Meth math: modeling temperature responses to methamphetamine

Abstract

Methamphetamine (Meth) can evoke extreme hyperthermia, which correlates with neurotoxicity and death in laboratory animals and humans. The objective of this study was to uncover the mechanisms of a complex dose dependence of temperature responses to Meth by mathematical modeling of the neuronal circuitry. On the basis of previous studies, we composed an artificial neural network with the core comprising three sequentially connected nodes: excitatory, medullary, and sympathetic preganglionic neuronal (SPN). Meth directly stimulated the excitatory node, an inhibitory drive targeted the medullary node, and, in high doses, an additional excitatory drive affected the SPN node. All model parameters (weights of connections, sensitivities, and time constants) were subject to fitting experimental time series of temperature responses to 1, 3, 5, and 10 mg/kg Meth. Modeling suggested that the temperature response to the lowest dose of Meth, which caused an immediate and short hyperthermia, involves neuronal excitation at a supramedullary level. The delay in response after the intermediate doses of Meth is a result of neuronal inhibition at the medullary level. Finally, the rapid and robust increase in body temperature induced by the highest dose of Meth involves activation of high-dose excitatory drive. The impairment in the inhibitory mechanism can provoke a life-threatening temperature rise and makes it a plausible cause of fatal hyperthermia in Meth users. We expect that studying putative neuronal sites of Meth action and the neuromediators involved in a detailed model of this system may lead to more effective strategies for prevention and treatment of hyperthermia induced by amphetamine-like stimulants.

derivatives of amphetamines are widely abused all over the world. After long-term use, cognitive, neurophysiological, and neuroanatomic deficits have been reported (10, 11, 47, 62, 66, 69, 75). Neurophysiological deficits are enhanced by hyperthermia (2), which is a major mortality factor in drug abusers (27, 74). Despite numerous studies investigating the mechanisms underlying methamphetamine (Meth)-induced hyperthermia, there are no specific treatments. A key barrier to the design of specific treatments is a lack of consensus regarding which brain regions and receptors are involved.

Meth has a complicated dose-related temperature response. Relatively low doses of Meth (≤1 mg/kg) cause a short-lived, but rapid, increase in body temperature (49, 59). As the dose of Meth increases, the dose-response curve is not linear. Rather, at 1–5 mg/kg Meth, peak temperatures do not increase, but the time at which temperature peaks progressively shifts to the right; for example, the peak temperature for 1 mg/kg Meth (38°C) occurs at 60 min, while the peak temperature for 5 mg/kg Meth (38°C) occurs at ∼180 min. At >10 mg/kg Meth, temperature once again rises rapidly, peaks at 60–90 min, decreases slightly, and then rises again and remains elevated at 5 h (49).

Importantly, temperature responses to injections of Meth are dependent on ambient temperature and may include hypothermic and hyperthermic phases (38). Similar complex temperature responses have been reported with other amphetamines, including the substituted amphetamine 3,4-methylenedioxymethamphetamine (MDMA) (56).

Collectively, these responses point out the complex pharmacology of amphetamines and, in particular, Meth. Meth increases multiple neurotransmitters, including dopamine, norepinephrine, acetylcholine, glutamate, and serotonin (32, 53, 72). Meth can also act directly on σ-opioid receptors (41) and trace amine receptors (78). Because of the multiple interactions between these neurotransmitters and receptors, it is difficult to study and understand the mechanisms underlying the temperature effects of Meth. Further complicating the analysis, body temperature is dependent on multiple thermoregulatory mechanisms and complex neuronal circuitry.

As acute complications (including fatalities) and chronic neurotoxicity from Meth are linked to its effects on temperature (2, 31), a better understanding of how Meth affects body temperature may provide insight into prevention and treatment of these effects.

When administered in low doses, amphetamines, in general, and Meth, in particular, induce an array of responses strikingly similar to those evoked by stimulation or disinhibition of neurons in the region of the dorsomedial hypothalamus (DMH) in conscious rats: tachycardia, mild hypertension, hyperthermia via an increase in thermogenesis and suppression of heat dissipation, and activation of locomotion [see Refs. 14, 51, 65, 68, and 81 (DMH) and 38, 48, and 58 (amphetamines)]. In turn, inhibition of the DMH with microinjections of muscimol significantly attenuated hyperthermia, tachycardia, hypertension, and locomotion evoked by a systemic dose of MDMA (58). The structural similarity between MDMA and Meth allows us to hypothesize that the DMH may also be involved in mediating responses to Meth.

In the past decade, DMH has emerged as a key hypothalamic effector region, the activation of which plays an important role in generating fever and stress responses (for reviews see Refs. 15–17, 22, and 77). The DMH exerts most of its autonomic effects through medullary structures: the rostral ventrolateral medulla (RVLM) (21) and ventromedial medulla (VMM) (7, 9, 63). Peripheral responses mediated by the DMH, including thermoregulatory responses, are predominantly transmitted through the raphe pallidus (RP) in the VMM. Among those effects are nonshivering thermogenesis, including thermogenesis in the interscapular brown adipose tissue (7, 81), shivering, which can result in production of a significant amount of heat (6, 39), and control of heat dissipation through cutaneous blood flow (43, 44).

The sources of input to the DMH are multiple (42, 70); however, their functional roles and relative importance in mediating specific components of thermoregulatory processes have not been described. Inhibition of the DMH can suppress responses to activation of the amygdala (67) and dorsolateral periaqueductal gray (PAG) (13). Stimulation of the amygdaloid region affects cutaneous blood flow (36), which is a major part of the thermoregulatory process. Whether those connections are direct and involved in mediation of stress, fever, or responses to drugs of abuse remains unknown. Therefore, we have described Meth as acting directly on the DMH, while it is possible that this is not the case.

Our experimental data contained clear evidence of the presence of the inhibitory drive (the response to the intermediate dose is weaker than the response to the low dose). The DMH and RP have inhibitory inputs: disinhibition of both areas by antagonists of GABA_A receptors evokes thermogenic responses (37, 81) and a decrease in heat dissipation via constriction of the cutaneous vasculature (43). One of the main sources of GABAergic projections to both areas is located in the preoptic area; however, the cells projecting to each area are not the same (40, 79). Inhibitory tone to the RP could also originate from the ventrolateral PAG (52) and RVLM (8). However, while the inhibitory component of responses to Meth could be due to activation of the inhibitory projection (presynaptic effect), it can also be mediated by activation of dopamine (most likely D₂) receptors (45, 55) or α₂-adrenergic receptors (34) located directly on neurons (postsynaptic effect). Without experimental support for any specific pathway or receptor involved, for clarity of description, we modeled our inhibitory component as an inhibitory drive to the RP.

Finally (46), we demonstrated that 5-HT_2A receptors in the spinal cord contribute to cutaneous vasoconstriction after a high dose of MDMA. The high-dose component is clearly present in our data: a high dose of Meth overrides the inhibition, and body temperature rises sharply and remains elevated for a long period of time.

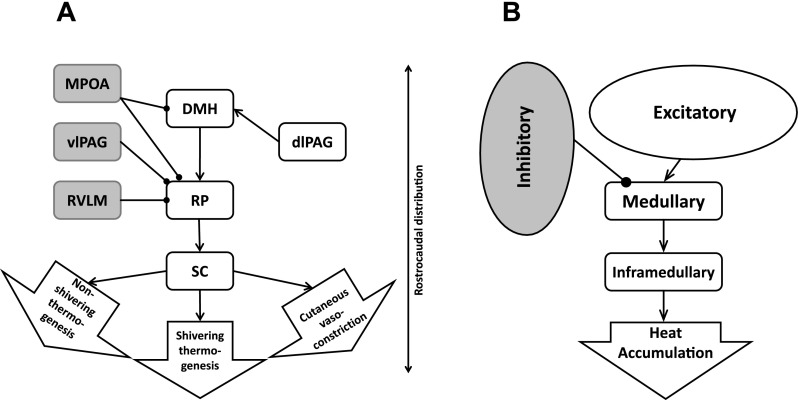
Previous studies pinpoint a few brain areas possibly involved in mediating the responses to Meth; however, in the following description, we avoid specific locations, as they have not been verified experimentally but, rather, rely on generic descriptors of nodes (Fig. 1). We refer to the DMH as the excitatory (Exc) node, and projection of the Exc to the medullary (Mdl) node will compete for activation of the Mdl node with the aggregate inhibitory drive, which is coming from the inhibitory (Inhib) node. The high-dose (HD) component, which cannot be inhibited by the inhibitory drive, enters the thermogenic pathway at the inframedullary sympathetic preganglionic neuron (SPN) node.

Fig. 1.

Neuronal circuitry involved in responses to amphetamines. A: actual anatomic structures. B: simplified conceptual network. Lines with arrows, excitatory projections (source is white); lines with circles, inhibitory projections (source is gray). MPOA, medial preoptic area; vlPAG and dlPAG, ventrolateral and dorsolateral periaqueductal gray; RVLM, rostral ventrolateral medulla; DMH, dorsomedial hypothalamus; RP, raphe pallidus; SC, superior colliculus.

Through an iterative process, we were able to create various neural networks, each of which closely models observed temperature responses from a range of Meth doses. Although they are obviously different from each other, these networks share a few core principles of organization, the most important of which is competition between converging excitatory and inhibitory drives.

METHODS

Experimental Procedures

All procedures were approved by the Indiana University Institutional Animal Care and Use Committee and followed National Institutes of Health guidelines.

Animal model.

Male Sprague-Dawley rats (280–350 g body wt) were individually housed with a 12:12-h light-dark cycle at a room temperature of 23–25°C; the animals had free access to food and water. All animals for which data are reported remained in good health throughout the course of surgical procedures and experimental protocols, as assessed by appearance, behavior, and maintenance of body weight.

Surgical procedures.

For measurements of core temperature, as well as heart rate and blood pressure, telemetric transmitters (model C50-PXT, Data Sciences International, St. Paul, MN) were implanted under isoflurane anesthesia, as previously described (82). A catheter was inserted into the abdominal aorta through the femoral artery, and the body of the transmitter was placed into the abdominal cavity and sutured to the abdominal wall. After ≥7 days of recovery, rats, still in their home cages, were brought to the experimental room. The cages were placed on telemetry receivers (model RPC-1, Data Sciences International), and the animals were given ≥2 h to adapt to the new environment.

Drugs.

Methamphetamine hydrochloride was obtained from Sigma-Aldrich (St. Louis, MO). It was dissolved in sterile saline at the time of injections and injected at a volume of 1 ml/kg.

Determining Temperature Responses to Meth

The temperature response to various doses of Meth was determined by randomization of animals receiving an intraperitoneal injection of saline or one of the four doses of Meth (1, 3, 5, or 10 mg/kg). Each animal received only one injection, with six rats per dose. Data were recorded every 2 min and transferred to Microsoft Excel, and 10-min averages were calculated using a template in Excel.

Statistical Analysis

Values are means ± SE. Data were compared using a one-way ANOVA with repeated measures followed by Fisher's least significant difference post hoc test, where appropriate. P < 0.05 was considered to indicate a significant difference in all comparisons. Baseline levels of activity, temperature, heart rate, and mean blood pressure did not differ between groups across the series of experiments, so changes from baseline were analyzed.

Model Construction

Three components were considered in constructing our model: 1) the pharmacokinetic time course of Meth concentration in the blood after an intraperitoneal injection, 2) a neural network, the activity of which depends on Meth concentration in the blood, and 3) a temperature control system that is driven by a signal from the neural component.

Pharmacokinetics.

Meth is rapidly absorbed from the peritoneum and then eliminated from the blood with a profile closely resembling a single-exponential process (23, 76). Our data do not contain independent information about the volume of distribution. Therefore, we have expressed the concentration in units of dose (mg/kg), and drug concentrations are described in the model by the following equations

$$\begin{array}{c}\frac{\text{d}x}{\text{d}t}=-\frac{x}{{\tau }_{\text{a}}}\\ \frac{\text{d}y}{\text{d}t}=\frac{x}{{\tau }_{\text{a}}}-\frac{y}{{\tau }_{\text{e}}}\end{array}$$ (1)

where t is time (in min), x(t) and y(t) are intraperitoneal and blood Meth concentrations, respectively, x/τ_a describes drug absorption with a time constant τ_a, and y/τ_e represents drug elimination with a time constant τ_e. Initial conditions are x(0) = D,y(0), given that a dose D is injected at time 0 (t = 0). With these initial conditions, the solution of Eq. 1 can be explicitly found as

$$y(t)=\text{D}{({\tau }_{\text{a}}/{\tau }_{\text{e}}-1)}^{-1}(e^{-\text{t}/{\tau }_{\text{a}}}-e^{-\text{t}/{\tau }_{\text{e}}})$$ (2)

which provides the Meth concentration in the blood at any given time.

Neural network.

The network schematic used in our model is based on previous research (see above) showing that neural populations in three key interconnected brain regions are responsible for normal rodent thermoregulation: excitatory drive is coming through the DMH to premotor sympathetic neurons in the VMM (Mdl node) and is relayed from the medulla to sympathetic preganglionic neurons in the spinal cord (SPN node). Activation of the SPN node results in an increase in body temperature via several mechanisms. In addition, we know from our data and data of others that temperature responses to amphetamines do not follow simple linear dose responses (35, 38, 46, 49, 59, 60). This can be seen in Fig. 2, where a low dose of Meth causes acute increases in temperature that are greater than increases caused by the two intermediate doses but lower than increases caused by the highest dose. Therefore, the excitation in the model can be suppressed by inhibitory drive, originating from supramedullary (preoptic nucleus or ventrolateral PAG) or intramedullary (RVLM) structures. We also know from the work of others that, at high doses, some amphetamines appear to act below the level of the medulla (46). For simplicity, our initial model factored in this postulated inframedullary effect by creating an additional Exc node that, as we hypothesized, would be activated only by higher doses of Meth (hence, the HD node).

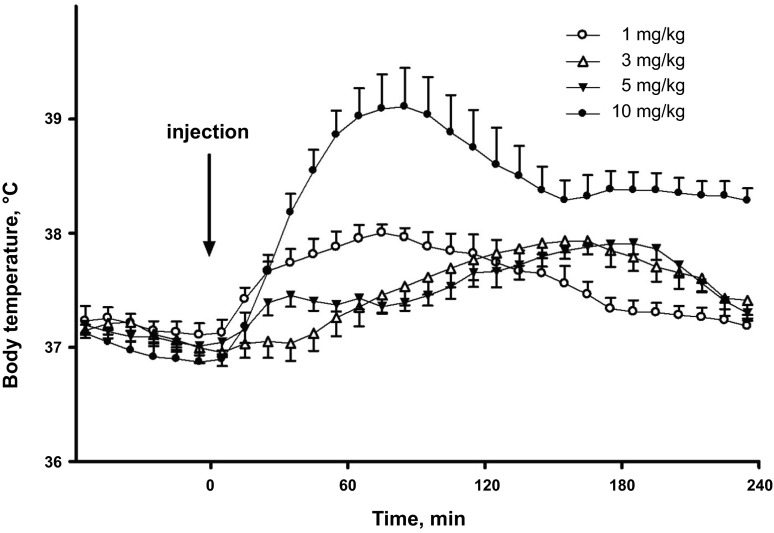
Fig. 2.

Dose dependence of temperature responses to methamphetamine (Meth). Meth was injected intraperitoneally at 0 min (t = 0) in a volume of 1 ml/kg.

This circuitry is depicted in Fig. 3A. The model takes the form of a feedforward artificial neural network. The outputs of “Meth-sensitive” supramedullary excitatory (Exc), inhibitory (Inhib), and high-dose-activated (HD) neural populations P_i (i = Exc, Inhib, and HD) were calculated using the following formula

$${\text{P}}_i(t)=\sigma [w_i\cdot y(t)+{\gamma }_i]$$ (3)

where σ(x) = (1 + tanhx)/2 is a sigmoidal activation function, w_i is a parameter of sensitivity to Meth, y(t) is the time dependence of the Meth concentration in the blood from Eq. 2, and γ_i defines basal excitability of P_i. Accordingly, the unit of sensitivity (w_Exc, w_Inhib, and w_HD) is (mg/kg)⁻¹ and γ_Exc, γ_Inhib, and γ_HD are dimensionless.

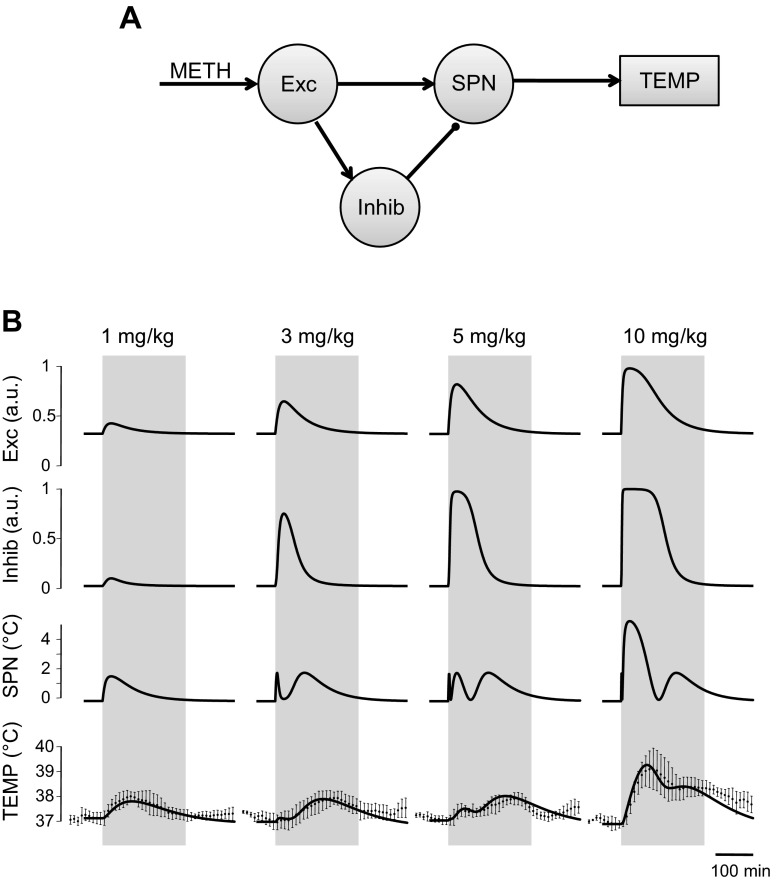
Fig. 3.

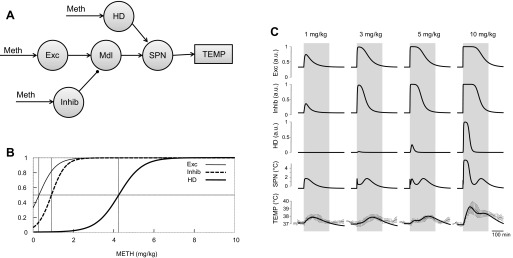
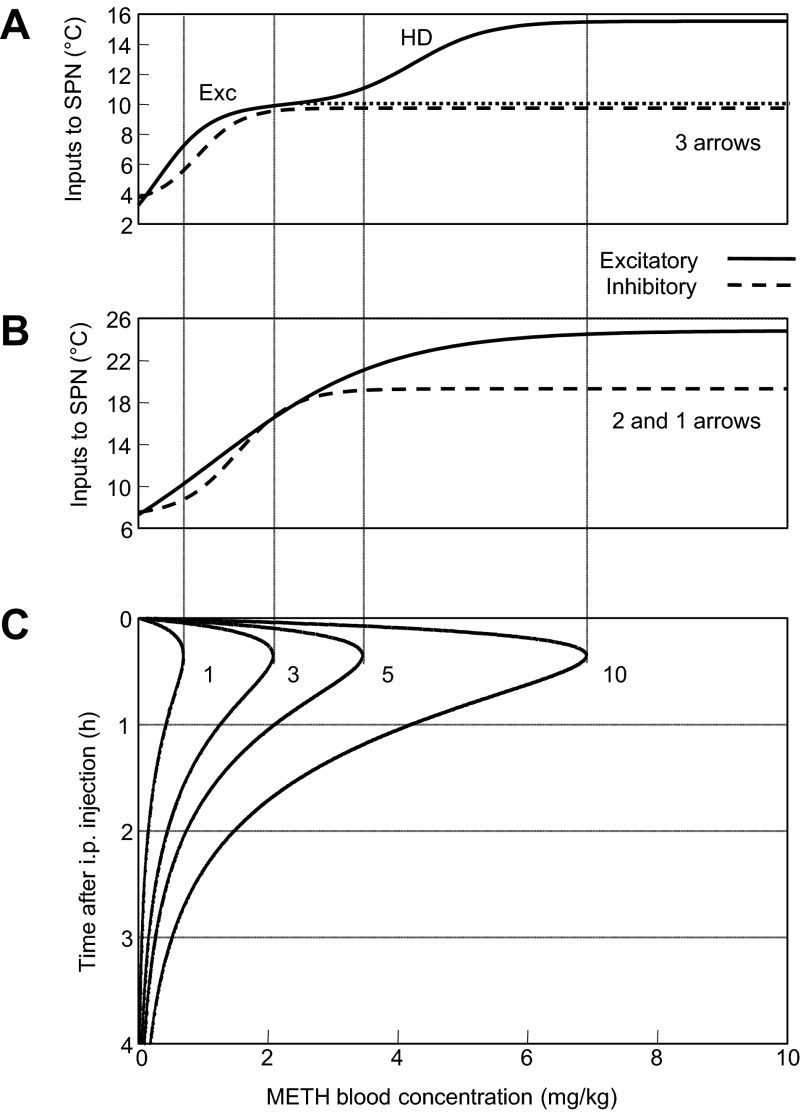
“Three-arrow” (circuitry-based) model. A: model schematic. Each circle represents a neural population. Meth-sensitive populations (“Meth”-labeled arrows) are modeled as an artificial neuron with sigmoidal activation function applied to its input (see text for a detailed description). Circuitry is a compilation of data from the literature. Exc, excitatory; Inhib, inhibitory; HD, high dose; Mdl, medulla; SPN, sympathetic preganglionic (or premotor) neuron; TEMP, temperature. B: activation functions of Meth-sensitive populations. Vertical lines show half-activation concentrations. C: reconstructed activity of neuronal populations included in the model, together with comparison of reconstructed dynamics of body temperature, after various doses of Meth, with actual experimental data used in fitting procedures. All reconstructed values of body temperature were within 1 SD of actual experimental data within the time period used for fitting procedures (220 min, gray bar). au, Arbitrary units.

The activity of the Mdl was described as

$${\text{P}}_{\text{Mdl}}(t)={\text{w}}_{\text{Exc}\to \text{Mdl}}\cdot {\text{P}}_{\text{Exc}}(t)-{\text{w}}_{\text{Inhib}\to \text{Mdl}}\cdot {\text{P}}_{\text{Inhib}}(t)$$ (4)

where w_Exc→Mdl is the weight of the excitatory projection from Exc to Mdl and w_Inhib→Mdl is the weight of the inhibitory projection from Inhib to Mdl. SPN then transmits the activity of Mdl, taking into account the additional contribution of the Meth-sensitive (HD) node

$${\text{P}}_{\text{SPN}}(t)={\text{P}}_{\text{Mdl}}\text{(}t\text{)}+{\text{w}}_{\text{HD}\to \text{SPN}}\cdot {\text{P}}_{\text{HD}}(t)+{\gamma }_{\text{SPN}}$$ (5)

where w_HD→SPN is the weight of the excitatory projection from HD to SPN and γ_SPN defines the basal excitability of the SPN neuronal node.

Temperature control.

The temperature response is modeled by a first-order linear ordinary differential equation and is driven by the SPN signal as follows

$${\tau }_{\text{T}}\frac{\text{dT}}{\text{d}t}={\text{P}}_{\text{SPN}}(t)-(\text{T}-{\text{T}}_0)$$ (6)

where T is body temperature (°C), τ_T is a time constant of the temperature response, and T₀ is the baseline body temperature. By design, activities of the Mdl and SPN nodes are measured in °C, as are the synaptic weights w_Exc→Mdl, w_Inhib→Mdl, and w_HD→SPN.

We make two major assumptions when we use Eq. 6 to describe temperature dynamics. Two terms of Eq. 6 represent heat production and heat dissipation, respectively. Heat dissipation occurs because of the difference between body temperature and environmental temperature. Accordingly, the dissipation term has to be proportional to the difference in the body and ambient temperatures and to the thermal conductivity of the skin. The latter is inversely proportional to τ_T in Eq. 6. Thermal conductivity is dependent on cutaneous blood flow, which can be regulated by cutaneous vasodilation to increase thermal conductivity in response to the temperature increase. At room temperature, the peripheral vessels are fully constricted, and sympathomimetic effects of Meth through central and peripheral neuronal mechanisms (3, 4, 58) will counteract effects of potential feedback caused by hyperthermia. So, our first assumption is that τ_T remains constant throughout all simulations. The physiological implication is that there is no afferent feedback through cutaneous vasodilation to the system. Our second assumption is that basal body temperature is an equilibrium temperature associated with basal metabolism and cannot be lowered by any feedback mechanisms related to hyperthermia. It is possible to make this assumption, since we model the system at room temperature; at room temperature, little additional heat is produced or few heat dissipation mechanisms are engaged at baseline due to close proximity to thermoneutrality.

Model parameter estimation.

To determine the optimal values of the model parameters to fit the experimental data, we minimized a cost function, which consisted of a residual sum of squares E(μ) and a regularization term R(μ)

$$\chi (\mathbf{\mu })=\text{E}(\mathbf{\mu })+\mathrm{R}(\mathbf{\mu })$$ (7)

where μ = τ_u, τ_d, τ_T, γ_Exc, w_Exc, γ_Inhib, w_Inhib, w_Exc→Mdl, w_Inhib→Mdl, γ_HD, w_HD, γ_SPN, and w_HD→SPN is the set of 13 parameters subject to optimization. We used the Broyden-Fletcher-Goldfarb-Shanno method (a multidimensional variable metric method) for minimization (50).

We had experimental time series of temperature responses to four doses of Meth _{[Tk(tl)]{l = 1}ⁿ, k = 1̄,4̄}, which were calculated from original data (10-min averages; see above). We used the residual sum of squares in the form

$$\text{E}(\mathbf{\mu })={\displaystyle {\sum }_{k=1}^4{{\displaystyle {\sum }_{l=1}^n\left[\text{T}(\mathbf{\mu },{\text{d}}_k,t_l)-{\text{T}}_k(t_l)\right]}}^2}$$ (8)

where T(μ,d_k,t_l) is the model's temperature response calculated by Eq. 6 at time t_l for the dose of Meth D = d_k for a particular set of parameter values μ.

The minimization of Eq. 5 is an ill-posed problem, because the model output depends mostly on the difference between Exc and Inhib projections to Mdl, and not on their absolute values. In addition, relatively low doses of Meth saturate Exc and Inhib activation. Therefore, the model output is weakly dependent on the sensitivity of these populations to Meth w_Exc and w_Inhib when their values are large. To overcome these difficulties, we used the Tikhonov regularization technique (71) by adding a regularization term

$$\text{R}(\mathbf{\mu })=\lambda ({\text{w}}_{\text{Exc}}^2+{\text{w}}_{\text{Inhib}}^2+{\gamma }_{\text{PSN}}^2+{\text{w}}_{\text{Exc}\to \text{Mdl}}^2+{\text{w}}_{\text{Inhib}\to \text{Mdl}}^2)$$ (9)

to the cost function (7). To determine an optimal value of the regularization factor λ, we used the L-curve method (24).

Model Reduction and Analysis

The original model was constructed on the basis of the hypothetical thermoregulatory circuitry available in the literature and had three Meth-sensitive nodes. Subsequent analysis of the model revealed several features redundant from a data assimilation perspective. Specifically, the experimentally observed temperature curves could be reproduced with comparable precision by use of the reduced circuitries receiving two or even one Meth-dependent input. Hereafter, we refer to these three models as the “three-arrow,” “two-arrow,” and “one-arrow” models, respectively.

Two-arrow model.

In our initial three-arrow model, we incorporated an inframedullary excitatory input that was activated only at high doses of Meth. While our decision was based, in part, on intuition and, in part, on previous data with MDMA (46), we also recognized that a more parsimonious model might be sufficient and would simplify its use. To test this, we derived a two-arrow model (see Fig. 5) from the original three-arrow model by setting w_HD→SPN = 0. This also had the effect of eliminating the parameters that described activation of the HD population, γ_HD and w_HD, resulting in the need to estimate only 10 parameters. This is possible from a conceptual standpoint, because elimination of the HD component essentially makes the inframedullary output directly dependent on the medullary output and, thereby, redundant for modeling purposes. Essentially, Mdl and SPN nodes were merged into a single SPN node; depending on the location, SPN can mean “sympathetic premotor neurons” (for the medullary location) or “sympathetic preganglionic neurons” (for the spinal cord location).

Fig. 5.

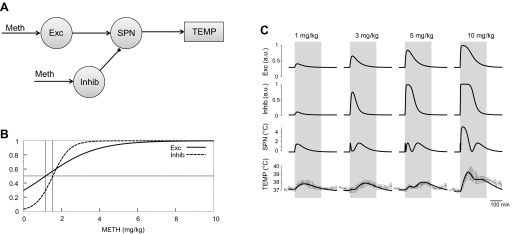
Two-arrow model. See Fig. 3 legend for details.

One-arrow model.

After confirming that the two-arrow model (without the HD and Mdl nodes) also accurately fit the observed data, we sought to simplify this model further. In the one-arrow model, only Exc is sensitive to Meth, and Inhib is now activated by projection from the Exc node (Fig. 6A). In this model, the activity of Inhib was described as follows

$${\text{P}}_{\text{Inhib}}(t)=\sigma \left[{\text{w}}_{\text{Exc}\to \text{Inhib}}\cdot {\text{P}}_{\text{Exc}}(t)+{\gamma }_{\text{Inhib}}\right]$$ (10)

where w_Exc→Inhib was the weight of the excitatory projection from Exc to Inhib. This parameter replaced the sensitivity of Inhib to Meth (w_Inhib). However, since the parameters of sensitivity of Inhib to Meth are replaced by parameters of sensitivity to descending excitatory input, the total number of parameters did not change compared with the two-arrow model.

Fig. 6.

One-arrow model. See Fig. 3 legend for details.

Variability of temperature responses.

To mimic experimentally observed animal-to-animal variability, we constructed model responses with varied model parameters. For every model parameter μ_i, we calculated the average sensitivity of the temperature to the relative parameter variation as

$${\text{S}}_i={\max }_{t\in [0,\text{L}]}\frac{\partial \text{T}(\mu ,\text{D},t)}{\partial {\mu }_i}{\mu }_i$$ (11)

where L = 220 min is the time interval used, the dose of Meth (D) = 10 mg/kg, and ∂T/∂μ_i is a partial derivative of the temperature at time t with respect to μ_i. We compared the calculated sensitivities and found that, for all three models, the calculated temperatures had the greatest sensitivity to variations in synaptic weights of the projections from Exc and Inhib nodes to Mdl. In addition, the three-arrow model has a comparable sensitivity to synaptic weight of the projection from HD to SPN. Accordingly, we chose w_Exc→Mdl, w_Inhib→Mdl, and w_HD→SPN as our control parameters for this analysis. Given the relative parameter variation κ, we multiplied w_Exc→Mdl (and w_HD→SPN for the 3-arrow model) and divided w_Inhib→Mdl by a factor of (1 + κ) to generate the greatest possible temperature response and the same parameters by a factor of (1 − κ) to obtain the lowest possible temperature response.

We have also considered situations when the inhibitory drive is significantly suppressed. For three- and two-arrow models, we have generated the model curves of the body temperature with all parameters being the same as in Table 1 but with w_Inhib→Mdl equal to 0 or one-half of its value in Table 1. The curves representing model responses to 1 and 3 mg/kg Meth in such situations are shown in Fig. 8.

Table 1.

Optimal model parameters with standard errors

	Model
Parameter	Three-arrow	Two-arrow	One-arrow
τa, min	8.25 ± 1.12	11.2 ± 1.1	11.3 ± 1.1
τe, min	57.5 ± 1.02	57.2 ± 1.2	57.1 ± 1.2
τT, min	89.2 ± 2.65	78.4 ± 2.8	79.2 ± 2.8
γExc, AU	−0.357 ± 0.006	−0.437 ± 0.002	−0.376 ± 0.005
wExc, (mg/kg)−1	1.225 ± 0.015	0.375 ± 0.002	0.337 ± 0.005
−γExc/wExc,* mg/kg	0.29	1.17	1.12
γInhib, AU	−1.335 ± 0.013	−1.746 ± 0.008	−4.27 ± 0.01
wInhib, (mg/kg)−1	1.463 ± 0.017	1.140 ± 0.007	N/A
−γInhib/wInhib,* mg/kg	0.91	1.53	N/A
wExc→Inhib, AU	N/A	N/A	7.47 ± 0.02
γHD, AU	−3.69 ± 0.05	N/A	N/A
wHD, (mg/kg)−1	0.872 ± 0.013	N/A	N/A
−γHD,* mg/kg	4.24	N/A	N/A
γSPN, °C	−3.35 ± 0.02	−7.20 ± 0.02	−7.62 ± 0.02
wExc→Mdl, °C	9.89 ± 0.03	N/A	N/A
wInhib→Mdl, °C	6.38 ± 0.04	N/A	N/A
wHD→SPN, °C	5.66 ± 0.12	N/A	N/A
wExc→SPN, °C	N/A	24.86 ± 0.04	23.82 ± 0.04
wInhib→SPN, °C	N/A	12.12 ± 0.05	10.44 ± 0.05

Optimization was performed as described in Model parameter estimation in methods.

N/A, not applicable; τ, time constant; a, absorption; e, elimination; T, temperature; γ, excitability; w, sensitivity; Exc, excitatory; Inhib, inhibitory; HD, high dose; Mdl, medulla; SPN, sympathetic preganglionic (or premotor) neuron.

^*Calculated half-activation Meth concentrations.

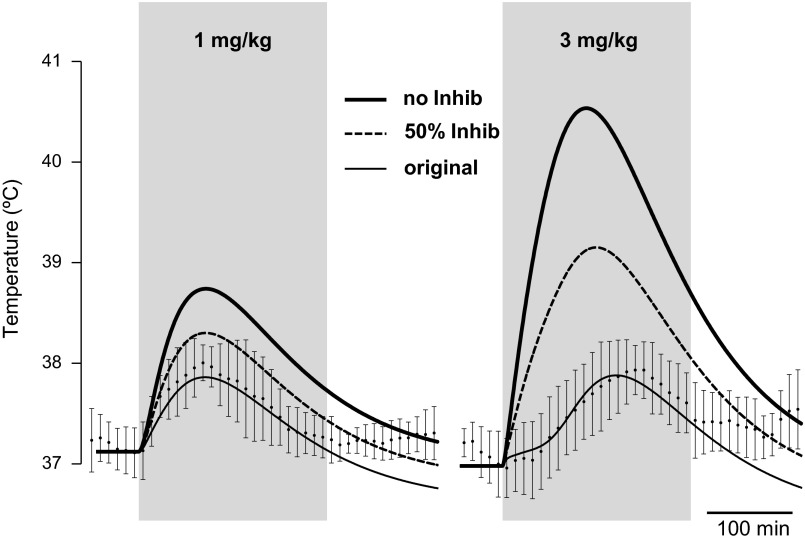
Fig. 8.

Modeling temperature responses to Meth (1 and 3 mg/kg) if inhibitory component is suppressed. ● with error bars represent experimental data. Thin solid line, best-fitting three-arrow model; dashed line, model with all parameters of thin solid line, except weight of inhibitory projection is considered 50% of the original value; thick solid line, model with all parameters of thin solid line, except weight of inhibitory projection is considered equal to 0.

RESULTS

Temperature Responses to Meth

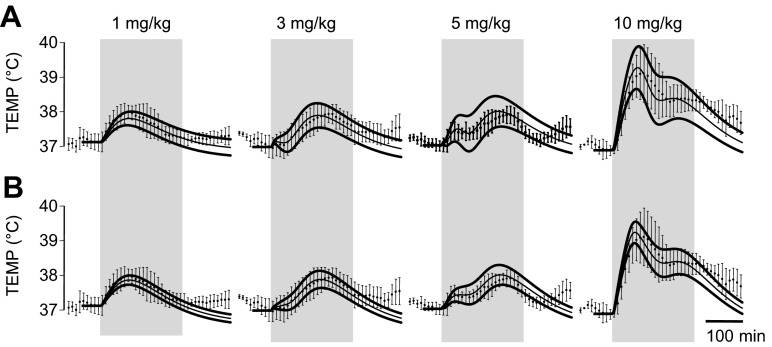
The doses of Meth (1, 3, 5, and 10 mg/kg) used in this study caused complex temperature responses (Fig. 2). At the lowest dose (1 mg/kg), temperature rose almost immediately after the injection, reached a peak (1°C above baseline) by 80 min, and retuned to baseline within 3 h. Increasing the Meth dose to 3 mg/kg delayed the response: temperature started to rise 40 min after the injection and peaked (also ∼1°C above baseline) at 150 min. Hyperthermia lasted for ∼4 h after 3 mg/kg Meth.

Similar to the low dose of Meth (1 mg/kg), 5 mg/kg Meth increased body temperature immediately after injection. The peak, however, was smaller (0.5°C) and occurred within 30 min. Temperature remained relatively constant for ∼1 h, began to rise again to a second peak (∼0.8°C above baseline) at 190 min, and, finally, returned to baseline within 4 h. Late phases of temperature responses to intermediate doses (t > 50 min for 3 mg/kg and t > 90 min for 5 mg/kg) were similar to the response to a low dose of Meth to the accuracy of a time shift.

Similar to 5 mg/kg Meth, the highest dose of Meth (10 mg/kg) caused an immediate increase in temperature. The increase, however, was greater (∼2°C above baseline) and required a longer period of time to peak (∼80 min). After reaching a peak, the temperature fell over the next 60 min and then, similar to the 5 mg/kg dose, peaked again, at least in some animals, or remained relatively constant for ∼60 min. In contrast to 5 mg/kg Meth, the second peak was not strongly expressed, and temperature slowly returned to baseline levels ∼6 h after injection (data not shown).

Collectively, these data show a complex multimodal temperature response to Meth that is highly dependent on the dose.

Estimated Parameters and Model Validation

Data shown in Fig. 2 were used to find the optimal set of parameters of each of the models, as described in methods. The calculated parameter values with their SE estimates are listed in Table 1. To evaluate the goodness of fit, we calculated the coefficient of determination (R², Table 2) for each model and all doses. R² can be treated as a fraction of the variance explained by the models, with a range of 65–95% for different doses and, on average, is ∼90% for all three models. We also calculated the ratio of the root mean square of the model residuals to the SDs of temperature responses over the group of animals (n = 6). These calculations are shown in Table 3 for all three models and all doses. Because, in all cases, this measure is much less than 100%, the model mismatch is well within experimentally observed animal-to-animal variability.

Table 2.

Coefficient of determination as a measure of goodness of fit

	Meth Dose
Model	1 mg/kg	3 mg/kg	5 mg/kg	10 mg/kg	Overall
Three-arrow	76.8	96.0	65.8	96.9	90.7
Two-arrow	66.9	95.4	64.4	94.7	87.8
One-arrow	65.9	94.9	63.8	94.8	87.6

Values are percentages. Goodness of fit is calculated as R² = 1 − Var(residuals)/Var(average temperature).

Table 3.

Model root-mean-square residual relative to the SD of temperature over the group of animals root-mean-squared over time of observation

	Meth Dose
Model	1 mg/kg	3 mg/kg	5 mg/kg	10 mg/kg	Overall
Three-arrow	41.9	17.7	55.7	17.4	29.0
Two-arrow	50.0	19.0	56.8	22.9	33.1
One-arrow	50.8	20.1	57.3	22.6	33.5

Values are percentages; n = 6 for each group.

To validate the model, we used k-fold cross-validation. Four temperature time series as a single data set were randomly divided into eight sets of points of equal size. Every set out of eight was used for validation, and the remaining seven sets were used to optimize the model parameters. The residuals for the validation sets were collected and root-mean-squared to be compared with the root-mean-square residuals for the training sets. The ratios of root-mean-squared residuals for the validation and training sets were 1.12 for the three-arrow model, 1.08 for the two-arrow model, and 1.09 for the one-arrow model. These ratios can be compared with the expected ratios in the case of linear regression. Each training set comprised 77 data points (n = 77). The models had 13, 10, and 10 parameters (p = 13, 10, and 10), respectively. Accordingly, the expected ratios of root-mean-squared residuals of validation and training sets, r = $\sqrt{(n+p)/(n-p)}$, were ∼1.18, 1.14, and 1.14. The values obtained were slightly less than the estimates, probably because of regularization used in our optimization procedure. In general, it evidences the robustness of the models.

Model Simulation and Interpretation

These parameters were used to simulate the dynamics of Meth concentration in the blood, activities of the neuronal populations, and temperature responses to different doses of Meth under various (patho)physiological conditions.

Pharmacokinetics.

The dependence of Meth concentration in the blood on time is described by Eq. 2, where τ_a defines a rate at which Meth is initially accumulated in the blood due to its absorption from the peritoneum and τ_e is responsible for the rate at which the drug is washed out. After parameter optimization to fit experimental data in all models, absorption appeared to be much faster than elimination (∼10 min vs. ∼60 min; see Table 1 for model-specific values). With such parameters, after an intraperitoneal injection of Meth, the blood concentration quickly peaks at a maximum of ∼70% of the dose and then exponentially decreases with a time constant of ∼1 h.

Activity in the Meth-sensitive nodes in the three-arrow model.

In the three-arrow model, which was able to accurately reproduce the observed temperature curves for all four doses of Meth (Fig. 3C), three neuronal nodes were stimulated by Meth directly (Fig. 3A): Exc, Inhib, and an excitatory projection to the SPN node, which was activated only at high doses of Meth (HD). The activation function of each Meth-sensitive population depended on two parameters: half-activation concentration and maximal slope. The slopes appeared to be comparable for all nodes, while half-activation concentration was lowest for Exc and highest for HD (Fig. 3B, Table 1, 3-arrow model).

Activation time courses of each of these nodes for each dose of Meth are shown in Fig. 3C. All doses of Meth were able to activate the Exc node, which reached 100% activity at 3 mg/kg for a short period of time. Each successively higher dose activated this node for a longer period of time. Similarly, the Inhib node was activated by all doses of Meth. The sensitivity of the Inhib node was less than that of the Exc node: the Inhib node required higher doses of Meth for full activation and had shorter durations of maximal activity at the higher doses. Finally, the HD component was activated only at the two highest doses of Meth (5 and 10 mg/kg).

Temperature responses to low and lower-intermediate doses.

The activity of the SPN, which defines an output of the system, can be viewed as a competition between excitatory and inhibitory drives. Excitatory drive in the three-arrow model is a sum of drives from Exc and HD that is offset by activity of the Inhib. To visualize how various doses of Meth result in activity of the SPN, Fig. 4 presents the activation function for combined excitatory drive and inhibitory drive (Fig. 4A) matched with pharmacokinetic profiles of Meth at various doses (Fig. 4C).

Fig. 4.

A and B: excitatory and inhibitory components of thermogenic activity in three- and two-arrow models as a function of Meth concentration in the blood. C: reconstructed time courses of Meth concentration in the blood for 1, 3, 5, and 10 mg/kg Meth. Vertical lines show maximal Meth concentrations in the blood for each dose in A and B.

At the lowest dose of Meth, Exc was the only activator of SPN in the model (curve 1 in Fig. 4C), and inhibition from Inhib was not sufficient to suppress excitation. Therefore, the activity of the SPN population followed the activity of Exc.

At ≥3 mg/kg Meth, the inhibitory input from Inhib was able to almost fully suppress the activity of the Mdl population, which mediated an activation of SPN. For this reason, no significant SPN activation, except a short-lived peak at the rising shoulder of Meth concentration, was observed immediately after injection of the lower-intermediate dose in Fig. 3C. The activity of SPN started to rise after the Meth concentration in the blood fell enough to deactivate Inhib, but the concentration transiently remained high enough to maintain Exc activity. Accordingly, the duration of the latency period to extended activation of the SPN was dose-dependent: the higher the dose, the longer it takes to wash out Meth. Thus our model suggests that, during the late phases of the responses, the SPN population exhibits activity patterns identical to the precision of the time shift, which monotonically increases with dose.

Temperature responses to higher-intermediate and high doses.

The maximal Meth concentration in the blood after the higher-intermediate dose (5 mg/kg) was sufficient to slightly activate the HD node (Fig. 4A, 3rd row of traces): ∼3.5 mg/kg at maximum is in the very beginning of the HD step (3rd vertical line in Fig. 3B). Accordingly, the activity of SPN becomes bimodal: the first maximum was evoked by a slight and immediate HD activation, and the second maximum was mediated by a mechanism identical to the delayed response to the 3 mg/kg dose, i.e., disinhibition of Mdl from Inhib during Meth washout in the continued presence of Exc activity.

As the dose increased from 5 to 10 mg/kg, the HD component was activated to a much greater extent (Fig. 3C). Interestingly, although the magnitudes of the two components of the excitatory drive (Exc and HD) are similar, activity of SPN was threefold greater with HD activation than with similar Exc activation, the effect of which was significantly attenuated by the activation of the inhibitory drive. At high doses, the inhibitory response was saturated and could not counteract excessive thermogenesis.

Reduced Models

The model schematic shown in Fig. 3A (3-arrows model) assumes that there are two distinct Meth-dependent excitatory nodes, Exc and HD, with significantly different sensitivities, that collectively determine the excitatory drive to the SPN node. Together, they form a two-step response curve (solid line in Fig. 4A), which can be treated as an activation curve of an aggregate population composed of both nodes. This allows for reduction of the model in such a way that two excitatory Meth-sensitive nodes can be combined into a single node characterized by a single sigmoidal activation curve (Fig. 4B). We call such a reduced model the two-arrow model according to the number of sites affected by Meth (Fig. 5A).

Two-arrow model.

By elimination of the HD node from the model schematic, the circuitry can be refigured as shown in Fig. 5A to have only two Meth-sensitive nodes. In addition, this allows combination of the Mdl and SPN nodes into a single SPN node. With the optimal set of parameters (Table 1) and corresponding activation curves for Meth-sensitive nodes (Fig. 5B), this two-arrow model also accurately reproduces the observed data (Fig. 5C), predicting temperature responses within 1 SD of the data for all times used for the fitting procedure (220 min; vertical gray bars in Fig. 5C).

To place activation functions of Exc and Inhib nodes in the context of effective concentrations of Meth, we have plotted them (Fig. 4B), together with matching pharmacokinetic profiles (Fig. 4C). The response of the Exc node to Meth injections does not saturate at the intermediate doses but, rather, continues to gradually increase as the dose increases. This results in the monotonically increasing curve of the excitatory component (solid line in Figs. 4B and Fig. 5B). The Inhib node, as in the three-arrow model, has a sigmoidal activation function (Fig. 5B).

In contrast to the three-arrow model, in the two-arrow model, the activation curves of the Exc and Inhib nodes have significantly different slopes (Figs. 4B and 5B, Table 1), which results in a different mechanism of the Meth dose dependence. After the lowest dose, SPN activity is increased by the excitatory drive, while the Inhib input barely reacts (Fig. 4B and Fig. 4C, line 1). With increasing dose, the Inhib node abruptly activates, the growth of inhibition prevails over a steady, but moderate, increase in excitation, and the SPN becomes silent (Fig. 4B and Fig. 4C, line 3). However, the inhibitory drive eventually saturates, while the excitatory input to the SPN continues to grow (Fig. 4B and Fig. 4C, lines 5 and 10), which results in activation of the SPN by sufficiently high doses of Meth.

One-arrow model.

In the two-arrow model, Exc and Inhib populations are affected by Meth independently. However, one can see that the entire range of Inhib sensitivity to Meth lies within the linear Exc response (the entire “step” of the dashed sigmoidal curve in Fig. 3B occurs while the solid curve is gradually increasing). From a modeling perspective, this means that we can leave only one Meth-sensitive input in the schematic and replace individual Inhib sensitivity to Meth with the excitatory input from Exc (Fig. 6A). Such a schematic is supported by known excitatory projections from the DMH to the RVLM (80).

At optimal parameter values (Table 1), this one-arrow model produces population activation patterns indistinguishable from those of the two-arrow model (compare Fig. 5C with Fig. 6B) and accurately predicts experimental observations.

Temperature Variability in Response to Parameter Variations

Experimental temperature curves exhibit significant animal-to-animal variability. For instance, after injection of 10 mg/kg Meth, the maximal temperature can differ by >2°C between animals (see SDs in Fig. 1). To evoke similar alterations in the model responses, we perturbed some model parameters relative to their optimal values in Table 1. Specifically, we varied synaptic weights of the projections from Exc and Inhib to Mdl in the two- and three-arrow models and, additionally, from HD to SPN in the three-arrow model, i.e., w_Exc→Mdl, w_Inhib→Mdl, and w_HD→SPN. The increase in w_Exc→Mdl and w_HD→SPN with a corresponding decrease in w_Inhib→Mdl produced the most exaggerated response, and a decrease in w_Exc→Mdl and w_HD→SPN with an increase in w_Inhib→Mdl attenuated the response. Figure 7 shows how a 3% change in the control parameters relative to their optimal values altered the temperature curves produced by the two- and three-arrow models. In both models, this change led to temperature variations on the same order of magnitude as experimentally observed variability (compare top and bottom thick solid curves with error bars representing experimental SDs in Fig. 7). Interestingly, such perturbations lead to noticeably greater temperature variations for the intermediate and highest doses in the two-arrow than the three-arrow model.

Fig. 7.

Variability of temperature responses to 1, 3, 5, and 10 mg/kg Meth due to model parameter perturbation. A: two-arrow model. B: three-arrow model. ● with error bars represent average and SD of experimentally measured core body temperature. Top and bottom solid lines are maximal and minimal temperature responses produced by the models after 3% change in key model parameters.

Significant suppression of the inhibitory drive results in dramatic amplification of Meth-induced hyperthermia (Fig. 8). In the absence of inhibition, the response to 1 mg/kg Meth approximately doubles, while a peak of the response to 3 mg/kg Meth exceeds 40°C and is close to life-threatening levels. With inhibition suppressed by 50%, hyperthermia is not so dramatic; however, after low Meth doses, body temperature reaches levels typical for responses to high doses.

DISCUSSION

Meth-evoked hyperthermia alone can cause death, but it also is known to aggravate neurological consequences of acute or chronic use of amphetamines. Despite significant efforts to determine reasons why some people develop life-threatening hyperthermia while the thermal response of most people is not a medical catastrophe, we do not have a clear idea of how hyperthermia develops. In this study, we attempted to develop an integrative model of temperature response to amphetamines, in general, and to Meth, in particular.

Dose dependence of the temperature responses to Meth appeared not to be trivial: intermediate doses (3 or 5 mg/kg; Fig. 2) caused less hyperthermia than the lowest (1 mg/kg) and highest (10 mg/kg) doses of Meth. Also, responses to the lowest and highest doses were virtually instantaneous, while responses to the intermediate doses were delayed. The highest dose evokes profound hyperthermia followed by a second temperature peak. Our results were qualitatively similar to those described by Myles et al. (38).

Our approach to mathematical description of responses was to model the involved neuronal circuitry in the form of an artificial neural network (1). Some of the nodes of the circuitry putatively corresponded to actual neuronal populations involved in thermoregulatory responses to amphetamines, in accordance with current physiological conception. All model parameters were chosen so that the model had the best fit to the experimental time series. When we used the optimal set of parameters, the simulated values of body temperature were within 1 SD of actual experimental data throughout all time courses for all doses (Table 3). Our model was additionally validated by comparing the “best-fit” values of some measurable parameters with experimental values available from the literature. For example, in all the models, Meth half-life in plasma was estimated to be ∼1 h (or, more precisely, 57 min); the same parameter in experimental studies was found to be 40–50 min (23) or ∼70 min (35).

More importantly, along with parameters that can be measured in experimental settings with relative ease, we reconstructed the responses of the involved neuronal ensembles. Such an approach may be a powerful tool for inferring the dynamics of individual functional populations, since there are limited options for measuring neuronal activity in conscious freely moving animals.

Mechanisms of Multimodal Responses in the Three-Arrow Model

Activities of the neuronal populations directly stimulated by Meth ultimately converge at the SPN population, the activity of which is treated as the term responsible for thermogenesis in Eq. 6. Increases in body temperature induced by Meth are compensated by heat dissipation, which is proportional to the difference from baseline body temperature: at baseline temperature, non-Meth-induced heat generation and dissipation are at equilibrium. For a specific Meth concentration in the blood, the activity of SPN (see patterns in the 4th row of traces in Fig. 3C) is defined by the difference between excitatory and inhibitory components. The dependence of the excitatory and inhibitory drives on Meth concentration in the blood (Fig. 4A) is shown against pharmacokinetic profiles for all four doses (Fig. 4C).

The lowest dose of Meth (1 mg/kg) activates neither the Inhib nor the HD node. Thermal output at this dose is dependent on activity of a single multisynaptic pathway from the Exc node through the Mdl to the SPN node. Activation of the Exc node follows the Meth concentration in the blood, as does the body temperature.

The increase to 3 mg/kg Meth is insufficient to activate SPN through HD, but it exceeds the threshold of activation of the inhibitory drive. Output of the Mdl is dependent on a balance between excitatory and inhibitory drives: the difference between the dotted line and the dashed curve in Fig. 4A becomes very small to the right from the second vertical line corresponding to the 3 mg/kg dose. Before the inhibitory drive kicks in, a short spike of supramedullary excitation (Fig. 3C) is successfully transmitted through the Mdl during the absorption phase, but this spike is very short and is not sufficient to cause a noticeable change in body temperature.

In experimental settings, inhibition of the medullary relay prevents downstream transmission of even maximal supramedullary (hypothalamic) excitation (7, 9, 44, 63). This quite fits our model data: the inhibitory drive successfully competes with the supramedullary excitatory drive, so at the lower-intermediate dose, there is no immediate increase in body temperature. Although the absence of an initial reaction may resemble a delay of the response, it is, in fact, a result of competition between two responses: excitatory and inhibitory.

Dose dependence of appearance of excitatory and inhibitory components is of critical importance for interpretation of dose dependence of responses to Meth. In a neuronal circuitry-based model, excitatory and inhibitory components differ in sensitivity to Meth. Most likely, such a difference is due to the predominant receptor mechanism responsible for the component. Meth evokes release of multiple neuromediators, with excitatory drive most likely mediated by dopamine (5, 28, 60). In turn, the inhibitory component could have multiple origins in monoaminergic systems, dopaminergic through D₂ receptors (45), adrenergic through α₂-adrenoreceptors (34), or even serotonergic through 5-HT_1A receptors (55, 56). Inhibition could be actually not direct but, rather, mediated by facilitation of the inhibitory GABAergic drive, tonically present in this circuitry (26). The variety of potentially involved mechanisms can explain differences of sensitivity of components of the model to Meth. Also, in our modeling, we assumed uniform distribution of Meth, while this assumption is not necessarily valid (33).

To discover specific mechanisms of physiological processes, a modeling approach allows generation of testable hypotheses. An assumption that the inhibitory drive is mediated by dopamine or adrenoreceptors allows prediction of the dynamics of the response to a specific dose of Meth under blockade of those receptors (Fig. 8).

It is noteworthy that the intermediate doses result in a sharp and very short-lived peak in Mdl/SPN activity at the rising shoulder of the blood Meth concentration profile before inhibition kicks in (Figs. 3, 5, and 6). This activation is so short that, because of inertia of the thermal system (τ_T ∼90 min), no significant increase in the body temperature occurs. The presence of this short-lived initial peak predicted by all models could be the source of misinterpretations in neuroanatomic studies, if a marker of neuronal activity such as c-fos immunoreactivity is used. Even though the peak is too short to evoke a significant thermal response, this short-duration (a few minutes) burst still could be sufficient to induce c-fos expression. Once expressed, c-fos is present in nuclei for a few hours (25). In such a situation, the marker of neuronal activity will be present without a clear physiological response.

The higher-intermediate dose (5 mg/kg) did not activate HD significantly, but for a short time the Meth level was elevated enough to evoke a mild HD response. This drove a short-lived activation of the SPN, which in turn resulted in a slight increase in the body temperature seen in Fig. 2 immediately after the injection. However, the HD-evoked activation does not last long, so temperature does not further increase after the initial rise.

Because of elimination, after the lower- and higher-intermediate doses (3 and 5 mg/kg), blood levels of Meth eventually drop below the threshold that is needed to maintain the inhibitory drive. However, these levels are still sufficient to maintain the Exc activity that serves as an excitatory drive for the Mdl. The latter, in turn, activates SPN, which drives hyperthermia. Since τ_e is significantly greater than τ_a (57 min vs. 8 min; Table 1), for t > τ_a the dynamics of the Meth concentration in the blood are defined almost exclusively by elimination. By the time Meth concentration in the blood falls to levels at which the excitatory input to the Mdl overcomes the inhibition, similar patterns of body temperature are observed for all low and intermediate doses, because pharmacokinetics of Meth are similar after this point. So the late phases of temperature responses to intermediate doses are virtually identical to the response to the lowest dose (see 1, 3 and 5 mg/kg in Fig. 2).

In contrast to the low and intermediate doses, the highest dose activates HD significantly. In fact, our model suggests that activation of HD provides remarkably stronger activation of the SPN than the supramedullary component (Fig. 3C, compare SPN activities at different doses). Interestingly, the Exc alone provides input of similar magnitude (see Fig. 4A, 1st step on the solid line), but it is significantly attenuated by its inhibitory counterpart (Fig. 4A, dashed line). This makes the slope of the temperature curve in the beginning of the response greater at the highest dose than at the other doses.

Sustained Exposure to Meth

The suggested model can be used to estimate the maximal body temperature that will be reached if thermogenic pathways are activated to the utmost extent for a prolonged period of time due to, for example, repeated Meth administration. The excess of this steady-state temperature above the baseline temperature (Eq. 6) is defined by the largest possible activity of the SPN node, which can be estimated as the difference between saturation levels of its excitatory and inhibitory inputs (see solid and dashed lines in Fig. 4A for high Meth concentrations). This difference is ∼5°C, which implies a highest possible temperature of 42°C. Evidently, high doses of Meth are able to evoke life-threatening hyperthermia, even at ambient room temperature.

The hyperthermia evoked by low doses can be estimated in a similar manner. If a low dose of Meth approximately equal to 1 mg/kg is maintained in the bloodstream for a long period of time (repeated administration), the excess of the steady-state temperature above the baseline will constitute ∼2°C (Fig. 4A), which means an absolute body temperature of 39°C. This, by itself, is not life-threatening but is definitely outside the normal temperature range for healthy animals kept at room temperature.

Interestingly, our model predicts milder or even no hyperthermia for sustained intermediate concentrations of Meth, since the excitatory input to SPN can be (completely) suppressed by the inhibitory input for Meth concentration in the blood of 2–3 mg/kg (solid and dashed lines almost coincide on Fig. 4A in this range).

Simplified Model With Two Inputs for Meth

In the original three-arrow model, the Meth-sensitive nodes are activated in a binary manner (Fig. 4A). They can be thought of as triggers switched on and off as the Meth concentration in the blood crosses its activation thresholds. The arrangement of the thresholds (half-activation concentrations) defines a temporal activation pattern of the network in response to a particular dose (Fig. 3, B and C, Table 1). Interestingly, the model predicts comparable slopes of the activation curves for all three Meth-sensitive nodes, w_Exc, w_Inhib, and w_HD (Fig. 3B, Table 1). The activation thresholds represent excitability of the corresponding neuronal populations, which can be controlled by a number of synaptic or intrinsic mechanisms.

A key feature of the model that defines the absence of a thermogenic response when the intermediate doses of Meth are maintained in the blood is that the activation curve of the Inhib component (dashed line in Fig. 4A) touches the curve of the Exc component (solid line in Fig. 4A). The same feature allows for a different modeling solution implemented in the two-arrow model (Fig. 4B). In this simplified model, we combined the low-dose Exc and the high-dose HD components into a single excitatory drive gradually activated throughout the entire range of Meth variation (Figs. 5A and 4B). We also combined the SPN with the Mdl into a single SPN node. In contrast to the three-arrow model, where all doses of Meth activate the Exc component to almost maximal values, in the simplified two-arrow model, different doses of Meth activate the Exc component to a different extent. Increasing the dose not only prolongs stimulation, but it also increases the amplitude. At the same time, the activation curve of the Inhib component is similar to that in the three-arrow model. Accordingly, after high doses, Inhib already saturates, while the activity of Exc continues to grow with dose, which creates an immediate “high-dose” component of hyperthermia (Fig. 4B and Fig. 4C, lines 5 and 10).

Model With a Single Input for Meth

As we mentioned above, the excitatory and inhibitory inputs in the two-arrow model as functions of the Meth concentration in the blood appear to have significantly different slopes (Figs. 4B and 5B). The inhibitory response curve is much steeper, which makes the excitatory response curve virtually linear in the corresponding range of Meth concentrations. Accordingly, the response of the Inhib population to the changes in Meth in the blood can be formed by the synaptic inputs from the Exc and is not due to its intrinsic sensitivity to Meth (Fig. 6A). This assumption, together with the assumption about actual neuroanatomic prototypes of the nodes of the model (Exc is the DMH, Inhib is the RVLM), is supported by the existing functional projections from the DMH to the RVLM (21, 80). This one-arrow model represents an extreme case, when the variety of possible temperature patterns is dictated by a specific network organization, while the system receives a single Meth-dependent input.

Which Model Is Correct?

In this initial approach to develop a mathematical model of temperature responses to amphetamines, we did not intend to create an all-inclusive “ultimate” model of the circuitry involved in those responses. We took this first step to break into potential mechanisms defining nontrivial dose dependence of responses to amphetamines. We showed that this complex phenomenon can be explained by relatively simple neural network architecture comprising a core of the temperature control system.

We considered it important that we present various potential circuitries that may underlie phenomena difficult to explain using the qualitative approach typical of pharmacodynamics. In our study, all three models replicated the experimental data with comparable precision. However, each model can be used to generate testable hypotheses for their subsequent experimental verification. One of the most obvious approaches to verify the models may be inactivation or activation of the putative anatomic structures involved in responses to Meth. For example, we hypothesize that the supramedullary node is the DMH; hence, the three-arrow model implies that inhibition of the DMH should prevent responses to the lowest dose and will not affect the initial phase of the response to the highest dose of Meth but will suppress the late phase of responses to the intermediate and highest doses.

Variability of Responses and Life-Threatening Hyperthermia

Our mathematical models can be used to gain insight into the potential mechanism of life-threatening hyperthermia induced by amphetamines. We found that a 3% change in certain parameters is sufficient to significantly modify responses (Fig. 7).

The HD component is relatively short-lived: <60 min after 10 mg/kg, which defines the maximum of intense hyperthermia. Prolongation of this component would make the rising shoulder after the high dose longer; therefore, body temperature will be able to reach life-threatening levels. Therefore, dramatically greater responses to amphetamines could appear due to purely pharmacokinetic, not pharmacodynamic, factors, such as an increase in half-life or repeated administration.

Importantly, “low dose” is not showing its power only due to prompt activation of the inhibitory drive. If not compensated by the inhibitory drive, the effect of the excitatory drive after low doses of Meth is comparable with the intensity of the average “high-dose” component of the response. This predicts that if, for any reason, the inhibitory drive is not activated by Meth, even low doses of Meth will evoke a high-dose-like response, with life-threatening levels of hyperthermia developing after “physiological” doses (Fig. 8). In the extreme situation, when no inhibitory drive is activated in the three-arrow model, the calculations show that 3 mg/kg Meth will result in a body temperature of 40.5°C in 100 min (Fig. 8). Catastrophic consequences of inhibitory failure may be a plausible explanation for a wide range of blood levels that can result in fatality after amphetamine overdose (12): some cases could be due to an actual overdose, while some could be due to an abnormal response to relatively low doses.

Missing Parts of the Model/Future Directions

In any of these models, we did not include a component associated with stress evoked by manipulations with an animal. In fact, the disturbance caused by intraperitoneal injection could significantly increase the body temperature of a conscious rat. The amplitude of the neuronal response to injection could be comparable to the amplitude of the response to the lowest dose of Meth, while usually it is significantly shorter. Interestingly, slight hyperthermia due to the stress of injection does not seem to appear at the intermediate doses (Fig. 1). Pathways that are involved in the response to amphetamines and stress are shared (58). With that in mind, it is quite logical that activation of the inhibitory pathway will suppress the excitatory drive induced by Meth and prevent stress-induced hyperthermia. For simplicity, we did not include a stress component in these studies; however, this is our plan for future developments.

In our models, our use of τ_T as a constant implies that no thermoregulatory changes, such as cutaneous vasodilation, occur in response to an increase in body temperature. In experiments performed at room temperature, rats normally do not thermoregulate through dissipation of heat. This mechanism only activates when the body temperature increases above a certain threshold (54). Activation of the sympathetic system by Meth (59) offsets this control mechanism toward higher thresholds, thus eliminating, or at least greatly attenuating, the feedback involved in hyperthermia.

Feedback mechanisms are activated when conditions are deviating from thermoneutrality; therefore, addition of feedback mechanisms to the model will be critical for proper description of responses at extreme conditions, first, in hot or cold environments. In such conditions, activity of already functional feedback mechanisms could be modified by the drug. For example, the amphetamine analog MDMA (ecstasy) suppresses cold-induced thermogenesis (55). Fortunately, afferent pathways and feedback mechanisms were extensively modeled previously (18–20, 29, 30, 64, 73). However, addition of such components to the model requires data obtained in varying environmental conditions and was beyond the scope of the current study.

When developing the model, we assumed that the medullary node is the RP. It is known that, even at ambient room temperature, inhibition of the RP results in a profound drop of the body temperature (82), which implies that the RP normally exhibits substantial tonic activity. The assimilation of such data will allow introduction of additional constraints on the model parameters.

It is known that administration of amphetamines results in thermodysregulation: at elevated ambient temperatures, animals become hyperthermic, while at low ambient temperature, they become hypothermic (60). This implies that pathways involved in responses to amphetamines and changes in ambient temperature are shared. However, inclusion of the ambient temperature as an independent parameter into the model will require formal description of thermoregulatory processes. We consider this to be the next step in constructing a closed-loop model of body temperature control, with the ultimate goal to explain how Meth modulates/disrupts temperature regulation.

Conclusion

Our interdisciplinary experimental and modeling study revealed that several relatively simple models are able to describe the complex pharmacodynamics of Meth. Our models had a few common features elucidating the essential mechanisms of Meth-evoked hyperthermia. 1) The thermal outcome is defined by the interaction of excitatory and inhibitory drives, both of which are activated by Meth. 2) The low-dose-induced component of the excitatory drive can be completely suppressed by the inhibitory drive. Inadequate activation of the Inhib component of the response to amphetamines may be the reason for fatal hyperthermia. 3) The high dose of Meth activates a component of the excitatory drive, which cannot be compensated by the inhibitory drive, either because of its location or insufficient strength of the Inhib component.

Perspectives and Significance

One of the most favorable outcomes of modeling is generation of a testable hypothesis. The common features of the models described here are, in fact, such testable hypotheses. While we developed the model with specific brain areas (e.g., DMH, RVLM, RP, and spinal cord) in mind, the actual representation of nodes remains untested. To test our hypotheses about involvement of the neuronal circuitry, it is necessary to experimentally target the activity of the above-mentioned neuronal populations. Also, the neuromediators involved in synaptic transmission between these nodes are yet to be determined. We expect that targeted modulation of activity of various brain structures and further pharmacological testing will reveal the real faces of those schematic nodes and arrows. The detailed model may provide a powerful tool for developing new strategies and therapies against amphetamine-evoked life-threatening hyperthermia.

GRANTS

This research was supported by National Institute on Drug Abuse Grants R01 DA-026867, IUPUI RSFG and iM²CS-GEIRE. This work was conducted in a facility constructed with support from National Center for Research Resources Grant C06 RR-015481-010.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Y.I.M. and D.V.Z. are responsible for conception and design of the research; Y.I.M. and D.V.Z. analyzed the data; Y.I.M. and D.V.Z. interpreted the results of the experiments; Y.I.M. and D.V.Z. prepared the figures; Y.I.M. and D.V.Z. drafted the manuscript; Y.I.M., M.V.Z., and D.V.Z. edited and revised the manuscript; Y.I.M., M.V.Z., and D.V.Z. approved the final version of the manuscript; M.V.Z. and D.V.Z. performed the experiments.