Mechanistic modelling suggests that the size of preneoplastic lesions is limited by intercellular induction of apoptosis in oncogenically transformed cells

Abstract

Selective removal of oncogenically transformed cells by apoptosis induced via signalling by surrounding cells has been suggested to represent a natural anticarcinogenic process. To investigate its potential effect in detail, a mechanistic model of this process is proposed. The model is calibrated against in vitro data on apoptosis triggered in transformed cells by defined external inducers as well as through signalling by normal cells under coculture conditions. The model predicts that intercellular induction of apoptosis is capable of balancing the proliferation of oncogenically transformed cells and limiting the size of their populations over long times, even if their proliferation per se were unlimited. Experimental research is desired to verify whether the predicted stable population of transformed cells corresponds to a kind of dormancy during early-stage carcinogenesis (dormant preneoplastic lesions), and how this process relates to other anticarcinogenic mechanisms taking place under in vivo conditions.

Introduction

Oncogenically transformed cells exhibit some of the features involved in multistep carcinogenesis, such as morphological changes, lack of contact inhibition, independence of their growth from specific growth factors, oncogene activation and tumour suppressor gene inactivation (reviewed in ref. 1–4). They are capable of inducing tumours in syngeneic or immunocompromised animals. However, cells isolated from such tumours differ from the initially injected transformed cells in two important ways: (i) much less of these cells, compared with the original cells transformed in vitro, are required for a new round of tumour induction, indicating a strongly increased tumorigenicity and (ii) the cells derived from tumours exhibit a much higher resistance against exogenous hydrogen peroxide (H₂O₂) and are capable of releasing prostaglandin E2 (5). These findings indicate that further phenotypical changes, crucial for tumour development, occur at later stages of carcinogenesis. Thus, oncogenically transformed cells represent an in vitro system mimicking the characteristics of early stage carcinogenesis in vivo; they ‘reflect the cell culture equivalent of initiation’ in carcinogenesis (6).

Oncogenically transformed cells constitutively produce superoxide (O₂ ^{− ·}) through membrane-bound NADPH oxidase (nicotinamide adenine dinucleotide phosphate-oxidase). Superoxide is involved in maintaining their transformed state and in controlling their proliferation (7); normal cells also use reactive oxygen species for the control of proliferation, but in contrast to transformed cells only in well-defined pulses within short intervals. Superoxide production is, on the other hand, the basis for a natural anticarcinogenic process potentially limiting the number of transformed cells, namely the induction of apoptosis in oncogenically transformed cells by signalling through surrounding cells (intercellular induction of apoptosis; reviewed in ref. 3,4,8).

Intercellular induction of apoptosis involves signalling by cytokines as well as reactive oxygen and nitrogen species (Figure 1). Through transforming growth factor type β (TGF-β) signalling, transformed cells trigger the release of peroxidase (POD) and nitric oxide (NO^·) in neighbour cells (thus triggering in neighbour cells their ‘effector function’ with respect to intercellular induction of apoptosis, step 1 in the process; Figure 1A). POD and NO^· may be produced also by transformed cells themselves (dashed arrows in Figure 1A), leading to autocrine apoptotic self destruction (9,10). Together with O₂ ^{− ·} produced by transformed cells, POD and NO^· enter into a cascade of biochemical signalling reactions (step 2), in which apoptosis inducers are produced in the vicinity of transformed cells. In the hypochlorous acid (HOCl) pathway (4,8,11; Figure 1B), O₂ ^{− ·} dismutates into H₂O₂, which, using abundant chloride ions, is converted by POD into HOCl. Upon reaction with O₂ ^{− ·}, HOCl yields hydroxyl radicals (·OH), potent apoptosis inducers. In the peroxynitrite pathway (4,8,11,12; Figure 1B), O₂ ^{− ·} reacts with NO^· to produce peroxynitrite (ONOO⁻), whose protonated form, peroxynitrous acid (ONOOH), decays yielding apoptosis-inducing ·OH and nitrogen dioxide. Consumption reactions may occur between H₂O₂ and HOCl and between NO^· and H₂O₂, leading to an interplay of the two pathways (4,9,10; schematically depicted in Figure 1B); POD also consumes H₂O₂ by converting it into water. Two further signalling pathways, namely the nitryl chloride pathway and metal catalyzed Haber–Weiss reaction, are of a minor importance only (4,8) and are not discussed in this work. Finally (step 3 in intercellular induction of apoptosis, Figure 1A), upon the attacks of ·OH, lipids in cell membranes are peroxidized, leading to local consumption of intracellular glutathione and through a cascade of further processes to the activation of mitochondrial pathway of apoptosis (8). The selectivity of intercellular induction of apoptosis with respect to the transformed phenotype is warranted by the short lifetime of superoxide, limiting the production of apoptosis inducers to the vicinity of transformed cells (4,8,11,12).

Fig. 1.

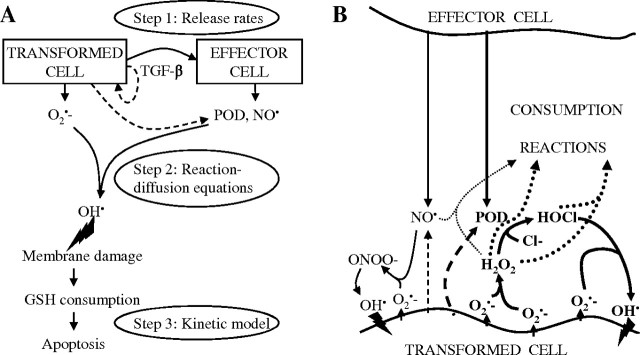
Mechanism of apoptosis induction in oncogenically transformed cells through signalling by surrounding cells (intercellular induction of apoptosis; reviewed in ref. 8). Panel A: Three steps in the mechanism of intercellular induction of apoptosis and their representation in the model. In step 1, transformed cells trigger, through TGF-β signalling, the release of POD and NO^· in neighbour cells, which thus become effector cells with respect to intercellular induction of apoptosis; also transformed cells themselves may serve as effector cells and release these species (dashed arrows). In step 2, a cascade of biochemical reactions occur between superoxide (O₂ ^{− ·}) produced by transformed cells and POD and NO^· released by effector cells, leading to production of ·OH in the vicinity of transformed cells. The two major pathways of the biochemical signalling cascade are depicted in detail in panel B; this work is focused on the HOCl pathway, highlighted in boldface. Finally, in step 3, the attacks of ·OH damage cellular membrane, which initiates an intracellular signalling pathway leading to apoptosis. In the model described in this paper, per-cell release rates of signalling species are considered in step 1, a set of reaction–diffusion equations is used to model step 2, and step 3 is represented by a non-linear kinetic model in which induction of apoptosis competes with cell proliferation.

A large variety of oncogenically transformed cells have been shown to be targets of intercellular induction of apoptosis, including rodent and human fibroblasts, epithelial, endothelial and haematopoietic cells, transformed by viruses, oncogene activation, irradiation or spontaneously (reviewed in ref. 8). Similarly, various cell types of murine and human origin are able to serve as effector cells in intercellular induction of apoptosis (i.e. release sufficient POD and/or NO^· upon TGF-β signalling), including fibroblasts, epithelial and endothelial cells, monocytes, B-cells and other cell types (8). On the other hand, tumour cells do not possess sensitivity to intercellular induction of apoptosis due to their expression of membrane-associated catalase, which inhibits signalling reactions in step 2, namely the HOCl pathway by removing H₂O₂ and the peroxynitrite pathway through decomposing peroxynitrite and oxidizing NO^· (9,10).

To help quantitatively understand the process of intercellular induction of apoptosis, enable extrapolations of experimental results to long-term behaviour and physiologically relevant conditions, and in particular to help estimate the role of this phenomenon as a control mechanism in carcinogenesis (3,8,13), a series of mechanistic modelling studies has been performed. Based on existing cell culture data, the model predicts that intercellular induction of apoptosis is capable of limiting the size of transformed cell population, providing support for an important anticarcinogenic role of this process. For simplicity, this paper is focused on the HOCl signalling pathway, the major pathway of intercellular induction of apoptosis in many transformed cell systems (9); an extension to the peroxynitrite pathway will be discussed elsewhere.

Materials and methods

A multiscale mathematical model of intercellular induction of apoptosis that follows its three-step mechanism (Figure 1) has been developed. The model takes into account the release of superoxide by transformed cells (target cells with respect to intercellular induction of apoptosis) and the release of POD (and NO^·) by their neighbours (this effector function being triggered by TGF-β signalling). The biochemical reaction cascade between these species (Figure 1B) is simulated using reaction–diffusion equations. The resulting yields of apoptosis inducers serve as input for the last module (step 3, Figure 1A), a kinetic model that accounts for the induction of membrane damage, its repair by the cell and non-linear triggering of apoptosis as a process competing with proliferation. The model is calibrated against cell culture data on the response of transformed and normal cells to defined externally added species involved in the given signalling as well as on induction of apoptosis in transformed cells cocultured with normal cells. The methods are described in detail below.

Experimental data used

Published data are analyzed on the extent and rate of apoptosis induced in 208F src3 transformed rat fibroblasts challenged by their parental (non-transformed) cell line 208F (11), measured in a coculture system with normal (non-transformed) cells pretreated with TGF-β and seeded in inserts with porous membrane ∼1 mm above transformed cells, excluding potential contribution of gap-junction communication (8). To help estimate model parameters, data on induction of apoptosis in these cells by externally added signalling species (14) are used. In all the experiments, apoptosis was scored by phase contrast microscopy using morphological criteria of membrane blebbing, chromatin condensation and fragmentation; correspondence to apoptosis was benchmarked by detecting free 3′ hydroxyl groups of DNA by the TUNEL assay (12).

Model scheme

Step 1: Triggering of effector function in neighbour cells through TGF-β released by transformed cells.

Pretreatment with TGF-β used in the analyzed experiments (10–20 ng/ml TGF-β for 1–2 days) significantly enhances cells’ capability to induce intercellular induction of apoptosis (9). Further increase in the amount or duration of this pretreatment does not enhance its effect (13), indicating that pretreated cells have already reached their full capacity of POD production. For the analyzed experiments, the model for Step 1 is thus reduced to considering constant POD release rates per effector cell, independent of additional TGF-β signalling by transformed cells. POD released by transformed cells (not pretreated with TGF-β) is neglected with respect to that from TGF-β pretreated normal cells (effector cells). Similarly, constant release rates of O₂ ^{− ·} per transformed cell are assumed; limited O₂ ^{− ·} production by non-transformed cells is neglected. Potential variations with cell cycle, passage number, etc are neglected. In the experiments with externally added signalling species, external species dominate over those released by cells, which are neglected accordingly.

Step 2: Intercellular signalling leading to the formation of apoptosis inducing species.

For coculture experiments, biochemical reactions involved in the HOCl pathway (Figure 1B; Supplementary Material, available at Carcinogenesis Online) are represented by standard reaction–diffusion equations. This set of non-linear partial differential equations accounts for cellular release of primary species (O₂ ^{− ·} and POD), their diffusion, mutual reactions leading to intermediates (H₂O₂ and HOCl) and inducers of apoptosis (·OH), lifetimes of all species in medium and absorption of inducers upon attacking cells and inducing membrane lipid peroxidation (LPO). In this work, a one-dimensional approximation to the full three-dimensional reaction–diffusion equations is used, in which temporal development of species concentrations in dependence only on the distance from the transformed cell plate is considered and individual cells (sources of primary species) are replaced with mean cell densities; detailed simulations have verified that this approximation represents the major system characteristics (results not shown).

For a given species (denoted here by A), the one-dimensional kinetic equation reads

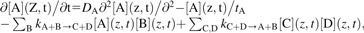(1)

where [A](z,t) denotes time-dependent local concentration of species A at distance z from the plane of transformed cells (and analogously for species B, C and D), t_A lifetime of species A, related to its rate of disappearance λ_A and half-life 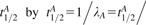ln(2), D_A its diffusion coefficient and 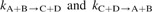rate coefficients of reactions in which species A is consumed or produced, respectively. Initial conditions for equation (1) are given by [A](z,t = 0) = 0 for all species except those present in medium or added externally. Boundary conditions are represented by fluxes j_A of species A released from transformed (at z_c = 0) or non-transformed cells (at z_c = 1 mm) and by consumption of apoptosis inducers upon attacking cells,

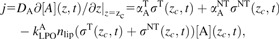(2)

j = 0 at the medium surface (z = 3 mm in the given experiments). Here, α_A^T and α_A^NTdenote the release rates of species A per transformed and non-transformed cell, σ^T and σ^NT densities of transformed and non-transformed cells at plane z = z_c and time t, k_LPO^A the reaction rate constant for initiation of LPO by inducer A, and n_lip denotes the molar amount, per cell, of membrane lipids exposed to these attacks (∼10⁻¹⁵ mol/cell, ref. 16).

For experiments on cellular response to externally added signalling species, the model for Step 2 is reduced essentially to spatially homogeneous decay kinetics of these species, as these dominate over those released from cells (Supplementary Material, available at Carcinogenesis Online).

During intercellular signalling leading to induction of apoptosis, ^·OH is the relevant inducer (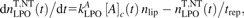 ref. 17); the levels of H₂O₂ and HOCl are rather low, so that they do not induce apoptosis directly but serve as intermediates only (14). In experiments with external species, much higher H₂O₂ concentrations were achieved at which it does induce apoptosis, presumably via a reaction with intracellular metal ions (e.g. Fe⁺⁺) producing ^·OH which finally induce LPO (17); in this work, the effects of all these processes are lumped together into effective rate constant 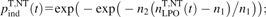in equation (2).

Step 3: Triggering and execution of apoptosis.

For simplicity, the present model works with two cellular states only, ‘living’ and ‘apoptotic’ cells, as also scored in the experiments. Neither the complex intracellular processes leading from membrane damage to apoptosis nor the detailed time course of apoptosis triggering and execution are represented. Only living cells (and not apoptotic cells) are assumed to release species involved in the given signalling [cf. equation (2)].

Density σ of living transformed (T) and non-transformed (NT) cells is modelled by

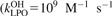(3)

The first term is a logistic model of cell proliferation, with rate 1/t_prolif modified by saturation effects with maximal cell density σ_max. The second term accounts for spontaneous apoptosis with rate 1/t_spont and for intercellular induction of apoptosis at maximal rate 1/t_ind modified by a factor 0 ≤ p_ind≤ 1 (discussed below). Density σ_ap of apoptotic cells is given by

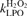(4)

with rate of removal of apoptotic bodies 1/t_rm.

The rate of apoptosis induction through intercellular signalling, p_ind/t_ind, is assumed to increase with the amount of LPO damage n_LPO caused by inducer attacks in a sigmoid manner,

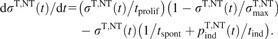(5)

this Gompertz function accounts for cellular ability to cope with a certain level of damage. All downstream intracellular processes leading to activation and execution of mitochondrial pathway of apoptosis are lumped into cell sensitivity parameters, n₁ and n₂.

The amount of induced damage is modelled by

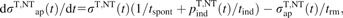(6)

with [A]_c(t) denoting concentration of inducer A (^·OH or H₂O₂ as discussed above) at outer cell surface, obtained from the reaction–diffusion equations describing the biochemical signalling scheme. Only LPO initiation events, i.e. the number of inducer attacks experienced so far, are considered. The propagation and termination phases of LPO reactions (18) are not modelled explicitly, as the resulting amplification of LPO (estimated as 10–15 propagation steps per initiation event, ref. 19) would lead to a multiplicative factor only, scaling the actual n_LPO and parameters n₁, n₂ but not influencing the results on kinetics of apoptosis. Cellular capability to repair lipid peroxides through glutathione peroxidases at the expense of glutathione (e.g. reviewed in ref. 18) is approximated by a first-order process, with characteristic time t_rep.

Summarizing the model scheme.

Density of living cells at a given time determines the amount of primary signalling species released. The biochemical signalling reactions lead to production of apoptosis inducers. In a complex non-linear way and with some delay, the spatially dependent concentration of inducers follows the density of transformed and non-transformed cells. Inducer attacks increase the probability of apoptosis triggering and execution, thus reducing the density of living cells that contribute to the signalling. This forms a feedback mechanism in intercellular induction of apoptosis. Within the model, this is translated into the given coupled set of differential equations.

Model application to experimental data.

Reaction rates and diffusion coefficients are taken from literature (Supplementary Material, available at Carcinogenesis Online). Signalling pathways are modelled in intercellular space only; diffusion of intermediate species across cell membrane is not considered. For experiments with externally added signalling species, cell-derived species are neglected accordingly, decay kinetics of added species described analytically and equations (3–6) solved numerically. Using MINUIT optimization tool (20), model calculations are fitted simultaneously to data for apoptosis triggered by (donors of) peroxynitrite and H₂O₂. This procedure enables estimating cellular sensitivity to apoptosis inducers n₁ and n₂, rate of apoptosis induction t_ind and species lifetimes t_A under in vitro conditions.

Cellular release rates of O₂ ^{− ·} and POD as well as parameters t_rm and t_rep are adapted to the observed kinetics of apoptosis under intercellular signalling and in cells exposed to H₂O₂-producing system complemented by myeloperoxidase (MPO) (cf. Results). For these experiments, the full set of partial differential equations, equations (1–6), is solved numerically.

As both transformed (208F src3) and normal (208F) cells proliferate with about the same doubling time t₂∼22 h (G. Bauer, unpublished data), equal proliferation rates 1/t_prolif = 1/(t₂ln(2)) are used for both phenotypes. However, the two phenotypes differ in the extent to which their growth is limited by contact inhibition. While the density of 208F cells is limited by σ^NT_max∼200/mm² (G. Bauer, unpublished data), transformed cells are even capable of growing on top of each other; thus, a higher maximal density (σ_max^T = 300/mm²) is assumed for 208F src3 cells in this work. Potential differences in t_spont, t_ind and/or t_rm between transformed and normal cells are neglected; t_spont = 15t_rm is taken to reflect the ∼5% fraction of apoptotic cells in control experiments. Transformed and normal cells respond to defined external donors of apoptosis inducers almost equally (14); identical sensitivity parameters n₁, n₂ are thus used for both phenotypes. As the specific POD that participates in intercellular induction of apoptosis and its reaction kinetics are unknown, published data for MPO are used as surrogate also for intercellular signalling. Specific information on limited turnover of this enzyme is lacking; lifetime of 10⁶ s is assumed.

Further details on the methods are given in Supplementary Material, available at Carcinogenesis Online.

Results

Cellular sensitivity to apoptosis inducer

Exemplary results of model calibration against data on apoptosis induction in 208F src3 transformed and 208F non-transformed fibroblasts by ·OH from the decay of peroxynitrite and by H₂O₂ (14) are shown in Figure 2A and B; further results are reported in Supplementary Material, available at Carcinogenesis Online. These species possess only small differences in their effects upon transformed 208F src3 and normal 208F cells (14); these are neglected in model calculations using the same sensitivity parameters, n₁ and n₂, for both phenotypes.

Fig. 2.

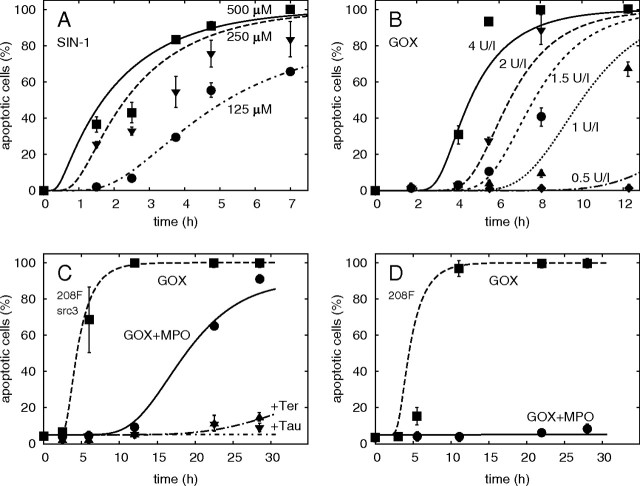
Apoptosis induced in 208F src3 transformed (A–C) or 208F non-transformed rat fibroblasts (D) by external donors of key signalling species involved in intercellular induction of apoptosis: selected examples illustrating the calibration of model calculations (lines) against data (points, error bars denoting standard errors of the mean from several repeats of the experiment, from (ref. 14); where not shown, were the errorbars smaller than the symbols). Additional results are reported in Supplementary Material, available at Carcinogenesis Online. (A) Kinetics of apoptosis induction by ·OH generated by decay of peroxynitrite produced from 0.125 to 0.5 mM 3-morpholino-sydnonimine (SIN-1). (B) Effect of H₂O₂ continuously produced by 0.5–4 mU/ml glucose oxidase (GOX) from glucose abundant in medium. (C) In transformed 208F src3 cells, apoptosis induced by H₂O₂ generated from 4 mU/ml GOX (dashed line) is delayed by adding 200 mU/ml MPO (GOX + MPO, solid line). Addition of HOCl scavenger taurine (Tau) or ·OH scavenger terephthalate (Ter) inhibits apoptosis induction. (D) In non-transformed 208F cells, the apoptosis-inducing effect of H₂O₂ from GOX is about the same as in 208F src3 cells, but addition of MPO completely abrogates apoptosis, as superoxide is not produced.

On the contrary, the responses of transformed and non-transformed cells are very different when MPO is added to the H₂O₂-producing glucose oxidase (Figure 2C and D); this system closely resembles the HOCl pathway of intercellular signalling. MPO converts H₂O₂ partly into HOCl (and partly into water). In the low concentrations produced, HOCl does not affect cell survival by itself (14) but yields apoptosis-inducing ^·OH upon reaction with transformed cell-derived superoxide. Compared with the fast effect of the high levels of H₂O₂ produced at this glucose oxidase concentration (Figure 2C, dashed line), apoptosis in transformed cells is induced less quickly by the HOCl pathway (Figure 2C, solid line), as only a part of H₂O₂ is converted into HOCl which has to react with superoxide and consumption reactions between H₂O₂ and HOCl occur (Figure 1A). Scavenging HOCl by taurine or ^·OH by terephthalate inhibits the induction of apoptosis in transformed cells (Figure 2C, dash-dotted lines). As non-transformed cells do not produce sufficient superoxide, addition of MPO inhibits the induction of apoptosis due to removal of H₂O₂ and synthesis of HOCl, without subsequent superoxide–HOCl interaction (Figure 2D).

Model parameters describing cellular sensitivity to apoptosis inducers and lifetimes of signalling species in vitro, estimated by fitting the data on apoptosis induction by defined externally added species (Figure 2 and Supplementary Material, available at Carcinogenesis Online), are listed in Table I.

Table I.

Model parameters estimated from a simultaneous analysis of experiments on apoptosis induction in rat fibroblasts by externally added signalling species (Figure 2 and Supplementary Material, available at Carcinogenesis Online) and from model adaptation to intercellular induction of apoptosis by the HOCl pathway in the coculture system with transformed and non-transformed cells (Figure 3)

Parameter		Value
n1	Characteristic level of membrane LPO leading to apoptosis induction (mol/cell)	10−17
n2	Rate of change in apoptosis induction probability with increasing LPO (1)	3.5
tind	Characteristic time of apoptosis induction (h)	1.7
trm	Characteristic time of removal of apoptotic bodies (h)	15
trep	Characteristic time of LPO repair (h)	15
tO2 − ·	O2 − · lifetime (s)	1.7
tH2O2	H2O2 lifetime (h)	2.7
tOH	·OH lifetime (μs)	3.4
tHOCl	HOCl lifetime (ms)	38
αO2 − ·	Release rate of O2 − · per transformed cell (mol/cell/s)	10−16
αPOD	Release rate of POD per TGF-β pretreated normal cell (mol/cell/s)	10−21

Parameters relevant for model calibration only are reported in Supplementary Material, available at Carcinogenesis Online.

Induction of apoptosis in transformed cells through signalling by normal cells

Due to their limited time span, the aforementioned reconstitution experiments provide no specific information on the characteristic times for the removal of apoptotic bodies t_rm and for the repair of peroxidative damage to membrane lipids t_rep, values >12 h yielding equally good results (t_rm = t_rep = 15 h used in Figure 2). These particular values and the release rates of POD per effector cell and of superoxide per transformed cell (10⁻²¹ and 10⁻¹⁶ mol/s, Table I) have been obtained by adjusting model calculations for the HOCl pathway (Figure 3A) to measured kinetics of apoptosis induced in 208F src3 cells by their parental cell line 208F. Experimentally, the release of NO^· and hence the peroxynitrite pathway of intercellular signalling were inhibited by two inhibitors of NO^· synthesis (11).

Fig. 3.

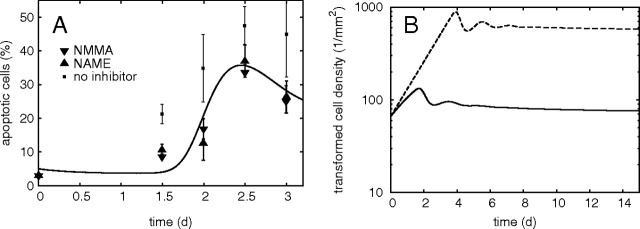
(A) Kinetics of apoptosis induced by the HOCl pathway in transformed fibroblasts 208F src3 upon coculture with non-transformed 208F cells. Model calculation (line) compared with data (triangles, ref. 11) obtained when the peroxynitrite pathway was inhibited by NO^· synthesis inhibitors N-omega-Nitro-l-arginine methylester hydrochloride (NAME) or N6-Methyl-l-arginine (NMMA); 40000 transformed cells per well (9.6 cm²) cocultured with the same number of non-transformed cells pretreated with 20 ng/ml TGF-β for 2 days. Data on apoptosis induction without inhibitors (squares) are also shown, although the present calculations are limited to the HOCl pathway only (cf. Discussion). Error bars were estimated from assays performed in duplicate (ref. 11). (B) The model predicts the existence of a stable long-term limit to the growth of transformed cell population, approached in a damped-oscillatory mode (solid line). Even if unlimited exponential growth of transformed cells and a reduced superoxide lifetime of 100 ms (21) are considered, limited population size is predicted (dashed line).

Compared with apoptosis induction by externally added species (Figure 2), apoptosis induced by intercellular signalling (Figure 3A) is characterized by a rather long, ∼2 days delay. The model predicts that this period corresponds primarily to the need for sufficient POD and H₂O₂ to accumulate in the system, as needed for optimal HOCl production. The prerequisite of sufficient H₂O₂ production translates into requiring a certain density of transformed cells that produce enough superoxide; dismutation of superoxide into H₂O₂ takes two O₂ ^{− ·} molecules, so that H₂O₂ production scales roughly quadratically with cell density. This non-linear nature of the HOCl pathway is further amplified by the need for another O₂ ^{− ·} molecule reacting with HOCl to yield apoptosis-inducing ^·OH. As illustrated in detail in Supplementary Material, available at Carcinogenesis Online, the density of transformed cells first increases by proliferation, leading to increasing superoxide release and enhanced production of H₂O₂ and in turn also of HOCl and ^·OH. As soon as the amount of LPO or rate of its induction exceeds the levels that cells can cope with, apoptosis starts to be triggered. The density of living superoxide-producing transformed cells is thus reduced. Consequently, also the production of H₂O₂, HOCl and apoptosis-inducing ^·OH diminishes, giving cells a chance to repair the LPO damage induced so far. Fewer cells are sent to apoptosis, and cell density increases by proliferation. Together with the removal of apoptotic bodies, this may lead to a reduction in the percentage of cells that exhibit apoptotic features, as shown in Figure 3A, in agreement with the data at ∼3 days coculture.

The model reproduces the observed selectivity of intercellular induction of apoptosis to the transformed phenotype (8): due to the short lifetime and hence diffusion length of superoxide, the majority of ^·OH are formed in a close vicinity to transformed cells; the model predicts that the ^·OH levels produced by the HOCl pathway decrease with distance from transformed cells by factors of 2–4 per 100 μm (Supplementary Material, available at Carcinogenesis Online).

The model also predicts the dependence of the extent and rate of intercellular induction of apoptosis via the HOCl pathway on initial cell densities, distance between transformed and non-transformed cell populations or the amount of medium (Supplementary Material, available at Carcinogenesis Online). Measurements addressing these issues could help verify model assumptions and the derived parameter values.

Predicted long-term behaviour

In Figure 3B, the long-term behaviour of transformed cell density, predicted based on the above-mentioned experimental data, is plotted. The model predicts the existence of a long-term stable state at which proliferation of transformed cells is counterbalanced by their apoptosis induced through signalling by neighbour normal cells. This steady state is approached in a damped oscillatory mode, based on the above-discussed feedback loop between transformed cell density and concentration of apoptosis inducers.

The equilibrium density as well as the amplitude and frequency of damped oscillations are given by system parameters, in particular by the release rates of signalling species, their lifetimes in the medium, cell sensitivities to inducers and rates of proliferation and apoptosis induction. To investigate the potential implications of intercellular induction of apoptosis for carcinogenesis under conditions closer to in vivo, the influence of larger parameter variations on the existence of a density limit and its value has been studied. The model predicts that intercellular induction of apoptosis is capable to balance the proliferation of transformed cells even if contact inhibition and other growth limitations are completely abolished and/or the lifetimes of signalling species shortened. This is illustrated in Figure 3B by a calculation with completely unlimited exponential growth of transformed cells (σ_max^T→∞), distance between transformed and non-transformed cells reduced to 0.1 mm and superoxide lifetime reduced to 0.1 s as estimated in blood (21). Although the extent of intercellular induction of apoptosis is reduced, the density of transformed cells is still limited; for the given parameter values the predicted limit amounts to ∼600 cells/mm² (Figure 3B).

Discussion

A detailed mechanistic model of intercellular induction of apoptosis has been developed. For the analyzed experiments, triggering of effector function in normal cells is approximated by constant release rates of signalling molecules. Detailed reaction kinetic model is used for the intercellular signalling reactions. Triggering of apoptosis increasing non-linearly with the amount of inducers attacking cells is considered. Although this apoptosis execution module is relatively simple and intracellular mechanisms of mitochondrial pathway of apoptosis are not represented explicitly, the assumed sigmoid response agrees with the behaviour predicted by detailed models of this apoptosis pathway (e.g. refs. 15,22). The model reproduces the kinetics of apoptosis as well as the dependence on the amounts of donors added or exposure duration (Figure 2 and Supplementary Material, available at Carcinogenesis Online).

Despite using data for a particular cell system, namely transformed 208F src3 cells derived from 208F rat fibroblasts, the model as well as qualitative features and conclusions discussed here are not cell-type specific, as qualitatively similar behaviour has been observed also with other cell systems (8,10,13).

By using literature-based reaction kinetics data, the model has verified the experimentally deduced intercellular signalling mechanism leading to apoptosis. The model confirms the critical role of superoxide production by transformed cells for both selectivity and efficiency of this process, pointed out in earlier experimental work (11,12,14; reviewed in refs. 4,8): Short lifetime of superoxide limits the production of apoptosis inducers to the vicinity of transformed cells, ensuring selectivity of intercellular induction of apoptosis to transformed phenotype. The efficiency of the HOCl pathway, which represents a dominant contribution to intercellular induction of apoptosis (cf. Figure 3), is driven by superoxide production: enough superoxide is needed for sufficient H₂O₂ formation and also for production of apoptosis-inducing ^·OH through HOCl–superoxide interaction.

Unfortunately, although the model works with mechanistically distinct parameters, not all of them could have been determined unambiguously from the limited data available; changes in some parameters can be compensated by adjusting others, as complex largely competing processes are involved (correlated parameters in terms of data analysis; cf. Supplementary Material, available at Carcinogenesis Online). The characteristic time for the removal of apoptotic bodies, for instance, can be compensated by characteristic time for the repair of lipid peroxidative damage, as both processes tend to reduce the number of apoptotic cells scored, though by very different mechanisms. This uncertainty in parameter determination could be reduced if some parameters were directly measured; e.g. the characteristic time for the removal of apoptotic bodies could be determined by recording the fate of individual apoptotic cells. Measuring local concentrations of diverse signalling species would be extremely challenging due to their large spatial variations. However, methods have been developed for single-cell measurements of superoxide release (23); peak values of ∼2 fmol/s and total releases of 50–100 fmol per non-transformed human fibroblast per burst (lasting over >2 min) after mechanical stimulation were reported (23). These values indicate that the release of 0.1 fmol/s O₂ ^{− ·} per 208F src3 transformed fibroblast estimated here (Table I) is not unrealistically high; direct single-cell measurements of superoxide release by transformed cells would benchmark this important model parameter.

The model calibration procedure is also hampered by the fact that the analyzed data correspond to a few (typically two to three) replicate experiments scored at a few time points only; improved statistics would help obtain more reliable parameter estimates. However, the lack of knowledge on specific parameter values is not critical for the present study. Although somewhat different parameter sets are consistent with the analyzed data, they lead to similar results for the equilibrium transformed cell density as well as the predicted damped oscillations (Supplementary Material, available at Carcinogenesis Online), as the main characteristics of the long-term behaviour are dictated by the observed onset of apoptosis at ∼2 days and reduction at ∼3 days of coculture.

The predicted long-term behaviour of the system represents the major result of the reported studies. A long-term stable limit is predicted for the density of transformed cells, i.e. a limited growth of preneoplastic lesions, due to the capability of intercellular induction of apoptosis to counterbalance the proliferation of transformed cells even if their proliferation per se were unlimited (exponential). This prediction extends the experimental results beyond the 3–5 days, after which the analyzed experiments with the transformed–non-transformed coculture system are spoilt by nutrient deprivation and/or build-up of toxic products. The present work has been limited to the HOCl pathway of intercellular induction of apoptosis; nevertheless, although in principle, a complex interplay of the two pathways may occur due to consumption reactions (Figure 1B), the data (cf. Figure 3A) as well as first calculations (24) including the peroxynitrite pathway show an enhanced percentage of apoptotic cells, i.e. a further strengthened density limit.

This long-term density limit is approached by the system in a damped oscillatory mode. Phenomenological description of the process using damped oscillations theory could be beneficial if only the kinetics of apoptosis or the resulting transformed cell density are of interest, e.g. for implementing intercellular induction of apoptosis into existing mechanistic models of carcinogenesis. Compared with the present model, such description would require four parameters only, namely lag time before apoptosis onset (period of undisturbed proliferation), equilibrium cell density (or percentage of apoptotic cells), damping ratio and period of oscillations. An approximate description of the predicted sizes of transformed cell populations could be based on sigmoid or step functions or even just the density limit, further reducing the number of parameters needed. The detailed model presented here relates these phenomenological parameters to mechanistic systems parameters describing experimental setup, initial cell densities, cellular sensitivity to inducers and release rates and lifetimes of signalling species.

To address potential implications of intercellular induction of apoptosis under conditions closer to in vivo, model calculations have been performed with an unlimited growth of transformed cells and lifetime of superoxide reduced from 1.7 s (derived for in vitro experiments) to 0.1 s estimated in blood (21). The model indicates (Figure 3B) that even in this case, intercellular induction of apoptosis is capable of limiting the size of transformed cell population. Note that this result still concerns the coculture geometry with transformed cells seeded in wells (i.e. in a plane) and effector cells on membrane inserts (i.e. in another plane, 1 mm separated). To model physiological conditions more realistically, spheroids or even irregular-shaped transformed cell populations surrounded by normal cells should be considered, and the signalling scheme (step 2) modelled in three-dimensional setup; these generalizations are straightforward though computationally expensive. Furthermore, a detailed representation of the TGF-β signalling (step 1) is necessary. A corresponding module is under development, considering TGF-β autoinduction, signal lifetime and a sigmoid increase in release rates of POD (and NO^·) with the amount of TGF-β signals; unfortunately, detailed experimental information on this process is still lacking.

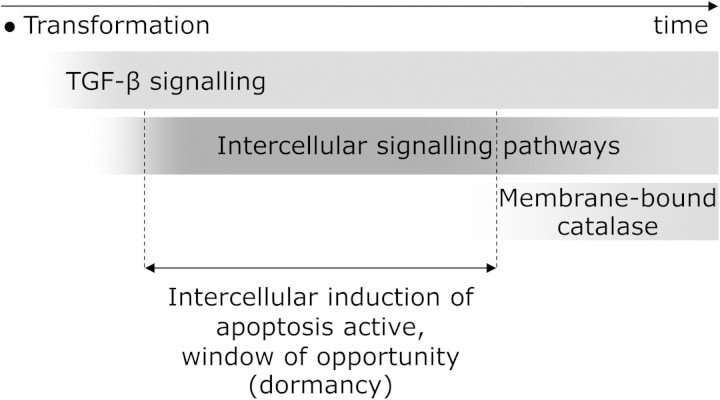
Nevertheless, already the present results indicate a potentially important role of intercellular induction of apoptosis in carcinogenesis and enable understanding the key processes deciding on its relevance. Triggering of effector function in surrounding cells by TGF-β released by the transformed cells decides on when the signalling reactions involved in intercellular induction of apoptosis become operational. In fact, gradually increasing release rates of primary species should be considered (contrary to constant releases assumed in this work), as the surrounding cells gradually respond to TGF-β released and/or activated by transformed cells. This would lead to time-dependent limits to cell densities; typically signalling would increase with time, leading to more stringent density limits. On the other hand, the system of intercellular induction of apoptosis is not active in tumour cells, as they express membrane-bound catalase, inhibiting the given signalling (9,10). Physiological relevance of intercellular induction of apoptosis thus critically depends on the time window available before membrane-associated catalase expression occurs as a phenotypical change in the transformed cell population (Figure 4). If catalase expression appears faster than triggering of effector function in surrounding cells by TGF-β from transformed cells, then there is no ‘window of opportunity’ for intercellular induction of apoptosis. However, if the onset of catalase expression needs longer time, e.g. several weeks or longer, then the present results suggest that intercellular induction of apoptosis probably represents a crucial anticarcinogenic process limiting the number of oncogenically transformed cells. Such a stable population of transformed cells (preneoplastic lesion with limited growth) resembles many features of dormant tumours (reviewed e.g. in ref. 25). Experimental research is needed to verify whether intercellular induction of apoptosis indeed contributes to the mechanism preventing their growth or whether its potential to specifically induce apoptosis in malignant cells is not effective under in vivo conditions.

Fig. 4.

Potential physiological relevance of intercellular induction of apoptosis as an anticarcinogenic mechanism. Following their oncogenic transformation, cells start TGF-β signalling, which in turn triggers the release of POD and NO^· in neighbour cells. These species together with superoxide produced by transformed cells undergo a cascade of biochemical reactions (Figure 1B). This intercellular signalling is rendered inactive when the transformed cells acquire further phenotypical change characteristic for tumour cells, the production of membrane-bound catalase, which removes H₂O₂ and peroxynitrite, key species in this signalling process. If catalase expression occurs with sufficient delay after the activation of intercellular signalling that leads to apoptosis induction, a dormant state results in which further growth of the transformed population is inhibited. This dormant state represents a window of opportunity for the action of other anticarcinogenic mechanisms.

Supplementary material

Supplementary Material can be found at http://carcin.oxfordjournals.org/

Funding

The research leading to these results has received funding from the European Atomic Energy Community's Sixth Framework Programme (FP6/2002-2006) under grant agreements FI6R-CT-2003-508842 (RiscRad) and FI6R-036465 (NOTE); and Seventh Framework Programme (FP7/2007-2011) under grant agreement no. 249689 (DoReMi).

Glossary

Abbreviations

TGF-β

transforming growth factor type-β

NO^·

nitric oxide

HOCl

hypochlorous acid

H₂O₂

hydrogen peroxide

·OH

hydroxyl radical

POD

peroxidase

MPO

myeloperoxidase

LPO

lipid peroxidation

O₂^−·

superoxide

ONOO-

peroxynitrite anion