Abstract
The analysis of stimulus/response patterns using information theoretic approaches requires the full probability distribution of stimuli and response. Recent progress in using information-based tools to understand circuit function has advanced understanding of neural coding at the single cell and population level. In advances over traditional reverse correlation approaches, the determination of receptive fields using information as a metric has allowed novel insights into stimulus representation and transformation. The application of maximum entropy methods to population codes has opened a rich exploration of the internal structure of these codes, revealing stimulus-driven functional connectivity. We speculate about the prospects and limitations of information as a general tool for dissecting neural circuits and relating their structure and function.
Introduction
Over the past twenty years, information theory has become a central part of the arsenal of analysis tools in neuroscience. Mutual information is a measure of the correlation between two variables [1] and allows one to evaluate the quality of a proposed neuronal representation. It therefore plays a dual role in neuroscience. First, it is a method for discovering and interpreting correlational structure in inputs and outputs. While the examples we will consider here focus on sensory coding, the developments we consider should ultimately allow for generalizations of the notion of input and output to correlated firing in complex circuits. Second, it is a normative theory, providing a well-defined quantity that a system—- via a coding strategy, a specific circuit dynamics, or even a behavior-- might be expected to maximize.
Here we will discuss recent developments in the applications of information methods to characterize neural coding at the single cell and population level. The evaluation of correlation using information depends on estimation of the entire probability distribution. Obtaining good estimates can be very challenging with limited data [2, 3**], and progress will depend on intelligent simplifications of high-dimensional distributions. We will highlight advances in the use of approximation methods that are moving toward an increasingly complete description of probabilistic encoding of inputs by populations of neurons. A very important open question is the interpretation of observed statistical correlations in terms of the structure of underlying neuronal circuitry. We review recent work that has begun to address the relationship between the statistics of neural firing and structure.
Information theory provides a formalism for quantifying the relationship between two (or more) random variables. A typical application in neuroscience is to quantify the codependence between an input s and a putative neural representation, r, where r might be the timing of a single spike, a spike pattern, the firing rate or a spatially averaged quantity such as the local field potential. The inputs and responses have distributions P(s) and P(r) respectively. If the response is predicted by s, knowledge about s should restrict the possible outputs r, P(r|s). This reduction in uncertainty is quantified by the mutual information, Eq. 2 and Fig.1.
Figure 1.
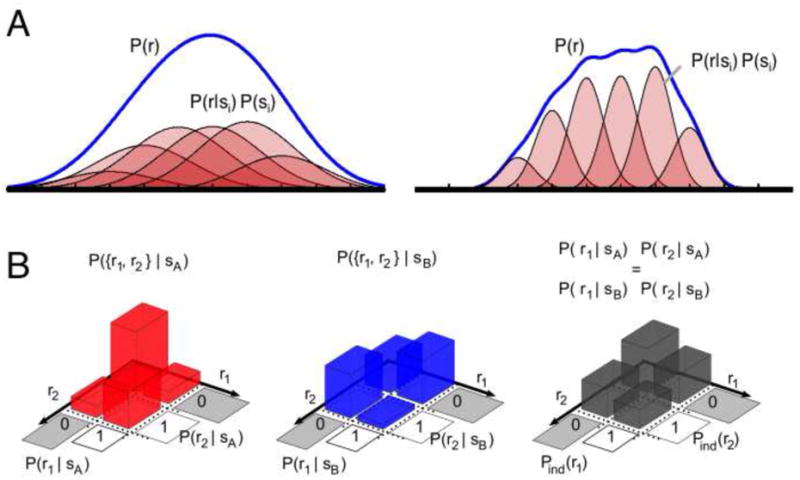
Information encoded by the neural response can be quantified by the mutual information between response and stimulus I(s, r). A. The response distribution is given by P(r) = ∫ P(si) P(r|si). When specifying a value of s, e.g. si, significantly reduces uncertainty, or narrows the distribution, about r, the mutual information between r and s is large (left). The more precisely that s specifies r, the larger the information (right). B. Information and correlations. Here, two stimuli sA and sB generate binary responses {r1,r2} with identical marginal distributions (p(r1|sA)=p(r1|sB) and p(r2|sA)=p(r2|sB)), yet differing joint responses (p({r1,r2}|sA) /= p({r1,r2}|sB)). If correlations are ignored, I(s, r) = 0; if correlations are maintained and the stimuli are equally likely, then I(s, r) ∼ 0.23 bits. From left to right: neural response to sA, with p(r1=1|sA)=p(r2=1|sA)=0.4 but response covariance p(r1r2=1|sA)-p(r1=1|sA)p(r2=1|sA)=0.14; neural response to sB, with p(r1=1|sB)=p(r2=1|sB)=0.4 but response covariance p(r1r2=1|sB)-p(r1=1|sB)p(r2=1|sB)=-0.12; the neural response neglecting covariances is identical for each stimulus, carrying no information.
Mutual information (MI) can be used to evaluate the ability of an output representation to convey stimulus information, without needing to invoke a decoding mechanism to extract that information, and in units that are stimulus-and response-independent [4*]. MI has been used to determine the temporal resolution of spike timing that carries maximal information [5, 6], to test the role of complex spike patterns such as bursts in conveying stimulus information [7], and to compare the information content of features of neural activity on different timescales, such as spike timing and the local field potential [8]. Different neural “symbols” may multiplex different components of stimulus information [9, 10]. Definitions of the mutual information can be generalized to multiple variables [11].
Information and receptive fields
The concept that neuronal receptive fields should minimize redundancy, or shared information (see Box) [12], in neural coding [13, 14] was used to predict that retinal receptive fields should act to cancel out common, or predictable, inputs [15, 16]. However, the underlying assumption of redundancy reduction has recently been challenged by the observation of considerable redundancy in retinal ganglion cells arising from the overlapping of their receptive fields [17]. Furthermore, while the filtering properties of RGC receptive fields do significantly decorrelate responses to natural images, neuronal threshold nonlinearities turn out to play an even more significant role [18].
Information measures.
The uncertainty in a distribution of a random variable S is quantified by its entropy,
| (1) |
The mutual information quantifies the average gain in certainty about one variable due to knowledge of the other:
| (2) |
When the response, R, is a binary variable, and the event is generally rare, the probability distribution of inputs associated with the non-event is very similar to the prior probability, and the information is approximated by the difference in entropy between the event-triggered stimuli and all stimuli. The MI between a spike and the stimulus can then be expressed as
| (4) |
which is the Kullback-Leibler divergence between the distribution of inputs, P(s), and those inputs which are associated with a spike.
When considering the output of more than one responder to an input, one can ask how much knowledge of the input is gained by measuring these responses simultaneously:
Synergy occurs when ⊕I > 0, and the two responses are more informative about the input when recorded together than when they are treated as independent. The responses are redundant when ⊕I < 0, which occurs when some of the information conveyed by the two responses is the same.
There are several other related quantities such the Fisher information that are used to quantify the success of decoding; we will not discuss these here.
Information can be used directly to evaluate how well receptive fields capture the true feature selectivity of neural systems. It thus also provides a method for searching for receptive fields. Eq. (4) can be used to quantify the information captured by a reduced model: that is, one that replaces the stimulus by its similarity to, or projection into, a low-dimensional feature space f [19, 20]. Maximizing Eq.(4) amounts to searching for a set of features f, Fig.2, that maximizes the difference between the entire set of stimuli, viewed in that basis, and the set of stimuli that are associated with spikes. These maximally informative dimensions (MID) then maximize the mutual information between the reduced stimulus and spike over the explored stimulus ensemble [21, 22].
Figure 2. Finding stimulus dimensions with information maximization.
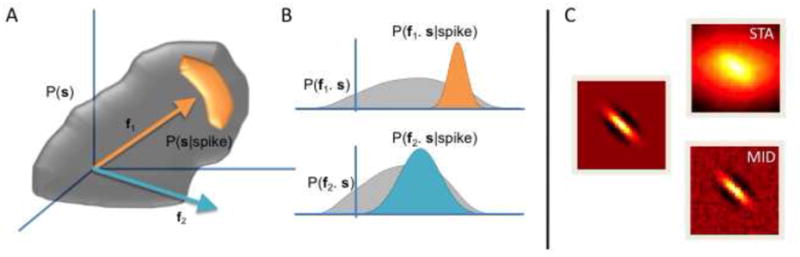
A. The MID method searches for a direction in stimulus space, ie. a filter f. The stimulus s is high-dimensional and is described by some distribution, the grey cloud P(s). One then takes the component of s along a direction f. B. This projected stimulus, f ⊕ s, has a (one-dimensional) distribution P(f ⊕ s). This is known as the prior distribution. The spike-triggered stimuli (denoted in orange), have distribution P(f ⊕ s| spike). The goal is to determine f such that the Kullback-Leibler distance (see Box) between these two distributions is maximized; here, direction f 1 improves the separation of the distributions compared with f2. Finding the direction f that maximizes the Kullback-Leibler distance is equivalent to maximizing the mutual information between the projected stimulus and the occurrence of a spike. C. For a model cell with the filter shown on the left and a sigmoidal nonlinearity, driven with natural images, the MID method recovers the true filter considerably better than the spike-triggered average (with thanks to T. Sharpee).
This powerful method liberates reverse correlation techniques for determining receptive fields from the use of Gaussian white noise stimuli. This allows one to estimate the feature selectivity of systems using more natural stimuli [23] –- in some cases driving neurons that may not even be well-stimulated using Gaussian white noise---and can expose changes in processing as a result of adaptation to the stimulus ensemble. For example, Sharpee et al. [24] found that the filtering properties of neurons in V1 adjust when processing natural images compared to with white noise.
The MID method can be applied to understand the transformations that occur between subsequent processing stages. According to the data processing inequality, a transformation of data cannot increase its information content [1]; however, the retina-LGN synapse was shown to preserve information almost perfectly, despite a reduction in firing rate [25]. Furthermore, this method can allow one to track changes in the structure or dimensionality of the feature set at different processing stages [26*]. Identification of multi-component receptive fields motivates and guides the search for specific circuit mechanisms of stimulus filtering. The MID method has two downsides, however, that may limit some practical applications. Estimating the required probability distributions, particularly for multiple stimulus dimensions, can require daunting amounts of data. Moreover, this optimization has no global solution and the procedure may get caught in local minima.
Population coding
The advent of high-throughput imaging and recording techniques allows simultaneous recording of hundreds of well-isolated single units. Information allows one to determine the statistical relationships between patterns of neural response and an input, whether that input is sensory or expressed in terms of the activity of another set of neurons. However, to apply these methods to neuronal populations, one must estimate the probability of occurrence of all combinations of stimuli and the responses {rj}J=1,N of a population of N neurons – P(r1, r2, …, rN; stimulus). Any direct approach requires sampling an enormous number of states that increases exponentially with N and rapidly outstrips the capacity of any possible experiment [27].
A possible resolution comes from the use of lower order approximations to the full population response. At the extreme, one might assume that each neuron responds independently: P(r1, r2, …, rN) ∼ ∏ Ni=1P(ri). In general, of course, this assumption is too strong: neurons are driven by common stimuli due to overlapping receptive fields. Thus, a weaker assumption is that neurons respond independently, once taking into account possibly overlapping stimulus sensitivities, or signal correlation: P(r1, r2, …, rN | stimulus) ∼ ∏ Ni=1 P(ri | stimulus).
However, neurons may share input variability that is not stimulus-related, and thus show correlations beyond those predicted by the input. This is known as noise correlation [12]. Noise correlations can have a significant impact on the efficacy of decoding information from observations [28, 29**]; depending on the form of this correlation, it may help or hinder decoding [30, 31], (PE Latham and Y Roudi, 2011, http://arxiv.org/abs/1109.6524v1).
Maximum entropy approaches
Thus, the next step in developing an improved approximation for the response distribution is to take into account noise correlations, but in direct attempts to capture P(r1, r2, …, rN | stimulus) we are still faced with a problem of unmanageable scale. One approach is to specify only pairwise noise correlations – dependencies among two cells at a time -- and to extrapolate from here.
Temporarily putting aside the question of stimulus dependence, let us first consider the response space, P(r). One would like to pose an approximate form for this potentially very complex distribution of responses that will take into account the observations one can reasonably make, while making minimal assumptions. The natural model that does this is known as the maximum entropy distribution, which is the distribution that has the most entropy and therefore makes the fewest assumptions about the structure of the distribution. It has the form:
| (5) |
where Z is a normalization factor, and the parameters hi, Jij ,…, are fixed to reproduce the observed moments. For example, knowing the mean (first-order) responses <ri> will fix the parameters hij. Including the terms with Jij allows one to match the second order moments, or the correlations between the firing of any neuron pair, <rirj>. One can then compare the observed frequency of specific patterns with the probability computed from this model. Such second-order models have been shown to improve the prediction of network patterns significantly [27, 28, 32, 33] over those of independent models.
Despite this improvement, the second-order maximum entropy description fails to completely capture the distribution of patterns in large networks, implying the need to incorporate higher-order structure. To capture these “beyond-pairwise” interactions, recent approaches retain selected higher-order terms in the probability model, Eq. (5). For example, the distribution of summed population spike count in somatosensory cortex – that is, the total number of simultaneously active units out of the 24 recorded – could be described by including third order terms [34*]. Encouragingly, this suggests that a relatively low-order correction may achieve the correct structure for significantly larger populations. Ganmor and colleagues [29**] aimed to capture not just the summed population output, but the entire distribution of spike patterns, in recordings of ∼100 retinal ganglion cells. Their insight was to only include in Eq. (5) selected terms corresponding to frequently occurring responses. This “reliable interaction” approach cleverly avoids the need to include every term at a given order. Equating the model probability of patterns that occur frequently to their well-sampled empirical frequencies produces a set of linear equations for the model parameters. This fit is thus rapid, easily learnable and is guaranteed by construction to reproduce the best-known observed probabilities.
Stimulus dependence
Ultimately, one needs to resolve response distributions as a function of the stimulus. Returning to the characterization of single neuron responses, one can again use the idea of the maximum entropy distribution to simplify stimulus dependence. Unlike maximizing information (Fig. 2), maximizing entropy is a convex and therefore relatively easily solved problem. One can then instead apply a maximum entropy approach to the response distributions, conditioned on the stimulus, also known as the noise entropy. The constraints will now apply not to the correlations between responses, but to correlations between stimulus and response [35*, 36**, 37]. Constraining only the first order correlation, < r s >–or the spike-triggered average—results in a logistic response function that depends on a single stimulus dimension. Including the next order terms means that the spike-triggered covariance [20] also appears in the logistic function, which allows for some of the complex multidimensional response functions that are observed in data [38]. Given this flexibility, such “minimal models” are likely to give good fits to a wide variety of sensory responses.
The correlated population models described previously have so far only captured fairly coarse-grained stimulus dependence. Third-order interactions were necessary to capture information about whisker vibrations in rat somatosensory cortex [34*]. In retina, spike-triggered average stimuli for the significantly correlated cell triplets or quadruplets differ from the spike-triggered averages of the constituent pairs, indicating that these higher-order interactions do convey distinct stimulus information [29**]. To date, these methods applied to populations do not fully take into account evolution in time. Ultimately, we expect that a maximum entropy approach that jointly constrains stimulus and response correlation and incorporates their temporal dynamics is a difficult but likely path to a complete population coding model [39].
One may also ask about the ability of a maximum entropy decoder to extract information from the observed responses (cf [40], [31], Latham and Roudi (2011)). In [29**], the use of selected higher order terms translated into a threefold speed increase in classifying new stimulus segments, compared with the pairwise model. On the other hand, Oizumi et al. [41] find that despite significant pairwise correlations in spike responses in RGCs, an independent decoder could extract 95% of the information present about the identity of a natural scene movie. Understanding and building intuition for how and why these cases differ is an important next step for information-based methods in neuroscience.
What do correlation measures reveal about circuit structure and mechanism?
Does the existence of higher-order interactions in Eqn. (5) predict the existence of corresponding features of the physical circuit? Answers to this question so far are mixed, and point to fruitful opportunities for future research. For example, a pairwise maximum entropy model produces extremely accurate descriptions of population activity in the retina [42], and the extent of statistical interactions agreed with general expectations from retinal anatomy. However, it has been shown that pairwise models can always be expected to fit population activity provided the firing rate is sufficiently low, regardless of the underlying circuit [43]. However, Barreiro and colleagues (2012, http://arxiv.org/abs/1011.2797v3) find examples in which purely pairwise inputs to triplets of cells can yield very strong third-order interaction terms, and Roudi et al. [44] find that in large, sparse network simulations, pairwise statistical interactions in maximum-entropy models do not predict direct synaptic connections.
We anticipate that further understanding of the relationship between structure and statistics will come from probabilistic models that adopt more mechanistic features than the statistical description of Eq. (5) - but without becoming so complex that they are impossible to fit (cf. [44]). One recent example is the dichotomous Gaussian method [45**], which has been fit to in vivo cortical slice data [46*]. Here, spikes are generated by passing a correlated Gaussian signal through a threshold - which may be viewed as a crude “binary” model of neural spiking in response to overlapping, common inputs (see Fig. 3). Surprisingly, this model contains the same number of parameters (∼N̂2) as the pairwise maximum entropy model (Eq. (5), truncated at second order), but is considerably more accurate in capturing population-wide spiking patterns (for up to 56 cells) and multichannel LFP patterns (approximately 100 channels). In related work, generalized linear models [47] using ∼Nˆ2 parameters have been successfully used to model population-wide activity in retina --- and have been able to recover qualitative features of circuit connectivity, such as the relative contributions of common input vs. reciprocal coupling [28, 48*].
Figure 3.
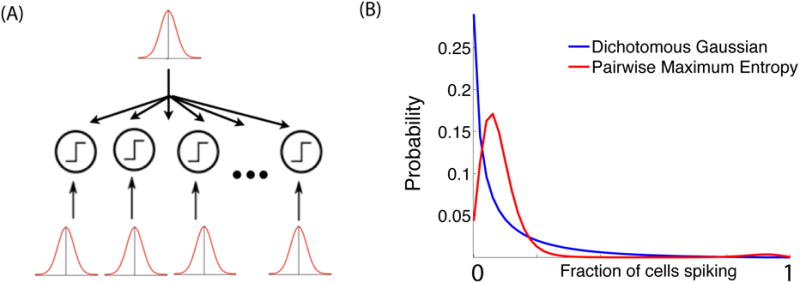
A schematic of the dichotomous Gaussian model of population activity (simplified version). (A) N cells receive a common Gaussian input, as well as independent inputs; the summed input is compared to a threshold to either generate a spike or silence at each timestep. (B) Intriguingly, the output of this idealized model of the thresholding mechanism of spike generation produces highly different population statistics than the corresponding pairwise maximum entropy model [45,46]. The red and blue lines show the fraction out of N=50 model cells that spike simultaneously in a given timestep; both models are fixed to have the same firing rate and pairwise correlation [45].
We anticipate further advances in the ability of these and related spiking models to uncover circuit connectivity, together with circuit mechanisms such as distributions of synaptic inputs (Barreiro et al., 2012, http://arxiv.org/abs/1011.2797v3). An important challenge for these models will be to identify the circuit mechanisms behind aspects of the population response that contribute most to encoding of stimuli. Models provide a rapid testbed for this question by allowing us to compare different circuit mechanisms that conserve basic features of the population response (such as firing rates and pairwise correlations) but differ in more subtle aspects – such as higher order statistics of the population response (cf. [48*, 49] and Fig. 3).
Normative models
Aside from stimulus/response characterization, one of the most intriguing if speculative and sometimes controversial uses of information is as an objective function to explain coding and behavioral strategies. The ability of many neural systems to encode stimuli in units that are rapidly normalized by a changing input range allows them to maintain high rates of information transmission [50]. Patterns in behavioral search strategies may be qualitatively predicted as a search for information; the zigzag flight pattern of a moth searching for the source of a plume of pheromone has been proposed to driven by “infotaxis”, an effort to reduce uncertainty about the stimulus [51, 52]. Similarly, the trajectories of eye movements are consistent with a theory in which they are driven by entropy reduction [53, 54].
Conclusions
Information theoretic tools are generating new methods to determine rich models for neural stimulus representation. The use of maximum entropy distributions has had tremendous recent impact, driving rapid progress in building complete population response models. As yet, these methods are limited in their ability to capture complex stimulus dependence and temporal dynamics. An interplay between these statistical methods and alternative generative models of network activity will be needed to interpret the observations of higher-order correlations and their significance in terms of underlying circuit motifs. However, such studies are likely to provide a framework for linking future connectomic data with functional models of stimulus representation.
Highlights.
Information theory requires the estimation of high-dimensional probability distributions of stimulus and response; enormous progress has been made recently using maximum entropy methods to find simplified approximations to these distributions.
Information theoretic methods allow the determination of receptive fields and approximate response models using natural stimuli.
Taking into account second-order correlations often provides remarkably good estimates of response distributions for neuronal populations, although new methods allow simple sampling of higher-order correlations.
Efforts to link correlational structure with anatomical circuit motifs are underway.
Acknowledgments
ALF acknowledges support from NSF 0928251 and NIH 1R21NS072691, and ESB from the Burroughs Wellcome Fund Scientific Interfaces Program and NSF Grants 1056125, 0818153, and 1122106. We thank Tatyana Sharpee for providing Figure 2C and David Leen (UW Applied Mathematics) for the algorithm and MATLAB coding that produced Figure 3B.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Adrienne Fairhall, Email: fairhall@uw.edu.
Eric Shea-Brown, Email: etsb@uw.edu.
Andrea Barreiro, Email: abarreiro@smu.edu.
References
- 1.Cover TM, Thomas JA. Information theory. New York: John Wiley & Sons, Inc; 1991. [Google Scholar]
- 2.Nemenman I, Bialek W, de Ruyter van Steveninck R. Entropy and information in neural spike trains: progress on the sampling problem. Physical Review E Statistical, Nonlinear, and Soft Matter Physics. 2004;69:56111. doi: 10.1103/PhysRevE.69.056111. [DOI] [PubMed] [Google Scholar]
- 3**.Ince RA, Senatore R, Arabzadeh E, Montani F, Diamond ME, Panzeri S. Information-theoretic methods for studying population codes. Neural Netw. 2010;23(6):713–27. doi: 10.1016/j.neunet.2010.05.008. This is an extensive review of recent literature applying information to characterize neural systems, particularly helpful for its discussion of multiple recent approaches to finite size corrections. [DOI] [PubMed] [Google Scholar]
- 4*.Quian Quiroga R, Panzeri S. Extracting information from neural populations: information theory and decoding approaches. Nature Reviews Neuroscience. 2009:10, 173–185. doi: 10.1038/nrn2578. This pedagogical review of information theoretic approaches focuses on the relationship between information and decoding methods. [DOI] [PubMed] [Google Scholar]
- 5.Reinagel P, Reid RC. Temporal coding of visual information in the thalamus. J Neurosci. 2000;20(14):5392–400. doi: 10.1523/JNEUROSCI.20-14-05392.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nemenman I, Lewen GD, Bialek W, de Ruyter van Steveninck RR. Neural coding of natural stimuli: information at sub-millisecond resolution. PLoS Comput Biol. 2008;4(3):e1000025. doi: 10.1371/journal.pcbi.1000025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Arabzadeh E, Panzeri S, Diamond ME. Whisker vibration information carried by rat barrel cortex neurons. J Neurosci. 2004 Jun 30;24(26):6011–20. doi: 10.1523/JNEUROSCI.1389-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Belitski A, Panzeri S, Magri C, Logothetis NK, Kayser C. Sensory information in local field potentials and spikes from visual and auditory cortices: time scales and frequency bands. J Comput Neurosci. 2010;29(3):533–45. doi: 10.1007/s10827-010-0230-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fairhall AL, Lewen GD, Bialek W, de Ruyter Van Steveninck RR. Efficiency and ambiguity in an adaptive neural code. Nature. 2001;412(6849):787–92. doi: 10.1038/35090500. [DOI] [PubMed] [Google Scholar]
- 10.Panzeri S, Brunel N, Logothetis NK, Kayser C. Sensory neural codes using multiplexed temporal scales. Trends Neurosci. 2010;33(3):111–20. doi: 10.1016/j.tins.2009.12.001. [DOI] [PubMed] [Google Scholar]
- 11.Schneidman E, Still S, Berry M, Bialek W. Network Information and Connected Correlations. Phys Rev Lett. 2003;91(23):238701. doi: 10.1103/PhysRevLett.91.238701. [DOI] [PubMed] [Google Scholar]
- 12.Schneidman E, Bialek W, Berry MJ., II Synergy, Redundancy, and Independence in Population Codes. J Neurosci. 2003;23(37):11539–11553. doi: 10.1523/JNEUROSCI.23-37-11539.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Barlow HB. Possible principles underlying the transformation of sensory messages. In: Rosenblith W, editor. Sensory Communication. MIT Press; Cambridge, MA: 1961. [Google Scholar]
- 14.Attneave F. Some informational aspects of visual perception. Psychol Rev. 1954;61:183–193. doi: 10.1037/h0054663. [DOI] [PubMed] [Google Scholar]
- 15.Srinivasan MV, Laughlin SB, Dubs A. Predictive coding: a fresh view of inhibition in the retina. Proc R Soc Lond B Biol Sci. 1982;216(1205):427–59. doi: 10.1098/rspb.1982.0085. [DOI] [PubMed] [Google Scholar]
- 16.Atick Could information theory provide an ecological theory of sensory processing? Network. 1992:3, 213–252. doi: 10.3109/0954898X.2011.638888. [DOI] [PubMed] [Google Scholar]
- 17.Puchalla JL, Schneidman E, Harris RA, Berry MJ. Redundancy in the population code of the retina. Neuron. 2005;46(3):493–504. doi: 10.1016/j.neuron.2005.03.026. [DOI] [PubMed] [Google Scholar]
- 18.Pitkow X, Meister M. Decorrelation and efficient coding by retinal ganglion cells. Nat Neurosci. 2012;15(4):628–35. doi: 10.1038/nn.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fairhall AL, Burlingame CA, Narasimhan R, Harris RA, Puchalla JL, Berry MJ., 2nd Selectivity for multiple stimulus features in retinal ganglion cells. J Neurophysiol. 2006;96(5):2724–38. doi: 10.1152/jn.00995.2005. [DOI] [PubMed] [Google Scholar]
- 20.Schwartz O, Pillow JW, Rust NC, Simoncelli EP. Spike-triggered neural characterization. Journal of Vision. 2006;6(4):484–507. doi: 10.1167/6.4.13. [DOI] [PubMed] [Google Scholar]
- 21.Sharpee T, Rust NC, Bialek W. Analyzing neural responses to natural signals: maximally informative dimensions. Neural Comput. 2004 Feb;16(2):223–50. doi: 10.1162/089976604322742010. [DOI] [PubMed] [Google Scholar]
- 22.Pillow JW, Simoncelli EP. Dimensionality reduction in neural models: an information-theoretic generalization of spike-triggered average and covariance analysis. J Vis. 2006;6(4):414–28. doi: 10.1167/6.4.9. [DOI] [PubMed] [Google Scholar]
- 23.Simoncelli EP, Olshausen BA. Natural image statistics and neural representation. Annu Rev Neurosci. 2001;24:1193–216. doi: 10.1146/annurev.neuro.24.1.1193. [DOI] [PubMed] [Google Scholar]
- 24.Sharpee TO, Sugihara H, Kurgansky AV, Rebrik SP, Stryker MP, Miller KD. Adaptive filtering enhances information transmission in visual cortex. Nature. 2006;439(7079):936–42. doi: 10.1038/nature04519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sincich LC, Horton JC, Sharpee TO. Preserving information in neural transmission. J Neurosci. 2009;29(19):6207–16. doi: 10.1523/JNEUROSCI.3701-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26*.Atencio CA, Sharpee TO, Schreiner CE. Receptive field dimensionality increases from the auditory midbrain to cortex. J Neurophysiol. 2012;107(10):2594–603. doi: 10.1152/jn.01025.2011. A recent example of the application of maximally information dimension methods to evaluate transformation in coding, finding an increase in the number of relevant stimulus dimensions. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schneidman E, Berry MJ, II, Segev R, Bialek W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature. 2006;440:1007–1012. doi: 10.1038/nature04701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pillow J, Shlens J, Paninski L, Sher A, Litke A, Chichilnisky EJ, Simoncelli EP. Spatiotemporal correlations and visual signaling in a complete neuronal population. Nature. 2008;454:995–999. doi: 10.1038/nature07140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29**.Ganmor E, Segev R, Schneidman E. Sparse low-order interaction network underlies a highly correlated and learnable neural population code. Proceedings of the National Academy of Sciences. 2011;108(23):9679–9684. doi: 10.1073/pnas.1019641108. Demonstrates a data-driven method for incorporating selected higher order interactions into a pairwise-maximum entropy fit in retina. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Abbott L, Dayan P. The effect of correlated variability on the accuracy of a population code. Neural Computation. 1999;11:91–101. doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- 31.Averbeck BB, Lee D. Effects of Noise Correlations on Information Encoding and Decoding. Journal of Neurophysiology. 2006;95:3633–3644. doi: 10.1152/jn.00919.2005. [DOI] [PubMed] [Google Scholar]
- 32.Shlens J, Field G, Gauthier J, Grivich M, Petrusca D, Sher A, Litke AM, Chichilnisky EJ. The structure of multi-neuron firing patterns in primate retina. The Journal of Neuroscience. 2006;26(32):8254. doi: 10.1523/JNEUROSCI.1282-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tang A, Jackson D, Hobbs J, Chen W, Smith JL, Patel H, Prieto A, Petrusca D, Grivich MI, Sher A, Hottowy P, Dabrowski W, Litke AM, Beggs JM. A Maximum Entropy Model Applied to Spatial and Temporal Correlations from Cortical Networks In Vitro. The Journal of Neuroscience. 2008;28(2):505–518. doi: 10.1523/JNEUROSCI.3359-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34*.Montani F, Ince RA, Senatore R, Arabzadeh E, Diamond ME, Panzeri S. The impact of high-order interactions on the rate of synchronous discharge and information transmission in somatosensory cortex. Philos Transact A Math Phys Eng Sci. 2009;367:3297–3310. doi: 10.1098/rsta.2009.0082. Computes mutual information between whisker vibration velocity and population level response in somatosensory cortex, showing that third-order interactions are sufficient to capture the information content in the response of a group of roughly 20 neural “clusters” (of 2-5 cells each) [DOI] [PubMed] [Google Scholar]
- 35*.Globerson A, Stark E, Vaadia E, Tishby N. The minimum information principle and its application to neural code analysis. Proc Natl Acad Sci USA. 2009:3490–3495. doi: 10.1073/pnas.0806782106. Introduces the concept of the minimum information principle, which determines the minimum information that a given set of observations contains about the stimulus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36**.Fitzgerald JD, Sincich LC, Sharpee TO. Minimal models of multidimensional computations. PLoS Comput Biol. 2011 Mar;7(3):e1001111. doi: 10.1371/journal.pcbi.1001111. Derives a minimal model of responses to neural stimuli by constructing maximum noise entropy (or minimum information) solutions that are constrained by successive order moments of the stimulus-response distribution. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fitzgerald JD, Rowekamp RJ, Sincich LC, Sharpee TO. Second order dimensionality reduction using minimum and maximum mutual information models. PLoS Comput Biol. 2011;7(10) doi: 10.1371/journal.pcbi.1002249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fairhall AL, Burlingame CA, Puchalla J, Harris R, Berry MJ., II Feature selectivity in retinal ganglion cells. J Neurophysiol. 2006;96(5):2724–38. doi: 10.1152/jn.00995.2005. [DOI] [PubMed] [Google Scholar]
- 39.Tishby N, Pereira FC, Bialek W. The information bottleneck method. Proceedings of the 37-th Annual Allerton Conference on Communication, sControl and Computing; 1999; pp. 368–377. [Google Scholar]
- 40.Latham P, Nirenberg S. Synergy, redundancy, and independence in population codes, revisited. The Journal of Neuroscience. 2005;25(21):5195. doi: 10.1523/JNEUROSCI.5319-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Oizumi M, Ishii T, Ishibashi K, Okada M. Mismatched decoding in the brain. Journal of Neuroscience. 2010;30:4815–4826. doi: 10.1523/JNEUROSCI.4360-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shlens J, Field GD, Gauthier JL, Greschner M, Sher A, Litke AM, Chichilnisky EJ. The structure of large-scale synchronized firing in primate retina. Journal of Neuroscience. 2009;29(15):5022–5031. doi: 10.1523/JNEUROSCI.5187-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Roudi Y, Nirenberg S, Latham PE. Pairwise Maximum Entropy Models for Studying Large Biological Systems: When They Can Work and When They Can't. PLoS Computational Biology. 2009;5(5):e1000380. doi: 10.1371/journal.pcbi.1000380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Roudi Y, Tyrcha J, Hertz J. Ising model for neural data: Model quality and approximate methods for extracting functional connectivity. Physical Review E. 2009;79:051915. doi: 10.1103/PhysRevE.79.051915. [DOI] [PubMed] [Google Scholar]
- 45**.Macke JH, Opper M, Bethge M. Common Input Explains Higher-Order Correlations and Entropy in a Simple Model of Neural Population Activity. Physical Review Letters. 2011;106(20):208102. doi: 10.1103/PhysRevLett.106.208102. Shows how beyond-pairwise correlations emerge in models with “pairwise” parameterizations from the operation of thresholding. [DOI] [PubMed] [Google Scholar]
- 46*.Yu Y, Yang H, Nakahara H, Sanstos GS, Nikolić D, Plenz D. Higher-Order Interactions Characterized in Cortical Activity. Journal of Neuroscience. 2011;31(48):17514–17526. doi: 10.1523/JNEUROSCI.3127-11.2011. Applies the model of Macke et al 2011 to array recordings in cortex, finding that it captures the underlying population structure at pairwise and higher orders of statistical interaction. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN. A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. J Neurophysiol. 2005;93(2):1074–89. doi: 10.1152/jn.00697.2004. [DOI] [PubMed] [Google Scholar]
- 48*.Vidne M, Ahmadian Y, Shlens J, Pillow JW, Kulkarni J, Litke AM, Chichilnisky EJ, Simoncelli E, Paninski L. Modeling the impact of common noise inputs on the network activity of retinal ganglion cells. J Comp Neurosci. 2011 doi: 10.1007/s10827-011-0376-2. [online only at present] An extension of the generalized linear model methods to allow for common noise inputs. Approaches like this will be important to combine with information theoretic measures to assess the importance of unobserved inputs. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Series P, Latham P, Pouget A. Tuning curve sharpening for orientation selectivity: coding efficiency and the impact of correlations. Nat Neurosci. 2004;7:1129–1135. doi: 10.1038/nn1321. [DOI] [PubMed] [Google Scholar]
- 50.Wark B, Lundstrom BN, Fairhall A. Sensory adaptation. Curr Opin Neurobiol. 2007 Aug;17(4):423–9. doi: 10.1016/j.conb.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Vergassola M, Villermaux E, Shraiman BI. ‘Infotaxis’ as a strategy for searching without gradients. Nature. 2007;445(7126):406–9. doi: 10.1038/nature05464. [DOI] [PubMed] [Google Scholar]
- 52.Agarwala Chiel H, Thomas P. Pursuit of food versus pursuit of information in a Markovian perception–action loop model of foraging. Journal of Theoretical Biology. 2012;304:235–272. doi: 10.1016/j.jtbi.2012.02.016. [DOI] [PubMed] [Google Scholar]
- 53.Renninger LW, Verghese P, Coughlan J. Where to look next? Eye movements reduce local uncertainty. J Vis. 2007 Feb 27;7(3):6. doi: 10.1167/7.3.6. [DOI] [PubMed] [Google Scholar]
- 54.Najemnik J, Geisler WS. Eye movement statistics in humans are consistent with an optimal search strategy. J Vis. 2008 Mar 7;8(3):4.1–14. doi: 10.1167/8.3.4. [DOI] [PMC free article] [PubMed] [Google Scholar]


