Improved corpus callosum area measurements by analysis of adjoining parasagittal slices

Abstract

The corpus callosum (CC) is a bundle of approximately 180 million axons connecting homologous areas of the left and right cerebral cortex. Because CC projections are topographically organized, regional CC morphological abnormalities may reflect regional cortical developmental abnormalities. We assess the variance characteristics of three CC area measurement techniques by comparing a single midsagittal slice versus three slices (midsagittal plus one parasagittal on each side) and five slices (midsagittal plus two parasagittal on each side). CC images were partitioned into five subregions using the Hofer–Frahm scheme under the three methods and variance was examined via two complementary data sets. In the first, to control for intersubject variability, 12 scans were acquired from a single subject over the course of 3 h. In the second, we used scans from 56 healthy male volunteers between the ages of 10 and 27 years (mean=17.47, S.D.=3.42). Increasing the number of slices from one to three to five diminished the coefficient of variation (CV) within subregions and increased the power to detect differences between groups. A power analysis was conducted for the sample under each method to determine the sample size necessary to discern a given percent change (delta) ranging from 1 to 20% iteratively.

1. Introduction

The corpus callosum (CC) is a bundle of approximately 180 million myelinated axons connecting homologous cortical regions of the left and right cerebral hemispheres (Tomasch, 1954). In a body of work containing over 300 publications, the size, shape, and/or developmental trajectory of the CC have been examined with respect to age, sexual dimorphism, and cognitive/behavioral correlates in typical and atypical development (Giedd et al., 2006).

Manual morphometric studies of the CC have typically reported the area of a single midsagittal slice. However, CC area measures may vary substantially with only slight changes in the angle of the chosen midsagittal slice or even as a result of within-scanner measurement drift (Takao et al., 2011). In this report, we examine the benefits of including parasagittal slices to decrease measurement error and increase power to detect group differences.

2. Methods

Our study consisted of two parts: (i) a single subject analysis in which repeated measures were used to compare variance across techniques, and (ii) an analysis of the power of each method to detect given percentages of between-group differences. All images were T1-weighted SPoiled Gradient Recalled echo (SPGR) pulse sequence collected on a 1.5 T scanner (GE Signa). Image volumes consisted of 124 1.5 mm-thick axial slices with an in-plane resolution of 0.9375 mm², TR=24 ms, TE=5 ms, and a flip angle=45°. Scan duration was 10 min.

Images were manually rotated into a standardized space using MIPAV's (Medical Image Processing, Analysis and Visualization, version 4.3.1; http://mipav.cit.nih.gov/) protractor alignment tool. In the axial plane, the posterior and anterior points of the longitudinal fissure were brought into vertical alignment such that the angle of deviation between the points was zero. In the sagittal plane, the deviation angle between the anterior-most and posterior-most points of the CC was set to zero. Similarly, in the coronal plane, the deviation angle between the medial–posterior pons and the superior-most point of the longitudinal fissure was set to zero. See Fig. 1 for an illustration of the spatial standardization procedure.

Fig. 1.

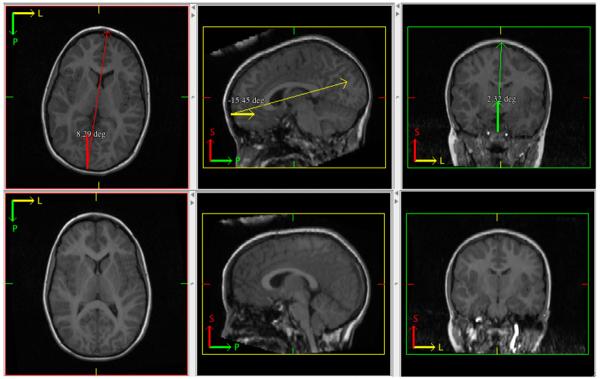
Illustration of manual tracing methods. Top: example of a brain in native space (deviation angles exaggerated for purposes of illustration) with MIPAV's protractor tool placed in each axis to execute spatial corrections. Bottom: result of spatial corrections.

2.1. Measurement schemes

Three manual measurement methods were compared: (i) a single midsagittal slice; (ii) the midsagittal slice with two additional parasagittal slices (one on either side of the midsagittal); and (iii) the midsagittal slice with two parasagittal slices from either side, lending five total slices to the measurements. We denoted these methods V1, V3 and V5, respectively. Thus, V3 included the V1 slice while V5 included V3 and V1 slices. Fig. 2 illustrates the three methods. Manual tracing of the CC was performed using MIPAV by two trained raters (BW and MM) with high intra-rater (both ICC>0.95) and inter-rater (ICC>0.9) reliabilities. We used the Hofer–Frahm guidelines (Hofer and Frahm, 2006) to partition the CC into five subregions across each slice included in the schemes, using an automated in-house MATLAB (http://www.mathworks.com/products/matlab/) program.

Fig. 2.

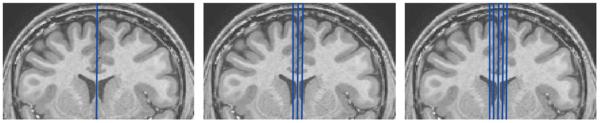
Illustration of slicing methods. Left: V1, midsagittal slice only. Middle: V3, midsagittal slice and two parasagittal slices. Right: V5, midsagittal slice and four parasagittal slices.

The Hofer–Frahm guidelines group White Matter (WM) bundles that traverse the CC into five vertically divided partitions along the anterior–posterior length of the callosum. Region I, the anterior-most sixth of the CC, contains fibers which project to the prefrontal cortex. Region II, which makes up the latter anterior half of the CC, is comprised of fibers that project to the premotor and supplementary motor areas. Region III is defined as the posterior half of the CC minus the posterior-most third and contains fibers that project to the primary motor cortex. Region IV is defined as the posterior third minus the posterior-most fourth and contains fibers projecting to sensory cortices. Region V is defined as the posterior fourth of the CC and contains fibers projecting to parietal, temporal and occipital cortex (Hofer and Frahm, 2006).

In order to calculate these partitions, a computer program, written in MATLAB first determined the anterior–posterior length of the CC mask (defined here as the difference between the position of the anterior-most and posterior-most CC voxels in each sagittal plane after all spatial alignment procedures have been performed). Then each voxel was classified into a subdivision based on relative anterior–posterior location according to the proportions proposed by Hofer and Frahm. If a voxel on the border of two subdivisions would have been classified as a mixture of two subdivisions, it was classified as the subdivision with the highest proportion. If both were equally represented, then it was classified as the more anterior region. See Fig. 3 for an illustration of the Hofer–Frahm partitioning scheme.

Fig. 3.

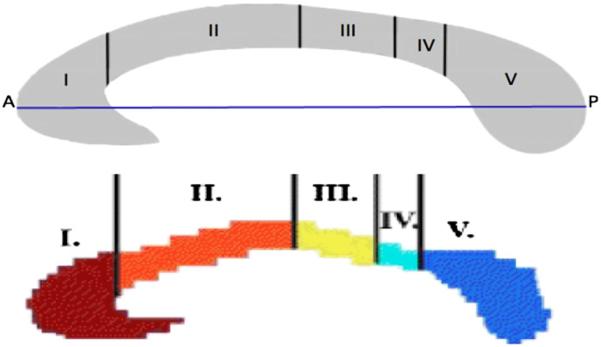
Original and adjusted Hofer–Frahm scheme. Top: illustration of Hofer–Frahm scheme subdivision proportions with A–P line in blue. Bottom: adjusted MATLAB division of proposed Hofer–Frahm scheme. Region I: prefrontal; region II: premotor and supplementary motor; region III: motor; region IV: sensory; region V: parietal, temporal, and occipital. A, anterior; P, posterior (Hofer and Frahm, 2006). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2. Single subject analysis

Variability of CC measures across multiple scans taken from a single individual within the same session of neuroimaging is unlikely to reflect true changes in CC size, and thus provides a direct index of measurement error. We applied V1, V3 and V5 measurement techniques to 12 SPGR brain scans taken from one subject during a single day using the same 1.5 T GE Signa scanner. Scans were acquired sequentially. Between scans, the subject was allowed to move her head however she was not removed from the scanner.

We obtained verbal and written assent from the child and written consent from the parents for participation in this study. The National Institute of Mental Health Institutional Review Board approved the protocol.

2.3. Single subject statistical methods

Relative variability of each CC subregion was assessed by comparing the coefficient of variation (CV), defined as the ratio of the standard deviation over the mean which was then multiplied by 100 to be expressed as a percentage, for each subregion under each method. Higher CV indicates greater variance in the data.

2.4. Multi-subject analysis methods

In order to gauge the efficacy of each manual method (V1, V3, V5) to detect finite, between-group differences, each was applied to a sample of 56 healthy male volunteers between the ages of 10 and 27 years (Mean=17.47, S.D.=3.42). All 56 SPGR scans were acquired on the same 1.5 T GE Signa scanner. Manual CC tracings for each scan were performed by two raters (BW and MM). We obtained written consent from the adult participants and obtained verbal or written assent from the child participants as well as written consent from the parents for participation in this study. The National Institute of Mental Health Institutional Review Board approved the protocol.

2.5. Statistical methods for multi-subject sample

For each method, we quantified the number of subjects needed to discern finite differences between two theoretical populations. Therefore, we performed a least squares regression on each method's subregion of the form $E[\text{Area}\mid \text{age}]={\beta }_0+{\beta }_1^{\ast }\text{age}$. A corrected measure of area was then calculated by adding the mean area back into the residuals, Area_corrected=residuals+mean. The corrected statistics were then used to execute a power analysis within the R statistical package [power t test (http://www.R-project.org) with an alpha of 0.05 and the power level of 0.95]. This was repeated iteratively, simulating 1–20% differences between group means.

3. Results

3.1. Single subject analysis

Table 1 presents the CV associated with each subregion based on each of the three measuring techniques.

Table 1.

Coefficient of variation by method and callosum subregion in single subject measures.

Method	Subregions
	1	2	3	4	5
V1	3.27	4.13	8.5	13.99	4.26
V3	2.85	3.33	5.96	11.6	4.35
V5	2.46	2.41	5.33	9.73	3.34

3.2. Multi-subject analysis

Results of the power analysis are presented in Table 2. Posterior CC segments, regions 3, 4 and 5 demonstrated consistent reductions in the predicted sample sizes necessary to detect differences between groups as slice count increased. Conversely, anterior CC segments, regions 1 and 2 showed slightly increased sample size requirements with increased slice count.

Table 2.

Sample size required as a function of percent delta, slice method and callosum subregion.

	Region 1			Region 2			Region 3			Region 4			Region 5
Number of slices included
Delta (%)	1	3	5	1	3	5	1	3	5	1	3	5	1	3	5
20	5	5	5	6	6	6	7	7	6	10	9	9	6	6	6
19	6	6	6	6	7	7	8	7	7	11	9	9	6	6	6
18	6	6	6	7	7	7	8	8	7	12	10	10	7	7	7
17	7	6	7	7	8	8	9	9	8	13	11	11	8	7	7
16	7	7	7	8	9	9	10	10	9	14	13	12	8	8	8
15	8	8	8	9	9	10	11	11	10	16	14	14	9	9	9
14	9	9	9	10	11	11	13	12	11	18	16	16	10	10	10
13	10	10	10	12	12	13	14	14	12	21	18	18	12	12	11
12	12	11	12	13	14	15	17	16	14	24	21	21	14	13	13
11	13	13	14	15	16	17	20	18	17	28	25	25	16	15	15
10	16	16	16	18	19	20	23	22	20	34	30	29	19	18	18
9	19	19	20	22	23	25	29	27	24	41	37	36	23	22	22
8	24	23	24	28	29	31	36	33	30	52	46	45	28	28	28
7	31	30	31	36	38	40	46	43	38	68	60	58	37	36	36
6	41	40	42	48	51	53	62	58	52	91	81	79	49	48	48
5	59	57	60	69	72	76	89	83	74	131	116	113	70	69	69
4	91	89	93	107	112	118	138	129	115	204	180	176	109	107	106
3	161	157	164	189	198	209	245	228	203	361	318	311	193	188	188
2	359	351	368	424	443	468	549	511	455	810	714	698	433	422	421
1	1433	1401	1468	1691	1767	1869	2190	2040	1814	3237	2852	2787	1726	1682	1679

Each intersection represents the sample size needed in each of two groups to reliably detect a percent difference between the g (delta). Entries above the single horizontal line reach a large Cohen's d effect size (> 0.8). Entries between the single and double lim medium in effect size (> 0.5), while entries below the double line are small in effect size.

4. Discussion

With this study, we have quantified the degree of variability in area measurements across several methods. In comparing data from one, three and five slices, we demonstrated a reduction in variance that occurs for the majority of the CC subregions when additional slices are utilized. We then calculated the sample size needed to detect particular degrees of between-group area differences ranging from gross differences upwards of 20% to minute group differences of 1%.

By fixing the structure of the CC as a constant, the single subject data provides an index of measurement error untainted by differences between subjects. Using this approach, we restricted the potential sources of variation primarily to rater error and repositioning of the head between scanning sessions.

The power analysis was conducted in an effort to provide investigators with the information needed to predict the sample size needed to detect a hypothesized delta. Interestingly, the power analysis revealed that not all CC subregions are less variable at higher slice counts. While regions 3, 4 and 5 experienced a 16.8%, 13.7% and 1.4% reduction in sample size requirement in the transition from V1 to V5, assuming a 5% delta respectively, regions 1 and 2 experience a 1.6% and 9.2% increase in sample size required under the same circumstances respectively.

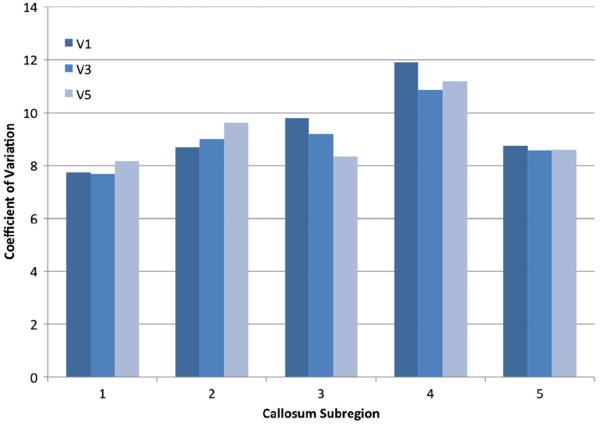
To investigate this differential anterior–posterior effect, we investigated the CV of the sample of 56 for each CC subregion under each method. However, rather than pooling sagittal slices where V1 is an element of V3 which is an element of V5, slices unique to each method were reported on separately. This way we could determine whether there was more information or noise being added with each addition of paired parasagittal slices. CV of unique slice pairs is reported in Fig. 4.

Fig. 4.

Coefficient of variation of unique slice pairs by callosum subregion.

The CV suggests that there is a differential anterior–posterior interaction between medial and lateral sagittal CC slices and CV. The anterior aspect of the CC, regions 1 and 2, show higher CV in lateral slices whereas posterior regions, 3, 4 and 5, decrease CV moving to lateral parasagittal slices. This would suggest diminishing returns when increasing slice count anteriorly while the opposite is true posteriorly. While CV of unique slice pairs explains how the anterior–posterior effect exists it does not explain why. It is reasonable to eliminate the alignment procedure as a source of differential anterior–posterior variation in our sample as all spatial transformations were linear and applied to the entire brain volume. However, it remains possible that this anterior–posterior difference exists purely by chance.

Interestingly, the single subject data did not reveal a differential effect between anterior and posterior subregions. Instead, the CV was reduced consistently across all subregions of the CC with the addition of parasagittal slices with the single exception of the transition from V1 to V3 in region 5. However, V5 CV was still lower than V1 and V3. It therefore remains unclear why there is a differential anterior–posterior CV effect in the sample used for the power analysis.

Yet, despite these exceptions in CV reduction, we posit that the five-slice method is more robust on the whole and should be utilized whenever possible. In our sample, the benefits of using V5 rather than V1 outweigh the negative effects with a 16.8%, 13.7% and 1.4% reduction in sample size needed for posterior regions 3, 4 and 5 respectively, weighed against a 1.6% and 9.2% increase in demand for anterior regions 1 and 2, respectively, at 5% delta, as previously stated. Moreover, while it is evident that the standard deviation of such measurements decrease in relation to increased data points, both the degree and pattern of this reduction is non-intuitive.

Finally, we do not investigate the significance of these reductions in the classical sense but instead report only on the magnitude of CV reduction across CC subregions. The significance of these reductions is a matter of the cost of time, labor and sample size saved to the researcher. It is also notable that the areas of parasagittal slices are highly correlated and therefore not entirely statistically independent. This correlated nature of adjacent slices would inflate our results had we reported on statistical significance, however, this is not the present case. We instead report on the more qualitative trending of CV reduction with increased slice counts which is untainted by the correlation between adjoining slices.

These results have implications for the design and interpretation of CC morphometry studies. While a large effect size (Cohen's d>0.8; Cohen, 1988) does not require more than 40 subjects for each group to be detected, the more subtle changes that qualify as medium- to small-effect size range (Cohen's d≤0.5) require exponentially larger sample sizes reaching into the thousands for small-effect sizes. Additionally, investigators performing multisite studies are subject to an added source of variance for which we have not accounted. One report in particular observed 11.7% CV between WM measures acquired on multiple scanners (Reig et al., 2009).

A limitation of the study was that the age range of our subjects was restricted to ages 10–27. No subjects below the age of 10 were included because we attempted to avoid steep WM growth curves associated with younger ages. While our sample does cover a widely studied age range, significantly younger or older samples might introduce higher variance, which would require larger sample sizes to detect between-group differences.

Additionally, while morphometry of the CC was analyzed in the sagittal plane, the images were acquired axially. Since slice thickness was 1.5 mm as compared to 0.9375 mm in-plane resolution, sagittal orientations would have offered superior resolution of the callosal boundaries.

We are also unable to pinpoint the cause of the differential anterior–posterior CV in our sample. Because we present reduction of CV in a qualitative manner, we are unable to eliminate the possibility that differential CV is purely due to random chance through use of statistical tests.

However, despite these limitations, this study provides a qualitative assessment of the benefits of including additional parasagittal slices in morphometric studies of the CC, which can be used in cost/benefit analysis of experimental designs.