Inhibition causes ceaseless dynamics in networks of excitable nodes

Abstract

The collective dynamics of a network of excitable nodes changes dramatically when inhibitory nodes are introduced. We consider inhibitory nodes which may be activated just like excitatory nodes but, upon activating, decrease the probability of activation of network neighbors. We show that, although the direct effect of inhibitory nodes is to decrease activity, the collective dynamics becomes self-sustaining. We explain this counterintuitive result by defining and analyzing a “branching function” which may be thought of as an activity-dependent branching ratio. The shape of the branching function implies that for a range of global coupling parameters dynamics are self-sustaining. Within the self-sustaining region of parameter space lies a critical line along which dynamics take the form of avalanches with universal scaling of size and duration, embedded in ceaseless timeseries of activity. Our analyses, confirmed by numerical simulation, suggest that inhibition may play a counterintuitive role in excitable networks.

Networks of excitable nodes have been successfully used to model a variety of phenomena, including reaction-diffusion systems [1], economic trade crises [2], epidemics [3, 4], and social trends [5]. They have also been used widely in the physics literature to study and predict neuroscientific phenomena [6–12], and have been used directly in the neuroscience literature to study the collective dynamics of tissue from the mammalian cortex in humans [13], monkeys [14], and rats [14–17]. The effects of inhibitory nodes, i.e. nodes that suppress activity, can be important but are not well understood in many of these systems. In this Letter, we extend such networks of purely excitatory nodes to include inhibitory nodes whose effect, on activation, is to decrease the probability that their network neighbors will become excited. We focus on the regimes near the critical point of a nonequilibrium phase transition that has been of interest in research on optimized dynamic range [6–11, 15], information capacity [14], and neuronal avalanches [13–18], and has also been explored in epidemiology where it constitutes the epidemic threshold [4]. At first pass, one would expect the inclusion of inhibition in excitable networks to lead to lower overall network activity, yet we find that the opposite is true: the inclusion of inhibitory nodes in our model leads to effectively ceaseless network activity for networks maintained at or near the critical state.

Our model consists of a sparse network of N excitable nodes. At each discrete time step t, each node m may be in one of two states s_m (t) = 0 or s_m (t) = 1, corresponding to quiescent or active respectively. When a node m is in the active state s_m (t) = 1, node n receives an input of strength A_nm. Each node m is either excitatory or inhibitory, respectively corresponding to A_nm ≥ 0 or A_nm ≤ 0 for all n. If there is no connection from node m to node n, then A_nm = 0. Each node n sums its inputs at time t and passes them through a transfer function σ(·) so that its state at time t + 1 is

$$s_n(t+1)=1\text{with probability}\sigma (\sum _{m=1}^N{A}_{nm}{s}_m(t)),$$ (1)

and 0 otherwise, where the transfer function is piecewise linear; σ(x) = 0 for x ≤ 0, σ(x) = x for 0 < x < 1, and σ(x) = 1 for x ≥ 1. In the presence of net excitatory input, a node may become active, but in the absence of input, or in the presence of net inhibitory input, a node never becomes active.

We consider the dynamics described above on networks drawn from the ensemble of directed random networks, where the probability that each node m connects to each other node n is p. In a network of N nodes, this results in a mean in-degree and out-degree of 〈k〉 = N_p. First, to create the matrix A, each nonzero connection strength A_mn is independently drawn from a distribution of positive numbers. While our analytical results hold for any distribution with mean γ, in our simulations the distribution is uniform on [0, 2γ]. Next, a fraction α of the nodes are designated as inhibitory and each column of A that corresponds to the outgoing connections of an inhibitory node is multiplied by −1. Many previous studies have shown that dynamics of excitable networks are well-characterized by the largest eigenvalue λ of the network adjacency matrix A, with criticality occurring at λ = 1 [7, 8, 12, 19]. In order to achieve a particular eigenvalue λ, we use γ = λ/[〈k〉 (1 − 2α)], an accurate approximation for large networks [20]. We explored a range of 0 ≤ α ≤ 0.3, which includes the fraction α ≈ 0.2, corresponding to the fraction of inhibitory neurons in mammalian cortex [21], and note that as α approaches 0.5, γ diverges. If excitatory and inhibitory weights are drawn from different distributions, larger fractions α are possible which we discuss in context below Eq. (4).

Our study focuses on the aggregate activity of the network, defined as S(t) = N⁻¹∑_n s_n (t), the fraction of nodes that are excited at time t. According to Eq. (1), if the entire network is quiescent, S = 0, it will remain quiescent indefinitely. In the excitatory-only case, the stability of this fixed point has been thoroughly investigated, finding stability for λ ≤ 1 and instability for λ > 1. Many studies have examined this phase transition in activity S, finding that many of the interesting properties occur at the critical point λ = 1 such as peak dynamic range [6–8, 15, 19] and entropy [14], and critical avalanches [12, 14, 15], and so our investigation is restricted to values of λ near 1.

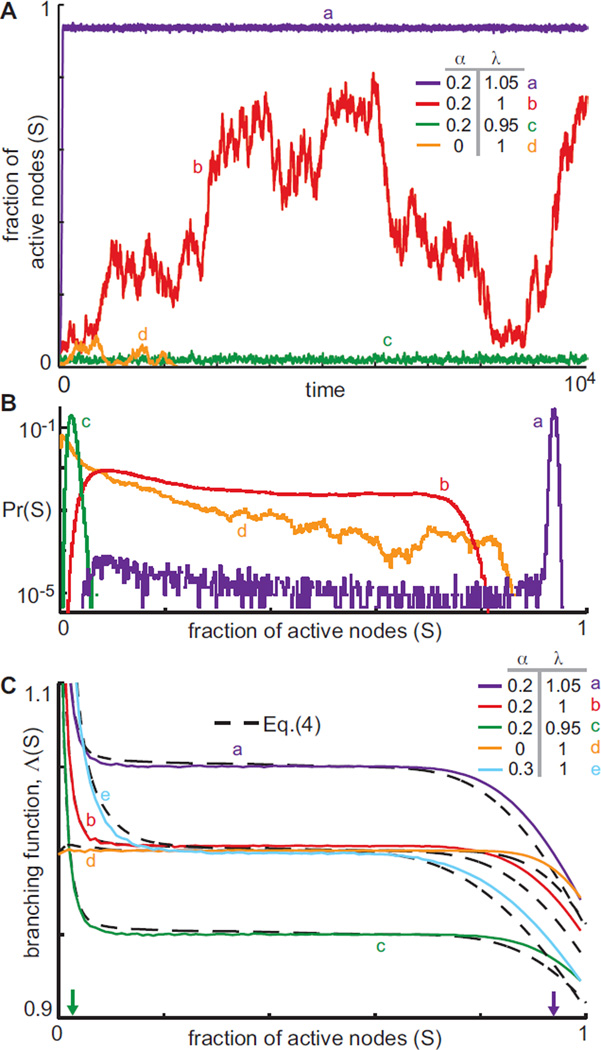
The main result in this Letter is that when inhibitory nodes are included, the state S = 0 is unstable. The representative time series of S(t) in Fig. 1A show that when α > 0, activity no longer ceases. Subcritical network activity fluctuates within a tight band near S = 0, supercritical network activity fluctuates within a tight band near S = 1, and critical network activity fluctuates widely, yet is repelled away from S = 0. Empirical distributions of system states are shown for each of these cases in Fig. 1B, highlighting the broad distribution for λ = 1, and narrow distributions otherwise. Importantly, Fig. 1B also demonstrates that for α > 0, network activity never reaches S = 0, while for α = 0 and λ ≤ 1, activity always eventually dies. A raster plot of self-sustained activity with λ = 1 is provided in Fig. S2 [23].

FIG. 1.

(Color online.) A) Time series of S(t) show typical behavior of this system: α > 0 causes the S = 0 state to become repelling, so that dynamics are self-sustaining. B) Empirical distributions of network activity show that states of critical systems are much more uniformly distributed while sub- and supercritical states fluctuate within tight bands. C) Predictions of branching function Λ [Eq. (4)] agree well with empirical measurements of S(t + 1)/S(t) for various λ and α. Three regimes corresponding to Λ > 1, Λ = 1 and Λ < 1 are visible, explaining dynamics from panels A and B. The Λ > 1 regime causes self-sustained behavior. Sub- and supercritical networks achieve Λ = 1 at a single S (arrows), around which dynamics fluctuates tightly; critical networks achieve Λ ≈ 1 over a wide range in S, allowing broad fluctuations. Λ < 1 for large values of S preventing activity from completely saturating. N = 10⁴, 〈k〉 = 200 for all panels.

In order to analyze and understand this behavior, we introduce the branching function Λ(S), which we define as the expected value of S(t + 1)/S(t) conditioned on the level of activity S(t) at time t,

$$\mathrm{\Lambda }(S)=S^{-1}\mathrm{E}[S(t+1)|S(t)=S].$$ (2)

We note that Λ is similar to the branching ratio in branching processes except that Λ varies with S. For values of S such that Λ (S) > 1, activity will increase on average, and for values of S such that Λ(S) < 1, activity will decrease on average. The expectation in Eq. (2) is taken overmany realizations of the stochastic dynamics. Noting that there is a set of many different possible configurations $\overrightarrow{s}={\{s_n\}}_{n=1}^N$ of active nodes that result in the same active fraction S, we define this set as 𝒮(S). Thus, Λ (S) = S⁻¹E_𝒮(S) [E [S(t + 1)|s⃗ (t) ∈ 𝒮(S)]], where the outer expectation averages over configurations in 𝒮(S) and the inner expectation averages over realizations of the dynamics for a given configuration. Using Eq. (1) we write

$$\mathrm{\Lambda }(S)=S^{-1}{\mathrm{E}}_{𝒮(S)}[\langle \sigma (\sum _m{A}_{nm}{s}_m(t))|\overrightarrow{s}(t)\in 𝒮(S)\rangle ],$$ (3)

where 〈·〉 denotes an average over all nodes n. A is a large network with uniformly random structure, so we approximate the expectation over 𝒮(S) by assuming each s_n (t) is 1 with probability S and 0 otherwise, independent of the other nodes. Since nodes differ in the number and type of inputs, this assumption is valid only for large, homogeneous networks. Thus, each node will have, on average, S〈k〉 (1−α) active excitatory inputs and S〈k〉α active inhibitory inputs. To account for the variability in the number of such inputs for any particular node (due to both the degree distribution of a random network and the stochasticity of the process), letting 𝒫(β) be a Poisson random variable with mean β, we model the number of active excitatory inputs as n_e = 𝒫(S〈k〉(1 − α)) and the number of active inhibitory inputs as n_i = 𝒫(S〈k〉α). We describe the total input to the transfer function using n_e and n_i draws from the link weight distribution. Replacing the argument of σ in Eq. (3), and taking the expectation over the distributions of n_e and n_i, as well as over the link weight distributions, we approximate

$$\mathrm{\Lambda }(S)\approx S^{-1}\mathrm{E}\left[\sigma \right(\sum _{j=1}^{n_e}{w}_j-\sum _{k=1}^{n_i}{w}_k\left)\right],$$ (4)

where w_j and w_k are independent draws from the link weight distribution. Eq (4) may be used for any function 0 ≤ σ ≤ 1, and w_j and w_k may represent draws from different excitatory and inhibitory link weight distributions.

Ceaseless dynamics are now explained by the shape of the branching function, shown in Fig. 1C. Specifically, for small S, Λ(S) > 1, so low activity levels tend to grow, thus preventing the dynamics from ceasing. The role of inhibition in this growth of low activity may be succinctly quantified as

$${\mathrm{\Lambda }}_0=\underset{S\to 0^{+}}{\text{lim}}\mathrm{\Lambda }(S)\approx \lambda \frac{1-\alpha }{1-2\alpha },$$ (5)

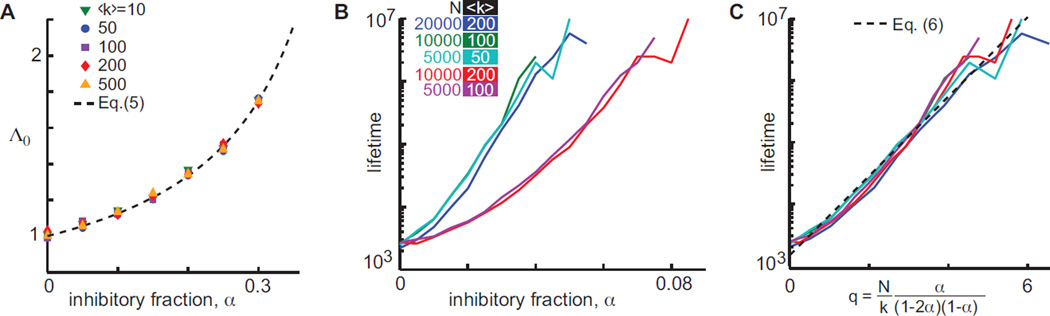
shown in Fig. 2A and derived in [23]. This estimate coincides with the dominant eigenvalue of the network adjacency matrix without inhibitory links, λ⁺, derived in [23]. Pei et al. proposed a different model in which a single inhibitory input is sufficient to suppress all other excitation and found that λ⁺ controlled dynamics for all activity levels in their model [19]. In contrast, we find that for moderate values of S, Λ (S) ≈ λ, and for large values of S, Λ(S) decreases further. For non-critical networks, Λ(S) = 1 at a single value of S, provided α > (1 − λ)/(2 − λ). Since Λ(S) is non-increasing, S(t) will stochastically fluctuate around that single point of intersection, Fig. 1C (arrows). On the other hand, for networks in which λ = 1, Λ(S) ≈ 1 over a wide domain in S, placing the network in a critical state where activity tends to, on average, replicate itself. For large values of S, Λ(S) < 1, imposed by system size.

FIG. 2.

(Color online.) A) Empirical measurements of Λ₀ (symbols) agree well with predictions, Eq. (S15), showing that as α increases, the S = 0 state becomes more repulsive. B) Lifetime of network activity increases with inhibitory fraction α for various N and 〈k〉. Simulations began with 100 active nodes, with lifetime calculated from the fraction of simulations that ceased prior to T = 10⁴ timesteps. (C) Lifetime scales correctly with q, as shown in Eq. (6), indicated by collapse of curves.

We find that when there are no inhibitory nodes (α = 0) network activity resulting from an initial stimulus ceases after a typically short time, in agreement with previous results [6–8]. However, as α is increased, activity lifetime grows rapidly. To understand the dependence of activity lifetime on model parameters, we simulated the critical case λ = 1 with various N, 〈k〉, and α, finding that the expected lifetime of activity after an initial excitation of 100 nodes grows approximately exponentially with increasing α, with growth rate proportional to N/〈k〉 (Fig. 2B). Thus large, sparse networks are likely to generate effectively ceaseless activity without any external source of excitation. The expected lifetime of activity τ, derived analytically (see [23]) by treating S(t) as undergoing a random walk with drift (Λ(S) − 1)S, is approximately given by

$$\tau ~C_1\text{exp}\left\{C_2\frac{N}{\langle k\rangle }\frac{\alpha }{(1-2\alpha )(1-\alpha )}\right\},$$ (6)

where C₁ and C₂ are two constants. Figure 2C shows collapse of numerically estimated τ for different values of N/〈k〉 when plotted against q = Nα/[〈k〉(1 − 2α)(1 − α)], in agreement with Eq. (6).

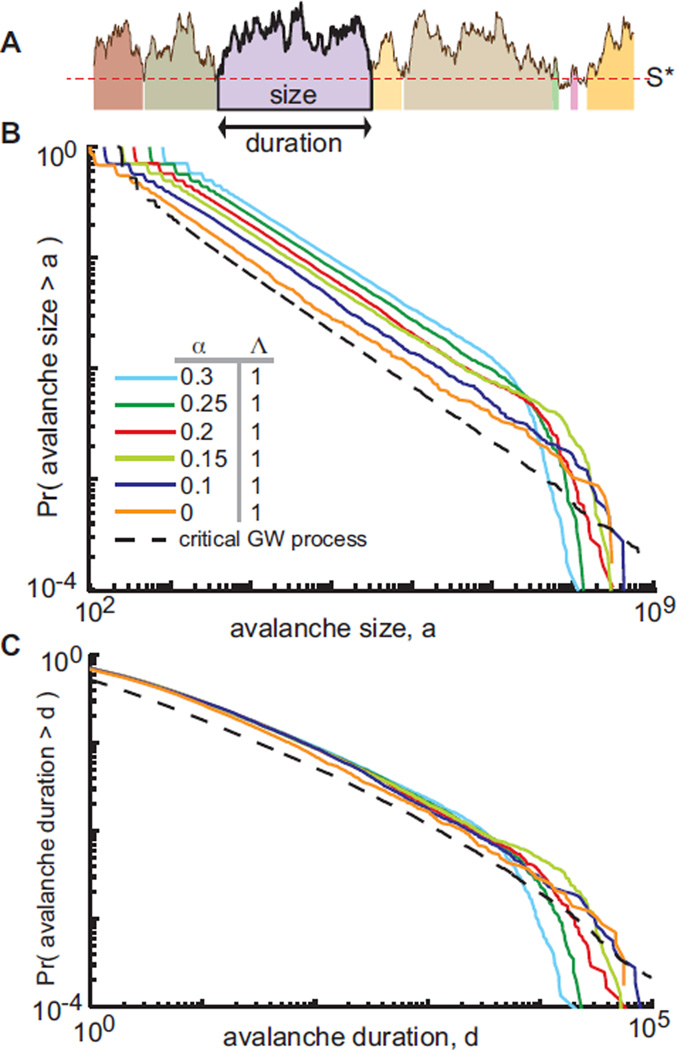
We now turn our attention to avalanches. For systems in which activity eventually ceases, an avalanche can be defined as the cascade of activity resulting from an initial stimulus, and thus in excitatory-only models, avalanches occur with well-defined beginnings and ends. Because our model generates a single ceaseless cascade, we define an avalanche as an excursion of S(t) above a threshold level S^* [22], fragmenting a ceaseless timeseries S(t) into many excursions above S^*, Fig. 3A. Avalanche duration is defined as the number of time steps S(t) remains above S^*, and avalanche size is defined as a = ∑S(t), summing over the duration of the avalanche. This definition corresponds to an intuitive notion of a lower threshold below which instruments fail to accurately resolve a signal. For λ = 1 and all α tested in the model, avalanche sizes are power-law distributed (Fig. 3B) with exponents that are consistent with critical branching processes and models of critical avalanches in networks [12], with size distribution P(a) ~ a^−β with β ≈ 1.5. This is equivalent to a complementary cumulative distribution function P (avalanche size > a) ~ a^−1/2 as displayed in Figure 3B. Exponents from numerical experiments [1] are shown in Table S1.

FIG. 3.

(Color online.) A) We define avalanches as excursions above a threshold S^*, with duration d the length of the excursion and size a the integral under the curve over the duration of the excursion. B) Distributions of avalanche size are power law for all α, P(a) ~ a^−3/2. The dashed line corresponds to sizes from a critical Galton-Watson branching process with S^* = 128. C) Durations are not power-law distributed but have the same distribution as durations from a critical Galton-Watson process. Durations do not show the familiar universal power-law exponent of −2 due to the conversion of ceaseless time series into avalanches (see text and [23]). Data shown: N = 10⁴ nodes over 3 × 10⁶ timesteps, 〈k〉 = 200.

Critical branching processes [25] and critical avalanches in excitatory-only networks [12] should have durations distributed according to a power law with exponent −2. However, as can be seen in Fig. 3C, avalanche durations, while broadly distributed, are not power laws, which we confirmed statistically [1]. Though at first glance this appears to disqualify dynamics as critical, we find that time series from a Galton-Watson critical branching process [25] that are fragmented into avalanches by thresholding show distributions like those shown in Fig. 3C, and not a power law with exponent− 2 [23]. Our predictions in both Figs. 3B and C therefore agree well with the criticality hypothesis (dashed lines). Our choice of S^* for cascade detection was the lowest value of S for which Λ(S) < 1.01, thus accounting for differences in the dynamics of the model for different α and acknowledging that for low activity, dynamics are not expected to be critical since Λ (S) is far from unity. These results are robust to moderate increases in S^*. Based on these observations, we note that to classify or disqualify dynamics as “critical” or “not critical” based on avalanche duration statistics may depend on precisely how avalanches are defined and measured.

The inclusion of inhibition in this simple model produces dynamics that may naturally vary between regimes. The low activity regime, where Λ(S) > 1, prevents activity from ceasing entirely while the high activity regime, where Λ(S) < 1, prevents activity from completely saturating. This may be understood in the following way. For an inhibitory node to affect network dynamics, it must inhibit a node that has also received an excitatory input. When network activity is very low, the probability of receiving a single input is small, and the probability of receiving both an excitatory and an inhibitory input is negligible. Thus, as network activity approaches zero, the effect of inhibition wanes and dynamics are governed by λ⁺. On the other hand, when network activity is very high, some nodes receive input in excess of the minimum necessary input to fire with probability one, and so input is “wasted” by exciting nodes that would become excited anyway, shifting the excitation-inhibition balance toward inhibition, Λ(S) < 1. The moderate activity regime, where Λ(S) ≈ 1, features activity that is on average self-replicating. For super- and subcritical networks, the moderate activity regime is a single point, but for critical networks where λ = 1, this regime is stretched, allowing for long fluctuations that emerge as critical avalanches. Thus, for large, critical networks, we find avalanches embedded in self-sustaining activity.

To conclude, in this Letter we have described and analyzed a system in which the addition of inhibitory nodes leads to ceaseless activity. Our findings may be particularly useful in neuroscience, where self-sustaining critical dynamics has been observed [18]. In experiments, networks of neurons exhibit ceaseless dynamics and optimized function (dynamic range and information capacity) under conditions where power-law avalanches occur [14, 15, 18], but it is not currently possible to directly test the relationship between cortical inhibition and sustained activity in vivo. One alternative may be to compare empirically measured branching functions from in vivo recordings with their in vitro counterparts, where more manipulation of cell populations is possible. This could also be done in model networks of leaky integrate-and-fire neurons, but while criticality [26] and self-sustained activity without avalanches [27] have been found separately, they have not yet been found together. The relation of our mechanism to more traditional “chaotic balanced” networks studied in computational neuroscience [28], and the ability of balanced networks to decorrelate the output of pairs of neurons under external stimulus [29] remain open. Outside neuroscience, our results may find application in other networks operating at criticality, such as gene interaction networks [30], the internet [31], and epidemics in social networks [5, 32].