Health, Education, and the Post-Retirement Evolution of Household Assets

Abstract

We explore the relationship between education and the evolution of wealth after retirement. Asset growth following retirement depends in part on health capital and financial capital accumulated prior to retirement, which in turn are strongly related to educational attainment. These “initial conditions” at retirement can have a lingering effect on subsequent asset evolution. We aim to disentangle the effects of education that operate through health and financial pathways (such as Social Security benefits and the general level of health) prior to retirement from the effects of education that impinge directly on asset evolution after retirement. We also consider the additional effects of education that are not captured through these pathways. We find a substantial effect of education on asset growth through each of the pathways as well as a substantial additional effect not captured by the identified pathways.

A large literature on the relationship between education, earnings, and the accumulation of wealth has developed over many decades. Most of this research has focused on how education affects earnings and the process of wealth accumulation during the working career. In this paper our goal is to understand the relationship between education and the evolution of assets after retirement. The education-wealth relationship after retirement may differ from that before retirement because many of the wealth-building mechanisms that operate at later ages are different from those at younger ages. Earnings are lower, or non-existent, in retirement, and income streams from Social Security and defined benefit (DB) pension plans are largely determined by pre-retirement earnings. These income streams also exhibit less cross-sectional variation than pre-retirement earnings.

We consider first how education affects the level of financial resources and health capital that are acquired prior to retirement. Wealth, health, Social Security benefits, DB pension benefits, and earnings potential are established by retirement and are related to the future evolution of assets. In particular, lifetime levels of real Social Security and DB benefits are fixed at retirement. We begin our analysis by estimating the relationship between these financial resource and health variables at the start of retirement and the subsequent evolution of assets. These variables are strongly related to education. For example, education exhibits a strong correlation with pre-retirement earnings which in turn determine Social Security benefits at retirement. The level of real Social Security benefits will affect asset spend-down decisions after retirement. We consider the accumulation of financial resources and health capital at retirement as one of the pathways through which education can indirectly affect post-retirement asset evolution.

A positive correlation between health and wealth accumulation has been documented by Smith (1999, 2004), Lee and Kim (2008), Michaud and van Soest (2008), and Coile and Milligan (2010). Recent surveys include Grossman (2006) and Cutler and Lleras-Muney (2008). In Poterba, Venti, and Wise (hereafter PVW) (2010) we suggest that the “asset cost of poor health,” the divergence between the path of assets for households in good and in poor health, exceeds the direct costs of medical care.

Many previous studies have tried to understand the mechanism by which education affects health, to measure education-related health inequalities, and to determine whether causality runs from education to health or from health to education. The proposition that education has causal effects on health has been buttressed by a large body of recent work that employs instrumental variable techniques to identify these effects, including Adams (2002), Lleras-Muney (2005), Oreopolous (2006), Silles (2009), Clark and Royer (2010), Fonseca and Zheng (2011), and Kemptner, Jurges and Reinhold (2011). There is also a growing body of work suggesting that health affects education. At young ages, shocks to health can affect educational attainment. Strauss and Thomas (1998) survey the early literature; more recent contributions include Behrman and Rosenzwieg (2004), Case, Fertig and Paxson (2005), and Currie, Stabile, Manivong and Roos (2010). The effect of health on formal education at older ages is less apparent, although poor health may impede informal learning, financial literacy, and cognitive skills.

Education may also influence the types of assets people invest in through its effects on risk-taking, financial literacy, and development of cognitive skills. McArdle, Smith and Willis (2009) explore the link between cognitive skills and the composition of wealth. Haliassos and Bertaut (1995), Bertaut and Starr-McCluer (2001), and Campbell (2006) show that more educated investors are more likely to own stocks. Ehrlich, Hamlen, and Yin (2008) find a correlation between a household’s education level and the portfolio share allocated to risky assets. They also find that more educated households earn higher returns.

We divide our analysis of the links between education and the late-life accumulation of assets into five parts, corresponding to sections of this paper. Section 1 presents the data that we analyze. The measurement of health and the development of the health index that plays a central role in our analysis are explained in section 2. Section 3 introduces descriptive data that motivates the estimation approach. The results are presented in section 4. Section 5 summarizes and concludes.

1. Data

The analysis is based on data from the Health and Retirement Study (HRS). The HRS is a longitudinal survey that resurveys respondents every two years. The current HRS is comprised of five entry cohorts. The original HRS cohort surveyed respondents age 51 to 61 in 1992 and the Asset and Health Dynamics of the Older Old (AHEAD) cohort surveyed respondents age 70 and older in 1993. Subsequent cohorts include the War Babies (WB) cohort, first surveyed in 1998 when respondents were between the ages of 51 and 56, the Children of Depression (CODA) cohort that was first surveyed in 1998 when respondents were between ages 68 and 74, and the Early Baby Boomers (EBB) cohort that includes respondents aged 51 to 56 in 2004. All cohorts were surveyed every second year through 2008, which covers nine waves for the HRS cohort, eight waves for the AHEAD cohort, six waves for the CODA cohort.¹ All three cohorts were well into retirement by 2008. The members of the HRS were age 69 to 79, members of AHEAD age 87 to 97, and members of the CODA were age 78 to 84 in that year.

The HRS is well-suited to the present analysis for several reasons. It provides detailed information on health conditions. The health variables used in our analysis are described in Section 2. The HRS also provides detailed information on assets and on income sources including Social Security benefits and defined benefit pension income. We construct a measure of total non-annuity wealth from respondent reports of holdings of home equity, other real estate, financial assets, business assets, and personal retirement accounts such as IRAs and Keoghs. All asset and income values have been converted to 2008 dollars using the CPI-U.

As explained in PVW (2011) and Venti (2011), the HRS data on 401(k) plan balances is incomplete. In addition, there is measurement error in the HRS wealth data. Venti (2011) shows that these data errors typically arise because either asset ownership is misreported or the value of an asset is misreported. The consequences of these data errors can be quite severe in longitudinal analyses when the wave-to-wave change in wealth is of interest. For this reason we have taken steps to minimize the impact of potential data errors, including “trimming” the data before calculating mean values. These steps are explained in later sections.

2. The Measurement of Health Status

Our analysis depends critically on measuring health status, which we do with a health index that is based on respondent-reported health diagnoses, functional limitations, medical care usage, and other indicators of health contained in the HRS. We use responses to the 27 questions that are shown in Table 1, and obtain the first principal component of these indicators of health status. The first principal component is the weighted average of the health indicators where the weights are chosen to maximize the proportion of the variance of the individual health indicators that can be explained by this weighted average. The variables in the table are ordered by the principal component loadings.

Table 1.

Health index weights (principal component loadings)

Variable	Loading
Difficulty walking several blocks	0.292
Difficulty lift/carry	0.276
Difficulty push/pull	0.272
Difficulty with an ADL	0.265
Difficulty climbing stairs	0.260
Health problems limit work	0.258
Difficulty stoop/kneel/crouch	0.258
Self-reported health fair or poor	0.255
Difficulty getting up from chair	0.248
Difficulty reach/extend arms up	0.210
Health worse in previous period	0.208
Ever experience arthritis	0.184
Difficulty sitting two hours	0.182
Difficulty pick up a dime	0.152
Back problems	0.152
Ever experience heart problems	0.148
Hospital stay	0.147
Home care	0.143
Doctor visit	0.139
Ever experience psychological problems	0.130
Ever experience stroke	0.124
Ever experience high blood pressure	0.120
Ever experience lung disease	0.118
Ever experience diabetes	0.107
Nursing home stay	0.065
BMI at beginning of period	0.064
Ever experience cancer	0.058

We have constructed similar health indices based on the first principal component of the HRS responses in our prior research, summarized in PVW (2010, 2011). In those analyses we constructed a separate index for each wave of the HRS. The index for a particular wave used information from both that wave and all previous waves. Thus, for example, the health index in the fifth wave depended on whether a respondent reported difficulty with an ADL in the first through fifth waves. In our current analysis, the health status index for a particular wave depends only on information provided in that wave. Also, in previous analyses we estimated separate principal component models for each wave. The estimated coefficients were very similar across waves, so in this analysis, we estimate a single principal component equation by pooling all respondents -- men and women -- from all of the waves. The estimated loadings for men and women were very similar when we estimated them separately, so we have combined them for our analysis.

We use data from all five HRS cohorts spanning the years 1992 to 2008 to estimate the principal component index. The estimated coefficients are used to predict a “raw” health score for each respondent. For presentation purposes we convert these raw scores into percentile scores for each respondent at each age. We assign each person in a two-person household the minimum percentile score in the household because household health expenditures are likely to depend on the health of the partner in poorest health. In PVW (2010, 2011) we used the average of the health of the two partners.

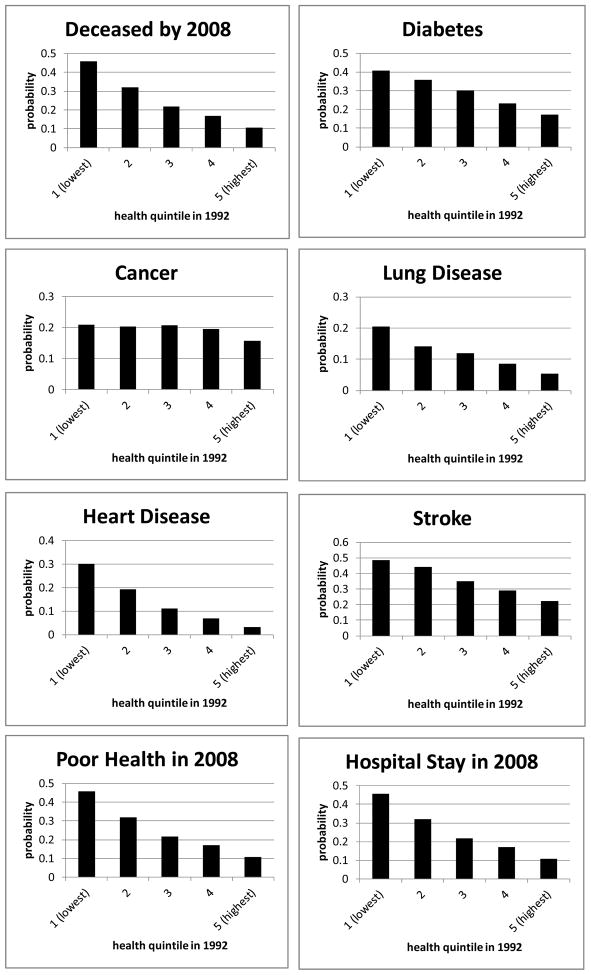
The health status index that we use in the regression analysis that we present later in this paper is a cardinal measure. It has several important properties. 1) It is strongly related to the evolution of assets, as shown in Figure 4 in the next section. 2) It is strongly related to mortality. The upper left panel of Figure 1 shows the relationship between the health index in 1992 and mortality in 2008 for members of the HRS cohort. Among those in the poorest health in 1992, approximately 46 percent are deceased by 2008. Among persons in the best health only about 10 percent are deceased by 2008. 3) It is strongly predictive of future health events such as stroke and the onset of diabetes, as is also shown in the remaining panels of Figure 1. The index value in 1992, however, has little predictive power for future episodes of cancer. 4) It is strongly related to economic outcomes prior to 1992, such as earnings, and to economic outcomes in later years.

Figure 1.

Probability of health events by 2008 by health quintile in 1992, all persons age 51 to 61 in 1992

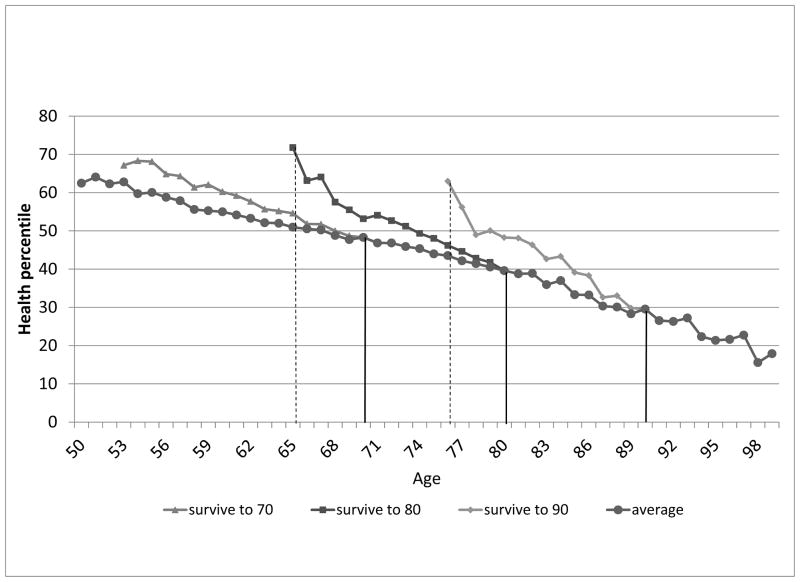
The health status index can be also be used to show the very strong persistence of health. Figure 2 shows the average health percentile of HRS respondents at each age - this is the heavy line with round markers. This average health trajectory reflects the offsetting effects of two forces. First, average health declines as people age. Most survey respondents report more health problems, and more limitations, as they age. Second, however, there is a selection effect (in the opposite direction) in moving from one HRS wave to the next: those in better health are more likely to survive from year to year. This may in part be due to underlying heterogeneity, and in part due to greater investment in life-extension by wealthy households, as described in Ehrlich (2000). This selection effect is illustrated by the other curves in Figure 2. These show the average health in prior ages of those who survived until at least age 70, age 80 and age 90. At each age those who survive longer are in better health. Those who survived until 80 had much better average health at age 65 than those who survived until 70. The health at age 75 of the persons who survive until 90 was, on average, much higher than the health of all those who survived until 80.

Figure 2.

The persistence of health; average health percentile by age and and prior health by survival in 2008

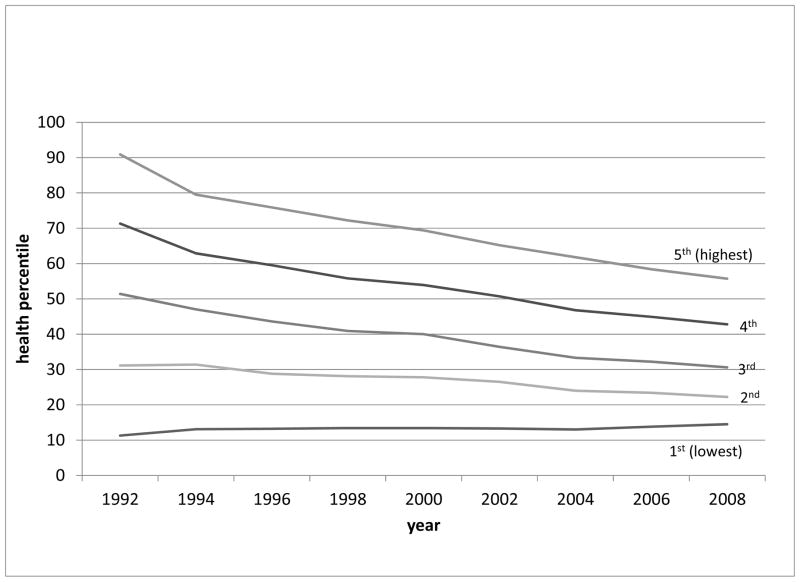
To set the stage for analysis presented below, we show the trajectory of health status by health quintile in 1992 in Figure 3. On average, those who approach retirement in good health experience a decline in health status over time. For those who begin with the worst health and survive in subsequent years their health remains roughly constant over time. Mortality is much greater for persons in the poorest health quintile in 1992, so that those who remain in subsequent years may be a highly select group of the least healthy 1992 respondents.

Figure 3.

Mean health percentile by health quintile in 1992, all persons age 51 to 61 in 1992

3. Descriptive Data

In earlier papers, notably PVW (2010, 2011), we explored the strong relationship between health and the evolution of assets. We focused on wealth at the beginning and end of each two-year interval between survey waves. For example, we followed persons aged 51 to 61 in 1992, and 53 to 63 in 1994, through ages 67 to 77 in 2008. We described the evolution of assets for eight two-year intervals between 1992 and 2008. Throughout our analysis the unit of observation was the person. For married households we included both partners (separately) in the analysis, but we associated household assets with each person. Finally, we classified each person in the survey as belonging to one of four possible family status groups defined by marital status at the beginning and end of the two-year interval. The groups are “continuously two-person” (married at both the beginning and end of the interval, but not necessarily to the same person), “continuously one-person” (single at both the beginning and end of the interval), transiting from a one-person household to a two-person household through marriage, and transiting from a two-person to a one-person household through divorce or death of a spouse. This analysis considers only the first two family status groups, which are the largest ones across all age categories.

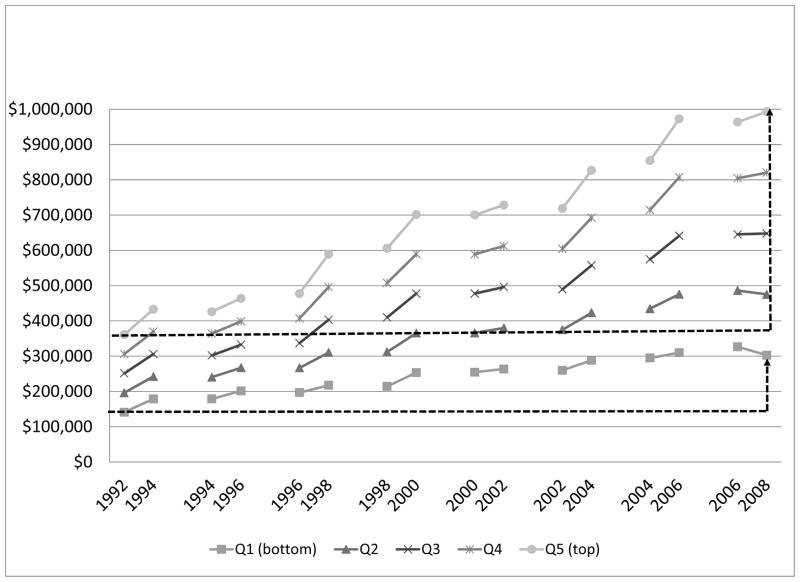
Figure 4 is taken from PVW (2011). It describes the change in assets between waves of the HRS cohort by quintiles of the health index in 1992. The figure pertains to two-person households who were aged 51 to 61 in 1992. The level of assets at the beginning and end of each interval are predicted based on the health index described above. The figure illustrates the relationship between health and wealth. Households in better health have substantially higher levels of wealth than households in poorer health. In addition, however, the evolution of assets is different for healthier and less healthy households: assets grow for healthy households, while they are stable or declining for others. Conditional on surviving until 2008, the increase in assets between 1992 and 2008 was about $632,000 (or 6.5 percent per year) for those in the top health quintile but only $161,000 (or 4.8 percent per year) for those in the bottom health quintile, as indicated by the dashed lines in the figure. Analysis of changing wealth levels over time is potentially confounded by survivor bias, the tendency of households with greater wealth to live longer than those with lower wealth levels. By stratifying households based on initial health status, we try to attenuate this bias.

Figure 4.

Predicted assets, persons in continuing two-person households age 51–61 in 1992, by health quintile

4. Results

As explained in the introduction, our goal is to understand the relationship between education and the evolution of assets after retirement. We distinguish two types of pathways through which education may matter. The first type involves effects of education on variables that are determined by pre-retirement behavior, and that are fixed at retirement and at subsequent ages. Examples of such pathways are effects on wealth and health at retirement, Social Security benefits, and defined benefit pension benefits. We label variables such as the level of Social Security benefits “pathway variables” to denote their role as links between education and circumstances at the time of retirement.

The second type of pathway involves an effect of education on the change in financial and health circumstances after retirement For example, the level of education may be associated with the change in health after retirement, which in turn affects spending needs and opportunities to earn income, or it might be associated with asset allocation patterns that directly affect wealth evolution.

To distinguish between the effects of education on post-retirement asset evolution that operate through these two types of pathways, we begin by estimating the effect of various “pathway variables” on the evolution of assets. Then we estimate the association between education and each of these variables, which allows us to compute the partial effect of education through each of these pathways. After estimating each of these pathway effects, we compute the component of asset evolution that cannot be explained by the effect of education operating through these pathways, and we then relate this “residual” to education as well. We interpret this last effect as an additional general effect of education on post-retirement asset evolution.

The dependent variable in our analysis is the level of household assets in a survey wave, A_w, where w denotes the survey wave. To frame our empirical specification, it is helpful to consider the standard inter-temporal budget constraint for the evolution of assets:

$${\mathrm{A}}_{\mathrm{w}}=(1+\mathrm{r}){\mathrm{A}}_{\mathrm{w}-1}+{\mathrm{a}}_{\mathrm{w}}+{\mathrm{e}}_{\mathrm{w}}-{\mathrm{c}}_{\mathrm{w}}$$ (1)

where r denotes the return on assets between waves w−1 and w, a_w and e_w are annuity income and earned income respectively, and c_w denotes consumption. Education can affect the level of assets by affecting annuity income, earned income, consumption, the rate of return, or the household’s level of assets in the previous year. The consumption effect, in turn, could arise from a number of sources, as education might be linked to an individual’s time preference rate, to spending on medical care or health-promoting activities, or to other components of consumption. We do not have data on consumption outlays, so we cannot estimate the effect of education on the consumption channel directly. We therefore study how a number of variables that may affect both health spending and other consumption spending are related to the level of household assets. It is important to recognize that one of the ways variables such as health status may affect the evolution of assets is through their impact on spending. In the framework of equation (1), out-of-pocket spending on medical care would be included with other consumption goods and would reduce asset accumulation.

We explain below how we estimate r for each person in our sample. Given this r̂, we calculate the value r̂A_w−1, which we think of as the estimated potential investment return at wave w, in dollars, on assets held in wave w−1. This return, which may include unrealized capital gains, along with annuity income from various sources and earnings if the household is still working, can be spent or saved. The evolution of assets is determined by the difference between these income flows and spending, which is likely to be a function of health status as well as a number of other factors.

We estimate the relationship between assets in wave w and a set of “pathway variables” that capture some of the channels through which education can affect asset accumulation: assets in w-1, health status, Social Security income, DB annuity income, earned income, as well as other variables. The specification is given by:

$${\mathrm{A}}_{\mathrm{w}}=\mathrm{k}+{\lambda }^{\ast }{\mathrm{A}}_{\mathrm{w}-1}+{\gamma }^{\ast }\widehat{r}{A}_{w-1}+{\alpha }^{\ast }{\mathrm{H}}_{\mathrm{w}-1}+{\beta }^{\ast }\mathrm{\Delta }{\mathrm{H}}_{\mathrm{w},\mathrm{w}-1}+a^{\ast }{\text{SS}}_{\mathrm{w}}+b^{\ast }{\text{DB}}_{\mathrm{w}}+c^{\ast }{\text{Earn}}_{\mathrm{w}}+m^{\ast }{\mathrm{M}}_{\mathrm{w}}+{\epsilon }_{\mathrm{w}}$$ (2)

The coefficient γ can be thought of as the marginal rate of saving out of the wave-to-wave investment return. H_w−1 and ΔH_{w, w−1} denote the level of health in the previous wave and the change in health since the last wave respectively. Higher levels of H and ΔH are expected to reduce the need to rely on assets to finance health care needs and thus are likely to be associated with a positive change in assets. Higher levels of Social Security benefits, DB annuity income, and earned income are also expected to be positively associated with asset change. The assumption is that persons with greater income can cover the cost of health-related and other expenses with less need to draw down their accumulated assets. M is an indicator of expected lifespan, which we discuss below, and ε_w is an error term.

We can calculate the effect of education through each pathway variable as the product of the estimated coefficient and the change in the pathway variable associated with education. For example, the effect of education on assets through Social Security benefits is the product of the effect of Social Security benefits on assets (dA_w/dSS, or the estimated coefficient a) and a measure of how Social Security benefits vary by level of education. We describe the latter part of this calculation in more detail below. The total effect of education (E) on assets is the sum of the effects through each of the pathway variables:

$$\begin{array}{l}\frac{{dA}_w}{dE}=\frac{{dA}_w}{{dA}_{w-1}}\frac{{dA}_{w-1}}{dE}+\frac{{dA}_w}{d(\widehat{r}{A}_{w-1})}\frac{d(\widehat{r}{A}_{w-1})}{dE}\\ +\frac{{dA}_w}{{dH}_{w-1}}\frac{{dH}_{w-1}}{dE}+\frac{{dA}_w}{d\mathrm{\Delta }H}\frac{d\mathrm{\Delta }H}{dE}\\ +\frac{{dA}_w}{\mathit{dSS}}\frac{\mathit{dSS}}{dE}+\frac{{dA}_w}{\mathit{dDB}}\frac{\mathit{dDB}}{dE}+\frac{{dA}_w}{\mathit{dEarn}}\frac{\mathit{dEarn}}{dE}\end{array}$$ (3)

Education may affect asset accumulation in retirement through each of the pathway variables in equation (2). We want to distinguish the effect of education through circumstances that are given at the time of retirement from the further effect of education through circumstances that change after retirement. For example, Social Security benefits and DB pension benefits are determined at retirement. Both are related to education because education affects earnings over working years, and possibly the age at which the individual claims benefits. These factors in turn determine Social Security and DB pension benefits. But the level of education has no further effect on the level of Social Security or DB benefits once a person has retired.

Still other effects of education operate through financial or health capital that are given at retirement but continue to evolve after retirement. Consider the role of health capital. Persons enter retirement with a given level of health, but health also evolves after retirement. The coefficient α in (2) captures the effect of the post-retirement level of health, H_w−1 in wave w − 1, on the level of assets in wave w. We can, in principle, decompose H_w−1 into two components: the level of health at retirement and the sum of changes to health after retirement. Education may influence the level of assets in wave w through either component. Our estimates allow for both the stock of health, and the change in health, to affect asset accumulation. Similarly, the post-retirement evolution of the level of assets may be determined in large part by the level of assets at retirement—which is related to education—as well as by the further effect of education on the change in the level of assets after retirement.

We present estimates of (2) in section 4–3 below. We find, however that the effect of education is not fully captured by the various “pathway effects” that we have described above. We demonstrate this by regressing the residuals from the specification in equation (2) on levels of education. The estimates reveal that education has substantial further effect on the evolution of assets, suggesting that there may be additional pathways that we have not identified.

To recognize the additional effect of education, the effect that is not captured by our pathways, we also tried adding the level of education directly to equation (2). We find that the estimated coefficient on education is substantial and statistically significant, and we also discover that including education in (2) reduces the absolute value of the estimated coefficients on most of the “pathway variables.” This finding raises the question of whether we should estimate the pathway effects using the coefficient estimates from (2), which excludes education, or the expanded specification that includes education. If educational attainment has a direct effect on assets that is not captured by any of our pathways, then the coefficient estimates on the included pathway variables will, through a standard left-out-variable-error analysis, be biased because they will reflect some of the direct effect of education. If, however, we have omitted some pathways that may be largely determined by the date of retirement, or if there is measurement error in some of the pathway variables, then these pre-retirement effects will in part be captured by the education variable in the expanded equation (2). This could lead to biased estimates of the post-retirement role of education. We do not believe that our specification has captured all possible pathways linking education to post-retirement asset holdings, so we therefore follow the first strategy. We compare the two strategies below.

We present the details of our analysis in five stages. First, we consider the relationship between education and the level of health at retirement and the relationship between education and the post-retirement changes in health. We later use these findings in conjunction with the estimated coefficients on H and ΔH in equation (2) to assess the effect of education through the health pathway. Second, we consider the relationship between education and the types of assets held in household portfolios, the implications for the potential differences in expected returns across education levels, and the magnitude of the implied potential differences in returns. These estimates provide the values for r̂ in r̂A_w−1 in equation (2). Third we present estimates of the effect of health and income on asset evolution—equation (2). Fourth, we use these estimated coefficients to estimate the effect of education on assets through each of the pathways. Finally, we explore the further effect of education not captured by these pathways by estimating the relationship between the education variables and the residuals from equation (2). To simplify the presentation, we show detailed results only for persons in two-person households.

4.1 Education and the Trajectory of Health

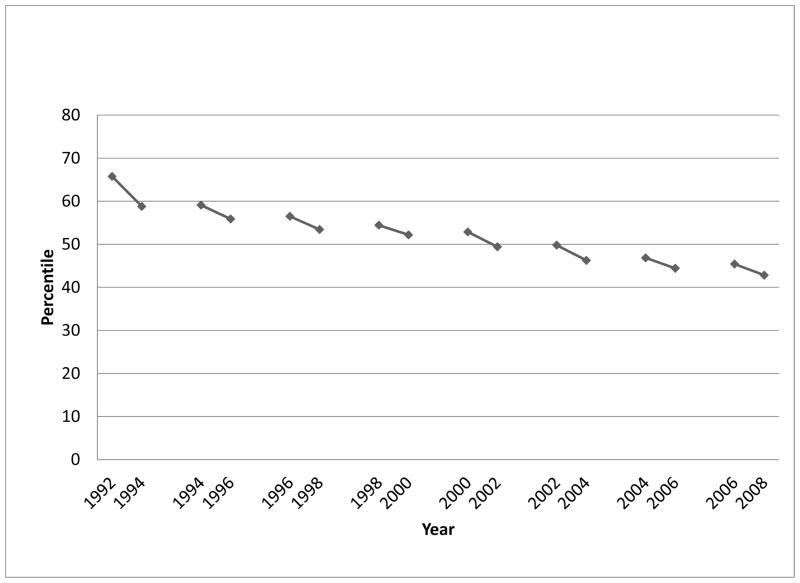
We begin our analysis by describing the relationship between educational attainment and the trajectory of health status at older ages. This relationship is a key input to our assessment of how education affects late-life asset evolution through the health pathway. Consider first the wave-to-wave change in health of the HRS cohort respondents, shown in Figure 5. The figure resembles Figure 4 above, but pertains to health rather than assets. For example, for persons in the sample in 1992 and 1994, the average health percentile declines from 65.8 to 58.8 between these two years. Health also declines within each of the subsequent intervals. The figure also reveals another important feature of the data. It is important to distinguish between the wave-to-wave changes in health shown by the line segments in the figure and the effect of differential mortality indicated by the “gaps” between segments. For example, persons present in both the 1992 and 1994 waves had mean health of 58.8 in 1994, but persons who were also present in both the 1994 and 1996 waves had mean health of 59.1 in 1994. The difference between 58.8 and 59.1 is the mortality selection effect—persons who survived through 1996 had better health in 1994 than persons who were alive in 1994 but did not survive through the next wave. The mortality selection effect between the end of one segment and the beginning of the next segment is evident for each of the adjacent segments.

Figure 5.

Health percentile by year, all persons age 51–61 in 1992

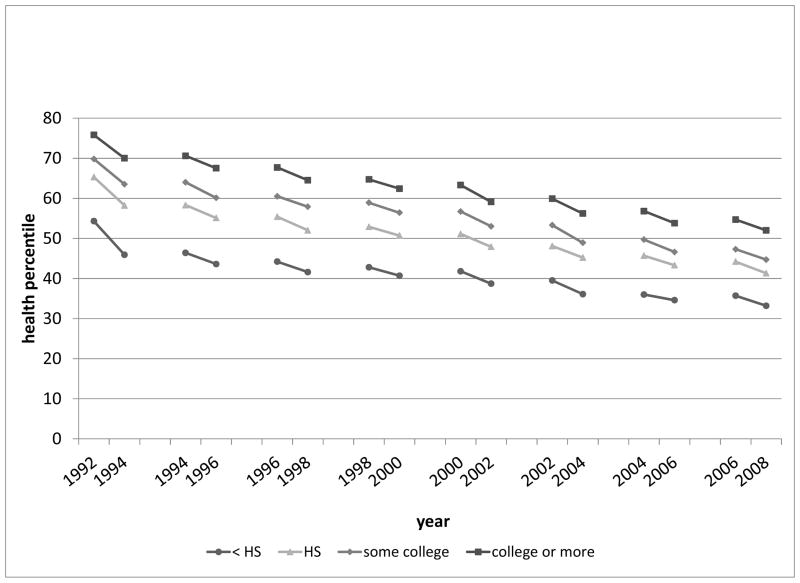
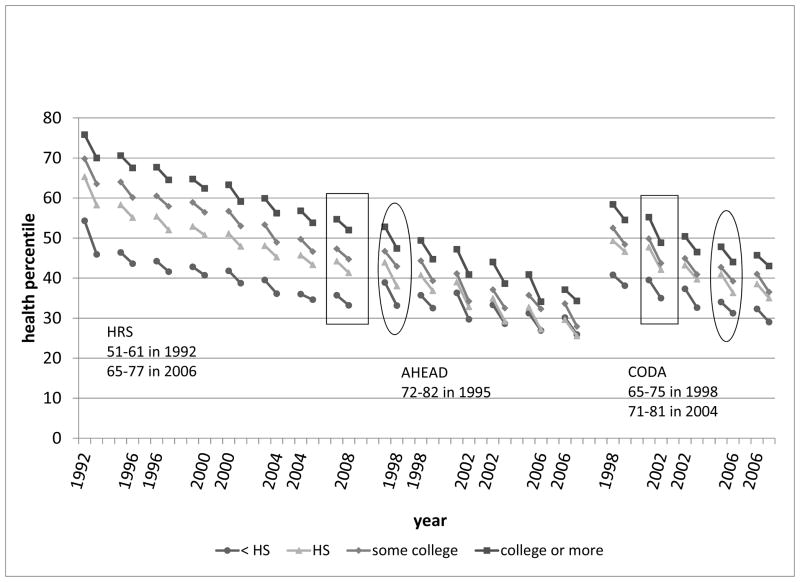
Our interest is in how these health trajectories differ by level of education. We show the data for three HRS cohorts. Figure 6 shows the within-interval changes in health by education group for the original HRS cohort age 51 to 61 in 1992. There are two important features of the data. First, when first observed in 1992, the differences in health by education group are very large. The mean health percentile in 1992 is 75.8 for persons with a college degree, 69.8 for those with some college, 65.3 for persons with a high school degree, and 54.3 for persons with less than a high school degree. The difference between the highest and lowest levels of education is 21.5 percentile points. The difference in 2008 is 18.8. The key conclusion is that the level of health in subsequent years is largely determined by the level of health when first observed in 1992. Over time, health declines by approximately the same amount (in percentiles) for persons at all levels of education. This suggests that there is little effect of education on the change in health after 1992, the first year members of this cohort were observed.

Figure 6.

Mean health trajectories by level of education for persons age 51 to 61 in 1992 (HRS)

More formal estimates of the wave-to-wave changes in health are presented below; they show that post-retirement wave-to-wave changes in health are essentially unrelated to education. But the levels of health are strongly related to the level of education when a person is first observed, in particular at the age of retirement as we see more clearly in the figures for other cohorts.

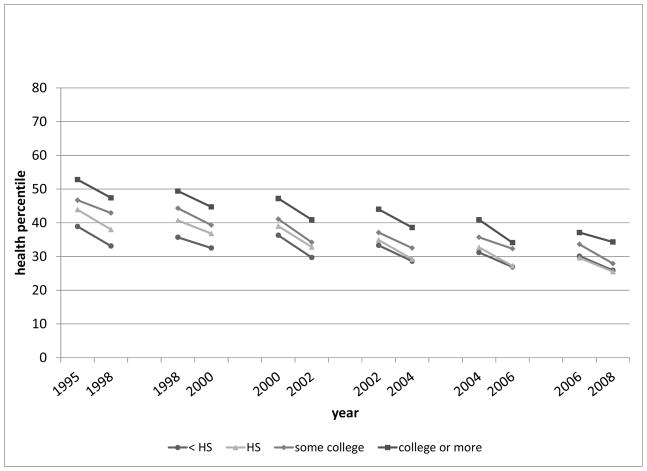
Comparable results for the AHEAD cohort are shown in Figure 7. This figure uses persons in the AHEAD cohort who were age 72 to 82 in 1995. Data for the AHEAD cohort were first collected in 1993 but, as noted above, there is insufficient data to construct a health index for 1993 and thus the data shown in the figure begin in 1995. Again there are large differences in health by education when respondents are first observed in 1995. The mean health percentile ranges from 52.8 for the college educated to a low of 38.9 for those with less than a high school degree. Again, the health trajectory in subsequent years shows only a limited relationship to education. The range narrows somewhat by 2008 when this cohort is age 83 to 93; at this age the range in mean health is from 34.3 for the most educated to 25.9 for the least educated.

Figure 7.

Mean health trajectories by level of education for persons age 72 to 82 in 1995 (AHEAD)

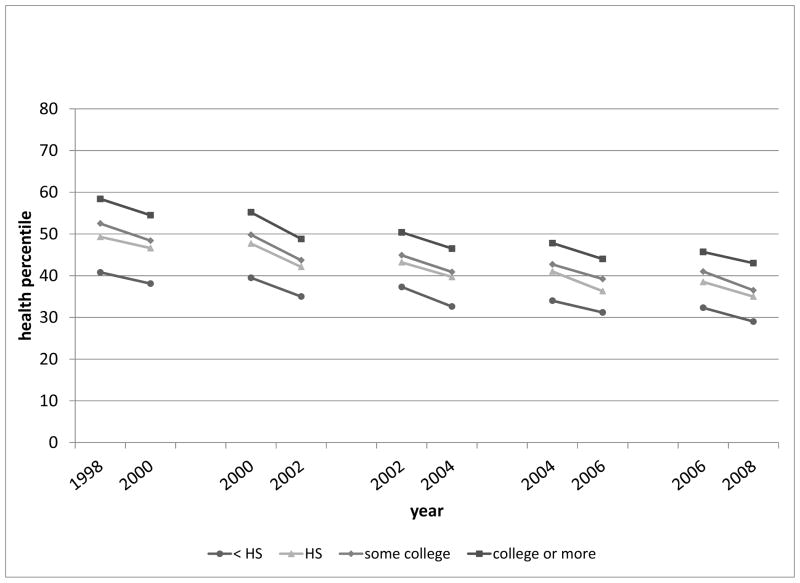
Figure 8 shows data for persons who were 65 to 75 in 1998. This group is primarily composed of persons from the CODA cohort (the youngest member of this cohort was age 68 in 1998), but also includes some older members of the HRS cohort. Again there are large differences in health in 1998—the mean health percentile is 58.4 for persons with college or more but only 40.8 for those with less than a high school degree—but the subsequent within-interval trajectories of health seem to differ only slightly by education group.

Figure 8.

Mean health trajectories by level of education for persons age 65 to 75 in 1998 (CODA)

Figure 9 shows the trajectories for all three cohorts on the same figure. The figure reveals two features of the data. First, for the HRS and CODA cohorts the spread in health by education does not change much with age (as shown above), but the spread in health by education level tends to decline with age for the older AHEAD households. Second, the cohort effects in health appear to be small. For example, health at each level of education in the AHEAD cohort that attained ages 72 to 82 in 1995 seems very similar to the pattern for persons in the CODA cohort that attained ages 71 to 81 nine years later in 2004 (circled in the figure). Similarly, the pattern by education for persons in the HRS cohort that attained ages 67 to 79 in 2006 is very similar to the pattern for persons in the CODA-HRS cohort that attained ages 66 to 77 eight years earlier in 2000 (shown by the rectangle in the figure).

Figure 9.

Mean health trajectories by level of education for all cohort (HRS, AHEAD, and CODA)

The figures above show large differences in health between high and low education groups in initial assets, but the slopes for the education groups are similar in subsequent years. Table 2 shows the mean wave-to-wave change in health by education group and by lagged asset quintile (the quintile of assets in the beginning year of each wave-to-wave change) for married persons. The breakdown by asset quintile will be useful for calculations later in this section. Separate estimates are presented for the three cohorts shown in Figure 9 as well as for all persons who were age 65 or older in 1998². As the figures suggested, there is no strong pattern associated with education. It does appear that the wave-to-wave changes are slightly more negative for persons in the highest lagged asset quintile, probably because persons in this quintile have the highest initial health. All but one estimate in Table 2 is statistically different from zero; the lone exception is for persons with less than a high school degree in the fifth asset quintile in the CODA cohort. We cannot reject the null hypothesis that the estimated effect for the fifth quintile equals that for the first quintile in any of the sixteen cases comparisons that can be made.

Table 2.

Estimated change in health between waves, by HRS cohort and by education group, two-person households, all years combined.

	Lagged Asset Quintile
	1 (low)	2	3	4	5 (high)
Age 51 to 61 in 1992 (HRS)
< HS	−3.79	−3.55	−3.96	−2.91	−3.69
HS	−3.61	−3.63	−3.80	−3.88	−2.92
Some college	−3.66	−4.22	−3.70	−3.83	−3.83
College or more	−4.28	−3.38	−3.89	−3.75	−3.38
Age 72–82 in 1995 (AHEAD)
< HS	−5.07	−6.00	−5.20	−4.10	−5.98
HS	−5.51	−4.87	−4.66	−5.04	−6.37
Some college	−2.49	−7.28	−5.37	−3.65	−4.02
College or more	−3.00	−4.02	−8.52	−4.37	−6.07
Age 65 to 75 in 1998 (CODA)
< HS	−3.52	−4.45	−4.52	−2.34	−2.79
HS	−3.33	−4.19	−3.23	−4.28	−4.22
Some college	−4.66	−3.93	−4.86	−4.01	−4.64
College or more	−3.31	−3.77	−6.29	−3.35	−4.47
Age 65+ in 1998
< HS	−3.57	−4.76	−4.81	−2.64	−3.50
HS	−3.80	−3.76	−3.63	−3.49	−4.60
Some college	−4.41	−4.02	−4.78	−3.18	−3.73
College or more	−2.95	−4.05	−4.12	−2.89	−3.78

4.2 Education and the Return on Assets

We now consider the relationship between education and portfolio allocation choices. We also explore how rates of return on total assets differ by education and we calculate how the expected dollar return on assets differs by education. These relationships highlight a second pathway through which education might affect the evolution of assets: households with different levels of education may make different financial decisions. Our analysis treats these differences as an effect of educational differences, although we recognize that both education choices and portfolio choices could be the result of underlying third factors.

Households with different education levels may make different portfolio choices and they may also earn different rates of return on the assets they invest in. While most analyses of household portfolio behavior assume that returns by asset classes are the same for all investors, we consider the possibility that education is related to those returns, either because more educated investors choose investments with, on average, a lower expense ratio, or because they choose different investments within an asset class. We first focus on how holdings of stocks, bonds, housing and other assets differ by education, and then explore the implications of these differences for expected returns on household wealth. This is another instance in which it is difficult to determine how much of the observed difference in post-retirement returns by education level is due to the level and allocation of assets at retirement and how much might be due to the change in allocation after retirement.

The return on a portfolio is a weighted average of the returns on component assets. If total assets $A={\displaystyle \sum _{a=1}^N}{A}_a$ where there are N assets, each denoted by a, then the average portfolio return is given by $r_A={\displaystyle \sum _{a=1}^N}\frac{A_a}{A}{r}_a$ where the A_a / A are the dollar weighted portfolio shares and the return on asset a is indicated by r_a. For most assets both the portfolio share and the return are related to a household’s level of education.

The portfolio shares for two-person households are shown in Table 3 for four education groups. The estimates are for all persons over the age of 65 in 2008. In results not reported here, we disaggregated the population into those with and without earned income; the results were similar for the two groups. The first four columns show mean assets in each asset category and the next four columns show portfolio shares. The top panel of the table shows shares for eight broad asset categories. The first four columns show large differences in asset holdings by education group. Total assets range from $344,000 for the lowest education group to over 1,490,000 for persons in two-person households with a college degree or more. The medians (not reported in the table) range from $132,000 to $763,000. There are also striking differences in portfolio allocations by education. Married persons with a college degree or more hold 20 percent of their wealth in personal retirement accounts (IRAs, Keoghs and 401(k)s) and another 34 percent in financial assets outside these accounts. Over half of their portfolio is in these financial instruments. Married persons with less than a high school degree have a combined 28 percent of assets in these same financial instruments. On the other hand, married persons with more education have a much smaller proportion of their portfolios invested in their primary residence, 26.5 percent for persons with a college degree or more and 35.4 percent for persons with a high school degree or less.³

Table 3.

Mean assets and portfolio shares by level of education, two-person households age 65 and over in 2008.

	Mean assets				Percent of total assets
Asset	Less than HS	HS	Some college	College or more	Less than HS	HS	Some college	College or more
Eight asset categories
IRAs and Keoghs	25,161	79,519	97,733	213,028	7.32	14.83	12.59	14.29
401(k)s	5,275	15,756	23,145	80,682	1.53	2.94	2.98	5.41
Other financial assets	66,582	134,821	246,583	512,063	19.36	25.14	31.77	34.35
Primary home equity	121,804	176,057	224,855	395,117	35.41	32.83	28.97	26.51
Second home equity	13,538	21,475	36,215	82,713	3.94	4.00	4.67	5.55
Other real estate	82,132	45,274	79,482	118,787	23.88	8.44	10.24	7.97
Business assets	31,853	65,757	71,733	92,036	9.26	12.26	9.24	6.17
Debt	−2,387	−2,445	−3,477	−3,915	−0.69	−0.46	−0.45	−0.26
Total	343,958	536,214	776,269	1,490,511	100.00	100.00	100.00	100.00
Total financial assets	97,018	230,096	367,461	805,773	28.21	42.91	47.34	54.06
Other financial assets--detail
Stocks	21,067	56,761	112,533	281,886	31.6%	42.1%	45.6%	55.0%
Checking	17,777	34,484	38,374	73,003	26.7%	25.6%	15.6%	14.3%
CDs	14,017	29,033	39,288	39,653	21.1%	21.5%	15.9%	7.7%
Bonds	3,755	5,214	12,260	52,032	5.6%	3.9%	5.0%	10.2%
Other	9,967	9,328	44,127	65,489	15.0%	6.9%	17.9%	12.8%
Total	66,583	134,820	246,582	512,063	100.0%	100.0%	100.0%	100.0%

To some extent the variation in portfolio shares reflects the wealth elasticity of demand for assets held in various ways - and for different types of assets. Households with less education are likely to accumulate less lifetime wealth, and households tend to invest first in owner-occupied housing, then in retirement accounts such as 401(k)s, and finally in other financial assets.

The bottom panel of Table 3 shows more detail on the allocation of “other financial assets” for married persons. Married persons with a college degree or more hold a much greater proportion in “risky” (but higher expected return) equities than those with less than a high school degree—55.0 percent versus 31.6 percent—and much less in low-return checking accounts and CDs—22.0 percent versus 47.8 percent.⁴ These results are consistent with Ehrlich, Hamlen, and Yin’s (2008) findings on the holdings of risky assets by different educational groups. The data in the bottom panel of Table 3 only pertain to financial assets held outside of personal retirement accounts. It is likely that more highly educated persons also hold higher proportions of equities within these accounts. Unfortunately detailed data are not available to make these calculations.⁵

The data in Table 3 show that the principal asset of many households is home equity, although more highly educated persons hold proportionately less home equity than persons with less education. We next investigate the wave to wave evolution of home equity by education level. We restrict our analysis to homeowners who do not move between waves. This excludes approximately 19 percent of the sample. Given this restriction, changes in home equity from one wave to the next reflect the change in the value of the home as well as the change in the amount of outstanding mortgage debt. Thus a household could display a large increase in home equity between waves if there was a sharp rise in the value of its home, with little or no change in mortgage indebtedness, or if it repaid mortgage debt, even if house prices remained the same. Educational attainment may be correlated with the rate at which house value changes, if households with different educational backgrounds on average live in different communities that face different economic conditions, or if they buy different types of homes, or borrow against their homes at different rates, or repay their mortgage debts at different rates in late life. One issue that we cannot address, given our data span of less than two decades, is whether differences in housing wealth accumulation patterns across education groups is a general finding, or just a pattern that emerges in the particular time period that we observe.

We report wave-to-wave changes in home equity for all persons who do not move between waves in Table 4 for two education levels (less than high school and college or more) and in Appendix Table 1 for all four education levels. These results suggest that growth in home equity is very strongly related to education. In some years, particularly during periods of rising house prices, the differences between education groups are substantial.

Table 4.

Wave to wave change in home equity of HRS households that do not move between the waves, means and medians (2008 dollars).

	Means			Medians
Interval and education	Beginning of interval	End of interval	Percent change	Beginning of interval	End of interval	Percent change
1996–1998
< HS	72,515	74,650	2.94	54,248	53,562	−1.26
College	179,345	195,348	8.92	139,097	147,295	5.89
1998–2000
< HS	72,119	69,665	−3.40	50,884	50,648	−0.46
College	175,715	202,564	15.28	133,905	145,613	8.74
2000–2002
< HS	72,024	82,562	14.63	50,648	54,488	7.58
College	204,723	249,020	21.64	145,613	181,627	24.73
2002–2004
< HS	80,767	95,099	17.74	54,488	51,958	−4.64
College	239,495	305,609	27.61	173,151	190,512	10.03
2004–2006
< HS	87,147	100,059	14.82	46,185	48,288	4.55
College	284,397	361,041	26.95	174,347	214,615	23.10
2006–2008
< HS	100,509	89,690	−10.76	48,181	49,000	1.70
College	361,239	356,820	−1.22	203,884	186,500	−8.53

Appendix Table 1.

Wave to wave change in home equity of HRS households that do not move between the waves, means and medians (2008 dollars).

	Means			Medians
Interval and education	Beginning of interval	End of interval	Percent change	Beginning of interval	End of interval	Percent change
1996–1998
< HS	72,515	74,650	2.94	54,248	53,562	−1.26
HS	110,340	119,902	8.67	90,413	93,733	3.67
Some college	136,136	151,517	11.30	107,105	107,124	0.02
College	179,345	195,348	8.92	139,097	147,295	5.89
1998–2000
< HS	72,119	69,665	−3.40	50,884	50,648	−0.46
HS	111,747	117,923	5.53	85,699	88,634	3.42
Some college	133,728	143,871	7.58	93,733	101,296	8.07
College	175,715	202,564	15.28	133,905	145,613	8.74
2000–2002
< HS	72,024	82,562	14.63	50,648	54,488	7.58
HS	120,568	126,734	5.11	88,634	96,868	9.29
Some college	147,192	153,960	4.60	101,296	117,452	15.95
College	204,723	249,020	21.64	145,613	181,627	24.73
2002–2004
< HS	80,767	95,099	17.74	54,488	51,958	−4.64
HS	124,006	137,377	10.78	90,814	95,833	5.53
Some college	149,677	181,876	21.51	108,976	115,462	5.95
College	239,495	305,609	27.61	173,151	190,512	10.03
2004–2006
< HS	87,147	100,059	14.82	46,185	48,288	4.55
HS	131,522	152,837	16.21	91,215	99,796	9.41
Some college	179,168	210,058	17.24	109,689	126,623	15.44
College	284,397	361,041	26.95	174,347	214,615	23.10
2006–2008
< HS	100,509	89,690	−10.76	48,181	49,000	1.70
HS	153,119	140,943	−7.95	101,942	97,000	−4.85
Some college	211,703	197,207	−6.85	128,769	120,000	−6.81
College	361,239	356,820	−1.22	203,884	186,500	−8.53

The period that we examine includes a historic house price run-up, and it may not provide a clear guide to the experience of future generations of older households. The data suggest however that there may be important differences in the way this house price boom—and the associated bust that began at the end of our sample—affected households at different points in the education and wealth distribution.

Appendix Table 2 decomposes the change in mean home equity into the change in home prices and the change in housing debt. The table shows that for four of the five two-year intervals prior to 2006, the highest education group repaid mortgage debt more quickly, or expanded mortgage debt more slowly, than households in the lowest education group. The most recent period, 2006–2008, which is characterized by more disparities in the housing market than earlier periods, shows a sharp decline in mortgage debt for the lowest education group. This may reflect an involuntary loss of mortgage debt, through foreclosures, or it may reflect a tightening of lending to this group.

Appendix Table 2.

Wave to wave percent change in home equity, house value, and mortgage debt (including home equity loans) of HRS households that do not move between the waves.

calculated from means
Interval and education	Home Equity	House value	House debt
1996–1998
< HS	2.94	3.38	6.65
HS	8.67	7.40	0.18
Some college	11.30	8.95	−0.95
College	8.92	5.61	−5.64
1998–2000
< HS	−3.40	−2.62	1.86
HS	5.53	4.14	−2.35
Some college	7.58	3.91	−7.65
College	15.28	9.15	−7.14
2000–2002
< HS	14.63	11.76	−3.62
HS	5.11	3.50	−4.25
Some college	4.60	3.06	−2.66
College	21.64	15.18	−5.57
2002–2004
< HS	17.74	15.57	3.05
HS	10.78	9.33	2.09
Some college	21.51	18.62	8.28
College	27.61	22.87	5.04
2004–2006
< HS	14.82	14.34	12.17
HS	16.21	12.73	−1.20
Some college	17.24	14.40	5.80
College	26.95	20.91	1.99
2006–2008
< HS	−10.76	−12.83	−22.07
HS	−7.95	−7.87	−7.48
Some college	−6.85	−7.48	−9.47
College	−1.22	−2.30	−6.46

One explanation for the findings in Table 4 is that more educated households earn higher rates of pre-tax appreciation on their homes than do their less-educated counterparts. There has been some tendency in the last decade for cities with more educated workforces, “science and technology based cities,” to fare better economically than cities that depended on traditional blue-collar industries. The disparities in housing returns may reflect in part differences in where households with different educational levels live.

The disparity of rates of return might also apply to other asset categories, in particular to financial assets. If more educated households have larger account balances on average, they may have better access to lower-cost mutual funds or to other investment vehicles with lower management costs, than less educated and (on average) less wealthy households. We do not have the data we need to assess this issue for non-housing assets, because wave-to-wave changes in these assets reflect buying and selling as well as pure investment returns. Unlike housing, for which we can eliminate the effect of buying and selling by restricting estimation to non-movers, the HRS does not include any information that would let us identify “non-traders” in financial assets.

While it is very difficult for us to determine whether households in higher education categories earn higher (or lower) returns on various types of financial assets than those in lower education tranches, we can use differences in the average portfolio structure of households in different education groups, along with data on the average returns to different asset classes, to estimate potential differences in the expected portfolio returns for these groups. We can also do such calculations using the actual returns on various asset categories in particular years. While this is likely to be a noisy measure of the actual return for any household, it provides some guidance on the return that the household may have earned. It is important to note that the variation across households in the returns earned on some asset categories, such as corporate stock, is likely to be much greater than the variation in other asset categories, such as government bonds.

In the analysis below we assume that, with the exception of housing, all education groups earn the same return on each asset. We use annual returns obtained from Ibbotson (2010) as our return measures. We use the return on large cap stocks to approximate the return on stocks and holdings of business assets (assumed to be similar in risk to stocks). For bond holdings we use the annual return on intermediate government bonds. For CDs and similar accounts and for debt we use the three-month Treasury bill rate. For checking and similar accounts we assume a zero rate of return. Other real estate is assumed to earn the same return as housing. We also assume that investments in personal retirement accounts are split evenly between stocks and bonds.

We can combine estimates of portfolio shares like those shown in Table 3 (but estimated separately for each person and for each year) with estimates of the mean return on housing by level of education shown in Table 4 and the external return data for other asset components to estimate the total portfolio return for each person. Table 5 shows the weighted average portfolio returns, the product of the percent in each asset component and the return on each asset component, by education group for married persons. On average the return for married households with a college degree or more is about 2.7 times as large as the return for those with less than a high school degree. However, the patterns are quite different in the individual years. In the downturn of 2000–2002 portfolio returns for the less educated exceeded returns for the highly educated who were much more heavily invested in risky assets, particularly stocks.

Table 5.

Mean two-year percentage return on total assets by interval and by education, for two-person households age 65 and over

	< HS	HS	Some college	College or more
1998–2000	4.3%	15.3%	18.6%	24.7%
2000–2002	8.6%	1.0%	0.4%	7.1%
2002–2004	13.0%	7.6%	13.1%	14.9%
2004–2006	13.2%	13.3%	13.5%	17.9%
2006–2008	−6.0%	0.8%	1.7%	7.3%
Average	6.6%	7.6%	9.5%	14.4%

Using the rate of return estimates, we compute the total dollar return from asset holding—essentially the percentage return between waves w−1 and w, times the stock of assets reported in wave w−1—for each household. More specifically, for each household and for each asset we multiply the dollar value of holdings in the asset in wave w−1 by the measured rate of return on that asset between w−1 and w. This yields the potential income from holding that particular asset. Then, for each household, we sum over all asset classes to obtain total dollar return from all asset holdings. Note that the use of actual dollar value holdings of each asset preserves the variation by education level in portfolio shares shown in Table 3. For example, among persons with the same total assets, those with higher levels of education will have larger dollar investments in stocks than persons with less education. The calculation uses the mean returns on housing, which also vary by education level, as shown in Table 4. However, for the return on other assets we use average rates of return from external sources that do not vary by education level.

These investment gains are shown in Table 6 for each wave-to-wave interval and for all years combined for married persons, in 2008 dollars. Separate estimates are shown for each education group and for each quintile of the distribution of lagged assets A_t−1. By presenting separate estimates by lagged asset quintile, we are able to show that even among persons who begin with the same initial A_t−1, those with more education earn higher returns. The last column shows the difference between the highest and lowest education groups.

Table 6.

Mean two-year potential dollar return on total assets (in 2008 dollars) by lagged asset quintile and level of education, for two-person households age 65 and over, by interval.

Lagged asset quintile	< HS	HS	Some college	College or more	Difference (college or more minus <HS)
1998–2000
1 (low)	−744	4,598	6,398	10,510	11,253
2	6,404	20,196	23,997	30,313	23,909
3	31,407	49,276	58,241	67,195	35,788
4	83,160	113,418	121,253	146,846	63,686
5 (high)	196,717	351,898	400,330	538,399	341,682
All	29,302	85,628	128,682	251,700	222,398
2000–2002
1 (low)	6,697	1,848	1,417	8,531	1,834
2	17,568	5,334	3,867	25,105	7,537
3	20,203	5,705	1,889	32,598	12,395
4	22,884	−8,101	−3,771	40,602	17,718
5 (high)	−51,408	−61,776	−55,113	37,950	89,358
All	8,299	−6,493	−10,292	33,650	25,351
2002–2004
1 (low)	8,565	5,650	9,855	14,480	5,915
2	25,293	15,521	28,836	38,816	13,523
3	37,783	26,860	47,313	59,702	21,919
4	61,937	43,957	73,682	92,531	30,594
5 (high)	155,375	91,426	166,326	229,816	74,441
All	32,761	30,415	66,997	125,173	92,412
2004–2006
1 (low)	7,716	8,671	9,262	13,842	6,126
2	23,366	24,876	26,284	41,044	17,678
3	44,016	46,988	50,132	69,730	25,713
4	82,178	85,311	89,237	120,326	38,148
5 (high)	240,837	212,144	239,661	332,339	91,502
All	38,382	60,368	84,730	171,670	133,288
2006–2008
1 (low)	−4,994	−2,792	−1,400	1,579	6,573
2	−10,554	−2,329	−1,662	11,198	21,752
3	−9,312	8,030	8,640	26,167	35,479
4	21,632	44,342	41,550	54,487	32,855
5 (high)	110,523	138,196	144,889	251,889	141,366
All	3,701	25,620	37,943	107,273	103,572
All intervals combined
1	3,624	3,490	5,003	9,594	5,970
2	12,842	12,565	16,358	28,427	15,585
3	26,027	27,255	32,281	49,456	23,430
4	55,382	53,921	65,347	89,166	33,785
5	120,490	144,853	176,825	272,235	151,745
All	22,970	38,264	60,666	134,441	111,472

Averaged over all years (bottom panel), the education effect (the difference between the potential investment gain of persons with a college degree or more and persons with less than a high school degree) ranges from $5,970 for persons in the lowest asset quintile to $151,745 for persons in the highest asset quintile. In other words, among persons in the same initial quintile of the wealth distribution, those with higher levels of education receive investment “income” that is more than two times as large as the investment “income” experienced by persons with the lowest levels of education. We place “income” in quotations because it includes both cash income, the interest on bonds and bank accounts and the dividends paid on corporate stock, as well as capital gains on housing and on financial assets.

There is considerable wave-to-wave variation in the estimated effect of education. In particular, between 2000 and 2002 when equity markets performed poorly, the education effects are relatively small. In periods of high returns on high-risk assets, such as 1998 to 2000, the education effects are substantial.

4.3 The Effects of Asset Levels, Health, and Income on the Evolution of Assets

The next step in our analysis is to estimate equation (2) above so that we can calculate the effect of education on the level of assets through each of the “pathway variables.”

We obtain separate estimates for each quintile of A_w−1 (lagged assets). We do this because the effects estimated in this model are specified in levels. Thus, for example we expect the effect of a unit change in health to have a larger effect on a person with large assets than on a person with low levels of assets. Because the specification includes the level of assets in wave w on the left side and the level of assets in wave w₋1 on the right side, the estimated effects will be very sensitive to reporting errors in either wave w−1 or w. To minimize the effect of reporting errors we “trim” the top and bottom one percent of the change in assets between wave w−1 and wave w. We also eliminate all households with lagged assets less than $1,000. This excludes slightly less than 4 percent of the sample. The results are shown in Table 7. The estimation sample includes all persons in all HRS cohorts in the 2000, 2002, 2004, 2006 and 2008 waves. This sample includes multiple observations on the same individual. We compute robust standard errors, and thus t-statistics, for this and subsequent tables to adjust for the possible correlation of unobserved individual effects.

Table 7.

Estimates of the effects of health, income, and subjective mortality on the the level of assets, for two person households age 65 and older

	1st (lowest) quintile		2nd quintile		3rd quintile		4th quintile		5th (highest) quintile
RHS variables	coeficient	t-stat	coeficient	t-stat	coeficient	t-stat	coeficient	t-stat	coeficient	t-stat
Assets lagged	0.810	12.3	1.096	10.4	0.789	10.65	0.734	15.52	0.916	37.76
r̂Aw−1	1.407	2.81	1.092	3.15	0.705	3.92	0.552	4.07	0.087	0.9
Health lagged	476	4.98	785	4.74	451	2.13	603	2.18	2,094	3.68
Change in healt	336	2.15	212	1.04	681	2.39	967	2.17	1,427	1.28
SS income	0.727	1.93	1.058	2.74	1.027	1.66	2.030	2.41	2.711	1.81
DB income	0.229	1.74	0.240	1.76	0.299	2.24	0.512	2.72	0.377	0.94
Earned income	0.293	2.44	0.456	2.14	0.876	4.22	0.429	1.97	1.473	4.23
Survival ratio	−414	−0.46	1,734	0.65	−93	−0.04	2,227	0.63	−5,653	−0.76
Age	881	2.17	1,485	2.26	−674	−0.8	−2,278	−1.87	−1,669	−0.58
2002	7,711	1.26	15,055	1.35	44,546	2.94	−18,728	−0.77	−194,938	−3.58
2004	8,710	1.43	13,183	1.37	22,375	1.69	19,430	0.85	−22,759	−0.55
2006	11,262	1.76	82	0.01	34,023	2.2	12,886	0.62	69,131	1.51
2008	14,676	2.07	19,910	1.33	−1,072	−0.06	11,043	0.44	−221,189	−4.31
intercept	−66,896	−2.2	−167,692	−3.39	92,238	1.36	234,778	2.35	−19,719	−0.09
N									23,952
R2									0.8467

There are several noticeable features of the results. First, as anticipated, assets in wave w are strongly related to assets in wave w-1 (lagged assets). In addition, with the exception of the fifth quintile, assets are importantly related to the expected income from lagged assets r̂A_w−1. The coefficients on this variable might be interpreted as the marginal propensity to save out of potential income from assets, with the marginal propensity declining with asset quintile. The estimated coefficients for the first and the second quintiles, however, are greater than one, although we do not reject the null hypothesis that the coefficient equals one in either case. The decline in the estimated coefficients with quintile may reflect differences in the composition of wealth across quintiles, as well as in the signal-to-noise ratio in our estimate of the return to asset holdings. Most of the wealth of the first four quintiles is housing equity which may be difficult to convert to consumption in the short run, even with the availability of home equity loans. On the other hand, much of the wealth of persons in the top quintile is in financial assets which may be much easier to turn into cash for consumption. Even more importantly, there are likely to be larger differences across households in the particular composition of financial wealth than in housing wealth. Within “corporate stock,” for example, there may be large differences in the ex post return to different households—even if their ex ante holdings have the same value. We were also concerned that the estimates for the 5^th quintile could be importantly affected by asset reporting errors—persons with transitorily high A_w−1 are more likely to be in this quintile and are also more likely to experience negative asset growth between waves w−1 and w. However, median regression estimates are essentially the same as those reported in the table.

In our specification, there are two ways that assets in the prior wave can affect assets in wave w. The first is the direct effect of lagged assets; the other is the effect through the expected return on lagged assets. That is, the effect of lagged assets depends not only on the level of the assets but also on the expected return on these assets. The total effect of the level of prior period assets is given by the direct effect of prior period assets plus the effect of the expected gain on the prior period assets times the rate of return on these assets, λA_w−1 + γr r̂A_w−1 = (λ + γr̂)A_w−1. Using the estimates for λ, γ, and the predicted value of r̂ for each person, we have calculated the combined coefficient on lagged assets. The combined coefficients are shown in Table 8 by asset quintile and by education level. With the exception of the second quintile the combined coefficients on lagged assets do not differ greatly by quintile or by education level.

Table 8.

Total effect of lagged assets on current assets (λ+γr) by lagged asset quintile and level of education, for two-person households age 65 and older

Quintile	Less than high school	High school	Some college	College or more
1	0.888	0.888	0.906	0.997
2	1.175	1.171	1.193	1.260
3	0.843	0.843	0.853	0.886
4	0.784	0.781	0.791	0.810
5	0.923	0.924	0.925	0.928

Second, prior assets can affect current assets through variation by asset level in the estimated effects of health, annuity income, and earned income, on asset accumulation. Each of these effects tends to increase with asset quintile. One more dollar of income from these sources is associated with a larger wave-to-wave increase in assets for those with higher initial asset holdings. The coefficients on these income flows in some cases are greater than unity, which suggests that they may be proxying for other sources of income as well. In addition, if the income in wave w is thought of as “lifetime” income that can be counted on until death—Social Security income in particular—the effect on asset withdrawal in wave w could be larger than income in wave w. A dollar for life is worth more than a dollar for a year.

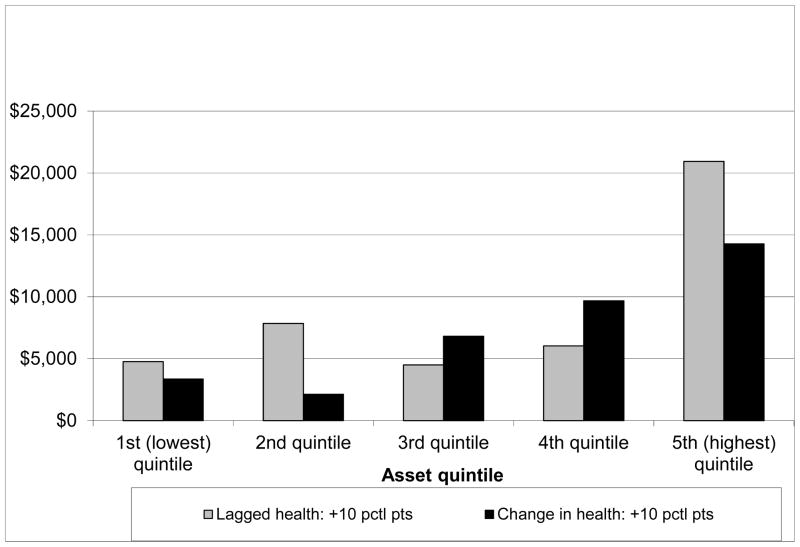
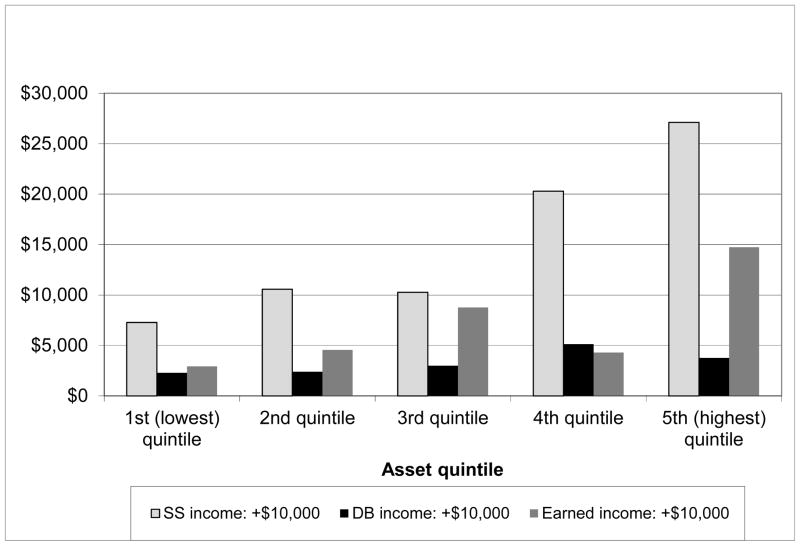
The estimates for lagged health, the change in health, Social Security income, and DB income are graphed in Figures 10 and 11. In each case with minor exceptions, the estimated effects tend to increase with asset quintile; in each the estimated effect in the 5^th quintile is much greater than the estimated effect in the 1^st quintile. The effect of DB income is much smaller than the effect of Social Security income. This may reflect the fact that receipt of DB income is much less certain than Social Security income; it is not consistently indexed to inflation and, according to Johnson, Uccello, and Goldwyn (2005), in about one-quarter of the plans for men and about two-thirds of the plans for women the benefit is not based on a joint life annuity. The estimates for health shown in the figure are very consistent with estimates of the asset cost of poor health reported in Poterba, Venti, and Wise (2010). Their estimates also show that the asset cost of poor health is much greater for those the highest asset quintile than for those in the lowest quintile.

Figure 10.

Estimated effect of health on asset evolution, two-person households age 65+

Figure 11.

Estimated effect of Social Security, DB, and earned income on asset evolution, two-person households age 65+

Third, most of the 25 estimated coefficients are statistically significant at the five percent level and a few at the ten percent level (17 and 5 respectively).

Fourth, the coefficients on the mortality ratio are never statistically different from zero and their sign varies across asset quintiles. In the standard life-cycle framework, asset holdings depend on expected longevity, and the rate of spending out of assets may also depend on this variable. Persons in poor health may accumulate fewer assets than persons in good health not only because they face higher health-related costs, but also because they anticipate a shorter lifespan. At the same time, conditional on the level of assets that households hold, those that expect to live a long time may spend at a slower rate out of their accumulated wealth. To control for this effect we have included a measure of each person’s subjective survival probability in the asset change equation.

The HRS asks each respondent to self-report the probability that they will survive for another ten years. Specifically, persons less than age 70 are asked for the likelihood that they will be alive at age 80; persons age 70 to 74 are asked if they will be alive at age 85; persons age 75 to 79 are asked if they will be alive at age 90, and so forth. Persons over the age of 90 were not asked this question. We use a “survivor ratio”, constructed by RAND (2010), that is the ratio of the respondent’s self-reported probability to the implied probability of living another ten years for a person of the same age and gender. The latter probability is obtained from the Vital Statistics life table. A lower value of M suggests that a person expects to live a shorter life than the average. If persons who expect to have shorter lives spend down assets more quickly, then the coefficient on M – the effect of the survivor ratio, conditional on lagged assets – would be positive.

The absence of a positive relationship between expected longevity and current assets, conditional on past assets, may suggest limitations of the lifecycle model, or it may signal shortcomings of our data. First, with regard to the model, it is possible that short life expectancy is positively correlated with the likelihood of substantial out-of-pocket medical costs or other late life expenses. If households have a precautionary demand for assets to cover such costs, they may seek to preserve assets when their life expectancy is short. In addition, bequest motives may attenuate the relationship between remaining life expectancy and asset draw-down. Second, with regard to data, it is possible that expected longevity is subject to substantial measurement error, and that the resulting estimate of the coefficient on this variable is therefore biased toward zero. A substantial body of previous work, including Hurd and McGarry (2002), Hurd, McFadden, and Gan (1998) and Hurd, McFadden, and Merrill (2001), nevertheless suggests that subjective mortality probabilities are strongly predictive of actual mortality. We also considered the possibility that our health status variable is collinear with expected longevity. When we excluded our health variable and re-estimated our basic model, the coefficient on the expected longevity variable remained statistically insignificantly different from zero. The absence of a subjective mortality effect of the expected sign thus remains a topic for further exploration.

Fifth, we are aware that the relationship between earned income and asset growth is more complex than our estimates reveal. Earned income is the product of the probability of working and the level of earnings if a person works. The estimates of these relationships (not reported here) show that whether a person works as well as earnings if working are positively related to health and negatively related to Social Security and DB income. Both the probability of working and earnings conditional on working are also positively related to the level of education, which is presumably a good measure of potential earnings.

Finally, for the fifth asset quintile the coefficients on the year indicator variables are large and negative for 2000–2002 and 2006–2008. We suspect that these effects reflect the two recent periods of decline in equity markets. The effect shows up strongly for the fifth assets quintile because equity holdings are much larger among household in the fifth quintile than in the other quintiles.

Given these estimates, we now consider how education affects assets though each of the pathways defined by variables in the regression. We do this by combining two components: (1) the estimates in Table 7 that show the effect of each pathway variable on the level of assets, and (2) an estimate of the relationship between education and the pathway variable. The second of these components is the difference between level of the pathway variable for persons with college or more education and the level of the variable for persons with less than a high school degree. For example, consider the health pathway. In terms of equation (3) above, the first component is dA_w / dH_W−1 (the estimated coefficient on lagged health) and the second component is dH / dE (from Table 2 above). We therefore define the effect of education on assets, through the level of health pathway, as

$$\frac{{dA}_w}{{dH}_{w-1}}\frac{{dH}_{w-1}}{dE}=\frac{{dA}_w}{{dH}_{w-1}}\left(H_{\mathit{College}}-H_{<HS}\right)$$

The estimated effect of education on assets through the “change in health” pathway is:

$$\frac{d{A}_w}{d\mathrm{\Delta }H}\frac{d\mathrm{\Delta }H}{dE}=\frac{d{A}_w}{d\mathrm{\Delta }H}\left(\mathrm{\Delta }{H}_{College}-\mathrm{\Delta }{H}_{<HS}\right)$$

Table 9 shows the effect of education through each of the pathways. Each row pertains to one of the pathways. The table shows separate results for each lagged asset quintile. The detail of the calculations is shown in Appendix Table 3. The total effect of education on assets through these pathways—the left-hand side of equation (3)—is shown in the last row. The total effect is greatest for the fifth asset quintile. In this quintile the pathway through lagged assets ($394,012, shown in the first row) accounts for 85 percent of the total effect of education ($466,451). The next two most important pathways for the fifth asset quintile are earnings and the level of health. For the first four asset quintiles the total effect of education is much smaller--$32,083, $50,560, $58,232, and $63,444 respectively. For these quintiles the most important pathways are lagged assets and the dollar return on assets. The post-retirement effect of education on assets through each of the other pathways appears to be small. One such post-retirement pathway is through the effect of education on the wave-to-wave change in health. The effect of this pathway is very small and negative for four of the five quintiles. Another possible post-retirement pathway is the dollar return on assets. But it is likely that most of the portfolio choices that determine this effect are established at retirement. The post-retirement level of health might also be affected by education, but data in Figures 6–9 above show that education-related differences in health in years subsequent to retirement are very similar to the differences when individuals are first observed. Thus the post-retirement level of health seems largely a carryover of the level health at retirement.

Table 9.

Estimates of the effect of education on the level of assets by pathway, by asset quintile, for two-person households age 65 and older--based on estimates in Table 7

	Asset quintile
	1 (low)	2	3	4	5 (high)
Lagged assets	$9,567	$15,331	$19,028	$25,785	$394,012
Dollar return on assets	$8,400	$17,019	$16,517	$18,649	$13,202
Mean level of health	$7,188	$8,321	$5,006	$6,090	$24,290
Change in health	−$386	$136	−$742	−$1,006	−$1,969
SS income	$337	−$979	−$765	$847	$1,743
DB income	$2,080	$3,850	$4,767	$8,184	$6,242
Earnings	$4,897	$6,882	$14,421	$4,896	$28,631
Total of pathway effects	$32,083	$50,560	$58,232	$63,444	$466,151

Appendix Table 3.

Estimates of the effect of education on the level of assets for each pathway, by variable and by asset quintile based on estimates in Table 7, two-person households age 65 and older

	Asset quintile
	1 (low)	2	3	4	5 (high)
Lagged assets
< HS	56,383	179,751	343,702	638,456	1,585,832
College or more	68,194	193,739	367,818	673,585	2,015,976
Coefficient	0.810	1.096	0.789	0.734	0.916
Estimated effect	$9,567	$15,331	$19,028	$25,785	$394,012
Dollar return on assets
< HS	3,624	12,842	26,027	55,382	120,490
College or more	9,594	28,427	49,456	89,166	272,235
Coefficient	1.407	1.092	0.705	0.552	0.087
Estimated effect	$8,400	$17,019	$16,517	$18,649	$13,202
Mean level of health
< HS	37.2	43.1	43.5	47.4	46.3
College or more	52.3	53.7	54.6	57.5	57.9
Coefficient	476	785	451	603	2,094
Estimated effect	$7,188	$8,321	$5,006	$6,090	$24,290
Change in health
< HS	−2.56	−4.25	−3.35	−2.27	−2.7
College or more	−3.71	−3.61	−4.44	−3.31	−4.08
Coefficient	336	212	681	967	1,427
Estimated effect	−$386	$136	−$742	−$1,006	−$1,969
SS income
< HS	17,102	19,425	20,371	20,974	22,565
College or more	17,566	18,500	19,626	21,391	23,208
Coefficient	0.727	1.058	1.027	2.030	2.711
Estimated effect	$337	−$979	−$765	$847	$1,743
DB income
< HS	4,947	7,323	10,965	10,904	8,923
College or more	14,032	23,363	26,909	26,888	25,480
Coefficient	0.229	0.240	0.299	0.512	0.377
Estimated effect	$2,080	$3,850	$4,767	$8,184	$6,242
Earnings
< HS	5,958	5,811	5,247	6,022	5,395
College or more	22,672	20,904	21,709	17,434	24,832
Coefficient	0.293	0.456	0.876	0.429	1.473
Estimated effect	$4,897	$6,882	$14,421	$4,896	$28,631
Total	$32,083	$50,560	$58,232	$63,444	$466,151

Note: Each panel pertains to one of the pathways. The first row in each panel shows the mean level of the pathway variable for persons with less than a high school degree and the next row shows the mean level of the pathway variable for persons with a college degree. The third row shows the estimated coefficient from Table 7 and the last row, labeled “estimated effect” is the product of the coefficient and the difference (college or more minus less than high school) in the pathway variable. Thus each row labeled “estimated effect” represents one of the terms on the right-hand side of Equation (2).

4.4. The Additional Effect of Education

The calculations above allocate the effect of education on asset growth following retirement to the several “pathway variables” included in the regression. We now consider effects of education that may not work through these pathways. We use two methods to estimate this additional effect of education.

One approach is to estimate the additional effect of education by a regression of the residuals from the specification reported in Table 7 on indicator variables representing levels of education. The results are shown in Table 10. The omitted category is less than a high school education. The estimated coefficients on education level suggest that education is strongly related to the level of assets even after controlling for the pathways described above.⁶

Table 10.

Regression estimation of residuals from specification in Table 7 on levels of education, for two-person households age 65 and older

Level of education	1st (lowest)		2nd quintile		3rd quintile		4th quintile		5th (highest)
	coeficient	t-stat	coeficient	t-stat	coeficient	t-stat	coeficient	t-stat	coeficient	t-stat
High school	12,828	2.86	24,884	3.98	10,500	1.06	−12,847	−0.66	44,749	1.01
Some college	18,453	3.17	30,559	3.32	26,463	2.28	−1,395	−0.07	64,090	1.42
College	49,998	4.12	63,426	4.55	49,472	3.42	34,241	1.67	139,326	3.15
Intercept	−11,724	−5.61	−25,001	−5.95	−20,574	−2.71	−5,717	−0.34	−90,088	−2.28
N									23,952
R2									0.0042

As noted above, we could capture the effect of education not accounted for by the pathways by simply including the level of education directly in the asset regression. This approach, however, makes it difficult to estimate the indirect effect of education—through its effect on pre-retirement levels of financial and health capital—on the post-retirement evolution of assets. Because health and financial capital at retirement are so closely linked to education, and because there may be measurement error in our recorded health and financial capital variables, adding the level of education to the specification reduces the estimated effect of health and financial capital on household assets. This suggests that the estimated coefficient on the education variable may be capturing part of the health and financial capital effects on subsequent asset growth that are attributable to education. We therefore focus on the strategy of relating the residuals from equation (2) to education, without including education directly in the asset equation.

We nevertheless estimate the alternative specification and compare the two sets of findings. When we add education to equation (2) the effects of the pathway variables (the absolute value of the coefficients) are reduced by about 18 percent on average. Similarly, the effects of education on asset growth through each of the pathways are smaller than those shown in Table 9. The total reduction in the “pathway effect” is more than twenty percent for households in the three lowest deciles of the wealth distribution, but less than five percent for those in the highest quintile. The “total” effect of education is unaffected by the estimation method, that is, the sum of the pathway effects from Table 9 and the “additional” effect of education from the residual regression in Table 10 is virtually identical to the sum of the pathway effects and the “direct” education effect obtained from estimates that include the education variables in equation (2). Thus the difference between the two methods is only how the effect of education is allocated. The pathway effects are smaller when education is included in (2)—and the proportion of the total effect of education “unexplained” by the pathways is correspondingly larger. Further detail on the relationships between the two methods is presented in Appendix Table 4.

Appendix Table 4.

Summary of results from two methods of estimating the “additional” effect of education, for two-person households age 65 and over

	Asset quintile
	1 (low)	2	3	4	5 (high)
Additional education effect--method 1	49,998	63,426	49,472	34,241	139,326
Additional education effect--method 2	58,772	78,761	62,846	42,338	153,543
Difference in estimates--method 2 minus method 1	$8,774	$15,336	$13,373	$8,097	$14,217
Reduction in the sum of pathway effects--method 2 minus method 1	−$8,600	−$14,766	−$12,381	−$8,031	−$14,363
Percent reduction in sum of the pathway effects--method 2 minus method 1	−26.8%	−29.2%	−21.3%	−12.7%	−3.1%

Note: The text discusses two methods of estimating the effect of education not accounted for by included pathways (“additional effect of education”). Method 1 obtains estimates by regressing the residuals from equation (2) on the education variables. Method 2 directly adds the education variables to equation (2). The table summarizes the estimated effect of education for each method, and shows how the effect of education is allocated to pathway and additional effects. The first two lines show the estimated effect of college education (versus less than a high school degree) for each method. The difference between the two is shown in the third line and ranges from $8,774 in the first asset quintile to $14,217 in the fifth quintile. The fourth line shows the corresponding reduction in the sum of the pathway effects associated with the health and resource circumstances given at retirement. One is essentially the mirror image of the other. The percent reduction is show in the last line of the table. The percent reduction in the sum of the pathway effects is very small for the top asset quintile because the indirect effect of lagged assets is very large for this quintile and the coefficient on lagged assets is affected very little by the addition of education levels to the regression.

Table 11 combines the results shown in Tables 9 and 10 for two-person households. Together, these two sets of results account for the total effect of education on the post retirement evolution of assets. The total of the effects of education through each of the pathways (from Table 9) ranges from $32,083 to $63,444 for the lowest four asset quintiles, but jumps to $466,151 for the top asset quintile. The “additional” effect of education (from Table 10)—presumably the effect of education through pathways not identified—ranges from $34,241 to $139,326. The total effect shown in the third row—the sum of the indirect effect through the identified pathways and the additional effect of education—for two person households ranges from about $82,000 for the first asset quintile to over $600,000 for the fifth asset quintile. Taken together, these results suggest that the post-retirement evolution of assets is strongly related to education. The last row shows the percent of the total effect that is not accounted for by the identified pathways. This percentage is much larger in the lower asset quintiles than in the higher asset quintiles.

Table 11.

Estimated pathway effects and additional effects of education on the evolution of assets, by pathway and asset quintile, for two-person households age 65 and over

	Asset quintile
	1 (low)	2	3	4	5 (high)
Total of pathway effects	$32,083	$50,560	$58,232	$63,444	$466,151
Additional education effect	$49,998	$63,426	$49,472	$34,241	$139,326
Sum of pathway and additional effects	$82,081	$113,985	$107,704	$97,685	$605,476
Additional effect as percent of total	60.9%	55.6%	45.9%	35.1%	23.0%

5. Summary and Conclusion

This paper presents evidence on the links between educational attainment and the evolution of assets in late life. Education affects income and saving over the life course in many ways. We focus on a set of health and financial pathways (such as Social Security income and the general level of health) through which education may affect asset growth for older households. Our goal is to estimate the effect of education on each pathway and to estimate the effect of each pathway on asset growth. In combination these estimates allow us to determine how education affects asset evolution through each pathway.

We acknowledge at the outset the difficulty of identifying the effects we are trying to measure. Our primary interest is the effect of education on asset evolution after retirement. Older persons with different levels of education may make different consumption and investment decisions in retirement and thus accumulate or draw down assets at different rates. However, asset growth in retirement also depends on choices made long before retirement. Such choices —which were strongly influenced by education—affect the financial and health capital that persons have upon entering retirement and will affect the future evolution of assets. For example, a person enters retirement with a general level of health and a level of annuity income—both are “pathways” through which education may affect subsequent asset growth, even though, for example, the influence of education on health and financial capital (principally through the effect of education on earnings) occurred long ago. It is particularly difficult to disentangle the effect of education on assets after retirement from the effect of education on financial and health capital acquired before retirement.

We estimate the relationship between each “pathway” variable, Social Security benefits for example, and the subsequent evolution of assets. The idea is that education affects Social Security benefits and these benefits in turn affect the post-retirement evolution of assets. However, we do not observe a change in education policy or a change in Social Security benefit rules. We are not able to randomly assign education levels to different households with similar levels of retirement income and wealth at retirement, and to study how their wealth evolves in their post-retirement years. Instead, we treat education as though it was pre-determined, and describe the differences in asset evolution across households that are associated with differences in education. Decisions about the level of education to acquire early in life may be related to family circumstances or to unobserved individual attributes that are also affected with late-life asset accumulation behavior. We do not have a way of evaluating the role of such unobserved heterogeneity.

These cautions notwithstanding, our findings suggest a strong relationship between financial capital and health capital accumulated at the age of retirement and the subsequent evolution of assets. Because much of the variation in health and financial capital at retirement is education-related, this at least suggests the possibility that changes in education early in life may have long-lasting effects. The level of education may also affect decisions made after retirement, including portfolio allocation and investment returns that have significant implications for asset accumulation.

We present separate results for households in five wealth quintiles. We first identify the effect of each pathway on asset growth. For two-person households, a 10 percentage point increase in the level of health is associated with a substantial increase in the level of assets from wave to wave—ranging from about $5,000 in the first asset quintile to about $21,000 in the fifth quintile. A ten percentage point increase in the change in health between the waves is associated with an increase assets ranging from about $3,000 in the first quintile to about $14,000 in the fifth quintile. More income is also associated with an increase in assets between waves. A $10,000 increment in Social Security income is associated with an increase in assets ranging from about $7,000 in the first quintile to $27,000 in the fifth assets quintile. An increment of $10,000 in earned income is associated with an increase in assets ranging from about $3,000 in the lowest to almost $15,000 in the highest asset quintile. Thus Social Security income in particular, but also earned income, are “protective” of assets; greater income reduces the need to withdraw assets to meet health and other expenses. Defined benefit pension and annuity income is much less important.

We calculate the “indirect” effect of education through each of the pathways we consider, as well as a substantial additional effect of education not captured by the identified pathways. The total effect is very large. For two person households the difference between the assets of college graduates and those with less than a high school diploma ranges from about $82,000 for the first asset quintile to over $600,000 for the fifth asset quintile. For households in the lower asset quintiles the “additional” effect accounted for slightly over half of the total effect of education on asset growth. Conversely, in the top quintile over three-quarters of the effect of education was through the identified pathways.

The results for one-person households are less consistent across financial resources and health capital, but they still show a strong relationship between health and the return on assets and the evolution of assets. The total effect of education—the indirect effect through the pathways plus the additional effect—is again very large, ranging from ranging from over $19,000 in the first quintile to almost $322,000 in the top quintile.

Two additional insights emerge about aspects of late-life health and financial status and educational attainment. First, health status is highly related to educational attainment, but the change in health status after retirement is not. Second, more educated households not only have more wealth on average in retirement but those with more education also allocate their wealth in a different way than their less-educated counterparts. They are more likely to hold financial assets such as stocks and bonds, which provide an opportunity for substantial returns. They also appear to experience more growth in housing equity during the sample period we study. This in part reflects a lower rate of home equity borrowing, and a higher rate of pay-down on existing mortgages. The result is a pronounced education gradient in the return to assets, with more educated households earning more, as a percentage of their asset holdings, than less educated households.

While we have considered a number of different pathways through which education can affect pre-retirement household behavior, and through those behaviors influence post-retirement asset evolution, our list of pathways is not exhaustive. There may also be important post-retirement channels for the influence of education on household behavior that we have not explored. For example, more educated individuals may have greater ability to adjust to changing technology, and consequently face better job prospects and higher potential earnings if they choose to work at older ages. This may, in turn, raise the probability that they work. We leave the study of this and other pathways to future work.