Dynamic Stability of Individuals with Transtibial Amputation Walking in Destabilizing Environments

Abstract

Lower limb amputation substantially disrupts motor and proprioceptive function. People with lower limb amputation experience considerable impairments in walking ability, including increased fall risk. Understanding the biomechanical aspects of the gait of these patients is crucial to improving their gait function and their quality of life. In the present study, 9 persons with unilateral transtibial amputation and 13 able-bodied controls walked on a large treadmill in a Computer Assisted Rehabilitation Environment (CAREN). While walking, subjects were either not perturbed, or were perturbed either by continuous mediolateral platform movements or by continuous mediolateral movements of the visual scene. Means and standard deviations of both step lengths and step widths all increased significantly during both perturbation conditions (all p < 0.001) for both groups. Measures of variability, local and orbital dynamic stability of trunk movements likewise all exhibited large and highly significant increases during both perturbation conditions (all p < 0.001) for both groups. Patients with amputation exhibited greater step width variability (p = 0.01) and greater trunk movement variability (p = 0.04) during platform perturbations, but did not exhibit greater local or orbital instability than healthy controls for either perturbation condition. Our findings suggest that, in the absence of other co-morbidities, patients with unilateral transtibial amputation appear to retain sufficient sensory and motor function to maintain overall upper body stability during walking, even when substantially challenged. Additionally, these patients did not appear to rely more heavily on visual feedback to maintain trunk stability during these walking tasks.

Introduction

People with lower limb amputation often experience considerable difficulty walking (Grumillier et al., 2008) and decreased physical capacity (van Velzen et al., 2006). More than 50% of community-dwelling amputees fall each year (Miller and Deathe, 2004) and younger patients fall as often as older patients (Miller et al., 2001). Amputation disrupts motor and proprioceptive function, leading persons with amputation to rely more heavily on visual feedback for standing balance (Fernie et al., 1978; Vanicek et al., 2009). Visual and somatosensory feedback are also thought to be critical for walking (Gandevia, 2001). However, walking and standing are very different tasks (Kang and Dingwell, 2006) and passive dynamics likely play a greater role during walking (Srinivasan and Ruina, 2006; Iida and Tedrake, 2010). Patients with unilateral transtibial amputation retain intact visual and vestibular input, and mostly intact proprioception and motor function in their proximal impaired limb and contralateral limb. Thus, it remains an important question whether these patients retain sufficient sensory and motor capacity to maintain adequate dynamic stability while walking.

Here, we define dynamic stability as the capacity of a system to respond to perturbations (Strogatz, 1994). “Local stability” refers to responses to very small (i.e., “local” in state space) perturbations that may arise from either external (e.g., irregular surfaces) or internal (e.g., neuromuscular noise) sources. For aperiodic systems, this local stability is quantified by local divergence exponents (Dingwell and Cusumano, 2000). For periodic (i.e., limit cycle) systems, maximum Floquet multipliers quantify the local stability of consecutive orbits around the limit cycle, often termed “orbital stability” (Strogatz, 1994; Dingwell and Kang, 2007). Because human walking is neither strictly periodic, nor strongly aperiodic, quantifying both measures provides a more complete description of the sensitivity of the system to small perturbations.

Healthy elderly are more locally unstable than young adults (Kang and Dingwell, 2008a; Hamacher et al., 2011) and elderly fallers may exhibit both increased orbital (Granata and Lockhart, 2008; Hamacher et al., 2011) and local (Toebes et al., 2012) instability compared to non-fallers. Compared to nondisabled controls, greater local instability has been demonstrated in patients with either transfemoral (Lamoth et al., 2010) or transtibial (Hak et al., 2013; Wurdeman et al., 2013) amputation. However, these studies did not control for walking speed, which can independently alter local stability (Dingwell and Marin, 2006; England and Granata, 2007; Kang and Dingwell, 2008a; Manor et al., 2008). Slower walking speeds are commonly adopted by elderly (Tsai and Lin, 2013) and many patient populations, including those with amputation (Paysant et al., 2006; Kendell et al., 2010). Conversely, faster walking speeds generally increase fall risk (Pavol et al., 1999; Troy et al., 2008; Faulkner et al., 2009; Callisaya et al., 2012). Separating differences in dynamic stability due to amputation from those due to changes in walking speed is therefore critical.

The most direct approach to assess dynamic stability is to impose perturbations that explicitly challenge subjects’ ability to walk and then quantify their responses. On irregular surfaces, patients with amputation walk with wider steps, but have exhibited inconsistent results for various measures of “stability” (Lamoth et al., 2010; Curtze et al., 2011; Gates et al., 2012; 2013). Perhaps either the stability measures used in those studies did not adequately capture the effects of the perturbations, or the perturbation paradigms imposed were not sufficiently challenging to elicit appropriate responses. We previously quantified how healthy subjects responded to substantially destabilizing mediolateral perturbations. Subjects exhibited highly significant increases in both kinematic variability (McAndrew et al., 2010) and dynamic instability (McAndrew et al., 2011), validating the idea that local divergence exponents and maximum Floquet multipliers captured these subjects’ increased sensitivity to the perturbations imposed. Hak et al. (2013) applied the same perturbation paradigm to patients with transtibial amputation. Although statistically significant, their data show only very small differences between subjects groups and perturbation conditions, likely due to methodological differences in how they calculated their local stability exponents.

This study therefore determined how lower limb amputation affects the ability to respond to well-controlled continuous visual or walking surface perturbations. We predicted that persons with transtibial amputations would be (a) more unstable than able-bodied controls during both unperturbed and perturbed walking, (b) would exhibit larger increases in instability than able-bodied controls when subjected to perturbations, and (c) would rely more heavily on visual feedback, resulting in greater increases in dynamic walking instability during visual compared to mechanical perturbations.

Methods

Nine persons with unilateral transtibial amputations (TTA) and thirteen able-bodied controls (AB) volunteered (Table 1). All TTA subjects walked without assistance using their own prostheses. All TTA patients were active duty military personnel undergoing comprehensive amputee care (Granville and Menetrez, 2010). Participants were screened by a physical therapist to ensure they had no orthopedic or neurological impairments (other than amputation) that might affect their walking. All subjects signed informed consent statements approved by both Brooke Army Medical Center and The University of Texas.

Table 1.

Subject characteristics

	AB (n = 13)	TTA (n = 9)
Sex (M/F)*	10/3	9/0
Age (years)*	24.8 ± 6.92	30.7 ± 6.75
Height (cm)*	174.8 ± 0.08	176.1 ± 0.11
Body Mass (kg)*	79.3 ± 11.56	90.2 ± 16.06
BMI (kg/m2)*	26.0 ± 3.96	28.86 ± 2.26
Leg Length (m)*	0.95 ± 0.05	0.94 ± 0.07
Cause of Amputation	---	8 Traumatic 1 Osteosarcoma
Time Since Amputation (mo)	---	19.8 ± 15.8
Residual Limb Length (%) †	---	55.1% ± 7.47%
Avg. Prosthetic Use (Hrs/Day)	---	13.94 ± 2.46
Pain Level (#)‡	---	1.75 ± 1.28

^*Note: t-tests for group differences: all p > 0.05

^†Residual Limb Length is defined as a percent of length of the lower leg (from the knee to the ankle)

^‡Pain ratings were taken on 10-pt visual analog scale (VAS). All subjects reported pain ≤ 3 at the time of testing.

Participants walked in a Computer Assisted Rehabilitation Environment (CAREN) (Motek, Amsterdam, Netherlands). Subjects walked on a 2 × 3m instrumented treadmill embedded in a 4m-diameter six degree-of-freedom motion platform inside a 7m-diameter dome (Fig. 1A) that created an immersive virtual environment (Sanchez-Vives and Slater, 2005).

Figure 1. Experimental Setup.

A: Example photo of a typical person with amputation standing inside the CAREN virtual reality system (Motek, Amsterdam, Netherlands). B: The visual scene used during CAREN trials, depicting a path through a forest with mountains in the background. Both sides the path were lined with 2.4 m tall white posts spaced every 3 m to increase motion parallax (Bardy et al., 1996; McAndrew et al., 2011; 2011).

The protocol was similar to previous studies (McAndrew et al., 2010; 2011). Each participant walked at a fixed speed scaled to their leg length (l): $v=\sqrt{0.16·g·l}$ (Vaughan and O’Malley, 2005), where l was defined as distance (m) from the great trochanter to the walking surface. This yielded an average walking speed of 1.22±0.03 m/s across subjects.

Subjects completed a 6-minute acclimation period followed by five 3-minute trials each under each of the following three conditions:

• NOP: Walking with no perturbations and normal visual optic flow.

• PLAT: Walking with mediolateral platform perturbations and normal visual optic flow.

• VIS: Walking on a stationary platform with mediolateral perturbations added to the visual optic flow.

Perturbations were generated as continuous pseudo-random oscillations using a sum of 4 sine waves with incommensurate frequencies ranging from 0.16 to 0.49 Hz (McAndrew et al., 2010; 2011):

$$A(t)=A_W\left[1.0sin(0.16·2\pi t)+0.8sin(0.21·2\pi t)+1.4sin(0.24·2\pi t)+0.5sin(0.49·2\pi t)\right],$$ (1)

where A(t) was the perturbation amplitude in meters, A_w was a weighting factor in meters and t was time in seconds. Perturbation magnitudes were scaled to A_w=0.04 for PLAT and A_w=0.45 for VIS conditions, respectively (Beltran et al., 2014), so as to elicit similar biomechanical responses to each type of perturbation (Terry et al., 2012; Sinitski et al., 2012). We applied medio-lateral perturbations because humans are laterally more unstable while walking (Bauby and Kuo, 2000; Dean et al., 2007; McAndrew et al., 2011).

Participants were instructed to focus on the horizon directly in front of them. Head orientation was monitored visually. The order of presentation of the conditions was randomized for each individual and balanced across subjects. Rest breaks were provided between conditions or at participants’ request.

Kinematic data were collected at 60Hz using a 24-camera motion capture system (Vicon Motion Systems, Oxford, UK) and 57 reflective markers (Wilken et al., 2012). Marker positions and digitized joint centers were post-processed using Vicon Nexus and Visual 3D (C-Motion Inc., Germantown, MD). Heel strikes were determined using a velocity-based detection algorithm (Zeni et al., 2008) and the first 150 strides for each trial were analyzed. Step lengths and widths were defined as the anterior-posterior and mediolateral distances, respectively, between the right and left heel markers at heel strike (Gates et al., 2012). We then computed means and standard deviations of step length and step width across all 300 steps (150 strides) for each trial, condition and subject.

To quantify kinematic variability and dynamic stability of trunk motions, the medio-lateral component of C7 marker movements was analyzed (Dingwell and Marin, 2006). We analyzed trunk motions because maintaining control of upper body movements is critical for walking (Zajac et al., 2003; Pandy et al., 2010). C7 marker velocities were analyzed to account for drifting of subjects on the treadmill (Dingwell and Marin, 2006). Additionally, for the PLAT trials, platform displacements were first subtracted from C7 marker displacements prior to calculating velocities (Sinitski et al., 2012).

Trunk variability was calculated as the mean standard deviation of the C7 position and velocity (MeanSD_pos and MeanSD_vel) according to (Dingwell and Marin, 2006):

$${SD}_j=\sqrt{\frac{{\sum }_{i=1}^{N_{\mathit{str}}}{\left(x_{ij}-{\overline{x}}_j\right)}^2}{N_{\mathit{str}}}},$$ (2)

$$\mathit{MeanSD}=\frac{1}{N_{int}}\sum _{j=1}^{N_{int}}{SD}_j,$$ (3)

where standard deviations, SD_j, were first computed across all N_str = 150 strides at each interval, j, of the gait cycle, where j ∈{0%,…,100%}. MeanSD quantities were calculated by computing the average standard deviation over all N_int = 101 intervals that comprised the complete gait cycle. Thus, MeanSD quantifies the mean of the standard deviations calculated across all strides at each 1% interval of the stride cycle.

For dynamic stability analyses, state spaces reconstructed using the method of delays (Sauer et al., 1991; Kantz and Schreiber, 2004). Each state space was reconstructed from the medio-lateral velocity of the C7 marker using the original data and their time delayed copies (Gates and Dingwell, 2009):

$$\mathbf{S}(t)=\left[v(t),v(t+\tau ),\dots ,v(t+(d_E-1)\tau )\right],$$ (4)

where S(t) is the d_E-dimensional state vector, v(t) is the original 1-dimensional data, τ is the time delay and d_E is the embedding dimension. Time delays were determined from the first minimum of the Average Mutual Information function, yielding an average time lag of 20 frames. An embedding dimension of d_E = 5 was used for all trials (Dingwell and Cusumano, 2000; McAndrew et al., 2011).

Dynamic stability of C7 velocity state spaces was quantified using both maximum Floquet multipliers (MaxFM) and local divergence exponents (λ^*_S). MaxFM quantifies the average rate at which system states diverge or converge from the average state in discrete time after one consecutive stride (Strogatz, 1994; Dingwell and Kang, 2007). Conversely, λ^*_S quantifies the rate at which infinitesimally close initial conditions diverge from away each other in real time both within and across strides (Kantz and Schreiber, 2004; Dingwell and Cusumano, 2000).

To compute MaxFM, C7 data were extracted for each individual stride and time-normalized to 0–100% gait cycle. A Poincaré map was defined at each percent of the gait cycle to determine how small perturbations from the average trajectory grew or diminished between consecutive strides (Strogatz, 1994; Donelan et al., 2004). The magnitude of MaxFM was calculated at each Poincaré section and then averaged over the gait cycle. MaxFM < 1 indicates that trajectories on average converge over consecutive strides and the system is orbitally stable. If MaxFM increases, but remains < 1, the system is less orbitally stable (Kang and Dingwell, 2008a).

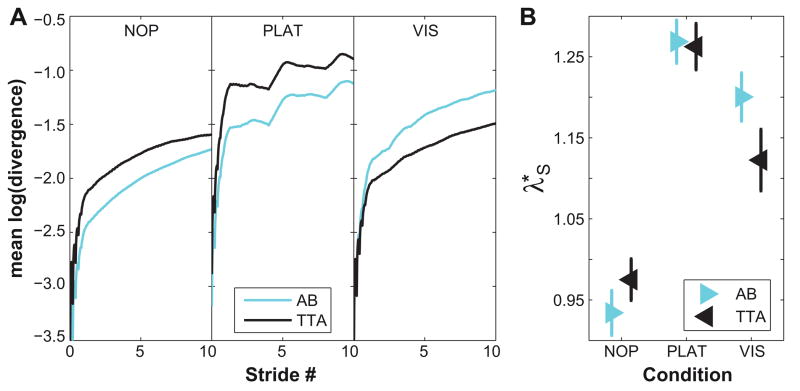
To compute λ^*_S prior to state space construction, the 150 continuous strides of data were first re-sampled to 15000 total data points (England and Granata, 2007; Bruijn et al., 2009). For each nearest neighbor in state space, the logarithmic distance between neighboring trajectories was calculated. These were then averaged over all nearest neighbor pairs (Rosenstein et al., 1993). A least-squares fit estimated the slope of the mean log divergence curve between 0–1 stride: λ^*_S (Dingwell and Cusumano, 2000). Positive λ^*_S exponents indicate that perturbations diverge over time and that the system is locally unstable. Larger exponents indicate greater local instability (Rosenstein et al., 1993; Dingwell and Cusumano, 2000).

Importantly, these local divergence curves are generally not linear (e.g., Fig. 5A), reflecting the fact that human walking is not “chaotic” (Rosenstein et al., 1993; Kantz and Schreiber, 2004). Hence, the λ^*_S computed here should not be interpreted as true “Lyapunov exponents” (Timmer et al., 2000; Kantz and Schreiber, 2004). The linear fits to these curves, however, still quantify the average exponential rate of divergence over the corresponding time scale. Thus, these λ^*_S still provide rigorous metrics for estimating the intrinsic sensitivity of human walking to small perturbations (Dingwell and Cusumano, 2000; McAndrew et al., 2011).

Figure 5. Short-Term Local Dynamic Stability (λ^*.

_S) of C7.

A: Exemplary mean local divergence curves for one typical healthy control subject (AB) and one person with amputation (TTA) for all three walking conditions (NP, PLAT and VIS). Short-term local divergence exponents (λ^*_S) were computed as the linear slopes of these curves over the region from 0 to 1 stride. B: Mean short-term local stability (λ^*_S) for all healthy controls (AB) and all amputees (TTA) separately for each walking condition. Error bars indicate the appropriate between-subject ± standard error.

For each dependent measure, repeated measures ANOVAs with the between-factor Group and the within-factor Condition were applied to determine differences between subject groups across conditions, separately for platform (NOP vs. PLAT) and visual (NOP vs. VIS) perturbation trials. All statistical analyses were performed using SPSS 19 (SPSS Inc., Chicago, IL).

Results

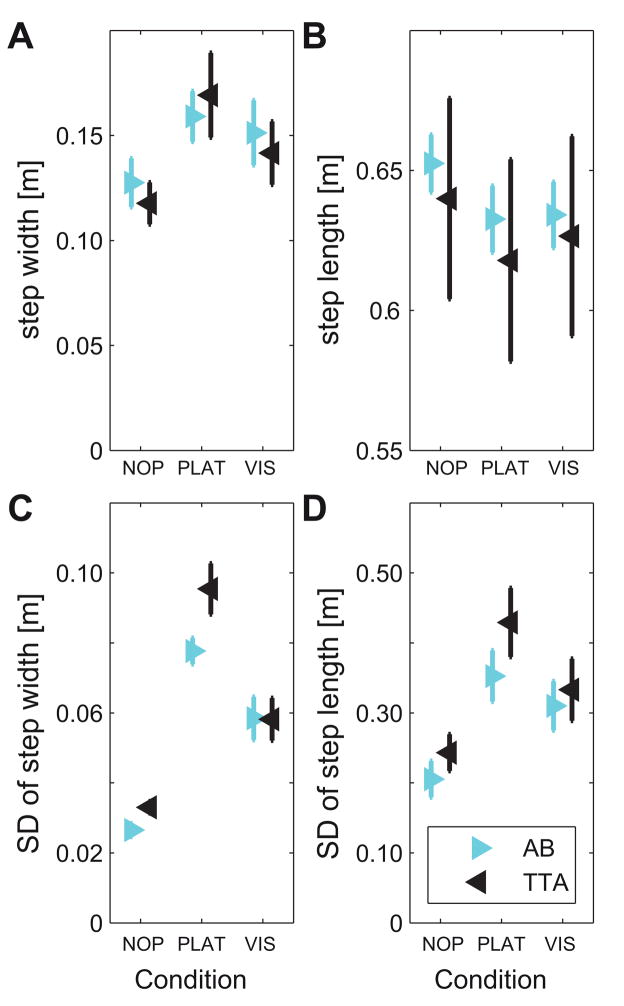
Subjects in both groups took significantly wider (Fig. 2A) and shorter (Fig. 2B) steps in response to both platform (Table 2A) and visual perturbations (Table 2B). Likewise, subjects in both groups exhibited significantly increased step width variability (Fig. 2C) and step length variability (Fig. 2D) in response to both types of perturbations. Step width variability was significantly greater for TTA than for AB when comparing the PLAT and NOP conditions (Table 2A; Fig. 2C).

Figure 2. Stepping Parameters (Step Length and Width) and Stepping Variability.

A: Mean step width, B: Mean step length, C: Step width variability, and D: Step length variability. Each graph shows data separately for all healthy controls (AB) and all amputees (TTA) for all three walking conditions. Error bars indicate the appropriate between-subject ± standard error.

Table 2.

ANOVA results

(A) between-factor: Age; within-factors: NOP and PLAT
	Group F (p-value)	Condition F (p-value)	Group x Condition F (p-value)
step length	0.31 (0.57)	88.97 (0.00)	0.002 (0.96)
step width	0.06 (0.81)	60.21 (0.00)	3.94 (0.06)
step length variability	2.01 (0.17)	57.42 (0.00)	0.67 (0.42)
step width variability	7.77 (0.01)	389.7 (0.00)	4.26 (0.05)
MeanSDpos	4.73 (0.04)	265.7 (0.00)	7.25 (0.01)
MeanSDvel	1.81 (0.19)	236.1 (0.00)	0.60 (0.45)
MaxFM	6.84 (0.02)	118.7 (0.00)	0.38 (0.55)
λ*S	0.26 (0.61)	236.7 (0.00)	1.36 (0.06)

(B) between-factor: Age; within-factors: NOP and VIS
	Group F (p-value)	Condition F (p-value)	Group x Condition F (p-value)
step length	0.18 (0.67)	39.02 (0.00)	2.30 (0.14)
step width	0.17 (0.68)	29.51 (0.00)	0.001 (0.96)
step length variability	0.15 (0.69)	14.79 (0.00)	0.48 (0.49)
step width variability	0.18 (0.67)	47.23 (0.00)	0.96 (0.34)
MeanSDpos	0.25 (0.63)	39.37 (0.00)	0.52 (0.48)
MeanSDvel	0.01 (0.93)	49.24 (0.00)	0.69 (0.42)
MaxFM	0.31 (0.59)	89.55 (0.00)	0.69 (0.42)
λ*S	0.22 (0.65)	125.7 (0.00)	10.36 (0.04)

^*Note: bold columns indicate significant differences (p < 0.05). Degrees of freedom are F(1,20) for all factors and for both ANOVAs

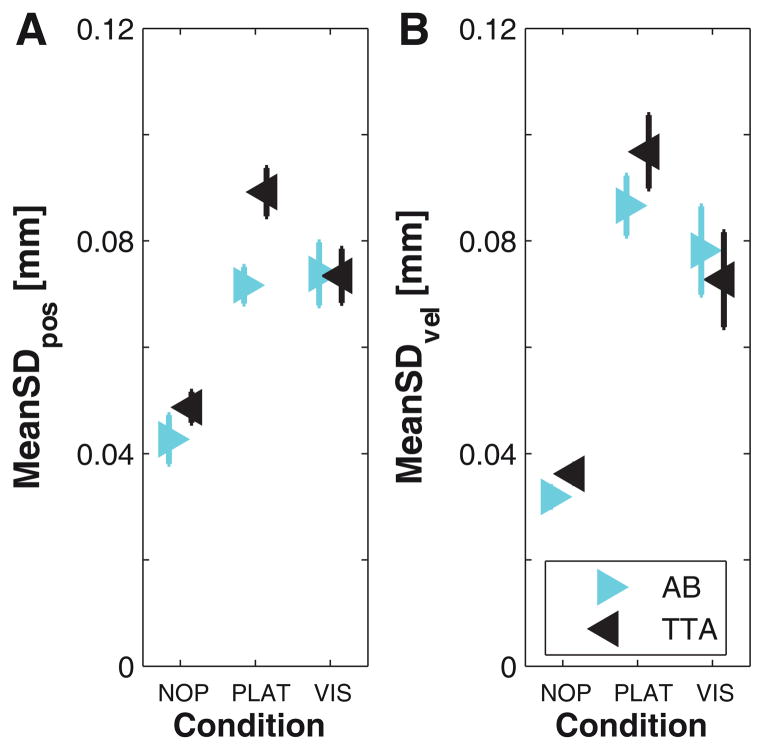
Able-bodied controls and individuals with amputations exhibited greatly increased trunk variability for both MeanSD_pos (Fig. 3A) and MeanSD_vel (Fig. 3B) from NOP to PLAT both and VIS (Table 2). For MeanSD_pos, TTA were slightly more variable than AB during NOP trials and increased their variability compared to AB during PLAT perturbations (Fig. 3A; Table 2A). For MeanSD_vel, both TTA and AB increased their trunk variability similarly, with TTA being slightly more variable in PLAT (Fig. 3B).

Figure 3. Kinematic Variability (MeanSD_pos and MeanSD_vel) of C7.

A: Mean standard deviation (MeanSD) of C7 vertebra marker displacements (position). B: MeanSD of C7 vertebra marker velocity. Each graph shows data separately for all healthy controls (AB) and all amputees (TTA) for all three walking conditions. Error bars indicate the appropriate between-subject ± standard error.

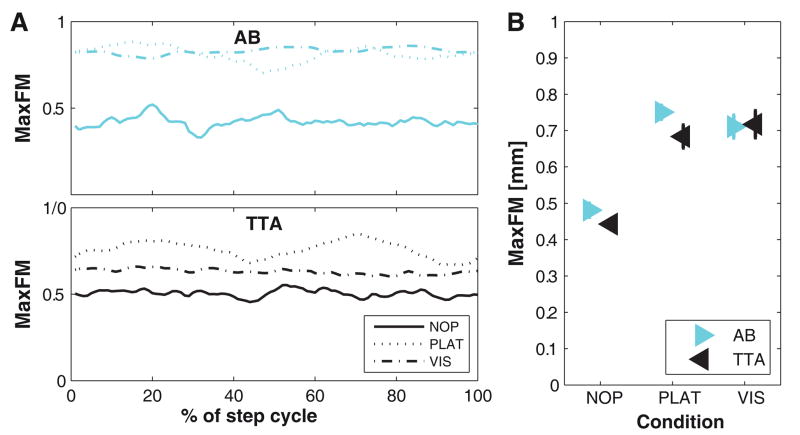
Across the gait cycle, raw MaxFM values fluctuated slightly but irregularly for NOP and VIS trials, but oscillated somewhat more systematically for PLAT trials (Fig. 4A), consistent with previous findings (Sinitski et al., 2012). However, no major qualitative differences were observed between subject groups. Both AB and TTA exhibited increased MaxFM when walking with either PLAT or VIS perturbations compared to NOP (Fig. 4B; Table 2). During NOP and PLAT, trunk movements of TTA were slightly more orbitally stable than those of AB (Table 2A); however, this difference did not reach statistical significance (Table 2A).

Figure 4. Orbital Dynamic Stability (MaxFM) of C7.

A: Maximum Floquet multipliers for all Poincaré sections (0–100% of gait cycle) for one typical healthy control subject (AB) and one person with amputation (TTA) for all three different walking conditions (NOP, PLAT< and VIS). B: Mean orbital stability (MaxFM) for all healthy controls (AB) and all amputees (TTA) separately for each walking condition. Error bars indicate the appropriate between-subject ± standard error.

Similar to orbital stability, local dynamic instability (λ^*_S) increased significantly for both AB and TTA groups when walking with either PLAT or VIS perturbations (Fig. 5A–B; Table 2). There were no significant main effects differences between groups, although the increase in local dynamic instability was slightly more pronounced in AB compared to TTA when exposed to VIS perturbations (Table 2B).

Discussion

Persons with lower limb amputation experience significant anatomical and neuro-motor compromise, including disrupted sensory feedback. These patients may slow down (Lamoth et al., 2010) and/or take shorter, wider steps (Gates et al., 2012; Hak et al., 2013), etc. to be more “cautious” (Tsai and Lin, 2013). However, they still experience a significantly high fall risk (Miller et al., 2001), indicating that these adaptations are not fully successful. Determining how persons with amputation respond to destabilizing situations is critical to better understand why they fall and to develop effective interventions. Previous studies report mixed results when comparing various measures of stability in patients with amputation to unimpaired controls during unperturbed walking (Lamoth et al., 2010; Wurdeman et al., 2013), when walking over irregular terrain (Lamoth et al., 2010; Curtze et al., 2011; Gates et al., 2013), or when explicitly perturbed (Hak et al., 2013). This study determined how patients with transtibial amputation responded to perturbations known to substantially destabilize walking humans (McAndrew et al., 2010; 2011).

All subjects responded very strongly and significantly to both the mechanical and visual perturbations. They exhibited substantial increases in stepping variability (Fig. 2C–D), trunk movement variability (Fig. 3), MaxFM (Fig. 4), and λ^*_S (Fig. 5) for both the PLAT and VIS conditions compared to NOP. Thus, these perturbations clearly destabilized subjects, precisely as intended (McAndrew et al., 2010; 2011). Likewise, these effects were unambiguously captured by the dependent measures analyzed here.

In response to these perturbations, both AB and TTA subjects appeared to adopt more “cautious” walking patterns (Tsai and Lin, 2013), taking wider (Fig. 2A) and slightly shorter (Fig. 2B) steps consistent with previous reports (Lamoth et al., 2010; McAndrew et al., 2010; Gates et al., 2012; Hak et al., 2013). However, in spite of changing their stepping behavior, subjects in both groups still exhibited increased variability (Fig. 2C–D; Fig. 3) and increased orbital and local instability (Figs. 4–5) of their trunk motions. When able-bodied subjects were explicitly instructed to walk with shorter or wider steps, they too initially became slightly more unstable (McAndrew Young and Dingwell, 2012). Therefore, taking shorter and/or wider steps alone did not fully mitigate the destabilizing effects of the perturbations imposed.

Despite the substantial and consistent responses to the imposed perturbations, the persons with TTA tested here did not exhibit greater orbital or local dynamic instability of their trunk movements than able-bodied controls (Figs. 4–5; Table 2). These TTA subjects exhibited orbitally slightly more stable C7 movements for the NOP vs. PLAT comparisons (Fig. 4B) and smaller increases in λ^*_S of C7 movements when subjected to VIS perturbations (Fig. 5B). Conversely, previous work demonstrated that elderly exhibited both greater variability (Kang and Dingwell, 2008b) and greater instability of trunk movements (Kang and Dingwell, 2008a) than young subjects during unperturbed walking. However, the present findings are consistent with work from both our lab (Gates et al., 2012; 2013) and others (Hak et al., 2013) showing that persons with TTA can effectively compensate to maintain appropriate control of upper/whole body movements, even during challenging walking tasks, like those imposed here (Beltran et al., 2014).

The small differences observed between these TTA and AB groups could have resulted from limited sample size (n = 9 TTA). However, this seems unlikely for several reasons. First, other studies reported either significant differences with equivalent samples (Lamoth et al., 2010; Hak et al., 2013), or non-significant differences for related measures with larger samples (Gates et al., 2012; 2013). Second, both subject groups exhibited very similar between-subject variability for stepping variability (Fig. 2C–D), trunk variability (Fig. 3) and both local and orbital stability (Figs. 4–5). Lastly, previous studies that used different implementations of the local stability analyses used here found either only very small (Hak et al., 2013) or even opposite effects (Lamoth et al., 2010) when subjects both with and without amputation walked in destabilizing conditions. In contrast, our analyses yielded dramatic increases in λ^*_S when subjects were perturbed (Fig. 5B; McAndrew et al., 2011), demonstrating that the stability measures calculated here are highly sensitive to changes in local/orbital dynamic stability when present.

An alternative possible explanation is that this study quantified local/orbital stability of only trunk movements. We focused on the trunk because controlling the motions of this large mass is paramount to maintaining whole-body balance (Dingwell and Marin, 2006; Pandy et al., 2010). In spite of their significant impairments, the persons with TTA tested here achieved similar trunk local/orbital stability, even when substantially perturbed (Figs. 4–5). However, it is possible these persons with TTA achieved these similar overall trunk movements by making different alterations in their lower extremity movements. Movements of inferior body segments (e.g. legs, feet) likely contribute to stabilizing superior segments (e.g. pelvis, trunk) (Prince et al., 1994; Kang and Dingwell, 2009a). The significant increases in stepping variability (particularly during PLAT perturbations) observed here (Fig. 2C; Table 2) support this view, as do results of a companion analysis of these same data, which showed increased means and variability of mediolateral margins of stability among persons with TTA, but only during PLAT perturbations (Beltran et al., 2014). Other studies have likewise reported increased local dynamic instability of leg movements in persons with unilateral TTA during unperturbed walking (Wurdeman et al., 2013) and also significantly increased stepping variability when walking over loose rocks (Gates et al., 2012).

In addition to their biomechanical impairments, persons with lower limb amputation also experience disrupted somatosensory feedback (Gandevia, 2001). Here, we tested whether findings that persons with amputation rely more heavily on visual feeback for standing (Fernie et al., 1978; Vanicek et al., 2009) also extend to walking. Greater reliance on vision would have resulted in greater differentiation between TTA and AB subjects during the VIS perturbation trials relative to NOP. However, these VIS perturbations yielded no between-group differences in stepping variability (Fig. 2C–D), trunk variability (Fig. 3), or orbital stability of trunk movements (Fig. 4B), consistent with previous findings (Beltran et al., 2014). These TTA subjects also exhibited less sensitivity to the VIS perturbations for local stability of trunk movements (Fig. 5B). This suggests these persons with TTA patients did not rely more heavily on visual feedback to maintain trunk stability during walking.

The persons with TTA tested here were all active-duty military service members, perhaps less typical of the broader population of patients with lower-limb amputations. This allowed us to control for walking speed, an important indicator of physical performance (van Velzen et al., 2006). Here, each subject walked at the same speed during all conditions and speeds did not differ between groups (p = 0.87). Thus, these TTA subjects achieved similar local/orbital dynamic stability of their trunk movements independent of any changes in walking speed. Thus, in the absence of other common co-morbidities, otherwise relatively healthy patients with unilateral TTA appear to retain sufficient sensory and motor function to maintain local/orbital stability of their upper body movements.

People with lower limb amputation exhibit increased fall risk and younger patients with traumatic amputation fall as often as older patients (Miller et al., 2001). This study demonstrated that a cohort of high-functioning persons with transtibial amputation did not differ substantially from able-bodied individuals in terms of local or orbital stability of trunk (C7) movements. The analyses applied here are highly responsive both to perturbations (McAndrew et al., 2011) and to age-related physiological changes that likely increase fall risk (Kang and Dingwell, 2008a; 2009b; Toebes et al., 2012). Thus, it is possible the increased fall risk in these young, otherwise relatively healthy patients may be more likely due to greater risk-taking associated with a more active lifestyle (Faulkner et al., 2009) than to the physical impairments directly related to their amputation itself, and/or possibly to impaired ability to properly regulate movements of the distal limb segments (Beltran et al., 2014).