Abstract
Studies employing functional connectivity-type analyses have established that spontaneous fluctuations in functional magnetic resonance imaging (fMRI) signals are organized within large-scale brain networks. Meanwhile, fMRI signals have been shown to exhibit 1/f-type power spectra – a hallmark of scale-free dynamics. We studied the interplay between functional connectivity and scale-free dynamics in fMRI signals, utilizing the fractal connectivity framework – a multivariate extension of the univariate fractional Gaussian noise model, which relies on a wavelet formulation for robust parameter estimation. We applied this framework to fMRI data acquired from healthy young adults at rest and performing a visual detection task. First, we found that scale-invariance existed beyond univariate dynamics, being present also in bivariate cross-temporal dynamics. Second, we observed that frequencies within the scale-free range do not contribute evenly to inter-regional connectivity, with a systematically stronger contribution of the lowest frequencies, both at rest and during task. Third, in addition to a decrease of the Hurst exponent and inter-regional correlations, task performance modified cross-temporal dynamics, inducing a larger contribution of the highest frequencies within the scale-free range to global correlation. Lastly, we found that across individuals, a weaker task modulation of the frequency contribution to inter-regional connectivity was associated with better task performance manifesting as shorter and less variable reaction times. These findings bring together two related fields that have hitherto been studied separately – resting-state networks and scale-free dynamics, and show that scale-free dynamics of human brain activity manifest in cross-regional interactions as well.
Keywords: Scale-free dynamics, Cross-temporal dynamics, fMRI, Intrinsic brain activity, Task modulation
1. Introduction
In recent years, functional-connectivity analysis applied to resting-state blood oxygen level-dependent (BOLD) fMRI has revealed a rich intrinsic functional architecture of brain activity, manifesting as large-scale, coherent brain networks that recapitulate the spatial patterns of task activations [1, 2, 3, 4, 5, 6, 7, 8]. The functional significance of fMRI resting-state networks (RSNs) has been demonstrated in various neurological and psychiatric diseases by showing that the degree of disruption of resting-state networks (RSNs) correlated with the severity of the disorder [9, 10, 11]. Moreover, repetitive training over period of days sculpts spontaneous activity of the resting human brain, suggesting dynamic reconfiguration of RSNs [12].
Most studies assessing functional connectivity so far have used either a seed-based region-of-interest (ROI) approach, in which the time series associated with a chosen ROI is used as a regressor to identify regions of similar temporal behavior across the brain [1, 5, 13], or an independent component analysis (ICA) – an exploratory approach for identifying spatial regions with temporally coordinated activity [14, 15, 16]. Each approach relies on either anatomically or statistically driven a priori assumptions (see [17]) for a general review of the pros and cons of both approaches). The seed-based method relies largely on the computation of linear Pearson correlation coefficients between the temporal fluctuations of BOLD signal in different brain regions. The ICA approach identifies spatial components that are maximally independent, each component grouping voxels with similar temporal dynamics [14, 17].
In nature, Pearson’s correlation is linear, static and global. Whether linear coupling is sufficient in describing interactions between brain regions or networks has been studied with care, using the functional integration index and mutual information [18, 19]. Definitive answers are still lacking, which depends on whether fMRI data are well modeled as Gaussian processes, and whether their dependence structure can be described by the sole correlation coefficient. It has been observed that depending on the spatial scale at which the correlation measure is assessed, departure from Gaussianity may be relatively minor (within-network) [18] or significant (between-network) [19].
Pearson’s correlation can also be considered a static measure of dependency since it does not provide practitioners with any information regarding the contributions of the different frequencies to correlation. To bridge that gap, the coherence function can be used to measure the relative contributions of the different frequencies to correlation [20, 21, 22].
The global nature of Pearson’s correlation prevents assessment of dependencies that vary over time. To overcome that limitation, local correlation coefficients can be computed via sliding windows [21, 22, 23] to access dynamic functional connectivity in humans or animals [23, 24]. It is however natural and efficient to combine local (time-varying) and frequency-dependent correlation measure into time-frequency or wavelet-based measures of correlation such as the wavelet transform coherence [21]. Indeed, temporal reconfigurations of fMRI RSNs have been recently observed over typical scan durations (several minutes) using time-resolved acquisitions and a cascade of spatial and temporal ICA [25], or sliding-window ICA or principal component analysis (PCA) [26, 27]. More recently, it has been demonstrated that the spatial signature of RSNs can be reconstructed from a few spontaneous coactivation patterns occurring at critical time points using a point process methodology [28] or a clustering algorithm [29].
In a separate vein, the temporal dynamics of brain activity has also been extensively studied. In both BOLD fMRI and electrophysiological recordings from the brain, a major component of brain activity is arrhythmic and demonstrates scale-invariance in temporal dynamics (i.e., “scale-free dynamics”), suggesting that no single time scale plays a predominant role [30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44]. Scale-free dynamics is associated with long-range dependence (also called “long memory”) and self-similarity in time [45] and a power-law distribution of the power spectrum (Γ(f) ∝ 1/fα with α > 0) in the frequency domain. Scale-free dynamics in fMRI signals have been shown to localize to grey matter (30–31), vary across behavioral conditions and brain networks [42, 43], alter with age [46], arousal state [47], and disease processes [48]. Moreover, long memory in fMRI signals, as quantified by Hurst exponent, decreases during task in both activated and deactivated brain regions [42]. In parallel, it has been shown that arrhythmic low-frequency fluctuations of brain electrical field potentials (< 4 Hz) are organized in the same intrinsic large-scale brain networks revealed by resting-state fMRI [35] and too demonstrate decreased long memory during task state [39]. Thus, analyzing scale-invariance in temporal dynamics may provide novel insights into brain mechanisms underlying cognition and behavior [31, 33, 34, 35, 39, 42, 43, 46, 48].
The present study aims at analyzing functional connectivity within and amongst RSNs beyond the use of the Pearson correlation coefficient ρXY by investigating scale-free cross-temporal dynamics. To this end, the fractal connectivity framework is used, which extends the classical univariate models of fractional Brownian motion (fBm)/fractional Gaussian noise (fGn) [49] into a multivariate setting and thereby allowing the investigation of scaling behaviors of cross-spectra [50]. More precisely, while the Hurst exponent H is classically used to quantify univariate scale-free temporal dynamics, scale-free cross-temporal dynamics between two regions X and Y are quantified by a scaling exponent αXY, related to the power-law decay of the cross spectrum. Exponent γXY = αXY − (HX + HY) + 1 is further defined to evaluate the extent to which cross-temporal dynamics contribute to functional connectivity: When γXY = 0, the cross spectrum contains no extra information beyond that carried by the auto spectra; in this case, functional connectivity between regions X and Y is said to follow fractal connectivity. Conversely, γXY ≠ 0 indicates that γXY conveys dynamical information not already contained in the static ρXY : It acts as a scale-free parameter to gauge the balance between different frequencies in their contributions to functional connectivity. Specifically, the recent formulation of fractal connectivity into a wavelet framework, referred to as wavelet fractal connectivity [51] is adopted here, as it allows the analysis of scale-free cross-temporal dynamics in a theoretically well-grounded and practically efficient manner. Hence, in the present work, functional connectivity in fMRI data is analyzed beyond the static correlation ρXY, under the additional light of the frequency balance parameter γXY.
2. Methods
Functional magnetic resonance imaging (fMRI) data were acquired from seventeen normal healthy young adults (9 females, age 18–27 years) at rest and performing a visual detection task. All subjects provided written informed consent. This data set has been previously published in separate studies [42, 52, 53]. Detailed methods can be found in SI Methods.
2.1. fMRI data acquisition
Blood-oxygen-level dependent (BOLD) fMRI data (4×4×4 mm3 voxels, TE 25 ms, TR 2.16 s) were acquired in 17 normal right-handed young adults (9 females, age 18–27 years) using a 3T Siemens Allegra MR scanner. All subjects gave informed consent in accordance with guidelines set by the Human Studies Committee of Washington University in St. Louis. Each subject completed 8 fMRI runs, each 194 frames (~ 7 min) in duration. They consisted of two alternating run types. The first run type was a resting-state study in which a white crosshair was presented in the center of a black screen. Subjects were instructed to look at the crosshair, remain still, and to not fall asleep. The second run type was a task study in which the identical crosshair was presented, but now it occasionally changed from white to dark gray for a period of 250 ms, at times unpredictable to the subjects. The subjects were instructed to press a button with their right index finger as quickly as possible when they saw the crosshair dim. Each of these button-press runs contained 20 crosshair dims time-locked to the scanner TR, with an inter-trial interval of 17.3–30.2 s. Subjects practiced this button-press task once in the scanner, prior to the onset of the functional scans. Anatomical MRI included a high-resolution (1×1×1.25 mm3) sagittal, T1-weighted MP-RAGE (TR 2.1 s, TE 3.93 ms, flip angle = 7°) and a T2-weighted fast spin-echo scan. This data set has been previously published in separate studies [42, 52, 53]. All analyses were carried out using custom-written codes in C++ and Matlab.
2.2. fMRI data preprocessing
fMRI preprocessing steps included, i.) compensation of systematic, slice-dependent time shifts, ii.) removal of systematic odd-even slice intensity difference due to interleaved acquisition (slice-timing correction); iii.) rigid body correction for inter-frame head motion within and across runs, and iv.) intensity scaling to yield a whole-brain mode value of 1000 (with a single scaling factor for all voxels). Atlas registration was achieved by computing affine transforms connecting the fMRI run first frame (averaged over all runs after cross-run realignment) with the T2- and T1- weighted structural images [54]. Our atlas representative template included MP-RAGE data from 12 normal individuals and was made to conform to the 1988 Talairach atlas [55]. Data were resampled to 3×3×3 mm3 voxels after atlas registration. The first four frames of each fMRI run were discarded in all further analyses. The fMRI time courses from each run were made zero-mean and the linear trend was removed. Lastly, the effect of head motion and its temporal derivative were removed by linear regression.
It is known that sudden head movements (like “spikes”) may have a strong influence in the estimated scaling exponents. To cope with this issue, a recent approach has been proposed in [56]. It consists of erasing segments of time series which are corrupted by very large head movements. This methodology turned out to be robust for Hurst exponent analysis at least using detrended fluctuation analysis (DFA) [57]. In this study, given the short length of time series, we first investigated the presence of large head movements. As detailed in Appendix A, we found that there were very few movement spikes, such that the removal of temporal segments containing them was unnecessary. Moreover, as detailed later, we rely on a wavelet framework for scaling exponent estimation, which further brings extra robustness against non-stationarities, compared to DFA cf. e.g., [58].
2.3. Definition of regions of interest (ROIs)
31 ROIs were obtained from a previous task-related functional neuroimaging studies or generated using coordinates from published fMRI studies, which included 10 pairs of homologous brain regions. These ROIs were the same as used in our previous study [42]. Their locations in the brain are shown in Fig. 1A (mapping to brain surface was done in CARET1). The regions were grouped into five cortical networks based on their known anatomical/functional properties (including attention, default-mode, motor, saliency and visual networks) and a separate group outside the neocortex including hippocampus, thalamus and cerebellum.
Figure 1. Networks definition and correlation structure.
Top (A): ROIs mapped onto the cortical surface, with each color denoting a different network. Middle (B): Group-averaged inter-regional correlation matrix at rest (p < 0.05, Bonferroni corrected). Regions are grouped by network to ease visualization. Details of the ROIs are provided in Table 1. Middle (C): Group-averaged inter-regional correlation matrix during the visual detection task (p < 0.05, Bonferroni corrected). Bottom (D): Difference of the correlation coefficients between rest and task (thresholded at p < 0.01, uncorrected, two-sample t-test for rest vs. task). The ROIs are grouped by networks whose names are given in Table 1; these networks correspond to the diagonal triangles surrounded by white dashed lines.
The anatomical locations, Talairach coordinates, references and associated networks of these ROIs are listed in Table 1. Specifically, the attention, motor, visual, thalamus and cerebellum regions were obtained from functional studies conducted in [59]. The default network regions were obtained from task-deactivation patterns from a meta-analysis of nine PET studies, which originally unveiled the default network [60]. To generate these ROIs, following methods described in [59], the activation or deactivation Z-score maps were subjected to an automatic peak search, peaks closer than 10 mm were consolidated by averaging their coordinates, and ROIs were defined around peaks by thresholding the map to yield regions of approximately 905 mm3, similar size as the coordinates-derived ROIs described below.
Table 1.
Anatomical information and references for each ROI. Note that the ROI appearance order below defines the order of ROI entries in the following functional connectivity matrices such as Fig. 1B.
| Network | ROI | Anatomical location | Talairach coordinates |
|---|---|---|---|
| Attention (AN) | vIPS[59] | (L and R) ventral intraparietal sulcus | −24, −69, 30 30, −80, 16 |
| pIPS[59] | (L and R) posterior intraparietal sulcus | −25, −63, 47 23 −65 48 |
|
| R TPJ | R temporoparietal junction | 49, −50, 28 | |
| MT[59] | (L and R) middle temporal region | −43, −70 −3 42 −68 −6 |
|
| FEF[59] | (L and R) frontal eye field | −26, −9, 48 32, −9, 48 |
|
| R DLPFC[61, 62, 63] | R dorsolateral prefrontal cortex | 43, 22, 34 | |
|
| |||
| Default Mode (DMN) | AG[60] | (L and R) angular gyrus | −51, −54, 30 45, −66, 27 |
| SFG[60] | (L and R) superior frontal cortex | −15, 33, 48 18, 27, 48 |
|
| PCC[60] | posterior cingulate cortex | −6, −45, 33 | |
| MPF[60] | medial prefrontal cortex | −6, 51, −9 | |
| FP[60] | frontopolar cortex | −3, 45, 36 | |
|
| |||
| Motor (MN) | L SII[59] | L second somatosensory area | −57, −27, 21 |
| L motor[59] | L primary motor cortex | −39, −27, 48 | |
| Broca[64] | Broca’s area | −42, 13, 14 | |
|
| |||
| Non-Neocortical (NC) | ThalamusciteHe07b | (L and R) thalamus | −15, −21, 6 9, −18, 9 |
| R Cerebellum[59] | R Cerebellum | 21, −54, −21 | |
| HF[65] | (L and R) hippocampal formation | −21, −25, −14 23, −23, −14 |
|
|
| |||
| Saliency (SN) | R FI[62] | R frontoinsular cortex | 36, 21, −6 |
| dACC[61] | dorsal anterior cingulate cortex | −1, 10, 46 | |
|
| |||
| Visual (VN) | vRetino [59] | (L and R) ventral retinal region | −15, −75, −9 15, −75, −9 |
| dRetino [59] | (L and R) dorsal retinal region | −6, −75, 9 9, −75, 12 |
|
The dosolateral prefrontal cortex (DLPFC), part of the frontoparietal attention network, and the saliency (also called “core task-control”) network regions were obtained from published coordinates in three studies [61, 62, 63]. The coordinates for Broca’s area and the hippocampal formation (HF) were obtained from [64] and [65], respectively. In cases where coordinates from multiple studies were obtained for one ROI, such as the R DLPFC and R TPJ (Table 1), the center-of-mass of these coordinates were used. A 6-mm-radius sphere ROI centered at these coordinates was created for each region. All regions used in the present study have been investigated in seed-based functional connectivity analyses applied to resting-state fMRI data by the author and, for ROIs in the attention and saliency networks as well as the HF, also in previous published studies [59, 62, 63, 65, 66] and have yielded networks consistent with those reported in the literature [1, 3, 7, 67].
2.4. Scale-free temporal dynamics modeling
Scale-free temporal dynamics is now a commonly observed property in brain activity [42]. To account for scale-free temporal dynamics in brain dynamics, these references propose quasi-exclusively, either implicitly or explicitly, to use fractional Gaussian noise (fGn), the celebrated model put forward by Mandelbrot [49] and massively used in many other scientific fields (see [68] for a review). In essence, fGn assumes that data have Gaussian marginal distributions and a power-law type spectral behavior, across a large range of frequencies:
| (1) |
where α is related to the Hurst parameter H as α = 2H − 1. This model is relevant when analyzing brain activity measured from univariate time series, each associated with a given region of interest. However, to assess functional connectivity, it is needed that a collection of time series each associated with a different region of interest, are studied jointly (or simultaneously), to measure for instance how they correlate one to another. It is thus natural to make use of a model inspired from the multivariate extension of fGn (mfGn), proposed e.g., in [69, 70]. In essence, this model assumes joint Gaussianity for the time series and power-law behaviors both for the auto- and cross-spectra, across a large range of frequencies.
For the sake of simplicity, the model is stated here in the bivariate case only, with a straightforward multivariate extension. Let X and Y denote two time series associated with two brain regions. Their auto- and cross-spectra are defined as, for fm ≤ |f| ≤ fM, fM/fm ≫ 1:
| (2) |
with parameters αX = 2HX − 1 and αY = 2HY − 1 confined to the range [0, 1]. Two important notes are now in order. First, mfGn theoretically further imposes that αXY = (αX + αY)/2 = HX + HY − 1. In the present work, we allow αXY to depart from (HX + HY) − 1 this is why the model used here is not strictly mfGn but rather inspired from. Second, the theoretical definitions of both fGn and mfGn, actually imply that their spectra exhibit power-law behavior in the limit of low frequencies: |f| → 0. Practically, however, power law behaviors are often assumed to hold across a large but finite range of frequencies: fm ≤ |f| ≤ fM (with possibly fm > 0). We will stick to that standard practice, while, with a slight abuse of language, continuing to refer to these processes as fGn and mfGn. While in the univariate case, this has little impact on the actual use of fGn as a model for real data, this is of much larger importance in the multivariate setting as this allows theoretically both positive and negative departures of γXY = αXY − (HX + HY − 1) from 0, thus providing us with a significant gain in versatility for analyzing spontaneous brain activity.
2.5. Coherence function
In the classical assessment of linear dependencies, the correlation coefficient ρXY is used. It consists of a static quantity that conveys no information related to the way the different frequencies contribute to the global correlation of X and Y. To overcome that limitation, the coherence function can naturally be used. It consists of a (sort of) frequency-dependent correlation coefficient [71]:
| (3) |
By definition, it takes values between −1 ≤ CXY (f) ≤ 1 and is proportional to ρXY. When |CXY (f)| = |ρXY|, ∀ f, all frequencies are equally or equivalently contributing to global correlation. Conversely, frequencies such that |CXY (f)| > |ρXY| contributes more to global correlation compared to frequencies where |CXY (f)| < |ρXY|.
2.6. Fractal connectivity
When X and Y follow the bivariate correlated scale-free model defined in Eq. (2), the coherence function becomes, for fm ≤ |f| ≤ fM:
| (4) |
Fractal connectivity is theoretically defined as the case where CXY (f) reduces to a (non-zero) constant over the range fm ≤ |f| ≤ fM, i.e.,
| (5) |
The intuition underlying fractal connectivity is that, for scale-free data, all frequencies are contributing to the correlation (and hence to functional connectivity) in an equivalent manner, or in a mfGn-type compatible manner. In that case, the coherence function does not bring any extra information compared to the sole static correlation coefficient. Conversely, assuming ρXY ≠ 0, γXY > 0 (resp., γXY < 0) indicates that low frequencies contribute more (resp., less) to correlation of X and Y than do high frequencies. Therefore estimating γXY and hence the coherence function brings complementary information related to the way temporal dynamics contribute to functional connectivity, compared to the sole static correlation coefficient ρXY .
Note that, in that context, low and high frequencies are defined in a relative manner: First, the range of frequencies, fm ≤ |f| ≤ fM, where scale-free properties are observed is estimated. Second, low and high refer respectively to the lower and upper sub-ranges of that scale-free range of frequencies.
Two interesting limit behaviors are worth being described:
When |ρXY| → 1 then necessarily γXY → 0 because 0 ≤ |CXY (f)| ≤ 1, ∀ f;
When |ρXY| → 0 then γXY is ill-defined as the cross-spectrum is identically zeros, and γXY is thus observed to be estimated with large variance [72].
2.7. The Wavelet estimation framework
It is now well-documented that the analysis of real-world data with scale-free properties can be conducted in a theoretically well grounded and and practically robust and efficient manner using wavelet coefficients, cf. e.g., [72, 73, 74, 75, 58] in general contexts and [36, 43, 76, 77] for brain activity analysis. Therefore, the fractal connectivity model proposed here is recast into a wavelet framework. This is detailed in Appendix B, which also discusses scaling parameter estimation.
2.8. Correction for multiple comparisons
Unless otherwise mentioned, all reported p-values for the statistical tests of correlation, self-similarity or fractal connectivity model where Bonferroni corrected for multiple comparisons. To this end, we divided the type-I error rate α = 0.05 by the number of simultaneous comparisons due to the 21 ×20/2 = 210 distinct region pairs. To control the family-wise error rate at level α (equivalent to 1.3 in a −log10 pval scale as shown in Fig. 6A–B for instance), we computed the corrected p-values by applying the following rule to uncorrected p-values pval-corr = min(1, 210 × pval-uncorr).
Figure 6. Cross-spectrum scaling exponents.
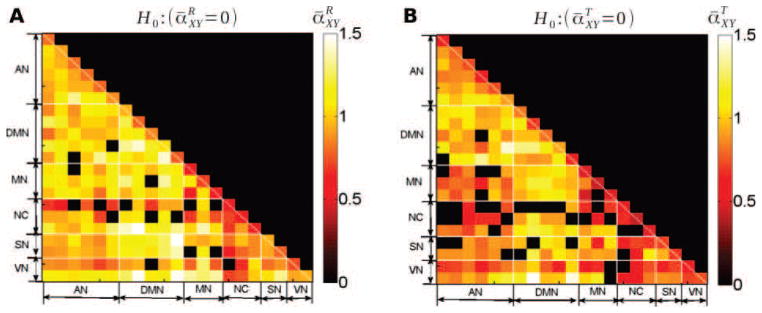
Group-average values of the scaling exponent of the cross-spectrum at rest (A) and during task (B), i.e. and , respectively. Only region pairs where the scaling exponent significantly departed from 0 (p < 0.05, Bonferroni corrected, one-sample t-test) are shown. Thus, scaling is significant for all cross-spectra associated with “hot squares”.
3. Results
3.1. Correlation-based functional connectivity analysis
The fMRI dataset comprised of seventeen right-handed subjects who were scanned at rest and during a visual detection task [42, 52, 53]. FMRI data was preprocessed before extracting signals from 31 ROIs obtained from previous task-related functional neuroimaging studies or generated using coordinates from published fMRI studies, which covered five brain networks [Attention, Default-mode (DMN), Motor, Saliency and Visual] as well as several non-neocortical ROIs (thalamus, cerebellum and hippocampus) (see SI). Projection of regions onto the cortical surface is shown in Fig. 1A. In following analyses, 10 pairs of homologous regions were each averaged together. This step was performed because we observed in preliminary analyses (see also [42]) that the time series of these homologous regions are highly correlated with each other and that their statistical properties are very similar. Thus, we averaged across homologous reigons in the same RSN in order to enhance statistical independence between investigated brain regions.
Correlation coefficients ρXY were estimated from the rest and task dataset separately for all pairs of regions, and were Fisher z-transformed (ZXY) for statistical testing. Group-level means of correlation coefficients were computed at rest ( ) and during task ( ) and mapped onto the significant one-sample t-tests and , respectively. Comparing Fig. 1B vs Fig. 1C, it can be seen that correlation remains high during task between regions belonging to a same network, whereas lower correlations are observed for between-network region pairs – specifically, between DMN and other networks, a result likely attributable to their respective task-deactivation and activation [3]. Fig. 1D shows region pairs with a significant change in correlation between rest and task (paired t-test across subjects; ). Significant (p < 0.01) differences between rest and task were observed mainly for pairs of regions consisting of one region located in DMN and the other in the decoupled networks (Attention, Visual, Motor, Saliency and the thalamus). Moreover, in all these region pairs, correlation was higher under rest than task ( ).
3.2. Scale-free univariate analysis
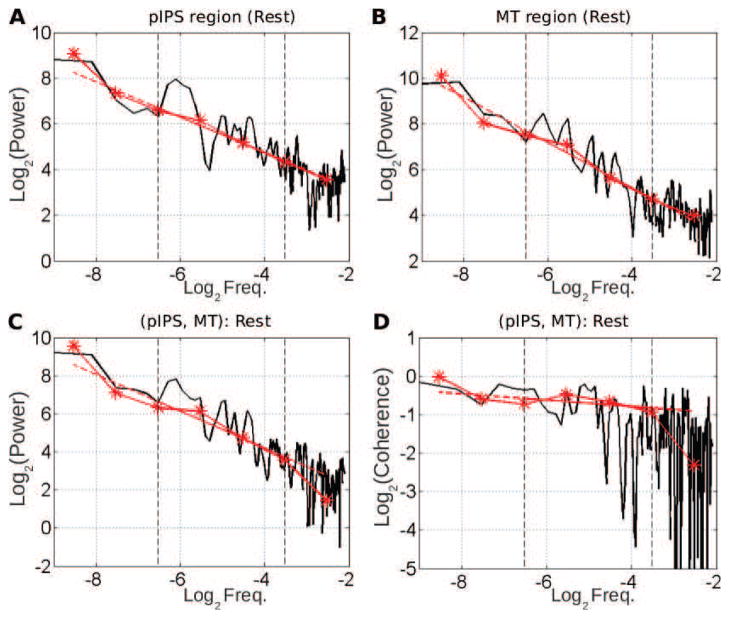
We first applied the wavelet spectrum estimation framework to investigate univariate temporal dynamics of fMRI signals. As an example, Figs. [2– 3]A–B shows the superimposition of the power spectrum estimated by the standard Welch-Periodogram and by wavelet method (log2 SX(2j) vs. log2 2j) for two regions [posterior intra-parietal sulcus (pIPS) and middle temporal area (MT)] located in the dorsal attention network (DAN) at rest (Fig. 2A–B) and during task (Fig. 3A–B), respectively. The match between the classical power spectrum and wavelet spectrum confirms that wavelet coefficients can serve as an efficient estimator for the spectrum. Both the classical and wavelet spectra exhibited power-law scaling behavior over the range of 0.01 < f < 0.1 Hz (corresponding to 3.3 < j < 6.6 with f = 2−j). Indeed, applying the goodness-of-fit assessment procedure described in Appendix C shows that, out of the 357 analysed time series (17 subjects ×21 regions), rejection of the null hypothesis that the wavelet auto-spectrum is well described by a power law in that range of scales, occurs for only 16% and 14% of cases, at rest and during task respectively. This confirms earlier finding in [42, p. 13788]. Also, similar results were obtained across ROIs and subjects, consistent with earlier reports [42, 43]. Henceforth, this range of frequencies is referred to as the scaling range.
Figure 2. Univariate (A–B) and multivariate (C–D) scale-free properties of fMRI signals at rest – example from a single subject.
A–B: Superimposition of the auto-power spectrum estimated by Welch-Periodogram (black) and wavelet method (red) for pIPS and MT. C: Superimposition of the cross-power spectrum between pIPS and MT estimated by Welch (black) and wavelet method (red) in log-log coordinates. D: Superimposition of the coherence function between pIPS and MT estimated by Welch (black) and wavelet (red) method. All exponents are estimated from linear regression based on the wavelet estimate (dashed red lines) in the scaling range defined by vertical dashed black lines (−6.6< log2 f < −3.3).
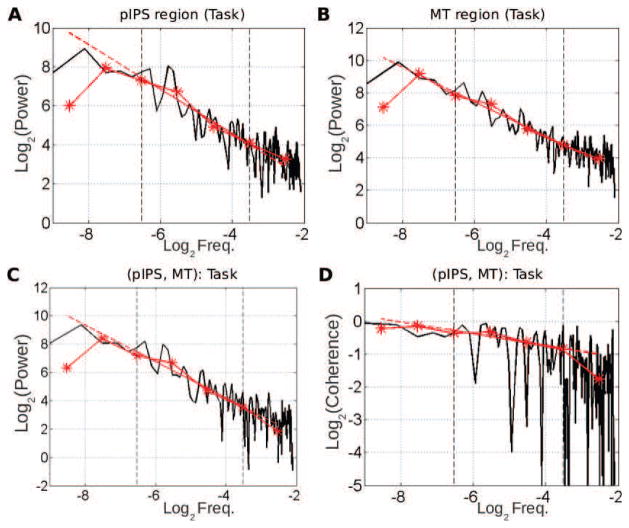
Figure 3. Univariate (A–B) and multivariate (C–D) scale-free properties of fMRI signals during task (same subject as in Fig. 2.
A–B: Superimposition of the auto-power spectrum estimated by Welch-Periodogram (black) and wavelet method (red) for pIPS and MT. C: Superimposition of the cross-power spectrum between pIPS and MT estimated by Welch (black) and wavelet method (red) in log-log coordinates. D: Superimposition of the coherence function between pIPS and MT estimated by Welch (black) and wavelet (red) method. All exponents are estimated from linear regression based on the wavelet estimate (dashed red lines) in the scaling range defined by vertical dashed black lines (−6.6< log2 f < −3.3).
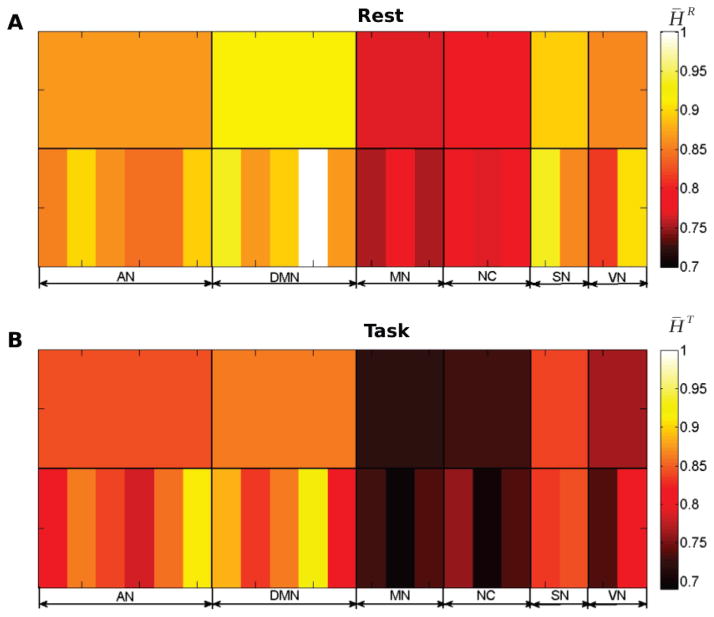
Hurst exponents were then estimated from the wavelet spectrum for each region and individual, separately for the rest (HR) and task (HT) dataset. Then, group-level means H̄R and H̄T were computed in each ROI to assess the overall effect. When averaged across ROIs within a network (Fig. 4), DMN exhibited the strongest long memory (H̄R, H̄T) = (0.91, 0.86), followed by the saliency (H̄R, H̄T) = (0.9, 0.83), attention (H̄R, H̄T) = (0.9, 0.83) and visual (H̄R, H̄T) = (0.86, 0.77) networks. The non-neocortical regions (H̄R, H̄T) = (0.78, 0.73) and the motor network (H̄R, H̄T) = (0.77, 0.72) exhibited the weakest Hurst exponents. These results are consistent with those previously obtained from the same data using detrended fluctuation analysis (DFA) [42]. Furthermore, the same network-level ordering was maintained during task while Hurst exponents in all ROIs systematically decreased from rest to task (comparing Fig. 4A and Fig. 4B).
Figure 4. Hurst exponents from scale-free univariate analysis.
Group-averaged region-wise (bottom row) and network-average (top row) wavelet-based estimates of Hurst exponent at rest (A) and during task (B). The color scale is the same for A and B, to illustrate the decrease of Hurst exponents from rest to task.
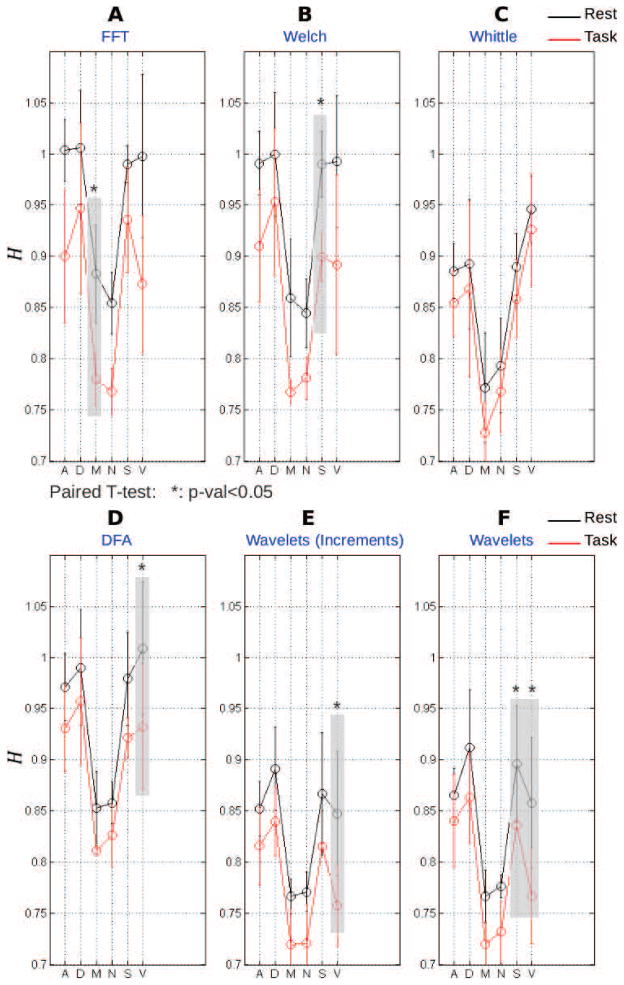
We further estimated Hurst exponents for each ROI and each subject, at rest and during task, using six different estimators: three based on spectral estimation (Direct FFT, Welch-Periodogram and Whittle), two relying on time domain representation (DFA and increments), one constructed on wavelet coefficients. Because it relies on a maximum likelihood principle, Whittle estimator theoretically yields the best estimates for Gaussian data, whereas the wavelet-based estimator has been observed to show significant robustness against additive non-stationary smooth and non-smooth trends. Fig. 5 shows that while the six group-averaged estimates take slightly different values, they are observed to systematically belong to the long memory range 0.5 < H̄ < 1. Moreover, Hurst exponents during task are systematically smaller compared with those at rest, regardless the estimation method: H̄T < H̄R. Using paired t-tests, we investigated the statistical significance of this effect and showed that the reduction of self-similarity from rest to task was found significant in the visual network by 3 estimation methods (DFA, increments and wavelets, all results were Bonferroni-corrected for multiple comparisons). The wavelet method additionally uncovered a significant change in the saliency network. These observations confirm, in a robust manner, earlier reports of long memory at rest and of a decrease in long memory during task [42, 43]. A decrease in the Hurst exponent during task implies an increased contribution of high frequencies to the temporal dynamics of fMRI signals.
Figure 5. Group-level network-average Hurst exponent at rest (black) and during task (red) using six different estimation methods.
A: Standard periodogram (squared fast Fourier transform normalized by the number of samples) and subsequent linear regression on the log-log power spectrum plot. B: Welch-based (i.e., averaged across overlapping windows) periodogram followed by linear regression on the log-log power spectrum plot. C: Whittle estimator, which consisted of a maximum likelihood estimator of power spectrum under fractional Gaussian noise model. D: Detrended Fluctuation Analysis (DFA). E: Time-domain increment-based Hurst exponent estimate. F: Wavelet spectrum estimate, where the Hurst exponent was estimated from a linear regression in the log-log plot where the log along the x-axis involves scales instead of frequencies. X-axis labels indicate networks: A, Attention; D, Default-mode; M, Motor; N, Non-neocortical; S, Saliency; V, Visual. The shaded areas outline the significant differences of Hurst exponents between rest and task. Significant differences are indicated by *-marks (p-val<0.05, Bonferroni corrected).
3.3. Scale-free multivariate analysis
To assess cross-regional temporal dynamics, we applied wavelet-based multivariate estimation to pairs of regions. For illustration, the Welch-Periodogram estimation of the cross-spectrum between MT and pIPS at rest and during task are illustrated in Figs.[2– 3]C, respectively, and superimposed with the wavelet estimation of the cross-spectrum (log2 SXY (2j) vs. log2 2j). The cross-spectra exhibited power-law scaling behavior, within a range of frequencies that matched the scaling range of univariate power spectra. Similar observations were obtained for almost all other region pairs as illustrated in Fig. 6A–B at rest and during task. Indeed, applying the Goodness-of-Fit assessment procedure described in Appendix C shows that, out of the 3570 = 17×21×20/2 analysed pairs of regions, the hypothesis that the wavelet cross-spectrum is well described by a power law was rejected only for 14% and 10% of cases, at rest and during task respectively.
These observations reveal that scale-free properties are not only characteristics of the univariate fMRI temporal dynamics but also of the multivariate cross-temporal dynamics, within the same scaling range: 0.01 < f < 0.1 Hz. Scale-invariance in univariate temporal dynamics implies that no frequency (in the scaling range) plays a dominant role in the temporal dynamics. Scale-invariance in the multivariate cross-temporal dynamics suggests that synchronization between different brain regions does not rely on a specific frequency, but instead on the intertwining of all frequencies within the scaling range. These findings raise two questions: First, do all frequencies contribute in a balanced manner to inter-regional correlation? Second, does task performance modify scale-free cross-temporal dynamics?
To address these questions, we normalized the cross-spectrum by the auto-power spectra to derive the coherence spectrum. The classical and wavelet-based coherence functions between MT and pIPS for rest and task are shown in Figs. 2–3D, respectively. Because coherence is estimated as the ratio of estimated quantities, it is necessarily noisier. For robustness, we estimate the scaling exponent of the coherence function from the auto- and cross- spectra (γXY = αXY − (HX + HY) + 1, where αXY is the power-law exponent of the cross-spectrum, and HX and HY are the Hurst exponents of the individual time series), rather than from the coherence function directly.
Using the wavelet-based framework, we estimated exponents αXY and γXY for all subjects and all region pairs, both at rest and during task. We then computed group-level means ᾱXY and γ̄XY. Fig. 6 reports the Bonferroni corrected p-values for the statistical test associated with the null hypothesis ᾱXY = 0, which was rejected for most region-pairs, both at rest (Fig. 6A) and during task (Fig. 6B). This result suggests that cross-temporal dynamics in most region-pairs exhibit a non-zero scaling exponent. Fig. 7A–B reports the Bonferroni corrected p-values for the test against the null hypothesis γ̄XY = 0 at rest and during task respectively. Several conclusions can be reached. First, the null hypothesis γ̄XY = 0 was rejected only for a few region-pairs, 18 at rest and 19 during task, out of 210 pairs (where, due to multiple comparisons, by chance 10 out of 210 may be rejected). Low rejection rate may stem from two reasons: Bonferroni correction for multiple comparisons yields a conservative result; and the statistical power for a test against γ̄XY = 0 has been shown to decrease when |ρ̄XY| decreases [51].
Figure 7. Cross-coherence scaling exponents.
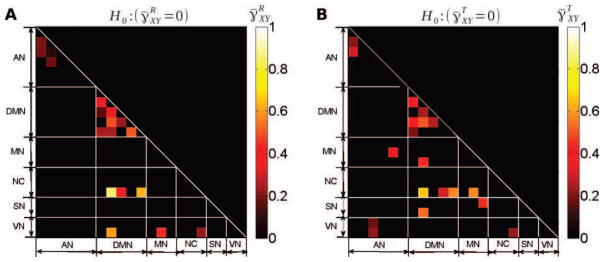
Group-average values of the scaling exponent of the cross-coherence function at rest (A) and during task (B), i.e. and , respectively. Only region pairs where the scaling exponent significantly departed from 0 (p < 0.05, Bonferroni corrected, one-sample t-test) are shown. So, scale invariance on the cross-temporal dynamics has a more complex structure than just averaging those coming from the ROI-based univariate time series in all “hot squares”.
However, for region-pairs where the null hypothesis (γ̄XY = 0) was rejected, a couple of interesting conclusions can be drawn. First, as shown in Fig. 7A–B, whenever departure from 0 was significant, γ̄XY was found to be positive; this was the case both at rest (Fig. 7A) and during task (Fig. 7B). Hence, for these pairs of regions, scale-free properties observed in the cross-spectra convey significant extra information beyond those carried by the auto-spectra: The lowest frequencies within the scaling range contribute substantially more to inter-regional correlation than the highest frequencies, consistent with earlier reports [21, 78, 79].
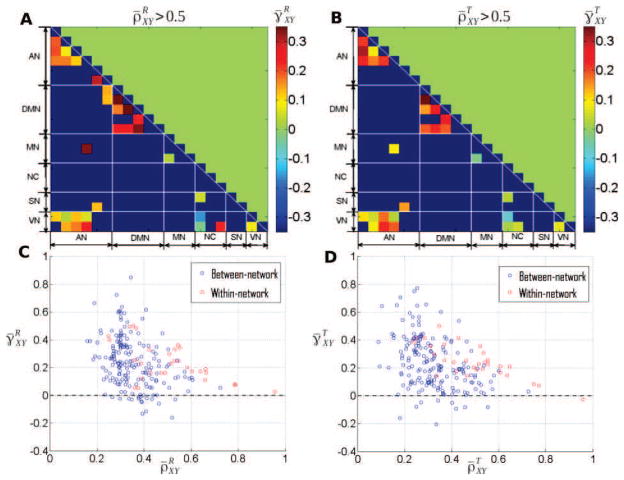
Second, while a priori ρXY and γXY are two independent parameters, it is worth noting that region pairs where γ̄XY = 0 was rejected also tended to show large ρ̄XY both at rest and during task; compare Fig. 1B–C to Fig. 7A–B. In addition, region pairs exhibiting high correlations (see Fig. 8A–B, arbitrary threshold of ) systematically showed . These observations indicate that a strong correlation involves dominant contributions of low frequencies to cross-temporal dynamics. Importantly, these observations are not a trivial effect of dependencies, as theoretically the limit ρXY → 1 imposes γXY → 0 (i.e., total correlation requires a balanced contribution from all frequencies): This effect can be seen in Fig. 8C–D, where as approaches 1, approaches 0.
Figure 8. Relationship between the cross-coherence scaling exponent and the linear Pearson correlation.
A–B: For region pairs with a relatively large Pearson correlation (ρXY > 0.5), the scaling exponent of the cross-coherence function is plotted as color, for rest (A) and task (B), respectively. C–D: Cross-coherence scaling exponent plotted against the linear correlation coefficient for all region-pairs at rest (C) and during task (D). Within- and between-network region pairs are shown in red and blue, respectively.
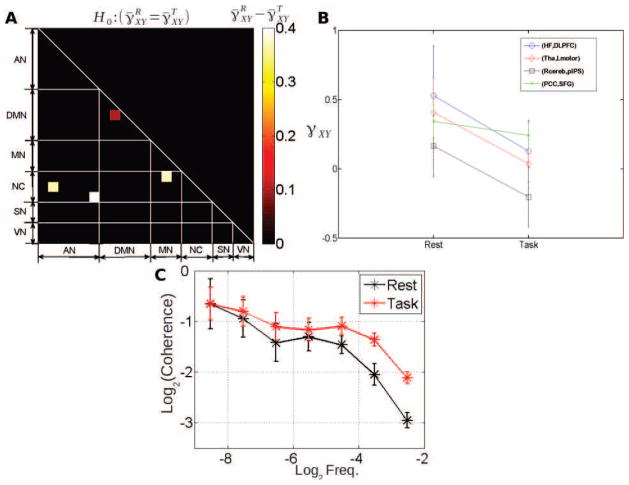
To further assess the evolution of γ̄XY from rest to task, a paired t-test across all subjects was applied to every region pair ( ). Four region pairs showed a significant (p < 0.05, Bonferroni corrected) difference between rest and task (Fig. 9A, R cerebellum – pIPS, hippocampus – R dorsolateral prefrontal cortex, thalamus – L motor cortex and posterior cingulate cortex – superior frontal gyrus). For all significant changes, we observed (Fig. 9B). In 3 out of the 4 regions pairs where the change of was significant, we observed which means that although task significantly modulated γ̄XY and made the contribution of high frequencies to correlation more important, the global correlation remains dominated by the contribution of low frequencies. In contrast, in the R cerebellum – pIPS pair, the switch to occurred during task, making the contribution of high frequencies to correlation more significant than that of low frequencies. Altogether, the more balanced frequency-range contribution to correlation during task suggests that cross-dynamics under task involves a larger contribution of the high frequencies, and is driven more by univariate temporal dynamics, since is converging to zero.
Figure 9. Comparison of cross-coherence scaling exponent between rest and task.
A: Significant differences in cross-coherence scaling exponent between rest and task (p < 0.05, Bonferroni corrected). B: For the four significant region-pairs in A, cross-coherence scaling exponent is shown for rest and task, respectively. Only one region-pair was within the same network (PCC – SFG, within the DMN). C: Grand average (with +/− standard deviations of the mean) of wavelet-based coherence functions between the Thalamus and Lmotor regions at rest (black trace) and during task (red trace).
For a representative region pair (thalamus – L motor cortex), the task-related change of the grand average (or group-level) wavelet coherence function is illustrated in Fig. 9C. As can be seen from Fig 9C, cross-temporal dynamics has larger contribution by high frequencies during task than at rest: the coherence function (red trace) is flatter during task. Comparing the results in Fig. 1D with Fig. 9A (paired t-tests for and for , respectively), we found only one region pair (hippocampus – R dorsolateral prefrontal cortex) showing a significant change in both linear correlation Z̄XY and coherence scaling exponent γ̄XY, with both quantities decreasing from rest to task.
3.4. Scale-free modulation and behavior performance
Lastly, we investigated the relationship between scale-free cross-temporal dynamics, as measured by cross-coherence scaling exponent γXY and behavioral performance as measured by reaction time (RT). Specifically, we assessed whether across subjects, predicts an individual’s response speed (mean of RT across trials) and response reliability (s.d. of RT across trials). Table 2A shows that, in 4 region pairs, is significantly correlated with the standard deviation of the recorded RT (p < 0.05, FDR-corrected). In all region pairs, the correlation coefficient was negative, suggesting that the larger the , the more reliable the subject’s response was across trials. Table 2B further indicates that is significantly and positively correlated to the mean RT for three region pairs. Thus, the smaller the difference , the shorter the mean RT. By contrast, no significant correlation was found between and the mean or s.d. of RT, after correcting for multiple comparisons.
Table 2. Correlation between scale-free cross-temporal dynamics and task performance. A.
Across-subject correlation between the cross-coherence scaling exponent during task and the s.d. of RT. B: Across-subject correlation between difference in cross-coherence scaling exponent between rest and task and the mean of RT. Only significant region-pairs are shown (p < 0.05, FDR-corrected). Group-average values (A) and (B) are reported in the first column. For full anatomical details of each ROI see Table 1.
| Group-average | ROIX | ROIY | Correlation coefficient | p-value | |
|---|---|---|---|---|---|
| A) vs. σRT | 0.09 | R TPJ | R Cerebellum | −0.79 | < 10−3 |
| 0.05 | pIPS | MPF | −0.74 | 10−3 | |
| 0.01 | R Cerebellum | dACC | −0.72 | 10−3 | |
| 0.19 | PCC | FP | −0.7 | 0.002 | |
|
| |||||
| B) vs. μRT | 0.06 | FEF | vRetino | 0.77 | < 10−3 |
| 0.13 | SFG | Thalamus | 0.74 | 10−3 | |
| 0.1 | pIPS | MPF | 0.72 | 10−3 | |
Recalling that a positive indicates that low-frequency range contributes more to correlations than high-frequency range, these observations suggest that a larger contribution of high frequencies to correlation corresponds to poorer behavioral performance. Conversely, the less a subject needs to mobilize high frequencies to accomplish the task, the better his/her performance. Comparing Table 2A and 2B, one can notice the specific role played by the pIPS – medial prefrontal cortex (MPF) pair, a link between the attention and DMN networks, which correlates with both the mean and the standard deviation of the reaction time. In addition, the significant positive correlation between mean RT and the measure in the frontal eye field (FEF) – ventral primary visual cortex (vRetino) pathway indicates that the stability of the scale-free cross-temporal dynamics in this region pair predicts the speed of task execution.
Altogether, these observations indicate that the extent to which task modulates inter-regional correlation and the balance between different frequencies’ contribution to global correlation is negatively correlated with behavioral performance. Thus, across subjects, the less the temporal dynamics of cross-correlation are altered during task, the better the performance.
4. Discussion
Using multivariate analyses of fMRI signals within the framework of scale-free dynamics, the present work sheds light on several characteristics of brain temporal dynamics.
First, scale-invariance is an important aspect of brain dynamics, being observed not only in univariate analysis of each region independently, but also in the cross-regional temporal dynamics. This observation links functional connectivity and scale-free dynamics in fMRI signals – two hitherto separately studied topics. In terms of neurophysiological interpretation, our findings have shown that the communication between distant brain regions, which is captured by the cross-spectrum, is brought by information/energy exchange over a range of frequencies in a scale invariant manner, without any dominant frequency between 0.01 and 0.1 Hz.
Second, the scale-free cross-temporal dynamics do not follow the fractal connectivity model in many region-pairs (Fig. 7), suggesting that: i) fMRI signals are not well described by the simple and direct multivariate extension of the classical fGn-type univariate models; ii) estimation of the cross-spectrum brings extra information beyond that contained in the auto-spectra; iii) low frequencies (close to 0.01 Hz) contribute more to functional connectivity, and thus to communication between regions, than high frequencies (close to 0.1 Hz). Several previous studies have also reported a stronger contribution of low frequencies to inter-regional correlation [21, 78, 79] by comparing the power in different frequency bands, yet without investigating the frequency-range balance quantified by scaling parameters. Our study thus significantly extends these previous reports by exposing the scale-invariance thereof and demonstrating a link between functional connectivity and scale-free dynamics. In particular, we observed that the scaling exponent measured from the cross-spectrum does not simply consist of an average of those estimated on auto-spectra, since the coherence scaling exponent (γXY) departs from zero. Also, we systematically observed that this deviation occurs in the same direction: γXY > 0, hence cross-temporal dynamics are driven by low frequencies. On a technical note, the lack of scale-invariance in prior reports was likely due to a methodological difference from our study, as the methods used there were not tailored to investigating long-range temporal behavior (e.g., Ref. [21] focused on the time-evolution of inter-regional correlations and Ref. [79] employed an autoregressive model which accounted only for short-range correlations).
Third, in addition to a decrease in linear correlation and Hurst exponent reported in previous work [42, 43], task induces a decrease of the cross-coherence scaling exponent γXY. In other words, cross-temporal dynamics are closer to fractal connectivity under task. From a neurophysiological perspective, this means that the temporal dynamics of communication between brain regions are altered under task performance in terms of frequency content. In additoin, these results are consistent with a previous study showing that increased attention induces a decrease of coherence between neuronal populations in macaques specifically in the low frequencies [80, Fig. 4]. Note that a priori the variations of these three parameters are independent; thus, the finding that they occur jointly in brain activity is nontrivial. These findings indicate that the decrease in correlation is accompanied by a stronger mobilization of high frequencies within the scaling range in both the univariate temporal dynamics and in the multivariate cross-temporal dynamics, the latter corresponding to a more balanced contribution of all frequencies to correlation (i.e., functional connectivity).
The current task was a very simple visual detection task, which engaged the visual, motor, saliency and attention systems as shown for instance in [42, Fig. 6, p. 13192]. This simple task already impacted functional connectivity between task-positive (attention, motor, saliency, visual) and task-negative (default mode) networks, as illustrated in Fig. 1D. The use of Bonferroni correction made these results very specific and reliable. The recourse to an alternative approach like FDR for addressing multiple comparisons would probably have shown larger functional connectivity differences between rest and task. Nonetheless, more demanding cognitive tasks, especially those with a learning component, may demonstrate a larger change in functional connectivity [12]. In the same spirit but focusing on scaling exponents instead of correlation measures, other contributions [81, 82] have shown that the multifractal properties of MEG source reconstructed time series continuously evolve with perceptual learning in the task-related networks associated with a visual discrimination task.
Fourth, we observed that across subjects, a larger increase of the high-frequency contribution to cross-temporal dynamics under task was associated with worse behavioral performance. Hence, a strong modulation of cross-temporal dynamics may indicate difficulty in performing the task, consistent with the idea that ongoing fluctuations captured by low-frequency functional connectivity are important for behavioral processes [83]. However, we also outlined that these findings may results from attention effects, as originally observed in macaques [80]. To further investigate such issues and disentangle attention from operative effects in the recourse to high frequencies, future work will be devoted to the analysis of another existing MEG dataset [84] for which complementary eye tracker recordings will permit to probe attention through measurements of ocular saccades in cunjonction with behavioral performance.
On a methodological note, we made use of 28 minutes of resting-state fMRI acquisition which is a relatively large amount of data compared to a typical resting-state fMRI experiments. However, the dataset was split in 4 alternating blocks of resting-state and task-related scans of 7 min each. Thus, we computed the scaling parameter estimates for each block individually, and then averaged the results over the 4 blocks for each condition (rest or task). This averaging increased the robustness of our analysis, compared with a single block analysis.
The use of the wavelet framework in the present work allows significant robustness in estimating univariate or multivariate scale-free dynamics in fMRI data, especially with respect to short sample size or the presence of slow superimposed trends [51, 74, 58]. In the present study, results were averaged across rest and task runs, respectively, which assumes that they were stable across time. This might hide a source of variability as suggested by recent studies on fMRI dynamic functional connectivity [21, 22, 23, 24, 25, 26, 27, 29] and a previous MEG study showing that the amount of self-similarity might change over time [82]. To address this issue, it would be informative for future studies to make use of high temporal resolution fMRI [85, 86, 87, 88], and to explore scale-free cross-temporal dynamics examined herein in a time-dependent manner.
Recent studies have also shown that functional connectivity can change over time [21, 22, 23, 24, 25, 26, 27, 29] suggesting the presence of nonstationarity in fMRI correlation structures. Future work should investigate whether the frequency-range balance of inter-regional connectivity is changing concomitantly at critical time points where functional connectivity is reconfigured (e.g., [29]) or whether these phenomena occur independently. This issue of nonstationarity further points out the need for continuation of the present work beyond a second-order stationary framework. First, potential time evolutions should be investigated (following, e.g., approach in [21]), yet tailored to scale-free dynamics. Second, extensions of this multivariate framework towards scale-free dynamics at higher statistical orders (referred to as multifractal properties) in fMRI signals [see Refs [36, 43] for univariate applications] should be investigated. This effort should help elucidating whether dependencies beyond correlation and second-order statistics play an active role in the dynamical reconfiguration of functional connectivity.
5. Conclusion
In conclusion, by showing that scale-free temporal dynamics manifest in the communication between brain regions, our results provide a bridge between two related, but so-far separate, fields - resting-state networks and scale-free dynamics, which have respectively studied spontaneous brain activity in the spatial and temporal domain. In particular, we observed that the lowest frequencies contributed more to inter-regional communication under both rest and task, but interestingly, this effect was ameliorated under task performance, with different frequencies contributing more equally to inter-regional correlation. Furthermore, we found that the degree to which task performance modulated the scaling behavior of cross-regional temporal dynamics was correlated, across subjects, with behavioral performance, such that smaller task modulation was accompanied by faster and more consistent reaction times. These results should inspire future studies of the interplay between scale-free brain dynamics and large-scale brain networks.
Highlights.
Scale-free dynamics and functional connectivity are intertwined in brain networks.
Scale-free dynamics in two different regions/networks can be related to each other.
Lower frequencies contribute more to inter-regional functional connectivity.
Task modulates cross-temporal dynamics by moderating lowest frequencies.
The smaller the magnitude of this modulation, the better the behavioral performance.
Appendix A. Spike detection procedure
We analyzed the movement parameter estimates by looking at translation and rotation separately. As regards translation, for each TR, run and individual, we computed the vector norm defined by the 3 translation parameters. Then, we computed the mean translation (μt) by averaging over all TRs in a given run. We extracted similarly the corresponding standard deviation (σt). Hereafter, we identified the number of TRs for which the translation movement exceeds α1 = μt +/− 2σt and α2 = μt +/− 3σt. We repeated this procedure over all rest and task-related runs for each individual so as to average the number of spikes per individual over the complete fMRI session. The grand average number of translation spikes was eventually computed by averaging over the 17 subjects who underwent the study. The outcomes of our spike detection procedure with respect to (wrt) translation movement are summarized in Table 3[Top]. They show that the presence of spikes is very negligible (less than 1% wrt α2 threshold both in rest and task related runs).
Table 3.
Results of our spike detection procedure with respect to translation and rotation movements. Grand average results are reported separately for rest and task runs after averaging first over all runs at the subject-level and then over all the individuals.
| Rest | Task | |||
|---|---|---|---|---|
| % spikes (α1) | % spikes (α2) | % spikes (α1) | % spikes (α2) | |
| Translation | 3.6% | 0.5% | 3.4% | 0.8% |
| Rotation | 1.4% | 0.7% | 1.4% | 0.6% |
As regards rotation, the problem is more complex. The difficulty lies in how to collapse the 3 rotation parameters in a single quantity describing a global 3D rotation. We decided to compute the global rotation matrix RG as follows:
| (A.1) |
where the Rx, Ry and Rz matrices match the pitch, roll and yaw movements, respectively. Of course, composing rotations is not a commutative operation so that any alternative composition will deliver distinct results. For each TR in each rest and task run, we computed the corresponding RG using Eq. (A.1). Hence, we extracted its spectral norm as follows:
| (A.2) |
where λmax(A) stands for the largest eigenvalue of matrix A. Since is positive semi-definite, all its eigenvalues are bounded below by zero. Clearly, Eq. (A.2) summarizes in a single scalar the largest rotation direction. By computing this value for all TRs and then extracting the meanμr and standard deviation (σr) over all volumes in a given run, we can therefore define the associated thresholds α1 = μr +/− 2σr, α2 = μr +/− 3σr for detecting rotation movement spikes. As done before for the translation movement, we repeated this procedure over all rest and task-related runs for each individual so as to average the number of spikes per individual over the complete fMRI session. The grand average number of rotation spikes was eventually computed by averaging over the 17 subjects who underwent the study. The outcomes of our spike detection procedure wrt rotation movement are summarized in Table 3[Bottom]. They show that the presence of spikes is even more negligible compared to what we found for translation (1.4% wrt α1 threshold and less than 1% wrt α2 threshold both in rest and task related runs).
Appendix B. The Wavelet estimation framework
Appendix B.1. Discrete wavelet transform
Let ψ0(t) denote a reference oscillating function with narrow supports in both time and frequency domains, referred to as the mother wavelet. It is characterized by its number of vanishing moment, a strictly positive integer Nψ defined as:
| (B.1) |
Also, ψ0(t) is chosen such that the {ψj,k(t) ≡ 2−j/2 ψ0(2−jt − k), j ∈ ℕ, k ∈ ℕ} form a basis of L2(ℝ). The discrete wavelet transform (DWT) coefficients of X are defined as:
| (B.2) |
Scale 2j qualitatively corresponds to the inverse of the frequency, 2j ~ f0/f, where f0 is a constant that depends on the choice of ψ0(t). For further details, readers are referred to e.g., [89].
Appendix B.2. Wavelet coherence function
Let X, Y denote a bivariate second order stationary processes. It has been shown that [73, 75]:
| (B.3) |
| (B.4) |
| (B.5) |
where Ψ0 stands for the Fourier transform of ψ0 and
 for the mathematical expectation. The quantities
for the mathematical expectation. The quantities
 dX(j, k)2,
dX(j, k)2,
 dY (j, k)2 and
dY (j, k)2 and
 dX(j, k)dY (j, k) can thus be read as the auto- and cross-wavelet spectra, measuring the frequency contents of data around frequency f = f02−j. Following [90], a wavelet-based coherence function can now be introduced as:
dX(j, k)dY (j, k) can thus be read as the auto- and cross-wavelet spectra, measuring the frequency contents of data around frequency f = f02−j. Following [90], a wavelet-based coherence function can now be introduced as:
| (B.6) |
When X, Y follow the bivariate model defined in Eq. (2), it yields:
and
Appendix B.3. Estimation procedure
Following [73, 75, 90], relevant estimators for the auto- and cross-wavelet spectra can be defined as time averages of the (squared) wavelet coefficients at scale 2j:
| (B.7) |
| (B.8) |
| (B.9) |
Therefore, the wavelet-based coherence function can be estimated as:
| (B.10) |
When X, Y follow the bivariate model defined in Eq. (2), one obtains:
and
Fig. 10, for synthetic data, and Figs. 2– 3, for the real data analyzed here, display log SX, log SY, log SXY and as functions of log2 2j = j and thus illustrate the corresponding power law behaviors for the auto and cross (wavelet) spectra and (wavelet) cross coherence. Following [74] or [72], estimation of the scaling parameters α̂X (hence Ĥx), α̂Y (hence Ĥy) and α̂XY stems from linear regressions performed in these log-coordinate plots, across the scaling range (j1 = log2 f0/fM; j2 = log2 f0/fm, tuned to match the frequency range fm ≤ |f| ≤ fM. Further, the estimate of γXY is obtained as γ̂XY = α̂XY − (Ĥx + Ĥy) + 1, and not as a linear regression of against log2 2j = j, cf. [51] for details.
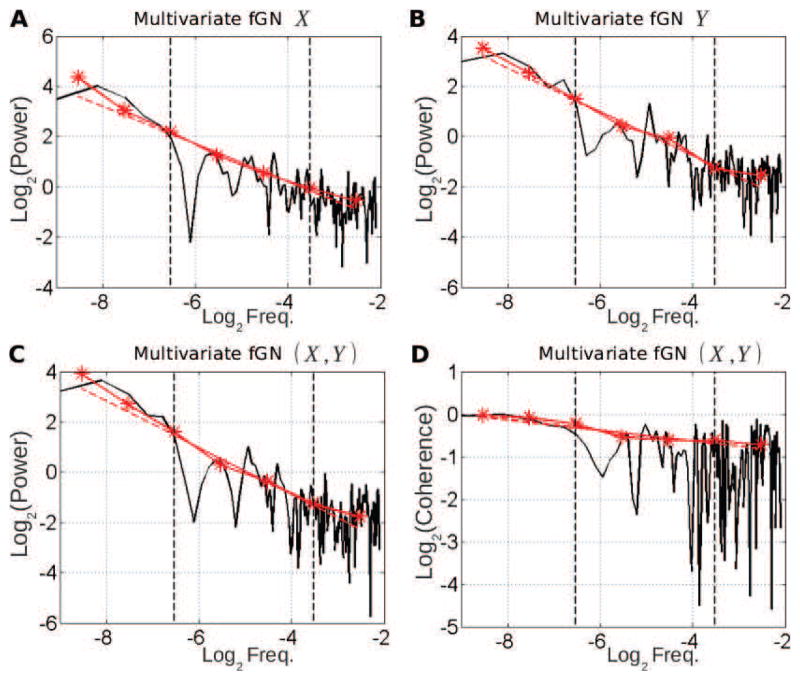
Figure 10. Univariate (A–B) and multivariate (C–D) scale-free properties of a multivariate fractional Gaussian noise (mfGn) process synthetised with the same scaling exponentγXY = as the one estimated on real fMRI data at rest; see Fig. 2.
A–B: Superimposition of the auto-power spectrum estimated by Welch-Periodogram (black) and wavelet method (red) for two of its components X and Y. C: Superimposition of the cross-power spectrum between X and Y estimated by Welch (black) and wavelet method (red) in log-log coordinates. D: Superimposition of the coherence function between X and Y estimated by Welch (black) and wavelet (red) method. All exponents are estimated from linear regression based on the wavelet estimate (dashed red lines) in the scaling range defined by vertical dashed black lines (−6.6 < log2f < −3.3)
Varying Nψ, this wavelet framework provides practitioners with an efficient and robust tool to estimate γXY and γ0 (and thus ρXY) on real-world data and is systematically used in the present work to produce the results.
Appendix B.4. Illustration on bivariate fractional Gaussian noise
The wavelet estimation framework is illustrated by application to synthetic bivariate fractional Gaussian noise, synthesized using the theoretical procedure and practical codes devised in [91], [92]. Parameters for synthetic data are chosen to match as closely as can be those estimated from the real data used to produce Fig. 2, and with same sample size. It permits to observe that estimated scaling from real data, in Fig. 2, are visually as convincing as those in Fig. 10 obtained from synthetic bivariate fractional Gaussian noise, with same parameters, known theoretically to have true scaling behaviors. Scaling relevance is further assessed by means of statistical tests as described in Appendix C below.
Appendix C. Goodness-of-Fit test for multivariate scaling
Following the methodologies outlined in [93, 42], we have implemented the following Goodness-of-Fit assessment procedure for each subject and each pair of regions:
estimation of the scaling and correlation parameters (HX, HY, αXY and ρ) is performed;
computation of the classical χ2 (sum of squared errors to the best fitted linear model) goodness-of-fit quantities for both the auto- and cross wavelet spectra is done;
1000 copies of synthetic bivariate fractional Gaussian noises, with same parameters as data, were simulated (according to the procedure theoretically devised in [91, 92]) and then for each copy, we performed estimation of HX, HY, αXY, and computed the classical χ2 goodness-of-fit quantity for both the auto-wavelet spectra and the cross-wavelet spectra;
the p-value, corresponding to the test aiming at rejecting the null hypothesis that true data have same auto- and cross-wavelet spectra as bivariate fractional Gaussian noise, with same parameters and same sample size, is computed as the percentage of times the χ2 goodness-of-fit value computed from synthetic data exceeds that computed from real data;
the null hypothesis is rejected at the 0.05 level.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Biswal B, Zerrin Yetkin F, Haughton V, Hyde J. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- 2.Xiong J, Parsons LM, Gao JH, Fox PT. Inter-regional connectivity to primary motor cortex revealed using mri resting state images. Hum Brain Mapp. 1999;8(2–3):151–156. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<151::AID-HBM13>3.0.CO;2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cordes D, Haughton VM, Arfanakis K, Carew JD, Turski PA, Moritz CH, Quigley MA, Meyerand ME. Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. Am J Neuroradiol. 2001;22(7):1326–1333. [PMC free article] [PubMed] [Google Scholar]
- 5.Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proc Natl Acad Sci USA. 2001;98(2):676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- 7.Damoiseaux JS, Rombouts SARB, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF. Consistent resting-state networks across healthy subjects. Proc Natl Acad Sci USA. 2006;103(37):13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Smith S, Fox P, Miller K, Glahn D, Fox P, Mackay C, Filippini N, Watkins K, Toro R, Laird A, et al. Correspondence of the brain’s functional architecture during activation and rest. Proc Natl Acad Sci USA. 2009;106:13040. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.He BJ, Shulman GL, Snyder AZ, Corbetta M. The role of impaired neuronal communication in neurological disorders. Curr Opin Neurol. 2007;20(6):655–660. doi: 10.1097/WCO.0b013e3282f1c720. [DOI] [PubMed] [Google Scholar]
- 10.Zhang D, Raichle ME. Disease and the brain’s dark energy. Nature reviews Neurology. 2010;6(1):15–28. doi: 10.1038/nrneurol.2009.198. [DOI] [PubMed] [Google Scholar]
- 11.Zhang L, Qi R, Zhong J, Ni L, Zheng G, Xu J, Lu G. Disrupted functional connectivity of the anterior cingulate cortex in cirrhotic patients without overt hepatic encephalopathy: a resting state fMRI study. Plos One. 2013;8(1 Article e53206):1–8. doi: 10.1371/journal.pone.0053206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lewis CM, Baldassarre A, Committeri G, Romani GL, Corbetta M. Learning sculpts the spontaneous activity of the resting human brain. Proc Natl Acad Sci USA. 2009;106(41):17558. doi: 10.1073/pnas.0902455106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci USA. 2003;100(1):253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol. 2005;360(1457):1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional MRI data using independent component analysis. Hum Brain Mapp. 2001;14(3):140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kiviniemi V, Starck T, Remes J, Long X, Nikkinen J, Haapea M, Veijola J, Moilanen I, Isohanni M, Zang Y, et al. Functional segmentation of the brain cortex using high model order group PICA. Hum Brain Mapp. 2009;30(12):3865–3886. doi: 10.1002/hbm.20813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cole DM, Smith SM, Beckmann CF. Advances and pitfalls in the analysis and interpretation of resting-state FMRI data. Frontiers in systems neuroscience. 2010 Apr;4:8. doi: 10.3389/fnsys.2010.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hlinka J, Palus M, Vejmelka M, Mantini D, Corbetta M. Functional connectivity in resting-state fMRI: is linear correlation sufficient? NeuroImage. 2011;54(3):2218–25. doi: 10.1016/j.neuroimage.2010.08.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Marrelec G, Bellec P, Krainik A, Duffau H, Pélégrini-Issac M, Lehéricy S. Regions, systems, and the brain: hierarchical measures of functional integration in fMRI. Med Image Anal. 2008;12(4):484–496. doi: 10.1016/j.media.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 20.Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philos Trans Trans R Soc Lond, B Biol Sci. 2005;360(4):937–946. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chang C, Glover GH. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage. 2010;50(1):81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD. Tracking whole-brain connectivity dynamics in the resting state. Cereb Cortex. 2013 doi: 10.1093/cercor/bhs352. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hutchison RM, Womelsdorf T, Gati JS, Everling S, Menon RS. Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum Brain Mapp. 2013;34:2154–2177. doi: 10.1002/hbm.22058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Majeed W, Magnuson M, Hasenkamp W, Schwarb H, Schumacher EH, Barsalou L, Keilholz SD. Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans. NeuroImage. 2011;54:1140–1150. doi: 10.1016/j.neuroimage.2010.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, Van Essen DC, Feinberg Da, Yacoub ES, Ugurbil K. Temporally-independent functional modes of spontaneous brain activity. Proc Natl Acad Sci USA. 2012;109(8):3131–3136. doi: 10.1073/pnas.1121329109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kiviniemi V, Vire T, Remes J, Elseoud AA, Starck T, Tervonen O, Nikkinen J. A sliding time-window ica reveals spatial variability of the default mode network in time. Brain connect. 2011;1:339–347. doi: 10.1089/brain.2011.0036. [DOI] [PubMed] [Google Scholar]
- 27.Leonardi N, Richiardi J, Gschwind M, Simioni S, Annoni J-M, Schluep M, Vuilleumier P, Van De Ville D. Principal components of functional connectivity: A new approach to study dynamic brain connectivity during rest. NeuroImage. 2013 doi: 10.1016/j.neuroimage.2013.07.019. in press. [DOI] [PubMed] [Google Scholar]
- 28.Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo D. Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Frontiers in Physiology. 2012;3(Article 15):1–12. doi: 10.3389/fphys.2012.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Liu X, Duyn JH. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc Natl Acad Sci USA. 2013;110:4392–4397. doi: 10.1073/pnas.1216856110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zarahn E, Aguirre GK, D’Esposito M. Empirical analysis of BOLD fMRI statistics. I. Spatially unsmoothed data collected under null-hypothesis conditions. NeuroImage. 1997;5(3):179–197. doi: 10.1006/nimg.1997.0263. [DOI] [PubMed] [Google Scholar]
- 31.Linkenkaer-Hansen K, Nikouline V, Palva J, Ilmoniemi R. Long-range temporal correlations and scaling behavior in human brain oscillations. The Journal of neuroscience. 2001;21(4):1370–1377. doi: 10.1523/JNEUROSCI.21-04-01370.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Thurner S, Windischberger E, Moser C, Walla P, Barth M. Scaling laws and persistence in human brain activity. Physica A. 2003;326(3):511–521. [Google Scholar]
- 33.Shimizu Y, Barth M, Windischberger C, Moser E, Thurner S. Wavelet-based multifractal analysis of fMRI time series. NeuroImage. 2004;22(3):1195–1202. doi: 10.1016/j.neuroimage.2004.03.007. [DOI] [PubMed] [Google Scholar]
- 34.Stam CJ, de Bruin EA. Scale-free dynamics of global functional connectivity in the human brain. Hum Brain Mapp. 2004;22(2):97–109. doi: 10.1002/hbm.20016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.He BJ, Snyder AZ, Zempel JM, Smyth MD, Raichle ME. Electrophysiological correlates of the brain’s instrinsic large-scale functional architecture. Proc Natl Acad Sci USA. 2008;105(41):16039–16044. doi: 10.1073/pnas.0807010105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ciuciu P, Abry P, Rabrait C, Wendt H. Log wavelet leaders cumulant based multifractal analysis of EVI fMRI time series: evidence of scaling in ongoing and evoked brain activity. IEEE Journal of Selected Topics in Signal Processing. 2008;2(6):929–943. [Google Scholar]
- 37.Wink AM, Bullmore E, Barnes A, Bernard F, Suckling J. Monofractal and multifractal dynamics of low frequency endogenous brain oscillations in functional MRI. Hum Brain Mapp. 2008;29(7):791–801. doi: 10.1002/hbm.20593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Miller KJ, Sorensen LB, Ojemann JG, den Nijs M. Power-law scaling in the brain surface electric potential. PLoS Comput Biol. 2009;5:e1000609. doi: 10.1371/journal.pcbi.1000609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.He BJ, Zempel JM, Snyder AZ, Raichle ME. The temporal structures and functional significance of scale-free brain activity. Neuron. 2010;66(3):353–369. doi: 10.1016/j.neuron.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Expert P, Lambiotte R, Chialvo DR, Christensen K, Jensen HJ, Sharp DJ, Turkheimer F. Self-similar correlation function in brain resting-state functional magnetic resonance imaging. J R Soc Interface. 2011;8:472–479. doi: 10.1098/rsif.2010.0416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Van de Ville D, Britz J, Michel CM. EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc Natl Acad Sci USA. 2010;107(42):18179–18184. doi: 10.1073/pnas.1007841107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.He BJ. Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J Neurosci. 2011;31(39):13786–13795. doi: 10.1523/JNEUROSCI.2111-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ciuciu P, Varoquaux G, Abry P, Sadaghiani S, Kleinschmidt A. Scale-free and multi-fractal time dynamics of fMRI signals during rest and task. Front Physiol. 2012;3(Article 186):1–18. doi: 10.3389/fphys.2012.00186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dehghani N, Hatsopoulos NG, Haga ZD, Parker RA, Greger B, Halgren E, Cash SS, Destexhe A. Avalanche analysis from multielectrode ensemble recordings in cat, monkey, and human cerebral cortex during wakefulness and sleep. Front Physiol. 3:Article 302. doi: 10.3389/fphys.2012.00302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Beran J. Statistics for long-memory processes. Chapman and Hall/CRC; Boca Raton, FL, USA: 1994. [Google Scholar]
- 46.Suckling J, Wink AM, Bernard F, Barnes A, Bullmore E. Endogenous multifractal brain dynamics are modulated by age, cholinergic blockade and cognitive performance. J Neurosci Meth. 2008;174(2):292–300. doi: 10.1016/j.jneumeth.2008.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tagliazucchi E, von Wegner F, Morzelewski A, Brodbeck V, Jahnke K, Laufs H. Breakdown of long-range temporal dependence in default mode and attention networks during deep sleep. Proc Natl Acad Sci USA. 2013;110:15419–15424. doi: 10.1073/pnas.1312848110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Maxim V, Sendur L, Fadili J, Suckling J, Gould R, Howard R, Bullmore E. Fractional Gaussian noise, functional MRI and Alzheimer’s disease. NeuroImage. 2005;25(1):141–158. doi: 10.1016/j.neuroimage.2004.10.044. [DOI] [PubMed] [Google Scholar]
- 49.Mendelbrot BB, Van Ness JW. Fractional brownian motions, fractional noises and applications. SIAM Review. 1968;10:422–437. [Google Scholar]
- 50.Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wendt H, Scherrer A, Abry P, Achard S. Testing fractal connectivity in multivariate long memory processes. 34th Proc. IEEE ICASSP; Taipei, Taiwan. 2009; pp. 2913–2916. [Google Scholar]
- 52.He BJ. Spontaneous and task-evoked brain activity negatively interact. J Neurosci. 2013;33:4672–4682. doi: 10.1523/JNEUROSCI.2922-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fox MD, Snyder AZ, Vincent JL, Raichle ME. Intrinsic fluctuations within cortical systems account for intertrial variability in human evoked brain responses. Proc Natl Acad Sci USA. 2007;56(1):171–84. doi: 10.1016/j.neuron.2007.08.023. [DOI] [PubMed] [Google Scholar]
- 54.Ojemann JG, Akbudak E, Snyder AZ, McKinstry RC, Raichle ME, Conturo TE. Anatomic localization and quantitative analysis of gradient refocused echo-planar fMRI susceptibility artifacts. NeuroImage. 1997;6(3):156–167. doi: 10.1006/nimg.1997.0289. [DOI] [PubMed] [Google Scholar]
- 55.Talairach J, Tournoux P. Co–Planar Stereotaxic Atlas of the Human Brain. 3-Dimensional Proportional System : An Approach to Cerebral Imaging. Thieme Medical Publishers, Inc., Georg Thieme Verlag; Stuttgart, New York: 1988. [Google Scholar]
- 56.Siegel J, Power J, Dubis J, Vogel A, Church J, Schlaggar B, Petersen S. Statistical improvements in functional magnetic resonance imaging analyses produced by censoring high-motion data points. Hum Brain Mapp. 2013:1–16. doi: 10.1002/hbm.22307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen Z, Ivanov P, Hu K, Stanley H. Effect of nonstationarities on detrended fluctuation analysis. Physical Review E. 65(4 Pt1) doi: 10.1103/PhysRevE.65.041107. [DOI] [PubMed] [Google Scholar]
- 58.Torres ME, Abry P. Comparison of different methods for computing scaling parameter in the presence of trends. CD Memorias XIV Congreso Argentino de Bioingeniería y III Jornadas de Ingeniería Clínica (SABI 2003); Argentina: Universitas, Córdoba; 2003. URL http://bioingenieria.edu.ar/grupos/ldnlys/metorres/metorres_files/SABI2003-074Torres.pdf. [Google Scholar]
- 59.He BJ, Snyder AZ, Vincent JL, Epstein A, Shulman GL, Corbetta M. Breakdown of functional connectivity in frontoparietal networks underlies behavioral deficits in spatial neglect. Neuron. 2007;53(6):905–918. doi: 10.1016/j.neuron.2007.02.013. [DOI] [PubMed] [Google Scholar]
- 60.Shulman GL, Fiez JA, Corbetta M. Common blood flow changes across visual tasks: II. Decreases in cerebral cortex. Journal of Cogn Neurosci. 1997;9(5):648–663. doi: 10.1162/jocn.1997.9.5.648. [DOI] [PubMed] [Google Scholar]
- 61.Dosenbach NU, Visscher KM, Palmer ED, Miezin FM, Wenger KK, Kang HC, Burgund ED, Grimes AL, Schlaggar BL, Petersen SE. A core system for the implementation of task sets. Neuron. 2006;50(5):799–812. doi: 10.1016/j.neuron.2006.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Seeley WW, Menon V, Schatzberg AF, Keller J, Glover GH, Kenna H, Reiss AL, Greicius MD. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci. 2007;27(9):2349–2356. doi: 10.1523/JNEUROSCI.5587-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Vincent JL, Kahn I, Snyder AZ, Raichle ME, Buckner RL. Evidence for a frontoparietal control system revealed by intrinsic functional connectivity. J Neurophysiol. 2008;100(6):3328–3342. doi: 10.1152/jn.90355.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Embick D, Poeppel D. Mapping syntax using imaging: problems and prospects for the study of neurolinguistic computation. In: Brown K, editor. Encyclopedia of language and linguistics. 2. Elsevier; Oxford, UK: 2006. pp. 484–486. [Google Scholar]
- 65.Vincent JL, Snyder AZ, Fox MD, Shannon BJ, Andrews JR, Raichle ME, Buckner RL. Coherent spontaneous activity identifies a hippocampal-parietal memory network. J Neurophysiol. 2006;96(6):3517–3531. doi: 10.1152/jn.00048.2006. [DOI] [PubMed] [Google Scholar]
- 66.Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA, Fox MD, Snyder AZ, Vincent JL, Raichle ME, Schlaggar BL, Petersen SE. Distinct brain networks for adaptive and stable task control in humans. Proc Natl Acad Sci USA. 2007;104(26):11073–11078. doi: 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc Natl Acad Sci USA. 2006;103(26):10046–10051. doi: 10.1073/pnas.0604187103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Wendt H, Abry P. Multifractality tests using bootstrapped wavelet leaders. IEEE Trans Signal Processing. 2007;55(10):4811–4820. [Google Scholar]
- 69.Didier G, Pipiras V. Integral representations and properties of operator fractional Brownian motions. Bernoulli. 2011;17(1):1–33. [Google Scholar]
- 70.Amblard P, Coeurjolly JF. Identification of the multivariate fractional brownian motion. IEEE Trans Signal Processing. 2011;59(11):5152–5168. [Google Scholar]
- 71.Marple SL. Digital spectral analysis with applications. Prentice-Hall; Englewood Cliffs, NJ: 1987. [Google Scholar]
- 72.Veitch D, Abry P. A statistical test for the time constancy of scaling exponents. IEEE Trans Signal Processing. 2001;49(10):2325–2334. [Google Scholar]
- 73.Abry P, Gonçalvès P, Flandrin P. Wavelets, spectrum estimation and 1/f processes. Springer-Verlag; New York: 1995. p. 103. wavelets and Statistics, Lecture Notes in Statistics. [Google Scholar]
- 74.Abry P, Veitch D. Wavelet analysis of long-range-dependent traffic. IEEE Trans Inf Theory. 1998;44:2–15. [Google Scholar]
- 75.Abry P, Baraniuk R, Flandrin P, Riedi R, Veitch D. Multiscale network traffic analysis, modeling, and inference using wavelets, multifractals, and cascades. IEEE Signal Proc Mag. 2002;3(19):28–46. [Google Scholar]
- 76.Bullmore E, Long C, Suckling J, Fadili J, Calvert G, Zelaya F, Carpenter T, Brammer M. Colored noise and computational inference in neurophysiological (fMRI) time series analysis: resampling methods in time and wavelet domains. Hum Brain Mapp. 2001;12(2):61–78. doi: 10.1002/1097-0193(200102)12:2<61::AID-HBM1004>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Fadili J, Bullmore E. Wavelet-generalized least squares: A new BLU estimator of linear regression models with 1/f errors. NeuroImage. 2002;15(1):217–232. doi: 10.1006/nimg.2001.0955. [DOI] [PubMed] [Google Scholar]
- 78.Sasai S, Homae F, Watanabe H, Taga G. Frequency-specific functional connectivity in the brain during resting state revealed by NIRS. NeuroImage. 2011;56(1):252–7. doi: 10.1016/j.neuroimage.2010.12.075. [DOI] [PubMed] [Google Scholar]
- 79.Shim WH, Baek K, Kim J, Chae Y, Suh J, Rosen BR, Jeong J, Kim YR. Frequency distribution of causal connectivity in rat sensorimotor network: resting-state fMRI analyses. J Neurophysiol. 2013;109(1):238–248. doi: 10.1152/jn.00332.2012. [DOI] [PubMed] [Google Scholar]
- 80.Mitchell J, Sundberg K, Reynolds J. Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron. 2009;63:879–888. doi: 10.1016/j.neuron.2009.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Zilber N, Ciuciu P, Abry P, van Wassenhove V. Modulation of scale-free properties of brain activity in MEG. Proc. of the 9th IEEE International Symposium on Biomedical Imaging; Barcelona, Spain. 2012. pp. 1531–1534. [Google Scholar]
- 82.Zilber N, Ciuciu P, Abry P, van Wassenhove V. Learning-induced modulation of scale-free properties of brain activity measured with MEG. 10th Proc. IEEE ISBI; San Francisco, CA. 2013; pp. 986–989. [Google Scholar]
- 83.Sadaghiani S, Hesselmann G, Friston KJ, Kleinschmidt A. The relation of ongoing brain activity, evoked neural responses, and cognition. Front Syst Neurosci. 2010;4:20. doi: 10.3389/fnsys.2010.00020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Zilber N, Ciuciu P, Gramfort A, van Wassenhove V. Supramodal plasticity optimizes perceptual learning. doi: 10.1016/j.neuroimage.2014.02.017. to appear in NeuroImage. [DOI] [PubMed] [Google Scholar]
- 85.Boyacioglu R, Barth M. Generalized iNverse imaging (GIN): Ultrafast fMRI with physiological noise correction. Magn Reson Med. 2012:1–10. doi: 10.1002/mrm.24528. URL http://www.ncbi.nlm.nih.gov/pubmed/23097342. [DOI] [PubMed]
- 86.Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PloS one. 2010;5:e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multi-band multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010;63(5):1144–1153. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Rabrait C, Ciuciu P, Ribès A, Poupon C, Leroux P, Lebon V, Dehaene-Lambertz G, Le Bihan D, Lethimonnier F. High temporal resolution functional MRI using parallel echo volume imaging. J Magn Reson Imaging. 2008;27(4):744–753. doi: 10.1002/jmri.21329. [DOI] [PubMed] [Google Scholar]
- 89.Mallat S. A Wavelet Tour of Signal Processing. Academic Press; San Diego, CA: 1998. [Google Scholar]
- 90.Whitcher B, Guttorp P, Percival BD. Wavelet analysis of covariance with application to atmospheric time series. J Geophys Res [Atmos] 2000;105:14941–14962. [Google Scholar]
- 91.Helgason H, Pipiras V, Abry P. Fast and exact synthesis of stationary multivariate Gaussian time series using circulant embedding. Signal Processing. 2011;91(5):1123–1133. [Google Scholar]
- 92.Helgason H, Pipiras V, Abry P. Synthesis of multivariate stationary series with prescribed marginal distributions and covariance using circulant matrix embedding. Signal Processing. 2011;91(8):1741–1758. [Google Scholar]
- 93.Clauset A, Shalizi C, Newman M. Power law distributions in empirical data. SIAM Review. 2009;51:661–703. [Google Scholar]