Random myosin loss along thick-filaments increases myosin attachment time and the proportion of bound myosin heads to mitigate force decline in skeletal muscle

Abstract

Diminished skeletal muscle performance with aging, disuse, and disease may be partially attributed to the loss of myofilament proteins. Several laboratories have found a disproportionate loss of myosin protein content relative to other myofilament proteins, but due to methodological limitations, the structural manifestation of this protein loss is unknown. To investigate how variations in myosin content affect ensemble cross-bridge behavior and force production we simulated muscle contraction in the half-sarcomere as myosin was removed either i) uniformly, from the Z-line end of thick-filaments, or ii) randomly, along the length of thick-filaments. Uniform myosin removal decreased force production, showing a slightly steeper force-to-myosin content relationship than the 1:1 relationship that would be expected from the loss of cross-bridges. Random myosin removal also decreased force production, but this decrease was less than observed with uniform myosin loss, largely due to increased myosin attachment time (t_on) and fractional cross-bridge binding with random myosin loss. These findings support our prior observations that prolonged t_on may augment force production in single fibers with randomly reduced myosin content from chronic heart failure patients. These simulation also illustrate that the pattern of myosin loss along thick-filaments influences ensemble cross-bridge behavior and maintenance of force throughout the sarcomere.

Introduction

Several physiological and pathological conditions (e.g. aging, muscle disuse, heart disease, lung disease, and cancer) are associated with reductions in skeletal muscle size and function, which contribute to the development of physical disability [12]. Reductions in myofilament protein content and/or function are potential effectors for these tissue-level changes, as these comprise 80% of muscle fiber volume [20] and generate the molecular forces that drive muscle contraction. Interestingly, recent studies have suggested that quantitative alterations in myofilament proteins may not be stoichiometric; more specifically, data from animal models and clinical populations have described a phenomenon of preferential depletion of the contractile protein myosin from muscle tissue/fibers relative to tissue/fiber size or volume [1, 11, 19, 24, 26, 32, 41]. Notably, the loss of myosin is functionally manifest as reduced contractile force per muscle size [11, 15, 26], presumably due to a reduction in the number of available cross-bridges. In this context, a selective loss of myosin may partially explain the reductions in whole muscle function in numerous physiological and pathological conditions that disproportionately exceed the loss of muscle size [2, 16, 39, 40].

Nearly all of the studies characterizing a selective loss of myosin from skeletal muscle have utilized biochemical measurements [1, 11, 19, 26, 32, 41], although our previous work also provided mechanical evidence for a loss of myosin [31]. An immediate question that arises from these observations is: how does the selective loss of myosin from the myofilaments manifest itself structurally? Early evidence supported a wholesale loss of thick-filaments from the myofilament lattice [24] and a complete dissolution of sarcomeric structure [26]. These changes, however, were described in conditions of surgical or pharmacological ablation of motor drive to the muscle via dennervation and neuromuscular blocking agents, which are more severe than most acute/chronic physiological or pathological conditions that lead to muscle dysfunction and disability. As an example, our recent findings in human patients with chronic heart failure show a similar preferential loss of myosin, but no gross ultrastructural changes in myofilament fractional content, thick-to-thin filament stoichiometry, or thick-filament length [31]. By default, we concluded that myosin was lost at random along the length of the thick-filament, in keeping with the notion that thick-filaments are remodeled along their length via removal and addition of myosin molecules [13, 42]. Anatomical evidence to support this conclusion, however, is beyond current methodological capabilities.

Computational modeling offers an opportunity to address biological questions in complex integrative systems, where current experimental methodologies may have a limited capacity to interrogate coordinated, multi-scale mechanisms underlying physiological function. As introduced above, variation in myosin content in muscle cells may modulate contraction, likely due to changes in the number or kinetic properties of bound cross-bridges. Similarly, contractility can vary with cross-bridge stiffness and thick-to-thin filament overlap at different sarcomere lengths, as these mechanical and structural properties of the myofilament lattice influence the upper limits of cross-bridge binding throughout the sarcomere. To investigate the roles of varied thick-filament structure, sarcomere-length, and cross-bridge stiffness on ensemble cross-bridge binding, force production, and kinetics, we used a computational model of the half-sarcomere to simulate muscle contraction in a system of Ca²⁺-regulated myosin-actin cross-bridge interactions between multiple thick- and thin-filaments [9, 37, 38]. While cross-bridge stiffness and sarcomere length influenced overall sarcomeric force production by affecting the number and kinetic properties of bound cross-bridges, these measures were influenced more by reductions in myosin content. Specifically, we found that random reductions in myosin content mitigated force decline due to increased t_on and fractional cross-bridge binding, which did not occur when myosin content was uniformly reduced from the Z-line end of thick-filaments. These observations support our prior speculations that myosin loss occurred randomly in human skeletal muscle fibers of heart failure patients [31], explaining the increase in t_on and maintenance of isometric tension [30].

Methods

The computational models used in this work build on a series of spatially-explicit models developed over the past 15 years that simulate muscle contraction within a network of linear springs [9, 10, 37, 38]. In summary, the current model comprises 4 thick-filaments and 8 thin-filaments of half-sarcomere length to model Ca²⁺-regulated actomyosin cross-bridge binding and force production (Fig. 1A). Periodic boundary conditions along the length of the half-sarcomere remove any edge effects along the longitudinal boundary of the simulation, which allows predictions of muscle contraction from a finite number of filaments to represent a sub-section myofilament lattice space. Monte Carlo algorithms drive kinetic state transitions for both thin-filament activation and cross-bridge binding. This kinetic scheme includes cooperative activation of thin-filaments from neighboring thin-filament regulatory units and bound cross-bridges [38]. As further described below, we have now: i) modified myosin organization along thick-filaments to represent the three-start helix of vertebrate thick-filaments (simple-lattice structure [5]), ii) added a linear elastic element between the free-end of thick-filaments and the Z-line to represent titin (Fig. 1B–C), and iii) developed two different algorithms for altering thick-filament structure to simulate the effect of reduced myosin content on predicted values of force, cross-bridge binding, ATPase, and myosin attachment time (t_on).

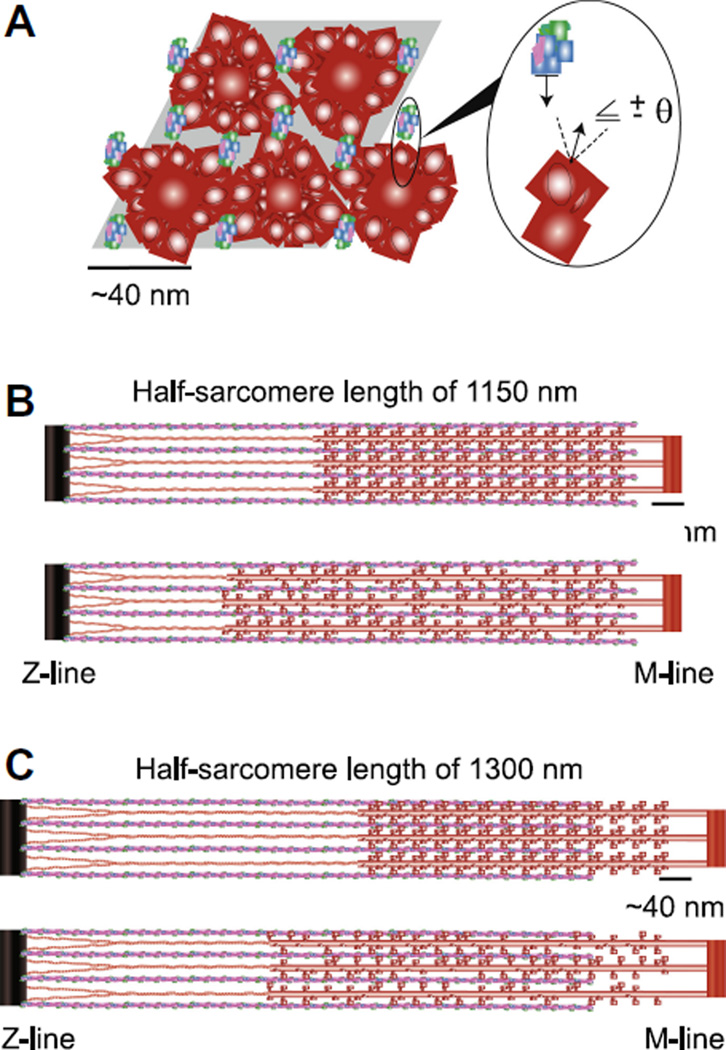
Figure 1. Model geometry and half-sarcomere organization.

A) The shaded parallelogram roughly outlines the cross-sectional view of modeled interactions between four thick-filaments (red) and eight regulated thin-filaments (actin=blue, troponin=green, tropomyosin=magenta) of half-sarcomere length. The expanded inset illustrates one potential myosin-actin cross-bridge interaction between two adjacent filaments. Axial, half-sarcomere illustrations show filament interactions for simulations of B) 1150 nm (=2.3 µm SL) and C) 1300 nm (=2.6 µm SL) for uniform (upper) and random (lower) reductions in myosin content at each SL. Titin is represented as the link between thick-filament backbones and the Z-line.

Myofilament mechanics and sarcomere architecture

Thick-filament backbones, thin-filaments, cross-bridges, and titin are represented as linear springs, such that motion, forces, and deformation within the myofilament network occur solely along the axial direction of the filaments (Fig. 1B–C). This affords a linear system of equations to calculate the one dimensional force balance throughout the half-sarcomere at each time-step (=1 ms). These assumptions of linearity allow this system of equations to be solved with linear algebra, which is computationally intensive relative to a mass-action model described by a system of ordinary differential equations [6, 33], but less computationally intensive than a multi-dimensional, non-linear force balance that must be solved using optimization algorithms [43–45]. Thick- and thin-filament spring constants were 6060 and 5230 pN nm⁻¹ for unstrained spring elements of length 14.3 and 12.3 nm, respectively. Half-sarcomere length thick-filaments were 860 nm (60 thick-filament nodes×14.3 nm) and thin-filaments were 1110 nm (90 actin nodes×12.3 nm). These thick-filament and actin node locations coincide with model structures that represent myosin crowns along thick-filament backbones from which myosin heads extend and sites for myosin binding with actin along thin-filaments, respectively.

Three myosin heads extend from each thick-filament node, with each myosin head rotationally spaced 120° apart, such that myosin heads extend from a thick-filament node to face 0, 120, and 240°. The helical pitch of myosin crowns in vertebrate striated muscle is a rotation of 40° every 14.3 nm [4, 5, 29], which was applied to thick-filament nodes in our current models. In relation to the thick-filament node described above, myosin heads extending from the adjacent thick-filament node 14.3 nm down the thick-filament backbone would face 40, 160, and 280°, and consistently, myosin heads extending from the node 28.6 nm down the backbone would face 80, 200, and 320°. As with the simple, hexagonal lattice structure of the myofilament lattice, only 1/3 of the myosin heads directly face neighboring thin-filaments that reside at hexagonal vertices (=0, 60, 120, 180, 240, 300°) around thick-filaments [5]. Physiologically, therefore, myosin must have some azimuthal flexibility to bind thin-filaments that are radially-misaligned with myosin heads. To account for this azimuthal flexibility in the model we introduced the parameter θ (=20°), which allowed myosin heads to bind with actin nodes if the pair were rotationally aligned to face each other within |θ| (outset, Fig. 1A).

When myosin heads bind with actin, they are assigned a cross-bridge spring constant (k_xb), which took values of of 1, 3, or 5 pN nm⁻¹ depending upon the simulation. These k_xb values were chosen because previous computational modelling efforts have shown that variations in k_xb influence the level of cross-bridge binding and cross-bridge kinetics [9, 10, 37, 38], which could have a combined influence on cross-bridge behavior as myosin content was reduced. Generally we focused on simulations when k_xb=3 pN nm⁻¹ as these have been most representative of measured experimental force and ATPase values in our prior computational studies [37, 38] and remains consistent with estimates of k_xb from cellular experiments [21, 28, 34].

Variations in sarcomere length (SL) were simulated by changing the M-line position with respect to the Z-line position. SL values of 2.3 or 2.6 µm were chosen for each simulation. The SL value of 2.3 µm represents almost complete thick-to-thin filament overlap (~860 nm) at a SL value on the plateau, near the start of the descending limb of the length-tension relationship [17]. The SL value of 2.6 µm is close to the 2.65 µm value used during our skeletal muscle measurements that prompted these simulations [30, 31]. Moreover, the 2.6 µm value maintains relatively large thick-to-thin filament overlap (~660 nm) and represents an overlap distance close to simulations where myosin content was uniformly reduced to 80% normal at 2.3 µm SL.

Myosin content was reduced throughout the half-sarcomere two ways: uniformly and randomly. Myosin content was reduced by uniformly deactivating myosin nodes (and their associated myosin heads) from the Z-line directed end of thick-filament backbones. This effectively mimicked reductions in myosin content as reductions in thick-filament length (upper half-sarcomeres, Fig. 1B–C). Random reductions in myosin content throughout the length of a thick-filament were simulated by randomly deactivating myosin heads along thick-filament backbones (lower half-sarcomeres, Fig. 1B–C). Specifically, individual myosin heads that extend from thick-filament nodes were not allowed to bind with actin nodes for the duration of a simulation, rather than knocking-out a whole thick-filament node for a simulation. Removal of cross-bridges did not influence the thick-filament stiffness value, although it is plausible that reduced myosin content could diminish thick-filament backbone stiffness.

The elastic link representing titin was assigned a spring constant of 0.1344 pN nm⁻¹and unstrained, rest-length values of 342 and 247 nm for half-sarcomere length simulations of 1300 and 1150 nm, respectively. These values provided relaxed (passive) force values of roughly 50 and 25 pN (=9 and 4.5 kPa, given the 5600 nm² modeled cross-sectional area) at the onset of simulations representing 2.6 and 2.3 µm sarcomere lengths (SL). These values were chosen to match our measured passive force values ranging from 5–12 kPa in skinned human skeletal muscle cells at SL=2.65 µm [Miller et al., unpublished data].

Thin-filament structures represent the helical pitch of native vertebrate thin-filaments (rotating 180° over 37.7 nm, [36]) and were modeled identical to prior studies [37, 38]. Regulatory unit activation span was set at 50 nm for all simulations, thereby activating the equivalent length of ~9 actin monomers, or 3 thin-filament nodes along one actin helix, subsequent to Ca²⁺-binding to troponin and tropomyosin movement.

Kinetics

The kinetic rates driving thin-filament activation and cross-bridge cycling were identical to the basic cooperative algorithms described previously [38]. Thin-filament activation represents three states: no Ca²⁺-bound to troponin (unavailable to bind myosin), Ca²⁺-bound to troponin (unavailable to bind myosin), movement of tropomyosin to expose actin-target sites along thin-filaments (available to bind myosin). Cross-bridge cycling represents three states: unbound; bound, low-force bearing cross-bridge; and bound, high-force bearing cross-bridge. However, the actual force generated by a cross-bridge depends upon the distance between thick- and thin-filament nodes and the strain borne by the cross-bridge spring element. All simulations used cooperative thin-filament activation parameters as previously described [38], with ψ=ζ=100. ψ and ζ coordinate effective strength of cooperative thin-filament activation and offset the effect of ψ on the rate of Ca²⁺-binding to troponin, respectively. Simulations used position-dependent cross-bridge rate transitions described previously [37, 38].

Data analysis

Identical to prior analysis [37, 38], steady-state data were gathered from each run by calculating the mean of the final 10% of the simulation for each metric (dashed lines Fig. 2A). ATP utilization was recorded at each time step as the number of cross-bridges that transitioned throughout the ‘forward cross-bridge cycle’ from the bound, high-force bearing state to the detached state. All normalized data relationships used the value at 100% of normal myosin content to normalize the data. However, predicted ATPase and fractional cross-bridge binding data are calculated using the number of myosin present throughout a simulation, and thus the denominator of these metrics varied with myosin content. In keeping with previous algorithms [37], 32 individual runs at pCa 4.0 were averaged to create the tension transients shown in Fig. 2A.

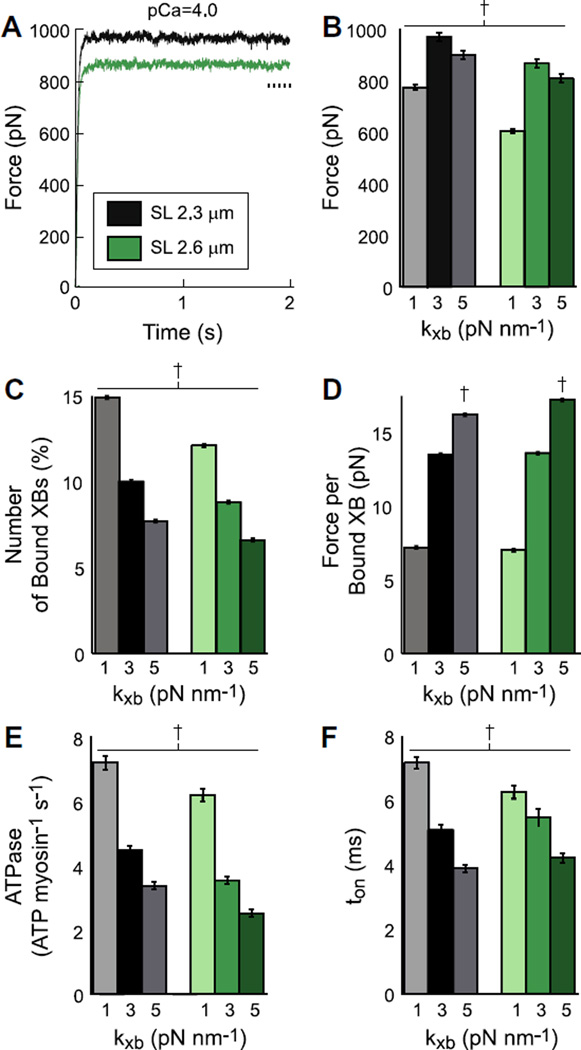
Figure 2. Simulations of contraction with normal myosin content and thick-filament architecture.

A) Average traces of Ca²⁺-activated force are plotted against time at pCa 4.0 (maximal force) for 2.3 and 2.6 µm sarcomere lengths (SL). Simulations represent 100% of normal myosin content and full thick-filament length at cross-bridge stiffness (k_xb) values of 3 pN nm⁻¹. Steady-state data were calculated from the final 10% of each run throughout a simulation (dashed line in panel A). Steady-state B) force, C) cross-bridge (XB) binding, D) force per bound XB, E) ATPase, and F) t_on at SL of 2.3 and 2.6 µm are plotted against k_xb. † denotes values that are different from all other values within each panel (mean±SD).

Consistent with the calculations of steady-state results described above, we count all unique, completed cross-bridge events during the final 10% of each run (i.e. cross-bridges that become attached and detached), which creates a pool of cross-bridge events from which an average myosin cross-bridge attachment time (t_on) was calculated for each run. Thus, the pool of completed cross-bridge events encompasses both events that underwent a full cross-bridge cycle and events that detached prior to completing a full cross-bridge cycle (i.e. exiting ‘backward’ from a bound, low-force bearing state to a detached state). A sub-set of simulations we tracked position and kinetic state of every thick- and thin-filament node throughout a simulation.

Statistical differences were assessed via one-way ANOVA followed by a Tukey-Kramer multiple comparison of the means (p<0.01). All simulations and analysis were performed using custom algorithms written in Matlab (The Mathworks, Natick, MA).

Results

Normal myosin content and thick-filament structure

To investigate the combined influence of cross-bridge stiffness (k_xb) and sarcomeric structure on myosin-actin cross-bridge kinetics and force production at maximal Ca²⁺ activation (pCa 4.0), we simulated muscle contraction while varying k_xb from 1–5 pN nm⁻¹ at sarcomere lengths (SL) of 2.3 to 2.6 µm. As simulations at 2.3 µm SL showed greater force development than 2.6 µm SL (Fig. 2B), due to greater thick-and thin-filament overlap, we initially describe the effects of varying k_xb at 2.3 µm SL. Peak steady-state force occurred at the intermediate k_xb of 3 pN nm⁻¹consistent with prior studies [9, 10, 37, 38]. This peak results from k_xb affecting the number of strongly bound cross-bridges and the force generated per cross-bridge, the product of which underlies steady-state force development. Increasing k_xb to 5 pN nm⁻¹ decreased cross-bridge binding (Fig. 2C), but increased force generated per bound cross-bridge (Fig. 2D). Together these data show that the most flexible cross-bridges confer the greatest levels of cross-bridge binding albeit a diminished capacity to generate or sustain force, and conversely for the stiffest cross-bridges. Varying k_xb also effects myosin-actin cross-bridge kinetics, as the kinetic rate-functions underlying cross-bridge state transitions depend upon cross-bridge distortion, or strain [37, 38]. Increasing k_xb decreased both cross-bridge ATPase (Fig. 2E) and myosin attachment time, t_on (Fig. 2F). These results show that varying k_xb alters myosin-actin cross-bridge kinetics and force production such that maximal single fiber force production is achieved at k_xb=3 pN nm⁻¹which is consistent with estimates from cellular experiments [21, 28, 34].

Increasing SL from 2.3 to 2.6 µm decreased the thick- and thin-filament overlap by 18.5% (810 vs. 660 nm), thereby reducing the number of cross-bridges able to bind actin (Fig. 1B–C). As SL increased from 2.3 to 2.6 µm, force decreased at each k_xb value (Fig. 2B), primarily due to the reduced number of strongly bound cross-bridges (Fig. 2C) because force per bound cross-bridge remained unchanged at k_xb values of 1 and 3 pN nm⁻¹ (Fig. 2D) for both SL values. As SL increased, there was a slight increase in force generated per bound cross-bridge at k_xb = 5 pN nm⁻¹. ATPase decreased as k_xb increased for both SL values, although ATPase values were lower for 2.6 µm SLs at each k_xb (Fig. 2E). Similar to the SL-dependent decreases due to diminished thick-to-thin filament overlap, the SL-dependent decreases in ATPase at 2.6 µm SL also follow from reduced cross-bridge binding. At each SL, t_on decreased as k_xb increased, although the range of t_on values was greater for 2.3 µm SL across all k_xb values. These data show that the influences of k_xb on force production and cross-bridge cycling were largely similar at both SL, which may indicate that steady-state contraction is more sensitive to variations in k_xb than variations in thick- and thin-filament overlap, 100% myosin content.

Effects of reduced myosin content

Myosin content was reduced (down to 50% of normal) either randomly along the length of the thick-filaments or uniformly from the Z-line end of the thick-filaments. As with the 100% myosin simulations (Fig. 2), we altered k_xb (Fig. 4) and SL (Fig. 5) to determine the effects of sarcomeric structure on cross-bridge kinetics and force production. We will first present results at k_xb=3 pN nm⁻¹ and SL = 2.3 µm (Fig. 3), as these conditions produced maximal force production at 100% myosin content (Fig. 2).

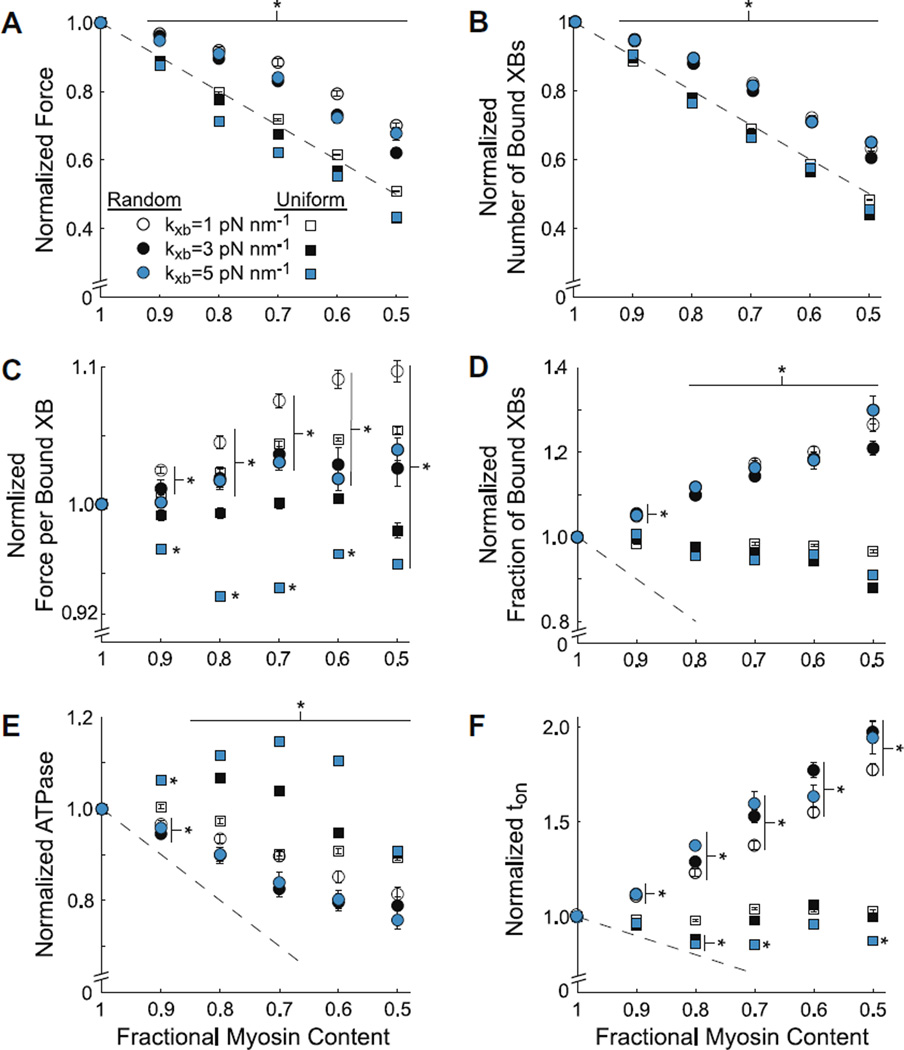
Figure 4.

Random vs. uniform reductions in myosin content as k_xb varied

Normalized steady-state values of A) force, B) cross-bridge (XB) binding, C) force per bound XB, D) fractional XB binding, and E) ATPase, and F) t_on are plotted against myosin content, as myosin was decreased randomly or uniformly from thick-filaments. Data represent simulations at pCa=4.0 and SL=2.3 µm as cross-bridge stiffness (k_xb) varied from 1–5 pN nm⁻¹. Data were normalized to values at 100% myosin for each k_xb value. * denotes differences from 100% myosin content (mean±SE).

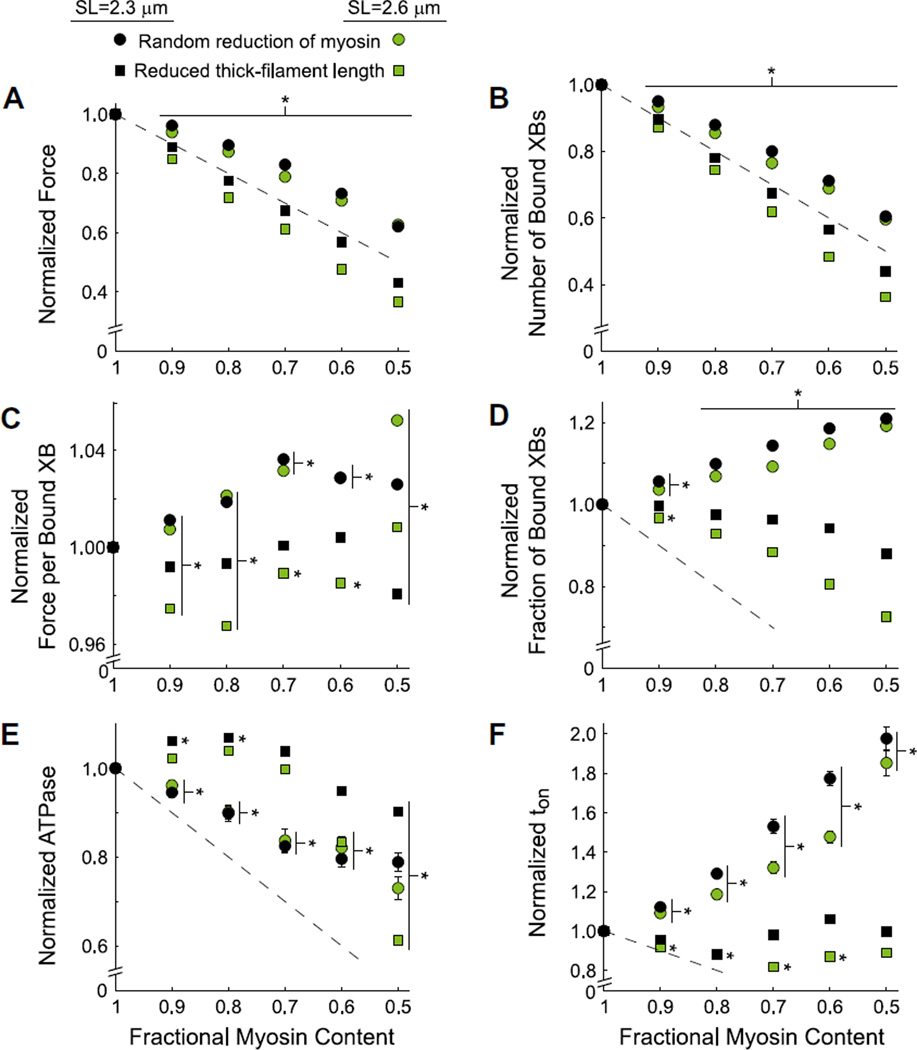
Figure 5. Random vs. uniform reductions in myosin content at 2.3 and 2.6 µm SL.

Normalized steady-state values of A) force, B) cross-bridge (XB) binding, C) force per bound XB, D) fractional XB binding, and E) ATPase, and F) t_on are plotted against myosin content, as myosin was decreased randomly or uniformly from thick-filaments. Data represent simulations at pCa=4.0 and k_xb=3 pN nm⁻¹ at SL values of 2.3 or 2.6 µm. Data were normalized to values at 100% myosin content for each SL. * denotes differences from 100% myosin content (mean±SE).

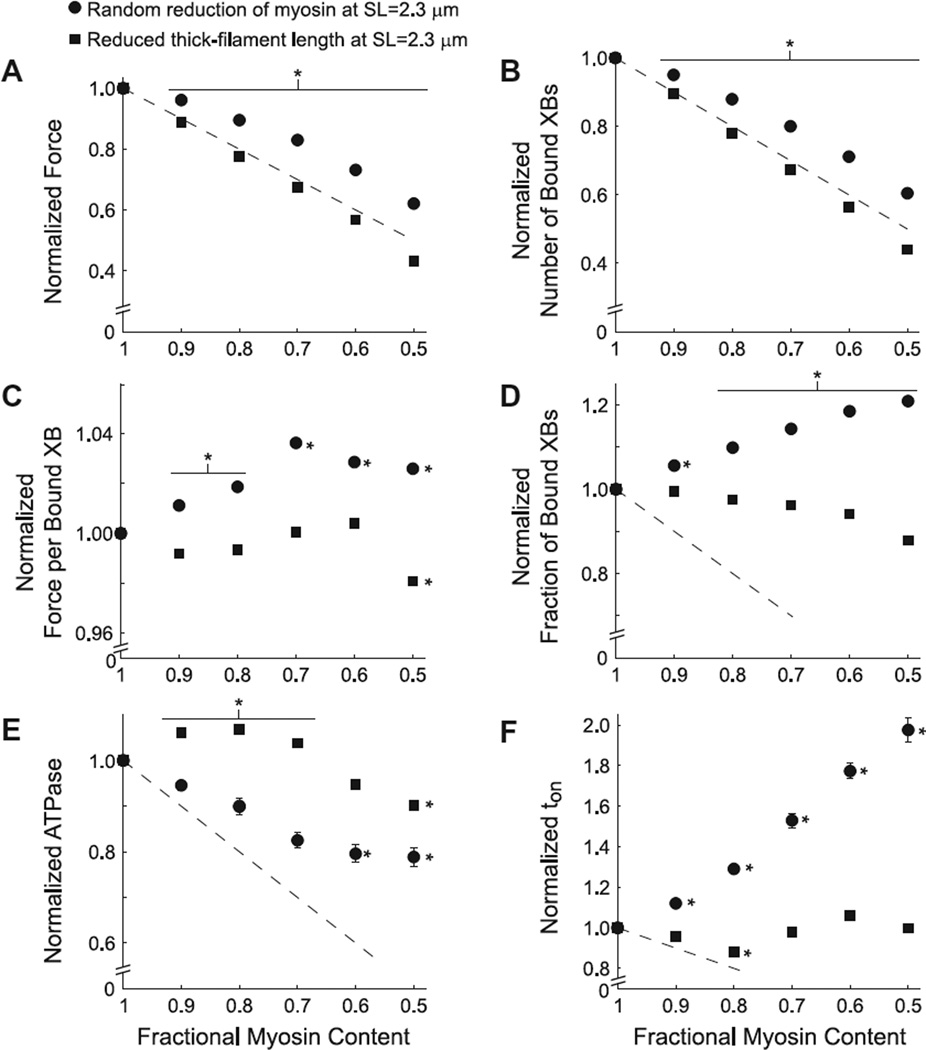
Figure 3. Random vs. uniform reductions in myosin content at a sarcomere length of 2.3 µm.

Normalized steady-state values of A) force, B) cross-bridge (XB) binding, C) force per bound XB, D) fractional XB binding, and E) ATPase, and F) t_on are plotted against myosin content. Myosin content was reduced two ways: randomly along thick filaments and uniformily from the Z-line end of thick-filaments. Data represent simulations at pCa=4.0 and k_xb=3 pN nm⁻¹normalized to values at 100% myosin content. * denotes differences from 100% myosin content (mean±SE).

Normalized force at pCa 4.0 decreased as myosin content was reduced randomly along the thick-filaments and uniformly from the Z-line end of thick-filaments (Fig. 3A). The overall decrease in force was less when myosin content decreased randomly (circles) than when myosin content decreased uniformly (squares), being above vs. slightly below the 1:1 decrease in force that would be expected from fewer available cross-bridges in each simulation (dashed line). Normalized decreases in the number of bound cross-bridges for random and uniform cross-bridge removal (Fig. 3B) were similar to the normalized force relationships (Fig. 3A). The consistency between the predicted force and number of bound cross-bridges arises from the modest variation in force per bound cross-bridge (< ± 5%) as myosin content decreased, both randomly and uniformly (Fig. 3C). These results demonstrate that random and uniform loss of myosin content from the sarcomere diminish force production.

The differences in force production with random vs. uniform reductions in myosin content (Fig. 3A) stem from the differential influences of myosin content on the normalized fraction of bound cross-bridges. Specifically, the fraction of bound cross-bridges increased with random decreases in myosin content, but decreased with uniform reductions in myosin content (Fig. 3D). As force per bound cross-bridge remained relatively unchanged with the amount or type of myosin that was removed from the sarcomere (Fig. 3C), the increased number of bound cross-bridges with random vs. uniform myosin removal would facilitate greater force production in muscle fibers.

Greater fractional cross-bridge binding for random vs. uniform myosin removal was driven by different cross-bridge kinetics as myosin content decreased in the sarcomere. Random reductions in myosin content led to linear reductions in ATPase at 90–70% myosin content, below which ATPase leveled off (Fig. 3E). Random reductions in myosin content also led to approximately linear increases in t_on (Fig. 3F). However, uniform reductions in myosin content produced slight increases in ATPase at 90–70% myosin content and a diminished ATPase value at 50% myosin content (Fig. 3E). Uniform reductions in myosin content minimally affected t_onwith the overall t_on-myosin content relationship being basically flat as myosin with uniform reductions in myosin content (Fig. 3F). In summary, these results indicate that random myosin loss influences ATPase and t_on (Fig 3E–F) to augment fractional cross-bridge binding (Fig. 3D), thereby providing a mechanism to ease force loss as myosin content decreases throughout the sarcomere (Fig. 3A). In contrast, uniform myosin loss has a relatively small effect on cross-bridge kinetics, and thus, fractional cross-bridge binding decreases as well.

An important caveat to this data, as described in the Methods, is that the reported ATPase values take on the traditionally reported units of ATPase myosin⁻¹ s⁻¹where “myosin⁻¹” represents the total number of myosin heads present in a simulation. Thus, the absolute number of ATP used throughout a simulation drops more sharply than shown in Fig. 3E (proportional to ATPase×fractional myosin content). In addition, we initially considered that thick-filament stiffness may decrease with reduced myosin content. Data from a subset of preliminary simulations, where thick-filament stiffness was reduced in-kind with myosin content, showed no significant differences, compared to simulations where thick-filament stiffness values were fixed.

Effects of reduced myosin content as cross-bridge stiffness varied

As prior computational studies have indicated a strong, inverse correlation between the number of bound cross-bridges and thick-filament stiffness [9, 10, 37, 38], we investigated the combined effects of reduced myosin content and cross-bridge stiffness (Fig. 4). Specifically, k_xb was varied from 1–5 pN nm⁻¹ as myosin was reduced randomly or uniformly. The k_xb = 3 pN nm⁻¹ values (black symbols) are identical to the data presented in Figure 3 and will first be compared to the results for k_xb = 1 pN nm⁻¹. Normalized force at k_xb=1 pN nm⁻¹ (open symbols) increased for random and uniform myosin loss at fractional myosin content values ≤ 70% of normal, compared to k_xb = 3 pN nm⁻¹ (Fig 4A). This increase in normalized force at k_xb=1 pN nm⁻¹ was due to an increase in force generated per bound cross-bridge (Fig. 4C), as the number of bound cross-bridges was relatively unchanged with cross-bridge stiffness (Fig. 4B). Cross-bridge kinetics were affected differently by changes in k_xb depending upon whether myosin was lost randomly or uniformly. At k_xb=1 pN nm⁻¹random reductions in myosin content led to a modest increase in ATPase (Fig. 4E) and decrease in t_on (Fig. 4F) compared to k_xb = 3 pN nm⁻¹. In contrast, the uniform reductions in myosin content produced relatively large decreases in ATPase (Fig. 4E) at intermediate values of myosin loss and basically no change in t_on (Fig. 4F) for k_xb=1 vs. 3 pN nm⁻¹.

As k_xb increased from 3 to 5 pN nm⁻¹ (cyan symbols, Fig. 4), simulation results were largely unaffected by random myosin loss, but greatly affected by uniform myosin loss. At k_xb=5 pN nm⁻¹uniform reductions in myosin content decreased force production (Fig. 4A), primarily due to decreased force per bound cross-bridge (Fig. 4C) as the number of bound cross-bridges remained unchanged (Fig. 4B). ATPase increased at k_xb=5 vs. 3 pN nm⁻¹ at intermediate myosin content values (Fig. 4E), and showed modest decreases in t_on at 50–70% myosin content (Fig. 4F). These data demonstrate that k_xb values indeed affect sarcomeric force production and cross-bridge behavior; however, reduced myosin content influenced these measures of contractility more greatly than k_xb.

Random vs. uniform reductions in myosin content at 2.3 and 2.6 µm sarcomere length

For random reductions in myosin content (circles), increasing SL from 2.3 to 2.6 µm had relatively minor effects on force production (Fig. 5A) and cross-bridge ATPase (Fig. 5E). The most significant kinetic effect of increased SL was a smaller increase in t_on as myosin content decreased at the longer SL (Fig. 5F). The slight reduction in t_on for 2.6 vs. 2.3 µm SL led to a slight decreases in normalized cross-bridge binding (Fig. 5B, D). Again, the effects of SL as myosin content was randomly reduced were slight in comparison to uniform reductions in myosin content.

When myosin was reduced uniformly (squares), the decline in normalized force was greater at 2.6 vs. 2.3 µm SL (Fig. 5A). This followed from a decrease in cross-bridge binding (Fig. 5B) as thick-to-thin filament overlap decreased, which led to greater decline in fractional cross-bridge binding as myosin content uniformly decreased along thick-filaments (Fig. 5D). The decrease in thick-to-thin filament overlap also influenced cross-bridge kinetics (Fig. 5E–F), with the most distinct SL-dependent difference showing up in the ATPase-myosin content relationships at the lowest myosin content values. Specifically, ATPase dropped off sharply at 50–60% myosin content for SL=2.6 µm (Fig. 5E), roughly 4X more sharply than SL=2.3 µm. These results indicate that reductions in thick-to-thin filament overlap considerably compromise force production and cross-bridge binding as myosin content uniformly decreased along thick-filaments.

Spatial effects of cross-bridge stiffness and myosin content on force production

To illustrate spatial effects of varied cross-bridge stiffness and myosin content throughout the half-sarcomere, we calculated average force borne along filaments and cross-bridges at each time-step during the first 100 ms of force development. Fig. 6 shows average force along thick-filaments (Fig. 6A–B), cross-bridges (Fig. 6C–D), and thin-filaments (Fig. 6E–F) for k_xb values of 3 and 1 pN nm⁻¹ at SL=2.3 µm. In general these data are consistent with previous studies [7, 10, 37], but the current presentation highlights spatial detail underlying i) diminished sarcomeric force production due to decreased cross-bridge force as k_xb decreased from 3 and 1 pN nm⁻¹ (Fig. 6), and ii) diminished sarcomeric force production with uniform vs. random reductions in myosin content even though cross-bridge force was similar at 70% myosin content for both types of myosin loss (Fig. 7).

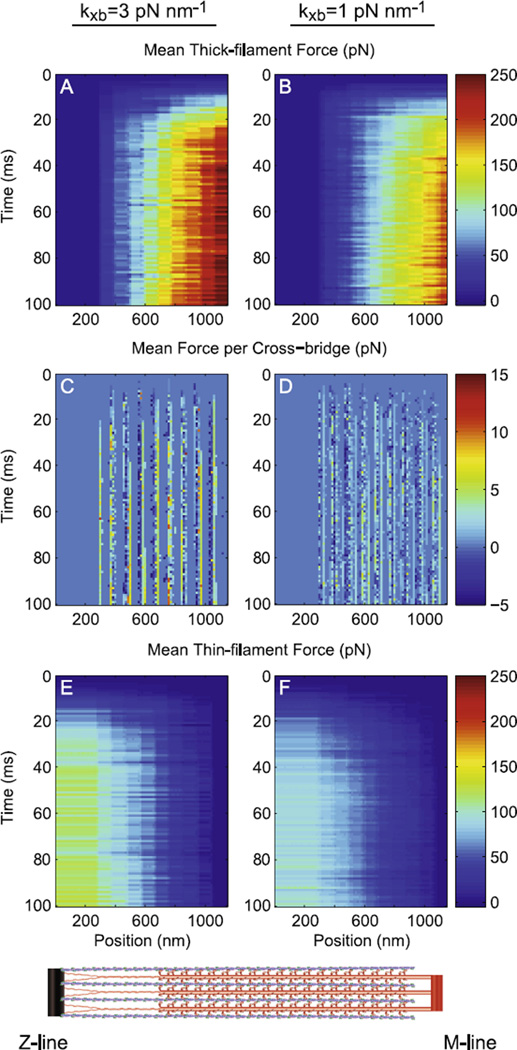
Figure 6. Force distribution throughout the half-sarcomere as k_xb varied.

Average force borne by A–B) thick-filaments, C–D) cross-bridges, and E–F) thin-filaments is shown for simulations with k_xb values of 3 (panels A, C, E) and 1 (panels B, D, F) pN nm⁻¹ (pCa=4.0 and SL=2.3 µm at 100% myosin content). Note that thick- and thin-filament color bars ranges 0–250 pN, while cross-bridge color bar ranges from −5–15 pN.

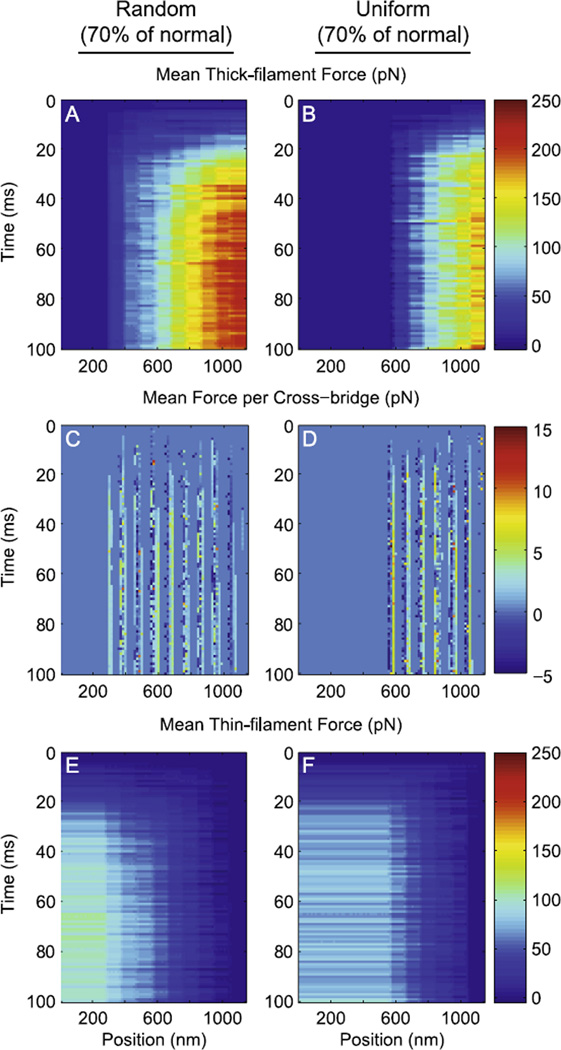
Figure 7. Force distribution throughout the half-sarcomere at 70% myosin content.

Average force borne by A–B) thick-filaments, C–D) cross-bridges, and E–F) thin-filaments is shown for simulations with k_xb values of 3 pN nm⁻¹when myosin content decreased randomly (panels A, C, E) and uniformly (panels B, D, F) along thick-filaments (pCa=4.0 and SL=2.3 µm). Note that thick- and thin-filament color bars ranges 0–250 pN (as in Fig. 6), while cross-bridge color bar range was reduced to −1.5–4.5 pN.

Force borne along thick-filaments is smallest towards the Z-line (=0, as passive force borne by the titin element was subtracted for panels A-B) and greatest near the M-line. Conversely, force borne along thin-filaments is greatest near the Z-line and smallest near the M-line (=0 at the free end, Fig. 6E–F). Note that force values borne by thick-filaments are roughly twice the force values borne by thin-filaments, due to thick-filaments interacting with six thin-filaments while thin-filaments only interact with three thick-filaments. Maximal forces along thick-(Fig. 6A–B) and thin-filaments (Fig. 6E–F) also reflect the maximal steady-state values of 971±17 and 775±10 pN shown in Fig. 2B, as k_xb was decreased from 3 to 1 pN nm⁻¹. As described earlier, diminished force production at k_xb = 1 vs. 3 pN nm⁻¹ arises from the diminished capacity of more compliant cross-bridges to generate/maintain force (Fig. 6C–D).

As predicted by others [7, 10, 14], cross-bridge binding occurred in ‘pockets’ or ‘hotspots’ along the length of the half-sarcomere where myosin heads and actin binding sites are well aligned. These regions can be envisioned through plots of average cross-bridge force throughout the half-sarcomere (Fig. 6C–D). Comparing between k_xb values of 3 and 1 pN nm⁻¹stiffer cross-bridge values lead to more sharply defined (less broad) regions of cross-bridge binding (Fig. 6C). Consistently, comparable thermal force distort compliant cross-bridges more greatly, broadening the regions of cross-bridge binding for k_xb=1 pN nm⁻¹ (Fig. 6D). While there are clear differences in the average cross-bridge force between k_xb values of 3 and 1 pN nm⁻¹ (Fig. 6C–D), the values within a panel are relatively consistent along the half-sarcomere and do not show any obvious differences near the M- or Z-line, in contrast with the force gradient along the filaments.

As myosin content was reduced to 70% of normal, thick- and thin-filaments bore greater forces for random (Fig. 7A, E) vs. uniform reductions in myosin content (Fig. 7B, F). Although random reductions in myosin content also reduced the force magnitudes borne along filaments (Fig. 7 A, E) compared to normal myosin content (Fig. 6A, E), average force borne per cross-bridge was similar for both conditions (within 4%, Fig. 3C). Moreover, the spatial distribution of cross-bridge binding throughout the sarcomere was consistent at 70% randomly reduced myosin content and 100% myosin content (Fig. 7C vs. 6C). In contrast, uniform reductions in myosin content eliminated the capability of cross-bridge binding at many thick-filament nodes (Fig. 7D), even though average force per cross-bridge was similar to the value at 100% myosin content (Fig. 6C). This spatial disruption in cross-bridge binding led to less force production along filaments (Fig. 7B, F) than either 100% myosin content (Fig. 6A, E) or a random reduction to 70% myosin content (Fig. 7A, E).

Therefore, randomly reducing myosin content does compromise force production, but less than comparable reductions in myosin content that occurred uniformly from the end of thick-filaments. A key difference between random vs. uniform loss of myosin content is the increase in t_on as myosin content decreased (Fig. 3F), which effectively increases cross-bridge binding with random myosin loss (Fig. 3B, D). Consistently, this increase in t_on leads to greater overall cross-bridge binding, which underlies greater forces borne along the filaments for random (Fig. 7A, E) vs. uniform (Fig. 7B, F) myosin loss. Mechanistically, this increase in t_oncross-bridge binding, and force production may be related to greater compliant filament realignment [7, 9, 10, 37, 38] in simulations of random vs. uniform myosin loss, as cross-bridge binding would take place along a the entire length vs. a fractional length of the thick-filament as myosin content decreases (Fig. 7A vs. B).

Discussion

The primary focus of this computational study was to assess how the pattern of myosin loss along thick-filaments influenced cross-bridge behavior and force development throughout the sarcomere. As myosin-actin cross-bridge performance underlies whole muscle contraction, understanding the effects of myosin loss due to disease, disuse, aging, and normal physiological remodeling is important and cannot be examined using conventional experimental methods (i.e. biochemical quantification, electron microscopy, muscle mechanics). Moreover, there are currently no genetic, pharmacological, or biochemical means whereby different patterns of myosin inactivation/loss can be modeled to assess its role in altering contractility. In this context, computational modeling offers the only viable means to investigate this phenomenon.

We found that force decreased with random reductions in myosin content, but this decrease in force was less than the decrease observed with uniform reductions in myosin content. Although the number of myosin heads available to bind actin decreased similarly for both types of simulations, the greater force production with random myosin loss arose from a greater cross-bridge binding due to a longer myosin attachment times (t_on). The mechanism that longer myosin t_on could help to mitigate force decreases as myosin is lost from the muscle fiber agrees with our previous findings in human skeletal muscle from heart failure patients [30, 31]. In addition, simulations showed reduced ATPase with random myosin loss, which would provide the chemomechanical advantage of more economical force production (economy=force per ATP consumed). Altogether, these data support a general model where myosin loss and replacement occurs randomly along thick-filaments during remodeling in single skeletal muscle fiber [13, 42].

Reduced myosin content

This series of computational simulations complement our empirical findings in human skeletal muscle fibers [30, 31]. Specifically, t_on decreased 14–19% without any isometric tension change in single fibers from chronic heart failure patients, compared to healthy, activity-matched controls [30]. These changes in t_on were associated with a 15–35% myosin loss that depended on fiber type [31]. As there were no differences in thick-filament length, myofibrillar area, and thick-to-thin filament ratio between patients and controls [31], we speculated that myosin content was likely lost at random along thick-filaments in heart-failure patients. Our computational findings support this speculation and provide additional molecular detail of cross-bridge mechanisms that enhance economical maintenance of fiber tension as myosin content decreased.

While these combined computational and experimental results help advance our understanding of the molecular mechanisms of muscle contraction, there are a number of pathological conditions associated with sarcomeric remodeling that are not addressed here. The idea that ambulatory disability with chronic heart failure may be diminished by prolonged t_on and fractional cross-brige binding, rather than increase in force per bound cross-bridge, is an important contribution to our understanding of this phenotype. However, other conditions [1, 11, 19, 26, 32] show decreased myosin heavy chain content and present a range of diminished contractile function that may be more severe than we observed in the heart failure patients. This may stem from the clinically stable heart failure patients showing mild to moderate, rather than severely dysfunctional contractility as might occur with the progression toward end-stage heart failure. Therefore, additional studies of other disease states or more severe heart failure will be useful as we continue to identify and describe the link between myofilament protein behavior and cellular/whole muscle function in this integrative, multi-scale mechanical system.

Varied cross-bridge stiffness

Although a series of previous computational studies have illustrated that cross-bridge stiffness can influence cross-bridge recruitment, thereby affecting force production and ATPase [10, 37, 38], this study reports the additional metrics of cross-bridge behavior: force per bound cross-bridge, fractional cross-bridge binding, and t_on. Due to thermal forces that influence cross-bridge distortion [10, 25], the most flexible cross-bridges explore the largest spatial volumes along thin-filaments, which leads to the greatest levels of cross-bridge binding. However, this increased cross-bridge binding does not necessarily translate into the greatest levels of force production due to a compromised capacity to generate force or maintain load, in comparison to stiffer cross-bridges. This arises because much of the chemomechanical energy transduction for the most flexible cross-bridges is lost as cross-bridge deformation rather than sustained force generation [37]. This leads to diminished force production throughout the sarcomere, both in magnitude (Fig. 6) and economy (as ATPase and cross-bridge stiffness were inversely correlated, Fig. 2). In contrast, stiffer cross-bridges deform less than flexible cross-bridges, restricting stiffer cross-bridge binding to the most well-aligned target zones throughout the sarcomere [7], which allows stiffer cross-bridges to transmit a greater fraction of their chemical energy into ‘useful’ mechanical force. Therefore, intermediate cross-bridge stiffness values, as presented here for 3 pN nm⁻¹benefit from moderate levels of cross-bridge binding and force generation, which led to the greatest steady-state force values at moderate t_on and ATPase values for both SL (Fig. 2). Therefore, economical skeletal muscle contraction may peak at cross-bridge stiffness values of 3–4 pN nm⁻¹consistent with estimates of cross-bridge stiffness from muscle fiber experiments [28, 34].

Altered thick-to-thin filament overlap

The sarcomere length values studied here encompass much of the potential thick-to-thin filament overlap distance that may occur throughout the 15–20% change in fiber length during a skeletal muscle contraction [3, 27]. Although we found that overall changes in force production and cross-bridge kinetics varied more greatly with k_xb than SL (Fig. 2), each k_xb value showed consistent decreases in force, cross-bridge binding, and ATPase as SL increased. These consistent decreases were primarily driven by the reduced capacity for cross-bridge binding as thick-to-thin filament overlap decreased 18.5% from 2.6 to 2.3 µm SL. Consistently, these relative reductions in thick-to-thin filament overlap also arose as similar reductions in cross-bridge binding as myosin content decreased. Specifically, fractional cross-bridge binding at uniform myosin content values of 50–80% for SL=2.3 µm almost exactly matched the values of 70–100% myosin content at SL=2.6 µm, which accounts for the ~20% decrease in thick-to-thin filament overlap. Therefore, the capacity for cross-bridge binding was not different with changes in thick-to-thin filament overlap or uniform reductions in myosin content from the Z-line end of the thick-filament, but the ensemble cross-bridge behavior and forced production throughout the sarcomere was not consistent. These functional differences that arise as the pattern of cross-bridge binding varied throughout the sarcomere highlights the complexity of the ensemble cross-bridge behavior as force develops throughout the sarcomere.

Recent computational studies of the length-tension curve [45] have demonstrated that the physiological length-tension response [17] arises due to reduced thick-to-thin filament spacing and diminished thick-to-thin filament overlap as SL increases. Williams et al. [45] were able to show that changing solely thick-to-thin filament overlap creates a more shallow length-tension response than the empirical relationship [17, 45]. For the specific sarcomere lengths used here, an isovolumetric reduction in force from 2.3 to 2.6 µm SL would be 5–10% greater than the ~20% reduction observed in Fig. 2 (k_xb=3 pN nm⁻¹) or by Williams et al. [45] when accounting for thick-to-thin filament overlap alone. Consistently, we might anticipate that the steady-state force would decrease more than reported between 2.3–2.6 µm SL (Fig. 2) and that force production might fall more steeply as myosin content was reduced at 2.6 µm SL (green symbols, Fig. 5A). However, a number of spatial, kinetic, and mechanical forms of cooperative thin-filament activation and cross-bridge binding in the current model that are not present or formulated differently in the models of Williams et al. [44, 45]. Without further speculation about varied model predictions due to differential effects of reduced thick-to-thin filament spacing vs. reduced thick-to-thin filament, it is clear that these mechanism of length-dependent force production remain important and minimally understood contributors to static and dynamic muscle function.

Sarcomeric structure influences ensemble cross-bridge behavior

The remarkable capacity of the sarcomere to robustly generate and bear force as variations in cross-bridge stiffness or myosin content vary can be appreciated by the data presented in Figs. 6 and 7. From the architectural standpoint of organizing a structure to facilitate force production we see that the highest loads are borne at the ends of thick- and thin-filaments. Filaments would integrate with a series of M- and Z-line proteins near these locations of greatest load, which may confer structural stability at regions of the sarcomere that are most prone to failure via overloading. Although simple beam-theory from an introductory mechanical engineering textbook may have illustrated these load profiles along the filaments, we had not envisioned that sarcomeric structure and elasticity (modest filament compliances, relative to the much more flexible cross-bridges) would lead to relatively uniform cross-bridge forces throughout the length of the sarcomere. If overall position-dependent sarcomeric load were calculated as the sum of thick-filament load + 2×thin-filament load, given there are twice as many thin-filaments, this would lead to all bound cross-bridges experiencing similar filament loads. Thus, the structural organization of the sarcomere appears to ‘normalize’ cross-bridge behavior throughout the length of thick-filaments, as there were no obvious spatial-dependencies in the mean load borne per cross-bridge from the M-line to the Z-line.

This uniformity of load borne by cross-bridges throughout the sarcomere carried forward as myosin content was randomly and uniformly reduced to 70% of normal (Fig. 7). However, random reductions in myosin content led to longer t_on values (Fig. 3F) and greater cross-bridge binding (Fig. 3B, D) that produced greater thick and thin filament loads (Fig. 7A,B,E,F) and steady-state force (Fig. 3A) for random vs. uniform myosin loss. Perhaps this stems from the fact that cross-bridges were capable of binding along the entire length of the filaments when myosin content was randomly reduced, which would enhance cooperative cross-bridge binding due to spatial, mechanical, and kinetic forms cooperativity. In contrast, similar mechanisms of cooperative cross-bridge binding would be limited to shorter filament regions upon uniform reductions in myosin content, thereby compromising cross-bridge recruitment and steady-state force production.

Increasing spatial, mechanical, and kinetic information has been included in model structures representing the sarcomere and myofilament proteins with each revision and update to the class of spatially-explicit models, as used here and developed over the past 15 years [7–10, 37, 38, 43, 44]. While this class of models remains far from a digital representation of the half-sarcomere or many sarcomeres, findings from these computational studies continue to show that spatial and mechanical coupling between cycling cross-bridges intrinsically affects ensemble cross-bridge behavior. Whether one classifies this cross-bridge behavior as ‘coordinated or coupled force-generators’ [9, 10, 37] vs. ‘independent force-generators’ [22, 23] remains an interesting question due to the unique structure of muscle. The fundamental “rules” underlying thin-filament activation and cross-bridge binding were set by rate functions that include spatial, mechanical, and kinetic information describing Ca²⁺-activated muscle contraction. These rate functions did not change as myosin was lost along thick-filaments, but ensemble cross-bridge kinetics and steady-state force production was significantly influenced by the pattern of myosin loss throughout the sarcomere. While specific mechanisms that coordinate vs. isolate cross-bridge force generation remain minimally characterized computationally and difficult to measure experimentally, it is becoming increasingly difficult to describe cross-bridges as independent force-generators given the highly-structured network of proteins that constitute the sarcomere.

Conclusions

In combination with experimental measurements [30, 31], these findings illustrate that the physiological response in chronic heart failure patients arises from random myosin decreases along thick-filaments, which augments fiber force production as myosin content decreases. Moreover, simulations also suggest that random reductions in myosin content confer more economical contraction due to prolonged t_on as myosin content decreased, which would support a model of random removal/replacement of myosin along the length of the thick-filament [13, 42]. From a clinical perspective, these two adaptations may be beneficial in maintaining normal muscle function in pathological conditions or muscle pathologies, which are often characterized by myofilament protein loss and energetic insufficiency [18, 35]. From a physiological perspective, while force production and fractional cross-bridge binding were clearly influenced by variations in cross-bridge stiffness and thick-to-thin filament overlap, the overall influences of variations in myosin content were much greater than either of these other two characteristics among all simulation results. Thus, our results highlight the potential for variation in myosin protein content as a potentially important modulator of contractile function in skeletal muscle fibers.

Highlights.

Myosin loss may diminish muscle fiber performance with aging, disuse, and disease

Computational models of myosin loss reduced cross-bridge number and fiber force

Random myosin loss resulted in a smaller fiber force decrements than uniform loss

Myosin attachment time and cross-bridge binding increased with random myosin

Results support prior findings in heart failure patients with random myosin loss