Abstract
Purpose
We systematically reviewed pharmacoepidemiologic studies published in 2012 that used inverse probability weighted (IPW) estimation of marginal structural models (MSM) to estimate the effect from a time-varying treatment.
Methods
Potential studies were retrieved through a citation search within Web of Science and a keyword search within PubMed. Eligibility of retrieved studies was independently assessed by at least two reviewers. One reviewer performed data extraction and a senior epidemiologist confirmed the extracted information for all eligible studies.
Results
Twenty pharmacoepidemiologic studies were eligible for data extraction. The majority of reviewed studies did not report whether the positivity assumption was checked. Six studies performed intention-to-treat analyses, but none of them reported adherence levels after treatment initiation. Eight studies chose an as-treated analytic strategy, but only one of them reported modeling the multiphase of treatment use. Almost all studies performing as-treated analyses chose the most recent treatment status as the functional form of exposure in the outcome model. Nearly half of the studies reported that the IPW estimate was substantially different from the estimate derived from a standard regression model.
Conclusions
The use of IPW method to control for time-varying confounding is increasing in medical literature. However, reporting of the application of the technique is variable and suboptimal. It may be prudent to develop best practices in reporting complex methods in epidemiologic research.
Keywords: inverse probability weighting, marginal structural models, pharmacoepidemiology
INTRODUCTION
A time-varying confounder is a time-varying risk factor for the study outcome which brings about changes in the treatment use under study.1 In the presence of time-varying confounders that are influenced by previous treatment, standard regression models may produce biased estimate of the total treatment effect.2,3 To obtain unbiased estimate in this situation, Robins et al. proposed the inverse probability weighted (IPW) estimation of marginal structural models (MSM).2,3 As the name indicates, IPW estimation attempts to control for confounding through assigning each participant a weight. The weight is proportional to the inverse probability of receiving observed treatment given the time-varying confounders and previous treatment history. The weights are then used to create a pseudo-population, in which participants receiving treatment and those not receiving treatment are balanced over the time-varying confounders but the relationship between treatment and outcome is not changed.3
After publication of the seminal papers on MSM, methodological studies have provided detailed insights regarding the types of bias this method handles well,4,5 the assumptions under which consistent causal effects can be identified,6–8 and the appropriate ways of constructing weights and building outcome models.9–12 IPW estimation has been increasingly used in medical research, possibly due to the straightforward interpretation of the parameters derived from MSM.12 Indeed, from 2000 to October 2009 Suarez et al. noted a 15-fold increase in the number of studies using this approach.13
Despite the increase in studies using IPW, the extent to which these studies conform to the recommendations proposed by methodological studies remains unknown. The purpose of this study was to systematically review pharmacoepidemiologic studies in which IPW was used to estimate the effect from a time-varying treatment. Based on information abstracted from these studies, we hope to provide a broader context for scientists considering using this approach through discussing the scenarios under which IPW method is preferred, appropriate procedures of conducting IPW analyses and contents which are critical to report when using IPW in medical literature.
METHODS
This study did not require ethics approval as no human subjects were involved.
Selection of articles
Our goal was to retrieve all pharmacoepidemiologic studies published in 2012 that used IPW to estimate effect from a time-varying treatment. To achieve this, we used two search strategies. First, using the Web of Science database, we retrieved all published studies citing any one of the seminal papers on MSM.2,3,9,14 Second, in case we missed any relevant studies which did not cite these seminal papers, we also conducted a keyword search within PubMed. To improve the methodological rigor of our search strategy, we worked with a research librarian and developed the following keyword search algorithm: (marginal structural model*) OR (“marginal structural Cox model”) OR (“inverse probability” AND (“weight” OR “weighted” OR “weights” OR “weighting”)) OR (inverse weight*). The following types of studies or publications were excluded from the review: (1) methodological or simulation studies, (2) studies assessing effect from a point-treatment, i.e., a treatment that was assumed invariant in the study period; (3) non-pharmacoepidemiologic studies, i.e., studies not focusing on pharmaceuticals, biologics, or medical devices as primary exposure; (4) letters, meeting abstracts, review articles, and editorials.
We followed the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines for this review.15 After excluding duplicate records, titles and abstracts of the remaining articles were assigned to two independent reviewers. Studies with titles and abstracts judged relevant by at least one reviewer underwent full-text review. Any discrepancy in eligibility judgment was resolved through discussion between the reviewers. One reviewer (SY) performed data extraction and a senior epidemiologist (KLL) confirmed the extracted information for all eligible studies.
Information abstraction
The following sections provide a brief description and rationale of each element of IPW method we chose to include in our data collection process. In particular, we extracted information about the type(s) of bias IPW was used to address, how the identifiability assumptions were assessed, how the weights were constructed and outcome models specified, and whether substantially different results were derived from IPW method and standard regression models.
Type of bias
As illustrated by Hernán et al.,4 compared to standard regression models, IPW has the advantages of eliminating bias from two sources when estimating the effect from a time-varying treatment. First, through applying inverse-probability-of-treatment weighting, IPW can control for the time-varying confounding while avoiding two types of bias that may arise in analyses with standard regression models.4 The first type of bias occurs when the time-varying confounder is simultaneously a confounder and intermediate variable. Conditioning analysis on such a variable (as performed in standard regression models) will block the indirect effect from previous treatment on study outcome that is mediated by this variable.3 Another type of bias (called collider-stratification bias16 or selection bias4) occurs in standard regression models when the time-varying confounder is a common effect (i.e., a collider) of previous treatment and an unmeasured risk factor for the study outcome. Conditioning analysis on this time-varying confounder induces a non-causal relationship between previous treatment and the unmeasured risk factor, which introduces bias in the effect estimate of previous treatment use.4
Second, through applying inverse-probability-of-censoring weighting, IPW can control for selection bias from informative censoring.4,5 Our review focused on the use of IPW for handling selection bias from artificially censoring participants with treatment noncompliance, e.g., discontinuing the treatment under study or switching to an ineligible treatment.5 Bias may be introduced when this artificial censoring depends on treatment history and also risk factors for the study outcome.17 Under certain conditions (discussed below), IPW can eliminate this bias by simulating a pseudo-population, in which all participants complete the follow-up but the effect of treatment on study outcome is the same as in the unweighted study population.18
Identifiability assumptions
There are three conditions or assumptions, under which consistent causal effects can be identified from non-experimental data: no uncontrolled confounding, consistency and positivity.9,19 Consistency is the assumption that an individual’s potential (or counterfactual) outcome under the observed treatment is precisely the observed outcome.20 Because consistency is often considered a reasonable assumption when estimating effects from medical treatments6, we did not extract information on this assumption.
When there are confounders (time-invariant or time-varying) that are not measured or measured with error, the IPW estimates will be biased by uncontrolled confounding. We looked for information about whether studies qualitatively discussed the susceptibility of their findings to uncontrolled confounding and whether they performed sensitivity analyses to test the robustness of their results when substantial uncontrolled confounding was suspected.
The positivity assumption states that each treatment level occurs with some positive probability at every level of observed confounders in the study population.7,21 For example, this assumption is violated when all (or almost all) patients with a specific contraindication (which is also a risk factor for the study outcome) are untreated with the medication under study. Among patients with the contraindication, the probability of receiving treatment will be zero (or close to zero), and the inverse probability will be inestimable (or a very large number). The disproportionate reliance on the experience of a few unusual individuals (i.e., treated patients with the contraindication) in the weighted population can result in imprecise and biased effect estimate.7 Thus, we extracted information about (1) whether studies reported that the positivity assumption was checked, (2) how the positivity assumption was evaluated, and (3) how violations of the assumption were handled (if detected).
Constructing weights
The validity of IPW estimates depends on correct construction of weights.3,19 There are two types of weights--unstabilized and stabilized. The unstablized weight is calculated as the inverse of conditional probability of receiving observed treatment given the history of time-varying confounders and previous treatment history (called weight denominator).3 The stabilized weight can be calculated as the product of the conditional probability of receiving observed treatment given baseline confounders and previous treatment history (called weight numerator) and the unstabilized weight. The stabilized weight is generally recommended because it can yield estimates with greater precision compared to the unstabilized weight.3 The conditional probability of receiving observed treatment (for weight numerator and denominator) is often estimated with a regression model (i.e., treatment model).
When non-compliance after treatment initiation is low, an observational intention-to-treat (ITT) analysis with IPW has been recommended.3,9,14 Specifically, this strategy assumes that once a participant initiates treatment, the participant will remain on treatment for the remainder of the study period. This assumption simplifies the process of estimating the probability of receiving observed treatment history, because only one model is needed to estimate the probability of treatment onset.22 In addition to ITT analyses, analogous to data analysis of a clinical trial, a non-experimental study can perform per-protocol and as-treated analyses using IPW.17 In a per-protocol analysis, a comparison is made only among those who adhere to the treatment under study and patients are censored when they deviate from the initial treatment. In an as-treated analysis, individuals are classified according to the treatment they receive during the follow-up rather than the treatment they initiate, and patients who stop or switch the treatment are also included in the analysis.
We extracted information about the analytic strategy each study adopted, and how they specified the treatment models for the weight numerator and denominator. For studies not assuming ITT, we assessed whether or not the authors modeled the multiphase of treatment use (e.g., treatment initiation, continuation, etc.) and how this was done.
Outcome model building
After weights are constructed, a weighted regression model (i.e., outcome model) is typically fit to estimate the effect of treatment on the outcome.9 All the variables included in the treatment model for the weight numerator should also be included in the outcome model, because they are not balanced between treated and untreated participants in the weighted population and thus can still bias the estimate.9 Substantive expertise should drive the selection of the functional form of exposure in the outcome model.22,23 For instance, under the assumption of a linear relationship between treatment duration and study outcome, studies can specify exposure as the total duration of previous treatment use, and the estimate then quantifies the effect from each additional time unit (e.g., one month) of treatment;3,17 studies performing ITT analyses can also specify exposure with an indicator for treatment initiation (yes or no) to estimate the average effect of initiating treatment in the follow-up period.17 In this review, we assessed what covariates were included in the outcome model and how they specified the functional form of exposure.
Discrepancy between IPW estimates and standard regression estimates
The review by Suarez et al. reported that more than half of the studies using IPW method yielded an estimate substantially different from that produced by standard regression models.13 However, the review did not provide information about how studies discussed reasons for such discrepancy. In this review, we assessed whether studies found a substantial difference in estimates between the two methods and further extracted information about how studies explained the discrepancy when it was noted. We considered a difference “substantial” if the difference was more than 20% of the IPW estimate13.
RESULTS
Figure 1 depicts the process of identifying studies eligible for the review. We retrieved 164 and 137 studies from citation search in Web of Science and keyword search in PubMed, respectively. After excluding duplicate studies (n=66), methodological or simulation studies (n=92), review studies (n=9), studies not focusing on a health-related outcome (n=12) or not using IPW (n=7), studies assessing effect from a point-treatment (n=66), and non-pharmacoepidemiologic studies (n=26), we had 23 pharmacoepidemiologic studies which applied IPW to estimate effect from a time-varying treatment. Among these 23 studies, three used IPW to evaluate effects from dynamic treatment regimens.24–26 Considering that weight construction for estimating effects from dynamic regimens is different from that for static regimens,27 we excluded these studies from the review. Data extraction was performed on the remaining 20 studies.28–47
Figure 1.
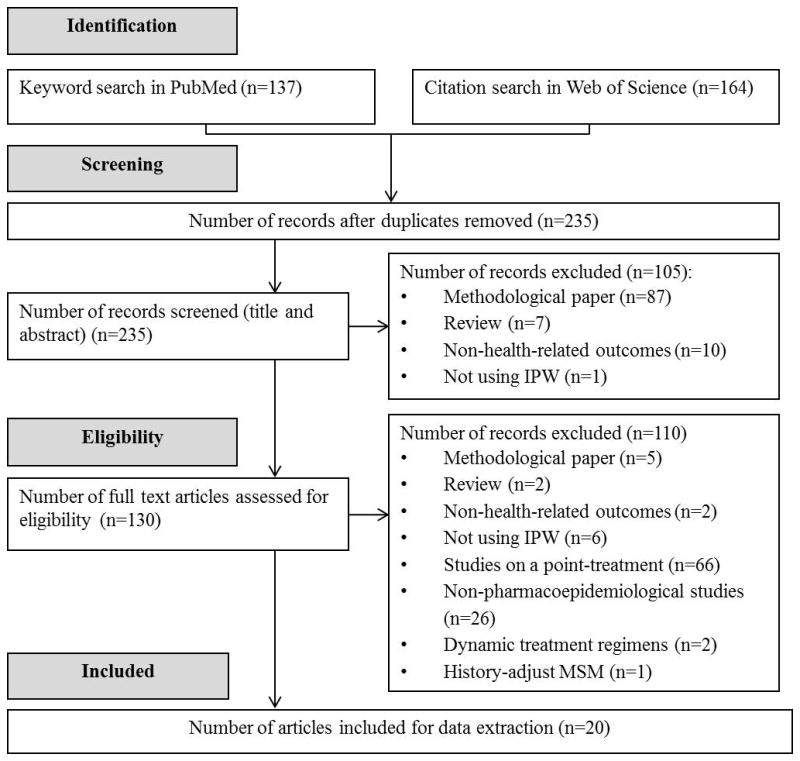
Identification of pharmacoepidemiolgoical studies using IPW to deal with time-varying confounding in 2012
Table 1 shows a brief description of the study design, primary exposure and outcome and potential time-varying confounders. Three studies compared treatments that were randomized to participants.28,38,44 However, they performed analyses as if data were collected from a non-experimental design, so we included them in the review. Half of the 20 studies assessed benefits or risks from antiretroviral therapy among HIV-infected patients31,33,36,37,39,43,47 or risk of HIV transmission from contraceptive use;34,40,42 five studies focused on treatment or prevention of cardiovascular diseases;28–30,32,44 two studies assessed treatments for chronic kidney disease;35,41 and there was one study assessing the effect of treatment for a protein metabolism disorder,45 schizophrenia,46 and breast cancer,38 respectively. The primary outcome of most studies was mortality (n=7) or first occurrence of a pre-specified event (n=12), and one study considered a repeated-measure outcome.47 With the exception of two studies,32,38 all reviewed studies provided information on the time-varying confounders.
Table 1.
General description of pharmacoepidemiologic studies published in 2012 and eligible for the systematic review
| Reference | Study design | Exposure & | Outcome & | Time-varying confounders |
|---|---|---|---|---|
| Cook et al.28 | Randomized controlled trial | Aspirin vs. no-treatment | CVD or CVD-related mortality | CVD risk factors, intermediate CVD events |
| Desai et al. 29 | Cohort | Candesartan vs. losartan | Mortality | Hospitalization |
| Gerhard et al. 30 | Cohort | Aggressive vs. conventional antihypertensive therapies | CVD or mortality | Blood pressure |
| Gsponer et al. 31 | Cohort | Switching to second-line ART vs. first-line ART | Mortality | CD4 cell count |
| Haukka et al. 32 | Cohort | Statins vs. no-treatment | Mortality | Not reported † |
| HCV working group of COHERE 33 | Cohort | Hepatitis C treatment vs. no-treatment | Mortality | CD4 cell count, HIV RNA level, platelet counts, alanine aminotransferase levels |
| Heffron et al. 34 | Cohort | Hormonal contraceptive vs. no-treatment | HIV infection | Pregnancy, unprotected sex |
| Hernández et al. 35 | Cohort | ACEI/ARB vs. no-treatment | Graft failure | Smoking, concurrent medication use |
| HIV-CAUSAL Collaboration 36 | Cohort | Nevirapine vs. efavirenz | Mortality | CD4 cell count, HIV RNA level, AIDS |
| HIV-CAUSAL Collaboration 37 | Cohort | ART vs. no-treatment | Tuberculosis | CD4 cell count, HIV RNA level, AIDS |
| Jin et al. 38 | Randomized controlled trial | Letrozole vs. no-treatment | Cancer recurrence | Not reported * |
| Kalayjian et al. 39 | Cohort | Tenofovir+ ritonavir-boosted protease inhibitor vs. efavirenz/nevaripine | Chronic kidney disease | CD4 cell count, viral load |
| McCoy et al. 40 | Cohort | Injectable hormonal contraceptive vs. no-treatment | HIV infection | Sexual behavioral risk, condom use, sexually transmitted infections |
| Miller et al. 41 | Cohort | Low dose vs. high dose paricalcital | Mortality | Parathyroid hormone, phosphorus, calcium |
| Morrison et al. 42 | Cohort | Oral contraceptive vs. non-hormonal use | HIV infection | Sexual behavioral risk, condom use, genital symptoms |
| Scherzer et al. 43 | Cohort | Tenofovir vs. no-treatment | Proteinuria | CD4 cell count, viral load, lipids, diabetes, hypertension |
| Shinozaki et al. 44 | Randomized controlled trial | Atorvastatin vs. no-treatment | CVD | Lipid profiles, HbA1c, blood pressure, BMI |
| Terrier et al. 45 | Cohort | Corticosteroid + rituximab vs. corticosteroid alone | Renal and immunological response | Vasculitis manifestations |
| Tiihonen et al. 46 | Cohort | Benzodiazepine vs. no-treatment | Mortality | Concurrent medication use |
| Young et al. 47 | Cohort | Tenofovir + ritonavir-boosted lopinavir vs. renofovir+efavirenz | eGFR | HIV-infection, diabetes, hypertension, hepatitis B or C infection, eGFR, CD4 cell count, virological failure |
ACEI: angiotensin-converting enzyme inhibitors; ARB: angiotensin II receptor blockers; ART: antiretroviral therapy; CVD: cardiovascular diseases; eGFR, estimated glomerular filtration rate.
Only the primary study exposure and outcome were reported in this table. “No-treatment” means not using the treatment under study.
This study did not describe any specific substantial time-varying confounders for which adjustment was needed.
This study used inverse probability of censoring weighting to deal with treatment crossover. Probability of treatment crossover was estimated based on baseline characteristics. Time-varying confounders were not mentioned.
In Table 2, the type of bias IPW addressed and details regarding the assumptions of positivity and no uncontrolled confounding are described for each study. Eleven studies used IPW owing to concerns that standard regression models might eliminate indirect effects mediated by time-varying confounders, five studies used IPW to deal with bias from the artificial censoring of noncompliance, and five studies did not provide further details other than stating that IPW was used because of “concerns of time-varying confounding”. The majority of studies did not report whether the positivity assumption was checked. Four studies truncated weights and one study trimmed weights to alleviate the impact of potential positivity violation. Most studies discussed qualitatively the susceptibility of their findings to uncontrolled confounding, but none reported performing formal sensitivity analyses to assess robustness of the results to uncontrolled confounding.
Table 2.
Type of potential bias and examination of identifiability assumptions
| Reference | Type of potential bias addressed | Positivity assessed | Weight truncated or trimmed | Uncontrolled confounding discussed |
|---|---|---|---|---|
| Cook et al.28 | Bias from blocking mediated effect | Mean: 1.01 Median (Inter Quartile Range): 1.00 (0.97–1.01) |
Weight truncation at 0.01th and 99.99th percentiles | Yes |
| Desai et al. 29 | Bias from blocking mediated effect; Selection bias owing to artificial censoring | Mean (Standard Deviation): 1.00 (0.06) | Not reported | Yes |
| Gerhard et al. 30 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| Gsponer et al. 31 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| Haukka et al. 32 | No details provided† | Not reported | Not reported | Yes |
| HCV working group of COHERE 33 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| Heffron et al. 34 | No details provided† | Mean (range): 1.07 (0.82–1.34) | Weight truncation at 1st and 99th percentiles | Yes |
| Hernández et al. 35 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| HIV-CAUSAL Collaboration 36 | Selection bias owing to artificial censoring | Not reported | Weight truncation at 99th percentile | Yes |
| HIV-CAUSAL Collaboration 37 | Bias from blocking mediated effect | Mean: 1.04 | Weight truncation at 10 | Yes |
| Jin et al. 38 | Selection bias owing to artificial censoring | Not reported | Not reported | No |
| Kalayjian et al. 39 | Selection bias owing to artificial censoring | Not reported | Not reported | Yes |
| McCoy et al. 40 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| Miller et al. 41 | Bias from blocking mediated effect | Not reported | Weight Trimming at 10 | Yes |
| Morrison et al. 42 | No details provided† | Not reported | Not reported | Yes |
| Scherzer et al. 43 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| Shinozaki et al. 44 | Bias from blocking mediated effect | Not reported | Not reported | Yes |
| Terrier et al. 45 | No details provided† | Not reported | Not reported | No |
| Tiihonen et al. 46 | No details provided† | Not reported | Not reported | Yes |
| Young et al. 47 | Selection bias owing to artificial censoring | Not reported | Not reported | No |
If studies reported “using IPW to control for time-varying confounding” without further specification of relationships between treatment, time-varying confounders and outcomes.
Table 3 includes information on the construction of weights and specification of outcome models. Six studies performed ITT analyses, three performed per-protocol analyses and eight performed as-treated analyses. None of the studies assuming ITT reported adherence levels after treatment initiation. The three “per-protocol” studies censored patients when they discontinued the treatment under study, and estimated the probability of treatment continuation (i.e., being uncensored) separately from treatment initiation. One of the eight “as-treated” studies modeled current treatment use stratified by previous treatment status.
Table 3.
Specification of treatment models and outcome models
| Reference | Analytic strategy* Adherence level | Multiphase of treatment use modeled | Variables in weight numerator / Stabilized | Variables in weight denominator/ Covariates selection | Covariates in outcome model | Functional form of exposure |
|---|---|---|---|---|---|---|
| Cook et al.28 | As-treated 73% stayed on initial treatment | Yes. Current use modeled by status of previous use | Baseline confounders, previous treatment | Baseline confounders, time-varying confounders, previous treatment | Baseline confounders | Most recent exposure |
| Desai et al. 29 | As-treated Not reported | No | Baseline confounders, previous treatment | Baseline confounders, time-varying confounders, previous treatment | Baseline confounders | Not reported |
| Gerhard et al. 30 | Intention to treat Not reported | Not applicable | Not reported /Yes | Baseline confounders, time-varying confounders, previous treatment | Not reported | Indicator of treatment initiation |
| Gsponer et al. 31 | Intention to treat Not reported | Not applicable | Not reported /Yes | Baseline confounders, time-varying confounders, previous treatment / Stepwise selection based on Akaike information criterion | Baseline confounders | Indicator of treatment “initiation”†; Time to treatment “initiation”† |
| Haukka et al. 32 | As-treated Treatment use covered 73% of study period | No | Baseline confounders | Baseline confounders, follow-up time | Not reported | Most recent exposure |
| HCV working group of COHERE 33 | Intention to treat Not reported | Not applicable | Not reported /Yes | Baseline confounders, time-varying confounders, previous treatment | Not reported | Indicator of treatment initiation |
| Heffron et al. 34 | As-treated 52.0% stayed on treatment | No | Not reported /Yes | Baseline confounders, time-varying confounders | Baseline confounders | Most recent exposure |
| Hernández et al. 35 | As-treated >85% stayed on treatment | No | Not reported / Not reported | Baseline confounders, time-varying confounders / Variables significantly associated with outcome | Not reported | Most recent exposure? |
| HIV-CAUSAL Collaboration 36 | Intention to treat Not reported | Not applicable | None/No | Baseline confounders, time-varying confounders, previous treatment | Baseline confounders | Initial treatment |
| HIV-CAUSAL Collaboration 37 | Intention to treat Not reported | Not applicable | Not reported / Yes | Baseline confounders, time-varying confounders, previous treatment | Baseline confounders | Indicator of treatment initiation; Cumulative exposure |
| Jin et al. 38 | Per-protocol 31% stayed on initial treatment | Yes. Treatment initiation and “treatment crossover” was considered separately | Not reported / Not reported | Baseline confounders, previous Treatment / Variables significantly associated with outcome and treatment crossover | Not reported | Initial treatment |
| Kalayjian et al. 39 | Per-protocol 64% stayed on initial treatment | Yes. Treatment initiation and discontinuation modeled separately | Not reported / Not reported | Baseline confounders, time-varying confounders, previous treatment | Not reported | Initial treatment |
| McCoy et al. 40 | As-treated 51.6% stayed on treatment | No | Unconditional probability of receiving observed treatment | Baseline confounders, time-varying confounders, previous treatment | Not reported | Most recent exposure |
| Miller et al. 41 | As-treated Not reported | No | Not reported / Yes | Baseline confounders, time-varying confounders, previous treatment | Not reported | Most recent exposure? |
| Morrison et al. 42 | As-treated 64.4% stayed on treatment | No | Not reported / Yes | Baseline confounders, time-varying confounders / Covariates significantly associated with outcome and treatment use and also predicted by past treatment use | Baseline confounders | Most recent exposure |
| Scherzer et al. 43 | Not reported | Not reported | Not reported / Yes | Not reported | Baseline confounders | Cumulative exposure; “Ever exposure” |
| Shinozaki et al. 44 | Intention to treat Not reported | Not applicable | Baseline confounders | Baseline confounders, time-varying confounders, previous treatment | Baseline confounders | Indicator of treatment initiation |
| Terrier et al. 45 | Not reported | Not reported | Baseline confounders | Not reported | Not reported | Most recent exposure |
| Tiihonen et al. 46 | Not reported | Not reported | Not reported/ Not reported | Not reported | Not reported | Not reported |
| Young et al. 47 | Per-protocol Not reported | Yes. Treatment initiation and discontinuation modeled separately | Unconditional probability of receiving observed treatment | Baseline confounders, time-varying confounders, previous treatment | None | Initial treatment |
If the study stated that “modeling the probability of receiving observed treatment at each time visit”, we assumed that the study was not making the assumption of intention-to-treat.
“Initiation” refers to switching to the second-line therapy after treatment failure with first-line therapy.
One study did not use stabilized weights, four did not report whether stabilized weights were used, and eight reported using stabilized weights but did not describe how it was done. The remaining studies reported stabilizing weights with unconditional probability of receiving observed treatment, or conditional probability given baseline covariates and previous treatment or given baseline covariates only. For the weight denominator, twelve studies estimated the conditional probability given baseline covariates, time-varying confounders and previous treatment, three did this given baseline covariates and time-varying confounders and two adjusted for baseline covariates plus “follow-up period” or baseline covariates only. Four studies selected variables in the treatment model for weight denominator based on a statistical criterion. Two studies included covariates with statistically significant associations with the study outcome and subsequent treatment use. One study included factors significantly associated with the study outcome only. One study used a stepwise procedure to select the treatment model which maximized Akaike information criterion.
Regarding the functional form of exposure in the outcome model, studies performing ITT and per-protocol analyses included an indicator of treatment initiation and the initial treatment status, respectively. Almost all studies performing as-treated analyses included only the most recent treatment status in the outcome model.
Table 4 shows crude estimates, and estimates from IPW and standard regression models for the associations between primary study exposure and outcome listed in Table 1. The last column contains information about whether the IPW estimate was substantially different from the standard regression estimate for any association assessed in the study, as well as how the study explained any noted discrepancies. Fourteen studies reported results from both methods and a substantial difference was found in six studies. Among studies reporting a substantial difference, three did not discuss reasons for the discrepancy, two considered IPW method correctly estimated the indirect effects from previous treatments, and one considered IPW method controlled for “confounding by indication”.
Table 4.
Primary exposure-outcome association† and discrepancy in IPW estimates and standard regression estimates
| Reference | Crude Hazard Ratio (95% Confidence Interval) | IPW Hazard Ratio* (95% Confidence Interval) | Standard regression Hazard Ratio* (95% Confidence Interval) | Discrepancy found Reason discussed |
|---|---|---|---|---|
| Cook et al.28 | 1.00 (0.89–1.14) | 0.93 (0.81–1.07) | 0.96 (0.84–1.09) | Yes Correction of blocked mediated effect |
| Desai et al. 29 | Adjusted for baseline covariates: 0.89 (0.7–1.06) | 0.79 (0.42–1.50) | Not reported | Not applicable |
| Gerhard et al. 30 | Adjusted for baseline covariates: 0.96 (0.87–1.07) | 0.81 (0.71–0.92) | Not reported | Not applicable |
| Gsponer et al. 31 | 0.52 (0.20–1.35) | 0.25 (0.09–0.72) | Not reported | Not applicable |
| Haukka et al. 32 | NR | 0.42 (0.37–0.47) | 0.39 (0.37–0.40) | No |
| HCV working group of COHERE 33 | 0.50 (0.35, 0.71) | 0.72 (0.43–1.21) | Not reported | Not applicable |
| Heffron et al. 34 | 1.73 (0.95–3.15) | 1.84 (0.98–3.47) | 1.98 (1.06–3.68) | No |
| Hernández et al. 35 | 0.77 (0.49–1.21) | 0.82 (0.52–1.32) | 0.80 (0.51–1.26) | No |
| HIV-CAUSAL Collaboration 36 | 1.46 (1.21–1.76) | 1.59 (1.27–1.98) | 1.38 (1.13–1.68) | Yes Not reported |
| HIV-CAUSAL Collaboration 37 | Adjusted for baseline covariates: 0.81 (0.67–0.97) | 0.56 (0.44–0.72) | 1.03 (0.86–1.24) | Yes Not reported |
| Jin et al. 38 | 0.68 (0.56–0.83) | 0.52 (0.45–0.61) | 0.58 (0.47–0.72) | Not reported as such |
| Kalayjian et al. 39 | Not reported | 3.35 (1.40–8.02) | 1.34 (0.75–2.40) | Yes Not reported |
| McCoy et al. 40 | 1.32 (1.00–1.74) | 1.34 (0.75–2.37) | 1.37 (1.01–1.85) | No |
| Miller et al. 41 | Not reported | 1.26 (1.19–1.35) | 1.07 (1.01–1.14) | Yes Confounding by indication |
| Morrison et al. 42 | 0.89 (0.55–1.44) | 0.84 (0.51–1.39) | 0.88 (0.49–1.30) | No |
| Scherzer et al. 43 | Adjusted for baseline covariates: 1.30 (1.22–1.37) | 1.24 (1.17–1.32) | 1.34 (1.25–1.45) | No |
| Shinozaki et al. 44 | Adjusted for baseline covariates: 0.65 (0.30–1.40) | 0.48 (0.19–1.16) | 0.75 (0.34–1.63) | Yes Correction of blocked mediated effect |
| Terrier et al. 45 | Not reported | 3.7 (1.3–10.6) | Not reported | Not applicable |
| Tiihonen et al. 46 | 1.61 (1.06–2.45) | 1.80 (1.02–3.20) | 1.91 (1.13–3.22) | No |
| Young et al. 47 | Beta coefficient of exposure term from linear model: −4.6 (−8.6 to −0.5) | Beta coefficient of exposure term from linear model: −2.6 (−7.3 to 2.2) | Not reported | Not applicable |
Primary exposure and outcome are listed in Table 1.
Adjusted for potential time-varying confounders.
We summarized the review results of the 20 studies in Table 5.
Table 5.
A summary of review results of the 20 pharmacoepidemiologic studies applying IPW method in 2012
| Elements of IPW method | No. of studies (percent#) |
|---|---|
| Types of bias IPW was used to address | |
| Blocking mediated effects by time-varying confounders | 11 (55) |
| Collider-stratification bias | 0 |
| Selection bias due to artificial censoring | 5 (25) |
| Assessment of identifiability assumptions | |
| Discussed qualitatively uncontrolled confounding | 17 (85) |
| Performed sensitivity analyses of uncontrolled confounding | 0 |
| Reported the weight distribution | 4 (20) |
| Reported truncating or trimming extreme weights | 5 (25) |
| Analytic strategy | |
| Intention-to-treat analysis | 6 (30) |
| Per-protocol analysis | 3 (15) |
| As-treated analysis | 8 (40) |
| Weight construction | |
| Reported use of stabilized weights | 15 (75) |
| Described how weights were stabilized | 7 (47†) |
| Described covariates in the treatment model for weight denominator | 17 (85) |
| Modeled the multiphase of treatment use | 1 (12.5&) |
| Functional form of exposure in outcome models | |
| Indicator of treatment initiation or initial treatment use | 9 (100^) |
| Most recent treatment use | 7 (100*) |
| Discrepancy in estimates between IPW and standard regression | |
| Discussed reasons for the substantial discrepancy | 3 (50§) |
The denominator is 20 unless indicated otherwise.
The denominator is 15 studies which reported using stabilized weights.
The denominator is 8 studies performing as-treated analyses.
The denominator is 9 studies performing intention-to-treat or per-protocol analyses. One study performing intention-to-treat analyses also specified cumulative exposure as an alternative.
The denominator is 7 studies performing as-treated analyses which provided information on the functional form of exposure.
The denominator is 6 studies reporting substantial difference.
DISCUSSION
Our review supports the notion that studies using IPW to deal with time-varying confounding continue to diffuse in the medical literature. In 2012, 49 studies used IPW to estimate the effect from a time-varying exposure on a health-related outcome. After reviewing 20 pharmacoepidemiologic studies, we found that the majority lacked sufficient details to evaluate the appropriateness of the application of the method. Most studies did not report that the positivity assumption was checked, and more than half did not report the type of weights (stabilized or unstabilized) applied or how the weights were stabilized. Furthermore, we found that more studies performed as-treated analyses than ITT analyses, but few of these studies considered the multiphase of treatment use in the process of weight construction and almost all chose the most recent treatment status as the functional form of exposure in the outcome model.
Assessment of positivity assumption
Surprisingly, the majority of reviewed studies did not report whether they checked the positivity assumption. The IPW method is more sensitive to positivity violations than standard regression models.7,9 Studies using simulated48 and empirical49 data have demonstrated that positivity violations could result in substantial bias and imprecision in IPW estimates. Estimated stabilized weights with the mean far from one or with very extreme values can be indicative of non-positivity.9 Thus, a thorough examination of the weight distribution is essential for checking the positivity assumption.9,13 However, a “well-behaved” weight distribution (i.e., with mean close to one and moderate range) is not sufficient to ensure the absence of positivity violations.7,50 Thus, Cole et al. recommended assessing the robustness of IPW estimates with weights truncated at certain percentiles (e.g., 99th, 95th and 90th) as sensitivity analyses.9
Assessment of uncontrolled confounding
Although it was difficult to judge the adequacy of control for confounding in the reviewed studies without knowledge in the specific datasets and subject areas, we did find that some studies reported adjusting for “follow-up period” as the only time-varying confounder or adjusting for only baseline covariates. If time-varying disease risk factors that cause changes in treatment use are not correctly measured and appropriately adjusted for, the IPW estimates will be biased. When substantial uncontrolled confounding is suspected, sensitivity analyses have been recommended to assess the robustness of the IPW estimates.8,51 To perform such sensitivity analyses, investigators need to specify a plausible function form which quantifies the direction and magnitude of uncontrolled confounding.8,51
ITT analyses
When non-adherence after treatment initiation is minimal, an ITT analysis may be preferred to as-treated analysis in terms of simplifying the weight construction and controlling for confounding.22,24,27 The ITT assumption simplifies the process of constructing weights, in that the treatment models only need to estimate the probability of treatment initiation. More importantly, for studies performing ITT analyses, the assumption of no uncontrolled confounding is satisfied as long as confounders for treatment onset are correctly measured and specified in the treatment model for weight denominator. This assumption may be viable for many pharmacoepidemiologic studies using healthcare database, because “information used by physicians to make a decision to initiate treatment is often captured in the database”.24 However, the ITT estimate merely measures the effect of treatment initiation instead of effect from actual treatment.18 High levels of non-adherence after treatment initiation may drive the ITT estimate away from the true treatment effect.22,52 For this reason, studies performing ITT analyses should report adherence measures for each treatment arm so that findings can be interpreted under appropriate consideration of the observed adherence patterns.53
As-treated analyses
Instead of estimating the effect of treatment initiation, we found that more studies performed as-treated analyses. Validity of “as-treated” estimates relies on the extent to which the study correctly models the relationships between confounders and the multiphase of treatment use.22 Because it is very likely that the influence of time-varying confounders on initiating a treatment is different from their impact on continuing or resuming the treatment, separate models for different treatment regimens are often needed for adequate control for confounding. However, when information on time-varying confounders that predict treatment changes after initiation is not well-recorded in the data sources or when the number of participants following each specific regimen is small, a correct estimation of the multiphase of treatment use will be difficult, if not impossible.22,24,27 In sum, when choosing between an ITT and an as-treated analytic strategy, investigators need to take into account adherence levels after treatment initiation and availability of information on the time-varying confounders that predict treatment changes during the study period.
Weight construction
Stabilized weights can generate estimates with greater precision than unstabilized weights and thus are recommended in data analyses.14 However, we still found that four studies did not report whether they used stabilized weights and one study used unstablized weights. It’s unknown to us why unstabilized weights were chosen. Regarding variable selection for treatment model in the weight denominator, we found that most studies chose covariates based on substantive knowledge, while four studies used some statistical criterion to select covariates significantly associated with treatment use and/or study outcome. A simulation study by Lefebvre et al. found that the performance of IPW method could be improved when the confounders and risk factors of outcome were included in the treatment model, whereas including pure predictors of treatment use (i.e., not confounders) led to biased and highly variable estimates, particularly in the context of small samples.10 These findings are consistent with the recommendation for variable selection for building propensity scores.54 Therefore, an advisable strategy in building treatment model for weight denominator may be to include variables considered to be direct risk factors for the outcome.
Functional form of exposure in outcome models
Almost all studies performing as-treated analyses included only the most recent treatment status in the outcome model. Most of these studies chose IPW method instead of standard regression models owing to the concerns that standard models would eliminate the indirect effect from previous treatments mediated by the time-varying confounders. This may imply that these studies were interested in estimating the effects from both recent and previous treatments. However, when treatment use is intermittent, including only the most recent exposure status in the outcome model will not correctly capture the effect from previous treatments. Furthermore, when the weights are stabilized with previous treatment history but only the indicator of most recent treatment use is included in the outcome model, the estimate may also be a biased one for the recent treatment effect, because the status of previous treatment is not balanced between recently treated and untreated patients and thus may bias the estimate.55 Finally, if only the most recent treatment effect is biologically plausible and is the focus of the study, standard regression models adjusting for time-varying confounders and previous treatment history can also produce unbiased estimate,14,50 even though there is disagreement regarding the difference in precision between estimates derived from IPW and standard regression models.56,57
Discrepancy in estimates from IPW and standard regression models
Similar to the previous review,13 we found nearly half of the studies, which provided estimates from both methods, reported that IPW estimates were substantially different from the standard regression estimates adjusted for time-varying confounders. Unfortunately, half of the studies reporting a substantial difference did not discuss reasons for the discrepancy. As mentioned in the section Type of bias, the discrepancy can be attributed to the correct estimation of total treatment effect or avoidance of collider-stratification bias by the IPW method, especially if the direction of discrepancy is consistent with the hypothesized relationships between exposure, outcome and time-varying confounders. In addition, the difference can be due to control for selection bias from informative censoring if censoring weights are incorporated in IPW analyses.
Non-uniform treatment effects
Several studies also noticed that substantial discrepancy in estimates could arise in the presence of covariates (or a summary of covariates like propensity score) which strongly predict treatment use and are also strong effect modifiers.49,58,59 Compared to the standard regression models, the IPW method gives much more weights to the covariate strata within which treatment status is almost completely determined by the covariates.60,61 If the effect sizes in these strata differ dramatically from other strata, the IPW estimates will be substantially different from the standard regression estimates.61 The nonuniform treatment effects across the covariates (or the propensity score) can be due to violation of positivity,49 unmeasured confounding58 or true effect-measure modification. When unmeasured confounding or positivity violation is the cause of non-uniformity, the IPW estimate will be biased and weight truncation or propensity score trimming should be applied to ameliorate the impact.49,58 In summary, when substantially different estimates are derived from IPW and standard regression models, investigators should take into account these alternative explanations before being assured that IPW method generates unbiased estimates.
Our review has some limitations. First, we included only pharmacoepidemiologic studies published in 2012. The findings may not be representative of all publications using IPW to deal with time-varying confounding. Second, the reporting practices of published studies may be influenced by journals’ requirements. Authors are reporting their findings given strict word limitations and as such may have limited space to provide details on these facets of the application of the method. Nevertheless, with complex methods such as IPW, such reporting is necessary to evaluate the extent to which the method has been appropriately applied.
In summary, the use of IPW estimation is increasing in the medical literature. Given the variable and suboptimal reporting of the application of the technique, it may be prudent to develop best practices in reporting complex methods in epidemiologic research and for journal editors to consider adopting such reporting guidelines.
Key points.
Reporting of the application of IPW method among pharmacoepidemiologic studies is variable and suboptimal.
It is essential for studies using IPW to assess positivity assumption through examining the weight distribution and address violations of positivity with weight truncation.
Studies performing intention-to-treat analyses should report levels of non-adherence after treatment initiation.
Studies performing as-treated analyses with IPW should take into account the multiphase of treatment use in the process of weight construction.
Acknowledgments
Funding source
This study was funded by the National Institute of Arthritis and Musculoskeletal and Skin Disease (Project number 268201000020C-1-0-1 entitled TAS::75 0888::TAS to Charles Eaton).
Footnotes
Conflict of interest
We have no conflicts of interest to declare.
This study has not been previously published or presented at conferences/meetings.
References
- 1.Platt RW, Schisterman EF, Cole SR. Time-modified confounding. Am J Epidemiol. 2009;170(6):687–694. doi: 10.1093/aje/kwp175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Robins JM. Association, causation, and marginal structural models. Synthese. 1999;121:151–179. [Google Scholar]
- 3.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 4.Hernán MA, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15(5):615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- 5.Robins JM, Finkelstein DM. Correcting for noncompliance and dependent censoring in an AIDS clinical trial with inverse probability of censoring weighted (IPCW) log-rank tests. Biometrics. 2000;56(3):779–788. doi: 10.1111/j.0006-341x.2000.00779.x. [DOI] [PubMed] [Google Scholar]
- 6.Hernán MA, Taubman SL. Does obesity shorten life? The importance of well-defined interventions to answer causal questions. Int J Obes. 2008;32(Suppl 3):S8–14. doi: 10.1038/ijo.2008.82. [DOI] [PubMed] [Google Scholar]
- 7.Petersen M, Porter K, Gruber S, et al. Diagnosing and responding to violations in the positivity assumption. Stat Methods Med Res. 2012;21(1):31–54. doi: 10.1177/0962280210386207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brumback B, Hernán MA, Haneuse SJ, et al. Sensitivity analyses for unmeasured confounding assuming a marginal structural model for repeated measures. Stat Med. 2004;23(5):749–767. doi: 10.1002/sim.1657. [DOI] [PubMed] [Google Scholar]
- 9.Cole SR, Hernán MA. Constructing inverse probability weights for marginal structural models. Am J Epidemiol. 2008;168(6):656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lefebvre G, Delaney JA, Platt RW. Impact of mis-specification of the treatment model on estimates from a marginal structural model. Stat Med. 2008;27(18):3629–3642. doi: 10.1002/sim.3200. [DOI] [PubMed] [Google Scholar]
- 11.Mortimer K, Neugebauer R, van der Laan M, et al. An application of model-fitting procedures for marginal structural models. Am J Epidemiol. 2005;162(4):382–388. doi: 10.1093/aje/kwi208. [DOI] [PubMed] [Google Scholar]
- 12.Moodie EE. Risk factor adjustment in marginal structural model estimation of optimal treatment regimes. Biom J. 2009;51(5):774–788. doi: 10.1002/bimj.200800182. [DOI] [PubMed] [Google Scholar]
- 13.Suarez D, Borràs R, Basagaña X. Differences between marginal structural models and conventional models in their exposure effect estimates: A systematic review. Epidemiology. 2011;22(4):586–588. doi: 10.1097/EDE.0b013e31821d0507. [DOI] [PubMed] [Google Scholar]
- 14.Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology. 2000;11(5):561–570. doi: 10.1097/00001648-200009000-00012. [DOI] [PubMed] [Google Scholar]
- 15.Moher D, Liberati A, Tetzlaff J, et al. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. BMJ. 2009;339:b2535. doi: 10.1136/bmj.b2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Greenland S. Quantifying biases in causal models: Classical confounding vs collider-stratification bias. Epidemiology. 2003;14(3):300–306. [PubMed] [Google Scholar]
- 17.Danaei G, Rodriguez LA, Cantero OF, et al. Observational data for comparative effectiveness research: An emulation of randomised trials of statins and primary prevention of coronary heart disease. Stat Methods Med Res. 2013;22(1):70–96. doi: 10.1177/0962280211403603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Toh S, Hernán MA. Causal inference from longitudinal studies with baseline randomization. Int J Biostat. 2008;4(1) doi: 10.2202/1557-4679.1117. Article 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hernán MA, Robins JM. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578–586. doi: 10.1136/jech.2004.029496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cole SR, Frangakis CE. The consistency statement in causal inference: A definition or an assumption? Epidemiology. 2009;20(1):3–5. doi: 10.1097/EDE.0b013e31818ef366. [DOI] [PubMed] [Google Scholar]
- 21.Westreich D, Cole SR. Invited commentary: Positivity in practice. Am J Epidemiol. 2010;171(6):674–677. doi: 10.1093/aje/kwp436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Platt RW, Brookhart MA, Cole SR, et al. An information criterion for marginal structural models. Stat Med. 2013;32(8):1383–1393. doi: 10.1002/sim.5599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee TA, Pickard AS. Exposure definition and measurement. In: Velentgas P, Dreyer NA, Nourjah P, editors. Developing a protocol for Observational Comparative effectiveness research: A User’s Guide. Agency for Healthcare Research and Quality; Rockville, MD: 2013. pp. 45–57. [PubMed] [Google Scholar]
- 24.Neugebauer R, Fireman B, Roy JA, et al. Dynamic marginal structural modeling to evaluate the comparative effectiveness of more or less aggressive treatment intensification strategies in adults with type 2 diabetes. Pharmacoepidemiol Drug Saf. 2012;21:99–113. doi: 10.1002/pds.3253. [DOI] [PubMed] [Google Scholar]
- 25.Shortreed SM, Moodie EE. Estimating the optimal dynamic antipsychotic treatment regime: Evidence from the sequential multiple-assignment randomized clinical antipsychotic trials of intervention and effectiveness schizophrenia study. J R Stat Soc Ser C Appl Stat. 2012;61(4):577–599. doi: 10.1111/j.1467-9876.2012.01041.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rosthoj S, Keiding N, Schmiegelow K. Estimation of dynamic treatment strategies for maintenance therapy of children with acute lymphoblastic leukaemia: An application of history-adjusted marginal structural models. Stat Med. 2012;31(5):470–488. doi: 10.1002/sim.4393. [DOI] [PubMed] [Google Scholar]
- 27.Cain LE, Robins JM, Lanoy E, et al. When to start treatment? A systematic approach to the comparison of dynamic regimes using observational data. Int J Biostat. 2010;6(2) doi: 10.2202/1557-4679.1212. Article 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cook NR, Cole SR, Buring JE. Aspirin in the primary prevention of cardiovascular disease in the women’s health study: Effect of noncompliance. Eur J Epidemiol. 2012;27(6):431–438. doi: 10.1007/s10654-012-9702-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Desai RJ, Ashton CM, Deswal A, et al. Comparative effectiveness of individual angiotensin receptor blockers on risk of mortality in patients with chronic heart failure. Pharmacoepidemiol Drug Saf. 2012;21(3):233–240. doi: 10.1002/pds.2175. [DOI] [PubMed] [Google Scholar]
- 30.Gerhard T, Delaney JA, Cooper-Dehoff RM, et al. Comparing marginal structural models to standard methods for estimating treatment effects of antihypertensive combination therapy. BMC Med Res Methodol. 2012;12:119. doi: 10.1186/1471-2288-12-119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gsponer T, Petersen M, Egger M, et al. The causal effect of switching to second-line ART in programmes without access to routine viral load monitoring. AIDS. 2012;26(1):57–65. doi: 10.1097/QAD.0b013e32834e1b5f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Haukka J, Niskanen L, Partonen T, et al. Statin usage and all-cause and disease-specific mortality in a nationwide study. Pharmacoepidemiol Drug Saf. 2012;21(1):61–69. doi: 10.1002/pds.2255. [DOI] [PubMed] [Google Scholar]
- 33.HCV working group of the Collaboration of Observational HIV Epidemiological Research in Europe (COHERE) in EuroCoord. Effect of hepatitis C treatment on CD4+ T-cell counts and the risk of death in HIV-HCV-coinfected patients: The COHERE collaboration. Antivir Ther. 2012;17(8):1541–1550. doi: 10.3851/IMP2263. [DOI] [PubMed] [Google Scholar]
- 34.Heffron R, Donnell D, Rees H, et al. Use of hormonal contraceptives and risk of HIV-1 transmission: A prospective cohort study. Lancet Infect Dis. 2012;12(1):19–26. doi: 10.1016/S1473-3099(11)70247-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hernández D, Muriel A, Abraira C, et al. Renin-angiotensin system blockade and kidney transplantation: A longitudinal cohort study. Nephrol Dial Transplant. 2012;27(1):417–422. doi: 10.1093/ndt/gfr276. [DOI] [PubMed] [Google Scholar]
- 36.HIV-CAUSAL Collaboration. The effect of efavirenz versus nevirapine-containing regimens on immunologic, virologic and clinical outcomes in a prospective observational study. AIDS. 2012;26(13):1691–1705. doi: 10.1097/QAD.0b013e328354f497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.HIV-CAUSAL Collaboration. Impact of antiretroviral therapy on tuberculosis incidence among HIV-positive patients in high-income countries. Clin Infect Dis. 2012;54(9):1364–1372. doi: 10.1093/cid/cis203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jin H, Tu D, Zhao N, et al. Longer-term outcomes of letrozole versus placebo after 5 years of tamoxifen in the NCIC CTG MA. 17 trial: Analyses adjusting for treatment crossover. J Clin Oncol. 2012;30(7):718–721. doi: 10.1200/JCO.2010.34.4010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kalayjian RC, Lau B, Mechekano RN, et al. Risk factors for chronic kidney disease in a large cohort of HIV-1 infected individuals initiating antiretroviral therapy in routine care. AIDS. 2012;26(15):1907–1915. doi: 10.1097/QAD.0b013e328357f5ed. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McCoy SI, Zheng W, Montgomery E, et al. Oral and injectable contraception use and risk of HIV acquisition among women in the Methods for Improving Reproductive health in Africa (MIRA) study. AIDS. 2013;27:1001–1009. doi: 10.1097/QAD.0b013e32835da401. [DOI] [PubMed] [Google Scholar]
- 41.Miller JE, Molnar MZ, Kovesdy CP, et al. Administered paricalcitol dose and survival in hemodialysis patients: A marginal structural model analysis. Pharmacoepidemiol Drug Saf. 2012;21(11):1232–1239. doi: 10.1002/pds.3349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Morrison CS, Skoler-Karpoff S, Kwok C, et al. Hormonal contraception and the risk of HIV acquisition among women in South Africa. AIDS. 2012;26(4):497–504. doi: 10.1097/QAD.0b013e32834fa13d. [DOI] [PubMed] [Google Scholar]
- 43.Scherzer R, Estrella M, Li Y, et al. Association of tenofovir exposure with kidney disease risk in HIV infection. AIDS. 2012;26(7):867–875. doi: 10.1097/QAD.0b013e328351f68f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shinozaki T, Matsuyama Y, Iimuro S, et al. Effective prevention of cardiovascular disease and diabetes-related events with atorvastatin in Japanese elderly patients with type 2 diabetes mellitus: Adjusting for treatment changes using a marginal structural proportional hazards model and a rank-preserving structural failure time model. Geriatr Gerontol Int. 2012;12(Suppl 1):88–102. doi: 10.1111/j.1447-0594.2011.00816.x. [DOI] [PubMed] [Google Scholar]
- 45.Terrier B, Krastinova E, Marie I, et al. Management of noninfectious mixed cryoglobulinemia vasculitis: Data from 242 cases included in the CryoVas survey. Blood. 2012;119(25):5996–6004. doi: 10.1182/blood-2011-12-396028. [DOI] [PubMed] [Google Scholar]
- 46.Tiihonen J, Suokas JT, Suvisaari JM, et al. Polypharmacy with antipsychotics, antidepressants, or benzodiazepines and mortality in schizophrenia. Arch Gen Psychiatry. 2012;69(5):476–483. doi: 10.1001/archgenpsychiatry.2011.1532. [DOI] [PubMed] [Google Scholar]
- 47.Young J, Schaefer J, Fux CA, et al. Renal function in patients with HIV starting therapy with tenofovir and either efavirenz, lopinavir or atazanavir. AIDS. 2012;26(5):567–575. doi: 10.1097/QAD.0b013e32834f337c. [DOI] [PubMed] [Google Scholar]
- 48.Barber J. Adjusting for time-varying confounding in survival analysis. Sociol Methodol. 2004;34(1):163–192. [Google Scholar]
- 49.Platt RW, Delaney JA, Suissa S. The positivity assumption and marginal structural models: The example of warfarin use and risk of bleeding. Eur J Epidemiol. 2012;27(2):77–83. doi: 10.1007/s10654-011-9637-7. [DOI] [PubMed] [Google Scholar]
- 50.Dumas O, Le Moual N, Siroux V, et al. Work related asthma. A causal analysis controlling the healthy worker effect. Occup Environ Med. 2013;70(9):603–610. doi: 10.1136/oemed-2013-101362. [DOI] [PubMed] [Google Scholar]
- 51.Chiba Y. Sensitivity analysis of unmeasured confounding for the causal risk ratio by applying marginal structural models. Commun Stat Theory Methods. 2010;39(1):65–76. [Google Scholar]
- 52.Cain LE, Cole SR. Inverse probability-of-censoring weights for the correction of time-varying noncompliance in the effect of randomized highly active antiretroviral therapy on incident AIDS or death. Stat Med. 2009;28(12):1725–1738. doi: 10.1002/sim.3585. [DOI] [PubMed] [Google Scholar]
- 53.Setoguchi S, Gerhard T. Comparator selection. In: Velentgas P, Dreyer NA, Nourjah P, editors. Developing a protocol for Observational Comparative effectiveness research: A User’s Guide. Agency for Healthcare Research and Quality; Rockville, MD: 2013. pp. 59–70. [PubMed] [Google Scholar]
- 54.Brookhart MA, Schneeweiss S, Rothman K, et al. Variable selection for propensity score models. Am J Epidemiol. 2006;163(12):1149–1156. doi: 10.1093/aje/kwj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lipkovich I, Mallinckrodt C, Faries D. The challenges of evaluating dose response in flexible-dose trials using marginal structural models. Pharm Stat. 2012;11(6):485–493. doi: 10.1002/pst.1540. [DOI] [PubMed] [Google Scholar]
- 56.Xiao Y, Abrahamowicz M, Moodie EE. Accuracy of conventional and marginal structural cox model estimators: A simulation study. Int J Biostat. 2010;6(2) doi: 10.2202/1557-4679.1208. Article 13. [DOI] [PubMed] [Google Scholar]
- 57.Bryan J, Yu Z, Van Der Laan MJ. Analysis of longitudinal marginal structural models. Biostatistics. 2004;5(3):361–380. doi: 10.1093/biostatistics/5.3.361. [DOI] [PubMed] [Google Scholar]
- 58.Stürmer T, Rothman KJ, Avorn J, et al. Treatment effects in the presence of unmeasured confounding: Dealing with observations in the tails of the propensity score distribution-A simulation study. Am J Epidemiol. 2010;172(7):843–854. doi: 10.1093/aje/kwq198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kurth T, Walker AM, Glynn RJ, et al. Results of multivariable logistic regression, propensity matching, propensity adjustment, and propensity-based weighting under conditions of nonuniform effect. Am J Epidemiol. 2006;163(3):262–270. doi: 10.1093/aje/kwj047. [DOI] [PubMed] [Google Scholar]
- 60.Greenland S, Maldonado G. The interpretation of multiplicative-model parameters as standardized parameters. Stat Med. 1994;13(10):989–999. doi: 10.1002/sim.4780131002. [DOI] [PubMed] [Google Scholar]
- 61.Stürmer T, Rothman KJ, Glynn RJ. Insights into different results from different causal contrasts in the presence of effect-measure modification. Pharmacoepidemiol Drug Saf. 2006;15(10):698–709. doi: 10.1002/pds.1231. [DOI] [PMC free article] [PubMed] [Google Scholar]


