Testing for Association with Multiple Traits in Generalized Estimation Equations, With Application to Neuroimaging Data

Abstract

There is an increasing need to develop and apply powerful statistical tests to detect multiple traits-single locus associations, as arising from neuroimaging genetics and other studies. For example, in the Alzheimer's Disease Neuroimaging Initiative (ADNI), in addition to genome-wide single nucleotide polymorphisms (SNPs), thousands of neuroimaging and neuropsychological phenotypes as intermediate phenotypes for Alzheimer's disease, have been collected. Although some classic methods like MANOVA and newly proposed methods may be applied, they have their own limitations. For example, MANOVA cannot be applied to binary and other discrete traits. In addition, the relationships among these methods are not well understood. Importantly, since these tests are not data adaptive, depending on the unknown association patterns among multiple traits and between multiple traits and a locus, these tests may or may not be powerful. In this paper we propose a class of data-adaptive weights and the corresponding weighted tests in the general framework of generalized estimation equations (GEE). A highly adaptive test is proposed to select the most powerful one from this class of the weighted tests so that it can maintain high power across a wide range of situations. Our proposed tests are applicable to various types of traits with or without covariates. Importantly, we also analytically show relationships among some existing and our proposed tests, indicating that many existing tests are special cases of our proposed tests. Extensive simulation studies were conducted to compare and contrast the power properties of various existing and our new methods. Finally, we applied the methods to an ADNI dataset to illustrate the performance of the methods. We conclude with the recommendation for the use of the GEE-based Score test and our proposed adaptive test for their high and complementary performance.

1 Introduction

Published genome-wide association studies (GWAS) have shown that single nucleotide polymorphisms (SNPs) associated with common diseases and complex traits are not easy to be detected. The main reason is due to their small e ect sizes: the odds ratios from the identified associations are often only 1.1-1.3. It is also realized that using only one single phenotype may not suffice to identify the underlying genetic mechanism, as a complex disease may exhibit its occurrence or progression in several syndromes. Thus, multivariate trait analysis is being increasingly recognized as a potentially useful strategy in genetic studies (Zhu and Zhang 2009). However, a dilemma in joint analysis of multiple traits is the inevitable power loss as more and more non-associated traits are being included; in practice, there is no guarantee that multiple traits being analyzed are all simultaneously associated with the same SNP. Therefore, a key issue in multivariate trait analysis is how to maximally maintain statistical power in the presence of many non-associated traits while gaining the power when many or most of the traits are associated with an SNP.

Various methods have been proposed and applied to multivariate trait analysis. Broadly speaking, any existing method for pedigree or longitudinal data analysis is applicable; see a recent nice review by Yang and Wang (2012). The methods can be classified into a few categories. The first category is to conduct univariate analysis on each trait, then combine their results (Yang et al 2010). For example, for any given SNP, one can conduct a single trait–single SNP analysis for each of the multiple traits, then take the minimum p-value from the univariate analyses with an adjustment for multiple testing. This is like the most commonly adopted approach to single trait–multilocus analysis in GWAS, the so-called UminP approach. The second class is based on dimension reduction on multivariate traits, usually by principal components analysis (PCA) (Lan et al 2003; Wang and Abbott 2007) or by principal components of heritability (PCH) (Klei et al 2008) and related methods (Wang et al 2008; Lin et al 2012). For PCA, a main issue is that a few top PCs may not capture su cient association signals (Aschard et al 2013). For PCH, the sample splitting strategy for population-based studies is not e cient (Yang and Wang 2012), though the modification of Lin et al (2012) overcomes this downside. Nevertheless, the interpretation with the use of a few principal components may not be straightforward, and it is debatable whether there exist a few PCs that can genetically capture a large proportion of trait variations. Importantly, it is not clear how robust these methods are in the presence of many non-associated traits, and how many components are needed. Canonical correlation analysis (CCA) also belongs to this class; it seeks the linear combination of all traits yielding the greatest association with a locus (Ferreira and Purcell 2009). Another special case is simply to take the average (or sum) of multiple traits and then conduct a univariate analysis with this single average (or sum) trait, which is called Average (or Sum) method and has been applied to neuroimaging genetic data recently (Shen et al 2012). As in the case for single trait–multilocus testing, the Average (or Sum) method su ers from severe power loss in the presence of opposite association directions between the traits and a locus (Pan 2009), or even worse, as to be shown later, in the presence of some non-associated traits. The third class includes some classical methods for multivariate data, such as MANOVA (Ferreira and Purcell 2009), which however is not applicable to non-Normal traits, e.g. binary traits. Linear mixed models (LMMs) or generalized least squares for quantitative traits, and generalized linear mixed models (GLMMs) for discrete traits provide a more general alternative (Laird et al., 1982; Fitzmaurize et al., 1993; Li et al 2011; Korte et al., 2012). However, these likelihood-based approaches require one to correctly specify a model, including the correlation structure among the multiple traits, which is often di cult, especially for non-Normal traits. Furthermore, fitting GLMMs is computationally demanding. Alternatively, the generalized estimation equations (GEE) methodology (Liang and Zeger, 1986) is convenient to use, only requiring a correct specification of a marginal mean regression model, not a variance or covariance structure and other higher moments of the traits. In particular, its (generalized) score vector is easy to calculate, in contrast to the intractability in GLMMs. The GEE framework is general and flexible: it can accommodate covariates and various types of traits (Liu et al., 2009; Chen et al., 2011; Lange et al., 2003). Yang and Wang (2012) commented that there may be inflated Type I errors in GEE; we show here that the problem is mainly with the Wald test (Pan 2001) while the Score test and other score-based tests seemed to work well. Hence, in this paper we adopt the GEE framework, applying some existing tests and developing some new ones, to test for association between a single SNP and multiple, possibly a large number of, quantitative traits.

A challenge in association testing with multiple parameters, such as in multilocus analysis or multivariate trait analysis, is the lack of a uniformly most powerful test. Depending on the unknown truth of the underlying association patterns, any given and fixed test may or may not be powerful. For example, depending on how many of a given set of multiple traits are associated with a locus, di erent tests may be more powerful: if only few of the traits are associated, then a univariate minimum p-value (UminP) method based on choosing the most significant p-value of the univariate tests on each of the multiple traits, similar to TATES (van der Sluis et al 2013), would be more powerful; on the other hand, if most or all of the traits are associated with the locus with similar e ect sizes, the simple Average method is expected to be more powerful. Our simulation results will confirm these points later. Accordingly, in multilocus association testing, adaptive tests based on weighting multiple loci di erently have been proposed (e.g. Lin and Tang 2012). However, due to the use of fixed weights, these adaptive tests may still su er from power loss under some situations. Here we propose a class of more highly adaptive tests with a wide range of weights on multiple traits. The goal is that, for a given situation with some unknown association patterns, we can find at least one set of the weights yielding a high-powered test. In our earlier example, if only one trait is associated with a locus, then assigning a large weight to the associated trait while assigning small weights to other traits would be optimal; on the other hand, if all traits are (almost) equally associated with the locus, we would like to assign an equal weight to all the traits. Our proposed class of tests are based on weighting the (generalized) score vector of a marginal generalized linear model (GLM) (McCullagh and Nelder 1983) in GEE; it maintains the computational simplicity of the Score test and the generality and flexibility of GLMs. Each of our proposed test statistics is a sum of powered score statistics, say SPU(γ), in which an integer γ indexes a set of weights on the multiple traits. Our adaptive SPU (aSPU) test essentially estimates and thus chooses the most powerful SPU test for a given dataset.

Another contribution of this work is to point out connections among the existing and new tests. Although some existing methods, such as classic ones like CCA and MANOVA, recently proposed ones like TATES (van der Sluis et al 2013), MultiPhen (O'Reilly et al., 2012) and kernel machine regression (KMR) (Maity et al 2012), and some potentially usable ones like MDMR (McArdle and Anderson 2001), have been suggested for analysis of multivariate traits, their relationships with each other are largely unknown. Here we analytically illuminate on how these existing tests and our proposed tests are related. In particular, when testing on association between multiple quantitative traits and a single SNP in the absence of other covariates, we point out that many existing tests are special cases of the SPU tests. For example, CCA, MANOVA and the GEE-Score test are equivalent, which in turn are closely related to MultiPhen; the Average method coincides with the GEE-SPU(1) test, while TATES is closely related to the GEE-SPU(∞); Under suitable conditions, both MDMR and KMR are the same as the GEE-SPU(2) test. These analytical results will be confirmed in our extensive simulation studies.

Finally we will apply these methods to the NIH Alzheimer's Disease Neuroimaging Initiative (ADNI) data. We aim to detect associations between SNPs and some multivariate neuroimaging phenotypes in several related regions of interest (ROIs). As both imaging and genotyping technologies advance, imaging genetics is emerging as a promising yet challenging field. In particular, due to numerous phenotypes measured for the ROIs, there is a high demand on developing and applying powerful association testing for multivariate traits, given limited multivariate methods available (Glahn et al., 2007). Shen et al. (2010) applied the simple Average method and confirmed two associated genes, APOE and TOMM40. We aimed to investigate how our proposed new tests perform as compared to other existing tests. We will demonstrate the advantages and potential usefulness of the GEE-based tests.

2 Methods

2.1 Generalized Estimating Equations

Suppose that for each subject i = 1, ..., n, we have k traits Y_i = (y_i1, y_i2, ..., y_ik)′, x_i = 0, 1 or 2 is the genotype score (i.e. count of the minor allele) for an SNP of interest, and z_i = (z_i1, z_i2, ..., z_iq) is a row vector of q covariates. Define the design matrices for the SNP e ects and covariates as

$$X_i=\left(\begin{array}{cccc}\hfill x_i\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill x_i\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill x_i\hfill \end{array}\right)=x_{i}I,Z_i=\left(\begin{array}{cccccc}\hfill 1\hfill & \hfill z_i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill z_i\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill z_i\hfill \end{array}\right),$$

where 0 is a row vector of all 0's. X_i is a k × k matrix, and Z_i is a k × k(q + 1) matrix including the intercept term. Define two regression coe cient vectors as β = (β₁, ..., β_k)′ for X_i and φ = (φ₁₁, ..., φ_1(q+1), ..., φ_k1, ..., φ_k(q+1))′ for Z_i, where the main interest is on β, the SNP e ects on the traits. The marginal means, E(Y_i|x_i, Z_i) = μ_i, the SNP and covariates are modeled through a marginal generalized linear model (GLM):

$$g\left({\mu }_i\right)={\eta }_i=Z_i\phi +X_i\beta =H_i\theta ,$$

with H_i = (Z_i, X_i), = (φ′, β′)′ and g(.) as a suitable link function.

The consistent and asymptotically Normal estimates of β and φ are obtained by solving the GEE (Liang and Zeger, 1986):

$$\begin{array}{c}\hfill U=U(\phi ,\beta )=\sum _i{U}_i(\phi ,\beta )=\sum _i\nabla {\mu }_i^{\prime }{V}_i^{-1}(Y_i-{\mu }_i)=0,\hfill \\ \hfill \nabla {\mu }_i=\partial {\mu }_i∕\partial {\theta }^{\prime }=\partial g^{-1}\left(H_i\theta \right)∕\partial {\theta }^{\prime },V_i=\varphi A_i^{1∕2}{R}_w\left(\alpha \right)A_i^{1∕2},\hfill \end{array}$$

where g⁻¹(.) is the inverse function of g(.), ϕ is a possible dispersion parameter, A_i = diag{v(μ_i1), v(μ_i2), ..., v(μ_ik)} with v(μ_im) = Var(y_im|x_i, z_i)/ϕ, and R_w = R_w(α) is a working correlation matrix that may depend on some unknown parameters α. Note that R_w does not have to be correctly specified; for convenience, a working independence model with R_w = I is often used, as done in this paper unless specified otherwise.

With a canonical link function and a working independence model (i.e. R_w = I), it is not di cult to obtain the (generalized) score vector and its consistent covariance estimate:

$$\begin{array}{cc}\hfill U=& {(U_{.1}^{\prime },U_{.2}^{\prime })}^{\prime }=\sum _{i=1}^n\nabla {\mu }_i^{\prime }{A}_i(Y_i-{\mu }_i)=\sum _{i=1}^n{(Z_i,X_i)}^{\prime }(Y_i-{\mu }_i),\hfill \\ \hfill \tilde{\Sigma }=& \widehat{\mathrm{Cov}}\left(U\right)=\sum _i{(Z_i,X_i)}^{\prime }(Y_i-{\widehat{\mu }}_i){(Y_i-{\widehat{\mu }}_i)}^{\prime }\left(Z_i{X}_i\right)=\left(\begin{array}{cc}\hfill V_{11}\hfill & \hfill V_{12}\hfill \\ \hfill V_{21}\hfill & \hfill V_{22}\hfill \end{array}\right),\hfill \end{array}$$ (1)

Where ${\widehat{\mu }}_i$ is an estimate of μ_i, $\tilde{\Sigma }$ is partitioned according to the score vector components U_.1 and U_.2 for φ and β respectively.

Binary Traits

For binary traits (coded as 0 and 1), we use the logit link function, and v(μ_im) = μ_im(1 − μ_im). The (m, l)th element of ∂μ_i/∂ θ′ is H_i,mlμ_im(1 − μ_im) with H_i,ml as the (m, l)th element of H_i. We have the score vector and its covariance estimate as

$$\begin{array}{cc}\hfill U=& \sum _i{\left(\frac{\partial {\mu }_i}{\partial {\theta }^{\prime }}\right)}^{\prime }{A}_i^{-1∕2}{R}_w^{-1}{A}_i^{-1∕2}(Y_i-{\mu }_i),\hfill \\ \hfill \tilde{\Sigma }=& \sum _i{\left(\frac{\partial {\mu }_i}{\partial {\theta }^{\prime }}\right)}^{\prime }{A}_i^{-1∕2}{R}_w^{-1}{A}_i^{-1∕2}(Y_i-{\widehat{\mu }}_i){(Y_i-{\widehat{\mu }}_i)}^{\prime }{A}_i^{-1∕2}{R}_w^{-1}{A}_i^{-1∕2}{\left(\frac{\partial {\mu }_i}{\partial {\theta }^{\prime }}\right)}^{\prime },\hfill \end{array}$$

with ${\widehat{\mu }}_i$ as an estimate of μ_i, A_i = diag(μ_i1(1 − μ_i1), ..., μ_im(1 − μ_im)).

Quantitative traits

We use the identity link g(μ_im) = μ_im and v(μ_im) = ϕ. Then we have

$$\begin{array}{cc}\hfill U=& \sum _i{H}_i^{\prime }{R}_w^{-1}(Y_i-{\mu }_i),\hfill \\ \hfill \tilde{\Sigma }=& \sum _i{H}_i^{\prime }{R}_w^{-1}(Y_i-{\widehat{\mu }}_i){(Y_i-{\widehat{\mu }}_i)}^{\prime }{R}_w^{-1}{H}_i.\hfill \end{array}$$ (2)

If we assume a common covariance matrix for Y_i's across all i, then a better covariance estimate is

$$\tilde{\Sigma }=\sum _i{H}_i^{\prime }{R}_w^{-1}(\sum _i(Y_i-{\widehat{\mu }}_i){(Y_i-{\widehat{\mu }}_i)}^{\prime }∕n)R_w^{-1}{H}_i,$$

which is used by default for its better finite-sample performance (Pan 2001).

2.2 Existing Tests in GEE

Our goal is to detect whether there is any association between any of the traits and the SNP via testing the null hypothesis H₀: β = (β₁, ..., β_k)′ = 0 versus H₁: β ≠ = 0.

To construct score-based tests with covariates Z_i, we first fit the GEE model under H₀, g(μ_i) = Z_iφ, to obtain $\widehat{\phi }$ and ${\widehat{\mu }}_i$. If we denote for subject i, U_i1 as the score vector corresponding to covariates Z_i, and U_i2 as the score vector for the SNP, then the score vector under the null hypothesis, with an assumed independent working correlation structure for the traits, is:

$$\begin{array}{cc}\hfill & U(\widehat{\phi },0)={(U_{.1}^{\prime },U_{.2}^{\prime })}^{\prime }=\sum _{i=1}^n{(U_{i1}^{\prime },U_{i2}^{\prime })}^{\prime },\hfill \\ \hfill & U_{.1}=\sum _{i=1}^n{U}_{i1}=\sum _{i=1}^n{Z}_i^{\prime }(Y_i-{\widehat{\mu }}_i),\hfill \\ \hfill & U_{.2}=\sum _{i=1}^n{U}_{i2}=\sum _{i=1}^n{X}_i^{\prime }(Y_i-{\widehat{\mu }}_i)=\sum _{i=1}^n{x}_i(Y_i-{\widehat{\mu }}_i).\hfill \end{array}$$

The null distribution of the score vector for β is asymptotically Normal under H₀:

$$U_{.2}\sim N(0,{\Sigma }_{.2}),{\Sigma }_{.2}=\widehat{\mathrm{Cov}}\left(U_{.2}\right)=V_{22}-V_{21}{V}_{11}^{-1}{V}_{12},$$ (3)

where V₁₁, V₁₂, V₂₁, V₂₂ are defined in (1).

The Wald test

$T={\widehat{\beta }}^{\prime }{\left(\mathrm{Cov}\left(\widehat{\beta }\right)\right)}^{-1}\widehat{\beta }$, where $\widehat{\beta }$ is the estimate of β in the GEE marginal model, and $\mathrm{Cov}\left(\widehat{\beta }\right)$ is the sandwich estimate. Under H₀, we have $T\sim {\chi }_k^2$ asymptotically. In spite of its simplicity and popular use, as well known (Pan 2001) and to be shown later, with a relatively large k, the Wald test in GEE may become too liberal with inflated Type I errors.

The Score test

$T=U_{.2}^{\prime }{\Sigma }_{.2}^{-1}{U}_{.2}$, where U_.2 and Σ_.2 are discussed above; it is asymptotically equivalent to the Wald test with the same null distribution ${\chi }_k^2$. Since we only need to fit the model under the null hypothesis, it is computationally simpler than using the Wald test, which requires fitting a full model. More importantly, as to be shown, the Score test controls the Type I error much better than the Wald test.

The UminP test

$T=\underset{j=1,\dots ,k}{\max }{U}_{.2,j}^2∕{\Sigma }_{.2,jj}$, where U_.2,j is the jth element of U_.2, and _.2,jj is the jth entry on the diagonal of _.2. Although a numerical integration-based method as for single trait–multilocus testing (e.g. Pan 2009) can be adopted, we use a simulation based method to calculate its p-value. Specifically, we simulate the score vectors U_(b) = (U_(b),1, U_(b),2, ..., U_(b),k)′ from its null distribution $U_{\left(b\right)}\sim N(0,{\Sigma }_{.2})$ for b = 1, ..., B, then calculate the null statistics $T^{\left(b\right)}={\max }_{j=1,\dots ,k}{U}_{\left(b\right),j}^2∕{\Sigma }_{.2,jj}$, and the p-value ${\sum }_{b=1}^{B}I(T^{\left(b\right)}>T)∕B$.

With a working independence model R_w = I, each component U_.2,j is equal to the score function for the univariate analysis on the jth trait. Hence, the GEE-UminP test is equivalent to the usual UminP test that combines the univariate analyses on the multiple traits.

2.3 New Tests in GEE

For association analysis of rare variants, weighting on the components of the score vector has been recognized as a general and effective approach to synthesizing information contained in the components of the score vector (Lin and Tang 2012). We borrow this idea and apply it to the current context, yielding a weighted score test:

$$T_W=\sum _{j=1}^k{w}_j{U}_{.2,j},$$

where the weights w_j's have to be specified, which is a key and challenging issue. Various choices of the weights have been proposed for analysis of rare variants, all of which are some fixed weights. Our goal is to specify a whole class of weights such that they can cover a wide range of situations: for any given data with unknown true association patterns, we hope that at least one member from the specified class of weights would yield a high-powered test. We reason that, since association information is largely contained in the score vector, the driving force of constructing various score-based tests (as reviewed above), it might be productive to use the score vector to construct the weights. Accordingly, we propose a class of weights $w_j=U_{.2,j}^{\gamma -1}$ for a series of values of γ = 1, 2, ..., ∂, leading to the sum of powered score (U) tests, called SPU tests:

$$SPU\left(\gamma \right)=\sum _{j=1}^k{U}_{.2,j}^{\gamma }.$$

As γ = 1, the SPU(1) test sums up the information in the multiple traits equally, just as the Average (Sum) test. As the power parameter γ increases, the SPU(γ) test puts higher weights on the traits with larger |U_.2,j|, while gradually decreasing the weights on the other traits with smaller |U_.2,j|. By statistical theory, we know that a trait associated with the SNP is expected to have a larger |U_.2,j| while a non-associated one has a smaller value. Hence, an increasing value of γ tends to put higher weights on those more strongly associated traits. An extreme situation is that, as γ → ∂ (as an even number), we have

$$SPU\left(\gamma \right)\propto {\left(\sum _{j=1}^k{U}_{.2,j}^{\gamma }\right)}^{1∕\gamma }\to \underset{j\in \{1,2,\dots ,k\}}{\max }\mid U_{.2,j}\mid \equiv SPU\left(\infty \right),$$

taking only the largest one. In our experience, an SPU(γ) test with γ> 8 often yields results similar to that of the SPU(∞) test. Hence, in all our following experiments, we only used γ ∈ Γ = {1, 2, ..., 8, ∞}.

While the SPU(1) is similar to the Average (Sum) test, the SPU(2) test is the same as the SSU test outlined by Yang and Wang (2012), an extension of the SSU test for single trait–multilocus analysis (Pan 2009) to the current context for multiple traits and a single SNP.

Suppose that the sample size is large enough for the asymptotic null distribution of the score vector to hold, we use a simulation method to estimate the p-value of an SPU test (Seaman and Mller-Myhsok 2005; Lin 2005). Suppose that T is the test statistic for an SPU(γ) test and ${\widehat{\Sigma }}_{.2}$ is the covariance matrix of the score vector based on the original data. We draw B samples of the score vector from its null distribution: $U_{.2}^{\left(b\right)}\sim MVN(0,{\widehat{\Sigma }}_{.2})$, b = 1, ...B, and obtain a null statistic $T^{\left(b\right)}={\sum }_{j=1}^k{U}_{.2,j}^{\left(b\right)\gamma }$. We then calculate $\text{p-value}={\sum }_{b=1}^{B}I(\mid T^{\left(b\right)}\mid >\mid T\mid )∕B$.

Since the result of an SPU(γ) test depends on the choice of the power parameter γ while in general it is unknown which value of is optimal for a given dataset, it would be convenient to have a test that data-adaptively and automatically chooses the parameter γ. We propose an adaptive SPU (aSPU) test to estimate and thus select the most powerful SPU test for given data. Because it is di cult to characterize the power curve of an SPU test, we use the p-value of a SPU test to approximate its power; this idea has been widely used in practice. Accordingly, the aSPU test statistic is the minimum p-value among all SPU tests:

$$T_{aSPU}=\underset{\gamma \in \Gamma }{\min }{P}_{SPU\left(\gamma \right)},$$

where P_SPU(γ) is the p-value of the SPU(γ) test.

The p-value of aSPU can be obtained based on simulations. It may appear that a double simulation procedure is needed, but indeed not necessary. As before, first, we simulate B independent copies of the null score vector U^(b) from $N(0,{\widehat{\Sigma }}_{.2})$ for b = 1, 2, ..., B. We then calculate the corresponding SPU test statistics $T_{SPU\left(\gamma \right)}^{\left(b\right)}$ and their p-values $p_{\gamma }^{\left(b\right)}={\sum }_{b_1\ne b}I(T_{SPU\left(\gamma \right)}^{\left(b_1\right)}>T_{SPU\left(\gamma \right)}^{\left(b\right)})∕(B-1)$. Thus, we have $T_{aSPU}^{\left(b\right)}={\min }_{\gamma \in \Gamma }{p}_{\gamma }^{\left(b\right)}$, and the final p-value of the aSPU test is $P_{aSPU}={\sum }_{b=1}^{B}I(T_{aSPU}^{\left(b\right)}<T_{aSPU})∕B$. Note that, in practice we can first use a smaller B, say B = 1000, to scan a genome, then gradually and repeatedly increase B for a few SNPs that pass an initial significance criterion (e.g. p-value < 5/B) in the previous step.

The aSPU test aims to data-adaptively approximate the most powerful SPU test among a set of versatile SPU(γ) tests with various values of γ, thus maintaining high power at any given situation. Although we use the minimum p-value to approximate the most powerful SPU test, other combining methods (e.g. Pan et al 2010) are also possible and may be explored. The aSPU test uses adaptive weights on the multiple traits to assess their aggregated e ects (while down-weighting the e ects of null traits).

The SPU and aSPU tests assume that the multiple traits are in the same scale; if not, e.g. when the variances of the traits vary a lot, one should first standardize the traits to have an equal sample variance. For example, when some null traits have larger variances than that of associated traits, an SPU test statistic will be dominated by the noises in the score components for the null traits, leading to concealing association signals and thus reduced power. Alternatively, to account for possibly different scales or variances of the multiple traits, one can use a variance-weighted SPU test (SPUw): for any γ ∈ Γ,

$$SPUw\left(\gamma \right)=\sum _{j=1}^k{\left(U_{.2,j}∕\sqrt{{\Sigma }_{.2,jj}}\right)}^{\gamma }.$$

Note that under the working independence model (R_w = I) in GEE, the SPUw(∞) test is equal to the UminP test. The adaptive SPUw (aSPUw) test can be accordingly defined as for the aSPU test.

2.4 Properties of the GEE Tests

We analyze how the proposed GEE-based tests are related to some existing tests in the absence of covariates while testing for association between a set of quantitative traits and a single SNP. By default (unless specified otherwise), we assume without loss of generality that both Y_i and x_i have been centered at 0; that is,${\sum }_{i=0}^n{Y}_i=0$ and ${\sum }_{i=0}^n{x}_i=0$. For simplicity we also assume that there is no missing data, and each subject has all k traits observed.

We expect that most of our below conclusions can be extended to the case for quantitative traits with covariates Z_i: we first regress Y_i on Z_i to obtain residuals r_Y,i, and regress x_i on Z_i to obtain residuals r_X,i; then we apply the same arguments below to regression of r_Y,i on r_X,i (instead of regression of Y_i on x_i).

2.4.1 Fitting a GEE Working Independence Model and an Equivalent Model

In the current context, the GEE model is

$$E\left(Y_i\right)=X_i\beta =x_i\beta$$ (4)

with β = (β₁, ..., β_k)′. Note that, due to centering both Y_i and x_i at mean 0, no intercept term is needed. To test H₀: β = 0, under the working independence model (i.e. R_w = I), we have the score vector and its empirical covariance estimate as

$$U=\sum _{i=1}^n{x}_i(Y_i-\stackrel{‒}{Y})=\sum _{i=1}^n{x}_i{Y}_i,\widehat{\mathrm{Cov}}\left(U\right)=\sum _{i=1}^n{x}_i^2{Y}_i{Y}_i^{\prime }.$$ (5)

As an alternative, we fit the below model:

$$E\left(x_i\right)=Y_i^{\prime }b$$ (6)

with b = (b₁, ..., b_k)′. To test H₀: b = 0, we obtain its score vector and empirical covariance estimate, which are exactly the same as in equation (5). Note that, due to the possible correlations among the components of Y_i and possibly non-Normality or non-constant variances of x_i (the latter of which is true because x_i is the genotype score), we have to use the empirical covariance estimate of the score vector. In summary, any test based on the score vector of fitting the GEE working independence model (4) can be equally constructed based on fitting a simple linear model (6). For example, a GEE-SPU(2) test based on the GEE model (4) is equivalent to the SSU test based on model (6) (Pan 2009).

We note that using the GEE score components and their variances to test for H_m,0: β_m = 0 separately for each trait m is the same as conducting a univariate Score test on each trait m individually. Hence, in addition to UminP, other methods could be applied to combine these univariate tests (Yang and Wang 2012); in fact, if R_w = I is used in GEE, all our proposed tests could be regarded in this way.

Finally, we note that the above conclusion holds for other GLMs with a canonical link function, under which the score vector maintains the same form as in (5) (McCullagh and Nelder 1983).

2.4.2 GEE-SPU versus GEE-SPUw tests

In the current context, based on (5), we have

$$\begin{array}{cc}\hfill & SPU\left(\gamma \right)=\sum _{j=1}^k{\left(\sum _{i=1}^n{x}_i{y}_{ij}\right)}^{\gamma },\hfill \\ \hfill & SPUw\left(\gamma \right)=\sum _{j=1}^k{\left(\frac{{\sum }_{i=1}^n{x}_i{y}_{ij}}{\sqrt{{\tilde{\Sigma }}_{jj}}}\right)}^{\gamma }\approx \sum _{j=1}^k{\left(\frac{{\sum }_{i=1}^n{x}_i^2{y}_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_i^2\mathrm{Var}\left(y_{ij}\right)}}\right)}^{\gamma }\propto \sum _{j=1}^k{\left(\frac{{\sum }_{i=1}^n{x}_i{y}_{ij}}{\sqrt{\mathrm{Var}\left(y_{ij}\right)}}\right)}^{\gamma },\hfill \\ \hfill & \mathrm{Var}\left(y_{ij}\right)=\mathrm{Var}\left(x_i\right){\beta }_j^2+{\sigma }_j^2=2f(1-f){\beta }_j^2+{\sigma }_j^2,\hfill \end{array}$$

where the Hardy-Weinberg equilibrium is assumed in the second equality for Var(y_ij), f is the MAF of the SNP, and ${\sigma }_j^2$ is the residual variance of trait j (after removing the e ect of the SNP). We also assume that Var(y_ij) does not depend on i (but may depend on j).

It is clear that the SPUw tests, but not SPU tests, are invariant to the scales of the traits. Hence, the SPUw and aSPUw tests can automatically account for different scales of the multiple traits, while the SPU and aSPU tests cannot, requiring one to standardize the (residual) variances of the traits if they di er a lot. On the other hand, if ${\sigma }_j^2’\mathrm{s}$ are all equal, for an associated trait j with β_j ≠ = 0, due to its larger Var(y_ij), any SPUw test would put a lower weight on it as compared to the corresponding SPU test, leading to power loss. However, for complex traits with typically small |β_j|, the power loss of the SPUw or aSPUw test is often negligible, resulting in almost equal power between the aSPUw and aSPU tests, as to be confirmed in our numerical examples.

2.4.3 Use of various working correlation structures in GEE

For quantitative traits, it is often reasonable to assume that the marginal covariance matrix Cov(Y_i|H₀) = V₀ does not vary over i. Under this assumption (and thus a equal cluster size dim(Y_i) = k), we can write the working covariance matrix V_w,i = A_i^−1/2R_wA_i^−1/2 = V_w,0, invariant to i. With any working correlation matrix R_w, the score vector and its covariance estimate are

$$\begin{array}{cc}\hfill U\left(R_w\right)=& \sum _i{x}_i{V}_{w,0}^{-1}(Y_i-Y_0),\hfill \\ \hfill \widehat{\Sigma }\left(R_w\right)=& \sum _i{x}_i{V}_{w,0}^{-1}(\sum _i(Y_i-Y_0){(Y_i-Y_0)}^{\prime }∕n)V_{w,0}^{-1}{x}_i,\hfill \end{array}$$ (7)

from which it can be seen that

$$\begin{array}{cc}\hfill T_{Sco}=& U{\left(R_w\right)}^{\prime }\widehat{\Sigma }{\left(R_w\right)}^{-1}U\left(R_w\right)\hfill \\ \hfill =& \left(\sum _i{x}_i{(Y_i-Y_0)}^{\prime }\right)V_{w,0}^{-1}{\left\{V_{w,0}^{-1}\sum _i{x}_i^2\left(\sum _i(Y_i-Y_0){(Y_i-Y_0)}^{\prime }∕n\right)V_{w,0}^{-1}\right\}}^{-1}{V}_{w,0}^{-1}\left(\sum _i{x}_i(Y_i-Y_0)\right)\hfill \\ \hfill =& U{\left(I\right)}^{\prime }\widehat{\Sigma }{\left(I\right)}^{-1}U\left(1\right).\hfill \end{array}$$

That is, the GEE-Score test is invariant to R_w, the working correlation structure.

Since in general U(R_w) ≠ U(I) and $\widehat{\Sigma }\left(R_w\right)\ne \widehat{\Sigma }\left(I\right)$ for R_w ≠ = I, the other GEE-based tests (except GEE-Score) are not necessarily invariant to R_w.

Surprisingly, as to be shown, the GEE-UminP, GEE-SPUw(∞) and GEE-SPU(∞) tests may lose power when the true correlation structure is used as R_w. Here we consider a simple example. Suppose that the first 5 traits are associated with a SNP while all other remaining k−5 traits are not; the true covariance matrix Cov(Y_i) has a compound symmetry structure CS(r): Var(y_ij) = 1 and Cov(y_ij, y_il) = r for any j ≠ l. The score vector U(R_w) = (U₁(R_w), . . ., U_k(R_w))′ is defined in (8) and $\widehat{\Sigma }\left(R_w\right)\approx {\sum }_i{x}_i^2{V}_w^{-1}\mathrm{Cov}\left(Y_i\right)V_w^{-1}$. Without loss of generality, we also assume x_i is standardized to have ${\sum }_i{x}_i^2=1$. Under the working independence model R_w = I, assume that E(U_j(I)) = 1 for 1 ≤ j ≤ k₁, and E(U_j(I)) = 0 for 5 < j k. Hence, with R_w = I, the component-wise signal magnitude (related to the non-centrality parameter for a univariate Score test on each trait) is

$${\lambda }_j=E{\left(U_j\left(I\right)\right)}^2∕\mathrm{Var}\left(U_j\left(I\right)\right),$$

which is 1 for 1 ≤ j ≤ 5, and is 0 otherwise. On the other hand, in the ideal case with V_w = Cov(Y_i), we have

$$E\left(U\left(R_w\right)\right)=\mathrm{Cov}{\left(Y_i\right)}^{-1}E\left(U\left(I\right)\right),\widehat{\Sigma }\left(R_w\right)=\mathrm{Cov}{\left(Y_i\right)}^{-1}.$$

Accordingly, we can calculate its component-wise signal magnitude λ_j = E(U_j(R_w ))²/Var(U_j(R_w)). Table 1 shows some examples.

Table 1.

Component-wise signal magnitude with various R_w and k in GEE.

Rw	I	R0: CS(r = 0.5)				R0: CS(r = –0.5)
k	≥ 5	5	10	40	400	5	10	40	400
E(U1)	1	0.3	1.091	1.756	1.975	−1	0.191	0.577	0.658
Var(U1)	1	1.667	1.818	1.951	1.995	0.333	0.571	0.649	0.665
λ 1	1	0.067	0.655	1.581	1.955	3.000	0.064	0.513	0.652
E(U6)	0	-	−0.909	−0.244	−0.025	-	−0.476	−0.090	−0.008
Var(U6)	1	-	1.818	1.951	1.995	-	0.571	0.649	0.665
λ 6	0	-	0.455	0.031	0.0003	-	0.397	0.013	0.0001
${\max }_{j=1}^k{\lambda }_j$	1	0.067	0.655	1.581	1.955	3.000	0.397	0.513	0.652

It is clear that, compared to using R_w = I, one may gain or lose with respect to componentwise information contents in the score vector by using a correct correlation matrix as R_w in GEE, depending on the value of between-trait correlation r and the number of traits k. In particular, with r > 0 and a small k, using a correct correlation matrix may give max_j λ_j < 1, leading to loss of power by the UminP test, as compared to its using the working independence model in GEE; as k increases (while keeping the number of associated traits fixed), it will gain by using the correct correlation matrix as R_w. This latter point is consistent with the theoretical result of Cai et al (2013) for a high-dimensional two-sample comparison problem.

2.4.4 Relationships between the new and existing tests

Our proposed tests cover several commonly used methods as special cases in the current context. A summary is given in Table 2, and the details are relegated to the Appendix.

Table 2.

Relationships between the existing and new tests.

Method	Model or test statistic	Relation to the new tests
The Average method (Shen et al 2011)	${\sum }_{j=1}^k{Y}_{ij}={\alpha }_0+{\alpha }_1{x}_i+e_i$, Applying the Score test on H0: α1 = 0.	Average = GEE-SPU(1).
TATES (van der Sluis et al 2013)	Yij = β0,j + β1,jxi + eij for j = 1, 2, ..., k. Testing for H0: β1,1 = ... = β1,k = 0 with analytical approximations to calculate a p-value.	TATES ≈ GEE-UminP ≈ GEE-SPUw(∞).
CCA=MANOVA (Ferreira & Purcell 2009; Yang & Wang 2012)	CCA seeks to maximize the correlation between a linear combination of (Yi1, ..., Yik) and xi. Test statistic: $B=S_{XX}^{-1∕2}{S}_{XY}{S}_{YY}^{-1}{S}_{YX}{S}_{XX}^{-1∕2}$	CCA=MANOVA=GEE-Score.
MDMR (Zapala & Schork 2012)	$D_{ij}=d(Y_i,Y_j),A=(-D_{ij}^2∕2)$, G = (I – 11′/n)A(I – 11′/n), H = X(X′X)–1X′, Test statistic: F = tr(HGH)/tr[(I – H)G(I – H)]	MDMR=GEE-SPU(2) if d(,) is Euclidean.
KMR (Maity et al 2012)	Test statistic: $T_{KMR}={(Y-\stackrel{‒}{Y})}^{\prime }{V}_0^{-1}K{V}_0^{-1}(Y-\stackrel{‒}{Y})$	KMR = GEE-SPU(2) if K = XX′ and Rw = Corr(Yi|H0).
MultiPhen (O'Reilly et al., 2012)	${\pi }_j\left(y\right)=Pr(x_i=j\mid Y_i=y),{\kappa }_j\left(y\right)={\sum }_{m=0}^j{\pi }_m\left(y\right)$ for j = 0, 1, 2, $\log \frac{{\kappa }_j\left(y\right)}{1-{\kappa }_j\left(y\right)}={\alpha }_j-y^{\prime }\beta$ for j = 0 and 1. Applying the Score (or likelihood ratio) test on H0: β = 0.	MultiPhen ≈ GEE-Score.
Generalized Kendall's tau (Zhang et al 2010)	uij = (Yi1 – Yj1, ..., Yiq – Yjq)′, ${\stackrel{‒}{u}}_i={\sum }_{j=1}^n{u}_{ij}∕n,\tau ={\sum }_{i=1}^n{x}_i{\stackrel{‒}{u}}_i$. Test statistic: $T={\tau }^{\prime }{V}_0^{-1}\tau$.	GK-tau = GEE-Score.

2.5 Simulation Set-ups

Unless specified otherwise, by default each simulated dataset consisted of n = 1000 subjects with a varying number (k) of correlated quantitative traits, including the first k₁ = 5 traits associated with the SNPs to be tested under the alternative hypothesis H₁ (while all other k − k₁ traits were not associated). For each subject, we generated a block of p = 11 SNPs in linkage disequilibrium (LD) and the first one was the causal SNP under H₁. Specifically, for each subject i, we first generated a latent vector G_i = (G_i1, ...G_ip)′ from a multivariate Normal distribution with a first-order auto-regressive (AR-1) covariance structure with parameter ρ = 0.5: Cov(G_ij, G_il) = ρ^|j−l|. Second, each latent element G_ij was dichotomized to 0 or 1 with probability Prob(G_ig = 1) as its minor allele frequency (MAF), randomly drawn from a uniform distribution (Pan 2009). The MAF of the causal (i.e. first) SNP was from U(0.3, 0.4), while the MAFs of the other SNPs were independently drawn from U(0.1, 0.5). In this way, we generated a haplotype for subject i. Similarly, we independently generated another haplotype for subject i; by combining the two haplotypes we obtained the genotype of the subject. We tested on each of the first few SNPs nearest to the causal SNP.

Similarly, we also considered smaller sample sizes n = 500 and n = 200, and rare variants (RVs) with MAF=0.01.

The phenotype for each subject i, Y_i = (Y_i1, ..., Y_ik)′ was simulated from a linear model:

$$Y_i={\beta }_0+x_i\beta +{∊}_i,$$

where β₀ = (β₀₁, ..., β_0k)′, β = (β₁, ..., β_k)′, x_i is the genotype score of the causal SNP, and ∈_i was independently drawn form a multivariate Normal distribution N(0, σ²R), with σ = 1 and R as either an AR-1 correlation matrix with parameter r or a compound symmetry (CS) matrix with parameter r; we considered r = ±0.3 or 0.5. In addition, we also considered using a correlation matrix estimated from the ADNI data. β_0m is the intercept for trait m. Under H₀, we had β = 0; under H₁, we had β_m ≠ = 0 for 1 ≤ m ≤ k₁, and β_m = 0 for k₁ < m ≤ k. The non-zero β_j's were randomly drawn from a uniform distribution U(0.2, 0.3) for weak e ects, or from U(0.8, 1) for strong e ects. That is, under H₁, only the first 5 traits were associated with the causal SNP, and we gradually increased the number of the non-associated (i.e. null) traits from 0 to 5, then 15, up to 35. Under each simulation set-up, 1000 datasets were independently generated and analyzed; we used B=1000 to obtain p-values for any simulation-based method. Unless specified otherwise, by default, the working independence model was used in GEE.

For comparison, in addition to the GEE-based tests, we also applied some representative existing tests, including the Average method, MultiPhen, TATES, MANOVA (based on the Wilks statistic) and MDMR (based on the L₁-norm or L₂-norm as the distance metric).

2.6 ADNI Data

Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their e ectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is the result of e orts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

3 Results

3.1 Simulations

3.1.1 CS

In Table 3, the multivariate traits had a compound symmetry (CS) correlation structure with parameter r = 0.3 or 0.5. All the tests, except the GEE-Wald test, could control the Type I error. As the number of the traits, k, increased, the GEE-Wald test gradually had a severely inflated Type I error; in contrast, the GEE-Score test performed satisfactorily. The poor performance of the Wald test and better performance of the Score test for finite-samples in GEE are well known (e.g. Guo et al 2005); due to its inability to control Type I errors, we will omit the discussion on the GEE-Wald test in the sequel.

Table 3.

Empirical Type I error rates when the multiple traits were correlated with a CS structure with correlation coefficient r. An independence working correlation structure was used in GEE.

									GEE
						MDMR						SPU(γ)
r	SNP	#traits	Average	MultiPhen	TATES	L 1	L 2	MANOVA	Wald	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
0.3	1	5	0.043	0.051	0.048	0.040	0.048	0.051	0.056	0.051	0.046	0.038	0.049	0.050	0.045	0.048	0.049	0.049	0.050
		10	0.053	0.060	0.055	0.059	0.058	0.060	0.076	0.060	0.053	0.049	0.057	0.051	0.049	0.047	0.052	0.046	0.051
		20	0.058	0.062	0.046	0.052	0.046	0.064	0.094	0.062	0.046	0.054	0.048	0.046	0.049	0.051	0.049	0.046	0.047
		30	0.049	0.034	0.047	0.059	0.052	0.036	0.102	0.034	0.042	0.051	0.049	0.051	0.052	0.049	0.045	0.045	0.049
		40	0.053	0.055	0.059	0.055	0.058	0.061	0.165	0.054	0.059	0.053	0.059	0.061	0.061	0.062	0.064	0.057	0.054
0.3	2	5	0.051	0.058	0.059	0.054	0.051	0.059	0.066	0.058	0.056	0.050	0.049	0.051	0.048	0.053	0.050	0.053	0.050
		10	0.050	0.046	0.043	0.044	0.048	0.047	0.061	0.046	0.047	0.050	0.042	0.047	0.046	0.048	0.046	0.050	0.045
		20	0.048	0.049	0.048	0.048	0.048	0.049	0.078	0.049	0.048	0.049	0.054	0.053	0.051	0.053	0.055	0.046	0.053
		30	0.041	0.048	0.045	0.041	0.039	0.050	0.102	0.048	0.045	0.045	0.041	0.042	0.039	0.041	0.042	0.050	0.043
		40	0.058	0.051	0.044	0.056	0.059	0.053	0.153	0.049	0.051	0.055	0.055	0.055	0.051	0.050	0.046	0.049	0.052
0.5	1	5	0.043	0.052	0.050	0.044	0.045	0.051	0.056	0.051	0.045	0.038	0.041	0.046	0.049	0.046	0.047	0.047	0.048
		10	0.053	0.060	0.045	0.049	0.049	0.060	0.076	0.060	0.048	0.047	0.049	0.054	0.053	0.050	0.048	0.051	0.048
		20	0.058	0.062	0.048	0.057	0.051	0.064	0.094	0.062	0.055	0.055	0.053	0.049	0.048	0.050	0.047	0.052	0.048
		30	0.049	0.034	0.045	0.055	0.055	0.036	0.102	0.034	0.055	0.054	0.048	0.050	0.054	0.054	0.053	0.062	0.055
		40	0.053	0.055	0.048	0.055	0.060	0.061	0.165	0.054	0.051	0.055	0.058	0.060	0.059	0.058	0.056	0.054	0.055
0.5	2	5	0.051	0.059	0.054	0.055	0.050	0.059	0.066	0.058	0.049	0.050	0.052	0.050	0.050	0.049	0.045	0.049	0.051
		10	0.050	0.046	0.045	0.047	0.053	0.047	0.061	0.046	0.047	0.050	0.048	0.045	0.049	0.046	0.046	0.047	0.046
		20	0.048	0.049	0.046	0.045	0.048	0.049	0.078	0.049	0.048	0.049	0.051	0.050	0.055	0.056	0.054	0.049	0.048
		30	0.041	0.048	0.043	0.042	0.037	0.050	0.102	0.048	0.046	0.043	0.040	0.040	0.039	0.041	0.042	0.051	0.046
		40	0.058	0.051	0.040	0.059	0.057	0.053	0.153	0.049	0.046	0.056	0.058	0.057	0.054	0.054	0.054	0.048	0.051

Table 9 shows the power performance of the tests when the causal SNP had strong genetic e ects on the associated 5 traits. Since the causal SNP and its nearest neighbor were strongly associated with (a subset of) the traits, the power of each test was close to 1 (not shown); hence, we tested on the second and third nearest SNPs next to the causal SNP. First, we can empirically verify our theoretical results derived earlier: i) the equivalence between MANOVA and the GEE-Score test, between MDMR(L2) and the GEE-SPU(2) test, and the Average and GEE-SPU(1) tests; ii) the similar performance between TATES and UminP (or SPUw(∞)), and between MultiPhen and the GEE-Score test. Since the traits had a multivariate Normal distribution, using the L₂-norm as the distance was more powerful than using the L₁-norm in MDMR; however, with other trait distributions, it is possible that the latter may edge over the former. Second, we note that the Average test, or equivalently the GEE-SPU(1) test, had the highest power when all k = k₁ = 5 traits were associated with the causal SNP (with similar e ect sizes and the same e ect direction); however, they quickly lost power as k increased, i.e. more non-associated traits were included. Third, as k increased, an SPU(γ) test with a larger γ had higher power than those with smaller γ. In particular, we highlight the case with k = 40: the power of the GEE-SPU(1) or GEE-SPU(2) test could be much lower than GEE-SPU(6) or SPU(∞); for example for SNP 2 and r = 0.3, the SPU(1), SPU(2) and SPU(6) tests had power as 0.084, 0.432 and 0.680 respectively. We also note that GEE-SPU(6) and SPU(∞) gave similar power, implying that using up to 6 or 8 (as done here) is good enough. Fourth, we see that, for any given situation, one of the SPU tests had high power, though its identity changed with the situation. Most importantly, the aSPU test seemed to be able to remain (nearly) most powerful across all situations.

Table 9.

Empirical power when the multiple traits were correlated with a CS(0.3) structure; the first five traits were associated with a causal SNP with log-ORs β_j ~ U(0.8, 1), while all others had β_j = 0. An independence working correlation structure was used in GEE.

							GEE
									SPU(γ)
n	SNP	#Strait	Average	MultiPhen	TATES	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
500	2	5	0.610	0.369	0.534	0.370	0.366	0.509	0.604	0.598	0.580	0.563	0.557	0.542	0.505	0.577
		10	0.316	0.389	0.427	0.393	0.386	0.419	0.318	0.528	0.507	0.530	0.514	0.510	0.479	0.495
		20	0.126	0.273	0.338	0.281	0.269	0.328	0.127	0.386	0.373	0.451	0.446	0.463	0.439	0.405
		30	0.089	0.209	0.291	0.229	0.208	0.280	0.090	0.261	0.279	0.390	0.380	0.417	0.412	0.370
		40	0.071	0.188	0.256	0.203	0.186	0.250	0.067	0.191	0.207	0.318	0.299	0.356	0.361	0.333
200	2	5	0.306	0.144	0.254	0.146	0.144	0.237	0.312	0.298	0.291	0.285	0.280	0.273	0.249	0.287
		10	0.160	0.151	0.197	0.163	0.149	0.182	0.155	0.235	0.230	0.247	0.237	0.243	0.225	0.229
		20	0.087	0.104	0.145	0.117	0.102	0.135	0.087	0.159	0.163	0.198	0.201	0.209	0.199	0.180
		30	0.066	0.070	0.122	0.089	0.068	0.116	0.066	0.104	0.121	0.155	0.158	0.168	0.163	0.146
		40	0.054	0.063	0.087	0.091	0.060	0.077	0.053	0.081	0.089	0.123	0.121	0.140	0.139	0.122

Between an SPU(γ) and SPUw(γ) tests for a fixed γ, the former one was more powerful (not shown). As analyzed in section 2, this was presumably due to the larger e ect sizes of the associated traits, giving lower weights to associated SNPs in an SPUw(γ) test than in an SPU(γ). Accordingly, the aSPU test was also more powerful than the aSPUw test.

Table 5 shows the results with weaker genetic e ects. Now the GEE-Score and related MANOVA and MultiPhen tests were more powerful than the SPU/aSPU tests. Note the puzzling phenomenon: the former tests could have lower power with all k = 5 associated traits than that with some additional non-associated traits; this problem of MANOVA was pointed out by Ferreira and Purcell (2009) and studied by Cole et al (1984). In addition, due to the smaller e ect sizes of the associated SNP, the SPU and SPUw tests, and thus aSPU and aSPUw tests, performed similarly (not shown).

Table 5.

Empirical power when the multiple traits were correlated with a CS structure with correlation coefficient r = 0.3, and non-zero β_j ~ U(0.2, 0.3). An independence working correlation structure was used in GEE.

								GEE
					MDMR					SPU(γ)
SNP	#traits	Average	MultiPhen	TATES	L 1	L 2	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
l	5	0.664	0.468	0.551	0.653	0.652	0.469	0.468	0.531	0.660	0.658	0.636	0.609	0.597	0.569	0.533	0.632
	10	0.263	0.574	0.452	0.441	0.506	0.576	0.573	0.437	0.267	0.501	0.460	0.493	0.472	0.481	0.444	0.456
	20	0.114	0.535	0.335	0.202	0.245	0.536	0.535	0.330	0.114	0.249	0.261	0.330	0.321	0.348	0.345	0.305
	30	0.084	0.458	0.283	0.126	0.158	0.462	0.456	0.282	0.085	0.162	0.188	0.254	0.262	0.288	0.293	0.257
	40	0.058	0.412	0.252	0.089	0.103	0.421	0.409	0.250	0.058	0.100	0.128	0.180	0.192	0.236	0.263	0.211
2	5	0.226	0.110	0.165	0.209	0.213	0.110	0.108	0.160	0.221	0.214	0.206	0.188	0.188	0.181	0.166	0.211
	10	0.087	0.142	0.120	0.098	0.117	0.143	0.142	0.115	0.088	0.117	0.116	0.129	0.129	0.128	0.122	0.118
	20	0.064	0.132	0.085	0.074	0.083	0.135	0.131	0.091	0.064	0.086	0.089	0.099	0.097	0.098	0.095	0.089
	30	0.058	0.130	0.098	0.063	0.069	0.131	0.129	0.097	0.060	0.071	0.076	0.086	0.092	0.098	0.102	0.087
	40	0.050	0.091	0.067	0.057	0.056	0.098	0.091	0.066	0.049	0.055	0.057	0.064	0.066	0.070	0.071	0.063

3.1.2 AR-1

Now we consider the case where the multivariate traits had an AR-1 correlation structure. Table 6 shows that all the tests could control the Type I error rates around the nominal level of 0.05 satisfactorily.

Table 6.

Empirical Type I error rates when the multiple traits were correlated with an AR1 structure with correlation coefficient r. An independence working correlation structure was used in GEE.

									GEE
						MDMR					SPU(γ)
r	SNP	#traits	Average	MultiPhen	TATES	L 1	L 2	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
0.5	1	5	0.037	0.051	0.051	0.049	0.051	0.051	0.041	0.042	0.043	0.033	0.035	0.034	0.037	0.037	0.040	0.036
		10	0.045	0.060	0.053	0.049	0.060	0.060	0.046	0.053	0.041	0.052	0.048	0.051	0.057	0.058	0.051	0.051
		20	0.060	0.059	0.046	0.040	0.059	0.064	0.041	0.044	0.059	0.048	0.055	0.052	0.053	0.047	0.043	0.050
0.5	2	4	0.048	0.058	0.052	0.060	0.058	0.059	0.041	0.040	0.050	0.045	0.042	0.041	0.041	0.041	0.040	0.040
		10	0.062	0.047	0.044	0.053	0.047	0.047	0.062	0.056	0.063	0.062	0.056	0.057	0.053	0.058	0.064	0.061
		20	0.046	0.047	0.052	0.048	0.047	0.049	0.048	0.052	0.043	0.058	0.053	0.053	0.054	0.051	0.060	0.053
0.3	1	5	0.037	0.051	0.040	0.047	0.045	0.051	0.041	0.042	0.039	0.034	0.034	0.037	0.037	0.038	0.039	0.036
		10	0.048	0.060	0.049	0.061	0.054	0.060	0.046	0.043	0.047	0.049	0.040	0.044	0.037	0.040	0.040	0.052
		20	0.059	0.062	0.050	0.050	0.048	0.064	0.041	0.058	0.060	0.042	0.062	0.047	0.062	0.055	0.057	0.058
0.3	2	5	0.049	0.058	0.057	0.056	0.060	0.059	0.041	0.049	0.051	0.050	0.040	0.043	0.046	0.044	0.044	0.042
		10	0.061	0.046	0.054	0.045	0.042	0.047	0.062	0.056	0.061	0.062	0.065	0.063	0.059	0.057	0.057	0.059
		20	0.051	0.049	0.044	0.050	0.047	0.049	0.048	0.062	0.051	0.058	0.051	0.053	0.056	0.059	0.062	0.056

For power (Table 7), regardless of the value of r, we reached the same conclusions. First, it is clear that the aSPU test was more powerful than the MultiPhen, TATES, Score and UminP test. As more null traits were added, power of all methods generally decreased and the aSPU test still maintained its advantage. The power of MultiPhen was close to that of the GEE-Score test, while that of TATES was close to that of the UminP test. For example, when testing the association between SNP 1 and k = 5 traits (with no null traits), MultiPhen had a power of 0.458, TATES had 0.554, GEE-Score test had 0.458, UminP had 0.522, while the aSPU test had 0.624, close to 0.661, the highest power given by the Average method, essentially the same as that of SPU(1) test at 0.651. However, as the total number of traits increased to 20 (with 15 null traits), the power of the Averaging method dramatically reduced to 0.217, compared to 0.286 of the GEE-Score test and 0.334 of the UminP, all much lower than 0.400 of the aSPU test. The results also confirmed that if the SNP of interest was physically farther away from the causal SNP, the power any test would be largely reduced. For example, when testing SNP 1 based on 10 traits, the power of the Score test was 0.388 and the aSPU was 0.516; but when testing SNP 2, their power decreased to 0.100 and 0.139 respectively.

Table 7.

Empirical power when the multiple traits were correlated with an AR1 structure with correlation coefficient r; the non-zero β_j ~ U(0.2, 0.3). An independence working correlation structure was used in GEE.

									GEE
						MDMR					SPU(γ)
r	SNP	#traits	Average	MultiPhen	TATES	L 1	L 2	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
0.5	1	5	0.661	0.458	0.554	0.629	0.634	0.459	0.458	0.522	0.651	0.630	0.624	0.594	0.582	0.564	0.525	0.624
		10	0.390	0.371	0.426	0.496	0.527	0.373	0.388	0.447	0.388	0.555	0.534	0.533	0.513	0.513	0.471	0.516
		20	0.217	0.262	0.332	0.362	0.365	0.263	0.286	0.334	0.214	0.414	0.390	0.427	0.397	0.402	0.343	0.400
0.5	2	5	0.223	0.113	0.165	0.202	0.201	0.113	0.113	0.153	0.220	0.206	0.193	0.182	0.178	0.173	0.162	0.208
		10	0.124	0.107	0.122	0.131	0.129	0.107	0.100	0.112	0.124	0.150	0.137	0.139	0.127	0.129	0.114	0.139
		20	0.084	0.080	0.105	0.121	0.118	0.081	0.069	0.104	0.090	0.113	0.106	0.122	0.109	0.116	0.103	0.111
0.3	1	5	0.780	0.547	0.571	0.698	0.706	0.571	0.546	0.551	0.774	0.706	0.709	0.647	0.637	0.602	0.551	0.737
		10	0.487	0.442	0.469	0.568	0.596	0.444	0.442	0.443	0.482	0.592	0.569	0.546	0.530	0.511	0.454	0.572
		20	0.274	0.309	0.366	0.448	0.490	0.312	0.307	0.349	0.277	0.478	0.456	0.467	0.438	0.434	0.368	0.459
0.3	2	5	0.245	0.129	0.154	0.177	0.179	0.129	0.127	0.146	0.244	0.180	0.185	0.165	0.164	0.153	0.149	0.190
		10	0.147	0.120	0.129	0.157	0.156	0.121	0.119	0.122	0.146	0.161	0.146	0.143	0.139	0.136	0.122	0.156
		20	0.077	0.085	0.093	0.121	0.126	0.087	0.085	0.087	0.078	0.131	0.113	0.115	0.098	0.103	0.091	0.113

It is confirmed that the SPU and SPUw tests, and thus aSPU and aSPUw tests, were always almost equally powered, presumably due to the small e ect sizes here (not shown). Given that the majority of common SNPs that are associated with common diseases and other complex traits have only small e ect sizes, we conclude that it is unlikely that the aSPU and aSPUw tests would perform much di erently in practice; we recommend the use of the aSPU test (after standardizing the correlated traits to the same scale if needed).

When the causal SNP had di erent e ect directions on di erent traits, and/or when the correlations among the multiple traits were possibly negative, it was confirmed that the Average, SPU(1), SPUw(1) (and more generally, any SPU(γ) or SPUw(γ) test with γ as an odd number) would lose power; the better performance of the GEE-Score (and related tests) over that of aSPU, or vice versa, depended on the situations (not shown), as previously shown for the cases with a CS correlation structure.

3.1.3 Using a more realistic correlation matrix

We also considered using a correlation matrix mimicking real data. Specifically, based on the ADNI data, we fitted a null model (with several covariates but no SNP) to a set of 26 neuroimaging traits and thus estimated their correlation matrix. These traits appeared to be strongly correlated with the first quartile, median and third quartile of pair-wise correlations at 0.34, 0.47 and 0.59 respectively. We generated simulated data as before except fixing the number of the traits at 26 with their true correlation matrix as the one estimated from the ADNI data. As shown in Table 8, under the null hypothesis, it is clear that the methods could control the Type I error rates satisfactorily (except the GEE Wald test, which was omitted). For power, we randomly picked up the first five traits to be associated with a causal SNP; we considered both strong and weak e ects from the causal SNP. The conclusions were the same as before. For example, when the SNP-traits were strongly associated, the aSPU test was more powerful than the Score test. On the other hand, if the causal SNP was weakly associated with the five traits, given that the traits were strongly correlated as for the previous simulation case with a CS structure, the Score test appeared to be more powerful than the aSPU test.

Table 8.

Empirical Type I error rates (for β = 0) and power (for β ≠ 0) for 26 traits with the true correlation matrix estimated from the ADNI data; for β ≠ 0, the first five traits were associated with a causal SNP with log-ORs β_j ~ U(0.8, 1) or ~ U(0.2, 0.3), while all others had β_j = 0. An independence working correlation structure was used in GEE.

						GEE
								SPU(γ)
β	SNP	Average	MultiPhen	TATES	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
β = 0	1	0.054	0.037	0.051	0.039	0.037	0.053	0.055	0.048	0.048	0.053	0.053	0.050	0.056	0.056
βj ~ U(0.8, 1)	2	0.116	0.565	0.614	0.574	0.564	0.618	0.113	0.416	0.501	0.659	0.650	0.711	0.716	0.679
	3	0.064	0.126	0.143	0.132	0.125	0.147	0.060	0.098	0.123	0.162	0.172	0.183	0.220	0.176
βj ~ U(0.2, 03)	1	0.071	0.619	0.302	0.629	0.617	0.317	0.068	0.115	0.151	0.205	0.235	0.272	0.339	0.270
	2	0.053	0.141	0.079	0.144	0.140	0.085	0.052	0.057	0.059	0.065	0.076	0.080	0.086	0.082

3.1.4 Other cases with smaller sample sizes and association parameters

We considered whether the sample size would change our conclusions. We used a smaller sample size n = 500 or n = 200 while the multiple traits had a CS(0.3) correlation matrix. As shown in Table 9, we reached the same conclusions. For example, the aSPU test was more powerful than the Score test in these cases.

So far we have always assumed that the association directions between a causal SNP and multiple traits are in the same direction. Next we considered the case where a subset of the traits were positively while another subset were negatively, and weakly associated with the causal SNP. We still used a CS(r) as the correlation matrix for the traits. As shown in Table 10, as expected, the Average method and any SPU(γ) test with γ being an odd number were always low powered. Between the Score and aSPU tests, if r = 0.3, then the Score test was more powerful; however, if r = −0.3, then the aSPU test was more powerful. Overall, either the Score test or the aSPU test was the winner.

Table 10.

Empirical power when the multiple traits were correlated with a CS(r) structure; the first five traits were associated with a causal SNP with log-ORs β_j ~ –(–1)^jU(0.2, 0.3), while all others had β_j = 0. An independence working correlation structure was used in GEE.

						GEE
								SPU(γ)
r	SNP	#trait	Average	MultiPhen	TATES	Score	UminP	γ = 1	2	3	4	5	6	7	8	∞	aSPU
SNP 1
0.3	1	5	0.084	0.926	0.671	0.928	0.626	0.085	0.817	0.442	0.754	0.558	0.712	0.595	0.685	0.631	0.739
		10	0.075	0.854	0.541	0.851	0.512	0.073	0.684	0.356	0.644	0.463	0.598	0.482	0.569	0.529	0.586
		20	0.058	0.713	0.397	0.718	0.392	0.058	0.503	0.237	0.511	0.327	0.477	0.366	0.452	0.416	0.420
	2	5	0.060	0.272	0.173	0.289	0.168	0.063	0.188	0.137	0.179	0.156	0.177	0.163	0.175	0.169	0.140
		10	0.062	0.230	0.120	0.227	0.126	0.062	0.143	0.111	0.145	0.128	0.146	0.133	0.141	0.137	0.115
		20 0.062	0.167	0.100	0.170	0.145	0.084	0.059	0.087	0.078	0.088	0.086	0.083	0.084	0.084	0.087	0.085
–0.3	1	5	0.152	0.567	0.587	0.571	0.553	0.147	0.730	0.402	0.668	0.479	0.626	0.512	0.599	0.557	0.646
		10	0.115	0.466	0.461	0.490	0.488	0.118	0.640	0.356	0.606	0.435	0.566	0.464	0.552	0.502	0.565
		20	0.078	0.308	0.352	0.329	0.365	0.081	0.511	0.237	0.497	0.316	0.458	0.340	0.435	0.375	0.426
	2	5	0.075	0.117	0.137	0.144	0.165	0.073	0.212	0.135	0.186	0.150	0.168	0.148	0.165	0.159	0.163
		10	0.072	0.121	0.136	0.108	0.121	0.071	0.164	0.119	0.160	0.126	0.143	0.130	0.134	0.129	0.145
		20	0.057	0.091	0.118	0.080	0.076	0.055	0.113	0.069	0.096	0.072	0.092	0.071	0.085	0.074	0.087

3.1.5 Rare variants

As suggested by a reviewer, we considered rare variants with MAF fixed at 0.01 when simulating genotypes, while all other aspects were the same as before. To be consistent with our focus here on single SNP testing, we tested on each RV separately, though testing on multiple RVs was expected to be more powerful. As shown in Table 11, the results were pretty much the same as those for common variants when the causal SNP was strongly associated with five traits. For example, it was confirmed again that the results between the Average and GEE-SPU(1), between TATES and GEE-UminP, and among MultiPhen, MANOVA and GEE-Score tests were almost the same respectively. More importantly, the aSPU test was much more powerful than the previous tests, especially as the number of non-associated traits increased.

Table 11.

Empirical Type I error rates (for β = 0) and power (for β ≠ 0) when the multiple traits were correlated with a CS(0.3) structure; for β ≠ 0, the first five traits were associated with a causal RV with log-ORs β_j ~ U(7.5, 8), while all others had β_j = 0. All the RVs had MAF=0.01. An independence working correlation structure was used in GEE.

							GEE
									SPU(γ)
β	SNP	#traits	Average	MultiPhen	TATES	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	7	8	∞	aSPU
β = 0	1	5	0.060	0.052	0.056	0.052	0.052	0.055	0.062	0.052	0.055	0.050	0.050	0.050	0.055	0.057	0.057	0.052
		10	0.049	0.055	0.047	0.056	0.055	0.042	0.049	0.050	0.051	0.049	0.047	0.048	0.047	0.049	0.043	0.043
		20	0.040	0.042	0.041	0.042	0.041	0.045	0.042	0.037	0.037	0.040	0.041	0.044	0.046	0.046	0.041	0.042
		30	0.047	0.048	0.051	0.049	0.047	0.051	0.049	0.054	0.055	0.054	0.059	0.058	0.057	0.056	0.057	0.057
		40	0.033	0.049	0.045	0.052	0.049	0.048	0.037	0.037	0.037	0.037	0.036	0.040	0.044	0.044	0.048	0.039
β ≠ 0	1	5	0.702	0.587	0.677	0.587	0.587	0.679	0.696	0.697	0.698	0.693	0.688	0.684	0.681	0.680	0.674	0.691
		10	0.596	0.551	0.634	0.552	0.550	0.624	0.594	0.688	0.684	0.698	0.694	0.695	0.690	0.689	0.680	0.679
		20	0.421	0.513	0.613	0.516	0.513	0.609	0.426	0.678	0.667	0.696	0.692	0.695	0.695	0.696	0.690	0.672
		30	0.263	0.463	0.579	0.465	0.461	0.575	0.265	0.657	0.649	0.685	0.674	0.692	0.689	0.693	0.680	0.667
		40	0.163	0.403	0.546	0.409	0.401	0.539	0.160	0.599	0.602	0.669	0.663	0.679	0.679	0.682	0.677	0.648

3.1.6 Using other working correlation structures in GEE

It is confirmed that using a non-diagonal correlation structure in GEE may or may not improve the performance of the GEE-based tests. For example, when the true CS correlation structure was used as the working one, the performance of the SPU and aSPU tests improved (Table 12); on the other hand, if R_w=CS was used for the case with an AR-1 as the true correlation structure, the power of the SPU and aSPU tests could be lower than that of using R_w = I (Table 12). On the other hand, in the current context, as shown in section 2, the GEE-Score is invariant to the use of R_w. We also note that the UminP and SPU(∞) (and SPUw(∞)) tests could have a severe loss of power with the use of a non-diagonal working correlation structure, even if the working correlation structure was the same as the true CS structure, as analyzed in section 2.

Table 12.

GEE methods with various true and working correlation matrices for non-zero β_j ~ U(0.2, 0.3).

Correlation							SPU(γ)
True	Rw	r	SNP	#traits	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
CS	CS	0.3	1	5	0.468	0.155	0.662	0.163	0.278	0.164	0.202	0.159	0.152	0.565
				10	0.594	0.374	0.294	0.595	0.385	0.513	0.375	0.447	0.375	0.536
				20	0.535	0.352	0.116	0.603	0.394	0.544	0.387	0.476	0.365	0.521
				30	0.456	0.362	0.084	0.530	0.416	0.512	0.412	0.466	0.374	0.487
			2	5	0.108	0.065	0.227	0.059	0.101	0.067	0.070	0.068	0.062	0.162
				10	0.133	0.108	0.102	0.144	0.102	0.138	0.102	0.127	0.113	0.135
				20	0.131	0.103	0.067	0.155	0.105	0.133	0.097	0.114	0.099	0.112
				30	0.129	0.123	0.060	0.138	0.109	0.144	0.119	0.133	0.122	0.120
AR1	CS	0.5	1	5	0.458	0.158	0.661	0.121	0.293	0.143	0.188	0.146	0.173	0.559
				10	0.371	0.296	0.345	0.422	0.363	0.369	0.316	0.345	0.307	0.442
				20	0.261	0.264	0.196	0.337	0.337	0.337	0.317	0.321	0.293	0.368
			2	5	0.113	0.062	0.221	0.056	0.096	0.056	0.076	0.060	0.070	0.163
				10	0.107	0.102	0.116	0.109	0.094	0.107	0.092	0.103	0.096	0.123
				20	0.080	0.094	0.065	0.124	0.113	0.115	0.099	0.106	0.100	0.121
AR1	CS	0.3	1	5	0.546	0.248	0.778	0.297	0.458	0.276	0.338	0.261	0.251	0.699
				10	0.442	0.323	0.486	0.468	0.482	0.424	0.402	0.387	0.325	0.549
				20	0.307	0.291	0.273	0.423	0.424	0.399	0.374	0.361	0.312	0.445
			2	5	0.127	0.081	0.242	0.073	0.123	0.080	0.097	0.081	0.084	0.163
				10	0.119	0.118	0.147	0.133	0.129	0.130	0.122	0.119	0.108	0.146
				20	0.085	0.084	0.080	0.126	0.111	0.116	0.095	0.103	0.088	0.125

3.1.7 Combining the GEE Score and aSPU tests

It has been shown that, depending on the correlation structure for multiple traits and association parameters between SNPs and traits, one of the GEE Score test and aSPU test was better than the other, but neither could dominate the other across all situations. In light of this result and that in practice it is unknown which test would be more powerful, it might be productive to combine the two tests. A simple strategy is to take the minimum p-value of the two tests, yielding an aSPU.Sco test with test statistic

$$T_{aSPU.Sco}=\min \{\underset{\gamma \in \Gamma }{\min }{P}_{SPU\left(\gamma \right)},P_{Sco}\},$$

where P_Sco is the p-value of the Score test (and P_SPU(γ) is the p-value of the SPU(γ) test). To calculate the p-value of the aSPU.Sco test, we do not need another level of resampling; we simply include the Score test along with the SPU tests in the simulation algorithm discussed earlier for the aSPU test.

Table 13 shows the results for the multiple traits with a CS(0.3) correlation matrix. First, it is clear that the new test could maintain a satisfactory Type I error rate. Second, the performance of the new test was always between the other two tests, often closer to the winner. For example, in the case of a causal SNP weakly associated with 5 traits: i) when testing on the five associated traits, the Score test was less power than the aSPU test with their power as 0.464 and 0.632 respectively, while the power of the new test was 0.612, very close to the aSPU test; ii) on the other ahnd, when testing on 10 traits, the power of the Score test was 0.569, larger than 0.456 of the aSPU test, and the new test achieved the power of 0.537, again close to the winner.

Table 13.

Empirical Type I error rates (for β = 0) and power (for β ≠ 0) for the multiple traits with a CS(0.3) correlation matrix; for β ≠ 0, the first five traits were associated with a causal SNP with log-ORs β_j ~ U(0.8, 1) or ~ U(0.2, 0.3), while all others had β_j = 0. An independence working correlation structure was used in GEE.

	β = 0			βj ~ U(0.2, 0.3)			βj ~ U(0.1, 1)
#traits	Score	aSPU	aSPU.Sco	Score	aSPU	aSPU.Sco	Score	aSPU	aSPU.Sco
5	0.051	0.050	0.051	0.468	0.632	0.612	0.682	0.865	0.832
10	0.060	0.051	0.059	0.573	0.456	0.537	0.684	0.795	0.777
20	0.060	0.047	0.048	0.535	0.305	0.463	0.611	0.757	0.741
30	0.032	0.049	0.042	0.456	0.257	0.394	0.528	0.703	0.693
40	0.054	0.054	0.057	0.409	0.211	0.321	0.424	0.639	0.628

3.2 ADNI data

We applied the methods to the ADNI cohort at baseline, which consisted of 680 non-Hispanic Caucasians with both genotype and phenotype data, including 192 healthy controls, 327 subjects with mild cognitive impairment and 161 patients with Alzheimer's disease. We would like to use a few structural MRI-derived multiple traits as intermediate phenotypes to assess their association with genetic variation. We downloaded from the ADNI website 56 cross-sectional FreeSurfer traits related to volumetric and cortical thickness measures at the baseline as processed by the UCSF team (Hartig et al 2012). For illustration, we only tested 20 SNPs shown by Shen et al (2010) to be marginally significantly associated with one or more of the FreeSurfer traits. Here we considered only 7 multivariate traits consisting of a varying number of univariate traits as shown in Table 14, which were singled out by Shen et al (2010) to be more significantly associated with some of the 20 SNPs. The 7 multivariate traits included each of the six multivariate traits in Table 14 at the right side of the brain plus one of them (MeanPar) at the left side of the brain too. The covariates included were sex, handedness, brain volume, education (in years), and age. There were in total 680 subjects.

Table 14.

Multivariate traits. A letter “L” or “R” is to be added to each trait's ID to indicate the left or right side of the brain.

Trait ID	Trait description
MeanCing	Mean thickness of caudal anterior cingulate, isthmus cingulate, posterior cingulate, and rostral anterior cingulate
MeanFront	Mean thickness of caudal midfrontal, rostral midfrontal, superior frontal, lateral orbitofrontal, and medial orbitofrontal gyri and frontal pole
MeanLatTemp	Mean thickness of inferior temporal, middle temporal and superior temporal gyri
MeanMedTemp	Mean thickness of fusiform, parahippocampal, and lingual gyri, temporal pole and transverse temporal pole
MeanPar	Mean thickness of inferior and superior parietal gyri, supramarginal gyrus, and precuneus
MeanTemp	Mean thickness of inferior temporal, middle temporal, superior temporal, fusiform, parahippocampal and lingual gyri, temporal pole and transverse temporal pole

We first used B = 10000 for any simulation-based method (i.e. GEE-UminP, GEE-SPU and GEE-aSPU tests) to calculate p-values. Then for those SNPs with p-value< 5/B, we gradually increased B to 10⁵, then to 10⁶, and finally up to 10⁷ if needed. Other tests used asymptotics to calculate their p-values.

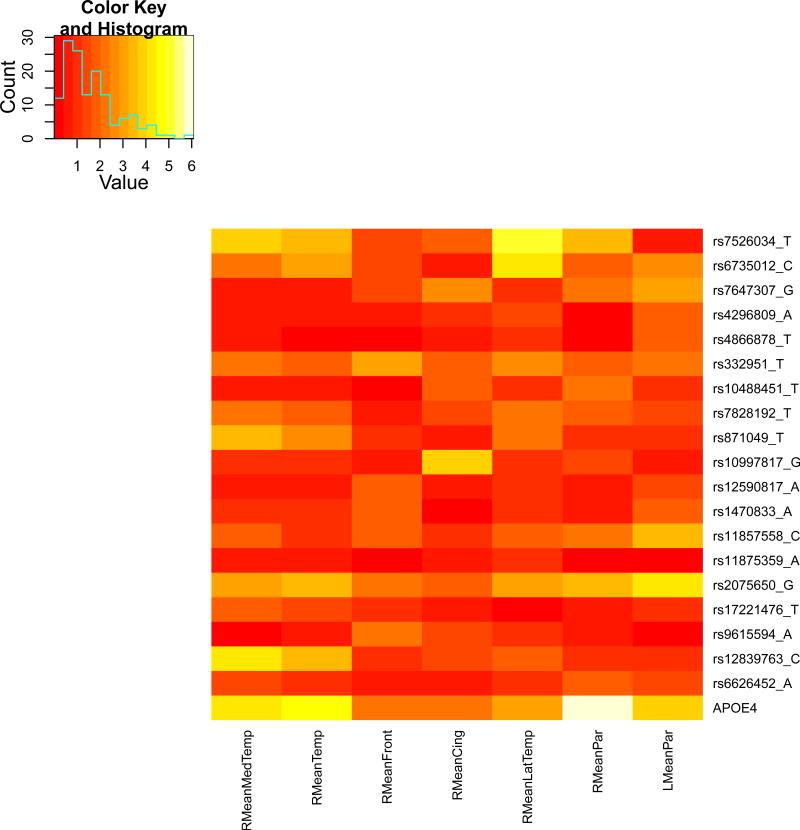
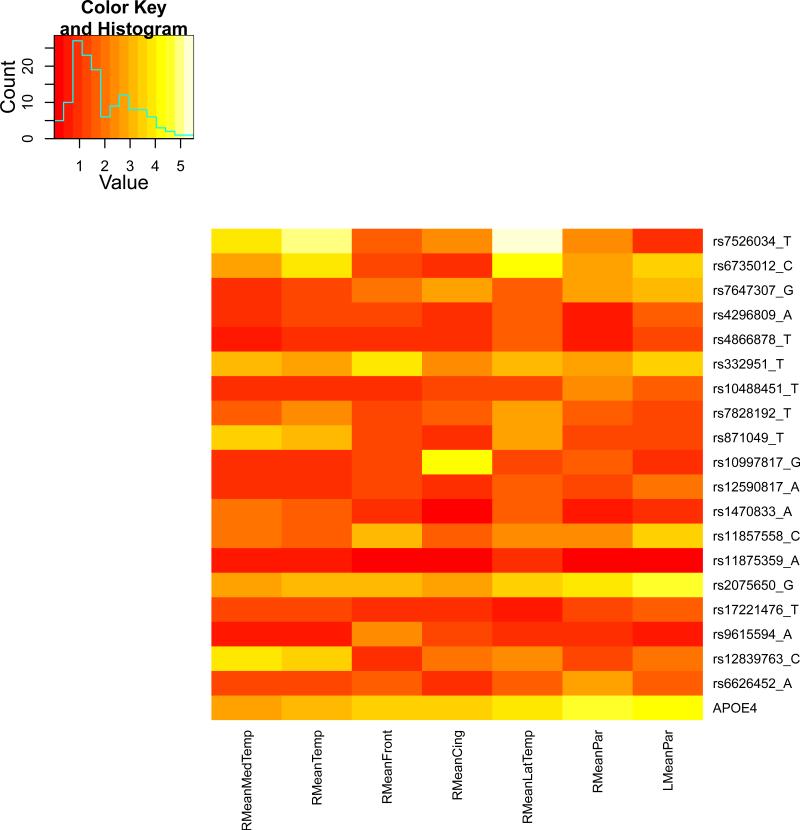
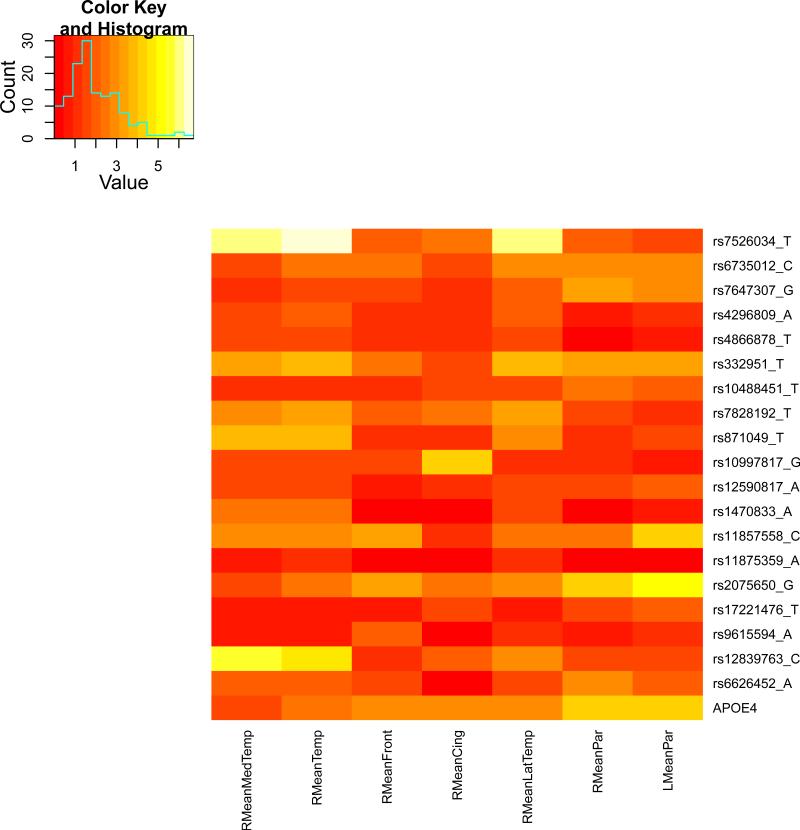
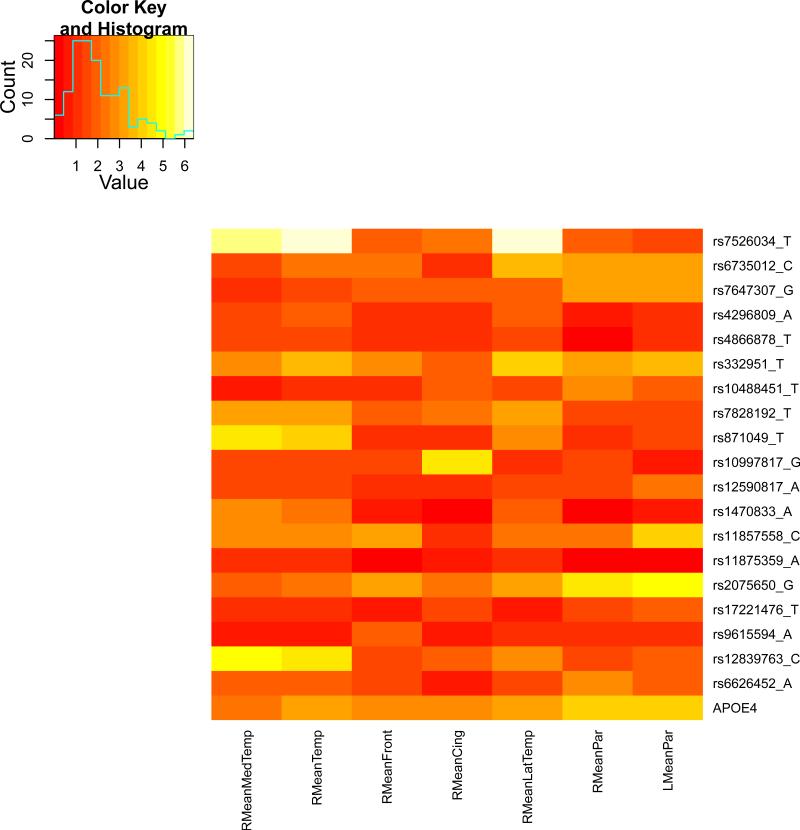
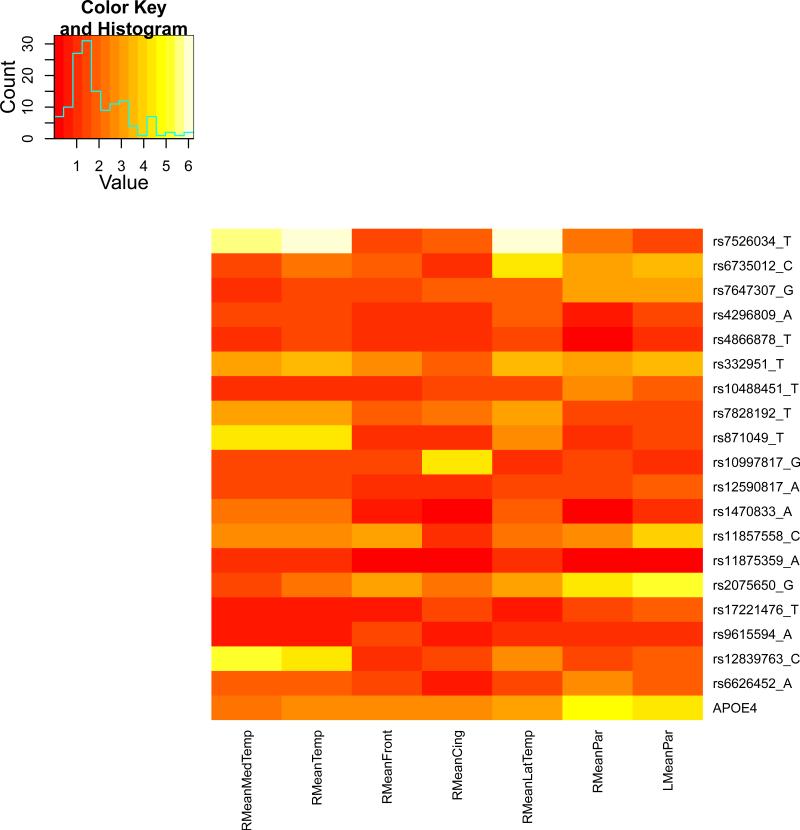
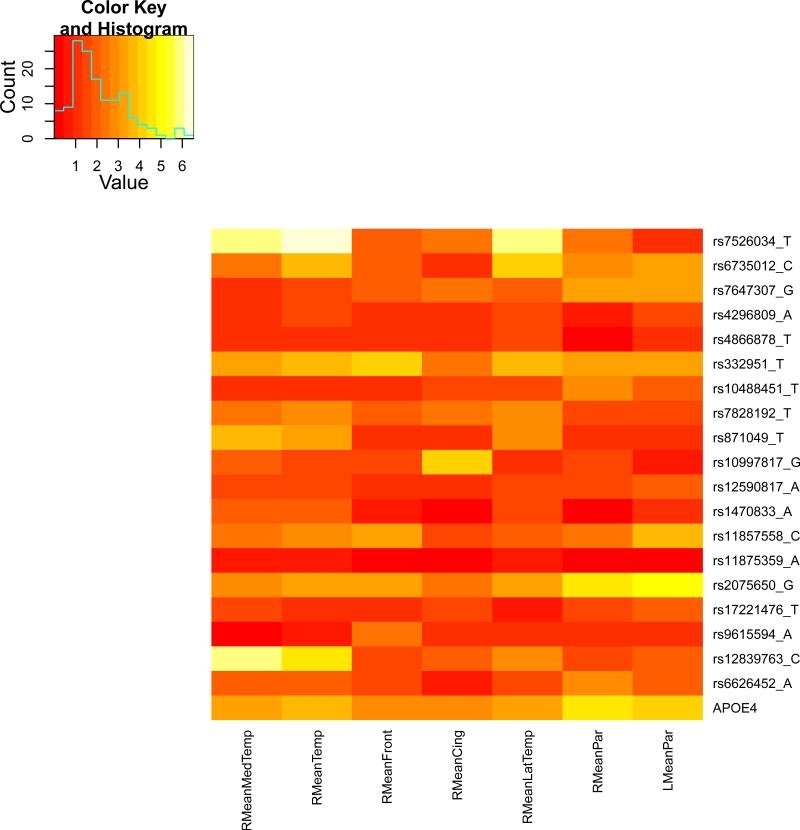
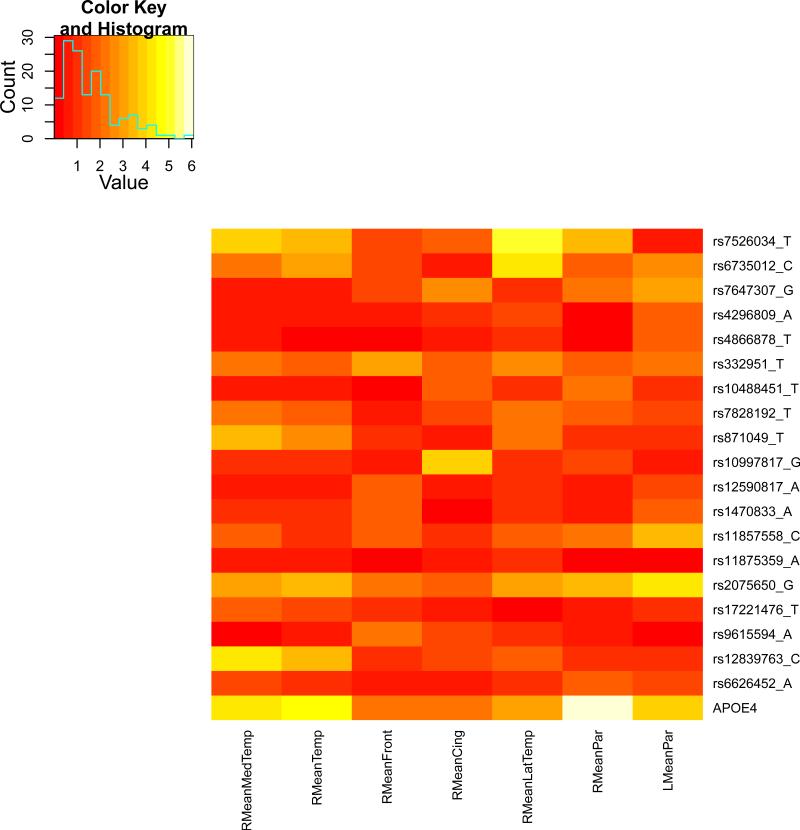
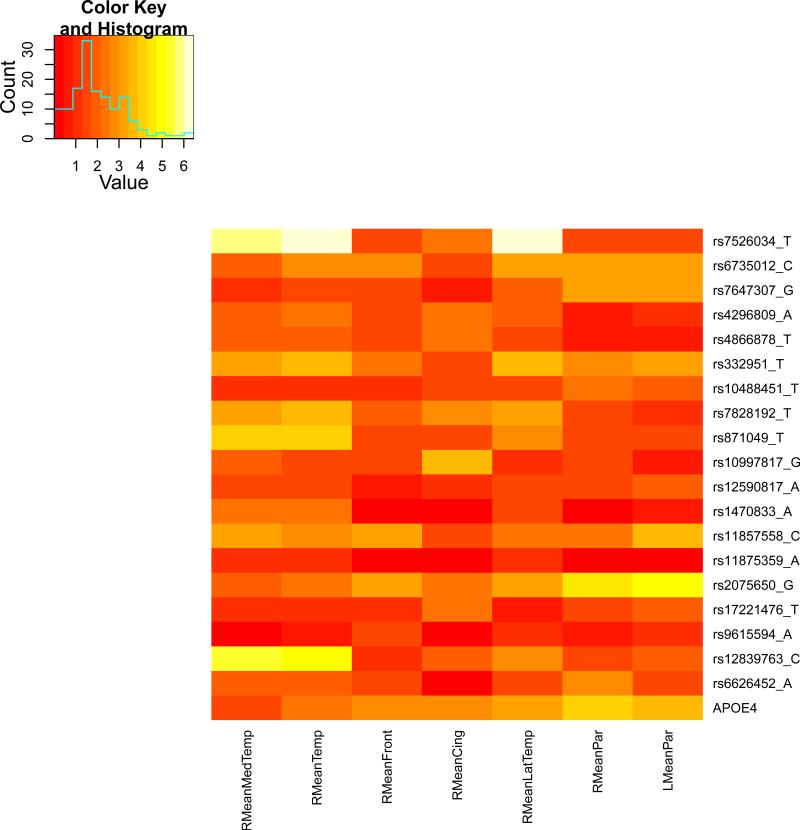
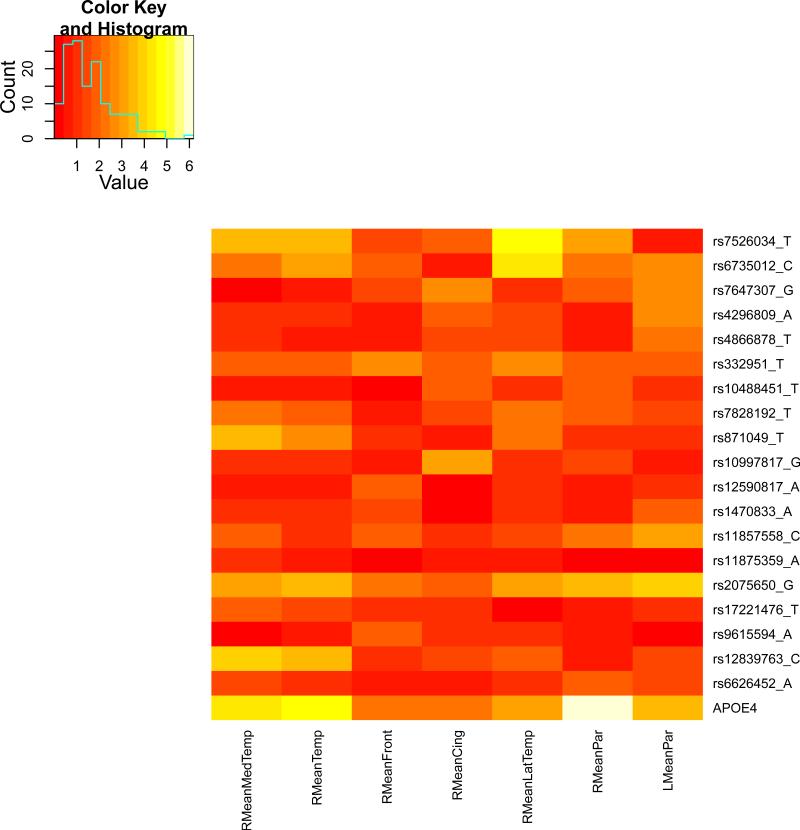
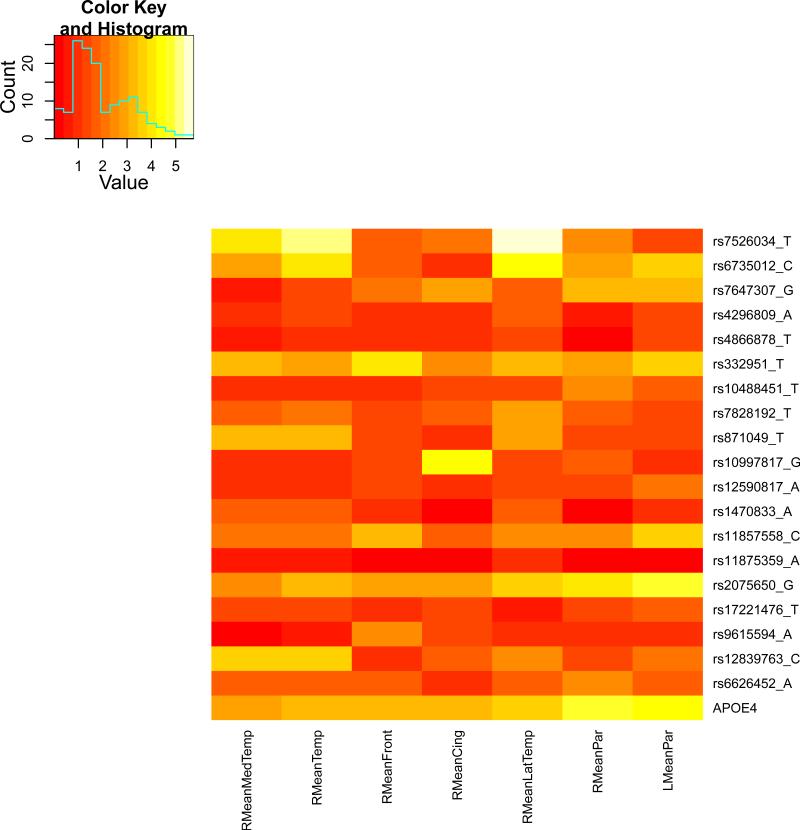
We present the heat maps of − log₁₀ (p-values) of the new methods in Figure 1; as a comparison, the results from four existing methods are shown in Figure 2. In agreement with our theoretical analysis and simulation study, it is confirmed that i) the GEE-Score test, MANOVA and MultiPhen, ii) the GEE-UminP test and TATES, and iii) the GEE-SPU(1) test and the Averge method, yielded similar results. For this dataset, it turns out that the GEE-SPU(2), GEE-aSPU and GEE-aSPUw tests also gave p-values similar to each other, and to those of GEE-SPU(1). However, the three groups i)–iii) of the tests did give quite di erent results. Below, taking the GEE-Score, GEEUminP and GEE-SPU(1) as a representative for each group, we show their identified marginally significant SNPs at p-values < 10⁻⁶ and < 10⁻⁵ respectively. i) The GEE-Score test identified an association between rs429358 (in gene ApoE) and RMeanPar (MeanPar at the right side of the brain) with a p-value of 8.45 × 10⁻⁷; it also gave a p-value of 8.13 × 10⁻⁶ for rs7526034 and RMeanLatTemp. ii) the GEE-UminP test detected rs7526034 marginally associated with RMeanLatTemp and RMeanTemp with p-values of 3.10 × 10⁻⁶ and 7.90 × 10⁻⁶ respectively; note neither is significant at the level of p-value< 10⁻⁶. iii) the GEE-SPU(1) test identified rs7526034 to be associated with three traits, RMeanTemp, RMeanLatTemp and RMeanMedTemp, with p-values of 2.00×10⁻⁷, 6.00×10⁻⁷ and 9.00×10⁻⁷ respectively, in addition to a marginal association between rs12839763 and RMeanMedTemp with a p-value of 2.00 × 10⁻⁶. As a comparison, the GEE-aSPU test gave results similar to the GEE-SPU(1) test: for the above 4 associations indicated by the SPU(1) test, the aSPU test gave p-values of 6.00 × 10⁻⁷, 9.00 × 10⁻⁷, 1.80 × 10⁻⁶, and 4.20 × 10⁻⁶ respectively; in addition, it also gave a p-value of 9.00 × 10⁻⁶ to rs2075650 and LMeanPar. In summary, it appears that the three groups of the tests could identify di erent sets of (marginally) significant associations, though TATES and GEE-UminP did not identify any association with p-value < 10⁻⁶, illustrating a possible loss of power in taking out only most significant univariate associations.

Figure 1.

The heatmaps of − log₁₀ (p-values) of the GEE-based tests for seven multivariate traits.

Figure 2.

The heatmaps of − log₁₀ (p-values) of the four existing tests for seven multivariate traits

As in the simulation study, the p-values obtained from the Average method and SPU(1) were very close. However, because the former was based on the asymptotic Wald test while the latter was a Score test based on simulations, their p-values might be slightly di erent. For example, for association between rs2075650 and LMeanPar, the Average method gave a p-value of 9.94×10⁻⁶, which was essentially the same as 1.10×10⁻⁵ by the GEE-SPU(1) test.

The similar results between the Average method (or SPU(1)) and SPU(2) or aSPU test were presumably due to the relatively small numbers of univariate traits consisting of the seven multi-variate traits. To investigate the robustness of the tests to a larger number of traits, we pooled all seven multivariate traits together to form a combined trait; after removing duplicated ones, a total of 26 univariate traits remained. Since all the methods indicated marginal associations between the rs7526034 and/or rs429358 and several traits, we focused on the two SNPs. As shown in Table 15, in agreement with earlier analyses of the seven individual multivariate traits, i) for SNP rs429358, the GEE-Score test and MultiPhen gave the most significant p-values; ii) for SNP rs7526034, the GEE-SPU(2) and aSPU tests yielded most significant results, followed by those given by TATES and GEE-UminP. However, the Average method and GEE-SPU(1) gave much less significant results, suggesting their non-robustness to a large number of non-associated traits as confirmed in the simulation study. In summary, it seems that the GEE-Score test (or equivalently MultiPhen) and the GEE-aSPU test could give complementary and useful results.

Table 15.

P-values of testing on a pooled set of 26 univariate traits.

				GEE
SNPs	Average	MultiPhen	TATES	UminP	Score	SPU(1)	SPU(2)	aSPU
rs7526034	1.40e-04	5.82e-04	1.72e-05	2.10e-05	5.86e-04	7.30e-05	7.00e-06	7.00e-06
rs429358	1.42e-04	1.68e-05	1.23e-04	1.50e-04	2.32e-05	1.10e-04	7.00e-05	1.60e-04

To demonstrate the feasibility of the new tests for GWAS, we conducted a genome-wide scan with a set of 31 FreeSurfer traits. Since the results did not o er additional new insights, to save space, we report the results in Supplementary Materials.

4 Discussion

In this paper we have developed a class of the so-called SPU tests for association analysis of multiple (correlated) traits and a single SNP. We have also proposed an adaptive test called the aSPU test to estimate and thus select the most powerful SPU test for a given dataset. For multivariate trait-single SNP analysis, based on a marginal regression model in GEE that allows the SNP to have different effect sizes and e ect directions on different traits, the aSPU test can adapt to the existence and the number of the null (non-associated) traits e ectively. With a larger power parameter γ, the SPU(γ) test reduces the influence of null traits and reinforces the associated ones. Thus this test can maintain high power in the presence of a large number of null traits. This property is especially useful for studies where many correlated phenotypes are collected but there are no established guidelines to selecting relevant phenotypes. On the other hand, in the presence of many associated traits, the SPU(γ) test with a smaller γ will be more powerful. In particular, SPU(1) is quite similar to the Average (or Sum) method as used in Shen et al (2012), while SPU(2) is an extension of the SSU test for single trait-multilocus association analysis to multivariate trait-single locus analysis. As noted, under suitable conditions the SPU(2) test is the same as MDMR or KMR. We have also pointed out how some existing methods, like CCA/MANOVA, TATES and MultiPhen are related to the various GEE-based tests. We emphasize that, many of the existing methods, such as CCA/MANOVA and MultiPhen, may not be applicable to discrete traits or multiple loci, while our proposed GEE-Score and GEE-aSPU tests can with their general modeling and inference framework of GEE. Our proposed tests are potentially useful for a large number of traits, as arising as intermediate phenotypes in neuroimaging studies, which has not been adequately considered in the genetics literature. We also note that our proposed GEE-aSPU test can be equally applied to multiple principal components after PCA or PCH dimension reduction on a large number of traits, though further studies are needed.

From simulation studies we observed that the relative performance of the GEE-based Score and aSPU tests varied with the degree of the correlations among the traits and with the e ect sizes of the causal SNPs. When the traits were somewhat more weakly correlated (e.g. with an AR-1 correlation structure), regardless of the e ects size of the causal SNP, the aSPU test was much more powerful than the Score test and UminP test. However, under some situations, e.g. when the traits had a compound symmetry correlation structure, the aSPU test might not be as powerful as the Score test when the e ect sizes were small; the opposite conclusion held with larger e ect sizes. We note that, the aSPU test largely combines the strengths of the SPU(1) (equivalently the Average method), SPU(2) (closely related to MDMR and KMR), and SPU(∞) (similar to UminP and TATES), but differing from the Score test and MultiPhen while the latter two (and CCA/MANOVA) perform similarly. Since currently we do not have a simple guideline on how to choose between the aSPU and Score tests in practice, we recommend the use of both; we have also explored combining the two tests with some promising preliminary results (see Table 13), though more studies are needed.

We have focused on multitrait association testing on a single SNP. A natural extenstion is to multitrait-multiple SNP testing. For univariate trait analysis, it has been established that testing on multiple SNPs simultaneously may gain power (Pan 2009), especially for RVs as evidenced by the increasing use of the burden tests and variance component tests (Basu and Pan 2011). Pan et al (2014) have proposed and studied an analogous aSPU test for RVs, which data-adaptively over-weights (unknown and estimated) associated RVs (while down-weighting non-associated RVs). In contrast, here our proposed aSPU test adaptively over-weights (unknown and estimated) associated traits (while down-weighting non-associated traits). It would be interesting to see whether combining the two ideas would work for multitrait-multiple SNP association testing, especially in the presence of large numbers of traits and of SNPs. An advantage of the aSPU test is its weighting on, rather than directly selecting, traits (or SNPs), in order to alleviate the e ects of non-associated traits (or SNPs) on diminishing the power of a test, expected to be present with many traits (or SNPs); given small e ect sizes of common variants (or small MAFs of RVs), weighting tends to outperform selection.

It seems to be a common belief that accounting for correlations among multiple traits would automatically increase power, which however may not be true, or at least not as simple as it may sound. Here are our arguments. First, using a non-independent working correlation matrix R_w ≠ I in GEE can be regarded as an attempt to account for correlations among multiple traits; however, as shown in Tables 1 and 12, in these situations a test may or may not have improved power. In particular, the GEE Score test is invariant to the use of the working correlation matrix (with an equal cluster size). Second, as directly shown numerically here (e.g. Table 9), the GEE-SPU(2) test could be more powerful than the GEE Score test, though the SPU(2) test statistic ignores the correlations among the components of the score vector (due to the correlations among the traits) while the Score test statistic does not. The same phenomenon is also observed in single trait-multiple SNP analysis (Pan 2009), in which the SSU test (or equivalently KMR) is known to be often, but not always, more powerful than the Score test. Pan (2009) offers an explanation based on a test's rejection region, which however is hard to visualize for high-dimensional testing while the power also depends on some unknown association parameters. Certainly this is a topic worth further investigation.

Finally, we have not compared our methods with those based on constructing latent composite traits such as PCA and PCH; a particularly interesting topic is to investigate how our proposed tests compare with the modified PCH method of Lin et al (2012) for high-dimensional neuroimaging traits.

Table 4.

Empirical power when the multiple traits were correlated with a CS structure with correlation coefficient r; the first five traits were associated with a causal SNP with log-ORs β_j ~ U(0.8, 1), while all others had βj = 0. An independence working correlation structure was used in GEE.

									GEE
						MDMR					SPU(γ)
r	SNP	#trait	Average	MultiPhen	TATES	L 1	L 2	MANOVA	Score	UminP	γ = 1	2	3	4	5	6	∞	aSPU
0.3	2	5	0.888	0.683	0.823	0.878	0.883	0.683	0.682	0.815	0.889	0.880	0.868	0.862	0.851	0.843	0.812	0.865
		10	0.567	0.685	0.727	0.786	0.826	0.686	0.684	0.708	0.567	0.830	0.777	0.819	0.796	0.807	0.772	0.795
		20	0.218	0.613	0.665	0.616	0.729	0.615	0.611	0.657	0.223	0.724	0.667	0.787	0.756	0.792	0.762	0.757
		30	0.116	0.528	0.607	0.435	0.574	0.531	0.528	0.591	0.117	0.577	0.541	0.725	0.695	0.742	0.738	0.703
		40	0.084	0.424	0.536	0.262	0.442	0.435	0.424	0.534	0.084	0.432	0.445	0.644	0.609	0.680	0.678	0.639
0.3	3	5	0.334	0.178	0.292	0.328	0.330	0.178	0.177	0.281	0.331	0.327	0.321	0.315	0.312	0.305	0.289	0.320
		10	0.184	0.167	0.203	0.240	0.269	0.167	0.167	0.197	0.182	0.273	0.260	0.282	0.267	0.273	0.244	0.249
		20	0.092	0.138	0.179	0.149	0.189	0.141	0.137	0.173	0.090	0.188	0.191	0.242	0.246	0.257	0.242	0.229
		30	0.074	0.121	0.143	0.107	0.120	0.127	0.119	0.146	0.079	0.128	0.141	0.185	0.184	0.203	0.204	0.181
		40	0.058	0.105	0.132	0.088	0.113	0.109	0.104	0.134	0.062	0.112	0.118	0.161	0.168	0.179	0.188	0.168
0.5	2	5	0.829	0.602	0.784	0.821	0.822	0.604	0.601	0.763	0.832	0.821	0.811	0.806	0.800	0.793	0.769	0.806
		10	0.424	0.725	0.694	0.629	0.729	0.728	0.725	0.685	0.430	0.734	0.714	0.766	0.750	0.765	0.737	0.723
		20	0.163	0.665	0.624	0.344	0.524	0.666	0.662	0.634	0.161	0.534	0.567	0.697	0.695	0.725	0.722	0.694
		30	0.093	0.570	0.549	0.186	0.318	0.577	0.570	0.570	0.093	0.319	0.440	0.593	0.609	0.666	0.707	0.653
		40	0.067	0.484	0.487	0.119	0.203	0.496	0.483	0.508	0.072	0.202	0.333	0.518	0.544	0.612	0.654	0.613
0.5	3	5	0.291	0.149	0.270	0.288	0.290	0.150	0.148	0.259	0.290	0.294	0.293	0.285	0.284	0.279	0.263	0.287
		10	0.129	0.181	0.209	0.171	0.207	0.182	0.180	0.201	0.126	0.203	0.223	0.245	0.249	0.255	0.245	0.223
		20	0.077	0.138	0.160	0.098	0.130	0.139	0.136	0.168	0.075	0.131	0.158	0.196	0.212	0.220	0.228	0.205
		30	0.067	0.117	0.129	0.077	0.092	0.121	0.117	0.139	0.065	0.091	0.118	0.144	0.156	0.166	0.195	0.181
		40	0.055	0.110	0.113	0.071	0.078	0.116	0.109	0.129	0.054	0.079	0.105	0.134	0.148	0.163	0.190	0.166

A Appendix: Relationships Between the New and Existing Tests

A.1 The Average (or Sum) test and the GEE-SPU(1) test

A simple dimension reduction method is to take the average (or sum) of the multiple traits and use it as a single trait to assess its association with a single SNP; we call the corresponding method as the Average or Sum method (Shen et al 2011; van der Sluis et al 2013). It is easy to see that the score vectors of the two methods in linear regression (or any GLM with a canonical link) are equivalent to each other (up to a constant) as

$$U_A=\sum _i{x}_i\sum _j{Y}_{ij},$$

which is equal to the SPU(1) test statistic under R_w = I in GEE. Hence, the Score test version of the Average or Sum test and GEE-SPU(1) tests (under R_w = I) are exactly the same. We implemented the Average test as a Wald test and used its asymptotic distribution to calculate its p-values while we used simulations to calculated the p-values for GEE-SPU(1), which led to some minor di erences in their results.

A.2 TATES, GEE-UminP, GEE-SPUw(∞) and GEE-SPU(∞) tests

It is easy to verify that the GEE-UminP and GEE-SPUw(∞) tests are exactly the same. It is noted that, under the working independence model, the GEE score vector and its covariance estimate are exactly the same as that for univariate analyses on each of the multiple traits separately. Hence, the GEE-UminP and GEE-SPUw(∞) tests are also closely related to univariate analysis-based TATES (van der Sluis et al 2013), but di er in two aspects: first, TATES uses Simes procedure for multiple testing adjustment, while the former two use an “exact” method for such a purpose; second, TATES uses a correlation matrix input by the user to estimate the null distribution of the test statistic, hence is computationally simpler but may be less accurate.

A.3 CCA, MANOVA and the GEE-Score test

To test for association between multiple traits and a single SNP (without any other covariates), CCA and MANOVA are equivalent (Ferreira and Purcell 2009; Yang and Wang 2012). They are based on the largest eigen-value ρ² of

$$B=S_{XX}^{-1∕2}{S}_{XY}{S}_{YY}^{-1}{S}_{YX}{S}_{XX}^{-1∕2},$$

where $S_{XX}=\widehat{\mathrm{Cov}}\left(x_i\right)$, $S_{XY}=\widehat{\mathrm{Cov}}(x_i,Y_i)$ and $S_{YY}=\widehat{\mathrm{Cov}}\left(Y_i\right)$ are sample variance-covariance matrices. In the current context with a single SNP x_i, since B is a scalar, we have ρ² = B.

With a working independence model R_w = I, the GEE-Score test statistic is

$$\begin{array}{cc}\hfill T_{Sco}=& {\left(\sum _i{x}_i(Y_i-\stackrel{‒}{Y})\right)}^{\prime }{\left(\sum _i{x}_i{S}_{YY}{x}_i\right)}^{-1}\left(\sum _i{x}_i(Y_i-\stackrel{‒}{Y})\right)\hfill \\ \hfill =& n{S}_{XY}{\left(S_{XX}{S}_{YY}\right)}^{-1}{S}_{YX}=nB,\hfill \end{array}$$

in which the second equality holds because S_XX is a scalar. Furthermore, as shown earlier, the GEE-Score test is invariant to R_w in the current context. Hence CCA and MANOVA are equivalent to the GEE-Score test, regardless of the working correlation matrix R_w being used in GEE.

A.4 MDMR, MANOVA and the GEE-SPU(2) test

MDMR is a nonparametric method as a generalization of Fisher's MANOVA (McArdle and Anderson 2001); it has been applied to detect association between a single trait and multiple SNPs, named as genomic distance-based regression (GDBR) (Wessel and Schork 2006). Schork and colleagues have outlined its application to analysis of longitudinal or multivariate traits (Zapala and Schork 2012). We briefly summarize its main steps as the following:

• Step 1. Calculate an n × n distance matrix for all pairs of subjec ts by D = (D_ij) with D_ij = d(Y_i, Y_j) and d(, ) being a distance or semi-distance metric.

• Step 2. Calculate A = (−D_ij²/2).

• Step 3. Obtain a centered similarity matrix G = (I − 11′/n)A(I − 11′/n), where 1 is an n × 1 vector of all 1's;

• Step 4. Denote X as the n × 1 vector of centered genotype scores with elements x_i (and ${\sum }_{i=1}^n{x}_i=0$).

• Step 5. Calculate the projection matrix H = X(X′X)⁻¹X′;

• Step 6. Calculate a pseudo F-statistic as

  $$F=\frac{tr\left(HGH\right)}{tr\left[(I-H)G(I-H)\right]},$$ (8)

  where tr(A) is the trace of matrix A.

To obtain a p-value, we recourse to permutations by shu ing X (or, equivalently, shuffling both the rows and columns of A simultaneously).

As discussed by McArdle and Anderson (2001), if G is an outer product matrix, say G = ZZ′ with an n × k matrix Z, the above F-test is simply testing H₀′ : B = 0 in a multivariate linear model

$$Z=1\mu +XB+∊,$$ (9)

where 1 is an n × 1 vector of all 1's, μ is a 1 × p vector of unknown intercepts, B is a 1 × p vector of unknown regression coe cients, and ∈ is an n × p matrix of random errors. Following the same argument in Pan (2011), it can be shown that

$$F\propto tr\left(Z^{\prime }X{X}^{\prime }Z\right)=tr\left({(Z-\stackrel{‒}{Z})}^{\prime }X{X}^{\prime }(Z-\stackrel{‒}{Z})\right),$$ (10)

which is the same as the GEE-SPU(2) test statistic for the multivariate linear model (9) under the working independence model. In particular, if the Euclidean distance (i.e. L₂-norm) is used as the distance metric d(, ), we have Z = Y ; thus, MDMR(L₂), the MDMR implementation with the Euclidean distance, is the same as the GEE-SPU(2) test. Importantly, as to be shown, GEE-SPU(2) loses power in the presence of many null traits, so does MDMR.

Furthermore, MANOVA is based on the same model (9) with Z = Y ; however, the (approximate) F statistics in MANOVA are di erent from (8). For example, the Wilks statistic is based on

$$\Lambda =\frac{\mid (I-H)G(I-H)\mid }{\mid (I-H)G(I-H)+HGH\mid },$$

with |B| as the determinant of B. For this reason, MANOVA and MDMR(L₂) will not be the same.

A.5 KMR and the GEE-SPU(2) test

KMR has been extended to multivariate quantitative traits (Maity et al 2012; Schifano et al 2012; Wang et al 2013). In the current setting, its test statistic is

$$T_{KMR}={(Y-\stackrel{‒}{Y})}^{\prime }{V}_0^{-1}K{V}_0^{-1}(Y-\stackrel{‒}{Y}),$$

where V₀ = Var(Y|H₀) and K is a kernel function. With a single SNP, it su ces to use a linear kernel with K = XX′, thus T_KMR is the same as the GEE-SPU(2) test statistic if the working correlation R_w is the true correlation structure of Y_i (i.e. R_w = Corr(Y_i|H₀)).

Since the extended KMR method is based on a mixed-effects model, it is not surprising to see that it requires specifying the correct correlation structure; in contrast, our proposed GEESPU(2) and other SPU tests only need a working, not necessarily correct, correlation structure R_w, maintaining the main advantage of the GEE methodology (while possessing its disadvantage of possible e ciency loss). Furthermore, it is not clear how to extend KMR to multiple discrete (e.g. binary) traits, while our GEE-SPU tests can be easily extended to other types of traits (as long as they can be modeled by GLMs). More importantly, as to be shown, GEE-SPU(2) loses power in the presence of many null traits, suggesting the same drawback of KMR.

A.6 MultiPhen and the GEE-Score test

MultiPhen (O'Reilly et al., 2012) is based on fitting a proportional odds model (POM). For simplicity, here we assume that x_i's are not centered or transformed; otherwise, we just need to modify some notation accordingly. Define π_j(y) = Pr(x_i = j|Y_i = y), and ${\kappa }_j\left(y\right)={\sum }_{m=0}^j{\pi }_m\left(y\right)$ for j = 0, 1 and 2. The POM is

$$\log \frac{{\kappa }_j\left(y\right)}{1-{\kappa }_j\left(y\right)}={\alpha }_j-y^{\prime }\beta ,$$ (11)

for j = 0 and 1. To test H₀: β = (β₁, ..., β_k)′ = 0, MultiPhen applies a likelihood ratio test. We can equally apply an asymptotically equivalent Score test. Following McCullagh (1980), after some algebra, we derive the negative score vector for the POM as

$$U_{POM}=\frac{-n_1-n_2}{n}\sum _{i:x_i=0}{Y}_i+\frac{n_0-n_2}{n}\sum _{i:x_i-1}{Y}_i+\frac{n_0+n_1}{n}\sum _{i:x_i=2}{Y}_i,$$ (12)

where $n_j={\sum }_{i=1}^{n}I(x_i=j)$ for j = 0, 1 and 2. In contrast, the Score vector for the GEE working independence model (4) can be written as

$$U_{GEE}=\frac{-n_1-2n_2}{n}\sum _{i:x_i=0}{Y}_i+\frac{n_0-n_2}{n}\sum _{i:x_i=1}{Y}_i+\frac{2n_0+n_1}{n}\sum _{i:x_i=2}{Y}_i.$$ (13)

Comparing the two score vectors U_POM and U_GEE, we see that they only differ in their weights on Y_i's for x_i = 0 and x_i = 2. Hence, we would expect that MultiPhen and GEE-Score test give similar results unless the MAF of x_i is extreme. The similarity of empirical performance between MultiPhen and MANOVA was observed by other authors (e.g. van der Sluis et al 2013), which is shown theoretically here, based on our earlier result on the equivalence between MANOVA and the GEE-Score test.

A.7 Generalized Kendall's tau and the GEE-Score test

Zhang et al (2010) proposed a nonparametric method to test association between multiple traits and a single SNP. The test statistic is a U-statistic as a generalized Kendall's tau (denoted as GKτ). Specifically, define u_ij = (f(Y_i1 − Y_j1), ..., f(Y_iq − Y_jq))′, where f() is an identity function for quantitative traits or binary traits, or a sign function for ordinal traits; in the former case, we have u_ij = Y_i − Y_j. Define ${\stackrel{‒}{u}}_i={\sum }_{j=1}^n{u}_{ij}∕n$. Then the GKτ statistic, after ignoring a constant factor, 2/(n − 1), is $\tau ={\sum }_{i=1}^n{x}_i{\stackrel{‒}{u}}_i$, which is asymptotically distributed as N(0, V₀) under H₀. The corresponding GKτ test is a score or Wald-type test: $T={\tau }^{\prime }{V}_0^{-1}\tau \sim {\chi }_k^2$ under H₀. With quantitative or binary traits, it is easy to verify ${\stackrel{‒}{u}}_i=Y_i-\stackrel{‒}{Y}=Y_i-{\sum }_{j=1}^n{Y}_j∕n$; under this condition we have exactly τ = U if a canonical link function and a working independence model are used in GEE, suggesting the equivalence between the GKτ test and the GEE Score test with R_w = I, which was confirmed by our numerical results (not shown). It is interesting to note that the nonparametric GKτ test coincides with our semi-parametric GEE approach.

This equivalence suggests a natural extension of the GKτ test to multiple SNPs (or markers): a new GKτ test statistic can be defined as the same as the score vector U for multiple SNPs in GEE with a canonical link function and a working independence model. This extension overcomes a conceptual di culty in generalizing Kendall's tau to two random vectors with unequal lengths. Furthermore, rather than using a score- or Wald-type test (which may be low-powered with a high dimensionality of kq), we can explore the power of the aSPU test as discussed before. Finally, our proposed approach di ers from the GKτ test in the case with covariates. The modified GKτ test with covariates (Zhu et al 2012) uses a weighting scheme to adjust for covariate effects, in contrast to our regression approach.