Mouse Visual Neocortex Supports Multiple Stereotyped Patterns of Microcircuit Activity

Abstract

Spiking correlations between neocortical neurons provide insight into the underlying synaptic connectivity that defines cortical microcircuitry. Here, using two-photon calcium fluorescence imaging, we observed the simultaneous dynamics of hundreds of neurons in slices of mouse primary visual cortex (V1). Consistent with a balance of excitation and inhibition, V1 dynamics were characterized by a linear scaling between firing rate and circuit size. Using lagged firing correlations between neurons, we generated functional wiring diagrams to evaluate the topological features of V1 microcircuitry. We found that circuit connectivity exhibited both cyclic graph motifs, indicating recurrent wiring, and acyclic graph motifs, indicating feedforward wiring. After overlaying the functional wiring diagrams onto the imaged field of view, we found properties consistent with Rentian scaling: wiring diagrams were topologically efficient because they minimized wiring with a modular architecture. Within single imaged fields of view, V1 contained multiple discrete circuits that were overlapping and highly interdigitated but were still distinct from one another. The majority of neurons that were shared between circuits displayed peri-event spiking activity whose timing was specific to the active circuit, whereas spike times for a smaller percentage of neurons were invariant to circuit identity. These data provide evidence that V1 microcircuitry exhibits balanced dynamics, is efficiently arranged in anatomical space, and is capable of supporting a diversity of multineuron spike firing patterns from overlapping sets of neurons.

Introduction

There is an ongoing discussion as to the nature and extent of microcircuit structure in mouse visual cortex. Murine primary visual (V1) microcircuitry exhibits retinotopic mapping (Dräger, 1975; Bonin et al., 2011), but the orientation tuning of neurons is not organized into anatomical columns (Bonin et al., 2011; Li et al., 2012; Ohtsuki et al., 2012). Orientation tuning has been used as evidence for columnar processing in primates, but the implication of a “salt and pepper,” or random, organization (Ohki et al., 2005, Van Hooser et al., 2005) on the structure and function of V1 in mouse is far less clear. Random assignment of orientation tuning implies a lack of architectural structure in cortex (Bonin et al., 2011) compared with the clear columnar organization in other areas of sensory neocortex, such as somatosensory barrel field and primary auditory cortex (Woolsey and Van der Loos, 1970; Bandyopadhyay et al., 2010). Further a “salt and pepper” organization may either suggest a lack of efficient circuit wiring or it may act to minimize the wiring costs necessary for connectivity between neurons while maintaining a full representation of the sensory space (Kaschube, 2014). Primary visual cortex has also been hypothesized to contain microcircuitry that is predominantly feedforward (Reid and Alonso, 1995). This property has been used in many V1 layer-specific network models to capture aspects of the cortical representation of visual information in cat and macaque (Miller et al., 1989). How these different organizational features manifest functionally at the mesoscopic scale, spanning lamina and comprising hundreds of neurons, remains unclear.

Spatiotemporally patterned spiking circuit activity has been shown to encode sensory input (Luczak et al., 2007), motor output (Churchland et al., 2007), and behavioral choice (Harvey et al., 2012). These patterns of activity are generated by specific circuits of interconnected neurons that interact with each other (Luczak and MacLean, 2012; Sadovsky and MacLean, 2013). How the structure of V1 microcircuitry determines the nature of temporally patterned activity in V1 remains unclear. Here we used two-photon microscopy in combination with calcium indicator dyes to study spontaneous multineuronal dynamics (Vogelstein et al., 2010; Sadovsky et al., 2011) with a dense unbiased sampling of large numbers of neurons (Sadovsky and MacLean, 2013) in mouse V1. To best sample functional microcircuitry (Milo et al., 2002), we maximized the number of neurons imaged while using a heuristically optimal scan path, which allowed us to achieve scan rates an order of magnitude greater than the traditional raster scan method (Sadovsky et al., 2011; Sadovsky and MacLean, 2013). By imaging the correlated spiking activity or activity flow at the mesoscale level, we generated functional wiring diagrams from mouse V1 describing reliable interrelationships in spike times. In addition, we evaluated the extent to which spiking activity of individual cells in V1 microcircuits is temporally stereotyped.

Materials and Methods

Preparation of V1 calcium indicator-loaded slices.

Fura-2 AM calcium indicator-loaded coronal and 15 degree angle off coronal axis primary visual cortex slices of C57BL/6 strain mice of both sexes were obtained in the same manner as previously described (Sadovsky and MacLean, 2013) on postnatal day ages 14–17. Animals were anesthetized by intraperitoneal injection of ketamine-xylazine, rapidly decapitated, and had their brains removed and placed in oxygenated ice-cold “cut” artificial CSF (contents in mm as follows: 3 KCl, 26 NaHCO₃, 1 NaH₂PO₄, 0.5 CaCl₂, 3.5 MgSO₄, 25 dextrose, 123 sucrose); 500-μm-thick coronal slices containing the sensory region of interest were cut using a vibratome (VT1000S; Leica). Slices were then placed in a 35°C oxygenated incubation fluid (Incu-ACSF; contents in mm as follows: 123 NaCl, 3 KCl, 26 NaHCO₃, 1 NaH₂PO₄, 2 CaCl₂, 6 MgSO₄, and 25 dextrose) for 30–45 min. Calcium dye loading was then achieved by placing all slices into a small Petri dish containing ∼2 ml of Incu-ACSF, an aliquot of 50 μg fura-2 AM (Invitrogen) in 13 μl DMSO, and 2 μl of Pluronic F-127 (Invitrogen) as previously described (Sadovsky et al., 2011). Experimental procedures were approved and performed in accordance with the Institutional Animal Care and Use Committee at the University of Chicago.

Data acquisition.

Experiments were performed in standard ACSF (contents in mm as follows: 123 NaCl, 3 KCl, 26 NaHCO₃, 1 NaH₂PO₄, 2 CaCl₂, 2 MgSO₄, and 25 dextrose, which was continuously aerated with 95% O₂, 5% CO₂). Whole-cell current-clamp recordings were made using Multiclamp 700B amplifiers (Molecular Devices). Rapid whole-field imaging of fura-2 AM-loaded neurons was achieved by taking multiple 5 min movies using the Heuristically Optimal Path Scanning technique and microscopy setup as previously detailed (Sadovsky et al., 2011), allowing us to monitor action potential generation within individual neurons. Our dwell time parameter for each experiment was fixed at a value of 16 samples/cell/frame for each experiment.

Spike and circuit event detection.

Spikes were inferred from the calcium traces of individual neurons using a modified version of fast non-negative spike deconvolution (Vogelstein et al., 2010). We examined the software's capability to correctly infer spikes in cells for which we also had simultaneous patch-clamp recording data and biased our inference toward minimizing false positives (MacLean and Yuste, 2009; calibration presented in Sadovsky et al., 2011). Spikes from each cell's calcium trace were then identified. Circuit events were defined as epochs where the network of cells was active for at least 500 ms. At least four circuit events were necessary for a field of view to be included in our dataset.

Statistical analysis.

All analyses were performed with MATLAB (MathWorks), with the exception of flow hierarchy, and figures of graphical networks, which were performed in Python using the NetworkX Python package. Data are presented as mean ± SD. Comparison p values were obtained using the Wilcoxon rank sum test, implemented via the MATLAB ‘ranksum’ function unless otherwise noted. For this and other tests, α = 0.05 was used as the cutoff for significance.

Functional graph creation.

Structure in the cross-correlation of neuronal spiking reflects structure in the underlying connectivity (Gerstein and Perkel, 1969). If we let each neuron be represented by a node, we can represent a functional microcircuit as a mathematical graphical object. Suppose cell A fires before cell B for some proportion of all the times that they fire. The reliability of this correlation between A and B can then be incorporated mathematically as a directed and weighted edge starting at node A and pointing to node B. This representation indicates that the order of firing is preserved and that there exists a functional connection between cell A and cell B, regardless of the actual neuroanatomical and physiological way this occurs (Gerstein et al., 1978). As described previously (Sadovsky and MacLean, 2013), functional directional edges were created for each dataset using single frame lagged correlated spiking with weight equal to the proportion, or reliability, of observing a pairwise lag correlation between two cells.

Anatomical identification and projection of functional connections into the imaged field of view.

We used biocytin-filled neurons as fiduciary markers in combination with measures of distance from pia to identify lamina. In addition, we used cell density measures from bright-field, biotinylated NeuN staining and two-photon calcium florescence to help confirm lamina location. To project functional connections (directed edges) onto pairs of component neurons in the imaged field of view, we used neuron centroid locations identified from two-photon imaging for the start and end points of a vector.

Columnar/laminar flow.

For each individual circuit event, directional flow between lamina was defined within a field of view where a statistically significant correlation existed between time frames and distance from the pial surface. Intercolumnar flow was determined similarly according to distance to an arbitrary line perpendicular to the pial surface not in the field of view. Events with significant correlations in both cases were considered to have both types of flow. Events with no significant correlation in either case were considered disperse.

Circuit peak detection.

Multiple peaks were defined as time points in the multiunit average where net spiking was greater than or equal to 90% and >2 frames away from the maximum peak.

Fuzzy clustering.

Fuzzy clustering was performed as in Sadovsky and MacLean (2013). We created binary representations of each circuit event, with 1 s indicating which cells were active at any point during the event and 0 s representing cells not active in that event. Fuzzy c-means (FCM) clustering was achieved using the MATLAB function ‘fcm’ with N clusters, where N ranged from 2 to the total number of events for a single slice. This function returns the membership function matrix indicating how strongly each event belongs to each of the N specified clusters. For our analysis, cluster sufficiency was defined as all events having at least one cluster membership larger than 1/N + (1/N)/4. This indicated that an event was unambiguously placed into a single fuzzy cluster. To obtain the number of clusters necessary to explain all the events in a region, we iteratively ran the fuzzy clustering method with increasing values of N, looking for the point in which all events fell under the definition of being sufficiently clustered. Because fuzzy clustering is dependent on initial seed, we took the average output of 100 runs of the fcm function, with each run consisting of either a maximum of 100 iterations or a clustering improvement of ≥0.00001.

Spike timing precision.

We established statistical significance of temporal stereotypy for each cell in a field of view by comparing all the individual spike trains of a cell obtained from every circuit event. Cells had to be active in at least 4 events to be considered for analysis. To compare spike trains, we used the D^spike metric (Victor and Purpura, 1996) with a time parameter (q) of 1 s. This comparison gave us a distance value corresponding to the amount each spike train needed to be modified to be identical across activations. Edit distance is inversely related to the temporal similarity of spike trains. To determine whether distance values were significantly smaller than what would be expected by chance we created a null hypothesis comparison by generating 5000 shuffled spike trains that preserved network firing rates and computing the edit distances. Shuffled spike trains were simulated with an inhomogeneous Poisson process with a rate that was equal to the average network firing rate across events. We then compared our observed metric value to those from the shuffled population to obtain a p value (e.g., see Sadovsky and MacLean, 2013). Cells showing a p < 0.05 were considered significant.

Rentian scaling.

Rentian scaling was performed using a 2D modification of the function “rentian_scaling” provided in the MATLAB Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/) implementing Bassett et al. (2010). To avoid boundary conditions, only partitions containing a sum of nodes less than half of the total population were used for analysis.

Results

Using high-speed multiphoton laser scanning microscopy, in combination with calcium indicator dye, we imaged the spiking activity (Vogelstein et al., 2010; Sadovsky et al., 2011; Sadovsky and MacLean, 2013) of large unbiased and densely sampled neuronal populations in V1. We imaged activity of up to 979 (mean = 734 ± 129; n = 11 datasets) neurons in a 1.1 mm diameter circular field of view in slices of mouse V1 neocortex (Fig. 1A) at speeds of 87 ± 15 ms per frame. We identified spontaneous, emergent, circuit activity that is the result of synaptic connectivity between neurons (Cossart et al., 2003; Sadovsky and MacLean, 2013). This top-down approach (from emergent dynamics to underlying structure) can delineate multiple possible functional relationships between neurons in a field of view (Luczak et al., 2007; Luczak and MacLean, 2012). To control for sampling bias resulting from slice angle, we created slices 15 degrees off the coronal axis for one-third of our experiments. We found no notable differences between data collected from this angle compared with coronal slices and pooled the data as a result. Spontaneous V1 circuit events (n = 104 events; Fig. 1C,D) spanned a range of circuit event sizes (populations of active neurons = 176 ± 94 cells) and durations (1342 ± 698 ms). Over the full time course of the experiment, spontaneous V1 circuit events engaged the vast majority of imaged neurons in every field of view (80 ± 12% across datasets) through multiple discrete circuit activations. We defined the overall flow direction of spiking activity during a circuit event by identifying statistically significant correlation between active neurons across imaged frames and distance from the pial surface. We found that a sizable portion (48%) of circuit events did not have a dominant flow vector as they progressed. However, 36% of events had a direct columnar flow, 8% had a directed laminar flow, and 9% demonstrated a combined columnar and laminar flow. When we whole-cell patch-clamped neurons in the field of view, we observed that imaged activity was accompanied by electrophysiological UP states in single cells (n = 56 up states; Fig. 1E) (Sadovsky and MacLean, 2013). Mesoscale imaging of large numbers of neurons without laminar bias allowed us to capture multiple and varied circuit events within a single field of view (Movie 1; Fig. 1F).

Figure 1.

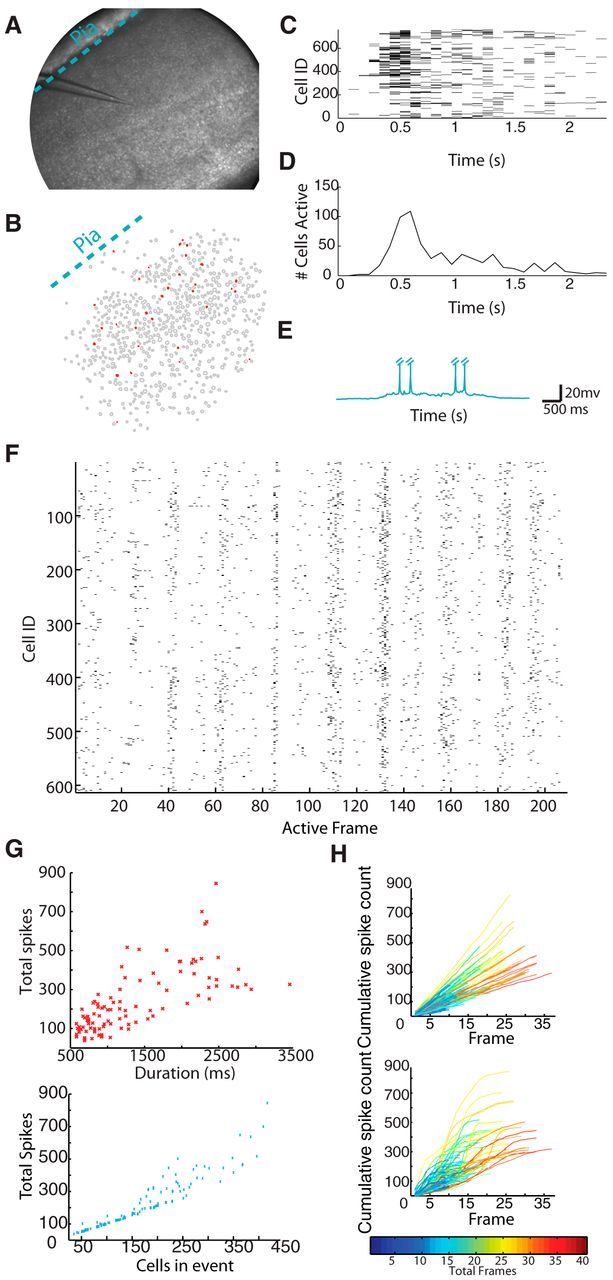
Visual cortex is capable of spontaneous circuit activity. A, Experimental preparation of a 1.1 mm diameter field of view of a V1 slice. B, Identified cells and single imaging frame example of activity from A. Active cells are in red. C, Spike raster of a single circuit event. D, Multiunit average of above raster. E, Single neuron whole-cell patch-clamp example of a visual neuron in an upstate during a circuit event. Action potentials have been truncated for presentation. F, Representative raster (quiescent intervals between events removed) of 14 circuit events observed in a single visual field of view. For each cell (n = 613), a black tick mark indicates a detected spike within a 72.8 ms imaging frame. G, Top, Each data point (red star) represents a single circuit event. Bottom, Each data point (blue x) represents a single circuit event. H, Plots showing cumulative firing across multiple circuit events in rate-matched Poisson (left) and V1 data (right). Each line represents a separate circuit event. Line color is normalized to event durations from short events (cool colors) to long events (hot colors).

Movie 1.

V1 example activity. Top, Filled red neurons are cells, which were active in a frame. Bottom, Representative raster (quiescent intervals between events removed) of 9 circuit events observed in a single visual field of view. For each cell (n = 764), a black tick mark indicates a detected spike within a 90 ms imaging frame. Movie time is altered for display. Top, Red line indicates current frame projected spatially.

The temporal progression of circuit activity in V1

Circuit dynamics, or the propagation of spiking activity through the network, have important implications for the organization of the underlying circuit (Roxin et al., 2011; Litwin-Kumar and Doiron, 2012). By imaging the activity of large neuronal populations during individual circuit events, we found that emergent circuit events in V1 began with a small initial group of active neurons (6 ± 7 cells in the first 85 ± 16 ms relative to even onset), which then rapidly recruited additional neurons up to a peak number of cells (39 ± 23 cells) before exponentially decaying (τ = 743 ms from average for all circuits) back to quiescence, with a full event comprised of a total of 176 ± 94 active cells. This neuronal recruitment pattern was common across circuit activations: 95% of events contained a single peak, which then decayed to quiescence (Fig. 1D; see Materials and Methods). Across circuit events, the peak occurred within the within the first 28 ± 15% (391 ± 150 ms) of the full duration of the total circuit activation. The discrete nature of each circuit event allowed us to determine whether overall duration of an individual circuit event was a linear function of firing (i.e., a similar scaled average firing rate within the circuit across multiple durations). We found a linear, correlative relationship between the number of spikes observed and the duration of the imaged events (Fig. 1G, top; r = 0.72; linear R² fit = 0.51). Similarly, we found a linear, correlative relationship between the number of cells active and the total number of spikes in a circuit event (Fig. 1G, bottom; r = 0.94; linear R² fit = 0.89). The relations between these variables describing V1 circuit dynamics in the majority of events indicated that the functional circuit did not have a specific or defining size and exhibited consistent dynamics over a large range of scales, possibly reflecting inhibition and excitation in balance with one another (Haider et al., 2006; Shew and Plenz, 2013). We did observe nonlinear effects at the upper end of our numerical circuit size. This may be due to some circuit events being so large that they involved cells outside our field of view, thus making these observations an undercount of the total number of neurons active.

We confirmed that these circuit dynamics reflect coordinated neuronal interactions by comparing these cumulative spike counts within recorded neurons to the cumulative spike counts generated from homogeneous Poisson networks. These null hypothesis populations were firing rate-matched to each cell in each circuit event dataset. Circuit firing properties in V1 resulted in sigmoidal-shaped cumulative progression of firing. In contrast, the cumulative progressions in each Poisson network were, as expected, nearly linear (Fig. 1H). These Poisson networks, which contain no interactions between model cells, did not mimic the cumulative progression of spiking activity observed in the interconnected neurons of V1 (Thomson et al., 2002; Perin et al., 2011).

Functional circuit flow of V1 circuitry indicates feedforward network properties

To further evaluate the neuronal interactions that generate V1 circuit dynamics and to reveal aspects of the organization of V1 microcircuitry, we used the pairwise temporal progression of action potentials between neurons (single frame lagged correlation) to generate functional microcircuit wiring diagrams: graphs whose weighted directed connections represented the probability of lagged spiking activity. Graph theory provided a mathematical framework and a set of established metrics for describing high dimensional networks (Bullmore and Sporns, 2009) and allowed us to quantify statistical features in the functional microcircuit topology of V1. Circuit activations in each field of view were translated into graph space with neurons acting as nodes, and single frame lagged spiking activity between two neurons resulting in directed edges, weighted by their reliability (see Materials and Methods) (Sadovsky and MacLean, 2013). Although not every edge in a functional graph reflects an underlying synaptic connection (Gerstein et al., 1978), we have previously found that functional topologies captured the distance dependent likelihood of a connection that is found in the underlying connectivity (Song et al., 2005, Perin et al., 2011; Sadovsky and MacLean, 2013), and when translated into actual connections in neuronal network models, they become capable of recapitulating experimentally measured dynamics (Sadovsky and MacLean, 2013).

In V1, we found that functional graphs were sparse, containing an average ratio of 13 ± 8 edges to each node. However, these edges were not distributed evenly, as we found neurons in each dataset that contained more edges than average, consistent with the idea of hub neurons (Picardo et al., 2011). Hubs with degree ≥1 SD of mean network degree equated to 10.6 ± 4% of all neurons (≥3 SDs, 1.6 ± 0.8%). We defined hub neurons according to the number of edges that a neuron possessed, and it remains to be seen what relation these neurons have to previously defined hubs in V1 (Yu et al., 2008; Folias et al., 2013). Nodes tended to be clustered together in a small-world-like fashion, where their directed clustering coefficient (Fagiolo, 2007) was significantly greater than that found in degree-matched random networks. For each dataset, 100 random networks were created with the same degree (Wilcoxon signed rank test: p = 9.8 × 10⁻⁴) while maintaining average path length (data = 2.7 ± 0.4 average path, random = 2.8 ± 0.7, Wilcoxon signed rank test p = 1). Thus, V1 functional networks were marked by nonrandom structure.

We quantified the recurrence of functional V1 circuit architecture using two metrics. As a null hypothesis, we used Erdős–Rényi random topologies in which edges between nodes are set with a fixed probability, to establish an expectation based on total node and edge count. For each dataset, we created 100 corresponding Erdős–Rényi graphs with equal numbers of nodes and an equal probability of connection as observed in the data (corresponding to 734 ± 129 nodes; p(edge) = 0.019 ± 0.012). As a second null hypothesis, we constructed V1 permuted networks that maintained out degree of each node but shuffled which nodes to which those edges connected. Both null hypotheses allowed us to evaluate whether circuit-specific patterns of node connectivity were biased toward recurrence or feedforwardness. We analyzed the aggregate structure of V1 graphs and found that V1 nodes had a low ratio of in to out degree, defined as the ratio of prefiring inward directed edges to postfiring outward directed edges. This indicated a bias toward outward flow. In contrast, Erdős–Rényi random graphs (V1-Random) were balanced (Fig. 2A). Because V1 microcircuitry demonstrated higher mean out degree edges, we next evaluated whether the overall topology, and all paths within it, were biased toward a feedforward flow. Specifically, we extended our graph analysis from path lengths of size 1, indicating pairwise functional connections between cells, to the largest possible path length in a given network, encompassing all circuit activity flow. To do this, we used the measure of flow hierarchy (Luo and Magee, 2011) that quantifies flow patterns through the wiring diagrams. Specifically, this metric quantifies the extent to which the flow propagates in a unidirectional manner. Because cycles reflect recurrent connections in the functional wiring architecture, we used this metric as a measure of recurrence in V1 functional graphs with highly recurrent networks having values close to zero, and highly feedforward networks having values close to 1. V1 contained a moderate level of flow recurrence compared with the null hypotheses (Fig. 2B). Random networks were entirely recurrent, probably because of the formation of a large interconnected network with multiple cycles (Newman et al., 2001). Interestingly, permuted V1 networks, where postsynaptic targets were randomized even as the total number of postsynaptic partners was maintained, were almost entirely feedforward, suggesting that the underlying V1 synaptic connections achieve a middle ground between these two extremes balancing feedforward structure with recurrent cycles.

Figure 2.

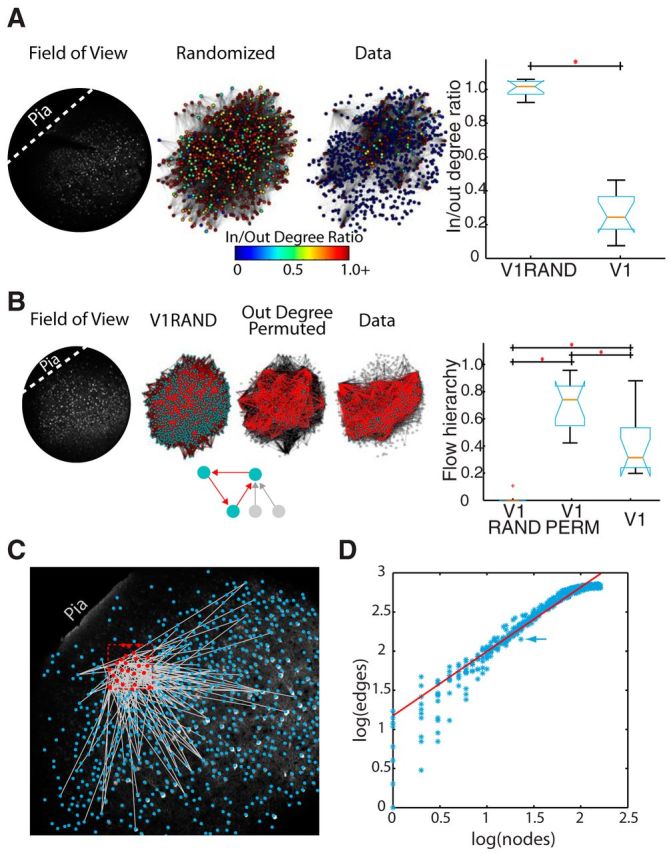
Circuit dynamics and functional graph properties. A, Left, Single example of the degree ratio of various neurons physically arranged in a field of view from V1 data, and Erdős–Rényi random graphs. Functional connectivity is displayed with pial surface toward the upper left (dashed line). Nodes represent cells and are colored by the degree ratio of that node as indicated in the key. Functional edges are drawn between nodes. For graphical display reasons, only edges with weight ≥ 0.2 are shown. All cells shown, even those without drawn edges, have at least 1 edge when weight constraints are removed. Right, Boxplot representing the significant difference (p = 8.1 × 10⁻⁵) in the average node ratio per dataset across all datasets for all edge weights (V1) and Erdős–Rényi random graphs (V1RAND). B, Left, Graphs showing the functional connectivity on a physical layout of neurons with pial surface toward the upper left (dashed line) for a single example dataset and single corresponding Erdős–Rényi and permuted graph. As in the inset: red represents cycle edges; teal represents nodes in cycles; gray represents edges and nodes without cycles. The inset would have a network flow hierarchy value of 2/5, or 0.4. For display reasons, only edges with weight ≥ 0.2 are shown. All cells shown, even those without drawn edges, have at least 1 edge when weight constraints are removed. Right, Boxplot representing the average feedforward value across Erdős–Rényi (V1RAND), data (V1), and permuted (V1PERM) datasets for all edge weights. Areas are significantly different from one another (Kruskal-Wallis: p = 2.6 × 10⁻⁶). C, Single partition Rentian scaling sample embedded into physical V1 slice space. Red dashed box indicates an example Rentian partition. Circles represent neuron centroids: blue if outside partition, red if inside. Gray lines indicate edges that transverse partition. Partition contains 23 nodes with 142 edges. Analysis is overlaid on two-photon slice image. D, Log–log plot of relationship of nodes to edges for multiple sized partitions. Each blue star represents a partition, with the partition in C indicated by an arrow. Red line indicates a linear fit (R² = 0.91, Rentian exponent [slope of line] = 0.82).

We then determined whether functional circuits were efficiently assembled in the physical space of cortex by studying functional wiring costs. To do so, we projected the functional graphs back into anatomical space (Fig. 2C) (Sadovsky and MacLean, 2013) and applied a measure of Rentian scaling (Basset et al., 2010). This measurement, originally designed to analyze very-large-scale integration circuitry, captures how efficiently a set of fixed structures with wiring between them is assembled in a physical space. This is achieved by creating random partitions of physical space, then measuring how often functional connections cross these partitions. The Euclidean field of view was randomly partitioned multiple times, and the number of nodes within each partition and the number of edges crossing each partition were counted (Fig. 2C). We found a linear relationship between these nodes and crossing edges on a log–log scale consistent with a modular, or Rentian, scaling of connectivity (Fig. 2D; linear fit across all datasets, R² value = 0.87 ± 0.13). These data indicated that functional circuits in V1 were embedded in physical space in such a way as to generate efficiently wired physical circuitry. Further, this result is consistent with the likelihood of a functional connection between neurons being dependent on spatial proximity while also maintaining topological features.

V1 is marked by a high number of differentiated circuits characterized by a variety of spatiotemporal firing patterns

We evaluated whether the spike trains of individual neurons were temporally stereotyped using a statistical test measuring spike train edit distance within individual neurons aligned perievent across multiple circuit events (Victor and Purpura, 1996; Kruskal et al., 2013; Sadovsky and MacLean, 2013). Using this method, V1 appeared to contain only a slightly above chance number of stereotyped neurons across all datasets (14 ± 7% neurons were significant at the 0.05 significance level). This indicated that individual cells fired at different times over multiple circuit activations. Thus, overall, individual neurons in V1 displayed a large diversity in their spike trains when considered in the context of all observed circuit events.

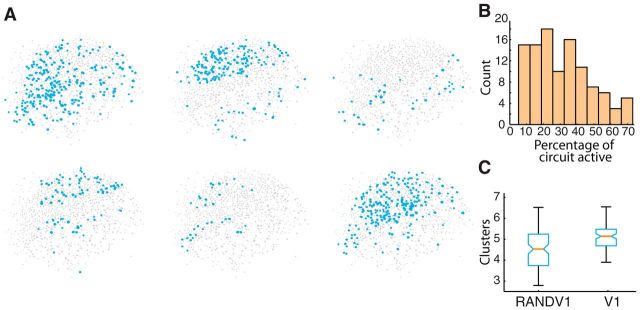
It seemed paradoxical that individual events were feedforward and demonstrated reliable firing patterns between cells yet had very little temporal stereotypy in individual neuron spike trains. We approached this paradox by determining whether this low amount of stereotypy indicated a large number of different groups of active cells (clusters) in the field of view. We computed the smallest convex region containing all active cells and found a range of convex hull areas in V1 (0.46 ± 0.08 mm), corresponding to 48 ± 9% of field of view size. Visually, the overall set of active cells in individual V1 circuit events appeared distinct from one another (Fig. 3A). We found that active circuits were interdigitated and they shared active neurons (average pairwise overlap of active neurons between any two circuits being 22 ± 11% in single fields of view). Circuits were numerically small, defined by total number of active cells as a percentage of all cells in the field of view (32 ± 17% cells active; Fig. 3B). Because the circuits appeared varied, we wished to see how they clustered into groups. We applied a fuzzy clustering metric (Sadovsky and MacLean, 2013) by observing separate, individual circuit activations (n = 104 total activations in n = 11 slices) and then determined whether there were groups of neurons that best described these circuits in the X-Y dimension. These groups can be thought of as neuronal event centroids, clusters, or a set of cells that best overlap across multiple circuit events. Every individual circuit event is assigned to one cluster, whereas the cells that make up that event can be part of multiple clusters. For a given field of view, N circuit events could be grouped into 1 to N clusters depending on the proportion overlap of cells active in each event. Our analysis demonstrated that V1 had more fuzzy groups, or circuits, in a single field of view than would be expected by random chance when conserving total spike count (Fig. 3C). The fact that even randomized, rate-matched, firing resulted in fewer fuzzy circuits than the real data suggested that the extent of the circuit variance we found in V1 did not simply reflect spiking properties of V1, but rather a specific property of network activation in this cortical region.

Figure 3.

Small clusters define V1. A, Examples of six spatially different circuit activations in the same slice. B, Histogram of circuit event sizes showing small size bias. C, Comparison of number of fuzzy cluster-derived circuit clusters observed in V1 compared with a randomized null hypothesis (p = 6.7 × 10⁻⁷).

Spatiotemporal activation reveals distinct, stereotyped circuits in V1

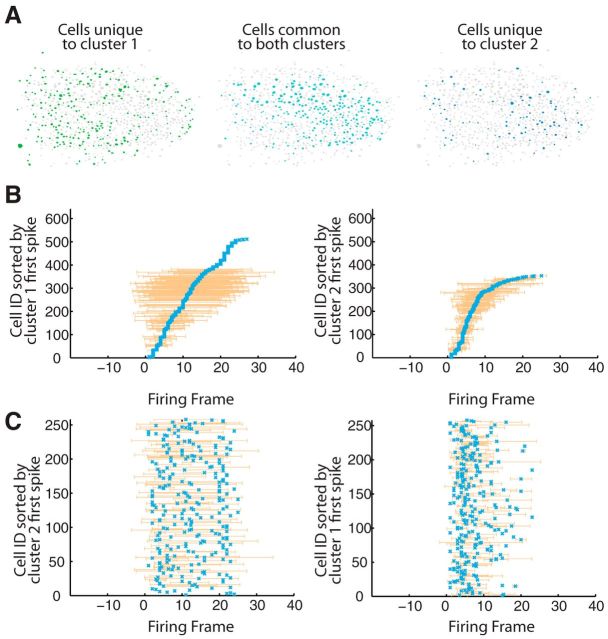
With these results in mind, we reevaluated our estimation of temporal stereotypy within individual neurons. While a small percentage of cells (12%) exhibited firing patterns that were similar across all circuit activations, we observed a greater number that appeared to fire more similarly within their unique fuzzy clustered circuits. To account for single-cell temporal stereotypy while taking into account these emergent spatial patterns, we determined temporal spiking similarity within spatially identified clusters, or circuits. We measured spike time precision within those spatially defined groups using the same spike distance metric that we used to measure temporal precision within individual neurons across all circuit activations. These results were significantly different from those that we arrived at with spatially agnostic designation of activity. V1 cells were significantly more stereotyped when spikes were assigned to one spatially defined circuit or another as appropriate. There was a significant increase in stereotyped neuronal spikes within each clustered circuit over nonclustered results (nonclustered significance = 13 ± 8%, clustered significance = 84 ± 9%, p = 5.5 × 10⁻⁰⁵). In the context of their numerous circuit clusters, V1 neurons spiked precisely. These analyses indicate that, whereas a small percentage of neurons showed temporally precise spikes regardless of which circuit was active, the majority of V1 neurons exhibit stereotyped and temporally precise activity that was specific to the active circuit. We next considered how stereotyped temporal spiking activity manifested across all cells active in a cluster (Fig. 4A). Again, circuit events were first clustered spatially and then active cells were ordered according to their mean first spike time across all circuit events within a cluster relative to the onset of event activity. Following this ordering, a structured sequence of neuronal activation became clear in each active cluster (Fig. 4B). Despite sharing a large number of neurons, each sequence was specific to each cluster. When neurons common to two spatially defined clusters were ordered by the mean first spike times corresponding to the alternate cluster, we found that the structured sequential activation was disrupted (Fig. 4C). Thus, individual circuit events have unique, overlapping spatial structure, and cells are capable of unique temporal firing dynamics dependent upon the circuit active. Spike times that were unique to one cluster or another are potentially dictated by other spatially patterned coactive cells.

Figure 4.

Spatial clusters exhibit different firing trajectories. A, Anatomical spatial representation of clusters. Left, Union of all cells in cluster 1 that are unique to cluster 1 indicated as green-filled cellular contours. Right, Union of all cells in cluster 2 that are unique to cluster 2 indicated as blue-filled cellular contours. Middle, Intersection of cells in cluster 1 and cluster 2 indicated as dark blue-filled cellular contours. B, Same cluster sorting of spike times. Left, Firing of circuit events in cluster 1 (n = 4 events, 511 cells) sorted by mean cluster 1 firing times. Right, Firing of circuit events in cluster 2 (n = 2 events, 353 cells) sorted by mean cluster 2 firing times. Frame duration = 89 ms. C, Alternate cluster spike time sorting. Firing of circuit events in cluster 1 sorted by mean cluster 2 firing times for shared neurons (n = 258). Right, Firing of circuit events in cluster 2 sorted by mean cluster 1 firing times for shared neurons (n = 258).

Discussion

The dynamics exhibited by neuronal circuits provide insight into the operational regimen of circuitry (Beggs and Plenz, 2003), the underlying topology (Roxin et al., 2011; Litwin-Kumar and Doiron, 2012; Vlachos et al., 2012), and information processing (Honey et al., 2007). Using multiphoton imaging, we studied emergent V1 microcircuit dynamics. These dynamics scaled linearly across circuit activations. We found that traditional anatomical boundaries did not strongly determine or shape the flow of circuit activity. Instead, V1 was fractionated into a number of functional circuits that were interdigitated and shared a number of neurons. We generated functional circuit wiring diagrams: graphs with nodes being neurons and directed connections being lagged correlated activity between neurons. Functional V1 microcircuit graph metrics were marked by a balanced prevalence of cycles and feedforward connections (Lamme and Roelfsema, 2000). These circuits are small world (Watts and Strogatz, 1998) and have short path lengths, which are embedded efficiently in anatomical space according to a measure of Rentian scaling (Bassett et al., 2010). It appears that circuits must balance minimization of wiring with topological structure, and the Rentian scaling relationship of functional graphs suggests that this is achieved with a modular circuit structure. We also evaluated the extent of temporally precise patterned activity in V1 microcircuitry. If we considered all circuit activations within an imaged field of view, a very small subset of neurons showed temporally consistent perievent spiking activity across all circuit activations. However, if we first considered the spatially defined circuit identity, we found a significant and substantial increase in the number of neurons that were temporally precise. In aggregate, this resulted in patterned multineuronal activations specific to each spatially defined functional circuit. Together, these data suggest that V1 microcircuitry has substantial potential for encoding multiple patterns of activity, which may be a beneficial strategy given relatively few total neurons in this brain region in the mouse species.

V1 circuitry has been described as a dichotomy between feedforward excitation and lateral inhibition, often in the context of orientation selectivity (Ringach et al., 1997). Our data suggest that the underlying connectivity of V1 expresses a combination of features from both of these classes. The reliability, stereotypical timing, and network average firing trajectories, together with flow topology metrics, indicate a strong feedforward drive, as previously described in juvenile mouse V1 (Ko et al., 2013). Yet this feedforward drive is also balanced with recurrence, as evidenced by V1 topology data falling midway between the random topology and the permuted topology in the calculation of flow hierarchy. This is consistent with the postulate that a minimal amount of recurrence is necessary to sustain multineuronal patterned activity or trajectories (Helias et al., 2013). Strict spatial constraints are not found in these networks, suggesting that multicolumnar processing is a major paradigm of network activation. As our activity was not matched to specific stimuli, it is unknown whether these functional circuits are the manifestation of orientation tuning or rather reflections of other processes. If the mouse functional columnar structure has been transformed into ontogenetic columns (Li et al., 2012; Ohtsuki et al., 2012), this would explain the rich dispersed, yet structured, activity which we observed in our data.

A theoretical study has suggested that anatomically structured connectivity is not necessary for the emergence of orientation selectivity in the visual cortex (Hansel and van Vreeswijk, 2012). Instead, the balance of inhibition and excitation can give rise to selective spike activity. Our data indicate that, although neurons with orientation selectivity are not spatially organized in mouse V1, functional microcircuitry has consistent and structured statistical features of organization. A previous study has demonstrated that neurons that exhibit correlated activity driven by natural scenes are more likely to be connected, consistent with a strong link between structure and function (Ko et al., 2011, 2013; Harris and Mrsic-Flogel, 2013). The tight link between function and synaptic connectivity suggests that the structure found in the functional graphs reflects structure in the underlying connectivity and is consistent with pairwise rules of connectivity in V1 (Harris and Mrsic-Flogel, 2013). The implication is that mouse V1 microcircuitry is highly nonrandom (Song et al., 2005).

We consider the slice preparation to be a self-contained system that allows us to isolate and then study the local connectivity that defines the cortical microcircuit. Future work toward understanding the role of connectivity in cortical dynamics and behavior will require a combination of research at the in vitro and in vivo level. Experiments using fluorescent beads as fiduciary markers (Ko et al., 2011, 2013) have already allowed researchers to make important headway combining these two levels of investigation.

Information processing is at least in part mediated by the spatiotemporal sequence of activation in neuronal circuits. Perhaps unsurprisingly, the identity and sequence of spiking in the preceding neuronal pool determine the time at which a neuron achieves threshold for action potential generation. We find that, although neurons are shared between multiple circuits, only a small subset of neurons show invariant peri-event spiking. Instead, the majority of neurons exhibit peri-event spiking activity that is unique to the circuit cluster that is active. Thus, circuit identity, rather than neuronal identity, dictates spike times. The ability for a neuron to participate appropriately in multiple circuit trajectories provides the potential for a large dynamic range of temporal patterns given a limited neuronal population to encode information.