Emphasis of spatial cues in the temporal fine structure during the rising segments of amplitude-modulated sounds II: single-neuron recordings

Abstract

Recently, with the use of an amplitude-modulated binaural beat (AMBB), in which sound amplitude and interaural-phase difference (IPD) were modulated with a fixed mutual relationship (Dietz et al. 2013b), we demonstrated that the human auditory system uses interaural timing differences in the temporal fine structure of modulated sounds only during the rising portion of each modulation cycle. However, the degree to which peripheral or central mechanisms contribute to the observed strong dominance of the rising slope remains to be determined. Here, by recording responses of single neurons in the medial superior olive (MSO) of anesthetized gerbils and in the inferior colliculus (IC) of anesthetized guinea pigs to AMBBs, we report a correlation between the position within the amplitude-modulation (AM) cycle generating the maximum response rate and the position at which the instantaneous IPD dominates the total neural response. The IPD during the rising segment dominates the total response in 78% of MSO neurons and 69% of IC neurons, with responses of the remaining neurons predominantly coding the IPD around the modulation maximum. The observed diversity of dominance regions within the AM cycle, especially in the IC, and its comparison with the human behavioral data suggest that only the subpopulation of neurons with rising slope dominance codes the sound-source location in complex listening conditions. A comparison of two models to account for the data suggests that emphasis on IPDs during the rising slope of the AM cycle depends on adaptation processes occurring before binaural interaction.

under many natural listening conditions, listeners perceive a single sound image originating from its source, despite the presence of multiple reflected copies of the sound arriving from different locations, milliseconds later. Although reflected sound energy may alter the width of the spatial percept, for speech signals, only the direct sound direction has an impact on the perceived location (“Haas effect”) (Haas 1951). This capacity to hear out the location (and other information) in speech sounds, particularly under noisy or reverberant conditions, is key to “cocktail party listening”—the ability to parse a conversation, even in the presence of competing sources with greater energy than that of the source to which a listener is attending. Nevertheless, speech—particularly reverberant speech—is a complex signal not easily parameterized, rendering difficult any systematic investigation of brain mechanisms underlying phenomena, such as the Haas effect. Consequently, many studies of reverberant listening have, instead, used pairs of click stimuli (Litovsky et al. 1999) to assess the neural basis of the related precedence effect (Wallach et al. 1949). In these studies, it is common to manipulate the spatial cues of leading and lagging sounds by altering the interaural time differences (ITDs) of each click pair to mimic sounds arriving directly from a source and later-arriving reflections. These more easily parameterized and reproducible stimuli facilitate investigation of neural mechanisms contributing to reverberant listening but at the expense of understanding how ongoing, modulated sounds, such as speech or music, are processed in reverberant environments.

Recently, with the use of a novel stimulus [amplitude-modulated binaural beats (AMBBs); Fig. 1] designed to mimic the temporal and interaural properties of reverberant speech with a deterministic (and easily parameterized) synthetic signal, we reported that human listeners appear to “glimpse” auditory spatial information arising during the early, rising slope of each amplitude-modulation (AM) cycle and not at the modulation maximum, where sound energy is greatest (Dietz et al. 2013b). The AMBB is generated in two steps: 1) two pure tones, one in each ear, with a small difference in frequency (f_beat) are used to generate a binaural beat; 2) the tones in each ear are AM, with an AM frequency (f_m) equal to the beat frequency (f_beat = f_m), with the result that the interaural-phase difference (IPD) of the binaural beat advances a full 360° during each AM cycle. This generates a fixed-phase relationship between the beat cycle (i.e., the IPD) and the AM cycle, which can be varied systematically by changing the start IPD at the beginning of the modulation cycle.

Fig. 1.

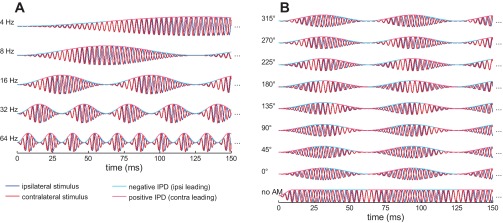
Subset of the amplitude-modulated binaural beat (AMBB) stimuli used in the experiment. Only the 1st 150 ms of the 1-s stimuli are plotted. For the stimuli in this figure, a mean carrier frequency of 288 Hz and of contralateral frequency (f_contra) > ipsilateral frequency (f_ipsi) was used. A: parametrical change of the AMBB frequency (left), affecting both amplitude-modulation (AM) rate and beat rate. In this panel, the start interaural-phase difference (IPD) at modulation minimum was kept constant at −90°. B: parametrical change of the start IPD (left). The start IPD is defined as the IPD in each modulation minimum. Here, the AMBB frequency was kept constant at 16 Hz. In addition to the fully AM binaural beats with 8 different start IPDs, a control condition with no AM was used (bottom row).

Dietz et al. (2013b) reported that psychoacoustic and brain-imaging [magneto-encephalography (MEG)] data were consistent in showing a dominance of those IPDs occurring just after the minimum in the modulation energy, essentially ignoring spatial information conveyed later in the modulation cycle. This preference for early-arriving spatial information in ongoing sounds suggests the involvement of an adaptation process at the neural level—whether spike-rate adaptation (Kiang et al. 1965) or temporal adaptation (Joris et al. 1994)—that emphasizes IPDs occurring in the rising portion of each AM cycle. Here, with the use of single-neuron recordings from the inferior colliculus (IC) of guinea pigs and from histologically verified recordings in the medial superior olive (MSO) of gerbils, we demonstrate the features of a neural “readout” that occurs early in each modulation cycle of an ongoing, modulated sound. Whereas previous investigations of the neural emphasis of spatial information have revealed the dominance of the stimulus onset, i.e., the start of the stimulation (Devore et al. 2009), the current study aims at generalizing this finding to the ongoing portion of an amplitude-modulated stimulus.

Devore et al. (2009) suggested several possible neural mechanisms underlying the dominance of stimulus onset in spatial information, which could operate before or after binaural interaction (although they pointed out that their data did not allow them to discriminate between these different mechanisms). Motivated by this open question, the second objective of the current study was to assess whether adaptation before or after binaural interaction underlies the localization dominance of stimulus onset or, in our case, the rising portion of the amplitude modulation. To disambiguate these two possibilities, we recorded rate-vs.-IPD functions to static IPDs and to AMBB stimuli. Through an analysis method similar to de-convolution, IPD readout-weighting functions were derived from these pairs of rate-vs.-IPD functions. A comparison of these readout-weighting functions with those derived from two different binaural processing models demonstrates that only adaptation before binaural interaction produces the observed temporal weighting of spatial information. Thus, although the ability to locate the source of a sound relies on interaural comparison, the ability to do so in reverberant conditions is a result of preceding sensitization of monaural inputs to the rising slopes of ongoing, modulated sounds.

MATERIALS AND METHODS

Stimuli.

The AMBB stimuli used in this study are identical to those introduced by Dietz et al. (2013b). This section briefly repeats the generation and the features of AMBBs.

Within a tone, each AM cycle is accompanied by a full 360° transition in IPD (Fig. 1A). To achieve this, the AM rate was set to be equal to the binaural beat rate, the latter determined by the frequency difference of the sinusoidal carrier for the left and right ear stimulus. The resulting stimulus thus contains a fixed relationship between instantaneous IPD and the phase of the AM cycle, which was varied systematically (Fig. 1B). The common rate of AM and binaural beating is referred to as the AMBB frequency.

Both possible beat directions were used by choosing the larger carrier frequency (f_c) in the ipsilateral (to the recording site) or contralateral ear. In addition to the AMBB, two different forms of control stimuli were required: binaural beats with no AM and AM tones with a fixed, static IPD.

Throughout, the polarity of the IPD was defined with respect to the AMBB beat direction: positive IPD means leading on the side with the higher carrier frequency. This nomenclature holds for start IPD, instantaneous IPD, and also for the static IPD compared with beat responses.

Single-neuron IC recordings.

Single-neuron recordings were made from 102 neurons in the IC of 17 adult guinea pigs (15 tricolored guinea pigs, 96 neurons; two albinos, six neurons) under urethane anesthesia (20% solution; 1.5 g/kg dosage ip) at the UCL Ear Institute (London, UK). These experiments were carried out in accordance with the Animal (Scientific Procedures) Act of 1986 of Great Britain and Northern Ireland and under Home Office Project Licence no. 70/6826. IC recording equipment and methods were similar to those used by Griffin et al. (2005).

Rimadyl (50 mg/ml solution; 2 mg constant dosage), a nonsteroidal, anti-inflammatory drug that also acts as an analgesic; Buprenorphine (0.3 mg/ml solution; 0.05 mg/kg dosage), an opioid; and Colvasone (2 mg/ml solution; 2 mg/kg dosage), a corticosteroid with an anti-inflammatory action, were administered subcutaneously at the beginning of each experiment. Supplementary doses of Buprenorphine were administered when an experiment continued beyond 10 h. Lignol, a local anesthetic containing lignocaine and lidocaine hydrochloride, was administered locally before any surgical incision. A tracheal cannula was inserted, and core temperature was maintained close to 37°C with a heating blanket (Harvard Apparatus, Kent, UK). Animals were placed in a sound-attenuating chamber (IAC Acoustics, Winchester, UK) and held in a stereotaxic frame with hollow ear speculae (modified from model 1730; David Kopf Instruments, Tujunga, CA). Before positioning the animal, the tragus of each ear was cut to obtain clear access to the tympanic membrane. A craniotomy was performed to expose the cerebral cortex overlying the IC, and the covering dura was removed. The bullae were vented by insertion of cannulae and sealed with Vaseline to equalize middle-ear and outside-air pressures. A parylene-coated tungsten microelectrode (1–2 MΩ; World Precision Instruments, Sarasota, FL) was positioned above the IC and advanced ventrally using a motorized micromanipulator (model SM-5; Luigs & Neumann, Ratingen, Germany), remotely controlled from outside of the recording booth. Stereotaxic coordinates were used, which, from experience, position the recording electrode within the low-frequency, dorsolateral aspect of the IC. Entry of the tip of the recording electrode into the central nucleus of the IC was adjudged by the appearance of robust, neural responses, well tuned for low sound frequencies and invariably, a preponderance of neuron sensitivity to ITDs conveyed in the stimulus fine structure. At the end of each experiment, animals were administered a lethal dose of pentobarbital sodium (200 mg/ml ip).

Sounds were produced using Tucker-Davis Technologies' (TDT; Alachua, FL) digital signal-processing hardware. TDT's Brainware software controlled the sequence and parameters of the stimuli that were computed on a RP2.1 processor (TDT), using the Real-Time Processor Visual Design Studio (RPvdsEx; TDT). Stimuli were generated with a 48.828-kHz sampling rate and scaled such that their peak voltages were 10 V at the digital-to-analog converter outputs. These signals were attenuated to achieve the desired level for the experiments using PA5 (System III) modules (TDT). Sounds were delivered by Etymotic ER-4S headphones with the common reference wire separated to abolish crosstalk. Microphones (FG-3452; Knowles Acoustics, Burgess Hill, UK) were used to measure the stimulus within a few millimeters of the tympanic membrane to ensure that the sounds delivered to each ear were well matched.

Electrical signals from the electrode were current amplified by a headstage (RA16AC; TDT) and further amplified, filtered, and digitized by a preamplifier (Medusa RA16PA; TDT) at a 25-kHz sampling rate. The signal was conducted by a fiber-optic cable to the RX5 base station for further digital filtering (300–3,500 Hz) and recording onto a personal computer. Spike data were displayed in real time using TDT's Brainware software and selected, according to manually adjusted criteria, to ensure that the analyzed data stem from a single neuron.

Single-neuron MSO recordings.

Single-neuron recordings were made from 18 neurons in the brain stem of five adult anesthetized Mongolian gerbils (Meriones unguiculatus) at Ludwig-Maximilians University, Department Biology II (Munich, Germany). Only those nine neurons, histologically confirmed as residing within the MSO, were used for further analysis. All gerbil experiments were approved by the German Animal Welfare (Tierschutzgesetz; AZ 2112531-40/01, AZ 55.2-1-54-2531-57-05), and methods were based on those described by Pecka et al. (2008).

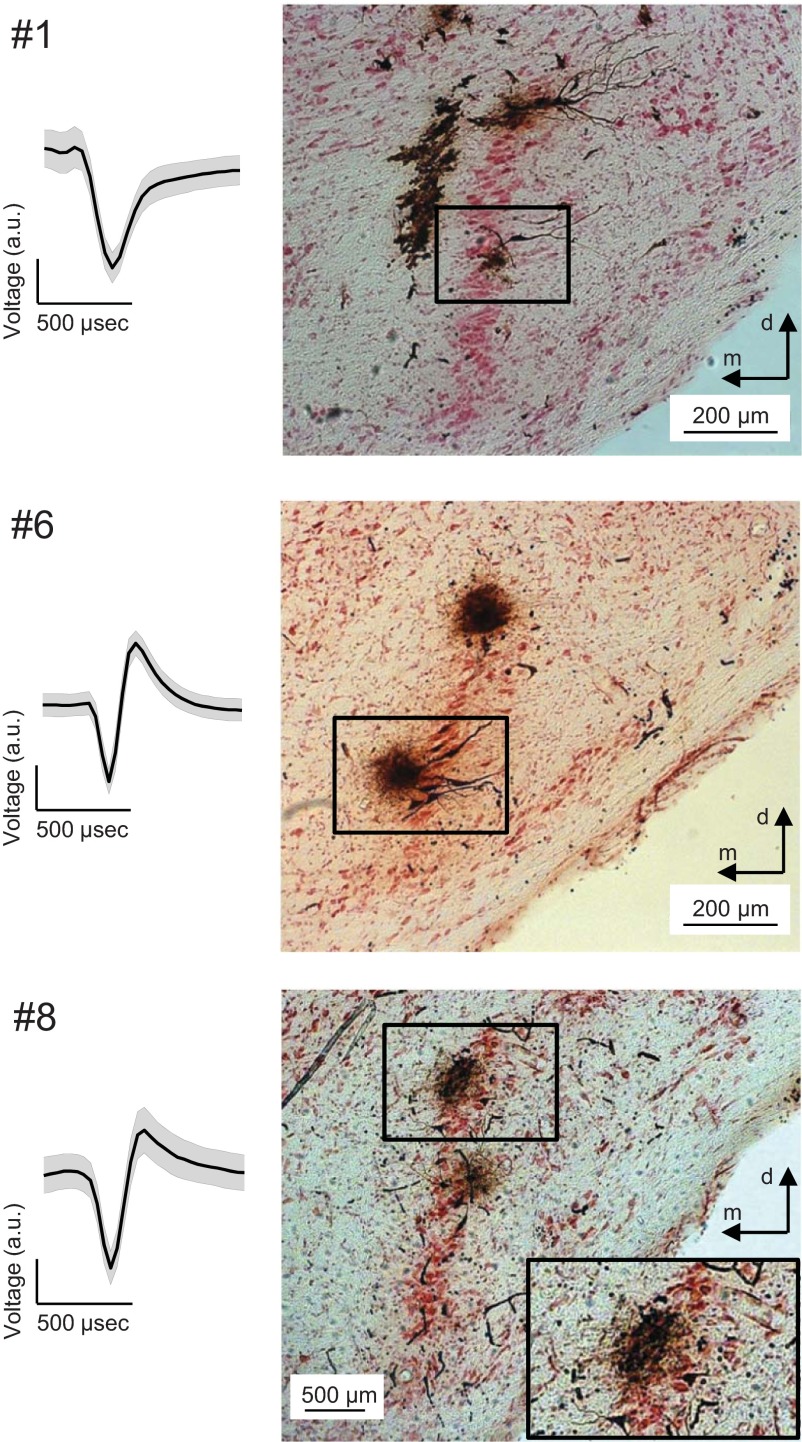
Gerbils were anesthetized initially with an intraperitoneal injection (0.5 ml/100 g body wt) of a mixture of ketamine (20%) and xylazin (2%), diluted in 0.9% NaCl solution. During surgery, a dose of 0.05 ml of the same mixture was administered subcutaneously every 30 min. During recording, animals were subcutaneously injected continuously with the same anesthetic via an automatic pump (801 syringe pump; Univentor, Zejtun, Malta) at a pump rate of 1.6–2.5 μl/min, depending on body weight. The animal was transferred to a sound-attenuated chamber and mounted in a custom-made stereotaxic frame (Schuller et al. 1986). The animal's position in the frame was standardized by stereotaxic landmarks on the surface of the skull (intersections of the bregmoid and lambdoid sutures with the sagittal suture in horizontal alignment). Constant body temperature was maintained at 37°C using a thermostatically controlled heating blanket. To gain access to the MSO, a craniotomy was performed just lateral to midline of the skull and caudal to the posterior aspect of the transverse sinus. The dura was opened, and the underlying cerebellum was partially aspirated to expose the floor of the fourth ventricle. The MSO was accessed with recording electrodes that were positioned with a micromanipulator, according to landmarks on the brain and in relation to lambda. Specifically, the coordinates used to traverse the MSO were 3,800–4,200 μm caudal and ≈1,300 μm lateral from lambda. The sound stimuli were delivered via earphones that were placed on the ear canal. After recording, a lethal dose of pentobarbital (20 mg/ml) was administered, and the animal was perfused intracardially with heparinized NaCl solution (0.9%), followed by a 4% paraformaldehyde solution. The brain was then sectioned in the coronal plane, and sections (50-μm thick) were stained for horseradish peroxidase (HRP) with diaminobenzidine (Adams 1977) and counterstained with Neutral red. The recording site was verified using light microscopy (Fig. 2). In total, six recording sites were located in the main cell band of the MSO, whereas three were located medial or lateral to it.

Fig. 2.

Examples of medial superior olive (MSO) action potential shape and histology. The shapes of the action potentials of 3 MSO neurons are displayed (left) as means. Shaded error bars are the SD. The respective recording site is displayed (right). MSO neurons #1 and #8 were located in the main cell band of the MSO, as shown histologically with horseradish-peroxidase (HRP) staining. MSO neuron #6 was located medial (m) to the main cell band of the MSO. Response properties of neurons #8 and #1 are shown below (see Figs. 5 and 6, respectively). Top: a large black trace is situated medial to the main MSO cell layer, corresponding to the electrode track of a different penetration. The HRP injections, dorsal (d) to the highlighted ones (top and middle), indicate recording sites of different penetrations, which were distinguished mainly by penetration depth. Bottom: the HRP injection, ventral to the highlighted one, indicates a recording site of a different penetration. a.u., arbitrary units.

Stimuli were digitally generated at a sampling rate of 50 kHz by TDT System III, converted to analog signals (RX6; TDT), attenuated to desired levels (PA5; TDT), and delivered to earphones (ER-2; Etymotic Research, Elk Grove Village, IL). A good seal between the ear canal and the output of the loudspeakers, as well as matching of the sounds delivered to each ear, was confirmed using microphones (ER-10B+; Etymotic Research) that measure the sound within the ear canal.

Single-neuron responses were recorded extracellularly with glass electrodes (5–15 MΩ; Harvard Apparatus), filled with 2% HRP in 10% NaCl. The recording electrode was tilted caudally by 20° and advanced under remote control, using a motorized micromanipulator (Digimatic; Mitutoyo, Neuss, Germany) and a PiezoDrive (Inchworm controller 8200; EXFO Burleigh Products Group, Victor, NY). Recordings were filtered, amplified, and fed to a computer via an analog-to-digital converter (RP2.1; TDT), running RPvdsEx (TDT). Isolation of action potentials from single neurons was guaranteed by visual inspection of amplitude and shape during the experiment and by offline spike-cluster analysis (Brainware; TDT). To mark a recording site after successful recording, HRP was iontophoretically ejected from the recording electrode (Fig. 2).

Methods identical to IC and MSO recordings.

Stimulus generation and data analysis were identical for IC and MSO recordings. The left and right carrier frequencies were set, such that one was above and one was below the characteristic frequency (CF) of the neuron, with equal distances from the CF on a linear scale. Stimuli were presented 25 dB above a neuron's estimated CF-tone threshold. Each neuron's CF and threshold were determined by recording a frequency-vs.-level response area [see Griffin et al. (2005) for details]. For each of the five different modulation frequencies (4, 8, 16, 32, and 64 Hz), 26 different configurations were recorded as a block, which contained eight static IPDs, eight right-beating stimuli, and eight left-beating stimuli. All stimuli in each of these 24 conditions were amplitude modulated and presented with eight different static IPDs (or start IPDs), spaced by 45°. Within the 24 conditions, the presentation order was randomized. A block finished with two unmodulated beat stimuli—one left beating and one right beating—with the beat frequency equal to the modulation frequency of the respective block. After the five modulation-frequency blocks were presented once and in random order, the entire presentation order was reversed, and the blocks were presented again. On average, 10 repetitions of the 130 stimulus conditions were recorded from each neuron. An exception is MSO neuron #1, where the 130 conditions were presented only once. Each stimulus duration was 1 s, and the interstimulus interval was at least 500 ms. Unmodulated beats were gated with 10 ms-squared cosine ramps; AM stimuli started and ended with AM minima. To exclude stimulus-onset effects, neural responses within first 250 ms were excluded from the data analysis.

Response latencies were estimated manually for each neuron by determining the best alignment of the peaks of the cycle histograms obtained from the unmodulated binaural beat stimuli (D and F of Figs. 3–6), with the peaks of the static IPD-tuning curve (redrawn in D and F in black from I) for all beat rates, simultaneously. The response latency includes both recording hardware and auditory pathway components and was subtracted from the neural response times before histograms were plotted. Note that the latency estimation is only critical for the correct positioning of the cycle histogram within the stimulus cycle. It influences neither the recorded static IPD-tuning curves nor the AMBB-tuning curves and is, therefore, not critical for deriving the estimated modulation-phase, IPD-weighting function.

Fig. 3.

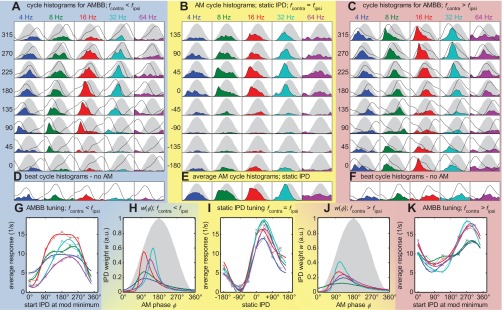
Response overview of inferior colliculus (IC) neuron #47; characteristic frequency (CF) = 320 Hz; 10 repetitions. All panels with blue backgrounds (left) belong to beating stimuli, with f_contra < f_ipsi; those with yellow backgrounds (middle) to AM tones with static IPDs; and those with red backgrounds (right) to beats, with f_contra > f_ipsi. A and C: latency-corrected cycle histograms (colored areas) for the 2 different beat directions of the AMBB. The 5 different columns of each panel represent different modulation (mod) frequencies (4, 8, 16, 32, and 64 Hz, from left to right). The 8 different rows show data for 8 different start IPDs (left). The sinusoidal envelope of the acoustic stimulus is plotted in gray. To provide information about where in the modulation cycle the best IPD occurs, fitted static IPD-tuning functions from I are replotted in the cycle histograms with black lines. Note that according to the start IPD of the different rows, this function occurs shifted in steps of 45°. B: respective data for the AM tones with various static IPDs (rows). E: mean histograms from B, averaged over the 8 static IPDs. D and F: beat cycle histograms for the unmodulated, binaural beats (start IPD = 180°). As in A and C, the fitted static IPD-tuning functions from I are replotted with black lines. I: neural responses to the AM stimuli, as a function of static IPDs, are shown for the 5 different modulation frequencies. Each data point corresponds to the pooled activity of 1 cycle histogram in B. Line colors indicate the modulation frequency corresponding to A–F. This neuron has its maximum response (best IPD) at ∼40°. G and K: neural responses to the AMBB stimuli as a function of start IPD. Each data point corresponds to the pooled activity of 1 cycle histogram in A and B, respectively. H and J: w(φ), IPD weighting as a function of the AM-phase φ, derived from the static-tuning curves (I) and the respective AMBB-tuning curve (G and K). G, I, and K: solid lines represent functions fitted according to Eq. 1.

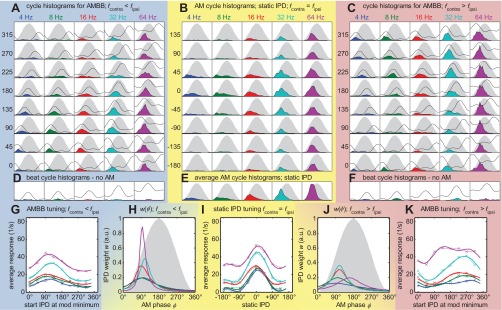
Fig. 6.

Response overview of MSO neuron #1; CF = 544 Hz; only 1 run. Same format as Figs. 3–5. The neuron has fully modulated-tuning curves, even for the AMBB stimuli. Compared with the other MSO example (Fig. 5), it has a higher rate of >100 spikes/s. It also has a high response rate to unmodulated, binaural beats (D and F). All of the above mentioned also occurs in some of the other 7 MSO neurons (see Fig. 2 for the corresponding histology).

Static-tuning curves [R_S(IPD); Fig. 3I] and AMBB-tuning curves [R_B(IPD_start); Fig. 3, G and K] were fitted with the function

$$\tilde{\text{R}}(\text{IPD})=\hspace{0.17em}\text{A}\hspace{0.17em}+\hspace{0.17em}\text{B}\hspace{0.17em}\sin (\text{IPD}\hspace{0.17em}+\hspace{0.17em}\text{C})\hspace{0.17em}+\hspace{0.17em}\text{D}\hspace{0.17em}\sin (2\text{IPD}\hspace{0.17em}+\hspace{0.17em}\text{E})$$ (1)

Five parameters (A–E) were determined, using the standard MATLAB fit function (fit.m) with the “trust region” algorithm that minimizes the root-mean-square (RMS) error between the fitted rate function [R̃(IPD)] and the measured response rate [R(IPD)]. The sin(2IPD) term was used to account for the sharply tuned or saw tooth-shaped, IPD-tuning function, which is not fitted well by a pure sinusoid. The magnitude of this term, specified by D, is typically 0.3–0.5 times the magnitude of the main term B.

The bin width for the cycle histograms was 15°, resulting in 24 bins for each histogram. Three-point averaging with a convolution kernel of [.2 .6 .2] was applied to all histograms. The average AM cycle histograms to static IPD stimuli (Figs. 3E–6E) were fitted with stable distributions (see below) to determine automatically and robustly their peak position. Symmetric fit functions, such as Gaussian or squared sinusoids, did not result in good fits, as the histograms were often skewed, showing a rise steeper than the fall. The so-called stable distributions (Nolan 2013) contain a parameter κ that allows the skew of the distribution to be adjusted. To keep the number of fit parameters to the minimal set of skew (κ), position (μ), and width (σ), the following distribution was used

$$\text{f}(\varphi )=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }\text{dx exp[i(}\mu -\varphi )\text{x}\hspace{0.17em}-|\sigma \text{x}|(1+2\text{i}\kappa \text{ sgn(x)}\hspace{0.17em}\log |\text{x}|/\pi )]}$$ (2)

where φ denotes the AM cycle phase. The average AM cycle histograms (e.g., Fig. 3E) were fitted with the distribution, maximizing the correlation coefficient between the fitted and the actual histogram.

An important aspect of the single-neuron data analysis is to derive the IPD weighting as a function of the AM phase (IPD-weighting function). This function w(φ) quantifies how strongly the instantaneous IPDs, at each part of the AM cycle, contribute to the total AMBB response (Fig. 3, H and J).

The following formulas describe how the IPD-weighting functions w(φ) (e.g., Fig. 3J) can be estimated from the fitted, static-tuning curve [e.g., R̃_S(IPD); Fig. 3I] and the fitted AMBB-tuning curve [e.g., R̃_B(IPD_start); Fig. 3K].

For any periodically amplitude-modulated stimulus, the total response R_out of a binaural coincidence neuron/AM cycle can be described as

$$R_{\text{out}}={\displaystyle \int d\varphi \hspace{0.17em}w(\varphi )\cdot R_S(\text{IPD}(\varphi ))}$$ (3)

For AMBB stimuli, the instantaneous phase IPD(φ) differs from the AM cycle phase φ by the offset IPD_start

$$\text{IPD}(\varphi )={\text{IPD}}_{\text{start}}+\varphi$$ (4)

By substituting IPD(φ) in Eq. 3, an equation for R_B(IPD_start) can be derived

$${\widehat{R}}_{\text{B}}({\text{IPD}}_{\text{start}})={\displaystyle \int d\varphi \hspace{0.17em}w(\varphi )\cdot {\tilde{R}}_{\text{S}}({\text{IPD}}_{\text{start}}+\varphi )}$$ (5)

The equation differs from a convolution integral only by the sign of φ in the R̃_S function. The sign is influenced by the definition of IPD with respect to the beat direction. In principle, therefore, the AMBB-tuning function can be expressed by a proper convolution of the static-tuning function and an IPD-weighting function.

The IPD-weighting function w(φ) is expressed by the same type of fit function as the cycle histograms f(φ) (Eq. 2). Since Eq. 5 cannot be easily solved for w(φ), an exhaustive search was implemented in a discrete, three-dimensional parameter space of skew (0 < κ < 0.9), position (0° < μ < 360°), and width (4° < σ < 120°): Eq. 5 was derived for all w(φ) functions possible with the three parameters. Then, the triplet of parameters was chosen for w(φ) that maximizes the correlation coefficient between the fitted-tuning curve R̃_B(IPD_start) and the set of derived tuning curves R̂_B(IPD_start). Typically, the maximized correlation coefficient is >0.98, so the derived IPD-weighting function can reconstruct the fitted AMBB-tuning curve almost perfectly from the static-tuning curve.

Computational model.

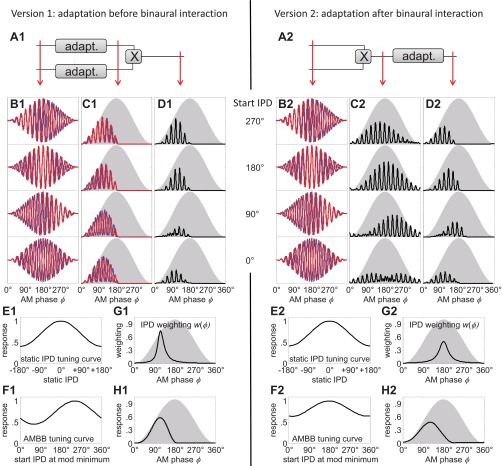
Two versions of a simple binaural model were compared to evaluate two possible explanations for the observed physiological results. The focus is on the effect of adaptation—resulting in an emphasis on the rising slope of the AM cycle—located either before or after binaural interaction. Both model versions consisted of simplified monaural preprocessing stages: band-pass filtering, compression, half-wave rectification, and low-pass filtering, as commonly used as front-end monaural components of binaural models (Bernstein and Trahiotis 1996; Breebaart et al. 2001; Klein-Hennig et al. 2011). Our implementation of this was identical to that used by Klein-Hennig et al. (2011), with a fourth-order gamma-tone filter centered at the mean carrier frequency of 500 Hz, a static power-law compression with an exponent of 0.23, half-wave rectification with subsequent square-law expansion, and 425 Hz, fourth-order, low-pass filtering. Binaural interaction was modeled by multiplying left and right inputs.

The dominance in the response of the rising slope of the modulation cycle was realized by multiplying the cycle histogram at the input of the slope, emphasizing stage with a half-wave-rectified sinusoid segment, shifted so that the resulting AM cycle had its peak at ∼90°, i.e., at maximum slope. This simple generator of slope emphasis does not describe any particular physiological mechanism, such as spike-rate adaptation, but serves, rather, to generate AM cycle histograms akin to those typically recorded in MSO neurons in response to 32 Hz AMBBs (e.g., Figs. 5E and 6E) and similar to the responses of MSO neurons reported inEq. 1 Fig. 11 in Joris (1996). This slope-emphasis stage was introduced just before (version 1) or just after (version 2) binaural interaction.

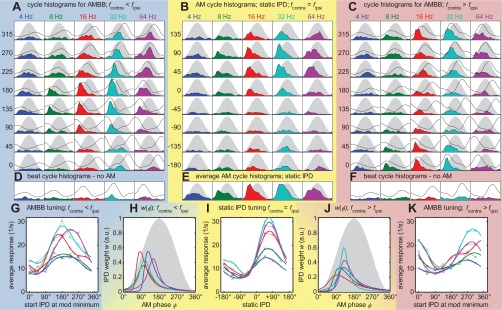
Fig. 5.

Response overview of MSO neuron #8; CF = 608 Hz; 8 repetitions. Same format as Figs. 3 and 4 (see Fig. 2 for the corresponding histology).

RESULTS

For neural recordings, the same AMBB stimuli as in human psychophysics (Dietz et al. 2013b) were used, with the exception that rather than binaural beats being centered at 500 Hz, neural responses were assessed, with binaural beats centered at the neuron's CF. CFs ranged from 96 to 1,312 Hz, with an average of 480 Hz.

A total of 102 single-neuron recordings was made from the IC of 17 guinea pigs. Figure 3 shows responses of a typical IC neuron to static IPDs and AMBBs, presented at CF (320 Hz). Figure 3B shows cycle histograms of action potentials to AM tones with various static IPDs and for AMBB stimuli with various start IPDs [Fig. 3A, contralateral frequency (f_contra) < ipsilateral frequency (f_ipsi); Fig. 3C, f_contra > f_ipsi]. For example, the stimuli shown in Fig. 1A are those used in Fig. 3C (270° start IPD). Those shown in Fig. 1B correspond with 16 Hz (Fig. 3C).

The AM cycle histograms for static IPDs (Fig. 3B) reveal that for 8 Hz and 16 Hz, the neuron responds maximally during the rising portion of the modulation cycle. They also reveal a strong binaural tuning, with a preference for positive IPDs (leading at the ear contralateral to the recorded IC).

Figure 3I shows the static IPD-tuning curve R_S(IPD), revealing this neuron's best IPD to be 40°. For this neuron, the static IPD-tuning curves are largely independent of the AM frequency. The total response to AMBB stimuli of both beat directions as a function of start IPD [R_B(IPD_start)] is shown in Fig. 3, G and K. Even though these stimuli contain all possible IPDs, there is a considerable change in the response rate as a function of start IPD. Note that the shapes differ between the two beat directions, to some extent explained by the asymmetries in the frequency-tuning functions when swapping the carrier frequencies, f_c, between the ears to change the direction of the binaural beat. As described in materials and methods, IPD-weighting functions (Fig. 3, H and J) were derived from the static-response functions and the responses to the AMBB to determine the region of IPD emphasis within the AM cycle.

Data from a second exemplary IC neuron are shown in Fig. 4. Compared with the example in Fig. 3, this neuron has its maximum IPD weighting slightly earlier in the modulation cycle (Fig. 4, H and J). Furthermore, the static AM cycle histograms (Fig. 4, B and E) are more heavily skewed toward the rising slope than for the example in Fig. 3. All cycle histograms of one neuron are scaled by the same factor. The factor is set so that the highest peak of all histograms fills the available space.

Fig. 4.

Response overview of IC neuron #98. Same format as Fig. 3; CF = 736 Hz; 8 repetitions. Rising slope dominance in both the period histograms panels (B and E) and in the IPD-weighting function (H and J) is strongest for 16 Hz, followed by 8 and 32 Hz, and only weak for 4 and 64 Hz.

In addition to the 102 IC neurons, recordings were made from nine histologically verified neurons, recorded in the MSO of anesthetized gerbils. These methodologically more-challenging experiments were conducted to determine whether the principle findings from the IC are also observed at this primary site of binaural interaction. Responses from the MSO neurons (see Figs. 5 and 6 for two examples) indicate that primary binaural neurons also have their maximum IPD weighting during a short and early segment of the modulation cycle.

Population analysis was performed on those conditions where the recorded data fulfilled selection criteria necessary to estimate robustly and automatically all of the response parameters. The empirically determined criteria were: 1) a clear, phase-locked neural response to the AM cycle [fitted to the average AM cycle histogram (Figs. 3E–6E) with σ ≤ 90°; see Eq. 2]; 2) an IPD-weighting function (Figs. 3, H and J–6, H and J) with a pronounced peak (with σ ≤ 90°); 3) clear binaural tuning to static IPDs [measured as vector strength, VS_static > 0.2, as described by van Hemmen (2013)]; and 4) an average response rate, R > 6 spikes/s, at best static IPD. In total, 205 conditions from 53 different IC neurons and 64 conditions from nine MSO neurons fulfilled all of these criteria. Many of the 4-Hz conditions were rejected, because they failed the two σ ≤ 90° criteria.

It might be assumed that selecting neurons with a relatively narrow IPD-weighting function (criterion 2) potentially favors neurons with an earlier maximum position. This assumption was tested by deriving the correlation between the width (σ) of the IPD-weighting function and the cycle position of the maximum IPD weighting. Practically no correlation (r = +0.02) was found in the IC data. A related, second hypothesis concerns a correlation between the width of the static AM cycle histogram (criterion 1) and the cycle position of the maximum IPD weighting. Here, a correlation of r = +0.18 (R² = 0.035) was found. Specifically, the grand average of “cycle position of the maximum IPD weighting” changes from 126° to 121° in the IC data when applying the filter for criterion 1. This small bias within the population data is appraised to be acceptable for filtering robust conditions. In the MSO data, all neurons have a narrow IPD weighting and a narrow AM cycle histogram anyway, with the result that the σ criteria filter out only very few conditions.

Importantly, in 198 of 205 IC conditions (Fig. 7A, ordinate) and 61 of 64 MSO conditions (Fig. 7D), the maximum IPD weighting was found during the rising portion of the modulation cycle (0–180°). One hundred forty-two of 205 (69.3%) IC and 50 of 64 (78.1%) MSO conditions have a maximum in the interval (0° − 135°) and are therefore classified as showing sensitivity to IPDs during the rising slope of the modulation cycle. The other 63 IC and 14 MSO conditions have a maximum in the interval (135° − 225°) and are classified as peak sensitive. No falling slope (225° − 360°) condition was found. The AM phase with the maximum IPD weighting is positively correlated, with the peak position in the AM cycle histogram. The correlation coefficient between these two very different measures is r = +0.66 for the IC (Fig. 7A), and r = +0.82 for the MSO conditions (Fig. 7D).

Fig. 7.

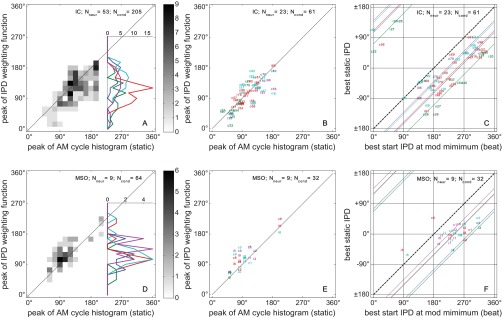
Summarizing data. A–C: IC data; D–F: MSO data. A and D: maximum IPD-weighting position (peak of the IPD-weighting function in Figs. 3, H and J–6, H and J) against the peak position of the static AM cycle histograms (Figs. 3E–6E). The vertical histogram insets contain a summation over the peak position of the static AM cycle histograms, leaving the maximum IPD-weighting positions as the only parameter of interest. They are separated by modulation frequency (color-coded as in Figs. 3–6). B and E: same as A and D but now with more restrictive criteria 1 + 2 [width (σ) < 60°], showing, therefore, fewer conditions (N_cond). This restriction was applied only to allow for the labeling of individual data points: modulation frequency is color-coded as in Figs. 3–6; the number identifies the neuron (N_neur), and letters “i” and “c” indicate the beat direction (i for f_contra < f_ipsi; c for f_contra > f_ipsi). C and F: peak of the AMBB-tuning curves (Figs. 3, G and K–6, G and K) against the peak of the static IPD-tuning curve of the corresponding condition (Figs. 3I–6I). The labels of the data points and the threshold criteria were identical to B and E. The format is analogous to that of the psychoacoustic data (Dietz et al. 2013b) (Fig. 3) to demonstrate the similarity between the psychophysical and physiological findings. The bold, dashed, diagonal lines indicate an offset of 180° between the static IPD and AMBB-tuning curves. This characterizes a hypothetical dominance of the IPD at the energy maximum. The colored, diagonal lines have an offset according to the across-neuron average of the maximum IPD-weighting position/modulation frequency (color codes as in previous figures). Data from the IC example neurons in Figs. 3 and 4 can be found in B and C marked “47” and “98,” and data from the MSO examples in Figs. 5 and 6 can be found in E and F marked “1” and “8”. Note that static IPDs are defined with respect to the beat direction (i.e., sign inverted when f_contra < f_ipsi). Therefore, data from the same neuron are plotted at 2 different best static IPD values (if both fulfill the criteria). For instance, IC neuron #81 (C: best IPD 88° contralateral leading) is either plotted at a best IPD of +88° (c81) or at −88° (i81).

In Fig. 7, C and F, each neuron's preferred static IPD (extracted from the data shown in Figs. 3I–6I) was plotted as a function of its best start IPD obtained from the AMBB-tuning curve (Figs. 3, G and K–6, G and K). The dashed, black diagonals in Fig. 7 plot the expected position of data points if the energy maxima of the AM would dominate the IPD weighting. A vertical offset from this diagonal is a simple estimate of how much the IPD dominance deviates from the energy maximum. The downward shift, observed in all cases, corresponds to dominance of IPDs within the rising segment of the AM. The colored diagonals indicate the average difference between best static IPD and best start IPD for each modulation frequency. Although this method is not as accurate a means of determining the dominance region as the estimation the IPD-weighting function using Eq. 5 and does not provide a measure of its width, this display is similar to that used for plotting the psychoacoustic data in Dietz et al. (2013b) (Fig. 3). In line with the psychoacoustic data, most neural data points are below the main diagonal at 180°, indicating that the neural response is dominated by IPDs occurring during the rising slope of the AM cycle.

The strong bias toward the rising slope of the AM cycle suggests that rapid adaptation is likely to reduce neural responses over the remainder of the cycle. The question remains whether adaptation before or after binaural interaction underlies the observed weighting of spatial information. A simple model considering both processing schemes illustrates that only adaptation occurring before binaural integration can explain the observed data (Fig. 8): whereas pre- and postbinaural adaptation influences the static AM cycle histograms [Fig. 8H1 is similar to Fig. 8H2, consistent with the data of Ingham and McAlpine (2004)], only adaptation arising before binaural integration shifts the maximum IPD weighting toward the rising slope (Fig. 8G1 differs from Fig. 8G2), so that in accordance with the neural data, the IPD-weighting function and the static AM cycle histogram have a similar peak position (peak of Fig. 8G1 identical to peak in Fig. 8H1).

Fig. 8.

Comparison of 2 processing schemes with an auditory model. Left: prebinaural adaptation (adapt.); right: postbinaural adaptation. Note that the processing stages do not refer to specific brain nuclei. Prebinaural can be, for example, in the auditory nerve, the cochlear nucleus, or the synaptic transmission at the MSO neurons. Postbinaural means the MSO output. A1 and A2: the 2 processing schemes. B1 and B2: 4 AMBB input stimuli with different start IPDs (blue represents the left and red the right ear's signal). C1 and C2: AM cycle histograms at an intermediate processing stage (C1: after peripheral processing and adaptation but before binaural interaction; C2: after peripheral and binaural processing but before adaptation). D1 and D2: AM cycle histograms at the model output (corresponding to the data presented in Figs. 3C–6C). E1 and E2: normalized static IPD-tuning curve of the model (corresponding to the data presented in Figs. 3I–6I). The model does not include an internal, interaural delay compensation, so its best IPD is 0. F1 and F2: normalized AMBB-tuning curve as a function of start IPD (corresponding to the data presented in Figs. 3K–6K). G1 and G2: IPD-weighting function derived from the 2 tuning curves in E1 and E2 and F1 and F2 (corresponding to the data presented in Figs. 3J–6J). H1 and H2: average AM cycle histogram (corresponding to the data presented in Figs. 3E–6E). It can be seen that the model with prebinaural adaptation has its highest response with start IPD = 270° (D1, top), whereas the postbinaural adaptation model has its maximum response with start IPD = 180° (D2, 2nd from top). This results in different IPD-weighting function with rising-slope dominance only observed with prebinaural adaptation (left), whereas the average AM cycle histograms of both models are very similar with peaks at 90°.

DISCUSSION

Our data indicate that ITD-sensitive neurons in the brain stem and midbrain show evidence of a readout window for ITD cues during each cycle of an ongoing, modulated sound. At least some neurons appear to glimpse spatial cues conveyed by the temporal fine structure during the rising portion of the modulation cycle, ignoring spatial information conveyed in later, higher-energy components of the ongoing waveform. This is likely beneficial for spatial listening in reverberant listening conditions, where late-arriving signals may contain spurious (and rapidly changing) spatial information. These single-neuron data from small mammals are consistent with recent behavioral and human-imaging data, indicating a readout window for spatial information during the early, rising portion of each modulation cycle comprising an ongoing, complex sound.

Relation to human data from AMBBs.

With the comparison of data from the current study with the psychoacoustic and MEG data recorded with AMBB stimuli (Dietz et al. 2013b), all four data sets (gerbil MSO, guinea pig IC, human MEG, and human psychoacoustics) indicate a strong dominance of IPDs during the rising portion of each modulation cycle (Table 1). The earliest dominance within the modulation cycle is observed at low modulation rates in the human psychoacoustic data (37° at 4 Hz and 40° at 8 Hz). There is then a systematic increase of the dominant cycle position with increasing modulation rate. At 64 Hz, the dominant position lies at 115° for the human psychoacoustic data and 138° for the human MEG data.

Table 1.

Summary of the maximum IPD-weighting position within the AM cycle for all methods

Method	Criterion	4 Hz	8 Hz	16 Hz	32 Hz	64 Hz
MSO	Cell mean	112°	98°	122°	123°	136°
	10th Percentile	68°	56°	89°	86°	105°
	90th Percentile	160°	138°	206°	174°	161°
IC	Cell mean	137°	99°	113°	143°	125°
	10th Percentile	55°	45°	72°	98°	85°
	90th Percentile	192°	160°	149°	193°	166°
Psycho	6 Subject mean	37°	40°	62°	83°	115°
MEG	7 Subject mean				108°	138°

A dominance of the rising portions (0–180°) in the ongoing envelope is found throughout all methods and modulation frequencies. A detailed explanation is given in the main text.

IPD, interaural-phase difference; AM, amplitude modulation; MSO, medial superior olive; IC, inferior colliculus; Psycho, psychoacoustic; MEG, magneto-encephalography.

The single-neuron recordings concur better with the MEG data in that the most dominant region observed with both of these methods occurs slightly later than in the psychophysical data but still during the rising slope. In contrast to the human data, the mean single-neuron data appear not to depend systematically on modulation frequency. Although many neurons show a strong IPD emphasis during the rising slope, there were also many neurons consistently showing an emphasis between 135° and 195° at all modulation frequencies. To quantify this finding, the data were, once more, analyzed in terms of slope-sensitive and peak-sensitive conditions. Table 1 shows the 10th and the 90th percentiles of the maximum IPD-weighting positions for each modulation frequency, indicating that for the slope-sensitive conditions (10th percentile), the maximum IPD-weighting position indeed increases systematically with modulation frequency. Notably, these values are similar to the (mean) human behavioral data. This is especially true for 8–32 Hz for both MSO and IC data. The maximum IPD-weighting positions at 4 Hz in the IC data and at 4 Hz and 64 Hz in the MSO data are different than the maximum IPD weightings observed in humans. The trend of the position change with changing AMBB frequency is also not apparent. We suggest that these modulation frequencies are a little beyond the frequency range for which “glimpsing” of IPD information during the rising slope is effective for these species. Similarly, these frequencies have been reported to be close to the limits of glimpsing in the human data (Dietz et al. 2013b), but for the current single-neuron data, the frequency range appears even more restricted. At the other end of the distribution (90th percentile), the maximum IPD-weighting positions are close to 180° and show no systematic frequency dependence.

Based on the variety of neural response types and the similarities of slope-type conditions and human perception, it might be speculated that slope-sensitive neurons contribute to the perceptual lateralization of sounds, whereas—perhaps even more speculatively—peak-sensitive neurons might be more important in encoding other features of the acoustic space, such as interaural coherence, from which subjects can obtain information about the acoustic scene (i.e., room size, number of sources, etc.). This dichotomy might also be conceptualized as coding of foreground vs. coding of background spatial information.

Relation to previous physiological studies.

Most previous studies of binaural hearing have focused their endeavors either on unmodulated, low-frequency stimuli or on high-carrier frequency AM stimuli [reviewed by Joris et al. (2004)], because perceptually, the lateralization cue of pure envelope ITDs in low-frequency AM stimuli is very weak compared with ITDs in the temporal fine structure (Bernstein and Trahiotis 1985). A few, more recent, physiological studies, examining neural sensitivity to high-frequency envelope ITDs, also focused on potential differences between the rising and the falling portions of the ongoing envelope of high carrier-frequency stimuli (Dietz et al. 2013a; Nelson and Takahashi 2010) and report a much stronger influence of the rising segment.

In contrast to the studies using high carrier-frequency AM stimuli, however, it is not the envelope ITD under investigation here but, rather, the influence of an in-phase envelope on dynamic ITD processing in the temporal fine structure. Sterbing et al. (2003) also investigated the influence of an in-phase AM on the IC response but only on (quasi-) static IPD processing. Consistent with the current data, they reported a maximum response early in the modulation cycle and that static IPD-tuning functions of unmodulated and modulated stimuli are similar in shape and best IPD position. Additionally, they reported that some neurons show a higher firing rate for unmodulated stimuli—an observation not reflected in the current data set. A likely explanation for this difference is that these authors measured neural responses for sounds with constant peak amplitude (i.e., the unmodulated tones had a higher RMS level), whereas the current study measured neural responses for a constant RMS level. Studies investigating binaural processing at the level of single neurons often use binaural beats of very low beat frequencies, usually 1 Hz (Fitzpatrick et al. 1997; Joris 1996; Sterbing et al. 2003; Yin and Chan 1990; Yin and Kuwada 1983). The slow beats have been used as quasistatic IPD, to obtain complete IPD-tuning curves efficiently with one continuous stimulus. In combination with AM (Sterbing et al. 2003), these stimuli are, in fact, slow binaural beats with an amplitude modulation but should not be confused with those of the current study, because the beating in their stimuli was not synchronized with the AM.

Binaural beats with high beat rates but without a synchronized AM have also been used in single-neuron recordings in the brain stem (Siveke et al. 2008), as well as at the level of the IC (Fitzpatrick et al. 2009), and reveal a high temporal resolution of the binaural system at these subcortical stages. In line with these studies, the unmodulated binaural beat control conditions in the current study also show a phase-locking at the highest tested beat frequency of 64 Hz in some neurons (e.g., Figs. 3, D and F, and 6, D and F).

Our data demonstrate that the position within the AM cycle that shows the maximum IPD weighting is correlated with the position of the response peak to static IPDs conveyed with an AM cycle. This can be interpreted as a linear and instantaneous coincidence detection (in line with, for example, van der Heijden et al. 2013) in primary binaural neurons (e.g., in the MSO): each neuron codes the IPD with a weighting, according to the characteristics of its response to the AM cycle. However, the main outcome from the current study is not only that these factors are correlated but also that both quantities are strongly dominated by IPDs within the rising slope of the AM cycle.

No existing physiological data are available to quantify the strength of adaptation to AM stimuli that occurs before the stage of binaural integration. (Latency-corrected, modulation-cycle histograms of bushy cells of the cochlear nucleus would be an important measure, but we are unaware of any published data to this effect.) However, even without latency correction, the skewed response of auditory nerve fibers to sinusoidally amplitude-modulated (SAM) tones (Joris and Yin 1992) suggests a strong dominance of the rising slope, resulting from spike-rate adaptation. Furthermore, recordings to a train of short tone pulses in fibers of the trapezoid body, which leave the cochlear nucleus to innervate the binaural nuclei, indicate that adaptation reduces the spike rate to approximately one-half of its maximum, <10 ms after the onset of a tone pulse (Fig. 7B in Joris et al. 1994). With tone-pulse repetition rates of 10 Hz, the temporal properties are indeed comparable with the current SAM cycle histograms at 8 Hz or 16 Hz. These data also suggest some form of temporal adaptation, in that action potentials generated earlier during the pulse train show higher temporal precision than those generated later during the pulse train. In terms of binaural coincidence detection, this would result in fewer coincidences at best IPD later during the pulse train or, here, occurring later within each modulation cycle. Thus both spike-rate adaptation and temporal adaptation likely contribute to the biasing of ITD sensitivity toward the rising portion of the AM cycle. This is consistent with Kuznetsova et al. (2008), who reported that at least in the avian auditory system, temporal adaptation in the cochlear nucleus plays a critical role in enhancing sensitivity to ITDs at stimulus onset.

Nevertheless, cellular mechanisms, contributing to enhanced slope sensitivity, remain unclear. Although low-threshold potassium channels are reported to shape response sensitivity for the rising stimulus slope in MSO neurons, thereby resetting the membrane potential during each stimulation cycle (Gai et al. 2009), these channels act on very short time scales. It seems unlikely that these channels contribute to the adaptation effects that we observed during AMBB stimulation, which by contrast, accumulated over multiple cycles of the temporal fine structure.

Implications for models of binaural interaction.

Many existing binaural models that account for perceived lateralization lack a realistic stage of preprocessing that includes the prebinaural adaptation necessary to model any dominance of the rising segments and are therefore unable to explain the perceived lateralization of the AMBB stimuli (Dietz et al. 2009; Stern and Shear 1996). Even models that include adaptation (Breebaart et al. 2001; Dau et al. 1996; Klein-Hennig et al. 2011) do not generate a significant imbalance between the rising and the decaying portions of the stimulus envelope. More physiologically based auditory models (Meddis 2006) do include a much stronger response enhancement during the rising segments of each AM cycle. Such models have been applied previously in binaural studies and revealed, for example, the influence of hair-cell adaptation on the precedence effect (Hartung and Trahiotis 2001). This model concept is supported by human data of evoked auditory brain stem and evoked otoacoustic emissions to precedence-effect stimulation paradigms (Bianchi et al. 2013), which emphasize the contributions of the cochlea to suppression of lagging transient sounds. Further studies need to be conducted to verify if and how such findings from these precedence-effect studies, which usually report lag suppression for delays of 1–12 ms, can be related to the rising slope dominance reported here.

Summary and conclusions.

1) The IPD sensitivity of both MSO and IC neurons is strongly emphasized during rising segments of AM sounds, at least for a subpopulation of neurons. The IPD sensitivity of many other neurons is maximal, just before the peak of each AM cycle. Fewer than 5% of the responses to all conditions showed a maximal IPD sensitivity after the modulation peak. No condition had a maximum IPD sensitivity >45° after the modulation peak. 2) The AM cycle position with the maximum IPD weighting correlated with the peak position of the static AM cycle response-rate histogram. 3) The similar frequency dependence of IPD weighting, observed in the 10th percentile of the most slope-sensitive IC and MSO neurons with that observed in the human behavioral data, suggests that this specific subpopulation of neurons might predominately contribute to the perceived spatial locations of amplitude-modulated sound sources. 4) Adaptation before binaural interaction is the most likely mechanism for the observed effect.

GRANTS

Support for this research was provided by the U.K. Medical Research Council Programme (grant G1002267 to D. McAlpine). Support for M. Dietz was provided by the Alexander von Humboldt Foundation with a Feodor Lynen Fellowship.

DISCLOSURES

The authors declare that there are no conflicts of interest.

AUTHOR CONTRIBUTIONS

Author contributions: M.D., T.M., and D.M. conception and design of research; M.D. and A.S. performed experiments; M.D. and T.M. analyzed data; M.D., T.M., and D.M. interpreted results of experiments; M.D., T.M., and A.S. prepared figures; M.D. drafted manuscript; M.D., T.M., A.S., M.P., B.G., and D.M. edited and revised manuscript; M.D., T.M., A.S., M.P., and D.M. approved final version of manuscript.