Similarities in error processing establish a link between saccade prediction at baseline and adaptation performance

Abstract

Adaptive processes are crucial in maintaining the accuracy of body movements and rely on error storage and processing mechanisms. Although classically studied with adaptation paradigms, evidence of these ongoing error-correction mechanisms should also be detectable in other movements. Despite this connection, current adaptation models are challenged when forecasting adaptation ability with measures of baseline behavior. On the other hand, we have previously identified an error-correction process present in a particular form of baseline behavior, the generation of predictive saccades. This process exhibits long-term intertrial correlations that decay gradually (as a power law) and are best characterized with the tools of fractal time series analysis. Since this baseline task and adaptation both involve error storage and processing, we sought to find a link between the intertrial correlations of the error-correction process in predictive saccades and the ability of subjects to alter their saccade amplitudes during an adaptation task. Here we find just such a relationship: the stronger the intertrial correlations during prediction, the more rapid the acquisition of adaptation. This reinforces the links found previously between prediction and adaptation in motor control and suggests that current adaptation models are inadequate to capture the complete dynamics of these error-correction processes. A better understanding of the similarities in error processing between prediction and adaptation might provide the means to forecast adaptation ability with a baseline task. This would have many potential uses in physical therapy and the general design of paradigms of motor adaptation.

the maintenance of accurate motor control is aided by the monitoring and processing of the errors of prior movements. Although this capability is most commonly studied with the phenomenon of motor adaptation (i.e., the ability to appropriately adjust motor commands in response to consistent, artificially exaggerated movement errors), such error-correction mechanisms are engaged continuously as we interact with the world around us. This implies that there may be signatures of motor adaptation in the dynamics of everyday normative (baseline) behaviors, even if those behaviors are not artificially stressed by adaptation paradigms.

Surprisingly, however, no such relationship has been clearly demonstrated between the trial-to-trial fluctuations in normative behavior (that is, the “noise” present across a given series of movements) and the capacity to adaptively alter movements when they become inaccurate. Although efforts have been made to characterize trial-to-trial learning in nonadaptation contexts (e.g., van Beers 2009; van Beers et al. 2013), they have tacitly assumed that this mechanism and the learning process that occurs during adaptation are identical. Wu et al. (2014) have recently taken a step in this direction by suggesting that the amount of variability exhibited during baseline reaching movements is correlated with the ability to adapt to a force field. However, it is unclear whether this relationship arises because subjects who have greater variability in their reaches inadvertently stumble upon the most appropriate solution to counteract the perturbation or whether the variability actually reflects the employment of a systematic trial-to-trial learning process.

Here we applied time series analysis to quantify the amount of structure present in the temporal order of consecutive movement amplitudes as evidence of an active learning process that operates across trials. We sought to confirm the existence of such a relationship between the constant recalibration processes occurring during normative (baseline, nonadaptive) behaviors and “learning” during adaptation paradigms. To do so, we used a particular type of baseline movement (predictive saccades) in which we have previously characterized the nature of these intertrial correlations (as having statistical long memory, manifest as a power-law decay of intertrial correlations; Wong and Shelhamer 2011a). We show that the intertrial correlations an individual exhibits in a series of stereotypical baseline movements reveals information about his or her capacity to adapt, suggesting that these two behaviors incorporate the same error-correction process.

Adaptation has been well studied in numerous motor systems and describes the process by which performance errors modify future behavior in order to maintain accurate long-term performance. The error signal that supports this learning process has recently been shown to be the difference between the observed movement outcome and the predicted movement outcome (Collins and Wallman 2012; Haith and Krakauer 2013; Mazzoni and Krakauer 2006; Miall and Wolpert 1996; Tseng et al. 2007; Wong and Shelhamer 2011b). This is illustrated particularly well with the saccadic eye movement system. Saccades are rapid eye movements used to bring objects of interest onto the fovea. Such movements typically occur with too short a duration to be influenced by online feedback corrections. Hence, error signals are primarily used to update the next generated movement (adaptation) rather than to directly influence the current movement (online feedback adjustments), and so each saccade may be treated as an approximate readout of the current state of the oculomotor system. Since perception of the visual scene is not available during a saccade (Matin 1974; Zuber and Stark 1966), the saccade double-step paradigm (in which a surreptitious target shift occurring during the saccade produces a larger-than-expected postsaccadic error, leading to an update of the gain-state of the saccadic system) provides a straightforward means of studying adaptation (McLaughlin 1967). In particular, this paradigm is useful for isolating the error signal that drives adaptation.

Adaptation is thought to drive changes in performance according to the current state of the motor system and an estimate of the error made on the current trial. This is typically modeled as a Markovian state-space process (autoregressive moving average, or ARMA) (Cheng and Sabes 2006). Although such a model captures many features observed during adaptation, state-space models are intended to fit stationary data (data that, in the weak sense, do not vary in their mean and variance across time; e.g., Box and Jenkins 1970). Thus it is problematic to fit a state-space model to adaptation data, which, by definition, arise from a nonstationary process. As a result, these models primarily fit the nonstationary adaptation learning curve and treat observed trial-to-trial fluctuations as noise—particularly those observed during stationary baseline behavior—rather than as arising from an underlying learning process. However, these error corrections during baseline movements made in the absence of any experimenter-imposed manipulation (e.g., a target double step during saccade adaptation paradigms that induces a particularly large movement error) are most reflective of the behaviors generated in daily life. As such, it is important that descriptions of error signals and learning processes that maintain movement accuracy during laboratory-induced adaptation phenomena also apply to baseline behavior.

Previous work (including our own with saccades; see Wong and Shelhamer 2011a) focusing on baseline behavior suggests that active error-correction processes exist and are related to efforts to maintain consistent long-term performance. During reaches and large gaze shifts, for example, van Beers et al. (2013) argued that a lack of correlation between consecutive movements suggests the presence of rapid learning that compensates for single-trial movement errors. The existence of an intertrial error-correction process in baseline behavior is particularly evident in the generation of predictive saccades. In this paradigm, subjects are asked to generate saccades between two fixed targets at a rapid, constant pacing rate (∼0.5–1 Hz). This stimulus strongly encourages subjects to automatically produce movements in anticipation of future target appearances, leading to eye movements that occur with very short or even negative latencies (<70 ms; Leigh and Zee 2006; Stark et al. 1962). Such short reaction times indicate that these saccades are initiated without use of visual information about the current target stimulus, and instead are produced by using a prediction of the movement that will be required on the next trial. Subjects are not aware that they make these predictive saccades, as they find it difficult to avoid producing one or two additional saccades when the targets abruptly shut off at the end of the paradigm (Joiner and Shelhamer 2006a). On the other hand, when subjects are asked to continue making saccades to remembered targets with the same amplitude and timing after the targets are turned off, saccade amplitude and timing accuracy rapidly deteriorate within a few trials (unpublished observation). This implies that an implicit error-correction process—not working memory—is used to adjust the performance of future anticipatory movements to keep each predictive saccade reasonably accurate. Because of these trial-to-trial error corrections, overall performance remains approximately statistically stationary (mean behavior and variance are constant over time), with no global behavioral change as might be observed for an adaptation paradigm. Therefore, fluctuations in behavior during this task may be appropriately modeled with the tools of time series analysis (Wong and Shelhamer 2011a).

The most natural error signal to use when modeling the predictive-saccade paradigm is the error of the predictive-saccade end point. Note that since a predictive saccade is aimed at the anticipated target location, the true target location can be considered a surrogate for the expected motor outcome and the predictive saccade is the observed motor outcome; then, the predictive-saccade error is by definition the difference between the actual and expected motor outcomes. Hence, the predictive-saccade paradigm is likely to invoke a learning signal comparable to that used in saccade adaptation (Wong and Shelhamer 2012), even though the generation of predictive saccades can be classified as a “baseline” task since an artificial stimulus perturbation is not imposed.

Investigation of the predictive-saccade process shows that the underlying error-correction mechanism may be far more complex than accounted for by state-space (ARMA) modeling and may instead benefit from examination using the tools of fractal analysis (notably, examination of the power spectrum to characterize intertrial correlations). Intertrial correlations in the predictive-saccade task, which describe the manner in which prior performance information influences future trials, decay much more slowly (as a power law) than those generated by a typical state-space process (exponential decay) (Joiner and Shelhamer 2006b, 2009; Wong and Shelhamer 2011a). This suggests that performance errors from very far in the past can strongly influence the manner in which future behavior is updated. Such power-law decay of intertrial correlations across time further indicates that the error-correction process may be best characterized as a fractal process (i.e., a process with scale invariance), in which the amount of intertrial behavioral fluctuation varies proportionally with the timescale across which those fluctuations are measured. That is, the power spectrum of a fractal process typically decays as a power-law function of frequency, and the strength of intertrial fluctuations is a power-law function of the timescale across which they are measured (Lowen and Teich 2005; see materials and methods).

Since fractal descriptions better characterize the error-correction process in baseline behavior (e.g., intertrial fluctuations during a predictive-saccade task), perhaps fractal models may also be used to describe some aspect of the adaptation process and in this way draw a link between the phenomenon of adaptation and the variations in baseline behavior. Here we show that this is indeed the case by demonstrating that a fractal parameter describing fluctuations in performance during a predictive-saccade task correlates with the rate of learning exhibited during a saccade adaptation paradigm. This correlation implies that baseline variability (“noise”) in behavior is actually meaningful, as its temporal structure contains information that can be used to characterize the error-correction process that is engaged during saccade adaptation. Such findings speak directly to the existence of a strong relationship between trial-to-trial variability (“noise”) during baseline tasks and the learning process that works to reduce a large consistent (artificially exaggerated) error across many trials during adaptation, likely arising from a common underlying error-correction process.

MATERIALS AND METHODS

Saccadic eye movement tasks were administered to 16 human subjects (12 subjects were recruited for this experiment, and data were also analyzed from 4 subjects who participated in a previous experiment whose methodology was consistent with the requirements of this study but whose data had not been analyzed in this fashion). All subjects (9 men, 7 women) provided written informed consent, and protocols were reviewed and approved by the local institutional review board.

The experiment involved separate prediction and adaptation tasks performed within the same testing session. “Baseline” intertrial error corrections were assessed with a standard predictive-saccade task (Wong and Shelhamer 2011a). This task encourages subjects to automatically generate a movement in expectation of the next target appearance (latency < 70 ms) before visual information about the target can be processed (Leigh and Zee 2006). During the predictive-saccade task, 300 horizontal saccades (10° amplitude) were made to alternating targets at fixed locations (±5°), paced at a constant rate (0.9 Hz). Intertrial correlations of successive primary-saccade amplitudes are quantified by methods developed for the analysis of fractal scaling, which assess behavioral fluctuations over time. One approach to characterizing the structure of these fluctuations is a power-spectrum analysis of the sequence of consecutive movement amplitudes (Beran 1994; Rangarajan and Ding 2000). For fractal processes, the power spectrum is expected to decay as a power-law function of frequency (i.e., power scales as a function of the frequency at which it is measured; this implies that the underlying process exhibits scale invariance, one of the hallmarks of fractal time series). The power spectrum, calculated as the squared magnitude of the Fourier transform of the time series, is also the Fourier transform of the autocorrelation function (Papoulis 1984) and thus equivalently provides a measure of the strength of intertrial correlations across different timescales.

Power-law scaling of the power spectrum suggests that intertrial correlations decay gradually, at less than exponential rate. In contrast, simple state-space (ARMA) processes generally exhibit intertrial correlations that decay exponentially and might be expected to exhibit power spectra that reflect such a decay. That is, exponential decay of the autocorrelation function should yield, via the Fourier transform, a power spectrum akin to a low-pass filter in that the power is constant at lower frequencies (Fig. 1; Stadnitski 2012). Power-law decay of the power spectrum suggests that intertrial fluctuations persist over all timescales and scale as a function of the time interval under examination (i.e., it is consistent with a fractal process). This stands in contrast to a state-space (ARMA) process, in which the timescales across which strong intertrial correlations exist must be predefined in the model. In practice, evidence for fractal processes is only available across the range of timescales that can actually be measured within a given experiment, in this case ranging from within-saccade kinematic changes and single-trial error corrections to a few hundred trials (or seconds to about an hour). It is left to the researcher to assume that such power-law behavior continues to exist across longer timescales. Nevertheless, we can be more certain about the presence of fractal structure in this behavioral process as we have previously shown for the predictive-saccade paradigm that our power-spectrum analysis returns results that are consistent with those of more complex forms of fractal analysis techniques, such as calculation of the Hurst exponent or autoregressive-fractionally integrated-moving average (ARFIMA) modeling (Wong and Shelhamer 2011a).

Fig. 1.

Comparisons of fractal and state-space models. A: examples of simulated time series for a fractal model {autoregressive-fractionally integrated-moving average [ARFIMA(0,0.22,0)], as suggested by Wong and Shelhamer 2011a, left} and a state-space model (parameters taken from Smith et al. 2006, right) were compared. B: power spectra for the 2 models were examined. Whereas the power spectrum decays linearly on log-log axes for the fractal model, there is a clear inflection in the power spectrum of the state-space model and it appears akin to that of a low-pass filter, as expected. This inflection can be confirmed by demonstrating a preferred piecewise-linear regression fit over a single linear regression fit according to the Bayesian information criterion (methods described in Wong and Shelhamer 2011a). C: detrended fluctuation analysis (DFA) analysis of the time series in A shows that whereas the fractal time series exhibits consistent scaling across all window sizes, the state-space time series exhibits a change in scaling depending on window size (note in particular the change in slope at large window sizes), consistent with the power spectra presented in B.

The strength of persistent intertrial correlations can be quantified by measuring β, the negative of the slope of a linear regression fit to the power spectrum across the entire frequency range when plotted on log-log axes (see Fig. 2). Larger β values indicate stronger intertrial correlations across very long timescales (statistically, long memory) or less resemblance to a white noise uncorrelated process (β = 0). Values of β > 0 are typically thought to reflect an underlying persistent process, meaning that successive observations tend to be more similar to each other and fluctuate about the mean less than a white noise process. An extreme example of a persistent process is a random walk, in which the value of the process tends to remain on one side of the mean for very long periods of time. When β is <0, the process is considered antipersistent, as it fluctuates rapidly about the mean at a rate more frequently than chance. Thus β reflects the rate of decay of intertrial correlations, consistent with its mathematical relationship to the rate of decay of the autocorrelation function. An example time series of predictive-saccade amplitudes and the corresponding power spectrum are presented in Fig. 2, A and B. The significance of an individual β value can be approximated with a bootstrapping technique in which, for a given time series, a large number of surrogates (e.g., 1,000) are generated by randomly shuffling the order of data points. By assessing β for each surrogate, a distribution of β values may be approximated; the probability of observing the true β value can be calculated from this distribution. Since these bootstrapped distributions are generally centered at zero (recall that β = 0 for a random white noise process; average of the means of the surrogate-β distributions for all subjects is 0.0004 ± 0.003), this analysis supports the claim that a given β value is different from zero. The strength of intertrial correlations may also be assessed with a time-domain approach such as detrended fluctuation analysis (DFA) (Peng et al. 1994), which serves as a complement to frequency-domain analyses like the power spectrum method although it requires more computational manipulation. DFA assesses long-range correlations by dividing the data into windows of fixed duration and measuring the average fluctuations within each window (e.g., the root mean square of the linear regression residuals within each temporal window). The DFA parameter α is the slope (on log-log axes) of these average fluctuations plotted against the size of the window. As with the power spectrum technique, fractal processes will exhibit fluctuations that increase as a power-law function of the window size (that is, it scales linearly on a log-log plot); state-space (ARMA) processes will be linear only for short timescales (Morariu et al. 2007). The DFA α value and the power spectrum β value are related by the equation β = 2α − 1. Thus DFA (as with the Hurst and ARFIMA modeling efforts in our prior work) may be used to confirm the evidence of fractal structure measured with the power-spectrum technique in these predictive-saccade data (see also Crevecoeur et al. 2010).

Fig. 2.

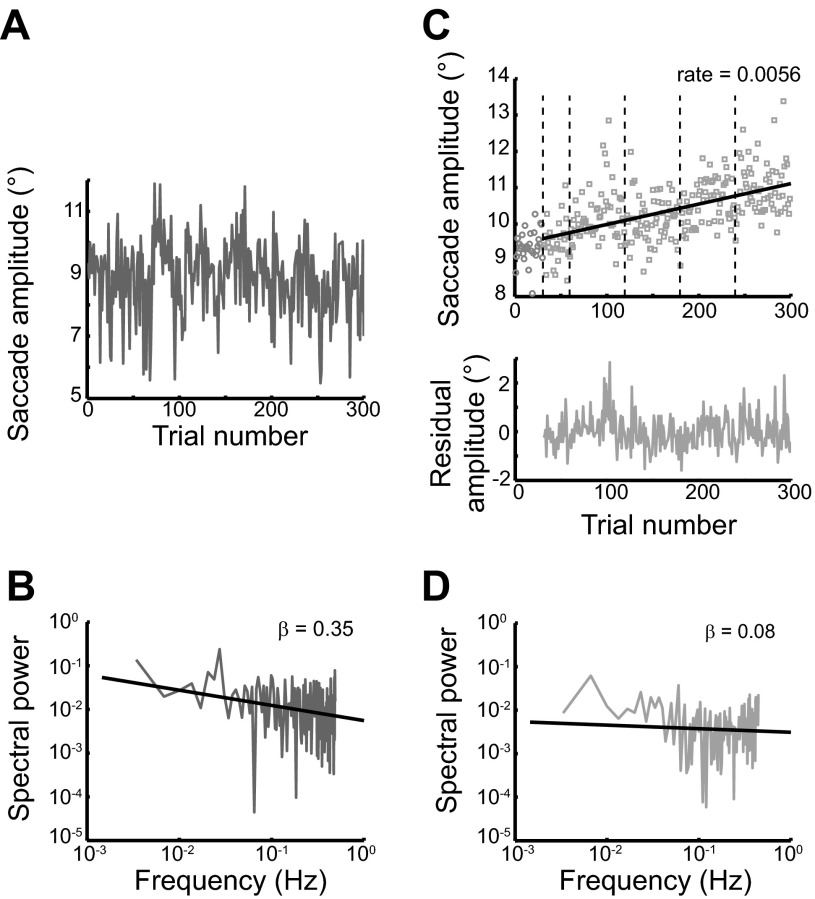
Structure of predictive saccades and adaptation. A: time series of predictive-saccade amplitudes from 1 subject. B: the corresponding power spectrum for the time series in A; power-law scaling of the power spectrum and a nonzero β value suggest fractal structure. C: adaptation data from 5 blocks (300 trials) for the same subject as in A. The double-step paradigm begins at trial 31; the first 30 trials are baseline assessments of movement gain. Adaptation rate is assessed with a linear regression fit to the data. When this fit is subtracted, the time series of adaptation residuals remains (bottom). D: power spectrum of the adaptation residuals shown in C.

The second portion of the experiment involved an assessment of adaptation using a conventional saccadic double-step task (McLaughlin 1967), in which a surreptitious displacement of the target during the saccade resulted in movement errors that were larger than expected. Repeated exposure to a consistent target shift (here, an outward displacement of 25% of the initial target jump) causes a systematic change of saccade gain (calculated as the primary saccade amplitude divided by the magnitude of the initial target jump) such that subjects learn to generate a saccade toward the displaced target in response to viewing the primary target (sample data are presented in Fig. 2). Subjects performed five adaptation blocks of 60 trials each. The first 30 trials of the first block contained no double step (10° amplitude, targets located at ±5°); these trials were used to assess preadaptation saccade kinematics. The remaining trials were adaptation trials, and saccades were made alternately to the right and left symmetrically across the vertical midline with a primary amplitude of 10° and a double step of 25% (2.5°). For example, starting from the fixation point located at 6.25°, the target initially stepped leftward by 10° to −3.75°; during the saccade, the target was further displaced by 2.5° to −6.25°. This then became the initial fixation point for the next rightward trial. Between blocks, subjects were given brief rest periods (∼30 s) during which they remained seated in darkness with their eyes closed to minimize deadaptation.

Adaptation data were analyzed in two ways. First, aspects of the adaptation process itself were examined. Adaptation rate was determined by fitting a regression to all adaptation trials (i.e., from trial 31 in the first adaptation block to the end of block 5). Linear regressions are reported because they consistently fit the data better than exponential regressions. Adaptation extent was computed as the difference in saccade gain of the last 30 trials of the adaptation session and the initial gain measured during the 30 nonadaptation trials (when no double step occurred), divided by that initial saccade gain. However, the adaptation session was brief enough that not all subjects may have fully adapted (i.e., reached an asymptote in their adaptation) by the end of the paradigm; hence, correlations with measures of percent gain change were not generally performed. Finally, kinematic changes during adaptation were evaluated. In particular, saccade peak velocity (i.e., the maximum velocity attained during the primary saccade) and duration (i.e., the time from saccade onset to the end of the saccade, as evaluated according to the velocity criterion mentioned below) were calculated for each saccade. Changes in these kinematic parameters were calculated by comparing saccades in the initial 30 nonadapting trials to the final 30 adaptation trials of the session.

Second, regression fits were subtracted from the adaptation data to obtain regression residuals; the correlation structure of these residuals was assessed with the same power-spectrum technique described above (data from 1 subject presented in Fig. 2, C and D). Although these residual data are concatenated from five short blocks instead of a single continuous data set and are thus not ideal for the application of fractal analysis techniques, these techniques are applied on a per-trial basis rather than a temporal basis (i.e., data are assessed in terms of trial number, not by the time of saccade occurrence). Furthermore, the short duration of breaks between blocks and the requirement to maintain eye closure while remaining seated in a completely dark room help reduce any dramatic deadaptive changes in saccade amplitude between blocks; the average amplitude difference for each subject between the end of the previous block and the start of the next block is quite minimal (0.09 ± 0.24°; not significantly different from zero, P = 0.13). Note that the correlation structure of the adaptation data cannot be directly analyzed with these fractal methods because the data are, by definition, nonstationary. Instead, we analyze the adaptation residuals (which have been detrended to remove to a large extent the nonstationarity; see Brockwell and Davis 2002) and infer from the correlation structure of the residuals what is occurring during the adaptation process.

In all experiments, subjects sat in a dark room in a stationary chair, and a bite bar was used to minimize head movements. Targets were rear-projected onto a screen 1 m in front of subjects with a mirror-controlled red laser dot 2 mm in diameter. Data were sampled at 1,000 Hz and acquired on a PC-compatible Pentium 166-MHz computer running real-time experiment control software developed in-house. Eye movements were recorded with a scleral search coil in a magnetic field (Robinson 1963) from either the right or left eye. Saccades were analyzed off-line with an interactive MATLAB computer program (The MathWorks, Natick, MA). Saccades were selected according to a velocity threshold (>15°/s) and subsequently verified by visual inspection. For each predictive-saccade or adaptation session, consecutive primary-saccade amplitudes were concatenated to form time series for analysis. When blinks occurred during saccades, those trials were discarded. Subjects were asked to refrain from blinking during saccades, although because of the length of individual blocks (especially the long predictive-saccade block) it is impossible to avoid blinking altogether. With the exception of one subject, on average this led to the removal of only 3% of all trials in a given time series because of blinks. (This single subject's data were found to be consistent with those of the other subjects in other respects despite the removal of ∼17% of all saccades and so were retained in these analyses.)

RESULTS

All subjects exhibited persistent behavioral fluctuations during the predictive-saccade task (average β ± SD: 0.26 ± 0.06), which reflect trial-to-trial amplitude modulations in response to errors. Although small, these fluctuations were different from a random, white noise process (as a group β > 0, t-test, P < 0.01; individually, the bootstrap analysis revealed that 12 of the 16 subjects' β values were large enough that they are <5% likely to have been observed if the data were uncorrelated white noise). Thus behavioral changes appropriately responded to prior performance fluctuations. DFA was used to confirm that these data exhibited fractal structure; DFA α values converted to equivalent β values were not significantly different from the measured power-spectral β values (paired t-test between β and β_{DFA-calculated}, P = 0.80). Furthermore, these β values were consistent with those previously reported for this task, in which we applied several additional fractal analysis techniques to confirm that the measured values were not artifactual (Wong and Shelhamer 2011a). Note that β values were not related to the quality of overall predictive performance. That is, β did not correlate with the average predictive-saccade amplitude at the conclusion of the task (r² = 0.004, P = 0.81). The β values also did not correlate with any change in amplitude that occurred across the task (r² = 0.3, P = 0.51), particularly as the predictive-saccade amplitude data were essentially stationary and exhibited no long-term trends (average regression slope of saccade amplitudes across the predictive-saccade task, −0.0005 ± 0.0015°/trial; not significantly different from zero, t-test, P = 0.22). Instead, β appears to quantify behavioral fluctuations across all timescales that arise from intertrial learning.

The interpretation of a β value comes directly from comparing the observed value to that of a white noise process (β = 0). β Values > 0 (i.e., persistent processes) exhibit relatively higher power in the low-frequency range; that is, a larger β value suggests a process that favors relatively short-term trial-to-trial consistency. Such fluctuations might be observed during an error-correction approach in which a portion of the current error is added to performance information accumulated from numerous previous trials in order to produce the next error correction; this keeps performance stable from trial to trial rather than overcompensating for any individual error. This is beneficial not only to ensure baseline behavioral consistency but also to speed error corrections in response to consistently observed errors as in the case of adaptation paradigms. All subjects exhibited this type of persistent behavior during the predictive-saccade task. In contrast, antipersistent β values (β < 0) arise from a process with relatively large high-frequency fluctuations. Such processes might be reflective of a cognitive strategy to fully correct each observed error on the next trial without regard for added movement noise that can cause overshoots, and without much retention of prior behavior to increase intertrial consistency. Hence, β describes the interplay between trial-to-trial and long-term behavioral fluctuations; in a sense, it may quantify the dynamics of the error-based learning process.

All subjects were also able to modify their saccade gains appropriately during the adaptation portion of the paradigm (average gain increase ± SD: 11.72 ± 4.45%). Measured adaptation rates were consistent with those previously reported in the literature (average rate ± SD: 0.003 ± 0.001°/trial; e.g., see Miller et al. 1981).

Subjects thus exhibited clear evidence of distinct adaptation abilities and fractal behavioral fluctuations during the predictive-saccade task. Therefore, we sought to explore whether these fluctuations—presumably reflecting the underlying error-correction process—were related to behavior during the adaptation task. The β value was found to be strongly related to the overall rate of change of saccade gain during adaptation (Fig. 3A; r² = 0.72, P < 0.01). This implies that measuring the intertrial correlation structure across a series of predictive saccades (β value) can accurately forecast an individual's adaptation rate because they quantify the same underlying error-correction process. In contrast, other measures of baseline movement variability (e.g., mean, standard deviation, kurtosis, and skew of predictive-saccade amplitudes) bore no relationship to adaptation rate (Fig. 4; r² < 0.15, P > 0.1). Hence, evaluation of the specific temporal structure of behavioral variability (i.e., β) is the critical feature that captures an appropriate description of the error-correction process. This correlation is consistent with the notion that greater intertrial correlations (larger β) reflect more carryover of information between trials; using more information to support appropriate changes in future performance allows for faster adaptive modification of behavior in response to systematic errors.

Fig. 3.

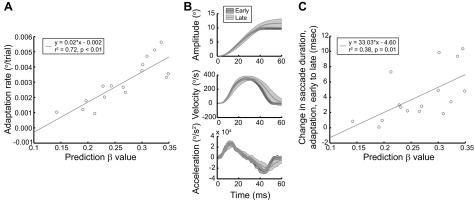
The structure of behavioral variability reveals motor learning dynamics. A: learning rate in the adaptation paradigm correlates with the β value assessed during the predictive-saccade paradigm. B: sample kinematic changes that occur during adaptation for 1 representative subject; each trace is an average of 20 trials, and the shaded region is the SD. Trials before adaptation (dark gray) exhibit smaller amplitudes and shorter durations; trials at the end of adaptation (light gray) exhibit longer durations, particularly due to a delay of the deceleration phase of the movement. C: the changes in duration (ms) that occur during adaptation correlate to predictive-saccade β values, indicating that (fractal) behavioral fluctuation structure relates fundamentally to motor changes that occur during learning (particularly regarding the effort to improve movement accuracy).

Fig. 4.

Alternative measures of behavioral variability. Common variability assessments (mean, A; standard deviation, B; kurtosis, C; skew, D) were applied to describe the fluctuations in predictive-saccade data. In all cases, there was no relation to adaptation rate, suggesting that the temporal structure of behavioral fluctuations, not gross behavioral variability, is the critical descriptor of the intertrial error-correction process.

Furthermore, β may relate to a fundamental change that occurs during adaptation: the adjustment of saccade kinematics. During gain-increase adaptation, movement amplitudes become larger primarily via an increase in saccade duration (Catz et al. 2008; Straube and Deubel 1995; see Fig. 3B for sample kinematic changes during adaptation). The data were suggestive of a correlation between the magnitude of these duration changes and the predictive-saccade β values (Fig. 3C; r² = 0.38, P = 0.01). Thus behavioral fluctuations during the predictive-saccade paradigm likely reflect the capacity to make gross motor changes, as β-value measures may relate to the magnitude of the fundamental kinematic adjustments that occur within individual saccades during adaptation.

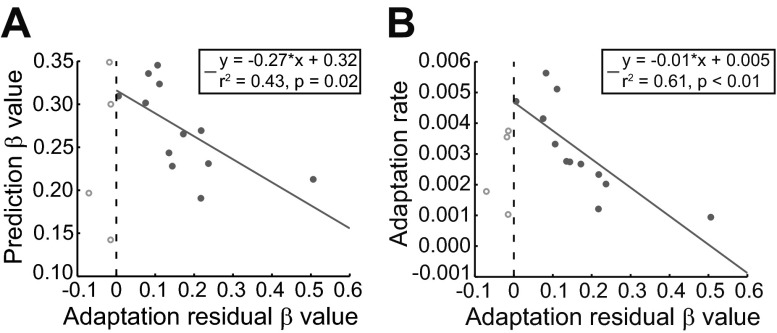
Finally, we investigated the residuals of the adaptation linear regression fit to examine the presence of any remaining structure after removing the dominant adaptation trend. Intertrial correlations were present in these residuals (β_res ± SD: 0.12 ± 0.14), as they also exhibited power-law (fractal) decay of the power spectrum. Although smaller than the predictive-saccade β values, β_res values of the population remained significantly greater than zero (t-test, P < 0.01), although in this case only 3 of the 16 subjects demonstrated a very large β_res according to the bootstrap analysis (probability of observing an individual β_res of at least that magnitude was <5% for only 3 subjects). For β_res > 0, the β_res value was found to be inversely correlated with β (Fig. 5A; r² = 0.43, P = 0.02). Thus it is not surprising that the correlation structure of the residuals was also inversely related to adaptation rate (note that this is the opposite trend from β and is consistent with observing fewer large β_res values across the subject population). In particular, when β_res > 0, larger β_res values corresponded to lower adaptation rates (Fig. 5B; r² = 0.61, P < 0.01). Recall that stronger predictive intertrial correlations (larger β) reflect greater use of behavioral information across trials in order to minimize errors, which can lead to more rapid adaptation in response to the consistent double-step stimulus. The associated low intertrial correlations in the adaptation residuals (small β_res) imply that all or most of the useful error information has been extracted from the saccade sequence in order to achieve these rapid adaptation changes; hence the residual fluctuations retain less information and therefore exhibit intertrial correlations more akin to a random white noise process. The opposite holds for large β_res values, which correspond to slower adaptation rates (and smaller β values). When β_res < 0, however, residuals are antipersistent: behavior fluctuates highly about the adaptation trend. This may reflect a quantitatively different kind of behavior. Indeed, there are two outliers that exhibit β_res < 0 and low adaptation rates; these subjects also exhibited small predictive-saccade β values. It appears that these two subjects may simply be poor learners across all motor tasks. Nevertheless, the complementary pair of β and β_res values can in general describe the use of prior information to adjust short-term and long-term behavioral changes, indicating the usefulness of fractal analysis techniques for forecasting individual adaptation capacity.

Fig. 5.

Fluctuations of adaptation residuals also describe learning. A: relationship between β measured for the predictive-saccade task and the adaptation residual β value (β_res). In general, β and β_res are inversely correlated, particularly when values of β_res are positive. B: relationship between adaptation rate and β_res values assessed for adaptation residuals. As in A, these β_res values can be divided into 2 regions. When β_res > 0 (persistent fluctuations), there is a correlation with adaptation rate; this agrees with the correlation between β and β_res for β_res > 0. When β_res < 0 (oscillatory, anticorrelated behavioral variations), we see that occasionally subjects exhibit poor learning in general (slow adaptation rates and near-zero predictive-saccade β values).

DISCUSSION

Here we demonstrate for the first time a strong link between error processing in the generation of predictive saccades and in the process of saccade adaptation, to the extent that it is possible to relate adaptation capacity to performance during a baseline prediction task. That is, there is a very strong relationship between the rate at which subjects adapt and the temporal structure of saccade amplitude fluctuations (β value) during a predictive-saccade task. This relationship likely arises from a common underlying error-correction mechanism used to adjust future behavior in response to current and previously observed errors. This mechanism may apply to all saccadic behavior—of which adaptation is a particular condition in which errors are artificially exaggerated—and produces a characteristic signature in the time course of behavioral fluctuations that may be quantified with the tools of fractal analysis. That is, adaptation may simply be a continuously stressed, consistent-error version of a recalibration process that occurs throughout daily life. Hence, the ability to detect characteristic signatures of this error-correction process within predictive saccades and other normative baseline behaviors with the appropriate assessment tools (e.g., fractal analysis techniques) may enable these forecasts of adaptation capacity to be made.

Fractal models may provide a better means of describing long-term learning, as β might be interpreted as representing the capacity of the motor system to balance short-term performance accuracy (correcting recent errors) and long-term behavioral consistency in the face of transient perturbations (recalling successful actions from the past). These notions run akin to a Bayesian framework in which prior expectations affect the interpretation of the importance of a given error in driving performance updates (e.g., Wei and Kording 2009), in that the ability of the current error to drive a behavioral correction (maintaining accuracy in the short term) is weighted by the accumulated set of prior behaviors (a “prior distribution” that defines the desired long-term performance to be consistently maintained). Managing these opposing goals of flexibility and stability is critical for performance in numerous tasks. Not surprisingly, therefore, (fractal) behavioral fluctuations have been observed in many other physiological processes (e.g., Lowen and Teich 2005; Stephen and Anastas 2011; West and Deering 1994). By establishing a relationship between this measure of behavioral variability structure and motor adaptation, we propose that the observation of fractal fluctuations across numerous behaviors is not simply an epiphenomenon but a reflection of systematic underlying learning processes in each of these physiological systems that respond to prior behavioral errors across short and long timescales. These fractal characterizations are somewhat puzzling, however, as the strength of an individual's intertrial correlations does not relate to any typical measure of task performance (e.g., spatial accuracy). Thus it is unclear what type of behavioral advantage they may convey. Nevertheless, the presence of intertrial correlations makes intuitive sense since the saccadic system must use prior information to produce an accurate prediction of the next expected movement; the reliance on this prior information should introduce correlations across successive movements. That such intertrial correlations decay as a power law merely suggests that the error-correction process may be best characterized as a fractal process (i.e., a process with scale invariance), in which the amount of intertrial behavioral fluctuation varies proportionally with the timescale across which those fluctuations are measured. The fractal structure implies that behavior across trials fluctuates in a correlated fashion, such that future behavior may be more similar (or less similar, depending on whether behavior is persistent or antipersistent, respectively) to current behavior than would be expected from a white noise, random process. In other words, within a time series, successive trials tend to fall consistently on the same side of the mean more (or less) often than chance, reflecting a process that retains information about prior performance far in the past and uses that information to drive future behavior. Fractal processes are particularly intriguing because they can almost be viewed as an expansion (and therefore a more complete description) of the commonly employed two-state adaptation model in which there is a fast state that learns quickly and forgets quickly and a slow learning state that learns gradually and forgets slowly (Smith et al. 2006); a fractal process exhibits fluctuations on all timescales, not merely two. It is certainly the case that although a majority of state-space models in the literature have only two states, additional states may be employed (e.g., Kording et al. 2006) such that these models may be tuned to achieve power-law behavior to any desired degree of fidelity (over a given temporal or frequency range). Our work—indeed any work on a physiological system with inherent constraints on temporal duration—cannot decisively rule out such models. However, the long-memory fractal modeling approach is in general more parsimonious and does not require the tuning of large numbers of parameters. Consequently, the numerous timescales suggested by the power-law decay of intertrial correlations in our data arise as a by-product of the fractal process itself rather than being explicitly defined by the number of “states” included within the model description, making a fractal model a convenient description of the error-correction process.

These arguments support the use of fractal models to describe learning processes such as adaptation, rather than state-space (ARMA) models. Indeed, adaptability likely reflects the capacity of an individual to make better performance adjustments according to information obtained from many previous trials, instead of relying solely on a Markov-type process that only uses the current state of the system and the most recent error to plan future movements. Hence, models should consider more complex error-correction processes that rely heavily on information from far in the past. For example, state-space models suffer from the flaw that they predict a complete washout of all learning after only a short time has passed (within a few time constants of the long-term process for a typical two-state model). In contrast, evidence suggests that relearning tends to occur more rapidly even if a long period of time or a long “washout” period has been imposed between the successive adaptation sessions (Zarahn et al. 2008). Fractal models, on the other hand, imply that prior experience from very far in the past may continue to have strong influences on future behavior. While it seems unlikely that our motor system does retain behavioral information extending throughout our entire lives, it is useful to consider a model that does not depend so heavily upon explicit definitions of time courses of learning. In this manner, a model that accounts for the presence of fractal long memory could support the enhanced capacity to relearn despite a long intervening washout period.

Although our data are supportive of the notion that behavioral fluctuations arise from a fractal process, it is admittedly difficult to prove that fractal structure exists. We have applied more than one analysis technique (in particular, see Wong and Shelhamer 2011a) to confirm the presence of fractals in the fluctuations of predictive saccades. Still, it is well recognized that all fractal analysis techniques can produce spurious results under certain conditions. For example, just as it is possible to produce an apparent power law by the addition of several exponential curves, intertrial correlations can appear to decay as a power law if they arise from the interaction of several processes that each exhibit exponentially decaying intertrial correlations (e.g., see Granger 1980; Wagenmakers et al. 2004). On a similar note, fractal models also face practical limitations: in particular, it is especially challenging to acquire data continuously across a sufficiently long time span to have confidence in establishing the existence of power-law decay of intertrial correlations. This is particularly true of biological systems, which are often not truly stationary processes, so assumptions must be made when analyzing these data. Related to this is the necessity of defining an appropriate time or frequency range across which power-law behavior is to be identified. Furthermore, the assumptions of fractal models are sometimes unrealistic, such as the troubling assumption that errors from infinitely far in the past are explicitly stored and used to modify current behavior. Despite these caveats, it is still useful to quantify intertrial fluctuations in this manner. Fractal models provide a succinct description of how behavior varies across all timescales spanning the data under examination, including those timescales that are relevant to learning experiments (ranging from single-trial corrections to changes occurring across ∼300 trials). A large advantage of doing so is avoiding the limitation of having to assume and explicitly predefine the number of relevant timescales within a model, as is done with a state-space model, since this impairs the forecasting of behavior at longer timescales of learning. Furthermore, fractal analyses allow the dynamics of behavioral fluctuations to be summarized within a single parameter, the scaling exponent (e.g., the β value) that can be correlated with other measures of interest such as adaptation rate. Thus, as long as the underlying assumptions of fractal models are met within the time span of interest and the results are found to be consistent across more than one fractal analysis method, it is helpful to describe motor behavior in this manner, as such models may still provide useful hypotheses for experimental testing and may prove to best describe learning phenomena (e.g., Drew and Abbott 2006).

It is interesting to note that, unlike the recent work of Wu et al. (2014), here we find no correlation between baseline variability (e.g., the standard deviation of predictive-saccade amplitudes) and adaptation rate. One possibility for this may be that whereas we quantify the variability of movement amplitudes along the primary movement direction, Wu et al. quantify variability of spatial displacements perpendicular to the primary movement direction. This could be a consequence of the task (adaptation of saccade gain vs. reaching in a force field), but variability may be controlled differently along the parallel and perpendicular axes depending on how task relevant those axes are in the context of reaching the target (van Beers et al. 2013). Another possibility may simply be that reaches and saccades are quite different in the manner in which they are controlled. While saccades are generally thought to be feedforward, reaches may be modified midflight with online observed errors. This might affect the nature of the variability measured during perturbation-free baseline movements. Finally, whereas Wu et al. bin subjects into groups and examine average adaptation performance of each group, we demonstrate correlations between baseline fluctuations and adaptation rate across subjects on an individual basis, suggesting that our correlation measures may be more sensitive to individual behavior. Nevertheless, these two studies together suggest that quantification of movement variability or intertrial fluctuations requires careful selection and application of appropriate analysis techniques.

Analysis of the adaptation residuals (i.e., after detrending the adaptation curve) provides additional insight into the adaptive process. Fractal structure remaining in the adaptation residuals inversely correlates with adaptation capacity, possibly reflecting additional error information that has not been adequately utilized by the motor system to drive adaptation. This is similar to the concept of classical estimation theory, in which the better a model or estimate fits the data, the less intertrial correlations remain; the optimal estimator should produce residuals that are white noise (Kailath 1981). Similarly, we find that the better a subject is at adapting (and therefore the better he or she is at extracting more usable error information to support that adaptation process), the more akin to white noise the residual intertrial correlations become. This supports the notion that subjects who are better adapters extract more useful information from movement errors (possibly by having a better internal model of the process leading to the observed errors)—which likely relies upon the accumulation of behavioral statistics across many trials in the past (e.g., through the use of a fractal process)—and therefore are able to rapidly adjust their behavior when necessary to resolve motor errors.

The insights afforded by these data are particularly helpful in that they provide a simple method that might be used to predict adaptation capacity without having to invoke learning (and a change in state) via an adaptation paradigm. This is an important feature that avoids problems associated with reassessments of adaptation capacity, including the as-yet poorly understood phenomena of savings (in which readaptation occurs more rapidly than learning during the initial exposure to the adaptation paradigm; Haith and Krakauer 2013; Huang et al. 2011; Kojima et al. 2004). Note, however, that the results presented here are currently limited to gain-increasing saccade adaptation mechanisms. Gain-decreasing and gain-increasing saccade adaptation may rely on different mechanisms (for review, see Prsa and Thier 2011). However, Golla et al. (2008) have speculated that gain-decreasing adaptation may not actually be a true “adaptation” in the sense of an intentional error-correction process; instead, what appears to be gain-decreasing adaptation may arise from a strategic lack of compensation for oculomotor fatigue. Thus it is yet to be determined whether the findings presented here should generalize to gain-decreasing adaptation and, if so, whether the relationship between β and adaptation rate should be preserved or reversed.

Nevertheless, the existence of such a relationship between β and adaptation rate is appealing since the baseline behavioral (predictive saccade) measurement is short (it takes ∼3 min to complete). Thus this assessment could save a great deal of time in evaluating the capacity of the system to adapt, instead of having to conduct a complete adaptation experiment (on the order of 30 min to an hour). For that reason, the existence of such a correlation, if it can also be demonstrated in other motor systems, is useful beyond the laboratory. One might use such knowledge of a relationship between baseline fluctuations and adaptation capacity of a given motor system in a rehabilitation setting when seeking to determine those behaviors that might be most amenable to adaptive changes (e.g., baseline fluctuations in gain of the vestibuloocular reflex may predict the capacity of this reflex for adaptation, which is useful since training the vestibuloocular reflex is a critical part of rehabilitation treatment for patients who suffer from dizziness). This could enable the design of improved training protocols based specifically on a person's adaptive capacity. Hence, these results provide insight into the process of maintaining movement accuracy by revealing a relationship between adaptation capacity and the intertrial updating of motor performance in response to errors during a baseline behavior of a given motor system.

GRANTS

This work was supported by National Science Foundation Grant BCS-1126957, National Institutes of Health Grants R21-EY-019713 and T32-DC-000023, and National Aeronautics and Space Administration (NASA) Grant NNX10AO19G.

DISCLOSURES

At the time these data were collected (in part under the support of a NASA-sponsored grant as mentioned in grants), M. Shelhamer was employed solely by Johns Hopkins University. However, within the past year M. Shelhamer has taken a position at NASA but has made no financial contributions to the work presented in this paper since that time. After assuming his position at NASA, M. Shelhamer has contributed to this work solely via reading and making edits to the manuscript; no part of the work presented in this manuscript was conducted as part of his official duties as an employee of the US Government.

AUTHOR CONTRIBUTIONS

Author contributions: A.L.W. and M.S. conception and design of research; A.L.W. performed experiments; A.L.W. analyzed data; A.L.W. and M.S. interpreted results of experiments; A.L.W. prepared figures; A.L.W. drafted manuscript; A.L.W. and M.S. edited and revised manuscript; A.L.W. and M.S. approved final version of manuscript.