Delayed suppression shapes disparity selective responses in monkey V1

Abstract

The stereo correspondence problem poses a challenge to visual neurons because localized receptive fields potentially cause false responses. Neurons in the primary visual cortex (V1) partially resolve this problem by combining excitatory and suppressive responses to encode binocular disparity. We explored the time course of this combination in awake, monkey V1 neurons using subspace mapping of receptive fields. The stimulus was a binocular noise pattern constructed from discrete spatial frequency components. We forward correlated the firing of the V1 neuron with the occurrence of binocular presentations of each spatial frequency component. The forward correlation yielded a complete set of response time courses to every combination of spatial frequency and interocular phase difference. Some combinations produced suppressive responses. Typically, if an interocular phase difference for a given spatial frequency produced strong excitation, we saw suppression in response to the opposite interocular phase difference at lower spatial frequencies. The suppression was delayed relative to the excitation, with a median difference in latency of 7 ms. We found that the suppressive mechanism explains a well-known mismatch of monocular and binocular signals. The suppressive components increased power at low spatial frequencies in disparity tuning, whereas they reduced the monocular response to low spatial frequencies. This long-recognized mismatch of binocular and monocular signals reflects a suppressive mechanism that helps reduce the response to false matches.

stereoscopic vision probably depends on binocular neurons in the primary visual cortex (V1), which encode binocular disparity based on the image patches inside the left and right receptive fields (RFs) (Barlow et al. 1967; Pettigrew et al. 1968). The fact that this calculation is based only on small image patches inevitably poses a problem for the encoded disparity; local variation inside the image patch may incidentally drive a neuron even when the image is not presented at the preferred disparity of a neuron (Fleet et al. 1996). These responses to “false” matches complicate the interpretation of activity in such neurons.

The problem of these false matches can be reduced by combining signals across neurons with a “push-pull-like” circuit (Read and Cumming 2007). We recently reported evidence of such a mechanism in primate V1 neurons (Tanabe et al. 2011). Here, we explore the dynamics of this interaction between excitation and suppression through both reverse correlation in the space domain (Jones and Palmer 1987; Ohzawa et al. 1990; Menz and Freeman 2004) and forward correlation in the Fourier domain (Ringach et al. 2003). The stimulus was a binocular sum-of-sinusoids in which each spatial frequency (SF) component was turned on or off randomly on each frame and each eye. Analysis of these data by reverse correlation was presented in Tanabe et al. (2011). Here, we used forward correlation, correlating the presence of an SF component jointly in both eyes with the ensuing spike train. Comparing this response with that when a component was absent from both eyes identifies suppressive responses to individual SF components, separate from excitation.

The dynamics of the response to the SF components provides a means to understand how monocular and binocular signals contribute to disparity responses. Reverse correlation studies have shown that disparity responses sharpen over time (Menz and Freeman 2003, 2004). However, there is a complication that monocular RFs also shift to finer SFs dynamically (Bredfeldt and Ringach 2002; Ninomiya et al. 2012). This shift in the scale of the monocular RF might affect the interpretation of binocular interaction. To separate the monocular and binocular contributions with reverse correlation, it is necessary to characterize space across both eyes and time. An adequate characterization with such a large number of stimulus dimensions would require an unrealistic amount of data if we were to use reverse correlation. Instead, we used forward correlation in the Fourier domain. This approach reduces the dimensionality of the stimulus by concentrating the dimensions to the ones that are most relevant for the neuron under study. With the forward correlation, our second objective was to directly compare the time evolution of monocular and binocular signals.

Finally, the decomposition into excitation and suppression, as well as into monocular and binocular, provides us with a unique opportunity to investigate a long-recognized discrepancy between V1 neurons and the disparity energy model. The model predicts a specific relationship between monocular SF tuning and the shape of disparity tuning, but previous tests have used quite different stimuli to probe the two properties. Here we estimate both functions from a single set of images and spikes. We could then explore whether the observed discrepancy can be explained by the interaction of excitation and suppression.

We find that suppressive inputs are delayed relative to excitatory ones, and thus responses to false matches are increasingly attenuated as the response develops. We also show that the combination of excitation and suppression can explain the difference in spatial scale between monocular and binocular responses. Combining these results produces the best account do date of the mechanisms responsible for disparity selectivity in V1.

MATERIALS AND METHODS

Subjects.

Two male rhesus macaques (Macaca mulatta) were implanted with head-restraining posts and scleral search coils in both eyes. After the subjects were trained on a standard fixation task, we implanted a recording chamber over the operculum of V1. The implantation surgeries were done while the animals were under general anesthesia and done under sterile conditions. All protocols were approved by the National Institutes of Health Institutional Animal Care and Use Committee and complied with Public Health Service Policy on the Humane Care and Use of Laboratory Animals.

We have previously published one analysis of these data (Tanabe et al. 2011). The stimulus generation and recording procedures are fully described there. Briefly, subjects viewed separate CRT monitors (Eizo Flexscan F980) with each eye through a haploscope. They were required to acquire fixation when a bright spot was turned on at the center of the screen. They had to maintain fixation for 2.1 s to earn a drop of liquid reward. The window of fixation was typically a box of 0.8 × 0.8° around the fixation spot.

The stimuli were generated on a Silicon Graphics Octane Workstation. Gamma-correction was used to linearize the luminance response. The mean luminance was 42 cd/m², the contrast was 99%, and the frame rate was 96 Hz.

Recording.

Single-unit recordings were made using tungsten microelectrodes (typically 1.0 MΩ at 1 kHz; Alpha Omega). The electrodes were lowered through the dura with a stepping-motor micromanipulator. Voltage signals were amplified (Bak Electronics) and band-pass filtered (0.1–10 kHz). Waveforms of possible spikes were sampled at 32 kHz and stored to disk (Datawave Discovery Systems). Single-unit isolation was checked offline with custom-built software.

The RF of the cell was initially hand mapped with a bright bar. We centered a patch of drifting grating on the RF of the cell and tested the ocular dominance, the orientation tuning, and the SF tuning. A thin strip of the optimal grating was then used to map the minimum response field quantitatively. The disparity tuning was tested with a dynamic random-line stereogram (RLS). We also interleaved monocular random lines and a binocularly uncorrelated RLS. The random lines were oriented to match the preferred orientation of the cell; thus the disparity axis was perpendicular to the preferred orientation. Cells were discarded from this study if the disparity tuning was not significant (ANOVA P > 0.05).

Stimulus.

The stimulus was randomly generated in the Fourier domain and then synthesized for presentation (Victor and Shapley 1979). The 10 SF components comprised a harmonic series {f₀, 2f₀, . . ., 10f₀}. The fundamental frequency f₀ was chosen for each cell, so that the harmonic series covered the SF pass band of the cell. The coefficient a_m^(L) of the left eye mth harmonic was a Bernoulli random variable, 0 or 1, each with a probability of 0.5. The harmonic phase ϕ_m^(L) was sampled uniformly from 0 ≤ ϕ_m^(L) < 2π. The image in the left eye on the ith frame was thus

$$l^{\left(L\right)}\left(x_i\right)=b_0^{\left(L\right)}+c{\displaystyle \sum _{m=1}^{10}}{a}_m^{\left(L\right)}\sin \left(2\text{π}{mf}_0{x}_i+{\text{ϕ}}_m^{\left(L\right)}\right),$$ (1)

where b₀^(L) was also a random variable with a mean of zero. The randomness of this term was not essential for the purpose of this study, and its calculation is described in Tanabe et al. (2011). The contrast of the sinusoidal components, c, was fixed at 0.17. With this value, the probability that an image would saturate the monitor was 0.005. On these image frames, the value of c was lowered such that the image did not saturate.

In the right eye, the amplitudes a_m^(R) and the DC component b₀^(R) were generated independently of the left eye on each video frame. The phase of the mth component in the right eye was the sum of the ϕ_m^(L) in the left eye and a randomized interocular phase difference Δϕ_m (IPD), thus

$$l^{\left(R\right)}\left(x_i\right)=b_0^{\left(R\right)}+c{\displaystyle \sum _{m=1}^{10}}{a}_m^{\left(R\right)}\sin \left(2\text{π}{mf}_0{x}_i+{\text{ϕ}}_m^{\left(L\right)}+\text{Δ}{\text{ϕ}}_m\right).$$ (2)

Δϕ_m was randomly sampled from a discrete uniform distribution with equal probability at [0, π/3, 2π/3, π, 4π/3, 5π/3]. The phases in each eye had a continuous uniform distribution, whereas the distribution of IPD took discrete values. The sum of these sinusoids forms a one-dimensional noise pattern with 21 independent values in each eye. Because the images were generated independently for each eye, there was no interocular correlation (on average).

Forward correlation.

In every monocular image, an SF component was either present or absent. This allowed us to use forward correlation to observe the dynamic response to the presence of individual components. Forward correlation is equivalent to calculating the stimulus-triggered average of firing rate (Ringach et al. 2003). The stimulus values consisted of a list of the random Fourier coefficients and the IPDs [a_m^(L)(t_i), a_m^(R)(t_i), and Δϕ_m(t_i); m = 1, 2, . . ., 10] on each video frame at t_i (I = 1, . . ., N_frame). For a binocularly presented mth component with Δϕ_m = 0 as an example, we take the time series Δϕ_m(t_i) and turn it into a binary sequence s_m^{(Δϕ_m = 0)}(t_i), in which a value of 1 indicates the presence of Δϕ_m(t_i) = 0. The spike times were also converted into a time series r(t) with binary values (0.1-ms sampling interval). Formally, forward correlation is the discrete version of the cross-correlation function,

$$\begin{gathered} R_m^{\left(\text{Δ}\text{ϕ}=0\right)}\left(\tau \right)=\frac{R_{\text{frame}}}{N_{\text{frame}}}{\displaystyle \sum _{i=1}^{N_{\text{frame}}}}{a}_m^{\left(L\right)}\left(t_i\right)\cdot a_m^{\left(R\right)}\left(t_i\right)\cdot \\ {s}_m^{\left(\text{Δ}\text{ϕ}=0\right)}\left(t_i\right)\cdot r\left(t_i+\hspace{0.17em}\text{τ}\right), \end{gathered}$$ (3)

where R_frame is the refresh rate of the monitor. Rather than calculating Eq. 3 in brute force, stimulus-triggered averaging takes advantage of the fact that the stimulus sequences are binary values. We triggered the spikes with every occurrence of the stimulus combination [a_m^(L)= 1, a_m^(R) = 1, s_m^{(Δϕ_m = 0)} = 1]. The binary spike series were averaged and then smoothed into a spike density function with a rectangular filter (10.4 ms, one video frame). We iterated the forward correlation for all combinations of m and Δϕ_m. This calculation resulted in a three-dimensional matrix, in which the dimensions represent time bin, SF component, and IPD. The values in the matrix are the firing rates. To avoid contamination by any onset transients, the first 100 ms of each trial was discarded before this calculation was performed.

The forward correlation for monocular presentations was calculated similarly. Consider the response to the mth component presented to the left eye only. We searched for stimuli in which that component was present in just the left eye [a_m^(L)= 1, a_m^(R) = 0]. The value of Δϕ_m was ignored for monocular conditions.

Importantly, we also calculated the response to the absence of an SF component in both eyes [a_m^(L)= 0, a_m^(R) = 0]. The absence condition was the reference when calculating the response amplitudes; the response to the absence condition was subtracted from the other responses. Thus a relative response less than zero at a given time indicates a firing rate that is lower than the average firing rate to images that do not contain a given SF component. These negative responses therefore identify suppression, indicating the effect of inhibition at some point in the pathway (but not necessarily inhibition at the recorded cell).

We tested the statistical significance of suppression using a random shuffling test. The null hypothesis is that the lowest response is one of the incidental troughs created by estimation error. We generated a null data set by randomly shuffling the trials of the stimulus sequence. Forward correlation was calculated for the randomized set, and we identified the lowest response in the same way as in the original data. The smoothing window of the spike density function was doubled in width (20.8 ms) to reduce the number of false troughs. We then iterated this randomization 1,000 times. The null hypothesis was rejected when the original trough was smaller than the 5th percentile of the 1,000 trough values. This is a one-tail test for testing the significance of the minimum response across conditions.

Our stimulus was an application of binary dense-noise (Reid et al. 1997; Anzai et al. 1999) to the subspace mapping technique (Ringach et al. 1997). Since multiple SF components were present in the stimulus, neurons could respond to higher order interactions between SF components, e.g., the simultaneous presentation of two particular SF components. The forward correlation cancels the responses to any such higher order interactions through averaging and thereby extracts the responses to individual SF components. The use of a binary sequence made it straightforward to trigger spikes when calculating forward correlation, as described above. Mathematically, forward correlation is equivalent to reverse correlation, when the spike-triggered average is converted to firing rate (Ringach et al. 2003).

Latency estimation.

Among the various possible patterns in the time course, the latency provides clues to the mechanisms behind the response generation. The difficulty in estimating latency is that it normally involves detecting the first signs of the response rising above the baseline firing. Straightforward detection methods, such as finding the time point at which the firing rate reaches a certain level above noise, can be influenced by response strength. They depend on not only the latency but also on the rate at which the firing rate rises after the true latency. We separated the latency from the rising rate by fitting a bilinear function to the smoothed time course in Eq. 3, as:

$$R_{\text{m}}^{\left(\text{Δ}\text{ϕ}\right)}\left(\text{τ}\right)=\{\begin{array}{cc}{\text{β}}_0& \text{for}\hspace{0.17em}0<\hspace{0.17em}\text{τ}\hspace{0.17em}\le {\text{β}}_1\\ {\text{β}}_2\cdot \hspace{0.17em}\text{τ}& \text{for}\hspace{0.17em}{\text{β}}_1<\hspace{0.17em}\text{τ}\hspace{0.17em}\le \hspace{0.17em}{\text{τ}}_{\text{halfmax}}\end{array},$$ (4)

where τ was bounded at the time-point τ_halfmax at which the firing rate reached half-way to the maximum. Three parameters (β₀, β₁, and β₂) were fitted to ∼50 data points (a time series of firing rate up till the τ_halfmax, in 1-ms intervals). The solution of β₁ was the estimated latency. This method of estimating latency was more robust to noise than using the time-to-threshold, because the fitting factors out the noise under reasonable assumptions. The fitting was based on the assumption that the noise should follow a Gaussian distribution (least-squares method). For estimating the latency of suppression, the time point τ_halfmax was when the firing rate reached half-way to the minimum.

Decomposition into excitatory and suppressive responses.

The time course of the response in the forward correlation might reveal stimuli that evoke predominantly excitatory responses, and other stimuli that evoke predominantly suppressive responses. Although such a differentiation is suggestive of a mechanism by which excitatory and suppressive components are combined, it is not sufficient to decompose the stimulus-response relationship into excitatory and suppressive components. The decomposition would only be accurate when the two components respond to completely nonoverlapping stimuli. In general, excitatory and suppressive components may be responsive to overlapping stimuli, producing a combined response to any given stimulus. We approached this problem by assuming that each component response was space-time separable, i.e., the excitatory component responds to any stimulus with the same time course, apart from a scaling factor. The same applies to the suppressive component, except that this one has a different time course than the excitatory counterpart. This simplification allowed us to solve the decomposition in two steps. Step 1 was to focus on a single time slice and reconstruct the spatial RFs in which the excitatory and the suppressive components were orthogonal. We used a spike-triggered covariance (STC) approach for this reconstruction.

This method is an extension of the reverse correlation to the second order statistics of the stimulus (de Ruyter van Steveninck and Bialek 1988). Reverse correlation is the characterization of the ensemble of images that preceded a spike by the average value at each position or delay, whereas the STC method characterizes the same ensemble of images by the covariance value between pairs of positions or delays (Touryan et al. 2002; Rust et al. 2005; Schwartz et al. 2006). The details of our method is described elsewhere (Tanabe et al. 2011). Briefly, the images in the left and right eyes (Eqs. 1 and 2) were concatenated back to back to create a single binocular image l(x_i) on each video frame. We subsampled the images at 42 equally spaced values (21 positions in each eye) along the position axis x_i. The subsampled images had zero correlation between any pair of positions. Henceforth, we will switch the notation of the images from a gray-scale value as a function of position l(x_i) to a vector of grayscale values l_i. For every spike, we extracted the video frame i that was presented τ ms before the spike. This long list of indices was the spike-triggered ensemble S_τ, using a delay of τ ms. First, we picked one value of τ and calculated the raw covariance matrix

$$\mathbf{V}=\frac{1}{N_{\text{spk}}-1}{\displaystyle \sum _{i=\left\{S_{\text{τ}}\right\}}}{\left({\mathbf{l}}_i-\overline{\mathbf{l}}\right)}^{\text{T}}\cdot \left({\mathbf{l}}_i-\overline{\mathbf{l}}\right).$$ (5)

We iterated this calculation for a range of delays τ = {20, 25, . . ., 95} ms. We selected the τ value that produced the strongest V, as measured by the variance over the elements in V. For the subsequent analyses, we fixed the τ to this value.

Having identified this covariance matrix for the best time delay, we identified the significant eigenvectors with a nested sequence of permutations (Schwartz et al. 2006; Tanabe et al. 2011). When the eigenvalue was greater than what would be expected from chance, the functional element is an excitatory component. Conversely, when the eigenvalue was smaller than the chance expectation, the functional element is a suppressive component.

After identifying the significant eigenvectors, a set of weights and an output nonlinearity were identified by estimating the neuronal response to feature contrast (details in Tanabe et al. 2011).

$$r_i\left(u_0,u_1\text{,. . .},u_M\right)=\left[{\text{β}}_0{\left[u_0\right]}_{+}^2+{\text{β}}_1\cdot u_1^2+\text{. . .}+{\text{β}}_M\cdot u_{\text{M}}^2\right].$$ (6)

The above description of how we estimated the model in Eq. 6 is a summary of the methods we described in Tanabe et al. (2011). We now add an additional step to estimate the time course of suppression and excitation. We calculated the response in Eq. 6 to every stimulus frame. The responses of the excitatory elements and the suppressive elements were pooled separately.

Step 2 of the decomposition was to reconstruct the temporal RFs that were associated with the models reconstructed in step 1. We used forward correlation in this step. We simulated the output of the excitatory and suppressive components and used those signals in a straightforward application of the forward correlation analysis. The outputs of excitatory elements were pooled separately from the outputs of suppressive elements. For the excitatory component, we first identified all frames for which excitatory pool response exceeded the 75th percentile. We then calculated a smoothed spike-density function triggered on these frame times, identifying the mean response to strong excitation. Second, we identified all frames associated with a weak response (less than the 25th percentile) and again calculated the spike density function. Finally, we subtracted the weak response from the strong response, to estimate of the excitatory component of the cell response. The suppressive component of the response was calculated similarly.

Disparity tuning with forward correlation.

The time course of the responses to individual SF components helps us understand the mechanism of how disparity tuning is generated. We sought to make direct comparisons between the responses to SF components and the disparity tuning. The forward correlation is advantageous for this purpose, because it allows us to test the disparity tuning of the cell using the exact same spike train. In fact, forward correlation is applicable to any feature of the stimulus. For disparity tuning in particular, we used the interocular crosscorrelation of the images as the trigger feature.

We converted the binocular image of every video frame into a crosscorrelation function. The crosscorrelation functions were then subsampled into 21 equally spaced values along the disparity axis. Each disparity had a distribution of correlation values over the entire recording session. We picked one disparity and set our trigger threshold at zero. The triggered spikes were then smoothed to obtain a spike density function for positive correlation. We also calculated the spike density function for negative correlation. We then calculated the difference of the two time courses, which provided our estimate of the response for one particular disparity. This forward correlation was then iterated over all 21 disparities.

RESULTS

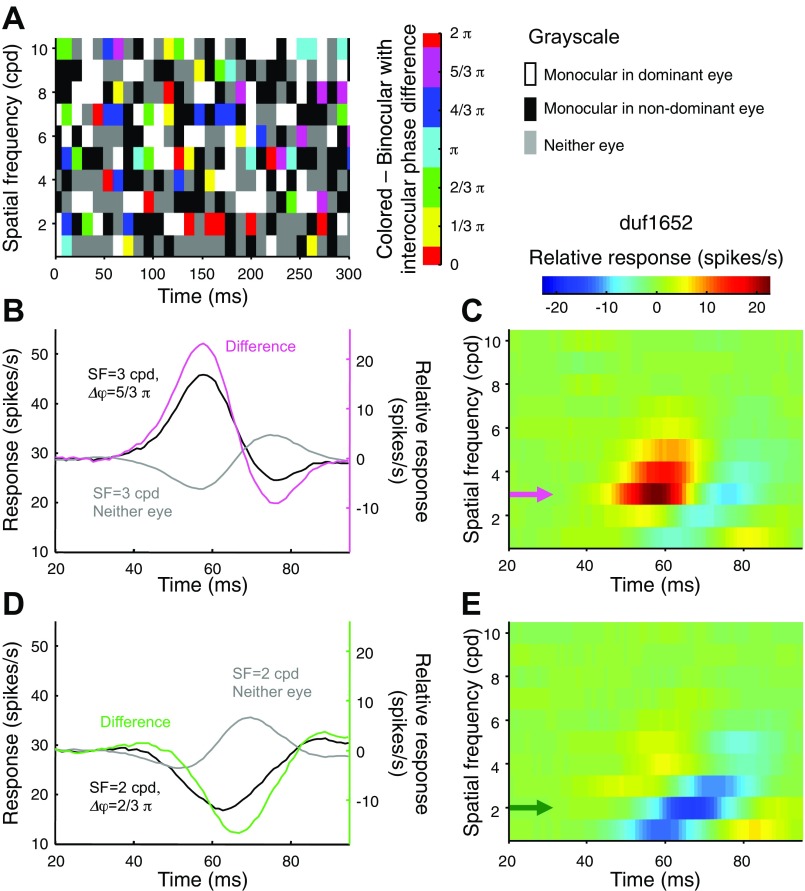
We recorded from 70 disparity selective cells (monkey duf: n = 38 and monkey ruf: n = 32) where we were able to maintain unit isolation long enough to complete the experiment. No other selection criteria were applied. Figure 1 shows an example of the steps involved in the analysis. Figure 1A illustrates a short segment of the stimulus sequence in a matrix using a multiplex colorcode. Each column of the matrix represents a video frame, and each row represents an SF component. The colored elements indicate the joint presence in both eyes. Their colorscale indicates the IPD. The grayscale represents the monocular and absent conditions. Only a quarter of the elements were binocular because the probability of an SF component of being present was 0.5 in each eye independently.

Fig. 1.

Responses of a primary visual cortex (V1) neuron to the stimulus randomized in the Fourier domain. A: color-coded matrix is a schematic illustration of the stimulus sequence. Each column represents 1 video frame. The random sequence of a spatial frequency (SF) component constitutes 1 row. The grayscale and the color codes are described at right. B: black and gray traces show the response time courses triggered by the presence of 1 SF component in both eyes [3 cycles/degree (cpd), Δφ = 5/3π] or the absence in both eyes, respectively. The gray trace serves as the baseline. The relative response is shown in magenta, with its y-axis shown at right. C: relative responses are shown for all the SF components with Δφ = 5/3π. The color code is given at top. The magenta arrow indicates the trace shown in B. D: responses are triggered by another SF component (2 cpd, Δφ = 2/3π). The relative response of this component was suppressive (green trace). E: relative responses are shown for all the SF components with Δφ = 2/3π. The green arrow indicates the trace shown in D.

Response maps with forward correlation.

As an example, we show the raw forward correlation to one condition. The solid black trace in Fig. 1B shows the mean response to all images in which the 3 cycles/degree (cpd) component was present in both eyes, and the IPD was 5/3π. The response rose from a baseline of 30 spikes/s to a peak of 45 spikes/s. It is important to note that this set of images contains all of the other SF components but in random combinations. Therefore, the baseline response is not a response to a blank screen but the overall mean response to all of these images. However, we can differentiate excitatory and suppressive effects of this SF component by comparing this spike density function with that produced by all images in which the 3 cpd component was absent in both eyes (gray trace). The difference of the two traces (magenta trace, right hand axis) estimates the cell response to one stimulus condition (Ringach et al. 2003). Negative values in the trace indicate suppression.

We repeated the calculation of relative response over all the SF components with this IPD (Fig. 1C). There were two notable features. First the responses were primarily excitatory (relative response >0). Second, the responses to higher SFs have longer latencies. These features are similar to what has been reported before in monocular studies (Bredfeldt and Ringach 2002). Figure 1, D and E, shows responses of the same neuron to the opposite IPD (2/3π). There are two striking differences. First, the response was primarily suppressive (relative response < 0). Importantly, “suppression” here does not merely indicate a weaker response than the average binocular response (it is inevitable that some IPD would satisfy this). Rather, relative responses less than zero here indicate binocular presentation of these SF components with this IPD produce lower firing rates than a stimulus in which the SF component is completely absent. The second striking feature in Fig. 1E is that that the suppressive responses were delayed and shifted to lower SF compared with the excitation shown in Fig. 1C.

In the subsequent analyses, we narrowed down our data set to neurons with high signal-to-noise ratio in these response maps. We estimated the disparity response amplitude by calculating the variance produced by IPD at each time instant. We calculated this variance at a time delay too short to contain any stimulus-driven response (the first time bin centered at τ = 5.8 ms) to estimate the noise. We compared this with the maximum variance found in the time interval of 20–100 ms. Fifty cells with ratios >3 were used as the population in all the subsequent analyses. All but one cell qualified as a complex cell, based on the presence of at least one significant eigenvalue in the STC analysis.

Excitatory and suppressive responses.

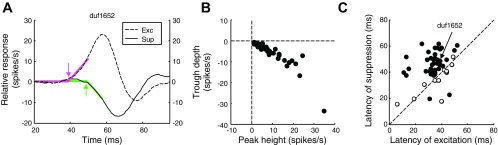
A subset of the combination of SF and IPD triggered an excitatory response, whereas another subset triggered a suppressive response. For each cell, we identified the stimulus combination that elicited the strongest response (largest peak) and the combination that produced the weakest responses, shown for the example cell in Fig. 2A. The weakest response was suppression (trough, relative response <0) for all the cells in the population (Fig. 2B). Out of the 50 cells selected for this study, the suppression was statistically significant in 34 cells (random shuffling test, P < 0.05). The two response magnitudes were well correlated; linear regression (type 2) shows a slope of −0.73. That is, the strength of suppression was typically 73% of that for excitation. The IPDs of the peak and trough were in antiphase in most cells (circular mean difference of 0.97π).

Fig. 2.

Latencies of excitation and suppression. A: 2 traces are the peak (strongest) and the trough (most suppressed) responses out of all combinations of SF and Δφ. The 2 traces are the same ones shown in Fig. 1B and 1D. Colored traces are the fits used to determine response latencies (bilinear functions). The suppressive response was delayed (green) compared with the peak response (magenta). B: peaks were positive and the troughs were negative in all the cells of the population (n = 50), indicating that all cells showed both excitatory and suppressive components. C: compares response latencies for excitation and suppression. The delay of the suppressive response was consistent across the population of V1 cells. The filled dots represent cells with significant difference in latency. We determined the significance of the peak difference when the 95% confidence interval of the joint values (an ellipse centered at the estimated latencies) did not cross the identity line (diagonal).

The example also shows a clear latency difference, with suppression delayed relative to excitation. To quantify response latency we fit a bilinear function with two segments to the onset portion of the response. The first segment had a value of zero (flat). The second segment extended from zero to a point where the response reached half its maximum amplitude, and the slope was a free parameter. We used the fitted breakpoint as our estimate of latency (Fig. 2A). The latency of the suppression was longer than the latency of the excitation in the example cell (Fig. 2A; upward and downward arrows, respectively). This was a systematic feature in the population data (Fig. 2C; median difference 10 ms; Wilcoxon's signed rank: P = 7.6 × 10⁻¹⁰). We checked whether the difference in delays might be explained by the differences in peak heights by normalizing both the peak response and the trough response to an amplitude of one. We obtained the same results (median difference: 10 ms). Finally, instead of comparing onset latencies, we compared time points at which suppression or excitation reached 50% of maximum. This showed a median difference of 6 ms. This latency difference suggests that the two signals arrive through separate binocular channels.

Tuning for interocular phase difference.

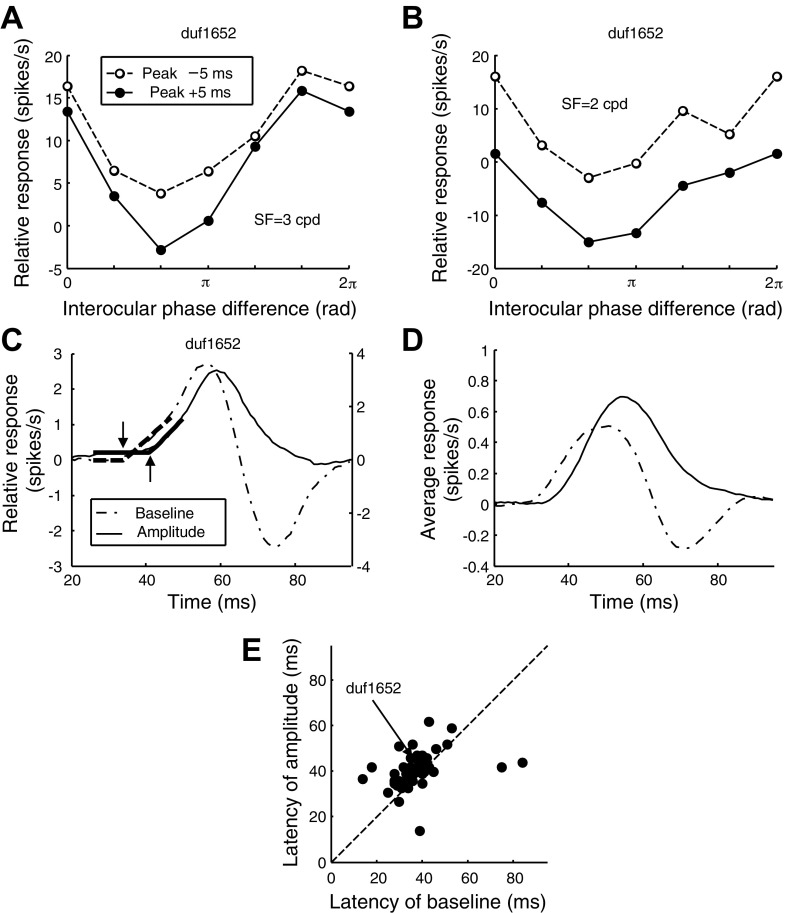
Figure 1 showed data for just two values of IPD, where it appears that the response dynamics are different for different IPDs (compare Fig. 1, C and E). This contradicts the prediction of the disparity energy model (Ohzawa et al. 1990), in which all IPDs should produce the same dynamics, apart from a scaling factor. We explored the IPD tuning to see if any of the deviations from the model might be related to the delayed suppression. Figure 3A shows the responses to all IPDs for the SF component (3 cpd) that produced the strongest excitatory response. Note two different changes in this tuning curve over time. First, the entire curve moves down (i.e., the baseline firing decreases), representing a decline in the excitatory response produced by the presence of this frequency, averaged across all IPDs. At the same time, the amplitude of modulation with IPD (peak to trough of the curve) increases. Figure 3B shows these responses for the SF component (2 cpd) that produced the greatest suppression. Here there is a larger change in baseline but little change in amplitude. Thus the time course of the baseline and the time course of the modulation amplitude are different. Figure 3, C and D, shows the time course of these two measures. The baseline and the amplitude of the IPD tuning were calculated from the zero-th and the first Fourier components, respectively. The baseline had a slightly shorter latency and reached a peak more quickly than the amplitude. However, the most dramatic difference occurred in the second half of the relative response where the baseline drops much more quickly and becomes negative, while the amplitude falls more gradually to zero (see Supplemental Video S1; Supplemental Material for this article is available online at the J Neurophysiol website). Both of these features were systematic properties of our population. Figure 3E compares the response latency for the mean response and the amplitude, showing a systematic difference with the amplitude delayed by a median of 4 ms (Wilcoxon's signed rank: P = 1.7 × 10⁻⁴).

Fig. 3.

Latencies of baseline and amplitude of interocular phase tuning. A: responses to binocular presentations of the 3 cpd component are plotted as a function of Δφ. The 2 functions are at different time slices. The tuning function amplitude continues to rise after the peak, whereas its baseline drops. B: tuning functions are shown for the 2 cpd component. There is no change in amplitude after the peak. This SF component is the same as in Fig 1D. C: amplitude of disparity tuning, combined across all SFs, follows a different time course (solid trace) from that of the baseline (dashed-dot trace). The fitted bilinear functions are superimposed (bold traces). The onset of the amplitude (upward arrow) was delayed to the onset of baseline (downward arrow). The y-scale at right measures the amplitude. D: population average time course (i.e., plots like C averaged over all cells). The delay of the amplitude is preserved in the average trace. E: delay of amplitude was consistent across the population of V1 cells.

The dissociation between the baseline and the amplitude we showed above is not compatible with the disparity energy model (Ohzawa et al. 1990). If separate excitatory and suppressive elements are combined, it is relatively straightforward to explain the dissociation during the second half of the response. Disparity-selective suppression can increase the response amplitude while reducing the baseline. Note that to increase amplitude, it is important that IPDs associated with maximal excitation must be associated with minimal suppression, i.e., the excitatory and suppressive responses need to be organized in a push-pull fashion, as we previously suggested (Tanabe et al. 2011). This same mechanism can in principle explain the difference in latency, if the suppressive contribution to disparity tuning makes a significant contribution even in the early part of the response. This requires substantial temporal overlap between the suppressive and excitatory responses. The method we use above is not well suited to characterizing this overlap. Although at individual time points we can determine whether the sum of excitation and suppression is positive or negative, we cannot say much about the individual components when both are present. An extension of our previous analysis of these data (Tanabe et al. 2011) provides a better way to examine this temporal overlap.

Decomposition into excitatory and suppressive responses.

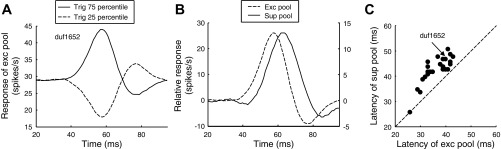
Our previous study ignored individual SF components and performed a spike-triggered analysis of the spatial noise patterns in one dimension. We only examined one time point and decomposed the response into functional elements using STC analysis. The elements were static models and were not meant to describe the dynamics of the response (Tanabe et al. 2011). Each element was identified as excitatory or suppressive based on its variance related to spikes. This method reconstructs the elements even when they act simultaneously. Here we make use of the reconstructed elements to explore the response dynamics by simulating the responses of the reconstructed elements to each frame of the actual stimulus. We then forward correlated the occurrence of a strong simulated output of the excitatory pool with the cell spike train (Fig. 4A, solid trace). We built a similar response with weak simulated output of the excitatory pool (Fig. 4A, dashed trace). The difference between these two averages estimates the time course of the neurons' response to putative excitatory inputs (Fig. 4B, dashed trace). We repeated the equivalent procedure to estimate the response to putative suppressive input, plotting the response to weak suppression minus the response to strong suppression (Fig. 4B, solid trace).

Fig. 4.

Decomposition into excitatory and suppressive responses. A: spike train was triggered on all stimulus frames where the pooled response of the excitatory elements was either greater than the 75th percentile (solid line) or less than the 25th percentile (dashed line). B: relative exictatory response (dashed line) was given by the subtracting the 2 traces in A. The solid line shows the equivalent calculation for suppression (weak suppression − strong suppression, so that positive values here indicate a reduction in spike rate). The relative response of the suppressive elements was delayed to the response of the excitatory elements of the example cell. The y-axis for the suppressive elements is at right. C: delay of the suppressive elements was consistent across the population (n = 26). This population had at least 1 significant excitatory element and at least 1 suppressive element.

For the example cell, the onset of the excitatory pool preceded the onset of the suppressive pool (Fig. 4B) by 7 ms, and the peak also occurred earlier with a similar difference. Importantly, these dynamics played no role in determining the spatial structure of the elements in our reconstructed model. The model was based only on the relationship between images and spikes at a single time delay −60 ms in this example neuron. The analysis of STC identified 26 cells with at least one significant excitatory and one significant suppressive element. Suppression lagged behind excitation in all but one cell (Fig. 4C), with a median lag of 7 ms. Out of the 50 cells selected in this study, suppressive elements were detected in 28 cells with the STC analysis. The forward correlation detected 34 cells with significant suppression. The majority of the cells detected with the forward correlation were also detected with the STC analysis (22/34 cells). Although this delay is both statistically and functionally significant, it is also important to note that there is substantial overlap in the time course of the two responses. For each neuron we calculated the ratio of this time delay to the response duration, and the median value was 0.16. These results reinforce the suggestion above that suppression is delayed with respect to excitation, but there is substantial temporal overlap.

Monocular response vs. binocular interaction.

Our analysis of responses to different SF components allows us to address another long-standing question relating to the generation of disparity selectivity in the visual cortex. In the traditional energy model, the shape of the monocular RFs constrains the shape of the disparity-selective response. One way in which this relationship can be tested is to compare the SF tuning (measured monocularly with grating stimuli) with the Fourier amplitude spectrum of a disparity-tuning curve (measured with a stimulus that is broadband in SF). Every attempt to do this has found that the disparity-tuning curve has more power at low SFs than predicted (Ohzawa et al. 1997; Prince et al. 2002; Read and Cumming 2003; discussed in Cumming and DeAngelis 2001). One difficulty with these comparisons is that they compare responses to very different stimuli at different times. Any number of nonlinearities (e.g., some form of normalization) might in principle explain this discrepancy (Ohzawa et al. 1997). Using our data, we can calculate monocular responses as a function of SF and estimate disparity selectivity, simply by applying different analyses to the same spike train recorded in response to the same stimulus.

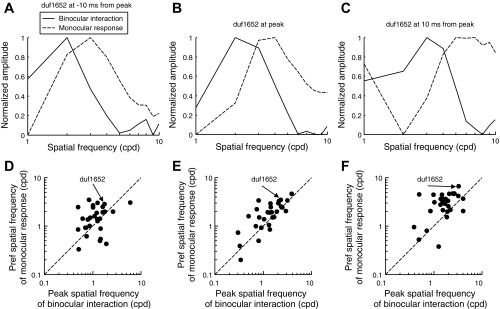
To estimate binocular interaction, we used the forward correlation of the spike train with the crosscorrelation function between left and right images. We constructed monocular responses as a function of SF by forward correlation based on the dominant eye's image. Figure 5, A–C, compares these two measures for the example cell at three different time delays. In each case, the amplitude spectrum of the binocular interaction peaked at a lower SF than the monocular response.

Fig. 5.

SF tuning of binocular interaction and monocular response. A–C: binocular interaction is the forward correlation with the cross-correlation of the left- and right-eye images. For the example cell, the SF spectrum of binocular interaction was shifted to lower frequencies than the SF tuning of monocular responses. This relationship was preserved across 3 different time slices around the peak time. Both functions shifted to higher SFs over time. D–F: peaks of the spectra and the tuning functions were consistently shifted across the population of cells.

We selected 29 cells in which the width of the amplitude spectrum of the monocular SF tuning was <2.5 octaves at peak time. The width of a spectrum was estimated in the same way as the standard deviation of a probability density function. The peaks were identified with spline interpolation. At all time delays, binocular interaction systematically peaked at lower SFs than the monocular SF selectivity (Fig. 5, D–F). As time evolved, both monocular and binocular responses moved to higher SFs but the difference remained. The difference in frequency spectra of monocular and binocular responses in analysis of spikes produced by a single image sequence demonstrates that this difference is not merely the result of incidental changes associated with using different stimuli in previous studies. As we discuss below, the interaction of excitation and suppression that we demonstrate above also provides a good explanation of this long-recognized discrepancy.

Mechanism of spatial-frequency mismatch.

In principle suppression might explain this discrepancy because it has quite different effects on the two measures. A suppressive element with power at a particular SF reduces monocular responses to that SF. However, if it does this in both eyes, it introduces a correlation between the monocular responses, which increases the power in the disparity response at that SF. Therefore, if the suppressive elements have more power at low SF than the excitatory ones, it will result in more power in the disparity response at low SFs than in monocular responses. When two signals are combined the power spectrum of the resulting disparity response also depends on the phase relationship. Combining excitation with a negative signal in antiphase produces the same signal as adding a positive signal with the same phase. Thus the suppressive subunits we find have the properties required to explain this SF mismatch.

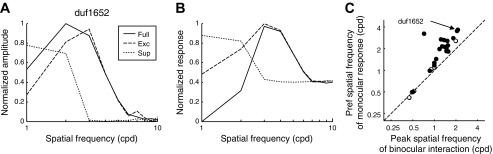
To test this explanation quantitatively, we simulated the responses of the reconstructed model, which was previously used in Fig. 4. The binocular interaction was simulated by calculating the average response to random-dot stereograms (500 frames in which every pixel was either bright or dark with 0.5 probability). The amplitude spectrum of the disparity tuning function is shown (Fig. 6A, solid curve). We analyzed the effect of suppression by switching off all the suppressive elements (dashed curve). When the suppressive elements were missing, the peak was near 3 cpd, which closely agrees with the peak in the forward correlation (Fig. 1C). The full model had a peak shifted to the left as we have predicted. The dotted curve shows the amplitude spectrum of disparity tuning when all the excitatory elements were switched off, which peaks at a lower SF. When the excitatory elements were missing, the peak was near 2 cpd, which closely agrees with the trough in the forward correlation (Fig. 1E).

Fig. 6.

The mechanism underlying the discrepancy of binocular and monocular signals. A: disparity tuning of the reconstructed model was simulated with random-dot stereograms to explore the contribution of each element. Plotted here is the amplitude spectrum of the tuning function. Inset: indicates which components were used for each curve. The amplitudes were normalized so that the spectra are bounded between 0 and 1. The peak of the full model was shifted to the left of the model using only excitation. B: drifting sinusoidal grating was presented to the dominant eye of the reconstructed model. The SF tuning of the full model was shifted to the right of the excitatory-only model. C: for each reconstructed model of the cell, the peak in the SF tuning is plotted against the peak in the amplitude spectrum of the disparity tuning. As in the neuronal data, there is a systematic shift, with most points lying above the identity line. The filled dots represent cells with significant difference in the SF peaks.

We also explored the responses of the reconstructed model to monocular drifting gratings in the dominant eye (Fig. 6B). As explained above, adding the suppressive elements had the opposite effect on monocular responses, reducing the response at low SFs and moving the peak response to a higher SF.

We performed this analysis with the reconstructed model for each cell. Two criteria were set for the selection of cells. First, the model identification recovered at least one excitatory and one inhibitory component. Second, the SF tuning of the full model had a clear peak (see paragraph on Fig. 5 for details). Twenty-five cells met these criteria. We fitted a log-normal Gaussian to the SF tuning and to the Fourier spectrum of the disparity tuning. In most cells (23/25), the monocular SF tuning of the recovered model had a higher peak SF than the peak of its disparity tuning (Fig. 6C). We determined the significance of the peak difference when the 95% confidence interval of the joint values (an ellipse centered at the peak SFs) did not cross the identity line (diagonal). Nineteen of the 23 cells above the diagonal showed a significant difference. The median ratio was 1.37. The recovered model reproduced the SF mismatch that we observed in the response of the cell (see Fig. 5), where the median ratio at the peak response time was 1.29.

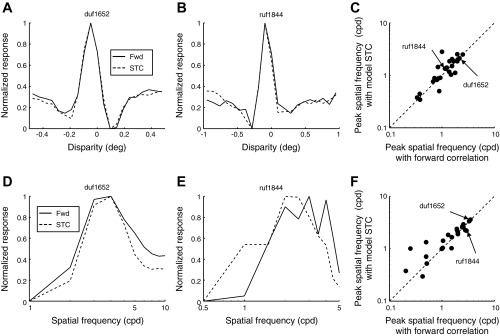
As a further check on the validity of this explanation, we compared the model disparity tuning curves with those for the neurons. These matched well in two example cells (Fig. 7, A and B). We characterized the respective tuning function with the peak SF of its Fourier spectrum. The peaks were identified using spline interpolation rather than the fitting in Fig. 6C. The peaks with the model plotted against the peaks of the cell lined up on the identity line (Fig. 7C), with a median ratio of 1.01. We then checked the monocular SF tuning, again comparing peak SF in the model with that observed in the cells (Fig. 7, D and E). These preferred SFs were also well matched, with a median ratio of 1.02 (Fig. 7F). Thus, the recovered model produced good description of both amplitude spectra in addition to explaining the difference between monocular and binocular responses.

Fig. 7.

Comparison of reconstructed model responses with observed forward correlation. A: disparity tuning calculated with forward correlation (solid curve) is superimposed with the disparity tuning of the spike-triggered covariance (STC)-reconstructed model (dashed curve). The 2 methods used the same time slice τ = 60 ms. The tuning functions were normalized to span between 0 and 1. B: same superposition of disparity tuning with another example cell. The time slice was τ = 55 ms for this cell. C: Fourier spectra of the tuning functions were in good agreement over the population. D: SF tuning calculated with forward correlation (solid curve) is superimposed with the SF tuning of the STC-reconstructed model (dashed curve). Both tuning functions are with monocular stimulation of the dominant eye. The time slice and the normalization was the same as in A and B. E: same superposition of SF tuning with the other example cell. F: SF tuning functions were in good agreement over the population.

DISCUSSION

This study applied subspace RF mapping to explore the mechanisms that produce dynamic evolution of the disparity selective responses in V1 neurons. Our approach allowed us to measure the temporal evolution separately for different SF components of a broadband stimulus. There were five striking and consistent results. First, 34/50 neurons showed significant suppressive effects for some SF component. Second, the strongest suppression was found at lower SF than the strongest excitation. Third, the suppressive response was delayed relative to the excitation, although this delay is small relative to the duration of the response. For most of the cells, excitation and suppression are both substantial. Fourth, the disparities associated with maximum excitation were usually associated with minimum suppression and vice versa. Fifth, the Fourier transform of the disparity selective response peaked at lower SFs than monocular responses calculated from the same image sequence. The push-pull organization of the disparity response, combined with the temporal delay, is able to explain the observed discrepancy between monocular and binocular responses.

Suppression is normally difficult to identify with extracellular recordings, especially in primary visual cortex, because spontaneous rates are low. This makes it difficult to differentiate negative responses from no response. White-noise approaches have proven useful in identifying suppression in several ways. First, the stimulus produces mean firing rate, which allows the response to zero input (a decline from the mean rate) to provide a baseline comparison. Reductions in activity beneath that baseline indicate suppression. Unlike earlier studies (Bredfeldt and Ringach 2002; Ninomiya et al. 2012) where this comparison was provided by a blank stimulus, we used a condition where a particular SF component was absent. Binocular presentation is also helpful, since continued drive from one eye facilitates the identification of the response to zero input from the other eye (Ninomiya et al. 2012).

Recent analyses provide a different way to identify suppressive responses. STC analysis decomposes the stimulus-response relationship into functional excitation and functional suppression (Rust et al. 2005; Tanabe et al. 2011). The assumption underlying these studies is that the functional components are orthogonal to each other (Schwartz et al. 2006). We previously used this technique to identify disparity selective suppression (Tanabe et al. 2011). Here we use a completely different analysis of the same data to demonstrate directly responses where suppression exceeds excitation. The binocular properties we found confirmed the main results that we had inferred from analysis of STC: suppression is produced by lower SFs and by disparities in antiphase. In that study we were only able to identify suppressive elements in approximately half of the neurons studied. We speculated that this might underestimate the prevalence of suppression because of statistical limitations of STC analysis. The forward correlation method we present here does not suffer from this limitation, and reveals that suppression is somewhat more widespread; we found evidence of significant suppressive input in 68% of the cells (34/50). We also discovered that suppression occurs later in time and were able to confirm this property for the elements revealed by STC.

In the current study, we searched through the stimuli and the delay times and identified suppression when the relative response fell to a negative value. Although this is evidence of suppression, it does not isolate suppression alone; the cell may also receive some level of input from excitatory mechanisms with that stimulus. The approach in our previous STC study was more neutral than this. We picked one delay time, whether or not the response was indicative of suppression (Tanabe et al. 2011). Within that time slice, we identified the axes in the stimulus space that had excitatory and suppressive influences. The axes were all orthogonal to each other, so the cell received no excitation with a stimulus that fell on a suppressive axis. This is true whether or not the axes actually correspond to underlying RF mechanisms. The isolation of suppressive axes is what sets the previous study apart from the current one.

Previous studies have reported that the disparity response sharpens over time (Menz and Freeman 2003; Tanabe et al. 2011). This phenomenon is of special interest because “coarse-to-fine” interactions have long been recognized as possible strategy for dealing with the stereo correspondence problem (Marr and Poggio 1979), and seem to play a role in determining perception (Wilson et al. 1991). Even if the spatial structure of excitatory and suppressive inputs was static, a time delay between them (which we find) could in principle explain this sharpening. However, we find that both suppressive and excitatory responses independently shift to higher SF over time. We did not see the sharpening of disparity tuning accelerate toward the end of the response. The current evidence suggests that the sharpening of disparity tuning can be fully explained by the shifting of SF tuning at the monocular level. This raises the possibility that the sharpening over time is largely the result of changes in monocular RFs over time (Bredfeldt and Ringach 2002; Ninomiya et al. 2012). In principle, this hypothesis could be tested by STC analysis, reconstructing binocular space-time RFs. Our data have too many stimulus dimensions to allow a simple analysis to do this, but we are currently exploring the use of regularization techniques to answer this question.

Our results, combined with several earlier studies (Bredfeldt and Ringach 2002; Rust et al. 2006; Tanabe et al. 2011; Ninomiya et al. 2012) make a strong case that the spatial responses of neurons in striate cortex (including the disparity selectivity) derive from the interaction of excitatory and suppressive influence. This scheme can explain results that are difficult to explain in a purely excitatory framework. We illustrate this here by a comparison of monocular selectivity for SF with the frequency composition the disparity-tuning curve. That these two measures differ has long been recognized as a puzzle in the framework of the disparity energy model, which uses only excitatory summation. The reconstructed disparity-energy model probably underestimated the effect of suppression, because the time slices used were too early for the suppression. On the other hand, the SF tuning of the cells was measured from the steady-state response, in which suppression was likely involved. It is the delayed suppression found in our study that reconciles this discrepancy between the reconstructed model and the actual tuning. Our measurement of the spatial properties of suppression shows that it has exactly the properties required for this explanation.

In the case of disparity selectivity, this combination of suppression and excitation avoids some of the negative consequences of fine disparity tuning. An important problem for stereovision is that noncorresponding features in the two eyes can drive simple binocular filters, giving rise to “false” matches (Marr and Poggio 1979). Finer spatial filters produce sharper disparity selective responses but also generate more numerous false matches. These false matches can be reduced by combining responses across spatial scales (Fleet et al. 1996). However, simply summing responses from lower SF filters produces coarser tuning. Suppression by low SFs both reduces the number of false matches (Tanabe et al. 2011) and sharpens the response function. This combination of binocular signals may be an adaptation for solving the stereo correspondence problem. They may also exemplify a more general principle: by combining excitatory and suppressive signals on different scales, it is possible to retain useful signals about important properties of the world (in this case disparity) while reducing responses to interfering signals (like false matches). This may be another reason why combinations of suppression and excitation are so often found to underlie activity in visual cortex.

GRANTS

This work was supported by the Intramural Program of the National Eye Institute. S. Tanabe was partially supported by the Long-Term Fellowship of the Human Frontier Science Program.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.T. and B.G.C. conception and design of research; S.T. and B.G.C. performed experiments; S.T. and B.G.C. analyzed data; S.T. and B.G.C. interpreted results of experiments; S.T. and B.G.C. prepared figures; S.T. and B.G.C. drafted manuscript; S.T. and B.G.C. edited and revised manuscript; S.T. and B.G.C. approved final version of manuscript.