Abstract
Identifying neurons and their spatial coordinates in images of the cerebral cortex is a necessary step in the quantitative analysis of spatial organization in the brain. This is especially important in the study of Alzheimer's disease (AD), in which spatial neuronal organization and relationships are highly disrupted because of neuronal loss. To automate neuron recognition by using high-resolution confocal microscope images from human brain tissue, we propose a recognition method based on statistical physics that consists of image preprocessing, parallel image segmentation, and cluster selection on the basis of shape, optical density, and size. We segment a preprocessed digital image into clusters by applying Monte Carlo simulations of a q-state inhomogeneous Potts model. We then select the range of Potts segmentation parameters to yield an ideal recognition of simplified objects in the test image. We apply our parallel segmentation method to control individuals and to AD patients and achieve recognition of 98% (for a control) and 93% (for an AD patient), with at most 3% false clusters.
A major advance in quantitative neuroanatomy comes from modern design-based stereological techniques supported by computer imaging methods, which use unbiased systematic random sampling to obtain estimates of global quantities, such as neuronal numbers, densities, areas, and volumes (1–3). A further advance comes from a more local analysis, such as the Dirichlet tessellation method, in which each particle is assigned a local density depending on the positions of all of its nearest-neighbor particles (4, 5). Recently, a 3D analysis of local spatial particle distribution has been coupled with a stereological approach (6).
The above methods present major advances in quantifying spatial distributions of neurons, glial cells, blood vessels, etc. in the cortex. However, to quantify a more subtle architectonic feature, such as the microcolumnar organization of neurons in the cortex, it is more powerful to apply a method that takes advantage of averaging over a population in a region of interest to get rid of statistical fluctuations that may obscure the results. Recently, a density map method based on statistical physics concepts was developed and successfully applied to study the microcolumnar structure of neurons in a higher-association cortex of a healthy human brain, and it was shown that this structure is disrupted in dementias such as Alzheimer's disease (AD) and dementia with Lewy bodies (7, 8). A modified cross-correlation density map method was developed to study the local spatial relationship between two different populations, and was applied to quantify neurotoxic effects of the fibrillar form of amyloid plaques in AD (9).
Density map methods require as input spatial coordinates of all of the neurons (or other populations) in the region of interest. The more subtle and short-range the spatial feature, the more samples are required to quantify it. The task of manually collecting neuronal positions from a given image is time consuming. For example, the number of neurons taken into account from the control human cortical lining of the superior temporal sulcus in the microcolumnar structure quantification was between 10,000 and 20,000 (7).
To decrease the human workload we need an automated method that takes a digitized image as input and outputs spatial coordinates of objects in the image. Such a method necessarily involves object (neurons, glial cells, plaques) recognition. Object recognition within an image can be made easier with software packages, such as National Institutes of Health image which can be downloaded at http://rsb.info.nih.gov/nih-image. Nonetheless, tedious manual and potentially subjective corrections are still necessary to achieve an adequate recognition accuracy. Traditional automated approaches, on the other hand, such as neural networks based on the work of Hopfield (10), are very elaborate and time consuming.
Which object recognition method to apply depends strongly on the object (in our case, neurons), acquisition technique, resolution, magnification, and quality of images. In this paper we consider confocal microscope images with 1-μm resolution of human brain tissue immunostained by anti-neu-N for neurons. These images show crisp neuronal bodies, while “hiding” all other cells in the tissue. Despite a high quality of images, simple image processing techniques, such as blurring, sharpening, and thresholding, are not sufficiently accurate to recognize neurons of different sizes, shapes, and textures. The challenge of neuronal recognition lies in the fact that more than one type of neuron is present in human brain tissue (large pyramidal neurons with many visible processes and small rounded neurons without visible processes), and neurons touch and visually overlap in parts of images.
Our goal is to automatically recognize neurons in a digital confocal microscope image of human brain tissue:
Step i: preprocess the image by using blurring.
Step ii: segment the preprocessed image into clusters of pixels with similar optical density.
Step iii: apply cluster selection criteria, based on the optical density, shape, and size distribution.
In step ii, we first map the preprocessed digital grayscale image on a discrete spin lattice and then apply Monte Carlo simulation using the inhomogeneous Potts model. In our approach we introduce a parallel Potts segmentation approach, which reduces the main source of recognition error that comes from parts of the image where two or more neurons overlap. Steps i, ii, and iii constitute a fully automated method that is capable of correctly detecting over 93% of neurons in confocal images of anti-neu-N immunostained human brain tissue.
The paper is organized as follows: in the first section of Methods, we describe the Potts segmentation method. This method in step ii has four adjustable parameters that influence the efficiency of the recognition. To find optimal parameters, we introduce a test image to “probe” the parameter space and introduce a quantity (deviation) to measure the efficiency of the recognition method. In the application to confocal microscope images, the Potts recognition method outperforms a simple automated neuron recognition method. However, it does not match our requirement. In the second section of Methods, we introduce the parallel Potts segmentation method to achieve the required recognition efficiency.
Methods
Potts Recognition Method.
Preprocessing, segmentation, and cluster selection.
The digitized grayscale image is mapped onto a 2D rectangular lattice of size Lx × Ly with a grayscale value gi ∈ [0, 255] at each plaquette i. Each lattice plaquette i has eight nearest neighbors: two along the x-axis, two along the y-axis, and two along each of the two diagonals. To reduce the background noise, in step i we preprocess the image by blurring: each grayscale value gi is replaced by the average of itself and the grayscale values of the eight nearest neighbors.
In step ii we segment the preprocessed image into clusters by (a) mapping the image onto a 2D lattice of Potts spins (11), such that each pixel of the image is represented by a spin on the lattice, and (b) finding a stable segmentation into clusters that is insensitive to the initial conditions. Clusters appear in Potts models (12–14) as regions of spins that are in the same spin state. There are q possible spin states (q ≥ 2) for each lattice plaquette (i.e., image pixel) instead of the original 256 possible grayscale levels. In our approach, we treat q as a parameter to be optimized for our particular segmentation problem. Intuitively, the more different segments (clusters) we want to distinguish, the larger the number of spin states q. The idea behind this approach (11) is to map two neighboring pixels with similar grayscale levels to two corresponding ferromagnetically bonded spins (which will belong to the same cluster in a stable state), and to map two neighboring pixels with very different grayscale levels to two corresponding antiferromagnetically bonded spins (which will belong to two different clusters in a stable state).
The q-state Potts model Hamiltonian (15) is defined as
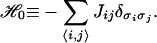 |
Two spins σi and σj interact only if they are nearest neighbors and are in the same spin state. δσiσj is a Kronecker δ function. The type (ferromagnetic or antiferromagnetic) and strength of the interaction are given by the interaction parameter Jij: for a positive Jij, the energy is lower if the spins are in the same spin state, whereas for a negative Jij, the energy is lower when the two spins are in different spin states. The difference in the grayscale levels of two neighboring pixels, gi − gj, is related to the interaction strength Jij between the corresponding neighboring spins, σi and σj:
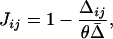 |
where
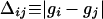 |
and Δ̄ is the average of Δij for the image. According to Eqs. 2 and 3, the interaction strength Jij is a linear function of the grayscale difference gi − gj and θ is a threshold parameter that changes the proportion of ferromagnetic versus antiferromagnetic bonds. (The threshold parameter was introduced into the model as a result of a personal communication with C. von Ferber in 2001.)
In analogy to neural systems that perform recognition tasks, we add an inhibition term (16, 17) to the Hamiltonian defined by Eq. 1. The total Hamiltonian is
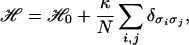 |
where κ is an inhibition strength. The sum is over all of the spin pairs in the entire system and not only the nearest neighbors. The inhibition term favors different spin states for spins in different clusters, and as such enhances the contrast of the final segmented image.
In total, there are four parameters in the model: temperature T, number of spin states q, threshold parameter θ, and inhibition strength κ. Note that kBT, κ, and Jij have the same units of energy, which we set to 1. Segmentation of our preprocessed grayscale image into clusters is now equivalent to superparamagnetic clustering (11) of Potts spins that interact by means of the Hamiltonian in Eq. 4. The final steady-state configuration depends strongly on the four model parameters. For example, we must choose a T low enough to avoid thermal fluctuations that would fragment the clusters. It has been shown that at T = 0 the relaxation process may stop at a metastable state that does not correspond to the lowest energy configuration (18). For T > 0, the final spin configuration is stable and does not depend on the initial conditions.
Initially, the Metropolis algorithm (19), in which each spin is updated individually, was used in Monte Carlo simulations. Swendsen and Wang (20) improved the efficiency of Monte Carlo simulations by introducing a cluster updating algorithm, which gave rise to many new efficient algorithms (16, 21–27). In this work we use an energy-sharing cluster update algorithm (17) which is up to 10 times faster than the original Swendsen–Wang algorithm.
In step iii of our neuron recognition method, we obtain a segmented image with clusters from which we must select those that correspond to neurons. We do this by applying (a) an optical density cutoff, (b) a shape criterion, and (c) a cluster size cutoff.
(a) Optical density cutoff.
To apply an optical density cutoff, we first calculate the average optical density of each cluster of the segmented image by averaging over the grayscale levels of the corresponding pixels of the preprocessed image. We then select only the clusters with the average optical density larger than 135, which is about half of the grayscale range. This way, we discard the clusters that form parts of the background or fainter objects that are out of focus.
(b) Shape criterion.
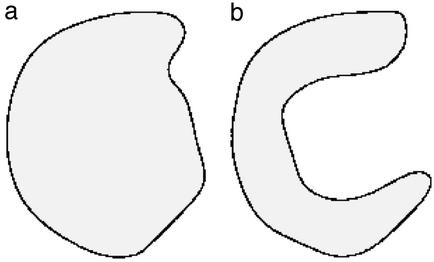
Neurons on the confocal image are of two types: smaller rounded ones and larger pyramidal neurons that are roughly diamond shaped and have many visible processes. In both types of neurons the neuronal body is a compact object of a spherical or rhomboidal shape. Because of an inner grayscale texture, the segmentation step iii may yield more than one cluster in place of one neuronal body; typically, one belongs to the compact neuronal body and the other one wraps around the body. To get rid of those clusters that wrap around neuronal bodies, we apply a shape criterion (Fig. 1) by which a cluster is selected only if it contains its center of mass.
Fig 1.
A schematic illustration of the shape criterion used in the step iii of our neuron recognition method: a cluster passes the shape criterion only when its center of mass belongs to the cluster. (a) A cluster that passed the shape criterion. (b) A cluster that failed the shape criterion.
(c) Cluster size cutoff.
After the optical density cutoff, the clusters that pass the shape criterion still have various sizes. To get rid of very small clusters that are far below a typical neuron size, we apply a lower size area cutoff of 7.5 μm2 (this corresponds to a linear size cutoff of 3 μm).
Parameter optimization.
We initially fix q and then optimize the values of the three model parameters T, θ, and κ involved in the segmentation step of our recognition method, i.e., we study the quality of the segmentation dependence on T, θ, and κ. We repeat this procedure for several different values of q. Below we will show that varying the number of spin states q results in a locally optimal value for q = 10.
To probe the parameter space (T, θ, κ), we introduce a test image, i.e., an image of well-separated square objects (see Fig. 2). To make the test image more realistic, we add uniform “white” noise to each pixel. If gi is the grayscale level of the pixel at the plaquette i (which is either 0 or 255) and ɛ is the noise level, then gi → |gi − η|, where η is a random integer number from the interval [0, ɛ). We use three different noise levels with ɛ = 30, 60, and 90.
Fig 2.
Test images, each consisting of 30 isolated squares of size 7 pixels × 7 pixels. The objects are of the highest optical density (255) and the background is of the lowest optical density (0) in the absence of noise. To this basic image we add three different noise levels, characterized by ɛ = 30 (a), ɛ = 60 (b), and ɛ = 90 (c).
The objective of our recognition method is to automatically determine the centers of the masses of these square objects in the test image. The efficiency of the recognition method can be measured by introducing a deviation δ, the sum of squared distances between the centers of the actual and recognized objects. Suppose the actual centers of the masses of objects are given by (Xi, Yi), i = 1, … , Nn, where Nn is the actual number of objects in the test image. These coordinates are known for the test image, where we choose the positions of these objects. The recognition method, on the other hand, may yield another set of coordinates for clusters that are recognized as objects, (X̃j, Ỹj), j = 1, … , Nc, where Nc is the number of clusters. For a 2D lattice with dimensions Lx × Ly, the deviation δ is defined as
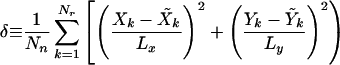 |
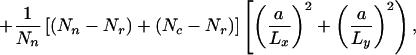 |
where a is a typical linear size of the object. The first term is a contribution from Nr correctly recognized objects (Nr ≤ Nc and Nr ≤ Nn). We count an object as correctly recognized if the center of the recognized object falls inside the perimeter of the real object. Thus this contribution is typically small. The second and third terms arise from false recognition and bring large contributions. There are Nn − Nr unrecognized objects and Nc − Nr false clusters that do not represent actual objects. Each unrecognized object and false cluster (with no real counterpart) contributes to δ the same quantity, which depends on the linear size of the object, a, and the image size Lx × Ly. Note that δ is a dimensionless positive quantity and normalized to be always smaller than 1. For ideal recognition, δ ≈ 0.
Using δ, we can determine the 3D volume of the Potts parameter space (T, θ, κ), which yields an ideal recognition of objects in the test image. In general, at high temperature T, large inhibition strength κ, large q, and small θ, there is a tendency to segment the image into many small clusters. At the other extreme, at low temperature T, small inhibition strength κ, small q, and large θ, there is a tendency for clusters to merge, and in the most extreme conditions, the clusters merge with the background clusters.
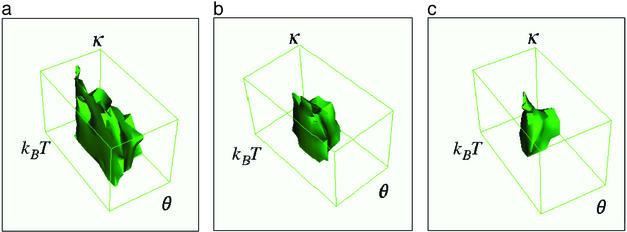
Here we determine the range of Potts model parameters that yields ideal recognition for the test image. At a fixed q = 10, we sample the three-parameter (T, θ, κ) space. For each sample point we apply the Potts recognition method and calculate the deviation δ of Eq. 5. An optimal point in this parameter space is defined as a point at which δ < δc = 1.8 × 10−4. The threshold deviation δc is chosen to correspond to the case where all of the objects in the test image are recognized exactly once, except one. From Eq. 5, we see that the value of the threshold deviation δc ≈ 2/NnA/(LxLy), where A is the object area, depends on the object's size and the number of objects in the image.
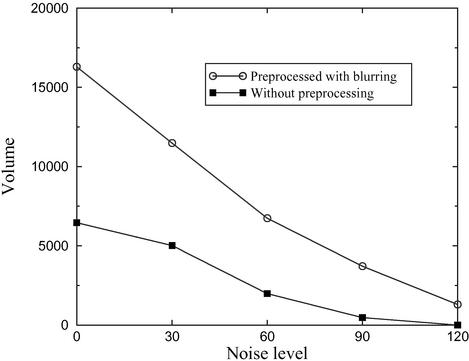
For each of the three noise levels superposed on the test image, we sample 7, 12, and 8 points for parameters T, θ, and κ, respectively, which gives 672 (7 × 12 × 8) points in the (T, θ, κ) parameter space. kBT ranges from 0.02 to 1.2, θ from 0.1 to 11, and κ from 0 to 3500. The optimal parameter space is presented in Fig. 3 for three different noise levels. For the test image with noise level ɛ = 60, for example, the optimal temperature range is [0.001, 0.800] at the optimal values of the parameters θ and κ. The parameter θ is optimal in the range [1, 6], and κ is optimal in the range [0, 1000]. As the noise level in the test image increases, the optimal parameter space shrinks as shown in Fig. 4, where we depict the volume of the optimal parameter space as a function of the noise level parameter ɛ. Preprocessing the image by blurring has the same effect as reducing the background noise, which increases the volume of the optimal parameter space.
Fig 3.
3D surface rendered parameter space within which each point represents the Potts model parameters that yield a perfect object recognition in the test image with three different noise levels, characterized by ɛ = 30 (a), ɛ = 60 (b), and ɛ = 90 (c). The box marks out the explored ranges: kBT = 0.02−1.2, θ = 0.1−11, and κ = 0−3500.
Fig 4.
The volume of the Potts model parameter space, which yields an ideal 100% recognition of the objects in the test image, as a function of the noise level parameter ɛ. Preprocessing the image by blurring has the same effect as reducing the background noise level.
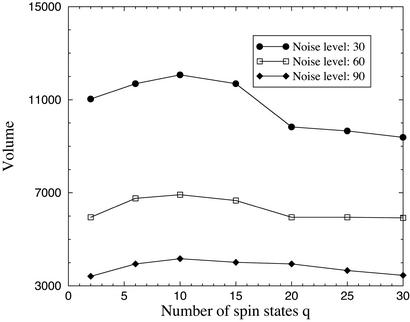
Finally, we study the dependence of the optimal parameter space volume on the Potts variable q. We vary q to explore the volume of the Potts model parameter space for ideal recognition, and we find that the volume assumes the maximum at q ≈ 10. Fig. 5 shows the parameter space volume versus the Potts variable q for three different noise levels.
Fig 5.
The volume of the Potts model parameter space that yields the ideal 100% recognition of objects in the test image as a function of the Potts parameter q for three different noise levels: ɛ = 30 (•), 60 (□), and 90 (♦).
Recognition efficiency.
Using these optimal parameters, we apply our neuron recognition method to automatically determine the (x, y) coordinates of neurons on the confocal microscope images of human neu-N-immunostained brain tissue. We choose five images from a healthy human subject and five images from an AD patient. We digitize each confocal microscope picture (447 μm × 447 μm) into an image of 512 pixels × 512 pixels.
To determine the efficiency of our neuron recognition method, we first manually locate the neurons in each image, then measure the recognition efficiency by two parameters: the percentage of actual neurons that get recognized by the Potts recognition method and the percentage of false clusters that do not coincide with actual neurons. There are Nn manually recognized neurons in the image and the method yields Nc clusters recognized as neurons, of which Nr clusters match to manually recognized neurons. Our recognition efficiency is quantified by parameters Nr/Nn (which we want to be close to 1) and (Nc − Nr)/Nc (which we want to minimize).
We calculate the two efficiency measures for each image separately, and then average over five control subjects and five AD patients. The Potts recognition method is capable of detecting an average of 86% (77% for an AD brain) of neurons, and there is an additional 5% (4% for an AD brain) of falsely detected objects that do not correspond to neurons. The main contribution to the error comes from the parts of the image with two or more touching or overlapping neurons.
Parallel Potts Segmentation Method.
The accuracy of the Potts recognition method with a single optimal parameter condition is not sufficient. We need a more efficient recognition of at least 90% neurons correctly recognized. Thus we developed a “parallel Potts segmentation method” based on the Potts recognition method. Step i of the image preprocessing remains the same, whereas in step ii, the parallel segmentation method uses simultaneous segmentations of the same image at several sets of slightly different Potts model parameters spanning the optimal range. The idea behind this approach comes from the observation that a typical confocal microscope image, even of the highest possible quality, still suffers from variations in contrast and focus, and also from neuron overlap because of the finite thickness of samples. Therefore, one single parameter condition cannot be optimal for all of the local parts of the image.
In step ii we choose four different temperatures (kBT = 0.1, 0.4, 0.7, and 1.0) combined with four different threshold parameters (θ = 0.5, 2.0, 3.5, and 5.0) and one inhibition strength κ = 10; the inhibition strength is a fixed parameter because the strength of the inhibition is not essential (see Discussion). After the parallel segmentation step, we have a set of 4 × 4 segmented images for the same original image. In some of these segmented images, overlapping neurons appear as a single cluster, but are correctly separated in other segmented images.
We apply step iii to these segmented images and get 4 × 4 sets of clusters that are candidates for actual neurons. Some sets of clusters cover the same part of the original image and we must apply some sort of logical “OR” operation in the further selection. Because the candidate clusters range from 10 to 40 pixels in area, and the typical neuronal size is 25 pixels in area, we give priority to clusters whose areas are closer to 25 pixels in the following selection. First, we choose the areas with 25 pixels and select all of the clusters from all of the 4 × 4 segmented images with this area. At the same time, we discard all of the nonselected clusters whose centers fall into the selected clusters. Next, we add to the selected clusters all of the clusters with areas of 24 and 26 pixels and again discard all of the remaining clusters whose centers are within these additional selected clusters. Next, we add to the selected clusters all of the clusters with areas of 23 and 27 pixels, etc. We repeat this procedure until all of the clusters are either selected or discarded. At the end of this step, we have a set of nonoverlapping clusters representing neurons. The recognition efficiency is improved by the present method because overlapping neurons are separated by the selection procedure based on typical neuron size, and the number of false clusters is minimized by the discarding procedure.
Results
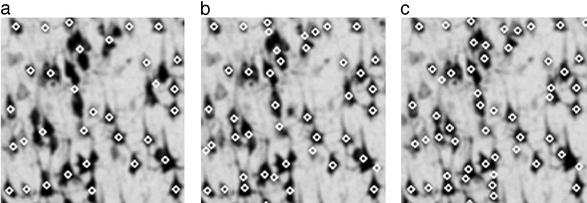
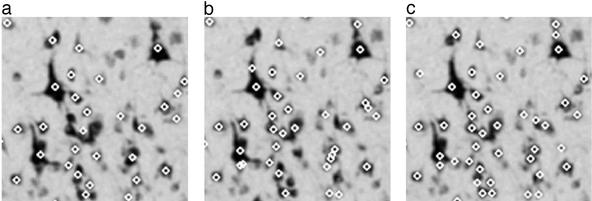
In Table 1 we compare the recognition efficiency of three automated methods: a simple recognition method, a Potts recognition method, and the present parallel Potts segmentation method. The simple recognition method is presented here for the purpose of comparison. It consists of blurring, grayscale thresholding, and applying the cluster shape criterion and a cluster size cutoff. This simple recognition method achieves its best performance with the grayscale threshold set to 155, and it can recognize ≈75% of neurons with 9% false clusters for threshold 155. Preliminary investigation shows that multilevel thresholding (28) does not give sufficient improvement. The Potts recognition method is capable of detecting an average of 86% (77% for an AD brain) of neurons with 5% (4% for AD) false clusters. By applying the parallel Potts segmentation approach, we achieve an accuracy of 98% (93% for AD) neuron recognition with 3% (2% for AD) false clusters. Examples in which the neurons are recognized by these three methods are presented in Fig. 6 for a healthy brain and in Fig. 7 for an AD brain. They show that the main error for the conventional methods (Figs. 6 and 7 a and b) comes from the parts of the image with overlapping neurons, and the parallel Potts recognition method improves the recognition efficiency by separating the overlapping neurons.
Table 1.
Comparisons of recognition methods
| Method | % recognition | % false clusters |
|---|---|---|
| Healthy brain | ||
| Simple segmentation | 74 | 9 |
| Potts segmentation | 86 | 5 |
| Parallel Potts segmentation | 98 | 3 |
| AD brain | ||
| Simple segmentation | 75 | 7 |
| Potts segmentation | 77 | 4 |
| Parallel Potts segmentation | 93 | 2 |
Fig 6.
Comparison of three neuron recognition methods applied to a healthy brain with shape criterion and cluster size cut-off (10 pixels) showing that as touching neurons are distinguished the recognition efficiency improves (e.g., the number of recognized neurons increases from 33 to 45 to 54.). Image size is 140 pixels × 140 pixels (122 μm × 122 μm). (a) Simple recognition (optical density cutoff 155). (b) Potts recognition (kBT = 0.4, θ = 2.5, κ = 10, and optical density cutoff 135). (c) Parallel Potts recognition with 4 × 4 sets of conditions (kBT = 0.1−1, θ = 0.5−5, κ = 10, and optical density cutoff 135).
Fig 7.
Comparison of three neuron recognition methods applied to an AD brain with shape criterion and cluster size cut-off (10 pixels) showing that as touching neurons are distinguished, the recognition efficiency improves (e.g., the number of recognized neurons increases from 30 to 34 to 46). Image size is 140 pixels × 140 pixels (122 μm × 122 μm). (a) Simple recognition (optical density cutoff 155). (b) Potts recognition (kBT = 0.4, θ = 2.5, κ = 10, and optical density cutoff 135). (c) Parallel Potts recognition with 4 × 4 sets of conditions (kBT = 0.1−1, θ = 0.5−5, κ = 10, and optical density cutoff 135).
Discussion
We studied neuron recognition on confocal microscope images of human brain tissue by introducing a parallel Potts segmentation method, which is based on superparamagnetic clustering data and the Potts recognition method (11, 17). We achieved a high recognition efficiency with more than 98% (±3%) correctly recognized neurons for a healthy control brain, and 93% (±2%) correctly recognized neurons for an AD brain. The lower recognition efficiency in an AD brain as compared with the control brain may be a reflection of the huge neuronal loss and disruption of the neighboring tissue caused by the volume change of the AD cortex.
To segment the image into clusters, we apply a q-state Potts model with spin–spin interactions that are related to the grayscale differences between the neighboring image pixels. Following the initial work of von Ferber and Wörgötter (17), we also include a global inhibition term into the Potts Hamiltonian, the purpose of which is to increase the contrast of the segmented image. When we excluded the inhibition term entirely, we found only a slight change of the final results: the Potts recognition method yields virtually the same recognition efficiency in both control and AD brains, whereas the parallel Potts segmentation method applied to control brain images improves from 95% (±5%) for κ = 0 to 98% (±3%) for κ = 10, with no significant improvement for images of the AD brain. We thus conclude that the inhibition term in our particular case of neuron recognition is not essential; however, it slightly improves the efficiency of our recognition results.
Although we do not discuss more general applications, our method can easily be extended to 3D, or used in a highly anisotropic milieu. We believe that our method will prove successful when applied to other types of tissue and material as well. To do that, however, the parameters of the model, which depend highly not only on the size of objects but also on their variability and inner “texture,” have to be optimized in each specific application separately.
In the present work we studied the cortical lining of the superior temporal sulcus, both in the control human and AD brain. It is of critical importance to be able to define the boundaries in the tissue at hand to perform an accurate quantitative assessment of specific brain regions. This cortical area is advantageous in our study because the boundaries can be defined by following anatomical landmarks rather than relying entirely on cytoarchitectural clues, which may suffer from severe disruption in the AD brain.
Finally, in this work we focused our study on the control and AD brain to test the robustness of our automated neuron recognition method. Given its success in the AD brain, where atrophy, autofluorescent lipofuscin, and degenerative changes decrease the quality of the image and thus effect the final efficiency of recognition, we anticipate that our method would be robust enough to apply to other degenerative disorders.
Supplemental data that include a detailed description of the method can be found at http://polymer.bu.edu/∼shypeng/Neu-Rec.
Acknowledgments
We thank C. von Ferber for helping with the implementation of the cluster update algorithm to the Potts model and D. Baker, N. V. Dokholyan, and S. V. Buldyrev for their helpful comments. This work was supported by National Institutes of Health Grant AG08487, The Neurological Foundation and Memory Ride, and the Adler Foundation.
Abbreviations
AD, Alzheimer's disease
References
- 1.West M. J. & Gundersen, H. J. G. (1990) J. Comp. Neurol. 296, 1-22. [DOI] [PubMed] [Google Scholar]
- 2.Harding A. J., Halliday, G. M. & Cullen, K. (1994) J. Neurosci. Methods 51, 83-89. [DOI] [PubMed] [Google Scholar]
- 3.Glaser J. R. & Glaser, E. M. (2000) J. Chem. Neuroanat. 20, 115-126. [DOI] [PubMed] [Google Scholar]
- 4.Duyckaerts C., Godefroy, G. & Hauw, J.-J. (1994) J. Neurosci. Methods 51, 47-69. [DOI] [PubMed] [Google Scholar]
- 5.Duyckaerts C. & Godefroy, G. (2000) J. Chem. Neuroanat. 20, 83-92. [DOI] [PubMed] [Google Scholar]
- 6.Schmitz C., Grolms, N., Hof, P. R., Boehringer, R., Glaser, J. & Korr, H. (2002) Cereb. Cortex 12, 954-960. [DOI] [PubMed] [Google Scholar]
- 7.Buldyrev S. V., Cruz, L., Gomez-Isla, T., Gomez-Tortoza, E., Havlin, S., Le, R., Stanley, H. E., Urbanc, B. & Hyman, B. T. (2000) Proc. Natl. Acad. Sci. USA 97, 5039-5043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jones E. G. (2000) Proc. Natl. Acad. Sci. USA 97, 5019-5021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Urbanc B., Cruz, L., Le, R., Sanders, J., Hsiao-Ashe, K., Duff, K., Stanley, H. E., Irrizarry, M. C. & Hyman, B. T. (2002) Proc. Natl. Acad. Sci. USA 99, 13990-13995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hopfield J. J. (1982) Proc. Natl. Acad. Sci. USA 79, 2554-2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blatt M., Wiseman, S. & Domany, E. (1996) Phys. Rev. Lett. 76, 3251-3254. [DOI] [PubMed] [Google Scholar]
- 12.Fortuin C. M. & Kasteleyn, P. W. (1972) Physica (Utrecht) 57, 536-564. [Google Scholar]
- 13.Coniglio A. & Klein, W. (1980) J. Phys. A 13, 2775-2780. [Google Scholar]
- 14.Wang S. & Swendsen, R. H. (1990) Physica A 167, 565-579. [Google Scholar]
- 15.Wu F. Y. (1982) Rev. Mod. Phys. 54, 235-267. [Google Scholar]
- 16.Opara R. & Wörgötter, F. (1998) Neural Comput. 10, 1547-1566. [DOI] [PubMed] [Google Scholar]
- 17.von Ferber C. & Wörgötter, F. (2000) Phys. Rev. E 62, 1461-1464. [DOI] [PubMed] [Google Scholar]
- 18.Fukunaga K., (1990) Introduction to Statistical Pattern Recognition (Academic, San Diego), pp. 533–549.
- 19.Metropolis N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. (1953) J. Chem. Phys. 21, 1087-1092. [Google Scholar]
- 20.Swendsen R. H. & Wang, J. S. (1987) Phys. Rev. Lett. 58, 86-88. [DOI] [PubMed] [Google Scholar]
- 21.Edwards R. G. & Sokal, A. D. (1988) Phys. Rev. D 38, 2009-2012. [DOI] [PubMed] [Google Scholar]
- 22.Niedermayer F. (1988) Phys. Rev. Lett. 61, 2026-2029. [DOI] [PubMed] [Google Scholar]
- 23.Wolff U. (1989) Phys. Rev. Lett. 62, 361-364. [DOI] [PubMed] [Google Scholar]
- 24.Kandel D. & Domany, E. (1991) Phys. Rev. B 43, 8539-8548. [DOI] [PubMed] [Google Scholar]
- 25.Machta J., Choi, Y. S., Lucke, A., Schweizer, T. & Chayes, L. V. (1995) Phys. Rev. Lett. 75, 2792-2795. [DOI] [PubMed] [Google Scholar]
- 26.Redner O., Machta, J. & Chayes, L. F. (1998) Phys. Rev. E 58, 2749-2752. [Google Scholar]
- 27.Tomita Y. & Okabe, Y. (2001) Phys. Rev. Lett. 86, 572-575. [DOI] [PubMed] [Google Scholar]
- 28.Clements J. D. & Buzy, J. M. (1991) J. Neurosci. Methods 36, 1-8. [DOI] [PubMed] [Google Scholar]