Improved Coarse-Grained Modeling of Cholesterol-Containing Lipid Bilayers

Abstract

Cholesterol trafficking, which is an essential function in mammalian cells, is intimately connected to molecular-scale interactions through cholesterol modulation of membrane structure and dynamics and interaction with membrane receptors. Since these effects of cholesterol occur on micro- to millisecond time scales, it is essential to develop accurate coarse-grained simulation models that can reach these time scales. Cholesterol has been shown experimentally to thicken the membrane and increase phospholipid tail order between 0 and 40% cholesterol, above which these effects plateau or slightly decrease. Here, we showed that the published MARTINI coarse-grained force-field for phospholipid (POPC) and cholesterol fails to capture these effects. Using reference atomistic simulations, we systematically modified POPC and cholesterol bonded parameters in MARTINI to improve its performance. We showed that the corrections to pseudobond angles between glycerol and the lipid tails and around the oleoyl double bond particle (the “angle-corrected model”) slightly improves the agreement of MARTINI with experimentally measured thermal, elastic, and dynamic properties of POPC membranes. The angle-corrected model improves prediction of the thickening and ordering effects up to 40% cholesterol but overestimates these effects at higher cholesterol concentration. In accordance with prior work that showed the cholesterol rough face methyl groups are important for limiting cholesterol self-association, we revised the coarse-grained representation of these methyl groups to better match cholesterol-cholesterol radial distribution functions from atomistic simulations. In addition, by using a finer-grained representation of the branched cholesterol tail than MARTINI, we improved predictions of lipid tail order and bilayer thickness across a wide range of concentrations. Finally, transferability testing shows that a model incorporating our revised parameters into DOPC outperforms other CG models in a DOPC/cholesterol simulation series, which further argues for its efficacy and generalizability. These results argue for the importance of systematic optimization for coarse-graining biologically important molecules like cholesterol with complicated molecular structure.

Introduction

Cholesterol serves diverse regulatory and metabolic functions in mammalian cells, including regulation of its own cellular concentration via multiple pathways.¹⁻⁴ In addition, much of cell biology is mediated by the physical properties of lipid bilayers, which can in turn be regulated by cholesterol. For example, cholesterol-mediated microdomains (“rafts”) are thought to facilitate trafficking of selected lipids and proteins in cells.⁵⁻⁷ In addition, cholesterol’s ordering effects are thought to be responsible for its inhibition of calcium channel SERCA2 ATPase activity,⁸ and cholesterol reduces leakage induced by cell-penetrating peptides.⁹⁻¹¹ Furthermore, high (>40%) concentrations of cholesterol in the plasma membrane can stimulate cholesterol recognition by proteins and trafficking to the endoplasmic reticulum (ER).¹²

Biophysical experiments and simulations are useful tools for understanding cholesterol function in cells, such as cholesterol-induced decreases in membrane fluidity and increases in membrane thickness, bending modulus, and lipid tail order.¹³⁻¹⁸ Computational models are important for predicting high-resolution structural and dynamic properties of the membrane that are not experimentally accessible. Currently, sterol-containing membranes can be simulated at atomic resolution for hundreds of nanoseconds.¹⁹⁻²⁶ However, the interactions of cholesterol with membrane proteins and its effects on membrane superstructure (e.g., vesicles, protein sorting and trafficking) occur on length and time scales of micro- to milliseconds and beyond. More scalable “coarse-grained” (CG) simulations are valuable tools for investigating such systems, provided they reproduce key properties measured from experiments and atomistic simulations where experimental data are not available.

Marrink and others developed the coarse-grained force-field MARTINI, which groups 3–5 heavy atoms into a single particle.²⁷⁻³¹ There are a few dozen MARTINI particle types that model a wide range of hydrophobicity and polarity levels, different hydrogen bonding properties, and charges.²⁸ In addition, smaller (2–3:1) particles are provided for modeling ring systems found in sterols, sugars, and aromatic groups.²⁸ So that the coarse-grained particles can be used in different classes of molecules, these particles are parametrized based on simple model systems. Bonded parameters are derived from atomistic simulations of model compounds, and nonbonded parameters are calibrated to match water/organic solvent partitioning coefficients of representative small molecules.^28,31 MARTINI has been broadly tested against experiment, and it qualitatively agrees with experimental thermal,³² elastic (e.g., bending modulus, area compressibility),²⁷ and dynamic²⁷ properties of DPPC membranes. Periole et al. provide an excellent review of the development and performance of MARTINI on membrane, protein, and other systems to date.³¹

Cholesterol presents a special challenge for coarse-graining due to its complicated local structure (see Figure 1B–C). Cholesterol has four rigid rings, which MARTINI has addressed with the smaller type “S” particles,²⁸ as well as two methyl groups perpendicular to the ring and a branched tail. Because of these methyl groups, cholesterol prefers to avoid self-interactions in the first coordination shell, and interactions in the second shell have 3-fold symmetry.³³ In atomistic simulations, removal of these groups reduces the 3-fold symmetry to 2-fold³³ and weakens the cholesterol-induced area condensation and lipid acyl chain-ordering effects.³⁴ Other simulations suggest that the smooth face prefers to interact with saturated lipid chains, while the rough face lacks such preferential interactions.³⁵

Figure 1.

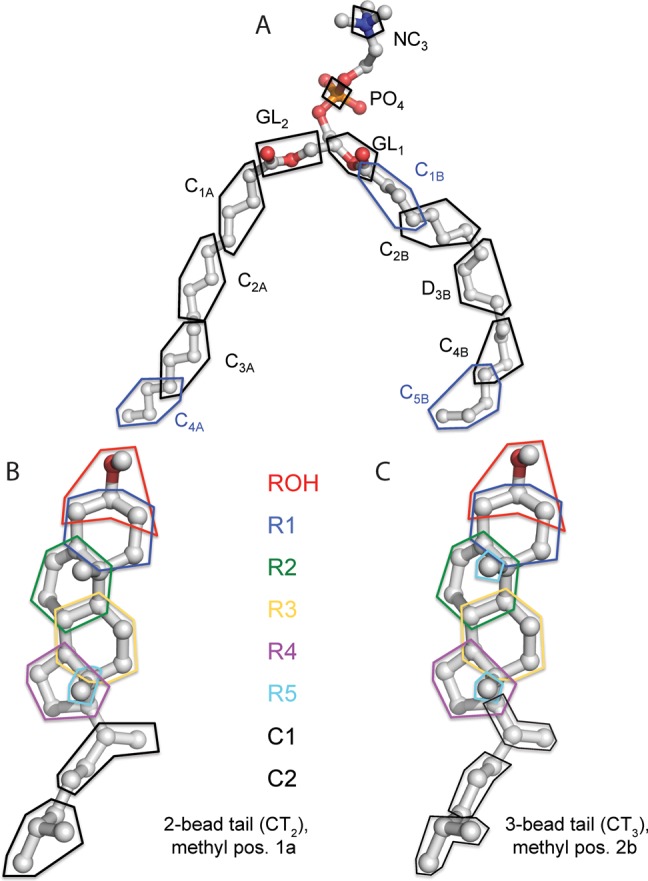
United-atom to coarse-grained mapping schemes for POPC and cholesterol. For each mapping, the polygon indicates a group of atoms that is mapped to a coarse-grained particle. For distance and angle calculations, the position of the coarse-grained particle is calculated by a weighted average of the positions of its constituent atoms. We assign a weight of 1.0 to an atom that belongs to only one coarse-grained particle and a weight of 1/N to an atom that is shared between N particles. The original UA-to-CG mappings of MARTINI are approximately illustrated in Marrink et al.²⁸

In this work, we assessed MARTINI performance on cholesterol containing palmitoyl-oleoyl phosphatidylcholine (POPC) bilayers. We consider POPC to be an important case study for physiologic membranes because of the introduction of the unsaturated alkane chain as is found in cellular membranes. By comparison to our published atomistic simulations,³⁶ we showed that MARTINI underpredicts bilayer thickening and lipid tail ordering at low cholesterol concentration and does not report the expected decrease in these observables at high concentrations. These are important considerations because they prominently affect the activity of membrane proteins.

Thus, we worked to improve MARTINI models for such bilayers by systematically varying selected force-field properties. First, we compared phospholipid conformations between MARTINI POPC and united atom (UA) POPC and adjusted the potentials for a few angles that agree poorly. We tested the resulting “angle-corrected” model against experimental determinations of the thermal, elastic, and dynamic properties used to validate the original MARTINI model. The angle-corrected model improves predictions of cholesterol-induced ordering at low cholesterol concentration, but its poor performance at higher concentrations suggests a problem with cholesterol-cholesterol interactions. Thus, we examined several key features of cholesterol coarse-grained structure, including tail angle corrections and, most importantly, representation of the small but critical rough face methyl groups and their effect on cholesterol self-avoidance. Then, we comprehensively compared all lipid and sterol models on a broad set of criteria (bilayer thickness, area per molecule, tail order parameters, radial distribution functions, and tilt) to identify the best model. Finally, to test for the generalizability of our revised model, we incorporated the parameters derived from UA POPC/cholesterol simulations into coarse-grained DPPC/cholesterol and DOPC/cholesterol binary simulations.

Methods

Lipid Topologies

United-Atom Simulations

The united-atom simulation data used in this work were collected in Olsen et al.,³⁶ and the force-field and simulation protocols are described in detail therein. Berger-Tieleman phospholipid tail parameters^19,37 were used for POPC, DOPC, and DPPC. The cholesterol topology was based on the original GROMOS topology from Holtje et al.,³⁸ with charges reparameterized using the QM/MM methods as described in Olsen et al.³⁹ Each united-atom trajectory is 400 ns long, and the last 200 ns were analyzed for the data presented in Olsen et al.³⁶ and this work. In addition to the 0–52% cholesterol trajectories from Olsen et al., we simulated additional trajectories at 60% cholesterol using the same method. We simulated a pure DPPC bilayer at 323 K.

Adjusted UA to CG Mapping

Figure 1A shows the UA-to-CG mapping we defined for POPC. Given the 4:1 mapping for MARTINI phospholipid.²⁸ we included some atoms in more than one CG particle (e.g., atom C47 is shared between CG particles C3A and C4A). For the alkyl regions of the tail, other mappings are possible, but for key functional groups we positioned the particles to include all relevant atoms. For example, we included in the GL1 and GL2 particles all the glycerol/fatty acid ester atoms in their respective chains, and we included in D3B all the atoms involved in the oleoyl double bond.

Starting from this mapping, we calculated reference CG bond and angle distributions from the UA simulation ensemble by first converting it to a “pseudo-CG” ensemble. To determine the position of each pseudo-CG particle from the UA simulation ensemble, we calculated a weighted average of the coordinates of its constituent atoms, where we assigned a weight of 1.0 to an atom that belongs to only one CG particle and a weight of 1/N to an atom that is shared between N particles. The topology files for all altered phospholipid and cholesterol models are included in the Supporting Information.

Adjustment of Bond and Angle Parameters Based on UA Simulations

In MARTINI, bond angle potentials are defined by E = (1)/(2)K_θ(cos(θ) – cos(θ₀))², where E, K_θ, and θ₀ are the angle potential energy, the force constant, and the equilibrium bond angle value, respectively. Table 1 shows that for most pseudoangles, MARTINI pure POPC simulations predict the average value within 10° of UA pure POPC simulations. However, Table 1 and Figure S1 show that MARTINI poorly predicts the distributions for the PO4/GL1/GL2 angle, the glycerol/glycerol tail angles (GL2-GL1-C1B and GL1-GL2-C1A), and the angle centered at the oleoyl double bond (C2B-D3B-C4B).

Table 1. Average Values of Pseudobond Angles in United Atom POPC and Coarse-Grained Variants^b.

		MARTINI			angle-corrected
angle	UA	eq. value (deg)	force constant (kJ/mol)	Δ from UA	eq. value (deg)	force constant (kJ/mol)	Δ from UA
PO4-GL1-C1B	145.0	180.0	25.0	0.2			7.1
PO4-GL1-GL2	72.5	120.0	25.0	39.2	a	a	0.8
GL2-GL1-C1B	120.3	-	-	32.3	120.0	45.0	8.1
GL1-GL2-C1A	123.4	-	-	10.5	120.0	45.0	9.5
C1B-C2B-D3B	152.1	180.0	25.0	7.1			6.7
C2B-D3B-C4B	147.8	120.0	45.0	23.9	145.0	45.0	6.3
D3B-C4B-C5B	147.6	180.0	25.0	5.9			5.4
GL2-C1A-C2A	148.0	180.0	25.0	2.5			2.6
C1A-C2A-C3A	151.0	180.0	25.0	6.3			5.9
C2A-C3A-C4A	148.8	180.0	25.0	6.2			5.5

^aFor the PO4-GL1-GL2 angle in the angle-corrected model, a bond of r = 0.513 nm is added between PO4 and GL2 in lieu of an angle potential given the acuteness of the equilibrium value. “Δ from UA” is the difference between the average value for a bond angle between the UA (pseudocoarse-grained) and MARTINI or angle-corrected pure POPC simulation.

^bThe united-atom to coarse-grained mapping is described in Figure 1. The form of the bond angle potentials is given in the Methods. Equilibrium values and force constants are provided for MARTINI POPC and for the angle-corrected model where MARTINI has been modified. The symbol ‘-‘ indicates that MARTINI does not include an angle potential for that triplet.

The PO4/GL1/GL2 angle averages 72.5° in the UA pure POPC simulation and is very sharply distributed (Figure S1). Since the average angle is acute and PO4, GL1, and GL2 are all covalently linked to the glycerol center, we introduced a 0.513 nm bond between PO4 and GL2 based on the average distance in the pseudo-CG ensemble. This stiff-bond potential is further supported by a very similar corresponding distance of 0.515 nm in the DOPC pseudo-CG ensemble and 0.512 nm in the DPPC pseudo-CG ensemble. For the glycerol/tail and oleoyl double bond angles, we corrected the equilibrium angle values to the nearest multiple of 5° observed in UA simulations, as indicated in Table 1. For example, for the C2B-D3B-C4B angle, we increased θ₀ from 120 in MARTINI to 145°. The values observed for these pseudoangles in UA DPPC and DOPC simulations are within 5° of the POPC values (data not shown).

MARTINI assigned K_θ = 45 kJ/mol for the C2B/D3B/C4B potential²⁸ because it is more sharply distributed in pseudo-CG ensembles than tail alkyl angles (Figure S1), for which MARTINI assigns K_θ = 25 kJ/mol. Because the GL/GL/tail angles are similarly sharply distributed, we also assigned their force constants as K_θ = 45 kJ/mol. With these corrections, the average value for PO4-GL1-GL2 improved to within 1° of UA, while GL2-GL1-C1B, GL1-GL2-C1A, and C2B-D3B-C4B improved to within 10°. In addition, Figure S2A shows that the angle correction significantly improves P₂ order parameters throughout the oleoyl tail (positions 1–5). The PO4-GL1/2 order parameters still remain about 0.15 higher than UA simulations for all coarse-grained models, but some deviation can be expected for these bonds since they span a tertiary center (C13) joining the headgroup and the two tails.

Coarse-Grained DOPC and DPPC Topologies

For CG DOPC/cholesterol and DPPC/cholesterol simulations, which are intended as an external validation of our revised POPC parameters, we copy all pseudobond and -angle potentials for angle-corrected DOPC and DPPC directly from the corresponding potentials in POPC. For example, for the double bond pseudoangles in the DOPC tails (C2A-D3A-C4A and C2B-D3B-C4B), we use the same potential as the double bond pseudoangle in the POPC oleoyl chain (C2B-D3B-C4B). Angle-corrected DPPC uses only the headgroup corrections since it has two palmitoyl tails. In addition, we use the same set of cholesterol topologies for DPPC/cholesterol, POPC/cholesterol, and DOPC/cholesterol sets of simulation series.

Fitting the Cholesterol Coarse-Grained Topology to the United-Atom Molecule

Two-Particle Tail

Figure 1B and Figure S3B illustrate our UA to CG mapping for cholesterol. We mapped the cholesterol ring and branched tail atoms into CG particles as explicitly as possible. For atoms shared between pseudo-CG ring and/or tail particles, we used the weighted average approach (described above for POPC) to calculate the pseudo-CG particle position. This mapping resulted in some small shifts in interparticle distances from the MARTINI cholesterol topology.²⁸ Significant changes include that ROH moves closer to R1 and R2, R3 moves away from R1 and closer to the tail atom C1, and R4 moves farther from R2 and closer to C1 (see Table S1).

For tail angle calibration, we followed a similar approach as for the phospholipid chains. For cholesterol with a two-particle tail (CT₂, Figure 1B), MARTINI only includes an angle potential for R3-C1-C2, which reasonably captures the average value and distribution seen in UA simulations (Figure S4 and Table S2). In UA simulations, the R4-C1-C2 angle is sharply distributed about 132.5°. Thus, we added a potential for this angle with K_A = 45 kJ/mol. Figure S4 shows that while the resultant coarse-grained distribution is not as narrow as the reference (UA) distribution, it fits better than MARTINI cholesterol. Table S2 also shows that both MARTINI and the best CG model overestimate the cholesterol CG tail order parameter S_R3-C1.

Three-Particle Tail

For CT₃, Figure S4 shows that the R3-C1-C2 angle is bimodally distributed in UA simulations, while MARTINI shows a single broad peak about 145°. While a statistical potential derived directly from the UA distribution better captures this peak, no corresponding improvement occurs in the membrane observables against which we test in the results (data not shown). Thus, we retained the original MARTINI potential for this angle. The reference distribution for R4-C1-C2 is sharper for CT₃ than CT₂ (Figure S4B). To address this, we increased K_A for this potential to 100 kJ/mol. Similarly, we added a potential for C1–C2–C3 with θ₀ = 180.0° and K_A = 50 kJ/mol. These two potentials captured the equilibrium values from UA to within 6° and 3°, respectively (Table S2). In addition, like CT₂, CT₃ also overestimated S_R3-C1, but S_C1–C2 and S_C2–C3 agree within 0.1 of UA.

Definition of Pseudomethyl Group Positions

Figure S5 illustrates our alternative UA to CG mappings for the pseudomethyl group of cholesterol, based on assignment of different weights to the two methyl groups (C18 and C19) and their corresponding attachment points (C13 and C10). Specifically, we used an internal coordinate system where the origin is at C13, the x-axis points toward C10 (1,0), and the y-axis points toward C18 (0,1). C19 is located at (1,1). We defined six pseudomethyl positions as follows: three “half-height” positions 1a at (0,0.5), 2a at (0.5,0.5), and 3a at (1.0,0.5) and three “elevated” positions 1b at (0,1.0), 2b at (0.5,1.0), and 3b at (1.0,1.0). Position 1a is closest to the original (relative) position of R5 in MARTINI.

Simulation and Analysis Protocol

For binary cholesterol/phospholipid simulations, initial structures were constructed from pre-equilibrated pure phospholipid bilayers by randomly replacing equal numbers of phospholipids with cholesterol molecules in the top and bottom leaflets. The total number of lipids (phospholipid + cholesterol) was 400 for all simulations. To remove steric clashes resulting from cholesterol insertion, the membrane was first stretched laterally 3.5-fold by scaling the position of the center of mass of each lipid in the bilayer plane. Then, the membrane was returned to its original size by a series of 24 energy minimization and small (5%) lateral compression steps. An approximately 2 nm-thick solvent layer was added on each side of the membrane, followed by 1000 steps of energy minimization.

Preliminary 10 ns equilibration runs were performed for each simulation using the Berendsen algorithm⁴⁰ and otherwise identical simulation conditions to the production runs. Production simulations were carried out for 200 ns using GROMACS 4.5,⁴¹ and the last 100 ns of the simulation were used for analysis. A time step of 20 fs was used since larger time steps cause simulations to be unstable at high (>30%) cholesterol concentrations. POPC/cholesterol and DOPC/cholesterol simulations were performed with velocity-rescale temperature coupling at 300 K with lipid (phospholipid plus cholesterol) and solvent coupled to separate heat baths. DPPC/cholesterol simulations were performed at 323 K. Semi-isotropic pressure coupling at equilibrium was performed using the Parrinello–Rahman algorithm.⁴²

Thermal Melting Simulations

Following Marrink et al.³² we estimated the liquid/gel phase transition temperature of coarse-grained POPC using two sets of simulations. The first “cooling” set of simulations started from an equilibrated liquid-disordered POPC bilayer at 300 K, well above T_m, which was instantaneously cooled to a series of target temperatures believed to bracket T_m. The second “heating” set of simulations started from an equilibrated gel-phase POPC bilayer at 200 K, well below T_m, which was instantaneously heated to a series of target temperatures. This approach is necessary since at the true T_m, liquid/gel transitions will occur on macroscopic length and time scales beyond the reach of even CG simulations,³² which will lead to hysteresis if a set of production simulations is run at a range of temperatures believed to bracket T_m, when started from a common initial configuration.

Given the nonequilibrium nature of liquid/gel transition simulations, we performed these with Berendsen pressure coupling. To prevent freezing of MARTINI water, 10 mol % “antifreeze particles” were added to the solvent. These particles prevent water freezing by disrupting crystal packing due to their larger size relative to standard MARTINI water.²⁸ Marrink et al. verified that 10 mol % antifreeze particles do not perturb any key properties (area per lipid, melting temperature, or lateral diffusion constant) of DPPC bilayers.²⁸

Membrane Structure Calculations

Bilayer Thickness

For the most comparison among experiments, united-atom, and coarse-grained simulations, we calculate bilayer thickness by twice the average height of the phosphate group from the membrane center, averaged between the leaflets. Due to undulations, which may cause the mean phosphate positions of the two leaflets to shift, we averaged the calculated thickness for each structure over a grid of cells with 1 nm spacing in the x and y (membrane plane) directions. Since not all grid cells contain a phosphate in both top and bottom leaflets, we performed a weighted average for each cell over a 3 × 3 grid of 1 nm cells, centered at the target cell, where each phosphate in the target cell is weighted 1.0 and each phosphate in a neighboring cell is weighted 1/8.

Radial Distribution Functions

Cholesterol-cholesterol radial distribution functions are calculated in two dimensions (the membrane plane) between the centers of masses of cholesterol molecules using the g_rdf script of GROMACS as described in the GROMACS manual.⁴¹ In addition, to compare two radial distribution functions G₁(r) and G₂(r), we define the metric ΔRDF

1

where the sum is taken over all radii between r_min and r_max, and N is the number of data points in this range of r. We choose r_min = 0.25 nm and r_max = 2.5 nm.

Order Parameters

We quantified the order of lipid tails by measuring the alignment of appropriate bonds along the membrane normal according to S_b = ⟨1.5cos²(θ_z) – 0.5⟩, where S_b is the order parameter of bond vector b, and θ_z is the angle of b with the membrane normal, averaged over both molecules and time. United-atom S_CH order parameters are calculated for each C–H vector for each carbon in the lipid tails. Coarse-grained second-rank (P₂) order parameters are calculated for consecutive bonds between coarse-grained particles in each lipid tail as in Marrink et al.²⁷

Order parameters cannot be directly compared between experiments and CG simulations. However, UA simulations can be compared to both experiments and CG simulations by calculating P₂ order parameters from the pseudo-CG simulation. Figure S7 shows that pseudo-CG P₂ and S_CH data are strongly linearly related with a scaling factor of about 2 and a near-zero intercept for each tail. Finally, to estimate experimental P₂ order parameters to which to compare the CG data, we rescale the data from Ferreira et al.⁴³ using the linear equations determined in Figure S7.

Bending Modulus

We calculated the bending modulus from the undulation spectrum of a large area of coarse-grained bilayer as described in refs (44 and 45). The bilayers from our united atom simulations are not sufficiently large to generate accurate bending modulus estimates. Following the protocol of Marrink et al.²⁷ from the original parametrization of MARTINI, we simulated 6400-POPC bilayers for 1 μs and obtained the undulation spectrum from the last 500 ns. Following Brandt et al.,⁴⁶ we converted the bilayer to two parallel discrete surfaces z₁(x,y) and z₂(x,y), with 64 bins each in the x and y directions. For a given grid cell, we calculated z₁(x,y) and z₂(x,y) by averaging z-coordinates of the phosphates in the top and bottom leaflets, respectively. The top and bottom surfaces are then averaged to produce a single surface:

For each frame in the trajectory, u(x,y) was Fourier transformed in two dimensions to produce a series of spectral intensities u²(m,n), which are the squares of the absolute values of the Fourier amplitudes. The two-dimensional space (m,n) is collapsed to a one-dimensional space q by

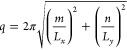where L_x and L_y are the box dimensions in x and y.⁴⁷u(q) was then normalized by (L_xL_y)². In the case of zero surface tension, the relation

holds for q < q₀, where q₀ ∼ 2π/d_HH and d_HH is the bilayer thickness.⁴⁵ In the above equation, k = Boltzmann’s constant, T = temperature, A = projected area, and k_c is the bending modulus. To obtain k_c, we fit ⟨u_and²(q)⟩ vs q according to the above equation for q < q₀ using the scipy.optimize.curve_fit function (www.scipy.org).

Area Compressibility

The area compressibility modulus K_A(48) measures the resistance of the bilayer to fluctuations in area per lipid. It is calculated as

2

where k is the Boltzmann’s constant, T is the temperature, and A₀ is the time-averaged bilayer area.

Results

Coarse-Grained Force-Field Optimization Goals and Approach

In this work, we critically assessed the performance of the MARTINI coarse-grained force-field against relevant metrics from united-atom (UA) simulations³⁶ and, where possible, experiments. We considered multiple observables including whole-bilayer properties like area per molecule (A_M) and bilayer thickness, macroscopic experimental properties like melting temperature, bending modulus, area compressibility, and microscopic properties like phospholipid acyl chain order parameters, lateral diffusion rate of lipids, and cholesterol-cholesterol radial distribution functions (RDFs).

We note that different types of UA and/or experimental reference data to which we compare have different levels of uncertainty. For example, bilayer thicknesses estimated from small-angle neutron^49,50 or X-ray⁵¹⁻⁵³ scattering (SAXS and SANS) provide a useful qualitative picture, but the fluid structure of bilayers limits their precision.⁵⁴ It is worth noting that recently developed scattering density profile analyses⁵⁵ can provide more precise thickness estimates for systems where both SAXS and SANS data are available. In addition, since areas per molecule are most readily observed in Langmuir monolayers⁵⁶ rather than in bilayers, these data likewise should be considered as a qualitative rather than quantitative target point for simulations. By contrast, lipid tail order parameters (S_C(D/H)) can be measured by NMR at atomic resolution, thus providing a rigorous test of simulation. Ferreira et al.⁴³ recently showed that simulations using the Berger lipid tail parameters¹⁹ accurately capture POPC tail ordering by low concentrations of cholesterol but tend to overestimate the ordering effect above 30% cholesterol. Finally, since UA simulations are themselves approximations designed from quantum and/or experimental data from model compounds, they must not be considered as target data per se but as a complement to low-resolution experimental data.

We revised the coarse-grained force-field properties separately for the phospholipids and cholesterol. POPC parameters are derived only from 100% POPC simulations, and cholesterol parameters are derived from 10% cholesterol/POPC simulations as described in the Methods. This calibration is the principal use of UA simulation data in this work. Figure 2 illustrates how three metrics (bilayer thickness, area per molecule (A_M), and order parameter) evolve between 0 and 60 mol % cholesterol. For reference, the solubility of cholesterol is ∼67% in phosphatidylcholine bilayers.^57,58 For these metrics, we compared experimental data (green) with UA (black), MARTINI (blue), and angle-corrected simulations (red) for cholesterol (circles) and optimized cholesterol (triangles). We also tested the POPC and cholesterol parameters on DOPC/cholesterol simulations as a test for transferability of our optimized parameters. Finally, we compare the original MARTINI²⁸ with corrected models on DPPC/cholesterol simulations. Using these examples, we evaluated how well the simulation of bilayer membranes containing cholesterol can be studied using a modified coarse graining approach.

Figure 2.

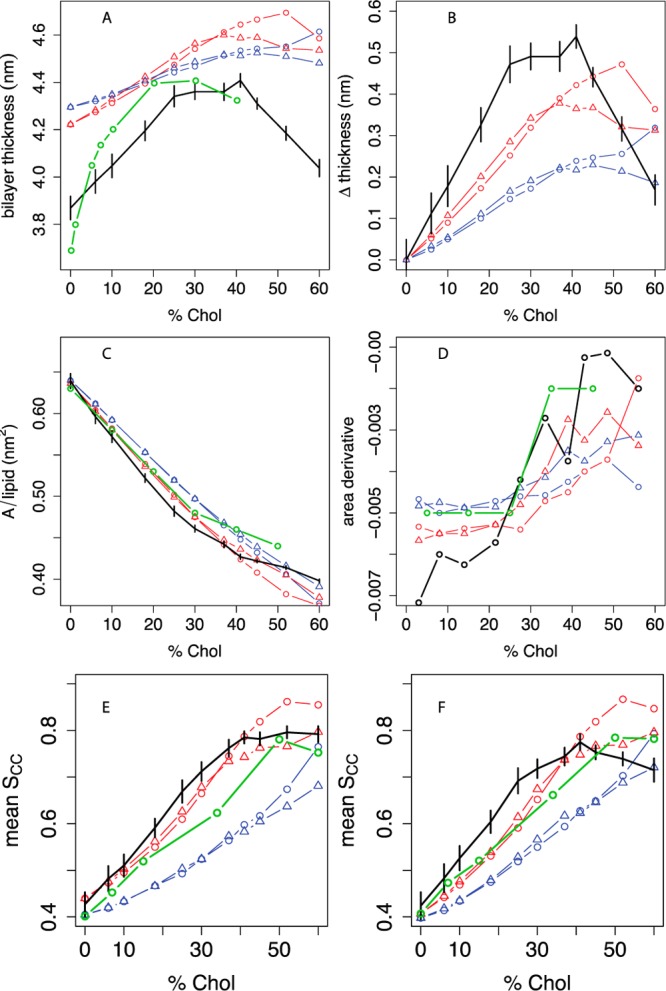
Thickness, area, and lipid tail order vs cholesterol concentration in POPC bilayers compared between experiment, united-atom, and different coarse-grained simulations. A: Bilayer thickness (phosphate-phosphate distance across the leaflets), averaged over a grid as described in the Methods; experimental headgroup-headgroup distance (d_HH) data are given from Hodzic et al.^52,53 B: Difference in bilayer thickness from 0% cholesterol. C: Projected area per molecule, with experimental areas in monolayers from Smaby et al. at a surface pressure of 30 mN/m;⁵⁶ D: estimated slope of the A_M curve as a function of mol % cholesterol; the slope between two consecutive X_cholx_i and x_i+1 is plotted at (x_i + x_i+1)/2. Panel E shows the C2B-D3B P₂ order parameter for the oleoyl chain and panel F shows the C2A-C3A P₂ order parameter for the palmitoyl chain. Experimental S_CH data from Ferreira et al.⁴³ (see Figure S8) are converted to estimated P₂ order parameters based on a linear model relating S_CH and P₂ calculated from UA simulations, as described in the Methods and Figure S7. For all panels, black indicates the united-atom model.³⁶ For coarse-grained simulations, the phospholipid model is indicated by blue lines (MARTINI) or red lines (angle-corrected POPC), while the sterol model is indicated by circles (MARTINI cholesterol) or triangles (optimized cholesterol, that is, CT₃-Me_2b). Where available, experimental data are indicated in green. Error bars indicate the standard deviation of each metric over simulation time.

Comparison of Atomistic and MARTINI POPC/CHOL Bilayer Properties with Experiments

Figure 2A-B shows the bilayer thickening induced by increasing cholesterol content in the membrane. Using small-angle X-ray scattering, Hodzic et al. (panels A and B, green curve) estimated that the headgroup-headgroup distance across the bilayer increases from approximately 3.7 nm at 0% cholesterol to 4.4 nm at 20% cholesterol, followed by a plateau from 20 to 40% cholesterol.^52,53 The thinning at high concentrations is related to the shorter height of increasingly abundant cholesterol relative to phospholipids. Simulations suggest that this results in phospholipid headgroup collapse to cover cholesterol⁵⁹ and increased lipid interdigitation between the leaflets due to free space under cholesterol molecules,³⁶ both of which would lead to thinning.

The UA simulations³⁶ (black) agree qualitatively with the experimental trend. Although the UA simulations produce a slightly smaller increase of 0.5 nm in thickness between 0 and 25% cholesterol, they clearly retain the plateau from 25 to 41% cholesterol. Above 40% cholesterol, the UA simulations produce a marked thinning between 40 and 60%. By contrast, MARTINI (blue circles) predicts a shallower, monotonic rise in thickness between 0 and 60% cholesterol; no plateau or decrease in thickness is predicted below 50% cholesterol. Though the resolution of SAX(N)s-derived bilayer thicknesses are limited, the plateau and/or thinning above 25% cholesterol is a qualitative feature we aim to capture in our revised model.

Figure 2C shows that Smaby et al.⁵⁶ (green) measured a monotonic decline in the area per molecule of POPC monolayers between 0 and 50% cholesterol, with a steeper slope above 30% cholesterol than below it. Since the tight spacing of A_M data hampers assessment of differences in the cholesterol area-condensation effect, Panel D shows the slope of the A_M curve vs cholesterol mole fraction X_chol. UA simulations predict A_M within 0.03 nm² of the experimental data between 0 and 60% cholesterol and a nearly monotonic increase in the slope of A_M between 0 and 52% cholesterol, qualitatively consistent with experiment. By contrast to the UA and experimental data,⁵⁶ MARTINI²⁸ predicts a constant slope of about −0.004 in this range.

Panels E and F show lipid tail order parameters. Ferreira et al.⁴³ recently showed that palmitoyl and oleoyl tail C–H order parameters steadily increase between 0 and 50% cholesterol (Figure S8). This figure also shows that atomistic simulations predict S_CH (for the middle carbons of the acyl chains) within 0.02 of the experimental values below 20% cholesterol and above 40% cholesterol, but the simulations predict S_CH values that are 0.05–0.10 too large between 25 and 45% cholesterol.

While coarse-grained simulations cannot be directly compared to atomic-scale experimental order parameters, the equivalent P₂ order parameters can be estimated from S_CH with the help of UA simulations, for which S_CH and P₂ are strongly correlated, as detailed in the Methods and Figure S7. Figure 2E shows that for both palmitoyl and oleoyl chains, MARTINI order parameters fall >0.1 below the estimated experimental P₂ at X_chol up to 52%, which is the opposite sign of error as the UA simulations in the same concentration region.

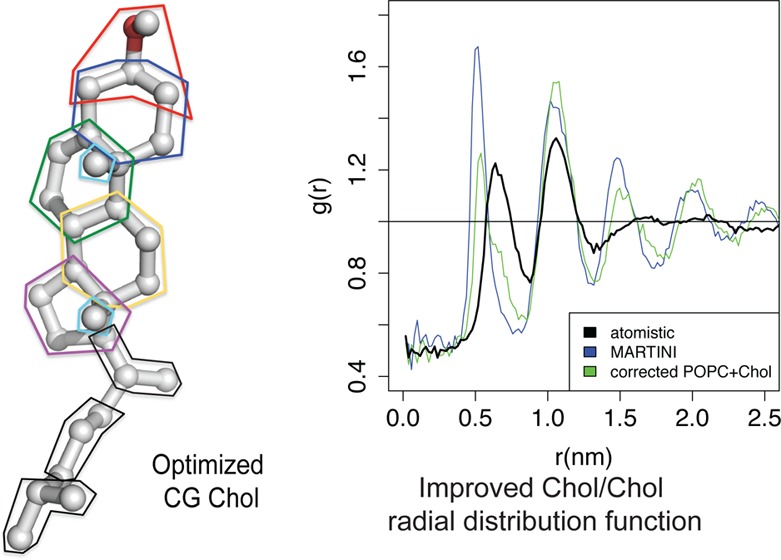
To assess the relative importance of short- versus long-range interactions between cholesterol molecules, we determined cholesterol-cholesterol radial distribution functions (RDFs) in our membrane simulations as described in the Methods. Figure 3 shows that UA simulations report a first-shell (nearest-neighbor) peak at about 0.7 nm at X_chol ≥ 41% and a second-shell peak at ∼1.0 nm for all concentrations. In MARTINI, the first-shell peak occurs at a smaller radius of about 0.5 nm and is noticeably higher at 41 and 52% cholesterol than in UA. This indicates excessive cholesterol self-association. In addition, at 52%, prominent third and fourth shell peaks that are absent in UA appear in MARTINI, which suggests excessive long-range lateral order.

Figure 3.

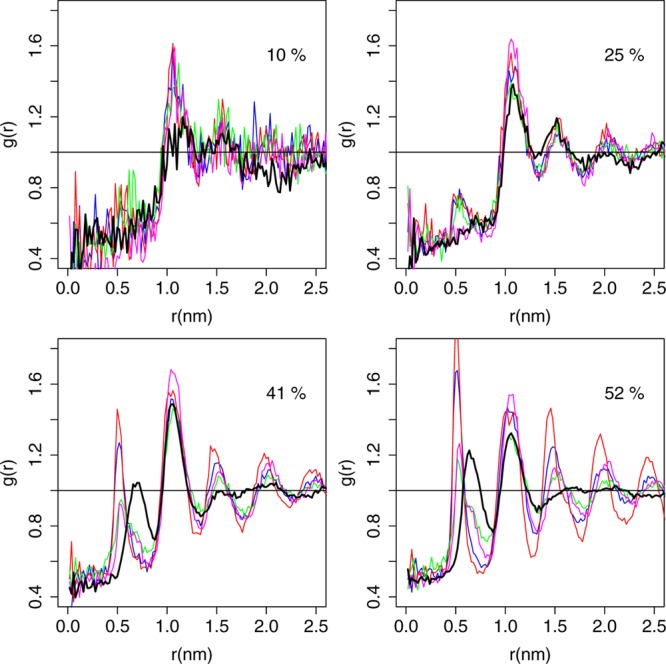
Cholesterol/cholesterol radial distribution functions. Radial distribution functions (RDFs) are calculated as described in the Methods. Black = UA, blue = MARTINI, red = angle-corrected POPC + MARTINI cholesterol, green = angle-corrected POPC + CT₂-Me_2b, and magenta = angle-corrected POPC + CT₃-Me_2b. The color scheme has been shifted from Figure 2 due to the close overlap between the RDF curves.

The natural position of cholesterol is upright, parallel to the membrane normal; we previously reported that 25-hydroxycholesterol, which is derived from cholesterol by oxidizing the tail, has a very different orientational distribution favoring configurations perpendicular to the membrane normal.³⁹ We defined tilt as the angle between a vector from the bottom to the top of the tetracycle and the membrane normal. Figure S9 shows the tilt distribution at 52% cholesterol. Panel A shows that for UA, the tilt distribution peaks between 15 and 20°, reflecting mostly upright orientations. Panel B reveals small secondary peaks at 90° and 170°. The population of inverted cholesterol (tilt >80°) is 0.7%. MARTINI reports an upright peak at the correct position, but this peak is slightly narrower than for UA; in addition, the inverted population is slightly higher.

Phospholipid Pseudobond Angle Corrections

The poor performance of MARTINI in predicting cholesterol-induced thickening, area condensation, and lipid tail ordering limits its applicability to the study of these important metrics by simulation. To improve MARTINI, we used UA simulations to determine appropriate adjustments in coarse-grained bond and angle potentials. To avoid overparameterization, we used only pure POPC UA simulations for this purpose. First, following the MARTINI recipe for coarse-graining,²⁸ we defined an explicit all-atom-to-CG mapping (Figure 1A) so that bond and angle potentials for the CG simulation can be derived from the UA simulation, as described in the Methods. The positions of the CG particles in space are illustrated in Figure S3. Then, as described in the Methods, we corrected the potentials for the PO4/(glycerol particle 1)/(glycerol particle 2) pseudoangles, the glycerol/glycerol tail angle, and the angle about the oleoyl double bond. We showed that these corrections improved the agreement of these pseudoangles’ distributions with UA simulations as well as predictions of P₂ order parameters throughout the lipid tail.

Effect on Bulk Membrane Properties

In addition, we tested the angle-corrected POPC model against a range of experimental bulk membrane properties as important “sanity checks” for physical realism, as Marrink et al. have done for MARTINI DPPC.^27,32 Following the protocol of Marrink et al.,³² we identified a range of temperatures at which liquid-to-gel and gel-to-liquid transitions will occur spontaneously on time scales accessible to CG simulations (<5 μs), as detailed in the Methods.

Figure S6 shows cooling and heating simulations used to estimate the phase transition temperature in angle-corrected POPC. We monitor transitions using A_M and define a transition as having happened in a cooling simulation when A_M contracts 95% from the starting value toward the gel-phase baseline, which occurs near 0.49 nm² for angle-corrected POPC. For heating simulations, we define a transition by 95% progress of A_M toward the liquid-phase baseline, which is about 0.60 nm² for angle-corrected POPC at 275 K. A simulation cooled from 300 to 250 K contracts to a gel phase within 350 ns, while a simulation cooled to 260 K transitions to the gel phase at about 1100 ns. A simulation cooled to 265 K does not experience such a transition even after 5 μs. Therefore, we estimate 260 K as the lower limit for the T_m. A simulation instantaneously heated from 200 to 275 K or higher experiences a gel-to-liquid transition within 115 ns, but a simulation heated to 270 K does not experience such a transition within 5 μs. Therefore, we estimate 275 K as the upper limit for the T_m. In the 260–275 K range, the system can exist as a supercooled liquid or a superheated gel on coarse-grained simulation time scales.³² Thus, we estimate a T_m of 267.5 ± 10.6 K for angle-corrected POPC. For MARTINI POPC, we estimate a T_m of 240.0 ± 7.1 K. Thus, the angle-corrected model agrees significantly better with the T_m of 271 K measured by differential scanning calorimetry.⁶⁰ Details for the T_m estimates for these two models are given in Table 2.

Table 2. Estimating Gel/Liquid Phase Transition Temperatures in MARTINI and Angle-Corrected POPC^a.

	cooling		heating
model	Tliq→gel (K)	time (ns)	Tgel→liq (K)	time (ns)
MARTINI	235	1310	245	456
AC	260	1090	275	115

^aT_liq→gel indicates the highest temperature in an instantaneous cooling simulation from 300 K to T for which a liquid-to-gel transition is observed within 5 μs. T_gel→liq indicates the lowest temperature in an instantaneous heating simulation from 200 K to T for which a liquid-to-gel transition is observed within 5 μs. Cooling transition times are defined by 95% progress from the area per molecule at t = 0 to its minimum value observed in the simulation; heating transition times are defined by 95% progress from the area per molecule at t = 0 to its maximum value observed in the simulation.

The bending modulus reflects the mechanical properties of a lipid bilayer, specifically the undulatory spectrum. Using the protocol described in the Methods, we obtained a bending modulus k_c of 1.7 and 1.2·10^–19 J for MARTINI and angle-corrected POPC, respectively. Both values are of the same order as the experimental value of 8.56·10^–20 J.^61,62 The area compressibility modulus K_A measures the fluctuation in area per lipid (see eq 2). For the 6400-lipid bilayer, we observed K_A of 306 and 252 mN/m for MARTINI and angle-corrected POPC, respectively. The angle-corrected POPC model agrees better than MARTINI with the experimental compressibility measurement of ∼243 mN/m, which is consistent over a wide range of lipid types and chain lengths.⁶³ Thus, angle-corrected POPC slightly outperforms MARTINI on prediction of bilayer mechanical properties.

To address the dynamic properties of the membrane, we calculated the phospholipid lateral diffusion constants D_L. For pure POPC, Filippov et al.⁶⁴ reported D_L = 8.2·10^–8 cm²/s at 298 K. From UA, MARTINI, and angle-corrected POPC simulations, we calculated D_L = 14.8 ± 4.8, 46.8 ± 0.2, and (40.7 ± 0.0)·10^–8 cm²/s, respectively, using the g_msd script of GROMACS.⁴¹ To avoid artifacts from subdiffusive transport at times below 100 ns,⁵³ we only consider the time between 200 and 390 ns for atomistic simulations and 100–190 ns for CG simulations. Since MARTINI samples configuration space at about four times the rate of the atomic-scale system,²⁸ we corrected the MARTINI and angle-corrected values by 1/4 to about 11.7 and 10.2·10^–8 cm²/s, respectively–both in good agreement with experiment. In summary, Table 3 and these experimental validations show that the angle-corrected model slightly outperforms MARTINI vs experiment in predicting thermal, elastic, and dynamic properties of POPC bilayers.

Table 3. Macroscopic Observables Compared between Experiment, UA, and Coarse-Grained Simulations for POPC Bilayers^a28.

parameter	experiment	UA	MARTINI	angle-corrected
melting temperature (K)	27160	NA	240	267
bending modulus (·10–19J)	0.8561,62	-	1.7	1.2
area compressibility (mN/m)	∼24363	268	306	252
lateral diffusion constant (·10–8 cm2/s)	8.264	14.8	11.7	10.2

^aCalculations of these thermal, elastic, and dynamic properties from our simulations are detailed in the Methods. Lateral diffusion constants for coarse-grained simulations are divided by 4 to reflect the faster time scale of coarse-grained vs atomistic simulations.

Effect on Binary POPC/Cholesterol Simulations

Figure 2A-B shows that the angle correction (red circles) slightly improves the accuracy of both bilayer thickness and its slope up to 25% cholesterol. However, rather than plateauing between 25 and 41% cholesterol, thickness continues to increase up to 52% cholesterol, with a slight thinning thereafter. Panels C and D show that the angle-corrected model slightly steepens the A_M curve and improves qualitative agreement with experimental data and the UA simulations, but as with MARTINI, the slope does not become less negative with increasing X_chol except above 40%. Panels E and F show that the angle-corrected model predicts tail order parameters at up to 40% cholesterol in better agreement with experiments than MARTINI and even UA simulations, but it predicts hyperordering at higher concentrations. The angle correction also slightly increases the excess height of both short- and long-range cholesterol-cholesterol RDF peaks (relative to UA simulations) at 41 and 52% cholesterol (Figure 3). Figure S9 shows that the peak of the cholesterol tilt distribution at 52% cholesterol is shifted to lower values than UA or MARTINI, and there is a higher inverted population than in MARTINI. An overabundance of inverted cholesterol molecules in MARTINI and the angle-corrected model may distort predictions of area and thickness at high concentrations; the abundance of this population is also linked to cholesterol desorption and flip-flop.⁶⁵ To address the poor performance of both MARTINI and the angle-corrected model at high cholesterol concentration, we further modified our coarse-grained representation of the sterol.

Adjustments to Cholesterol

To assess and optimize coarse-grained cholesterol, we first defined a UA-to-CG mapping for cholesterol with a two-particle tail (CT₂) as for POPC (see Figure 1B) and corrected bond angle potentials as necessary, as described in the Methods. We evaluated this and other revised cholesterol models on the criteria described above. In addition, to simplify comparison of cholesterol-cholesterol RDFs between CG and UA, we defined the metric ΔRDF (eq 1). We also applied tail angle corrections as described in the Methods.

Surprisingly, this relatively small change in UA to CG mapping increased ΔRDF at 52% cholesterol from 0.320 for the angle-corrected model to 0.451 (see Table 4, position 1(a). Figure S10A shows that this increased ΔRDF primarily reflects an increase in the height of long-range (≥3rd shell) cholesterol-cholesterol and POPC-cholesterol RDF peaks. The remapped model also showed excess thickness, increased tail order, and inverted cholesterol population comparable to the angle-corrected model. Based on the ΔRDF results, we hypothesized that excessive cholesterol self-association is occurring for the remapped model and to a lesser extent for MARTINI and the angle-corrected model.

Table 4. Comparison of Observables between United-Atom and Coarse-Grained 52% Cholesterol Simulations with Different Pseudomethyl Positions^a.

chol tail length	methyl position	ΔRDF	Δthickness (nm)	Δtilt	panti (%)	ΔSoleoyl	ΔSpalmitoyl
	UA	0.000	4.185	17.58	0.7	0.801	0.739
2	MARTINI	0.253	0.366	–3.12	1.8	–0.127	–0.036
	AC	0.320	0.509	–7.05	3.3	0.061	0.128
	1a	0.451	0.517	–9.49	3.0	0.076	0.153
	1b	0.272	0.434	–4.37	3.2	–0.018	0.042
	2a	0.460	0.566	–10.52	2.4	0.091	0.163
	2b	0.127	0.356	1.29	6.2	–0.144	–0.086
	3a	0.424	0.522	–10.19	1.0	0.074	0.147
	3b	0.239	0.558	–5.42	7.3	–0.001	0.061
3	2b	0.174	0.354	–2.32	0.2	–0.024	0.041

^aThe different methyl positions are defined in the methods and illustrated in Figure S5. Reference values for each observable from the 52% cholesterol UA simulation³⁶ are given in the first line. For the CG models in remaining lines, we give differences from these reference values, except for the p_anti column. ΔRDF is defined in eq 1. p_anti is the fraction of cholesterol molecules with a tilt angle greater than 90°. Position 2b, especially when using the 3-particle tail, performs best across the entire set of metrics.

In atomistic simulations, Martinez-Seara and colleagues have shown that the off-plane methyl groups of cholesterol (C18 and C19) are important for limiting direct interactions between cholesterol molecules.³³ Given this observation and the relative smoothness of the coarse-grained MARTINI cholesterol by comparison to the all-atom molecule, we examined more closely the relationship between cholesterol self-interaction and the coarse-grained representation of the off-plane methyl groups. We created and tested six different positions for the coarse-grained methyl group (R5) that vary the roughness of the rough face, as described in the Methods and Figure S5.

While MARTINI uses two very slightly off-plane particles that include the two respective methyl groups,²⁸ in our revised CG model, we used one particle for both atomic methyl groups since the MARTINI type “S” particle is intended for 2–3:1 mapping.²⁸ This strategy also allows us to optimize the position of the methyl group, as described below. First, we created position 1a (described above), which is midway between the C18 atomic methyl group and its attachment point, C13, as the closest approximation of the slightly off-plane position of R5 in MARTINI. We also considered position 3a, which is midway between C10 and the C19 methyl, and position 2a, which is an average of positions 1a and 3a and is designed to account for the effects of both atomic methyl groups. We compared the performance of these three models with MARTINI and the angle-corrected model (see Table 4). These three “half-height” models had ΔRDF > 0.4 at 52% cholesterol, which indicates excessive self-association. These models also exhibit excess thickness and tail order (vs UA simulations) slightly higher than the angle-corrected model.

Based on the results of Martinez-Seara and colleagues, we also created cholesterol models with three other pseudomethyl positions 1b, 2b, and 3b that are “elevated” to the height of the atomic methyl groups, under the hypothesis that these models would experience greater self-avoidance than the half-height models. Table 4 shows that these models predict RDFs, tail order parameters, and, for models 1b and 2b, bilayer thickness, in better agreement with UA simulations than the angle-corrected and other half-height models. Position 2b even outperforms MARTINI and the angle-corrected model on ΔRDF. However, positions 2b and 3b showed a > 6% population of inverted cholesterol molecules, which was nearly 3 times higher than for the angle-corrected model and could affect the accuracy of whole-bilayer properties like area and thickness.

Given these tilt results and the branched structure of the cholesterol tail, we also created a model with three tail particles and the methyl at position 2b (CT₃-Me_2b, Figure 1C). Unlike MARTINI and CT₂, which used a type C1 particle for the C2 cholesterol tail atom, we used the same smaller particle type as the cholesterol ring (SC1) for C2 and the added terminal particle C3; we also adjusted the bond distances accordingly. The tail angle corrections for this variant are described in the Methods. Table 4 shows that CT₃-Me_2b performs comparably to CT₂-Me_2b on ΔRDF and thickness, but it greatly outperforms on other metrics, while CT₃-Me_2b eliminates the excess population of inverted cholesterol and improves the agreement of S_C2B–C3B and S_C2A-C3A with UA simulations. Combined with the results for the ring methyl groups, these results suggest that for accurate predictions, higher resolution is required for regions with branched structure than those with linear structure (e.g., phospholipid tails).

Summary Comparison of Models

Figure 2 summarizes the global results for the optimal cholesterol model (CT₃-Me_2b) in the context of MARTINI (blue) vs our angle-corrected phospholipid (red). The results for MARTINI POPC with the new optimized cholesterol (blue triangles) show that, even in the absence of correct phospholipid conformations, our optimal cholesterol improves prediction of the slopes of the bilayer thickness (panels A and B) and P₂ order parameter curves (panels E and F) at high X_chol, by comparison to experiment and UA simulations. However, with this combination of force-fields, the magnitude of tail ordering is still severely underestimated across the entire 0–60% cholesterol range. By contrast, when the new angle-corrected POPC and the new optimal cholesterol are combined (red triangles), the thickness shift curve (panel B) and its slope agree significantly better with UA simulations than for any other pairing. The same is true for A_M and its slope; i.e., the condensation effect is best captured with the new force-fields. Most notably, with this pairing, the oleoyl and palmitoyl order curves closely match experiment across the entire 0–60% cholesterol concentration range with agreement better than that achieved by UA simulations. These results, combined with the pseudomethyl optimization results in Table 4, indicate that the combination of our angle-corrected POPC and the new CT₃-Me_2b cholesterol is the best model across a broad set of evaluation criteria.

Cholesterol Accessibility

Figure 4 addresses cholesterol solvent accessibility, which we previously showed increases significantly above 40% cholesterol.³⁶ Since the UA and CG lipid and sterol molecules have very different particle sizes, their solvent accessibilities cannot be directly compared. Instead, we calculated SASA from the pseudo-CG trajectory using a CG probe radius (0.241 nm). With MARTINI cholesterol, whether MARTINI or the new angle-corrected POPC is used, the predicted slope of the curve is too small relative to the pseudo-CG SASA curve (black). Using MARTINI POPC and the new optimized cholesterol, the slope is better captured, but as with bilayer thickness and order parameters, the best prediction occurs with the new angle-corrected POPC and the new optimized cholesterol. These results show that our best coarse-grained model can capture cholesterol-induced changes in the membrane surface.

Figure 4.

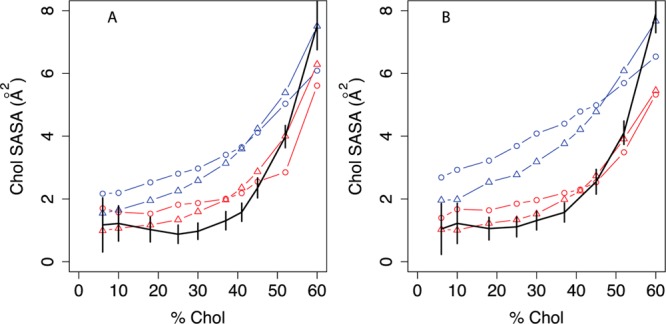
Cholesterol accessibility in united-atom and coarse-grained simulations. Cholesterol SASA is calculated with APBS⁷⁵ using the van der Waals radius of MARTINI cholesterol particles (2.41 Å) as a probe radius. For UA simulations (black), the plotted areas are determined from the pseudocoarse-grained trajectory to ensure the most direct comparison possible. Black indicates the united-atom model.³⁶ For coarse-grained simulations, the phospholipid model is indicated by blue lines (MARTINI) or red lines (angle-corrected phospholipid), while the sterol model is indicated by circles (MARTINI cholesterol) or triangles (optimized cholesterol, that is, CT₃-Me_2b). Error bars indicate the standard deviation of SASA over simulation time. A: POPC/cholesterol simulations; B: DOPC/cholesterol simulations.

External Validation

One strength of MARTINI is its general applicability to different lipid types and other kinds of biomolecular systems like proteins.^28,31 To test that our revised POPC and cholesterol models retain this generalizability, we run DPPC/cholesterol and DOPC/cholesterol simulations with the same parameters for equivalent bonds and pseudoangles that we derived for POPC. Figure S11A shows that for angle-corrected DPPC, the bilayer thickness curve is downshifted 0.1–0.15 nm from MARTINI DPPC. The angle-corrected value of 3.88 nm agrees better than MARTINI with the experimental headgroup-headgroup distance of 3.8 nm⁶⁶ and the value of 4.05 nm obtained from a pure DPPC simulation. However, as the trends of thickness vs X_chol are very similar and absolute thicknesses have limited meaning in CG models, it is impossible to judge a better model on this criterion alone. Panel B shows that the angle correction increases A_M by 0.01 nm² between 0 and 30% cholesterol, which is within the resolution limit of experiments. MARTINI is slightly closer to the experimental value of 0.631 nm² for pure DPPC at 323 K.⁶⁶ Panels C and D show that the P₂ order parameters for the two palmitoyl chains are very similar and change little between MARTINI and AC DPPC. Clarke et al. measured S_CD = 0.33 for the eighth carbon of the palmitoyl chain at 50% cholesterol,⁶⁷ from which we estimate a P₂ order parameter between the second and third beads of about 0.66 using the relation derived in Figure S7. The combination of angle-corrected DPPC and optimized cholesterol estimates P₂ ∼ 0.76 for this bond at 50% cholesterol, which exceeds the estimated experimental value but by considerably less than if MARTINI cholesterol is used. The smaller difference between simulations using MARTINI and angle-corrected DPPC than for MARTINI vs AC POPC likely results from the fact that there are no corrections to the tail pseudoangles for palmitoyl chains. In summary, these results show that the angle-corrected and MARTINI DPPC perform similarly and that optimized cholesterol reduces predictions of hyperordering at high X_chol by MARTINI cholesterol.

Figure 5 compares bilayer thickness, area per molecule, and order parameters from the different DOPC/cholesterol systems to all-atom and experimental data by analogy to the POPC/cholesterol data in Figure 2. Panel A shows that the UA DOPC/cholesterol simulations from Olsen et al.³⁹ qualitatively capture the absolute thickness measured by Kucerka et al. using SANS^50,65 in the 0–30% cholesterol range. Their data above 30% cholesterol may be affected by multilamellar vesicles^50,65 and are not included. Panel B shows that simulations with angle-corrected DOPC better capture the experimental change in thickness between 0 and 30% cholesterol, and the slope of this change, than simulations using raw MARTINI DOPC. In addition, the best UA/CG agreement across the 0–60% cholesterol range is achieved using angle-corrected DOPC + CT₃-Me_2b cholesterol.

Figure 5.

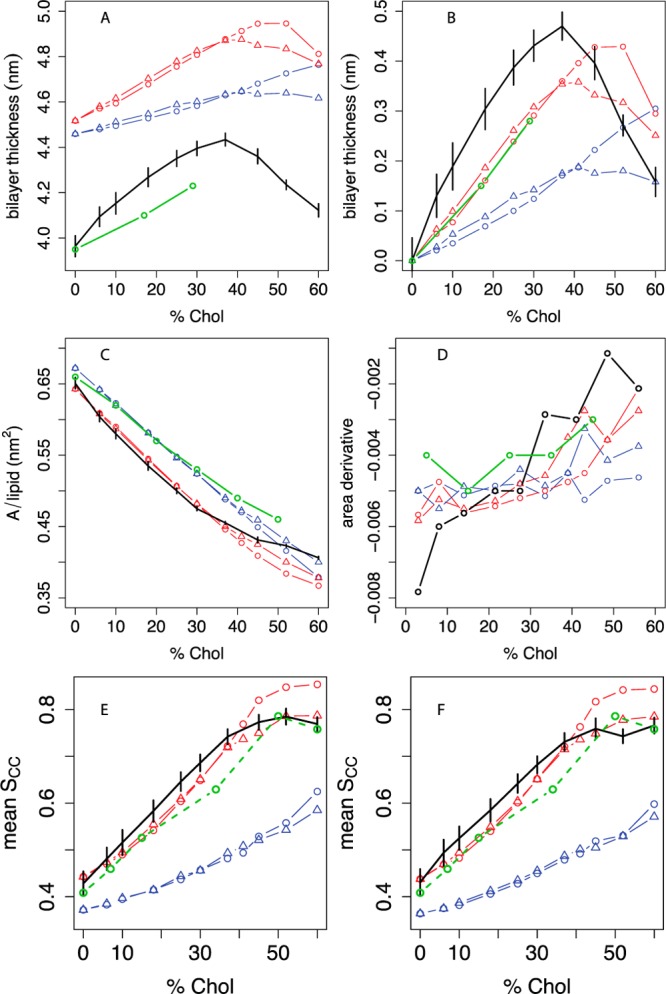
Thickness, area, and lipid tail order vs cholesterol concentration in DOPC bilayers compared between experiment, united-atom, and different coarse-grained simulations. A: Bilayer thickness (phosphate-phosphate distance across the leaflets), averaged over a grid as described in the Methods, with experimental data from Kucerka et al.⁵⁰ We estimated headgroup-headgroup distances (d_HH) from their data by d_TOT – d_H, where d_TOT is the total bilayer thickness measured in their paper and d_H = 1.0 nm is the estimated thickness of the headgroup layer.⁷⁶ B: Difference in bilayer thickness from 0% cholesterol. C: Projected area per molecule, with experimental areas in monolayers from Smaby et al. at a surface pressure of 30 mN/m;⁵⁶ D: estimated slope of the A_M curve as a function of mol % cholesterol; the slope between two consecutive X_cholx_i and x_i+1 is plotted at (x_i + x_i+1)/2. Panel E shows the C2A-D3A P₂ order parameter for the sn-1 oleoyl chain, and panel F shows the C2B-D3B P₂ order parameter for the sn-2 oleoyl chain. For all panels, black indicates the united-atom model.³⁶ The estimated experimental POPC oleoyl chain P₂ order parameter data derived from Ferreira et al.⁴³ (Figure 2E) are included in both panels as an approximate experimental reference. For coarse-grained simulations, the phospholipid model is indicated by blue lines (MARTINI) or red lines (angle-corrected POPC), while the sterol model is indicated by circles (MARTINI cholesterol) or triangles (optimized cholesterol, that is, CT₃-Me_2b). Where available, experimental data are indicated in green. Error bars indicate the standard deviation of each metric over simulation time.

Panel C shows that as with POPC, the UA and CG computational models agree only qualitatively with the absolute monolayer A_M data of Smaby et al.⁵⁶ for this lipid. MARTINI agrees best with the absolute areas, but this may be coincidental given the poor agreement with experiment on other criteria. Panel D shows that among the CG models, the combination of angle-corrected DOPC and CT₃-Me_2b cholesterol better reproduces the slope of the A_M vs X_chol curve areas from experiments and UA simulations than any other combination. Panels E and F show that the predicted P₂ order parameters for both oleoyl chains are very similar to the estimated experimental order parameters for the oleoyl chain of POPC (Figure 2E). Among all CG models, angle-corrected DOPC + CT₃-Me_2b cholesterol best predicts order parameters vs (estimated) experimental data and UA simulations. Finally, as in POPC/cholesterol simulations, this combination also best predicts the cholesterol SASA seen in DOPC/cholesterol UA simulations across the 0–60% cholesterol range (Figure 4). In summary, the DPPC/cholesterol and DOPC/cholesterol results suggest that our new CG POPC and cholesterol parameters derived from 0% cholesterol and 10% cholesterol UA simulations, respectively, are applicable to different lipid types.

Discussion

The MARTINI force-field was developed based on thermodynamic data from experiments and UA simulations on model compounds.^27,28,30,31 Because of this, MARTINI makes qualitatively accurate predictions for a variety of types of molecular systems such as proteins,^68,69 carbohydrates,⁷⁰ polymers,^71,72 and nanoparticles.⁷³ However, in cholesterol/monounsaturated phospholipid systems, where the structural nuances of cholesterol have been shown to be critical for its effects on membranes,^33,34 MARTINI fails to capture the evolution of key metrics of bilayer structure with increasing cholesterol concentration. In the present study, we improved the MARTINI coarse-grained model for lipids and sterols by adjusting inaccurate or missing parameters for key details of molecular structure based on reference atomistic simulations.

POPC Pseudobond Angle Corrections

Our analyses showed that MARTINI POPC simulations accurately captured the UA distributions for alkyl angles but poorly captured the glycerol/glycerol/tail pseudoangles and the pseudoangle centered at the oleoyl double bond (Table 1 and Figure S1). By correcting selected POPC pseudobond angle potentials based on UA pure POPC simulations, we improved predictions of bilayer thickening and ordering between 0 and 30% cholesterol (Figure 2B,E,F). DOPC/cholesterol simulations using the same corrected glycerol/glycerol/tail and oleoyl double bond pseudoangle parameters also showed improved performance on these metrics, which argues for the generalizability of our revised parameters. These results indicate the importance of lipid conformations for capturing the initial response of phospholipid bilayers to increasing cholesterol concentration: using optimized cholesterol with the original MARTINI POPC produced no change in the results for this concentration region. Our results indicate that coarse-grained bond angles are more difficult to parametrize than their all-atom counterparts because, while atomic-scale bond angles are fixed to within 1–2°, coarse-grained bond angles also incorporate flexible dihedral contributions from the atomic scale. The angle corrections in our model maintain or slightly improve the agreement of MARTINI with experiments for thermal, elastic, and dynamic properties of POPC bilayers (Table 3).

Validation and Performance of Coarse-Grained Cholesterol

Lipid–lipid and lipid–sterol interactions dominate over sterol–sterol interactions at low concentrations up to 30% where the largest lipid-ordering and membrane-thickening effects occur. However, as X_chol increases above 40% and cholesterol-cholesterol interactions become more abundant (and thus more important), the tail order of angle-corrected POPC exceeds the experimental and UA simulation values and the bilayer hyperthickens relative to UA simulations. The high cholesterol-cholesterol RDF peaks of MARTINI cholesterol at high X_chol suggest that MARTINI cholesterol is excessively self-associative. Our observation that a small change in the UA-to-CG cholesterol mapping causes a substantial increase in ΔRDF further supports this interpretation. Similarly, Martinez-Seara and colleagues showed that the rough face methyl groups of cholesterol are important for minimizing first-shell cholesterol-cholesterol self-interactions.³³

Guided by this observation, we systematically optimized the position of the coarse-grained pseudomethyl group in cholesterol. Motivated by similar concerns, Hadley and McCabe developed a coarse-grained cholesterol force-field that treats the rings and tail at 3–4:1 resolution but considers the hydroxyl and the C18 and C19 methyl groups at atomic resolution.⁷⁴ Their model accurately reproduced atom–atom RDFs from simulations of crystalline cholesterol. Our model resembles MARTINI in the treatment of both off-plane methyl groups as a single coarse-grained particle, but our model more closely resembles Hadley’s and all-atom models in that the pseudomethyl particle has a higher elevation than in MARTINI. Since Hadley’s coarse-grained simulations⁷⁴ and the atomistic methyl deletion studies of Poyry et al.³⁴ showed that both atomic methyls are important to the ordering and area condensation effects of cholesterol, we considered a variety of positions for the pseudomethyl group with different weights for the C18 and C19 atoms. The pseudomethyl at position 2b, which evenly weights the C18 and C19 methyls, performed best across a broad set of metrics, providing further evidence for the importance of both methyl groups.

Furthermore, we observed that simulations with CT₂-Me_2b, the best two-particle tail model, exhibit less lipid tail order than UA simulations at 52% cholesterol, which also occurs in the original MARTINI model. The CT₂-Me_2b model also predicted a high population (6.2%) of inverted cholesterol molecules, compared to only 0.7% in UA. The use of three particles instead of two for the branched tail (Figure 1C) eliminates both of these problems. The new CT₃-Me_2b model significantly outperforms MARTINI and the CT₂-Me_2b model on tail order, bilayer thickness, and the area condensation effect across 0–60% cholesterol (Figure 2) and removes the hyperordering effects of the angle-corrected model above 40% cholesterol. These results demonstrate that CT₃-Me_2b is the best-performing revised cholesterol model and that the 2–3:1 particle resolution is important for the tail and ring moiety to accurately predict cholesterol effects on lipid bilayers. These results also show the importance of systematic optimization for coarse-graining molecules like cholesterol with complicated molecular structure.

Conclusions

Coarse-graining is important for scalability of simulations to model biologically important large systems beyond the time and length scales of atomistic simulations. Here, we revised the MARTINI coarse-grained force-field to simulate cholesterol-containing lipid bilayers. Most importantly, the revised models capture the ordering and thickening effect of cholesterol on POPC bilayers between 0 and 60% cholesterol and reproduce experimental macroscopic properties of pure POPC bilayers slightly better than MARTINI. By revising the pseudobond angle potentials of POPC, we improved prediction of these effects between 0 and 30% cholesterol; however, because of excessive cholesterol self-interaction, this model predicts hyperordering at 40% cholesterol and higher. To address this excessive ordering behavior, we raised the position of the rough face pseudomethyl group relative to the cholesterol rings to better capture the repulsive properties of the methyl groups. Combined with a higher-resolution mapping for the cholesterol tail, the resulting optimized model predicts radial distribution functions, bilayer thickness, and lipid tail order at high cholesterol concentrations that agree more closely with united atom simulations than MARTINI. The observation that a model incorporating our revised parameters into DOPC outperforms all other CG models in a DOPC/cholesterol simulation series further argues for its efficacy and generalizability. While no molecule can be perfectly coarse grained, our results argue for the importance of decreasing the number of UA atoms represented by each coarse-grained particle for cases where branched structures like the cholesterol ring methyl groups and tail are suggested to be functionally important. Increased accuracy will allow for closer connection between coarse-grained simulations and experiments, which can explore long length- and time-scale phenomena more easily than atomic and molecular-scale simulations.

Supporting Information Available

Table S1: Average interparticle distances in MARTINI cholesterol and coarse-grained variants. Table S2: Average values of pseudobond angles in united atom cholesterol and coarse-grained variants. Figure S1: Representative bond angle distributions for united atom and different coarse-grained pure POPC simulations. Figure S2: coarse-grained carbon–carbon order parameters for different phospholipid models. Figure S3: UA to CG mapping schemes for POPC and cholesterol in 3D. Figure S4: Representative bond angle distributions for united atom, coarse-grained, and corrected coarse-grained models of cholesterol. Figure S5: Schematic illustration of all-atom cholesterol methyl groups and different coarse-grained representations. Figure S6: Cooling and heating phase transition simulations in angle-corrected POPC. Figure S7: Fit of pseudo-CG order parameters to UA S_CH. Figure S8: Order parameter comparison between UA simulations and experiments. Figure S9: Cholesterol tilt distributions for different models at 52% cholesterol. Figure S10: Excessive cholesterol self-associativity in the initial remapped model of cholesterol. Figure S11: Thickness, area, and lipid tail order vs cholesterol concentration in DPPC bilayers compared between MARTINI and angle-corrected models. The topology files for all altered phospholipid and cholesterol models. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States