One-laser interferometric broadband coherent anti-Stokes Raman scattering

Abstract

We introduce an interferometric technique for eliminating the nonresonant background of broadband coherent anti-Stokes Raman scattering (CARS) microscopy. CARS microscopy has been used for imaging a number of biological samples and processes, but the studies are mostly limited to detecting lipids in biological systems by probing the C-H stretch. Nonresonant background and incoherent noise sources can easily overwhelm less intense signals from other molecular vibrations. In this study, we demonstrate a one-laser broadband interferometric technique that separates the spontaneous Raman scattering-related component of the CARS signal from the nonresonant background using liquid benzonitrile as a model system.

1. Introduction

Coherent anti-Stokes Raman scattering (CARS) microscopy was first demonstrated by Duncan et al. [1], but its currently burgeoning popularity was spurred by the implementation of a simplified co-linear optical geometry [2,3]. CARS microscopy uses molecular vibrations as contrast and it has many attractive features for biological and materials imaging. It provides excellent sensitivity, high spatial resolution and inherent chemical specificity. The CARS process gives similar vibrational spectral information as spontaneous Raman scattering, but it is orders of magnitude more efficient [4]. This property allows CARS microscopy to be performed noninvasively at low laser power, which is important when imaging delicate biological specimens.

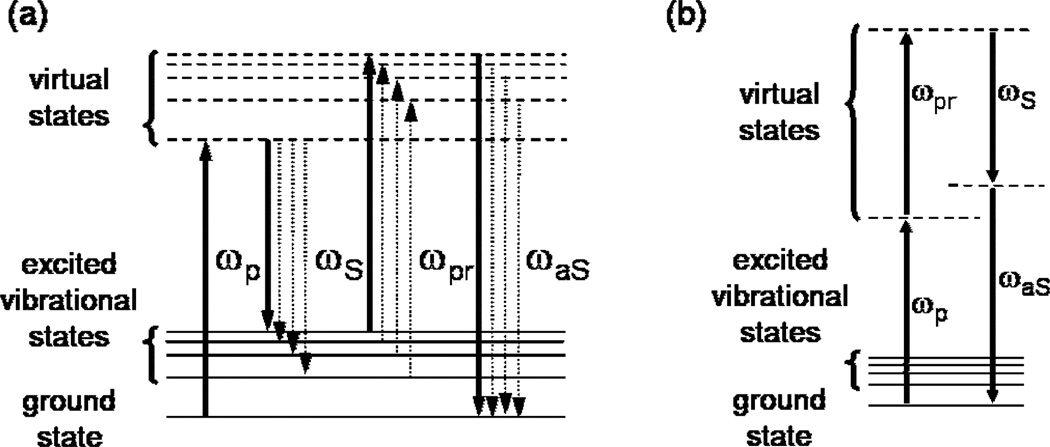
CARS is a nonlinear scattering technique in which pulsed light having at least two frequencies is mixed within a sample. Pump, Stokes and probe light at frequencies ω_p, ω_S, ω_pr overlap temporally and spatially to produce anti-Stokes light at frequency ω_aS = ω_p – ω_S + ω_pr. Fig. 1a provides the energy-level diagram for the CARS process. The anti-Stokes signal is proportional to the third-order nonlinear susceptibility, χ⁽³⁾, which has both vibrationally resonant (χ_R⁽³⁾) and nonresonant (χ_NR⁽³⁾) components; χ_R⁽³⁾ is the component of interest and it is related to the Raman-scattering cross section. Fig. 1(b) provides one of the 40 possible energy-level diagrams for the nonresonant processes [5]. As the diagram illustrates, the nonresonant scattering contains no information about the vibrational energy levels of the molecule. Furthermore, the nonresonant scattered light interferes coherently with the resonant signal so as to distort the bandshapes (as compared to natural spontaneous Raman bandshapes). Although the signal contribution originating from the nonresonant background is often sufficient to obscure weak resonant signals, narrow-band CARS has been demonstrated to be effective in biological [4,6,7] and materials imaging [8], provided that resonant signal strength is sufficiently high with respect to the nonresonant background.

Fig 1.

Energy-level diagram for narrow-band CARS: solid vertical arrows; broadband CARS: solid and dashed vertical arrows. Symbols: ω_p, pump; ω_S, Stokes; ω_pr, probe; ω_aS, anti-Stokes light. (b) Energy-level diagrams for a nonresonant process generating light at the same wavelength as is produced in the process depicted in (a).

The ability to characterize chemical species or biological components noninvasively within a complex heterogeneous system is of great interests in the physical and life sciences. CARS microscopy has the potential to fill this need; owing to its contrast mechanism, it has tremendous chemical resolving power since each chemical component within a sample has a unique spectral signature. The actual chemical resolving power rests in spectral bandwidth, spectral resolution and signal-to-noise levels. In response to the need for increased spectral bandwidth, multiplex [9–11] and broadband [12–14] CARS methods have been introduced recently, demonstrating single-shot spectral bandwidths ranging from 250 cm⁻¹ to more than 2500 cm⁻¹. Signal-to-noise issues can be dominated by nonresonant background, particularly for broadband CARS. Spectral features in the fingerprint region are often weak, and are usually obscured by noise from nonresonant background when imaging biological systems.

The presence of nonresonant background reduces the sensitivity of CARS. The nonresonant contribution to the total signal cannot be discarded using a baseline correction method. This is due to mixing of the resonant and nonresonant components in the third order nonlinear polarization, as will be discussed in the “Theory” section below. Many approaches have been established for reducing nonresonant background, including polarization control [15], temporal delay of probe with respect to the pump and Stokes fields [16], and epidetection [17] of the CARS signal. The former two suffer from significantly decreased signal levels, and the latter is applicable only to features that are small compared to the wavelength of the scattering light. Heterodyne and interferometric methods (see below) are also effective in reducing nonresonant background [18–23]; they appear to hold the greatest promise for general use for the following reasons. These methods can be used to selectively suppress the nonresonant background while enhancing the resonant signal, and they allow separation of the real and imaginary parts of the resonant signal (χ_R’⁽³⁾ and χ_R’’⁽³⁾), as well as linearization of the resonant signal with respect to concentration of analyte in the sample.

Yacoby et al. [18] were among the first to show that the nonresonant background associated with a signal of interest could be suppressed by interfering it with a nonresonant background that is generated separately. Xie et al. [19] applied a similar approach to multiplex CARS microscopy with a fairly straightforward experimental arrangement; however, the signal of interest and the nonresonant local oscillator were generated in separate samples, so it was necessary to account for the differential phase shift or differential chirp between the local oscillator and signal; this was later overcome with lock-in analysis [20].

Silberberg [21] has demonstrated a reduction in nonresonant background through interfering different spectral components of a single pulse using a pulse-shaping approach. Leone et al. [22] have improved on this method. An advantage of this method is that all light transverses the same beam path, so there are no issues that arise due to differential chirp in a broadband or multiplex measurement. A slight disadvantage of this approach is that the number of elements in the spatial light modulator limits the product of spectral resolution and spectral range. Boppart [23] has demonstrated a narrowband interferometric CARS method in which the local oscillator is generated by an optical parametric amplifier (OPA). The CARS signal and local oscillator are coherent, and are combined in a Mach-Zehnder interferometer. This technique gives a clear interferometric differentiation between the resonant CARS signal and the nonresonant four-wave-mixing signal; however, temporal jitter is a major source of noise due to intrinsically long arm-lengths (OPA source has up to 1 m pathlength) of the interferometer.

We present a new technique for interferometric suppression of the nonresonant background generated along with CARS. In the approach outlined below, the nonresonant local oscillator and the resonant signal are generated in the same spot of the sample. Therefore, there are no artifacts due to differential chirp between the signal and local oscillator. Another attractive feature of this approach is that the interferometer used in this study can have very short arms; we have used an arm-length of 65 mm, but this could be reduced somewhat. The short arm-length allows the instrument to have low temporal jitter. CARS spectra that are free of nonresonant background can be extracted with this interferometric technique. In this proof-of-principle study, neat liquid benzonitrile is selected as a model system due to its prominent peaks throughout the vibrational spectrum [24].

2. Theory

When sufficiently intense light of at least two frequencies interacts with a material, a third-order nonlinear polarization, P_i⁽³⁾, is generated along some polarization direction i in the sample according to

$${\mathbf{P}}_i^{(3)}=\sum _{j,k,l}{\chi }_{i,j,k,l}^{(3)}({\omega }_p+{\omega }_{pr}-{\omega }_S):{\mathbf{E}}_p^j({\omega }_p){\mathbf{E}}_{pr}^k({\omega }_{pr}){\mathbf{E}}_S^l{({\omega }_S)}^{*}$$ (1)

where E are the electric field vectors, the subscripts p, pr, and S indicate pump, probe, and Stokes light respectively, and symbols j, k, l indicate polarization directions. In the collinear CARS geometry, only two polarizations need to be considered. The sum is over all four combinations of driving field polarizations [15].

Each element of the third-order nonlinear susceptibility, χ⁽³⁾, has a frequency-independent (nonresonant) component, which is entirely real, and a frequency-dependent (resonant) component, which is composed of a real (χ_R’⁽³⁾) and an imaginary part (χ_R’’⁽³⁾).

$${\chi }^{(3)}={{\chi }_{NR}}^{(3)}+{{\chi }_{R\text{'}}}^{(3)}+i{{\chi }_{R"}}^{(3)}$$ (2)

The imaginary part χR’ ’⁽³⁾ contains elements with the same bandshape as the spontaneous Raman signal, and it is the component of interest to us. This component, however, cannot be extracted directly from the CARS signal I, because I_i ∝ | P_i⁽³⁾|², thus the real and imaginary parts are convolved. The χ_R’’⁽³⁾ can be extracted from the overall CARS signal using interferometric methods.

For light traveling along the z-axis, the x-polarized component of each field (E_m) in Eq. 1 may be described by:

$${\mathbf{E}}_m^x=E_m^x\text{exp}[-i({\omega }_{m}t+{\varphi }_m)]$$ (3)

An analogous relation could be written for the component of light polarized along the y-axis. The phase term does not have a superscript indicating polarization; the phase relationship between the×and y-polarized components is determined by the overall polarization state of the light. The i-polarized component of the overall third-order nonlinear polarization can be written as

$${\mathbf{P}}_i^{(3)}=\sum _{j,k,l}{\chi }_{i,j,k,l}^{(3)}({\omega }_p+{\omega }_{pr}-{\omega }_S)\times E_p^j{E}_{pr}^k{E}_S^l\text{exp}(-i[({\omega }_p+{\omega }_{pr}-{\omega }_S)t+({\varphi }_p+{\varphi }_{pr}-{\varphi }_S)]$$ (4)

In the approach described here, we generate two separate CARS signals with two orthogonally polarized pump/probe pulses with temporal widths of 100 fs and 750 fs. One of the CARS signals can be used as the local oscillator, provided that it has a reduced (preferably absent) resonant component. The 100 fs and 750 fs transform-limited pump/probe pulses are assigned subscripts 1 and 2 respectively. We must consider four distinct CARS driving fields, with p, pr = 1,1; 1,2; 2,1; 2,2. There is only one Stokes field, with a subscript 3. The term ϕ₃ is dropped because it is identical for each of the driving fields, and will not contribute to the behavior of the interferometric response. Since ϕ₂ is fixed and only the relative phase between the pulses is of concern, we further simplify our analysis by assigning ϕ₂ to be equal to zero. Finally, we substitute ω_aS for (ω_p + ω_pr − ω₃) since ω₁ and ω₂ are degenerate. These simplifications allow us to write

$${\mathbf{P}}_i^{(3)}=\sum _{p=1}^2\sum _{pr=1}^2[\sum _{j,k,l}{\chi }_{i,j,k,l}^{(3)}({\omega }_{aS})E_p^j{E}_{pr}^k{E}_3^l\text{exp}[-i({\omega }_{aS}t+{\varphi }_p+{\varphi }_{pr})]]$$ (5)

Recognizing that it is the real part of the complex electric field expression that is of interest, we can use Euler’s formula to write an expression for the interferometric CARS signal intensity $\left(I_i\right({\varphi }_1)=\underset{0}{\overset{2\pi }{\int }}|{\mathbf{P}}_i^{\left(3\right)}{|}^{2}dt)$ as a function of the phase of beam 1 as:

$$I_i({\varphi }_1)={\int }_0^{2\pi }{[C_{1,1}^{NR}\text{cos}(t\text{'}+2{\varphi }_1)+C_{1,2}^{NR}\text{cos}(t\text{'}+{\varphi }_1)+C_{2,1}^{NR}\text{cos}(t\text{'}+{\varphi }_1)+C_{2,2}^{NR}\text{cos}(t\text{'})+C_{1,1}^{R\text{'}}\text{cos}(t\text{'}+2{\varphi }_1)+C_{1,2}^{R\text{'}}\text{cos}(t\text{'}+{\varphi }_1)+C_{2,1}^{R\text{'}}\text{cos}(t\text{'}+{\varphi }_1)+C_{2,2}^{R\text{'}}\text{cos}(t\text{'})+C_{1,1}^{R"}\text{sin}(t\text{'}+2{\varphi }_1)+C_{1,2}^{R"}\text{sin}(t\text{'}+{\varphi }_1)+C_{2,1}^{R"}\text{sin}(t\text{'}+{\varphi }_1)+C_{2,2}^{R"}\text{sin}(t\text{'})]}^{2}dt\text{'}$$ (6)

where t’ = ω_aS t, and each coefficient C_p,pr represents the pre-exponential term in Eq. 5 for each pump/probe pair, e.g. $C_{1,1}^{NR}=\sum _{j,k,l}{\chi }_{NR;i,j,k,l}^{(3)}({\omega }_{aS})E_1^j{E}_1^k{E}_3^l$ These coefficients are complex, with resonant and nonresonant components, analogous to the χ⁽³⁾ values of Eq. 2. The integrated expression describes the interferometric CARS signal and it has five groups of terms with respect to the dependence on ϕ₁.

$$I_i({\varphi }_1)=2\pi \text{cos}({\varphi }_1)\sum _{\alpha =1}^2\sum _{\beta =1}^2\sum _{\underset{\gamma \ne \beta }{\gamma =1}}^2[C_{\alpha ,\alpha }^{r"}{C}_{\beta ,\gamma }^{r"}+(C_{\alpha ,\alpha }^{nr}+C_{\alpha ,\alpha }^{r\text{'}})(C_{\beta ,\gamma }^{nr}+C_{\beta ,\gamma }^{r\text{'}})]+2\pi \text{sin}({\varphi }_1)\sum _{\alpha =1}^2\sum _{\beta =1}^2\sum _{\underset{\gamma \ne \beta }{\gamma =1}}^2{(-1)}^{\alpha }[C_{\alpha ,\alpha }^{r"}(C_{\beta ,\gamma }^{nr}+C_{\beta ,\gamma }^{r\text{'}})-C_{\beta ,\gamma }^{r"}(C_{\alpha ,\alpha }^{r\text{'}}+C_{\alpha ,\alpha }^{nr})]+2\pi \text{cos}(2{\varphi }_1)[C_{1,1}^{r"}{C}_{2,2}^{r"}+(C_{1,1}^{nr}+C_{1,1}^{r\text{'}})(C_{2,2}^{nr}+C_{2,2}^{r\text{'}})]+2\pi \text{sin}(2{\varphi }_1)[C_{1,1}^{r"}(C_{2,2}^{nr}+C_{2,2}^{r\text{'}})-C_{2,2}^{r"}(C_{1,1}^{nr}+C_{1,1}^{r\text{'}})]+\text{const}.$$ (7)

The terms with a 2 ϕ₁ dependence arise from the interactions between the 1,1 and 2,2 (1,1:2,2) components. The terms with a ϕ₁ dependence, however, are derived from the interactions between the (1,1:1,2), (1,1:2,1), (2,2:1,2), and (2,2:2,1) components. The CARS signals represented by C_2,2 and C_1,2 are generated by a 750 fs probe pulse, and are therefore high-resolution spectra. The CARS signals represented by C_1,1 and C_2,1 are, on the other hand low-resolution spectra since they are generated with a 100 fs probe pulse. In the scheme we have devised, the low-resolution spectra serve as a slightly non-ideal local oscillator, and the high-resolution spectra serve as the signal of interest.

The ϕ₁-dependent and the 2ϕ₁-dependent signals are analogous, as indicated by the organization of Eq. 7. In fact, ϕ₁ and 2ϕ₁ give the same bandshape, as will be demonstrated in the “Results and discussion” section. For a purely nonresonant signal, the sin(ϕ₁) and sin(2ϕ₁) terms vanish. This fact is used to calibrate the differential phase as a function of wavelength (see below). In the presence of a resonant signal, the sine terms primarily represent the interaction between the local oscillator and the imaginary part of the resonant signal. This would be the only signal represented in these terms in the limit of an ideal local oscillator (no resonant components of C_1,1 or C_2,1). A similar argument can be made for the cosine terms – they primarily represent the interaction between the local oscillator and the real component of the resonant signal. The contribution of each group of the terms described in Eq. 7 can be extracted from experimental data by Fourier transform.

3. Experimental

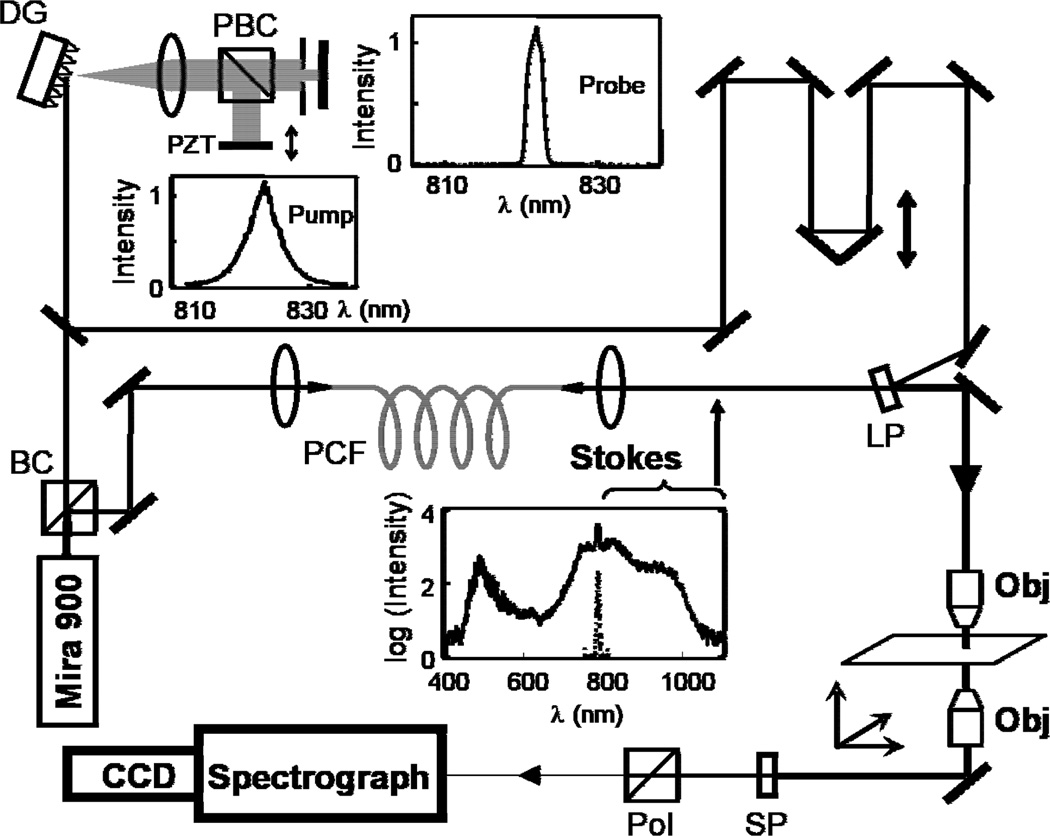
The experimental setup is shown in Fig. 2. It employed a single titanium sapphire oscillator (Coherent Mira 900F) pumped by a 10-W Nd:YVO₄ laser (Coherent Verdi), producing 100 fs pulses centered at 820 nm, with a repetition rate of 76 MHz [25]. After passing through an optical isolator, the oscillator output was split into two parts by a beam splitter. One beam was directed into a combined dispersionless filter/interferometer [13]. This component of the oscillator output was dispersed with a diffraction grating (1200 lines/mm), and collimated with a lens (f = 500 mm). The collimated beam was then separated into the two arms of an interferometer by a polarizing beamsplitter cube. The horizontally polarized component was retro-reflected by a mirror mounted on a piezo-electric transducer. This light constituted the low spectral resolution pump/probe (pulse width of 100 fs, bandwidth of 150 cm⁻¹). The bandwidth of the vertically polarized component, was limited by a slit placed near the Fourier plane to approximately 20 cm⁻¹ (pulse width of 750 fs), and retro-reflected by a mirror placed at the Fourier plane. This light was used as the high spectral resolution pump/probe. The two reflected beams were slightly displaced vertically to allow recovery from the dispersionless filter. The second part of the oscillator output was introduced into a photonic crystal fiber (Crystal Fibre) to create a continuum that spans the range 500 nm – 1100 nm [25]. The portion of the continuum at wavelengths longer than 820 nm was used as Stokes light. The polarization of the Stokes light was set to be 45° from pump and probe light. Pump, probe and Stokes light were combined through a long wave pass edge filter (Semrock) and then directed onto the sample, which consisted of neat benzonitrile (Sigma-Aldrich) in a 1 mm-thick sample cell [25]. The anti-Stokes signal generated by these three pulses was separated with the use of a short-pass filter. The vertically polarized portion was selected using a polarizer and then dispersed onto a spectrograph where interference between the various CARS signals occurred. Interferograms from each column of pixels were collected and recorded by an electron multiplying CCD camera (Princeton Instruments) [25]. Each CARS spectrum required an acquisition time of 80 ms, and each interferogram consisted of 256 spectra.

Fig 2.

Experimental configuration: BC, beamsplitter cube; DG, diffraction grating; PBC, polarizing beamsplitter cube; PZT, piezo-electric transducer; PCF, photonic crystal fiber; LP, long wave pass edge filter; Obj, microscope objective; SP, shortpass filter; Pol, polarizer. The inset spectra are (from top) probe, pump (Mira 900 output), and output of PCF. The PCF feed light is arbitrarily scaled and superimposed on the PCF output spectrum.

4. Results and discussion

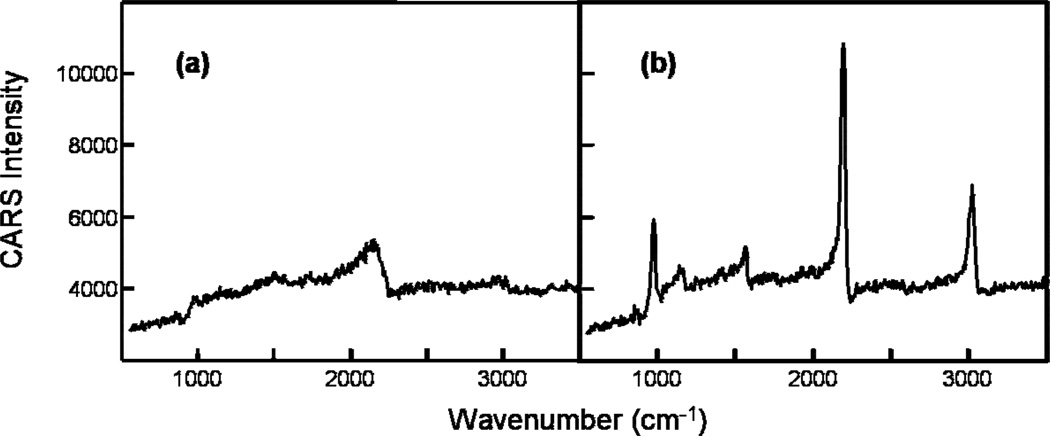
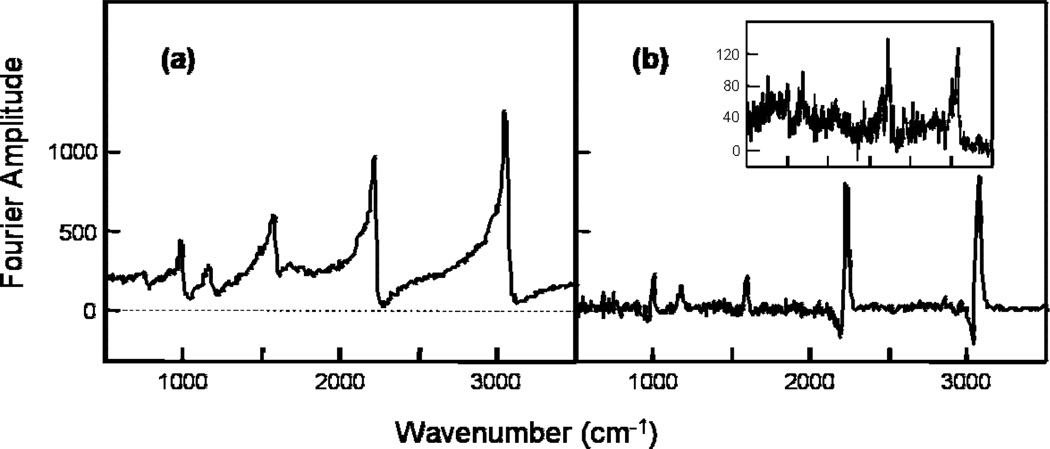
The broadband CARS spectra of benzonitrile generated individually by pump/probe light from the two arms of the interferometer are presented in Fig. 3. The spectrum in Fig. 3a is obtained by using 100 fs pulses as both pump and probe, where 750 fs pulses are used to acquire the spectrum in Fig. 3b. The spectral resolutions are 150 cm⁻¹ and 20 cm⁻¹, respectively. The acquisition time for each broadband CARS spectrum is 20 ms. In this interferometric CARS scheme, the spectrum shown in Fig. 3a is used as the local oscillator to interfere with the signal (Fig. 3b). The electric fields of these two signals interfere with one another at each CCD camera pixel. Figure 4a shows interferograms generated at two particular pixels by changing the length of one arm of the interferometer (i.e. by changing ϕ₁, see Eq. 6 and 7).

Fig 3.

Broadband CARS spectra of benzonitrile from each of the two arms of the interferometer. The spectra are generated by using (a) 100 fs pulses (spectral width 150 cm⁻¹) and (b) 750 fs pulses (20 cm⁻¹) as pump & probe.

Fig 4.

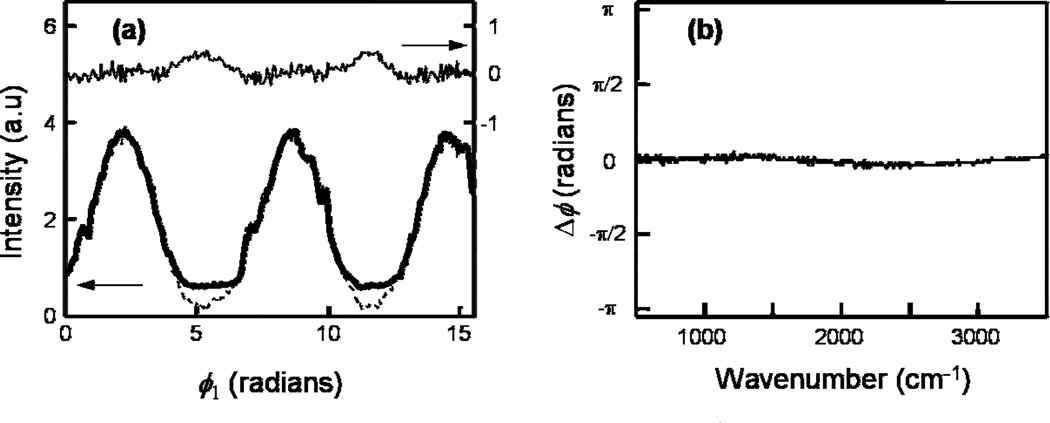
(a) CARS interferograms of benzonitrile – at 3070 cm⁻¹, (resonant, b solid curve), 2500 cm⁻¹, (nonresonant, dash) and the difference between the interferograms (thin solid). (b) Differential chirp between the local oscillator and signal as a function of wavenumbers, see text for details.

The dash curve in Fig. 4a is an interferogram recorded at 2500 cm⁻¹ where there is no vibrational resonance. The solid curve is an interferogram obtained at 3070 cm⁻¹ where the aromatic C–H stretch vibrational resonance occurs in benzonitrile. The vibrational resonance contributes sin(ϕ₁) and sin(2ϕ₁) components to the interferogram, and it is evident that the two interferograms have different waveforms. We extract the amplitudes of the individual sine terms by Fourier analysis, which necessitates a priori knowledge of the phase of the nonresonant component at each anti-Stokes wavelength. This wavelength-dependent phase information is obtained by collecting interferograms for a purely nonresonant spectrum generated by replacing the sample with a glass coverslip. Interferograms obtained in this manner are referenced to an interferogram that is simultaneously obtained by mixing the 100 fs and 750 fs pump beams on a photodiode. This calibration procedure yields a differential chirp, Δϕ(ω), (Δϕ(ω) = ϕ_NR(ω) − θ), where ϕ_NR(ω) is the phase of the interferograms of a nonresonant sample (glass cover-slip) at ω and θ is the phase of the reference interferogram. The Δϕ(ω) for our experimental configuration is presented in Fig. 4b; the average value is zero with a standard deviation of 0.06. The mild frequency dependence of Δϕ(ω) is a result of the fact that the local oscillator and the signal are generated in the same spot on the sample. This is an attractive feature of the instrument because the absence of a significant differential chirp will not result in artifacts in the interferograms.

Fourier transform of the interferograms yields the real and imaginary components of the χ⁽³⁾ signals, as shown in Fig. 5. As established in Eq. 7, the interferograms contains two signals with the same spectral bandshape with ϕ₁ and 2ϕ₁ dependences, where ϕ₁ is the interferometric phase delay. The results presented in Fig. 5 are derived from the interferometric signals with a ϕ₁ dependence. This signal is selected because it has a higher modulation amplitude than the signal with a 2ϕ₁ dependence, resulting in a higher signal-to-noise ratio. The real part of the χ⁽³⁾ signals is shown in Fig 5a and it consists of the nonresonant background and the real component of the nonlinear susceptibility χ⁽³⁾. Fig. 5b represents the imaginary component and hence the imaginary part of χ⁽³⁾. Note that the baseline of this spectrum is zero, free of nonresonant background. All the characteristic peaks of benzonitrile are recovered by the interferometric CARS technique [24]. The peaks at 2230 cm⁻¹ and 3070 cm⁻¹ have a negative amplitude component, as shown in Fig 5b. In our experimental configuration, the (non-ideal) local oscillator contains both real and imaginary components. The negative amplitude observed in Fig. 5b arises from the interaction between the imaginary parts of χ⁽³⁾ generated by the 100 fs and 750 fs pulses, as demonstrated by the sin(ϕ₁) term in Eq. 7. The asymmetry in the negative amplitude components is probably due to a slight difference between the central wavelengths of the 100 fs and 750 fs pulses. In the limit that the local oscillator has only real components, the bandshape of the recovered peaks will be similar to those of spontaneous Raman scattering. This is particularly important when CARS is used for identification of chemical species. In multiplex and broadband CARS, the nonresonant background and the resonant signal mix in the sample to distort the spectral profile of the peaks, as shown in Fig. 3b. This distortion of the spectral profile causes a shift in the peak positions, potentially introducing errors in spectral identification.

Fig 5.

(a) Real and (b) imaginary components of χ⁽³⁾ of benzonitrile determined by Fourier analysis of the ϕ₁ dependent interferometric signals (see text for details). The inset in (b) is the imaginary component of χ⁽³⁾ determined from the interferometric signals oscillating at 2ϕ₁.

Another advantage of using interferometric detection, in addition to recovering the bandshapes of the vibrationally resonant peaks, is to increase detection sensitivity. Interferometric/heterodyne methods are often used to increase the detection sensitivity by mixing the signal field (E_sig) with a strong local oscillator field (E_lo). In the case that the local oscillator field is significantly stronger than the signal field, i.e. E_lo >> E_sig, it is well known that the noise of the interferometric signal approaches the shot noise of the signal field. In the current experimental configuration, the local oscillator field is comparable to the signal field, thus the signal-to-noise ratio of interferometric CARS data is not considerably higher than in the case of broadband CARS. In order to improve the signal-to-noise ratio significantly, a strong local oscillator field must be used. A potential source of strong local oscillator field is broadband supercontinuum, e.g. supercontinuum generated by optically pumping a photonic crystal fiber, as shown in Fig. 2. An attempt was made to use this light source as local oscillator but the coherence of the supercontinuum from 630 nm to 820 nm was insufficient to produce an interferometric signal when mixed with the broadband CARS signal. Other approaches for producing a strong local oscillator field are currently implemented to increase the sensitivity of the interferometric CARS technique.

Considerable improvement of data acquisition rate must be achieved to facilitate microspectroscopy experiments. In this proof-of-principle experiment, the slow acquisition rate of interferograms is impractical for any micro-spectroscopy experiments, but studies are underway to increase the data acquisition rate significantly by using a strong local oscillator. With increased data acquisition rate, detection sensitivity, along with elimination of the nonresonant background, we expect that interferometric broadband CARS microscopy will become an important noninvasive technique in biological imaging that uses molecular vibrations as contrast.

5. Conclusion

We have demonstrated a one-laser interferometric technique that separates the nonresonant background from the CARS signal. In this simple interferometric CARS approach, there exists essentially no differential chirp between the local oscillator and signal. This attractive feature is due to the simultaneous generation of the two interfering parts at the same location on the sample. This technique has potential to become a robust biological imaging tool because the sensitivity, chemical species-identification ability, and rate of data acquisition can be improved significantly with existing methods.