Sparse Representation for Prediction of HIV-1 Protease Drug Resistance

Abstract

HIV rapidly evolves drug resistance in response to antiviral drugs used in AIDS therapy. Estimating the specific resistance of a given strain of HIV to individual drugs from sequence data has important benefits for both the therapy of individual patients and the development of novel drugs. We have developed an accurate classification method based on the sparse representation theory, and demonstrate that this method is highly effective with HIV-1 protease. The protease structure is represented using our newly proposed encoding method based on Delaunay triangulation, and combined with the mutated amino acid sequences of known drug-resistant strains to train a machine-learning algorithm both for classification and regression of drug-resistant mutations. An overall cross-validated classification accuracy of 97% is obtained when trained on a publically available data base of approximately 1.5×10⁴ known sequences (Stanford HIV database http://hivdb.stanford.edu/cgi-bin/GenoPhenoDS.cgi). Resistance to four FDA approved drugs is computed and comparisons with other algorithms demonstrate that our method shows significant improvements in classification accuracy.

1. Introduction

Since the disease of AIDS (Acquired Immunodeficiency Syndrome) was first recognized in the US in the early 1980s, it has become a severe worldwide epidemic¹. Based on the life cycle of the infectious agent human immunodeficiency virus (HIV), many inhibitors were constructed to treat AIDS. These inhibitors can retard the entry, replication or maturation of the virus. Therefore all of them are effective as anti-AIDS drugs.

The inhibitors of HIV protease have proved to be potent anti-viral drugs², since the protease plays an important role in the maturation of the virus³. Up till now, nine HIV protease inhibitors have been approved by the FDA (Food and Drug Administration): amprenavir (APV), indinavir (IDV), lopinavir (LPV), nelfinavir (NFV), ritonavir (RTV), saquinavir (SQV), atazanavir (ATV), tipranavir (TPV) and darunavir (DRV).

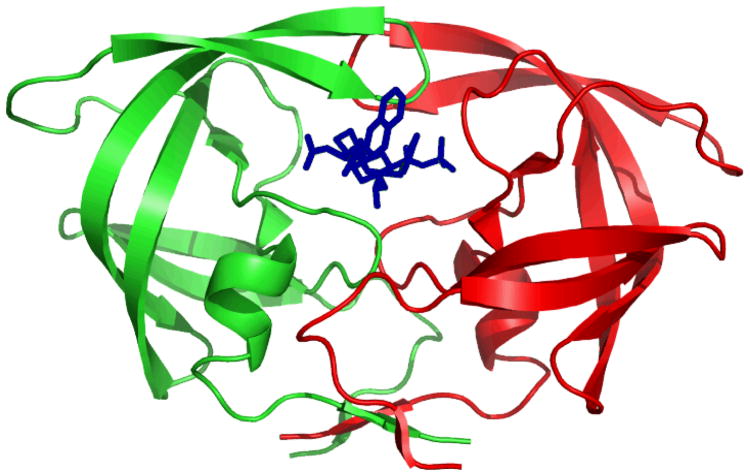
The structure of the HIV-1 protease is shown in Figure 1. HIV protease is a homodimer, and each monomer has 99 residues. The inhibitors bind inside the active site in the center of the dimer by hydrogen bonds and van der Waals interactions and prevent the cleavage of viral precursor proteins. Therefore, the virus cannot form mature particles and thus cannot infect other host cells^4,5.

Figure 1.

The structure of HIV-1 protease with Saquinavir. Two monomers are shown in red and green. Saquinavir is shown in blue.

However, because HIV has deficient proofreading⁶ and a high rate of replication⁷, mutations evolve rapidly in its genome. Such mutations lead to drug resistance or decreased susceptibility to certain drugs, though in some rare cases the drug efficacy was observed to increase for certain mutations⁸. Hence, resistance testing is recommended for AIDS patients due to the decreased susceptibility for certain drugs⁹ Mutations associated with resistance are found in almost half the protease residues. They are located around the active site of the protease where they can alter the interactions with inhibitors and throughout the structure¹⁰. Multiple mutations accumulate over time. Due to the huge number of possible combinations of mutations, it is a challenge to predict which protease sequences will cause resistance to specific inhibitors. Accurate predictions would be valuable for prescribing the most effective drugs for infections with resistant HIV.

Most existing approaches to predict HIV drug resistance from sequence data use only the sequence data and often only selected sets of mutation sites, such as geno2pheno¹¹, REGA¹², Stanford HIVdb¹³, ANRS¹⁴, and HIV-GRADE¹⁵. In this paper we incorporate structural data into the predictions. The structural information improves the quality of the predictions by representing interactions between physically adjacent mutation sites that are not adjacent in sequence unlike other methods.

The resistance can be assessed for HIV strains by experiments growing the infected cells in the presence of different drugs. However, even minimal wet lab experiments to measure the antiviral efficacy of individual inhibitors are time consuming and expensive. Therefore, it would be valuable develop computer methods to predict whether a mutant is drug-resistant or not.

In the field of extracting information, the sparse signal representation has emerged in recent years as a promising research area. Indeed, the sparsity is a hidden prior information for most of the signals in the physical world and the related philosophy and algorithms have been applied in a diverse areas^16,17. Sparse signal representation can be visualized as a technique for extracting the essential features from the data while simultaneously minimizing the effects of the noise in the data. For example, a sparse signal representation of audio data would extract the continuous sound waves while suppressing the uncorrelated and non-continuous background noise.

Therefore, in this paper, we apply the sparse signal technique in the prediction of HIV-1 protease drug resistance from sequences. In the BACKGROUND section, a brief background of the sparse signal representation is presented; in PREVIOUS WORK, we briefly review the area; in METHODS section, the details of our proposed classification algorithm are introduced. Following that, the RESULTS and DISCUSSION sections describe the outcomes and related discussions.

2. Background

Compressive sensing uses sparse signal representations to eliminate noise and non-critical features from the data^16,17. The data are expanded in terms of an orthogonal basis – often a Fourier or wavelet basis for conventional signals – and the critical features extracted based on the magnitudes of the coefficients of the expansion. A classical expansion, like the Fourier transform, is not always the optimal basis for expansion and therefore the choice of an optimal basis is done using optimization¹⁷. The optimal basis for machine learning with protein sequence and structure data is defined in terms of a dictionary of exemplars which are determined with the singular value decomposition KSVD¹⁸ as described in the methods below.

The idea of the above compressive sensing and sparse signal representation has achieved very exciting results in many areas such as signal acquisition¹⁹, signal representation¹⁸, pattern classification²⁰, and image processing²¹. In this work the idea of dictionary learning and classification is extended and applied in the problem of predicting drug resistance from HIV-1 protease sequence data.

3. Methods

In this section, we first provide a vector representation for the protein structure, and then the sparse dictionary is used to perform the classification task.

3.1 Data sets

A total of 11731 phenotype results from 1727 isolates were obtained from Genotype-Phenotype Datasets on the Stanford HIV drug resistance database¹³ (http://hivdb.stanford.edu/cgi-bin/GenoPhenoDS.cgi).

In this experiment, four protease inhibitors, SQV, TPV, IDV and LPV, were tested.

For SQV, IDV and LPV, among all these genotype sequences, those mutants with the relative resistant fold < 3.0 were classified as non- resistant, denoted as 0; while those with the relative resistant fold ≥ 3.0 were classified as resistant, denoted as 1²².

For TPV, those mutants with the relative resistant fold < 2.0 were classified as non-TPV resistant, denoted as 0; while those with the relative resistant fold ≥ 2.0 were classified as TPV resistant, denoted as 1²³.

3.2 Preprocessing of the datasets

In order to unify the data in the original datasets, those sequences with an insertion, deletion, or containing a stop codon relative to the consensus have been removed so that the data represent proteases of 99 amino acids.

Due to the limitations of the sequencing assay or presence of multiple viral sequences in the same sample, many of the sequences in the dataset have multiple mutations at the same sites yet share the same drug-resistance characteristics. An individual protein molecule can only have one type of amino acid at one location. Therefore, we need to expand the data to multiple sequences with single amino acids at each location. For instance, among the 99 letters of a sequence, 97 of them have a single amino-acid. However, at one site there are two different types of amino-acids, and another site has three. In this case, this record must be expanded to a total of 6 = (2 × 3) different sequences, each of which has only one amino-acid for each of its 99 residues, sharing the same drug resistance of the original sequence. In this work, we designed a fast way to perform this expansion, which significantly enriches the test data.

Without loss of generality, for a sequence in the original data set, we denote the number of variations on each of its 99 sites to be J_i, i = 1,2, …,99. Therefore, this sequence can be expanded to a total number of $P=\underset{i=1}{\overset{99}{\Pi }}{J}_i$ different sequences, each of which has only one type of amino acid at each position. In order to generate them all, equivalently, for any p ∈ {1,2,…, P}, we need to pick a unique combination among the 99 positions.

This choice can be done with a simple recursive implementation. Unfortunately, it has so high a complexity that in practice, we only obtain roughly 5k sequences within 24 hours on an Intel Core i7 workstation. In order to improve this speed, we designed a new method for this expansion by analogy to the base-conversion problem. For a simple example, assume J_i = 2 for all i = 1,2, …,99 Then, the task of listing all the 2⁹⁹ sequences, though a huge number, can be done by simply finding the representation of each p ∈ {1,2, …,2⁹⁹}, under base 2 and picking the 1st (resp. 2nd) amino acid on each site if a 0 (resp. 1) is encountered on that digit. By analogy, in this task, we need to convert a decimal number p to a mixed-base number: its i-th digit is a J_i-based number.

This can be done, similarly to the decimal-binary conversion, by successive short division. However, the difference is that instead of dividing by 2, here J_i should be used for the i-th division. The short division is repeated and the remainders are recorded in a reversed order, which finally gives a 99-digit mixed-base representation of p, denoted as π. Then, for each site, we just pick the amino acid according to the i-th digit of π.

With this new scheme, we generated a total of 1.5 × 10⁵ sequences in less than 10 seconds on the same machine. This significantly enriches the available data for the subsequent analysis.

3.3 Protease structure representation

It is necessary to use a representation of the structure that is invariant with respect to the arbitrary choice of origin and orientation of the molecule. Therefore, the procedure in²⁴ was used to convert the HIV-1 protease structure into a 210-dimensional vector.

The structure of wild type (consensus) HIV protease with SQV (PDBID: 3OXC²⁵) was obtained from the Protein Structure Database at www.pdb.org. Then, the position of each residue was represented by its alpha carbon position. Because the wild-type HIV-1 protease has 198 residues in the dimer, the α-carbon positions consist of 198 three-dimensional vectors, C⃑ = {C₁,C₂, …, C₁₉₈: C_i ∈ ℜ³}. The Delaunay triangulation is then performed on the C⃑ and a graph G =〈 C⃑, E〉 is obtained. Then, for the edge e ∈ E, the two residues it connects are denoted as A_i and A_j where A_i, A_j ∈ A being the set of all the 20 amino-acids. We then recode the distance between C_i and C_j as d(A_i, A_j). This process is repeated for all the edges in G and the distances computed for the same pair of amino-acids are averaged. Finally, the averaged values are filled into the corresponding positions of a matrix D ∈ ℜ^{20 × 20}. For example: D(1, 2) and D(2, 1) contains the average distance between the amino-acids A₁ and A₂ appearing in the graph G.

Evidently, the matrix D is symmetric. Therefore, it has a total of 210 degrees of freedom (upper triangular part plus the diagonal). Those 210 values are concatenated in a row-wise manner to form a 210-dimensional vector, which will be termed “structure vector” for short. The subsequent learning and classification are based on such structure vectors.

3.4 Sparse dictionary classification

From the brief introduction of the compressive sensing/sparse representation, it can be seen that for a more accurate signal reconstruction, rather than using some existing fixed basis/frames such as the Fourier basis, it is very important to find a suitable basis/frame Ψ, so that the signals of interest have sparse representations in Ψ. In the signal processing community, such a frame is also called a dictionary. Given a group of signals, the task of finding a dictionary that can represent the group of signals sparsely is called the dictionary construction.

The use of the signal dependent frame, as opposed to the generic frames/basis such as Fourier, wavelet, etc., gives us a new approach to the signal reconstruction problem. Indeed, one can view the construction of the signal dependent frame (dictionary) as a process of building a sparse, nonlinear model for the signals at hand. As a result, the fidelity of reconstructing a new signal from the dictionary can then be considered as a measure of how the new signal fits the model represented by the dictionary. Therefore, this can be used under a classification framework: Assume we have n groups of signals, for example (but not limited to) n=2 in our drug-resistant/non-resistant case. Then, we can construction two dictionaries as the models for the resistant/non-resistant groups, respectively. After that, a new signal (the “structure vector” described in the above section), is fit to the two models by reconstructing it using the two dictionaries. The reconstruction errors using different dictionaries are compared and the smaller error indicates that the signal fits to that specific dictionary better than to the other. As can be observed, there is no limitation on n being 2 and therefore the proposed method can be viewed as a nonlinear multi-group classification scheme. In addition, the sparsity of the representation makes the classification more efficient. In what follows, we present the details of the proposed algorithm.

Denote u₁,u₂,…,u_M, v₁, v₂,…,v_M as the training sets and u_M+1,u_M+2,…, u_{M + N}, v_{M + 1}, v_{M + 2},…,v_{M + N} as the testing sets. In order to learn and encode the information of the vectors belonging to SQV group (resistant to SQV), we construct an over complete dictionary J from u₁,u₂,…,u_M. To that end, the K-SVD algorithm is employed and shown in Algorithm 1.

The dictionary J records the information of the SQV group and similarly, the other over-complete dictionary K, which learns and encodes the information of non-SQV group, is constructed from v₁,v₂,…,v_m also with the K-SVD algorithm.

	Algorithm 1 K-SVD Dictionary Construction18
1:	Initialize J by the discrete cosine transformation matrix
2:	repeat
3:	Find sparse coefficients Λ(λi′s) using any pursuit algorithm.
4:	for j = 1, 2, …, update ji, the j-th column of J, by the following process do
5:	Find the group of vectors that use this atom: ζi: = {i: 1 ≤ i ≤ M, λi(j) ≠ 0}
6:	Compute where Ej: = Q − Σi ≠ j ji ΛiT where ΛiT is the i-th row of Ë
7:	Extract the i-th columns in Ej, where i ∈ ζj, to form $E_j^R$
8:	Apply SVD to get $E_j^R=U\Delta V$
9:	ji is updated with the first column of U
10:	The non-zeros elements in ${\Lambda }_T^j$ is updated with the first column of V × Δ(1,1)
11:	end for
12:	until Convergence criteria is met

In this work, we used the orthogonal matching pursuit algorithm to find the sparse coefficients²⁶. The two dictionaries encode the information in either group of vectors. Therefore, intuitively, a vector belonging to the SQV group could be represented by J with high fidelity and vice versa for the non-SQV group. Formally, a new vector w⃑ ∈ℜ²¹⁰ with unknown category, is reconstructed by both dictionaries J and K. To that end, the orthogonal match pursuit algorithm is used to find a sparse coefficient Λ and Γ, such that

$$\stackrel{\rightharpoonup }{w}\approx J\Lambda \text{s}.\text{t}.\Lambda \in {\Re }^{210},{\Vert \Lambda \Vert }_0<k$$

$$\stackrel{\rightharpoonup }{w}\approx K\Gamma \text{s}.\text{t}.\Gamma \in {\Re }^{210},{\Vert \Gamma \Vert }_0<k$$

However, the two dictionaries could represent w⃑ with different accuracy. The representation errors are recorded as:

$$e_{\mathit{\text{SQV}}}={\Vert \stackrel{\rightharpoonup }{w}-J\Lambda \Vert }_2$$

$$e_{\mathit{\text{non}}-\mathit{\text{SQV}}}={\Vert \stackrel{\rightharpoonup }{w}-K\Gamma \Vert }_2$$

and finally

$$e=e_{\mathit{\text{SQV}}}-e_{\mathit{\text{non}}-\mathit{\text{SQV}}}$$

Therefore, if e > 0, the new vector w⃑ could be represented better by the dictionary constructed from the vectors of the SQV group. Hence, it is classified to be resistant to the SQV. The overall algorithm is listed in Algorithm 2

	Algorithm 2 Drug resistance classification algorithm
1:	repeat
2:	Randomly choose m vectors from SQV group, the rest n being training data
3:	Construct dictionary J using Algorithm 1
4:	Randomly choose m vectors from none group, the rest n being training data
5:	Construct dictionary K using Algorithm 1
6:	for each vector v in testing data do
7:	computing the sparse representation of v using both dictionaries J and K
8:	computing the representation errors using the two dictionaries
9:	if the error of using J is larger then
10:	v is resistant to SQV
11:	else
12:	v is NOT resistant to SQV
13:	end if
14:	end for
15:	Compute the confusion matrix
16:	until For 9 times

4. Experiments and Results

4.1 k-fold validation

In order to fully use all the data, a k-fold cross-validation was performed in all the experiments for all the four drugs. Specifically, $\raisebox{1ex}{$k-1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.$ of all the sequences are used for training the classifier and the remaining $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathit{\text{k}}$}\right.$ data are used for testing. We pick k to be 5 for all the tests. For each of the four types of the drugs, we then have approximately 10k “structure vectors”, half are resistant and the other half are non-resistant. Accordingly, there are about 2k testing vectors for each drug.

4.2 Support vector machine

The support vector machine (SVM) is a framework for the supervised learning and classifying task. After its proposal by Vapnik²⁷, the SVM has been used widely in the machine learning/pattern classification filed.

When feeding the encoding result into SVM, 5-fold cross validation tests were performed implemented in MATLAB SVM toolbox^28,29. We tested several choices for the SVM kernel and the linear kernel has the best performance, as reported in Table 1 (choice of kernel is further discussed in Section 4.8). Care was taken to insure that all positive and negative instances of a given protein were removed from either training or testing dataset when generating a set for cross-validation. This avoided the potential problem of having negative instances associated with a positive test item or positive instances associated with a negative test item and thus generating systematically optimistic (and incorrect) assessments of the training accuracy.

Table 1. Mean accuracy, specificity and sensitivity using SVM.

	IDV	LPV	SQV	TPV
Accuracy	0.961	0.959	0.950	0.961
stddev (×102)	0. 233	0. 251	0. 249	0. 402
Sensitivity	0.951	0.947	0.947	0.958
stddev (×102)	0. 469	0. 348	0. 424	0. 463
Specificity	0.971	0.973	0.953	0.964
stddev (×102)	0. 368	0.341	0. 325	0. 369

4.3 Artificial Neural Networks

The same testing strategy was applied with the Artificial Neural Networks (ANN) to classify data. Specifically, the three-layer feedforward network was used in Matlab^29-31. The network had one hidden layer of 20 nodes and was trained with backpropagation with a maximum of 50 training epochs. Similar to SVM, 5-fold cross validation was also used for ANN and the result is shown in Table 2.

Table 2. Mean accuracy, specificity and sensitivity using ANN.

	IDV	LPV	SQV	TPV
Accuracy	0.961	0.963	0.957	0.951
stddev(×102)	0.857	0.641	0. 723	1.27
Sensitivity	0.960	0.965	0.958	0.953
stddev(×102)	1.16	0.741	0.483	1.89
Specificity	0.963	0.961	0.956	0.950
stddev(×102)	0.981	0.598	1.06	0. 672

4.4 Proposed sparse dictionary classifier

Following the approach described in METHODS, the sparse representation was also implemented and 5-fold cross validation was performed. The result is shown in Table 3.

Table 3. Mean accuracy, specificity, and sensitivity using sparse representation.

	IDV	LPV	SQV	TPV
Accuracy	0.969	0.974	0.970	0.990
stddev(×102)	0.151	0. 292	0.139	0.277
Sensitivity	0.951	0.957	0.959	0.984
stddev(×102)	0.529	0.494	0.604	0.423
Specificity	0.989	0.992	0.981	0.995
stddev(×102)	0.297	0.361	0.692	0.199

For clarity, the mean accuracy of all the above methods is compared in Figure 2. From it we can observe that the mean accuracy of the proposed dictionary classifier is higher than for other methods.

Figure 2.

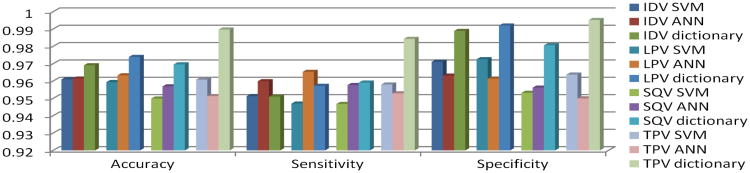
Comparison of accuracy, specificity and sensitivity of sparse dictionary, SVM and ANN.

While Figure 2 visualizes the comparison among the mean accuracies, sensitivities and specificities, we further conducted statistical tests for all the 5-fold cross validation results. At the significant level of 0.01, the accuracy, sensitivity and specificity of the proposed method are higher than for both SVM, and ANN.

4.5 Comparison with other methods

Furthermore, we have tested several state-of-the-art methods including HIV-GRADE (Version 12-2009), ANRS-rules (Version 7/2009), Stanford HIVdb (Version 6.0.6), Rega (Version 8.0.2), and geno2pheno (version December 13, 2000), which are available at http://www.hiv-grade.de/cms/grade/, using the same datasets described above. Since the original dataset obtained from Stanford HIVdb are all protein sequences, and all these servers take nucleotide sequence, the sequence manipulation suite³² was used to convert the protein sequences into nucleotide ones. When parsing the output of these methods, the output term with “susceptibility”, is considered as non-resistant, whereas output of “resistance” is considered as being resistant. Accuracies are presented in Table 4. For the HIV-grade, there are outputs termed “Intermediate”. When calculating the accuracies, “Intermediate” is considered as resistant, and the result is shown in the table 4. In the table, N/A indicates that there is no output for this method-inhibitor.

Table 4. Accuracy compared to other methods.

	IDV	LPV	SQV	TPV
HIV-grade	0.851	0.805	0.802	0.728
ANRS	0.851	0.870	N/A	0.597
HIVdb	N/A	0.839	N/A	0.768
Rega	0.856	0.840	0.693	N/A
Sparse	0.969	0.974	0.970	0.990

From the comparison we can observe the high accuracy achieved in our proposed sparse method. The consistent high level of accuracy demonstrates that including structural information and sparse encoding is a promising new alternative approach to only using sequence information for this important task of predicting drug resistance.

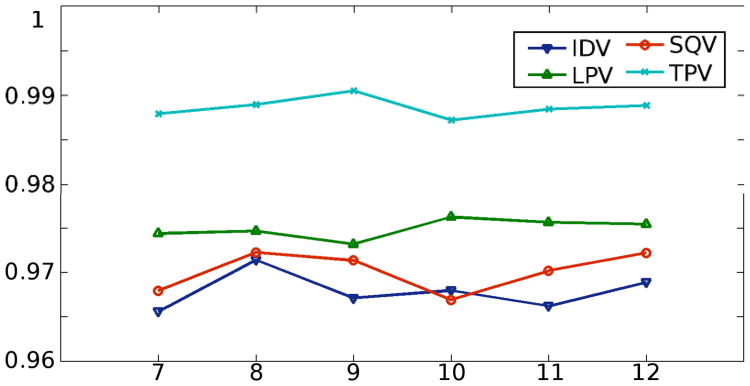
4.6 Mean accuracy with respect to different sparsity

The parameters of the algorithm, in particular the sparsity and the dictionary size, affect the final classification outcome. The sparsity controls how many atoms are used to re-construct a given vector. If it is large, then both dictionaries would give smaller representation errors. Therefore, it is a parameter that can be tuned. By varying from 7 to 12, we repeated the learning and classification steps. Then the mean accuracy was measured and plotted in Figure 3. It is noted that for all the tests here, the dictionary size is fixed at 250.

Figure 3.

The accuracy changes with respect to the change of the sparsity. The lines are the mean accuracies of the k tests with different sparsity. The dictionary size is fixed at 250.

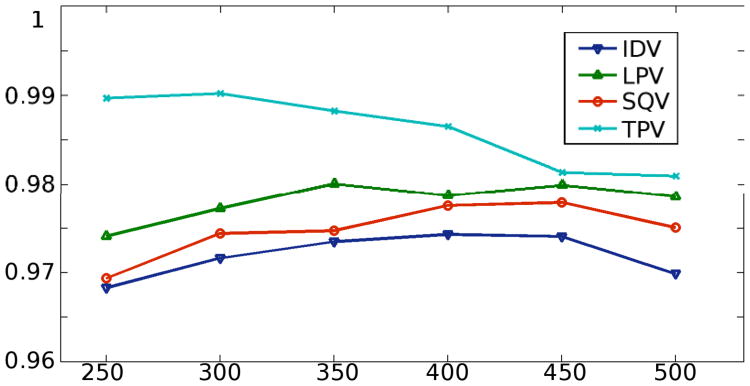
4.7 Mean accuracy with respect to dictionary size

The dictionary is an over-complete set of vectors (atoms) and the number of atoms in it is also a parameter that affects the learning and classification performance. Therefore, similar to the tests for the sparsity above, tests with different dictionary sizes were conducted (varying from 250 to 500) and the resulting accuracies are recorded in Figure 4. Moreover, for these tests, the sparsity value was fixed at 9.

Figure 4.

The accuracy changes with respect to the change of the dictionary size. The lines are the mean accuracies of the k tests with different dictionary sizes. The sparsity is fixed at 9.

From the tests we can observe that with further parameter tuning, the proposed algorithm has the potential of reaching even higher accuracy.

4.8 Computational Performance

As mentioned in Section 4.1, we have approximately 10k training “structure vectors” and 2k testing vectors for each single classification task. As can be seen in Table 5, although the proposed algorithm achieves better classification accuracy, it also takes longer to finish. For the SVM, any choice of kernel other than the linear one does not lead to convergence within 10⁴ seconds.

Table 5. Running times for training.

Method	SVM (linear)	SVM (non linear)	ANN	proposed
Training Time (Sec)	20.6	no convergence (>104)	21.9	358
Testing Time (Sec)	0.4	N/A	0.1	2

5. Discussion

Given a mutant strain of HIV-1, in order to establish whether it is resistant to certain drugs, wet lab biological experiments are conducted. However, this process is both time and resource consuming. Therefore, performing such experiment in silico will save much time and resources. Hence, in this work we propose an algorithm to predict the drug resistance property of the mutant HIV-1 protease from its sequence. It is based on the signal sparse representation theory. Essentially, we learn the characteristics of resistant and non-resistant mutants of the HIV-1 protease by constructing two over-complete dictionaries. Then, given the sequence of a new mutant, we measure how accurately this new sequence can be represented by the two dictionaries. The category of the dictionary with smaller error is assigned to the new mutant. The algorithm is tested on 1.5 ×10⁴ different sequences, and the result was compared with the common classification tools SVM and ANN. The result shows that the proposed sparse dictionary classifier can distinguish between drug resistant and non-resistant sequences significantly better than the other methods. Moreover, this new method outperforms existing approaches in terms of accuracy. This method for in silico prediction of resistance may be a promising way to select effective drugs in AIDS therapy without performing the actual biological experiments. In our on-going and future research, we will extend the bi-partition algorithm to multiple class classification. This would enable grouping the proteins in more finely divided and more accurate sub-categories.