Modeling Variability in Individual Development: Differences of degree or kind?

Abstract

The proper use of statistical models for analyzing individual change over time is critical for the progress of developmental science. Latent curve models, hierarchical linear growth models, group-based trajectory models, and growth mixture models constitute increasingly important tools for longitudinal data analysis. To facilitate their understanding and use, this paper clarifies similarities and differences between these models, with particular attention to the assumptions they make about individual development. An example shows how the results and interpretation vary across model types. Discussion centers on reviewing the strengths and limitations of each approach for developmental research.

It has long been recognized that longitudinal studies are of fundamental importance to child development research. Until recently, however, the types of hypotheses researchers could evaluate using longitudinal data were greatly restricted by the available statistical methods (e.g., repeated measures analysis of variance). Fortunately, advances in statistical theory and more efficient computers have allowed for the development of new approaches for modeling individual development (e.g., latent curve models, hierarchical linear models, group-based trajectory models, and growth mixture models) that overcome many of the conceptual and statistical deficiencies associated with previous methods (Bollen & Curran, 2006). In this paper, we review and compare three such modeling approaches, broadly construed. Each approach assumes that the course of individual development, referred to as a trajectory, is continuous over time and that there are individual differences in trajectories of change. What distinguishes the approaches we review is how they describe these individual differences.

The first approach we consider assumes that individual differences fall along a continuum. That is, individual trajectories differ by degree, characterized by quantitative variation in a common trajectory shape. Subsumed within this general approach are multilevel or hierarchical (generalized) linear models (Bryk & Raudenbush, 1987; Raudenbush & Bryk, 2002) and latent curve analysis (Bollen & Curran, 2006, Meredith & Tisak, 1990). In contrast, the second approach is (typically) motivated by the assumption that individuals differ qualitatively rather than quantitatively. In other words, individuals differ in kind, with one type of person exhibiting one trajectory and other types of people exhibiting other trajectories. This approach is therefore designed to capture differences in trajectories of change across homogeneous groups of individuals. Paradigmatic of this approach is the Semi-Parametric Groups-based trajectory Model (SPGM) of Nagin (1999). Finally, the third general approach for modeling individual trajectories that we discuss allows for both qualitatively different patterns of change as well as quantitative differences within each pattern. This third approach allows for heterogeneity by degrees within groups that differ in kind. Muthén's (2001) General Growth Mixture Model (GGMM) is the prime exemplar.

Because these three analytic approaches are quite flexible, models can often be specified to closely match our theories of individual development (Curran & Willoughby, 2003). Consequently, as software programs capable of fitting these models have become more widely available, research using these methods has proliferated (Bauer, 2007). Unfortunately, papers using or demonstrating these approaches often do not clearly justify their choice of method or explain how the assumptions of the chosen model relate to developmental theory. Researchers may therefore find it difficult to select among competing modeling approaches, especially when encountering disagreements among methodologists about the pros and cons of each approach. For instance, no less than five recent papers on group-based models or GGMMs have been followed by contentious commentary (see Bauer & Curran, 2003a; Connell & Frye, 2006; Eggleston Laub & Sampson, 2004; Nagin & Tremblay, 2005a, 2005b).

In the current paper, we attempt to provide a comparative framework that can be used to guide researchers as they explore the broader literature on these approaches. First, we try to clarify the connection between the statistical assumptions of each modeling approach and theoretical models of individual development. Graphical depictions are favored over technical explanations or equations in an effort to more clearly convey the implications of different assumptions for individual development. Second, we show how each model is applied and interpreted by fitting each to a common longitudinal data set on antisocial behavior. The results help to show what each approach offers the analyst, and how the three modeling approaches compare to one another. We begin by describing this data set in further detail.

A Motivating Example: The Development of Antisocial Behavior

Our sample includes 894 children from the National Longitudinal Study of Youth – Child Sample (Center for Human Resource Research, 2004) assessed biennially from 1986 to 1992 and who were between 6 and 8 years old in 1986. The primary dependent variable was mother-reported antisocial behavior, measured somewhat crudely as the sum of six three-point items from the Behavior Problems Index (Peterson & Zill, 1986). Change in antisocial behavior is modeled as a function of chronological age minus 6 (subtracting 6 will allow us to interpret the intercept of our trajectory model as the expected level of antisocial behavior at six years of age). For simplicity, only two predictors were considered, sex (0 = female, 1 = male), and a measure of cognitive and emotional support within the home obtained at the first assessment (from the Home Observation for Measurement of the Environment, scaled to M = 0 and SD = 1.5; higher scores indicate more support).

We now describe and demonstrate each modeling approach with this data. All models were fit using Mplus version 5.1 with maximum likelihood estimation (Muthén & Muthén, 2006).

Three Modeling Approaches

Inspection of individual trajectory plots and comparisons of model fit for different trajectory shapes (e.g. flat vs. linear vs. quadratic) suggested that age-related changes in antisocial behavior from 6 to 15 years of age could be described by a simple straight line. Accordingly, for all three modeling approaches, Antisocial Behavior (AB) at time t for person i is expressed as a linear function of time as follows:

$$A{B}_{ti}={\beta }_{0i}+{\beta }_{1i}Ag{e}_{ti}+r_{ti}$$ (1)

The coefficients β₀₁ and β_1i are interpreted as the intercept and slope of the individual trajectory, respectively, and r_ti is a residual term. More specifically, β_0i denotes an individual's level of antisocial behavior when Age = 0 (6 years), or “initial status.” The linear change in antisocial behavior that occurs with each year of age, or “rate of change”, is in turn represented by β _1i.

Every individual has his or her own trajectory of change in antisocial behavior and hence a unique intercept and slope (thus the i subscript on β_0i and β_1i). Our primary interest is not, however, in the trajectory of a particular individual, or even all of the individuals in our sample; we are most interested with making inferences about change over time in the population as a whole. That is, we want to know how and why individuals differ from one another in their trajectories of change over time (i.e., intercepts and slopes).

In each of the modeling approaches we consider here, the collection of intercept and slope values across all individuals in the population is described by a distribution, and the goal is to estimate the parameters of this distribution. These estimates will permit us to make inferences about patterns and mechanisms of change in the population as a whole, not just the sample. What distinguishes the three modeling approaches we consider here are the assumptions made about the nature of the distribution of intercepts and slopes. Put more simply, these models differ in how they summarize variation in β_0i and β_0i across individuals: as quantitative, qualitative, or both.

We focus here on how the trajectory parameters β_0i and β_1i are modeled because it is this choice that is most reflective of our conceptual model of individual development. In practice, equal attention should be paid to the residual term r_ti. Although the residuals are seldom of theoretical interest, inferences about β_0i and β_1i can be compromised if the distribution assumed for the residuals is incorrect. For our example we adopt the conventional assumption that the residuals are normally distributed. Alternative assumptions are possible, but they are usually motivated statistically (e.g. based on the scale of the dependent variable) rather than conceptually. For instance, antisocial behavior is a crudely measured variable that is rather skewed, making our assumption of normal residuals somewhat unrealistic. Complicating our analyses by choosing a less familiar distribution (e.g., censored normal) might bolster confidence in our results, but would also distract from the conceptual distinctions between modeling approaches that we wish to emphasize here. Thus, for expository purposes, we retain the normality assumption for the residuals for our analyses, and return to the issue of measurement at a later point.

Approach 1: Differences of Degree

The first general modeling approach we consider assumes that all individuals in the population follow the same general pattern of change (e.g. linear) and that individual differences in change over time are quantitative in nature (i.e. they fall along a continuum, differing by degree). Included in this approach are multilevel or hierarchical (generalized) linear models (Byrk & Raudenbush, 1987) and latent curve analysis (Bollen & Curran, 2006; Meridith & Tisak, 1990). More formally, differences in intercept and slope values across individuals in the population are assumed to follow some continuous distribution, almost always a normal distribution. Assuming that the intercepts and slopes are normally distributed allows us to summarize individual differences using mean and variance parameters. The mean intercept and mean slope trace out the trajectory of the average individual, whereas the variances of the intercepts and slopes (and their covariance or correlation) quantify the extent to which individuals differ in initial status and rate of change relative to the average. The covariance between intercepts and slopes tells us whether the rate of change is related to initial status.

Fitting this model to the antisocial data results in the parameter estimates reported in Table 1. The mean intercept and slope indicate that antisocial behavior generally starts out at a low level (1.88 ) and increases at the meager rate of .05 units per year. More interesting, the variances of the individual intercepts and slopes are both statistically significant, indicating that individuals reliably differ both in level of antisocial behavior at age 6 and rate of change in antisocial behavior over time. Some individuals increase more rapidly than the average trajectory, others show little change, and still others show slight decreases. There is a positive (but ns) association between intercepts and slopes, such that children with high levels of antisocial behavior at age 6 also tend to show slightly steeper increases in antisocial behavior over time (r = .29, computed by rescaling the covariance estimate).

Table 1.

Results of Approach 1, assuming quantitative differences among individual trajectories

Parameter	Estimate (SE)
Average Trajectory Parameters
Intercept	1.88 (0.07)**
Slope (Age)	0.05 (0.01)**
Variance / Covariance Parameters
Intercept	1.43 (0.25)**
Slope (Age)	0.02 (0.01)*
Covariance	0.05 (0.04)
Residual	2.09 (0.14)**

Note. Robust standard errors reported

^*p < .05

^**p < .01

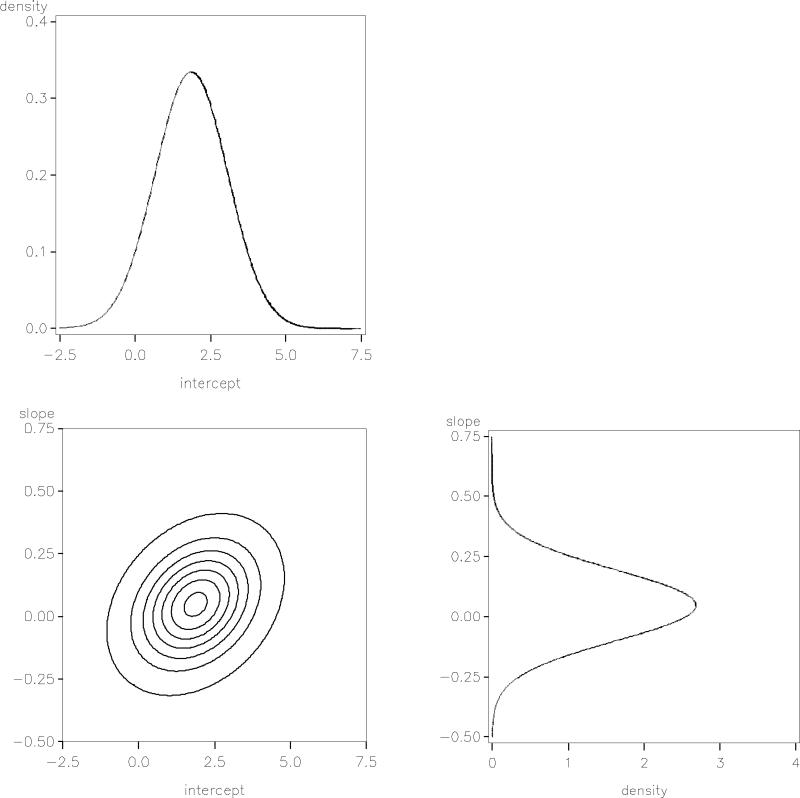
To understand these effects better, and to help contrast this model with those to follow, we provide two graphical representations of the results. Figure 1 aims to communicate the statistical assumptions of the model. The top panel shows the normal distribution assumed for the individual intercepts, whereas the right panel shows the normal distribution assumed for the individual slopes. The contour plot in the lower left shows the joint, bivariate normal distribution of the two trajectory parameters. Some readers may be unfamiliar with contour plots. Like a contour map, a contour plot provides a two-dimensional representation of a three-dimensional surface by using concentric rings to indicate ‘elevation’, that is, density of observations. The innermost rings of the plot represent pairings of intercept and slope values that are very common (this is where most of the dots would be in a scatterplot), whereas the outer rings represent pairings that are less common (in a scatterplot, there would be progressively fewer dots in rings further from the center). The ellipsoid shape of the contour plot reflects the assumption of bivariate normality, with the upward tilt of the ellipse reflecting the positive linear association between intercepts and slopes.

Figure 1.

Univariate and bivariate normal distributions for trajectory parameters implied by Approach 1 (bivariate distribution depicted via a contour plot)

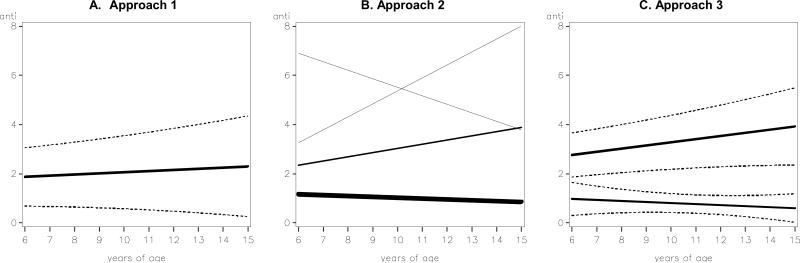
Whereas Figure 1 emphasizes the statistical assumptions of the model, Figure 2 more meaningfully depicts what these assumptions imply about individual differences in development. In Figure 2, the mean trajectory is depicted as a solid line and a SD above or below the mean is depicted by a dashed line (enclosing 68% of the individual trajectories at any given age). The dashed lines convey that the individual trajectories are assumed to be continuously and symmetrically distributed around the mean trajectory.

Figure 2.

Model-implied trajectories. A: Approach 1 (mean ±1 sd); B: Approach 2 (trajectory width proportional to class size); C: Approach 3 (mean ± 1 sd for each class).

To explain some of the observed differences in change over time, we next incorporated sex and cognitive and emotional support in the home as predictors of the intercepts and slopes of the individual trajectories. For brevity, we provide only a textual summary of the results here: boys and children who experienced less supportive early home environments displayed significantly higher levels of antisocial behavior at six years of age (the effects of sex and home environment on the intercept were significant). The rate of change in antisocial behavior from age six to fifteen was similar for boys and girls (the effect of sex on the slope was not significant), but steeper increases were observed for children experiencing less supportive early home environments (the effect of home environment on the slope was significant). Note that with this approach we are predicting differences in the degree of change, whereas the approach we consider next centers on different kinds of trajectories.

Approach 2: Differences in Kind

The second modeling approach we consider assumes that the individual trajectories can be summarized by a small number of group trajectories, often referred to as latent classes. Included in this approach are SPGM, latent class growth analysis, and latent class regression models (Nagin, 1999; Muthén, 2001; Vermunt & van Dijk, 2001).

For the development of antisocial behavior, we can motivate the idea of groups by drawing on Moffitt's (1993) theory. In Moffitt's taxonomy, the adolescent-limited pattern involves an increase in antisocial behavior during adolescence and then decline during the transition to young adulthood. In contrast, the life-course persistent pattern is characterized by childhood onset and high antisocial behavior throughout adolescence and into adulthood. Apart from these two groups, others might more or less abstain from antisocial behavior. These qualitative differences (i.e. differences between groups of individuals who share the same kind of trajectory) are represented statistically by latent trajectory classes. Each class is assumed to be homogeneous with respect to change, e.g., all individuals on the life-course persistent path must exhibit the same high levels of antisocial behavior over time.

Equation 1 continues to provide a model for the course of individual development in antisocial behavior. It is worth noting, however, that, the pattern of change need not always be the same for all groups (e.g., one group trajectory might be flat, requiring only the β_0i term, another might be linear as in Equation 1, and a third could be quadratic, requiring the addition of β_2iAge²). Unlike Approach 1, which assumed that the intercepts and slopes in Equation 1 were continuously and normally distributed across individuals, Approach 2 assumes that there is a small number of groups, within which all individuals share the same intercept and slope values. The distribution of the intercepts and slopes is then discrete (multinomial, to be exact), with G possible pairs of intercept and slope values for the G groups. In practice, the number of groups is determined by the analyst, usually by comparing the suitability of models fit with more or less latent classes. Whether the obtained groups really differ qualitatively, as is usually hypothesized, or not is a matter of interpretation. In some cases, the groups may simply mark points on a continuum, similar to splitting a continuous variable into four or five ordered-categorical levels.

To demonstrate this approach, we fit a sequence of models to the antisocial data varying the number of classes and allowing for both linear and quadratic patterns of change. Although the limited age range of our example data does not permit us to discriminate trajectories based on age of desistence, we expected that we might still observe groups differing in early levels of antisocial behavior (due to differential timing of onset), or rate of escalation of antisocial behavior over time. Based on comparing model fit statistics, parsimony, and substantive interpretability, we ultimately selected a four-group linear model as best for our data. As shown in Table 2, for each group (or class) we obtain an estimate of class size as well as an intercept and slope that summarize the trajectory of change in antisocial behavior for all of the individuals belonging to that group.

Table 2.

Results of Approach 2, assuming qualitatively different trajectory type.

	Latent Class
Parameter	“High Increasing”	“Low Increasing”	“High Declining”	“Low Stable”
Class Size
Proportion of Population	.08	.25	.04	.63
Sample N	70	222	39	562
Trajectory Parameters
Intercept	3.27 (0.92)**	2.35 (0.22)**	6.89 (1.98)**	1.17 (0.07)**
Slope (Age)	0.53 (0.20)**	0.17 (0.04)**	−0.34 (0.37)	−0.03 (0.01)*
Variance Parameters
Residual a	2.02 (0.10)**	2.02 (0.10)**	2.02 (0.10)**	2.02 (0.10)**

Note. Robust standard errors reported in parentheses.

^*p < .05

^**p < .01

^aConstrained to be equal across classes

Two groups are characterized by increasing antisocial behavior over time: one (8% of the population) is characterized by high initial antisocial behavior and rapid increases with age (high increasing), and the other (25%) has lower initial antisocial behavior and increases at a slower rate with age (low increasing). The third group (4%) has the highest initial levels of antisocial behavior which then rapidly decrease over time (high declining). The standard error for the slope is, however, also quite large (owing in part to the small size of this group), such that the decline is not statistically significant. Finally, the fourth and largest group (63%) exhibits little antisocial behavior at any age (low stable).

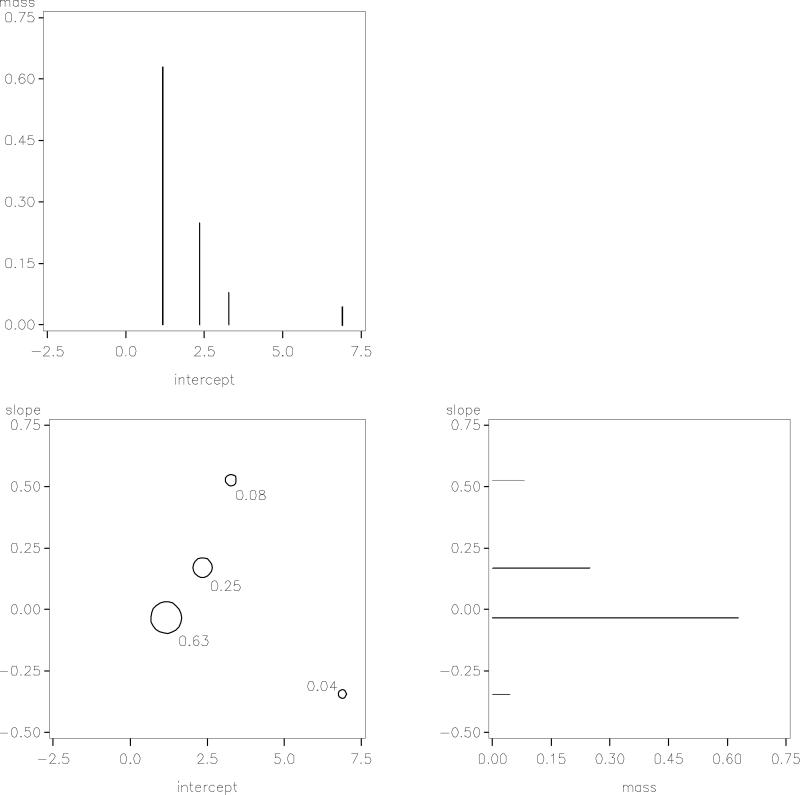
These results are presented graphically in Figure 3 to facilitate the contrast with Approach 1. As in Figure 1, the top and right panels of Figure 3 depict the distributions of the intercepts and slopes. Note that Approach 2 assumes these distributions to be discrete, so that each is composed of four point masses (the vertical or horizontal bars) indicating the relative frequency of each group. Across the four groups, the intercept distribution is skewed, with most cases observed in classes with low initial levels of antisocial behavior, whereas the slope distribution is more symmetric. The bivariate distribution of intercepts and slopes is represented via a bubble plot in the lower left panel of Figure 3. This plot is similar to a scatterplot but where the point size (or bubble) is proportional to the percent of individuals in the population belonging to the class. The positive association between intercepts and slopes observed with Approach 1 is reflected in the bubble plot by Classes 1, 2 and 4, but Class 3 is somewhat distinctive, displaying a high but declining trajectory. This unexpected “early desistance” trajectory was not represented in the results obtained from Approach 1, probably because it characterizes very few individuals (4% of the population). The differences between the two approaches are also made clear in Figure 2. Whereas Approach 1 depicts individual differences in change over time as a continuum (Panel A), Approach 2 depicts these differences by a small set of group trajectories (Panel B).

Figure 3.

Univariate and bivariate discrete distributions for trajectory parameters implied by Approach 2 (4 classes; bivariate distribution depicted via a bubble plot with bubble size proportional to class size; the proportion of the population within the class is indicated adjacent to the bubble).

We next added predictors to the model. Whereas in Approach 1 we were concerned with predicting quantitative variation in intercepts and slopes, with Approach 2 we are instead concerned with predicting group membership, that is, who has which trajectory. The inclusion of predictors thus produces odds ratios of belonging to each group relative to a reference group, here chosen to be the normative “low stable” class. Summarizing the results, the odds of belonging to the low stable group as opposed to any of the other three groups are higher for girls and children of experiencing supportive early home environments.

Approach 3: Differences of degree and kind

The third modeling approach we consider includes GGMM, structural equation mixture models (SEMM), and linear mixed models with heterogeneous random effects (Muthén, 2001, Verbeke & LeSaffre, 1996). Like Approach 2, this model allows for latent groups that follow qualitatively distinct trajectories. However, individuals within a latent class are not assumed to follow precisely the same trajectory. Instead, similar to Approach 1, individual intercepts and slopes are assumed to be continuously and normally distributed within groups. This approach therefore allows for both qualitative differences between groups of individuals who belong to different trajectory classes, and quantitative differences between individuals who belong to the same trajectory group. Thus with Approach 3 we have average trajectory parameters for each group as well as variance parameters characterizing within group variability.

With respect to the antisocial data, we can again draw on Moffitt's theory to motivate Approach 3. The average change patterns of the latent classes would reflect the proposed trajectory types (life-course persistent, adolescent-limited, abstainers). Additionally, within each groups individuals might differ quantitatively. For instance, within the adolescent limited group, some individuals might increase in antisocial behavior more quickly (and to higher levels) than others.

For the antisocial data, the best fitting version of this model included two groups, each characterized by the linear change model given in Equation 1, but with different mean trajectories and different variances for the intercepts, slopes, and within-person residuals, as presented in Table 3. One group (50% of the population) has higher initial levels of antisocial behavior and increases in antisocial behavior over time. In this “Increasing” group there is significant individual variability in initial levels of antisocial behavior but not in rates of change. The average level of antisocial behavior at age 6 in the second group (50%) is lower and this group slightly decreases over time. This “Decreasing” group is characterized by significant individual variability in both initial levels of antisocial behavior and in rates of change. The results are roughly consistent with Moffitt's theory, under the argument that the available age range is insufficient to distinguish between the adolescent-limited and life-course persistent types.

Table 3.

Results of Approach 3, assuming both qualitatively different trajectory types and quantitative variation within each type.

	Latent Class
Parameter	“Increasing”	“Decreasing”
Class Size
Proportion of Population	.50	.50
Sample N	445	449
Average Trajectory Parameters
Intercept	2.77 (0.13)**	0.98 (0.09)**
Slope (Age)	0.13 (0.03)**	−0.04 (0.02)**
Variance / Covariance Parameters
Intercept	0.83 (0.42)*	0.43 (0.10)**
Slope (Age)	0.02 (0.02)	0.01 (0.004)*
Covariance	0.01 (0.07)	−0.06 (0.02)**
Residual	3.55 (0.32)**	0.62 (0.07)**

Note. Robust standard errors reported in parentheses.

^*p < .05

^**p < .01

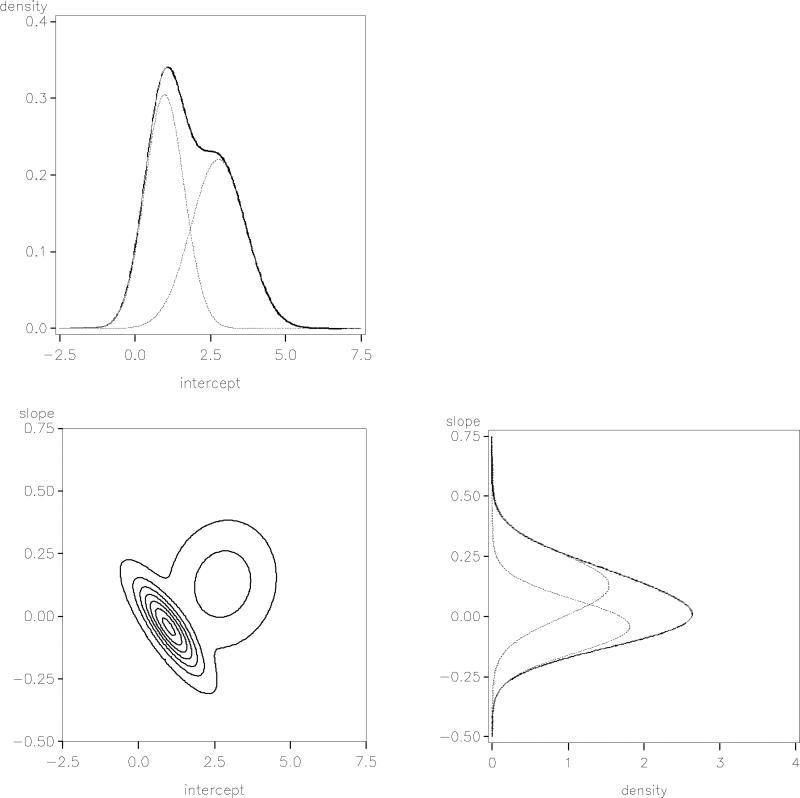
To facilitate comparison across the approaches, we again provide two graphical representations of these results. Figure 4 communicates the statistical assumptions of Approach 3, for comparison to Figures 1 and 3 for Approaches 1 and 2, respectively. The top and right panels of Figure 4 show that the overall intercept and slope distributions are the summation of the two normal distributions for the two latent groups. As with Approach 2 (Figure 3), it is the intercept distribution that is seen to be most skewed. The bivariate distribution, shown by a contour plot similar to Figure 1, shows a strong negative correlation between intercepts and slopes in the decreasing group (r = -.83) but relative lack of relationship between intercepts and slopes in the increasing group (r = .10). Pooling across the two groups, the association is positive, consistent with the results of the other approaches. The high declining group from Approach 2 is not, however, observed with Approach 3 (nor was it observed with Approach 1). Note also the variability within group: Within the “decreasing” group there are actually some individuals with increasing trajectories, whereas the opposite is true for the “increasing” group. In contrast, Approach 2 assumed that there was no individual variability within groups.

Figure 4.

Univariate and bivariate normal mixture distributions for trajectory parameters implied by Approach 3 (2 classes; bivariate distribution depicted via a contour plot)

Panel C of Figure 2 translates these distributions into a depiction of the individual trajectories implied by Approach 3. The mean trajectories of the two groups are plotted with solid lines, whereas within-group variability is represented by the dashed lines. Similar to the plot for Approach 1 (Panel A), the dashed lines in Panel C represent one standard deviation above and below the mean for the group and hence include 68% of the individual trajectories within the group at any given point in time. In comparison to Panels A and B, Panel C clearly illustrates the hybrid nature of Approach 3 as it depicts both multiple trajectory classes as well as individual variability within those classes.

The inclusion of predictors within Approach 3 also reflects the hybrid structure of this approach. As in Approach 2, we may predict which group an individual belongs to, or between-group qualitative differences. In addition however, we may also want to predict the differences within each group, or within-group quantitative variability. Simultaneously interpreting these between- and within-group effects can be challenging. For instance, we find that males are significantly more likely to belong to the increasing group. Additionally, within the increasing group being male is associated with higher initial levels of antisocial behavior, whereas within the decreasing group being male is associated with both higher initial levels and more rapid declines in antisocial behavior. Experiencing a supportive home environment early in development increases the odds of belonging to the declining group, but does not significantly explain within-group differences in either group.

Choosing an Approach

It is reassuring that, in broad strokes, the results we obtained from each approach were similar. Each approach reaffirmed that being male and experiencing low levels of cognitive and emotional support early in development are risk factors for increased levels of antisocial behavior between age six and fifteen years of age. But the interpretation of these results is quite different depending on the approach taken to the analysis. In Approach 1, these are predictions about graded differences among individuals, whereas with Approach 2 one is instead differentiating groups in a developmental taxonomy. Approach 3 blends the two conceptions. Hence choosing a modeling approach can greatly influence how one presents and interprets the results.

At this point, we might be expected to repeat the oft-used phrase that researchers should select the statistical model that most closely matches their theoretical model of individual development. On this recommendation, one would make a theory-based argument for why individuals are most likely to differ quantitatively, qualitatively, or both, and thereby choose a modeling approach. Although such a conclusion would be clear and unambiguous, it would also be overly simplistic. The waters are a bit muddier.

First, mapping between theory and method with these models is not always as clear cut as we have heretofore suggested. Approach 1, which we characterized as providing for quantitative differences, can in fact also capture qualitative differences between population subgroups, so long as these subgroups are adequately differentiated by predictors (Curran, Bauer & Willoughby, 2004). Thus, even if one expects heterogeneity in developmental pathways for subgroups of the population, Approach 1 may still prove useful if there is a strong theoretical model for the etiological origins of the subgroups. Similarly, even if one believes that individual differences in growth are continuous, Approaches 2 and 3 may still be reasonable choices for the data. Approach 2 can be used to yield ordered points along the continuum, whereas Approach 3 flexibly models the continuous distribution of individual trajectory parameters using a mixture of normal distributions. Either approach might be useful for situations in which the individual trajectories are unlikely to be normally distributed, as is conventionally assumed with Approach 1. Thus, although Approaches 2 and 3 are usually motivated from the idea that qualitative groups exist, they can also be used even when individual differences are strictly quantitative in nature. Methodologists disagree about the merits of Approaches 2 and 3 in this situation; Bauer (2007) argues in favor of Approach 1 because it is provides robust and stable inferences at the sample sizes characteristic of most psychological research, whereas Nagin (2005) offers an opposing view.

A second, greater difficulty arises when theory is ambiguous concerning the nature of individual differences in development. Indeed, in this situation, the very objective of the analysis may be to determine whether variation is quantitative or qualitative. The selection and use of a single modeling approach could then lead to a confirmation bias for the preferred hypothesis (e.g., I hypothesize there are groups characterized by different trajectories, I apply Approach 2 which assumes just this, and, lo, my results “confirm” that there are groups). A better strategy is to fit each type of model to the data and compare the results in terms of statistical fit and substantive interpretability. Unfortunately, it can be rather difficult to empirically adjudicate between the three approaches based on statistical fit alone (Bauer, 2007). For example, the analyses presented here cannot resolve the question of whether individual differences in the development of antisocial behavior are quantitative or qualitative in nature. Judged by statistical fit (e.g., Bayes’ Information Criterion), Approach 3 carries the day. Yet comparisons of statistical fit reflect not only the assumptions that were varied across models, but also those that were not. For instance, all of our analyses assumed that the residuals were normally distributed, an assumption that is almost certainly incorrect given our crude measure of antisocial behavior. Elsewhere, we have argued that measures with floor or ceiling effects can give the appearance of latent groups (in terms of superior statistical fit) even when variation is strictly quantitative in nature (Bauer, 2007). Approach 3 might not have fit best if we had used an alternative distribution for the residuals, or applied a normalizing transformation to the dependent variable prior to the analysis. Ultimately, determining whether variation in development is quantitative or qualitative (or both) is quite difficult and requires programmatic construct validation research (Bauer & Curran, 2003a, 2003b; Muthén, 2003).

Notwithstanding these complications, it is important to recognize that longitudinal data analysis has undergone a hugely beneficial transformation over the past several decades. Researchers no longer need accept statistical models that fail to reflect the richness of their developmental theories; they can chose among several new alternative models, each offering compelling advantages relative to past practice. It is our hope that readers will be encouraged by this paper to explore the broader literature on these models, thoughtfully consider the differences between them, and judiciously apply them in their own work.