Dose Escalation with Overdose Control using a Quasi-Continuous Toxicity Score in Cancer Phase I Clinical Trials

SUMMARY

Escalation with overdose control (EWOC) is a Bayesian adaptive design for selecting dose levels in cancer Phase I clinical trials while controlling the posterior probability of exceeding the maximum tolerated dose (MTD). EWOC has been used by clinicians to design many cancer Phase I clinical trials, see e.g [1-4]. However, this design treats the toxicity response as a binary indicator of dose limiting toxicity (DLT) and does not account for the number and specific grades of toxicities experienced by patients during the trial. Chen et al. (2010) proposed a novel toxicity score system to fully utilize all toxicity information using a normalized equivalent toxicity score (NETS). In this paper, we propose to incorporate NETS into EWOC using a quasi-Bernoulli likelihood approach to design cancer Phase I clinical trials. We call the design escalation with overdose control using normalized equivalent toxicity score (EWOC-NETS). Simulation results show that this design has good operating characteristics and improves the accuracy of MTD, trial efficiency, therapeutic effect, and overdose control relative to EWOC which is used as a representative of designs treating toxicity response as a binary indicator of DLT. We illustrate the performance of this design using real trial data in identifying the Phase II dose.

1. INTRODUCTION

Phase I cancer clinical trials are one of the most important steps in drug development. In these trials, patients are accrued sequentially and treated with a new agent or combination of existing agents. Dose escalation or de-escalation depends on the DLT status of previously treated patients after one cycle of therapy. For cytotoxic agents, it is known that as the dose of the drug increases, its therapeutic effects usually improve, but often at the cost of increased toxicity. Therapeutic effects are usually not assessed within one cycle of therapy. Consequently, the major goal of a cancer Phase I trial is to determine the MTD of a new drug that is associated with an acceptable level of DLT [5].

The majority of cancer Phase I trials treat DLT as a binary indicator of toxicity. Typically, DLT is defined as grade 3 or 4 non-hematologic and grade 4 hematologic toxicity, see the National Cancer Institute (NCI) common toxicity criteria [6] for the definition of the different grades of toxicity. Patients in these trials can experience different types and grades of toxicities varying from 0 for no toxicity to 5 for death but such information is disregarded when the DLT status is treated as a binary indicator of toxicity. For instance, a patient experiencing multiple grade 2 toxicities would be classified the same as a patient exhibiting a single grade 2 toxicity or a patient exhibiting one or more grade 1 toxicities. Such an approach may be inefficient when controlling the safety of the trial and estimating the MTD. Ideally, one would use all grades of toxicities experienced by the patients when allocating doses to future patients. The goal of this paper is to extend a Bayesian adaptive design known as EWOC [7-9] by accounting for all grades and types of toxicities experienced by the patients during the trial in order to determine the MTD. A normalized equivalent toxicity score system which was developed by Chen et al. [10] will be used to summarize the information from all toxicities experienced by the patients and to estimate dose allocation and the MTD at the end of the trial. The resulting design is termed EWOC-NETS.

The methodology uses the EWOC algorithm where the indicator of DLT is replaced by a quasi-continuous toxicity score in the Bernoulli likelihood function, which results in a quasi-likelihood function, see for example [11, 12]. After specifying a proper prior distribution for the MTD, we estimate the Phase II dose using the median of the quasi-posterior distribution of the MTD. A similar approach has been implemented in the continuous reassessment method (CRM) by Yuan et al. [13] where the toxicity grades were transformed into a numerical score according to hypothetical severity weights elicited by clinicians. This gives us a simple solution to estimate the MTD by taking into account all grades of toxicities exhibited by all patients. A full likelihood approach can be considered where the corresponding quasi-continuous toxicity score is modeled as a parametric or non-parametric distribution.

The manuscript is organized as follows. In Section 2, we give a brief review of EWOC and the definition of NETS and describe the design EWOC-NETS. Performance of this design including its operating characteristics and comparison with EWOC will be presented in Section 3. The performance of EWOC-NETS compared with that of EWOC is further evaluated with data from a real Phase I clinical trial in Section 4. The article ends with discussion and some concluding remarks.

2. EWOC-NETS DESIGN

In this section, we review EWOC, a Bayesian adaptive design for dose finding based on a binary indicator of DLT; and a normalized equivalent toxicity score NETS system introduced by Chen et al. [10] for designing cancer Phase I trials by taking into account all grades of toxicities experienced by the patients in the trial. Then, we describe EWOC-NETS, a new design for dose finding based on EWOC adapted to a quasi-continuous toxicity score NETS.

2.1. EWOC

Denote by x the dose of the drug in the trial and y the binary indicator of DLT, y = 1 if a patient exhibits DLT and y = 0 otherwise. The MTD γ is defined as the dose that is expected to produce DLT in a specified proportion θ of patients:

$$P(y=1\mid x=\gamma )=\theta .$$ (1)

A logistic based dose-toxicity model is assumed for modeling the relationship between dose and probability of DLT,

$$P(y=1\mid x)=\frac{\exp ({\beta }_0+{\beta }_{1}x)}{1+\exp ({\beta }_0+{\beta }_{1}x)},$$ (2)

where we assume that β₁ > 0 so that the probability of DLT is an increasing function of dose. The parameters β₀ and β₁ in the dose-toxicity relationship model have no clear clinical meaning. Therefore the logistic dose-toxicity relationship model is re-parameterized using the parameters of clinical meanings such as: MTD (γ), probability of DLT (ρ₀) at the starting dose (X_min), and the target toxicity level TTL (θ) as below:

$$\mathrm{logit}({\rho }_0)={\beta }_0+{\beta }_1{X}_{\min },$$ (3)

$$\mathrm{logit}(\theta )={\beta }_0+{\beta }_1\gamma .$$ (4)

From the equations 3 and 4, we can express the unknown terms of β₀ and β₁ in terms of ρ₀, γ, and θ as below:

$${\beta }_0=\frac{1}{\gamma -X_{\min }}[\gamma \mathrm{logit}({\rho }_0)-X_{\min }\mathrm{logit}(\theta )],$$ (5)

$${\beta }_1=\frac{1}{\gamma -X_{\min }}[\mathrm{logit}(\theta )-\mathrm{logit}({\rho }_0)].$$ (6)

These parameters can be easily interpreted by clinicians and investigators because γ is the parameter of interest (MTD), θ is the pre-specified highest acceptable toxicity level, and a meaningful informative prior for ρ₀ can be selected based on some preliminary studies conducted at or near the starting dose. Other model reparameterizations are possible. For instance, one can reparameterize the model in terms of the MTD γ and the dose effect β₁ since this parameter controls the steepness of the curve. The prior distributions of γ and ρ₀ are taken to be independent. The priori information about γ and ρ₀ from preclinical data or similar Phase I trials can be easily implemented in the model.

Dose levels are selected between X_min and X_max, the minimum and maximum doses anticipated in the trial. Let D_k = {(x_i,y_i), i=1,…,k} be the data after enrolling k patients in the trial, h(ρ₀, γ) be a prior distribution for ρ₀ and γ on [0,θ]×[X_min, X_max], and Π_k(x) the posterior cdf of the MTD γ given the data D_k. Dose allocation proceeds as follows. The first patient in the trial receives the dose x₁ = X_min and if y₁ = 0, then the kth patient receives the dose $x_k={\prod }_{k-1}^{-1}(\alpha )$ so that the posterior probability of exceeding the MTD is equal to the feasibility bound α. Convergence properties, design operating characteristics, comparison of EWOC with other Phase I designs, and examples of Phase I trials using EWOC can be found in [1-4, 7-9, 14-17].

2.2. NETS

The adjusted grade of the j^th toxicity G_i,j, j=1,…,J_i of the i^th patient is defined as 0 for grade 0 toxicity, 1 for grade 1 toxicity, 2 for grade 2 toxicity, 3 for grade 3 non DLT, 4 for grade 4 non DLT, 5 for grade 3 DLT, and 6 for grade 4 DLT, see Chen et al. [10]. Let G_i,max=max(G_i,j, j=1,…,J_i). The NETS, S_i, for patient i is defined to be 0 if patient i has no toxicity, equals to 1/60 if patient i has only one grade 1 toxicity, or

$$S_i=\frac{1}{6}\left[G_{i,\max }-1+\frac{\exp \left\{-2+\beta \left(\sum _{j=1}^{J_i}\frac{w_{i,j}{G}_{i,j}}{G_{i,\max }}-1\right)\right\}}{1+\exp \left\{-2+\beta \left(\sum _{j=1}^{J_i}\frac{w_{i,j}{G}_{i,j}}{G_{i,\max }}-1\right)\right\}}\right],$$ (7)

otherwise. In the above definition, the index i means the i^th patient, index j is the j^th toxicity of all J_i toxicities of the i^th patient. G_i,max is the worst toxicity with the highest adjusted grade among all the toxicities of the i^th patient. The NETS varies between 0 and 1 with logit equal to a weighted average of all toxicities experienced by patient i. The parameter w_i,j represents the weight for the correlation of the j^th toxicity with other toxicities for the i^th patient. Chen et al. [10] discuss the choice of the slope parameter β and weight w_i,j extensively and recommend using β values between 0.1 and 0.5. It can be easily seen that if l is the maximum adjusted grade of the worst toxicity exhibited by patient i, l =2,…,6, then the NETS S_i ∈ [(l-1)/6, l/6). Table 1 lists the range of S_i according to the worst toxicity grade experienced by a patient. When l = 0 or 1, the corresponding range listed in Table 1 follows from the above definition of S_i.

Table 1.

Mid-range of NETS and Probability of Most Severe Toxicity under Five Scenarios

Most severe toxicity	Maximum adjusted grade	Range of NETS	Mid-range NETS	The target toxicity profile for MTD in different scenarios
				Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5
Grade 0	0	0	0	0.070	0.07	0.07	0.67	0
Grade 1	1	[1/60 – 1/6)	0.092	0.150	0.24	0.06	0	0
Grade 2	2	[1/6 – 1/3)	0.25	0.150	0.18	0.12	0	0
Grade 3 non DLT	3	[1/3 – 1/2)	0.417	0.150	0.12	0.18	0	0
Grade 4 non DLT	4	[1/2 – 2/3)	0.583	0.150	0.06	0.24	0	0.67
Grade 3 DLT	5	[2/3 – 5/6)	0.75	0.165	0.22	0.11	0.33	0
Grade 4 DLT	6	[5/6 – 1)	0.917	0.165	0.11	0.22	0	0.33
TNETS for each scenario				0.476	0.410	0.526	0.25	0.69

Analogous to the definition of the MTD in (1) for a binary indicator of DLT, we define the MTD γ as the dose which corresponds to a prespecified target normalized equivalent toxicity score (TNETS). Determination of TNETS depends on the target toxicity profile which relies heavily on clinician’s input. Clinicians will be asked 4 specific questions (see the Section 3 of Chen et al. [10]) in order to define a target toxicity profile. The target toxicity profile consists of proportion of patients exhibiting DLT when treated at the MTD and the target probability that adjusted grade l toxicity is expected to be the worst toxicity when a patient is treated at the MTD, l = 0, 1,…,6. For example, Chen et al. [10] propose eliciting the expected probability of the worst adjusted grade l (or maximum adjusted grade) toxicity when a patient is treated at the MTD, l=0,1,…,6. For purpose of the simulation studies, a total of 5 different scenarios are created and summarized in Table 2. The last five columns of Table 1 list the target toxicity profiles of the 5 created scenarios in Table 2 for these probabilities when the expected proportion of patients exhibiting grade 3 or 4 DLT is 33%. The target normalized equivalent toxicity score is defined as

$$\stackrel{\sim }{\theta }=\sum _{l=0}^6{m}_l{p}_l$$ (8)

where m_l is the mid-range of NETS and p_l is the target probability corresponding to the maximum adjusted grade l toxicity. Using the choices of the target probabilities from Table 1, the corresponding TNET score is θ̃ = 0.476 for scenario 1, θ̃ = 0.410 for scenario 2, θ̃ = 0.526 for scenario 3, θ̃ = 0.25 for scenario 4, and θ̃ = 0.69 for scenario 5.

Table 2.

Probability that Adjusted Grade l Toxicity Is the Worst When a Patient Is Treated at a Given Dose Level

	The “worst” toxicity / Maximum adjusted grade		Dose level
			1	2	3	4	5	6
Scenario 1	0	0	0.11	0.09	0.07	0.05	0.03	0.01
	1	1	0.2	0.16	0.15	0.12	0.1	0.05
	2	2	0.2	0.17	0.15	0.13	0.1	0.06
	3 non DLT	3	0.2	0.17	0.15	0.13	0.1	0.06
	4 non DLT	4	0.21	0.17	0.15	0.13	0.11	0.06
	3 DLT	5	0.04	0.12	0.165	0.22	0.28	0.38
	4 DLT	6	0.04	0.12	0.165	0.22	0.28	0.38
	Probability of DLTs for the dose		0.08	0.24	0.33	0.44	0.56	0.76
	NETS for the dose		0.341	0.427	0.476	0.54	0.607	0.713
Scenario 2	0	0	0.11	0.09	0.07	0.05	0.03	0.01
	1	1	0.324	0.268	0.24	0.204	0.164	0.092
	2	2	0.243	0.201	0.18	0.153	0.123	0.069
	3 non DLT	3	0.162	0.134	0.12	0.102	0.082	0.046
	4 non DLT	4	0.081	0.067	0.06	0.051	0.041	0.023
	3 DLT	5	0.06	0.16	0.22	0.3	0.37	0.51
	4 DLT	6	0.02	0.08	0.11	0.14	0.19	0.25
	Probability of DLTs for the dose		0.08	0.24	0.33	0.44	0.56	0.76
	NETS for the dose		0.269	0.363	0.41	0.483	0.556	0.67
Scenario 3	0	0	0.11	0.09	0.07	0.05	0.03	0.01
	1	1	0.081	0.067	0.06	0.051	0.041	0.023
	2	2	0.162	0.134	0.12	0.102	0.082	0.046
	3 non DLT	3	0.243	0.201	0.18	0.153	0.123	0.069
	4 non DLT	4	0.324	0.268	0.24	0.204	0.164	0.092
	3 DLT	5	0.02	0.08	0.11	0.14	0.19	0.25
	4 DLT	6	0.06	0.16	0.22	0.3	0.37	0.51
	Probability of DLTs for the dose		0.08	0.24	0.33	0.44	0.56	0.76
	NETS for the dose		0.408	0.486	0.526	0.593	0.653	0.751
Scenario 4	0	0	0.92	0.76	0.67	0.56	0.446	0.24
	1	1	0	0	0	0	0	0
	2	2	0	0	0	0	0	0
	3 non DLT	3	0	0	0	0	0	0
	4 non DLT	4	0	0	0	0	0	0
	3 DLT	5	0.8	0.24	0.33	0.44	0.56	0.76
	4 DLT	6	0	0	0	0	0	0
	Probability of DLTs for the dose		0.08	0.24	0.33	0.44	0.56	0.76
	NETS for the dose		0.06	0.18	0.25	0.33	0.42	0.57
Scenario 5	0	0	0	0	0	0	0	0
	1	1	0	0	0	0	0	0
	2	2	0	0	0	0	0	0
	3 non DLT	3	0	0	0	0	0	0
	4 non DLT	4	0.92	0.76	0.67	0.56	0.446	0.24
	3 DLT	5	0	0	0	0	0	0
	4 DLT	6	0.8	0.24	0.33	0.44	0.56	0.76
	Probability of DLTs for the dose		0.08	0.24	0.33	0.44	0.56	0.76
	NETS for the dose		0.61	0.66	0.69	0.73	0.77	0.84

2.3. EWOC-NETS

Following the framework of EWOC described in Section 2.1, we develop EWOC-NETS by taking into account all toxicity information for each patient by measuring quantitatively the severity of a patient’s toxicity response with a NETS and using it in a “quasi likelihood” function instead of a binary indicator of DLT (0 vs 1) to update the posterior distribution function of MTD γ. The MTD γ is defined as a dose corresponding to a pre-specified target normalized equivalent toxicity score (TNETS), θ̃ as follows:

$$\mathit{TNETS}=\mathit{NETS}{\mid }_{\mathit{Dose}=\gamma }=\stackrel{\sim }{\theta }.$$ (9)

Figure 1 shows the relationship between NETS and dose and TNETS and γ. We model the relationship between dose and NETS as:

$$S_i=F({\beta }_0+{\beta }_1{x}_i)$$ (10)

where F is a specified distribution function, called a tolerance distribution. We further assume that β₁ > 0 so that the NETS is a monotonic increasing function of dose and that F is a logistic function. Monotonicity is assumed for the relationship between dose and overall toxicity response which is composed of the risk of the most severe toxicity and number of toxicities effect as indicated in (7) to calculate NETS for each patient. As in Section 2.1, we reparameterize the model in terms of γ and ρ₀, parameters clinicians can easily interpret. As shown in Figure 1, a parametric function, such as logistic, is used to model the monotonically increasing relationship between the dose and its corresponding overall toxicity severity in term of NETS score instead of probability of DLT. In a Phase I trial, a certain dose range from X_min to X_max will be tested to estimate a MTD in consideration of safety and efficiency. The ρ₀ is a measurement of toxicity level in term of NETS when patients are treated at the starting dose X_min and γ is the estimated MTD corresponding to a target highest acceptable toxicity severity level in term of NETS, θ̃. The reparameterization of EWOC-NETS is similar to that of EWOC in Section 2.1. Using the new definition of the MTD in (9) and the new model reparameterization, one can show that

$$\mathrm{logit}(S_{x_i}\mid \mathit{Dose}=x_i)=\frac{\mathrm{logit}({\mathrm{\rho }}_0)(\mathrm{\gamma }-x_i)+\mathrm{logit}(\stackrel{\sim }{\mathrm{\theta }})(x_i-X_{\min })}{\mathrm{\gamma }-X_{\min }}$$ (11)

Figure 1.

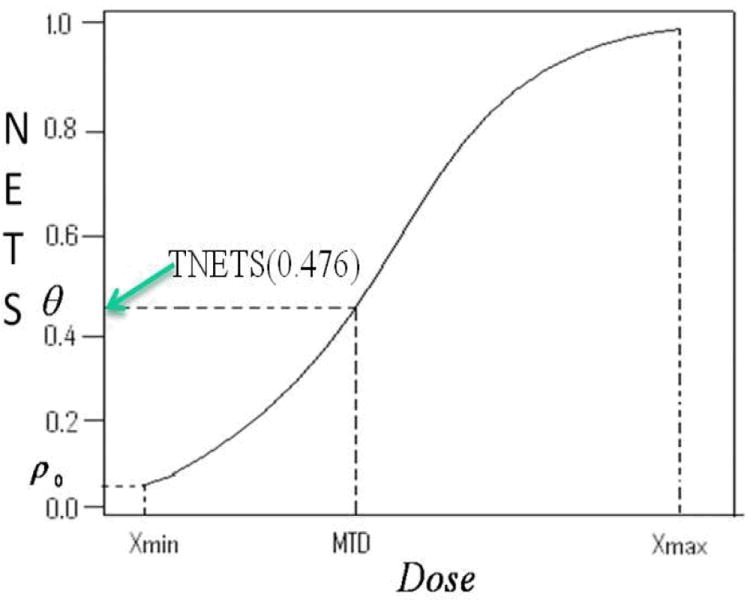
The Normalized Equivalent Toxicity Score (NETS) as a Function of Dose

2.3.1. Quasi-Bernoulli likelihood

NETS can be viewed as fractional events. The quasi-Bernoulli likelihood constructed using a family of “quasi” probability distributions without true distributions can provide a simple way to incorporate NETS into parametric models. When the “quasi” distributions belong to the linear exponential families such as the binomial family, quasi maximum likelihood estimates (QMLEs) obtained by maximizing the quasi-Bernoulli likelihood function are strongly consistent [11, 12]. A quasi-likelihood approach has been used in Bayesian generalized linear models [18] and another example of using Quasi-Bernoulli likelihood in CRM was reported by Yuan and Chappell [13].

Let D_k ={(x_i, S_i), i = 1, 2, …, k} be the data after observing of k patients, where x_i is the dose administered to the i^th patient and S_i is the NETS calculated using the definition in (7). The quasi-Bernoulli likelihood of (ρ₀, γ) given D_k is

$$\begin{array}{ll}\stackrel{\sim }{L}({\rho }_0,\gamma \mid D_k)=& \prod _{i=1}^k{\left(\exp \left\{\frac{\mathrm{logit}({\rho }_0)(\gamma -x_i)+\mathrm{logit}(\stackrel{\sim }{\theta })(x_i-X_{\min })}{\gamma -X_{\min }}\right\}\right)}^{S_i}\\ & \times {\left(1+\exp \left\{\frac{\mathrm{logit}({\rho }_0)(\gamma -x_i)+\mathrm{logit}(\stackrel{\sim }{\theta })(x_i-X_{\min })}{\gamma -X_{\min }}\right\}\right)}^{-1}.\end{array}$$ (12)

Here, S_i is the NETS of the i^th patient and is a quasi-continuous variable with a range from 0 to 1 instead of a binary variable in the regular Bernoulli likelihood. Therefore the above function L̃ is called a quasi-Bernoulli likelihood. Obviously, the true distribution in EWOC-NETS is not really Bernoulli. However, if the dose-toxicity model is correctly specified, the quasi-maximum likelihood estimate will be strongly consistent because the Bernoulli distribution belongs to the binomial family. The convergence of EWOC-NETS is similar to that of EWOC.

2.3.2. Markov Chain Monte Carlo (MCMC) for updating posterior distribution

Let h(ρ₀, γ) be a prior distribution on [0,θ]×[X_min, X_max]. The quasi-posterior distribution of (ρ₀, γ) given D_k is defined as

$$\stackrel{\sim }{\pi }({\mathrm{\rho }}_0,\mathrm{\gamma }\mid D_k)=\frac{\stackrel{\sim }{L}({\mathrm{\rho }}_0,\mathrm{\gamma }\mid D_k)h({\mathrm{\rho }}_0,\mathrm{\gamma })}{{\iint }_{[0,\theta ]\times [X_{\min },X_{\max }]}\stackrel{\sim }{L}({\mathrm{\rho }}_0,\mathrm{\gamma }\mid D_k)h({\mathrm{\rho }}_0,\mathrm{\gamma })d{\mathrm{\rho }}_{0}d\mathrm{\gamma }}.$$ (13)

Let Π̃_k(γ) be the marginal quasi-posterior cdf of γ given D_k. An MCMC sampler is devised to estimate features of the marginal quasi-posterior distribution of γ. This is based on the Metropolis–Hastings algorithm implemented in the same way as described in Tighiouart et al.[8]. The proposal distributions for the parameters ρ₀ and γ were taken to be the same as the corresponding prior distributions for these parameters. The first 1000 samples were discarded and an additional 4000 draws were used to estimate features of the posterior distribution of the MTD γ.

2.3.3. Trial Design

Dose levels in the trial are selected in the interval [X_min, X_max] as follows. The first patient receives the dose x₁ = X_min. If the patient exhibits DLT within one cycle of therapy, as defined by the clinician in the protocol, we recommend that the trial be stopped. Otherwise, the NETS S₁ for this patient is calculated using (7). Next, we calculate the quasi-posterior density of the MTD γ, π̃(γ ∣ (x₁, S₁). The second patient received the dose $x_2={\stackrel{\sim }{\mathrm{\Pi }}}_1^{-1}(\alpha )$ so that the posterior probability of exceeding the MTD is equal to the feasibility bound α. In general, the k^th patient receives the dose $x_k={\stackrel{\sim }{\mathrm{\Pi }}}_{k-1}^{-1}(\alpha )$. The number of patients in each cohort can be different and all patients in the same cohort will receive same dose. The trial proceeds until a pre-determined number of patients are enrolled to the trial or the same dose level has been recommended for the new cohorts for M (such as 4) times in a row. At the end of the trial, we estimate the MTD as the median of the posterior distribution of γ.

3. SIMULATION STUDIES

In order to evaluate the performance of EWOC-NETS, simulation studies are carried out comparing EWOC-NETS with EWOC under different scenarios. The primary comparison outcomes are the proportion of trials recommending a given dose level as the correct MTD, average trial sample size, therapeutic effect in term of percent of patients treated at true MTD, overdose control in terms of percent of patients overdosed and percent of patients with DLT.

3.1 Simulation Scenarios

We assume that there are 6 dose levels in the trial and a DLT is defined as Grade 3 DLT or Grade 4 DLT, corresponding to an adjusted grade of 5 or 6. We consider 5 scenarios for the target toxicity profiles, and in each case, the probability of DLT is 33%. These scenarios are included in Table 2 and differ in terms of the probability of the maximum adjusted grade l toxicity, l=0, 1,…, 6. Under the same profile of probabilities of DLT, the scenario 1 is assumed as an “ideal” scenario under which the probability being the “worst” toxicity for each kind of non-DLT toxicities is the same (ratio=1:1:1:1) and that for each kind of DLTs is the same too (ratio=1:1). The toxicity profiles of other 4 scenarios deviate from that of the scenario 1. Scenario 2 is kind of a medium under toxic scenario under which toxicity profile skews to low grade toxicity and each dose level is less toxic than the corresponding one in scenario 1. On the contrast, scenario 3 is kind of a medium over toxic scenario under which the toxicity profile skews to high grade toxicity and each dose level is more toxic than the corresponding one in scenario 1. Scenario 4 and 5 are the extreme cases of scenario 2 and 3, respectively. For example, scenario 2 assumes that the probability of DLT (defined as grade 3 DLT or grade 4 DLT) is 33% and the probability that the maximum adjusted grade toxicity is l = 3 when a patient is treated at dose level 2 is 0.134. Scenario 1 assumes equal probabilities of maximum adjusted grade 1, 2, 3, and 4 toxicities at dose level 3. Scenarios 2 and 3 introduce skewness in the probability of maximum adjusted grade toxicities at dose level 3. Scenario 4 is an extreme case where we assume that the probability mass is allocated to adjusted grade 0 at dose level 3 and the last scenario allocates this mass to the adjusted grade 4 toxicity. The toxicity profile of the “Dose level 3” column in Table 2 is the same as the target toxicity profile column in Table 1 for the same scenario. Therefore, the dose level 3 is true MTD in the simulations presented in Table 3.

Table 3.

Percent of Trials Recommending a Dose Level as the MTD and Average Trial Sample Size when Different TNETS in Table 1 Are Used for Its Corresponding Scenario Respectively.

Dose level	Percent of Trials Recommending Dose Level d as the MTD
	All scenarios (1 to 5)	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5
	EWOC*	EWOC-NETS**
All dose levels over toxic***		0	0	0	0	19
1	6	1	1	0	1	6
2	24	12	20	20	15	7
3	46	65	47	55	54	56
4	22	22	32	25	26	12
5	2	0	0	0	4	0
6	0	0	0	0	0	0
All dose levels under toxic****	0	0	0	0	0	0
Sample size Mean (SD)	25.8 (7.7)	22.7 (6.1)	24.6 (8.7)	23.1 (6.3)	24.6 (7.8)	47.4 (14.9)

^*EWOC is targeted with TTL ≤ 0.33.

^**EWOC-NETS is targeted with different TNETS for Scenario 1 (0.476), 2 (0.41), 3 (0.526), 4 (0.25), and 5 (0.69), respectively.

^***:All the 6 pre-specified dose levels are determined to be over toxic and the recommend MTD from simulation trial is a dose lower than the lowest pre-specified dose level (level 1).

^****: All the 6 pre-specified dose levels are determined to be under toxic and the recommend MTD from simulation trial is a dose higher than the highest pre-specified dose level (level 6).

EWOC is implemented as described in [9]. We carried out simulation studies to explore model operating characteristics under different scenarios for the toxicity profiles but keeping the probability of grade 3 or 4 DLT equal to 33%. There are two possible situations in the real practice with EWOC-NETS so that two different sets of simulation studies are conducted accordingly. The first one is that the scenario of toxicity profile may be different in the different trials so that the target toxicity profile for MTD and TNETS change accordingly because the TNETS defined by equation (8) depends on the anticipated probabilities of different grades of toxicities. Therefore, we conduct the first set of simulations in which the target TNETS differs across the 5 scenarios. Specifically, EWOC-NETS proceeds as described in Section 2.3.2 targeting NETS of 0.476, 0.410, 0.526, 0.25, and 0.69 for scenarios 1, 2, 3, 4, and 5, respectively. At each stage of the trial, the NETS responses are generated as follows. If patient i has been treated at dose level d_i, d_i = 1,…,6, randomly select the maximum adjusted grade l_i = 0,1,…,6 according to the true probabilities listed in Table 2. Next, generate the NETS S_i for patient i as a uniform random variable in the interval [(l_i-1)/6, l_i/6), see Table 1 for the range of NETS as a function of the maximum adjusted toxicity grade. The results of the first set simulations are summarized in the Table 3. In the second situation, we may want to determine the operating characteristics of the Phase I clinical trial designed with EWOC-NETS under different possible scenarios of toxicity profile. For this purpose, the target toxicity profile for MTD will be kept the same under different scenarios and the corresponding TNETS is constant across scenarios. Therefore, we also conduct the second set of simulation studies in which same target toxicity profile for MTD (TNETS=0.476) is used under all 5 different scenarios. The NETS responses are generated in the same way as the one in the first set of simulations. The results of the second set of simulations are summarized in Table 4.

Table 4.

Percent of Trials Recommending a Dose Level as the MTD and Average Trial Sample Size when the Same TNETS (0.476) is used in all Scenarios.

Dose level	Percent of Trials Recommending Dose Level d as the MTD
	All scenarios (1 to 5)	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5
	EWOC*	EWOC-NETS**
All 6 dose levels over toxic***	0	0	0	0	0	37
1	6	1	0	6	0	59
2	24	12	5	45	0	4
3	46	65	24	42	1	0
4	22	22	65	7	31	0
5	2	0	6	0	65	0
6	0	0	0	0	3	0
All 6 dose levels under toxic****	0	0	0	0	0	0
Sample size Mean (SD)	25.8 (7.7)	22.7 (6.1)	21.9 (4.8)	23.4 (6.9)	22.5 (6.6)	23.4 (5.7)

^*EWOC is targeted with TTL ≤ 0.33.

^**EWOC-NETS is targeted with same TNETS for all 5 scenarios.

^***:All the 6 pre-specified dose levels are determined to be over toxic and the recommend MTD from simulation trial is a dose lower than the lowest pre-specified dose level (level 1).

^****: All the 6 pre-specified dose levels are determined to be under toxic and the recommend MTD from simulation trial is a dose higher than the highest pre-specified dose level (level 6).

For each scenario, 1000 trial replicates are simulated. The feasibility bound, α, is set to start at 0.25 for both EWOC and EWOC-NETS with an increment unit of 0.05 after each new patient cohort is enrolled in the trial up to a maximum value of 0.5, see [15]. Three patients per cohort are used and the trial stops when the same dose has been recommended for 4 consecutive cohorts or a total of 20 cohorts have been enrolled. Since we are using discrete dose levels, the dose recommended by EWOC and EWOC-NET are rounded downward to the next available discrete dose. The simulation results about dose recommendation and safety of the trials using EWOC and EOWC-NETS under different scenarios are summarized in Table 5.

Table 5.

Dose Recommendation and Overdose Control of EWOC and EWOC-NETS under Different Scenarios.

Dose level	Percent (%) of patients treated at each dose level*
	EWOC	EWOC-NETS (Scenario)
	All scenarios (1 to 5)	1	2	3	4	5	2	3	4	5
	TTL**	Different TNETS***					Same TNETS*** (0.476)
	33%	0.476	0.41	0.526	0.25	0.69
1	0.1	0.8	1	0	0.5	31.7	0.1	4	0	59.4
2	17.5	10.6	16.1	16.3	11.1	12.7	4.2	50.4	0.3	30.1
3	41.9	61.5	49.4	56.4	50.4	46.1	34.7	31	6.8	10.5
4	35.7	27	32	26.4	35	9.5	54.8	13.6	42.8	0
5	4.8	0.1	1.5	0.9	3	0	6.2	1	47.7	0
6	0	0	0	0	0	0	0	0	2.4	0
% of DLT	31.9	32.3	32.2	31.6	32.0	23.5	35.5	28.9	44.8	15.3
% of >TNETS	NA	51.2	44.8	51.7	32.0	23.5	42.6	57.7	44.9	99.9

^*: The bold percentages with underline are the percentages of patients treated at the true MTD under different scenarios.

^**: TTL is the target toxicity level in term of probability of dose limiting toxicity.

^***: TNETS is the target normalized equivalent toxicity score when measuring toxicity response with a quasi- continuous score.

3.2 Simulation Results

Table 3 gives the percent of trials that recommend each dose level as being the MTD for each design under each scenario when different TNETS is used for EWOC-NETS in different scenario. The simulation results from the 5 different scenarios are the same for EWOC treating toxicity response as a binary indicator of DLT since the target DLT depends only on grade 3 or 4 DLT. In all 5 scenarios, EWOC-NETS has higher percent of MTD recommendation compared to EWOC, and the absolute difference in these proportions can be as high as 19%. This suggests that the design EWOC-NETS treating toxicity response as a quasi-continuous variable and fully utilizing all toxicities information improves substantially the accuracy of MTD estimation than EWOC treating toxicity response as a binary indicator of DLT under the entertained scenarios. The last row of Table 3 give the average sample size used in the trial for each design under the 5 scenarios. Except in scenario 5, EWOC-NETS uses slightly fewer patients than EWOC suggesting that EWOC-NETS can improve the efficiency of trial and reduce its length by fully utilizing all toxicity information. Scenario 5 is an extreme scenario because it is unlikely that the maximum adjusted grade toxicity can only be grade 4 non-DLT or grade 4 DLT when a patient is treated at all 6 dose levels.

Table 4 summarizes the corresponding simulation results when same TNETS (0.476) is used for EWOC-NETS in all 5 scenarios. With the same target toxicity profile and TNETS for MTD, the correct MTDs are dose level 3, 4, 2, 5, and 1 under the scenario 1, 2, 3, 4, and 5, respectively. EWOC-NETS can “recognize” the deviation of toxicity profile and correctly estimate dose level 4, 2, 5, and 1 as the MTD under the scenario 2, 3, 4, and 5, respectively. But EWOC fails to recommend the correct MTD when the toxicity profile deviates in scenarios 2 to 4 because it treat toxicity response as a binary indicator of DLT and only utilize the probability of DLT without further differentiating the detailed toxicity profile. Similarly, EWOC-NETS uses slightly fewer patients than EWOC in all 5 scenarios and further confirms that EWOC-NETS can improve the efficiency of trial and reduce its length most of the cases.

The percent of patients treated at each of the 6 dose levels, percent of patients with DLT, and percent of patients with NETS score above the TNETS of the trial under different scenarios are summarized in Table 5. EWOC-NETS always treats higher percent of patients at true MTD (46.1% ~61.5%) than EWOC (41.9%) under all different scenarios, suggesting that EWOC-NETS may provide better therapeutic effect for participated patients than EWOC. Under the 5 scenarios in which different TENTSs are used and the dose level 3 is the true MTD, EWOC-NETS treats lower sum percentages of patients at dose levels above the true MTD (dose levels 4, 5, and 6) than EWOC and the percent of patients with DLT is similar between EWOC-NETS and EWOC, except in scenario 5 which is an extreme case. There is no direct way to compare the overdose control of EWOC-NETS and EWOC under the scenarios (2, 3, 4, and 5) in which same TENTSs are used and different dose levels are the true MTD. For EWOC-NETS, the percent of patients with NETS score above the TNETS of trial vary from 23.5% to 99.9% under different scenarios depending on their exact true toxicity profiles.

From the above simulation results (Table 3, 4 and 5), we can see that EWOC-NETS using a quasi-continuous toxicity score can outperform EWOC in terms of MTD recommendation, trial efficiency, therapeutic effect, and overdose control characteristics.

4. ILLUSTRATION OF EWOC-NETS WITH REAL TRIAL DATA

In order to further evaluate the usefulness of EWOC-NETS in real Phase I clinical trials, we generated a total of 5000 pseudo-trials using EWOC-NETS and data from study A09712 in Table 6 of Chen et al. [10]. For the purpose of comparison, we also generated 5000 pseudo-trials using EWOC in a similar way with the data. The dose ranges from 0 to 350 mg/kg and a fixed total number of 9 pre-specified dose levels are tested. There were 41 eligible patients enrolled in the trial and the number of toxicities experienced by these patients varies from 0 to more than 20. The highest toxicity grade was Grade 3 DLT. A pseudo-trial was generated as follows. The first cohort of 3 patients is given dose level 1 and we randomly select 3 patients with replacement from the patients that were treated at dose level 1 in the A09712 trial and record their toxicities. Next, for each of the three patients, the NETS S_i is calculated using equation (7) with w_ij = 1 and the next dose is estimated using the α-th percentile of the quasi-posterior distribution of the MTD. The feasibility bound, α, is set to start as 0.25 for both EWOC and EWOC-NETS with an increment unit of 0.05 until 0.5 as in Section 3.1. In general, at each dose level recommended by the algorithm, the toxicity responses are generated by randomly selecting 3 patients for each patient cohort with replacement from the data of the real trial and the corresponding NETS are calculated. For EWOC, if one of the patients’ toxicities is Grade 3 DLT, then the binary indicator of response for that patient is 1. Otherwise, it is 0. The TNETS is 0.476 in all pseudo-trials using EWOC-NETS and the target probability of DLT is θ = 33% in all pseudo-trials using EWOC. The same stopping rules described in Section 3.1 are adopted here. Finally, we used different values for the slope parameter β (see equation (7)) when calculating NETS in order to explore the sensitivity of the estimated MTD.

The simulation results are summarized in Table 6. The original trial using the standard “3+3” recommended dose level 6 as the MTD, which is an under-toxic dose level when θ = 33% [10]. EWOC recommends dose level 7 as the MTD 50% of the time and dose level 8 as the MTD 35% of the time. On the other hand, between 90 and 98% of the trials using EWOC-NETS recommend dose level 8 as the MTD. The observed proportion of DLTs in the trial is 19%, far below the target probability of DLT of 33%. The original trial was designed using the “3+3” design and recommended dose level 6 as the MTD. This was clearly an underestimate of the MTD as was shown later in a Phase II trial, which was adjusted using dose level 8 for studying treatment efficacy. In fact, only 1 out of 6 patients exhibited Grade 3 DLT. The recommended dose levels by EWOC and EWOC-NETS are different since we targeted a TNETS based on the target toxicity profile of scenario 1. Based on the simulation results of Section 3.2, we conclude that the MTD is dose level 8.

Table 6.

Simulation Results Using Data from Study A09712^* with Different Values of β and w_ij=1 for all Toxicities.

Dose Level	Treatment	Total Dosage	Percent of Trials Recommending Dose Level d as the MTD
			EWOC (Binary)	EWOC-NETS
				β=0.1	β=0.25	β=0.5
1	1.7mg/kg/dose M-F*3w	25.5	0	0	0	0
2	1.7mg/kg/dose MWF*6w	30.6	0	0	0	0
3	1.7mg/kg/dose M-F*6w	51	0	0	0	0
4	1.9mg/kg/dose M-F*6w	57	4	0	0	0
5	3.4mg/kg/dose M-F*6w	102	0	0	0	0
6*	4.4mg/kg/dose M-F*6w	132	11	0	0	0
7	5.5mg/kg/dose M-F*6w	165	50	2	6	10
8**	7.1mg/kg/dose M-F*6w	213	35	98	94	90
9	9.2mg/kg/dose M-F*6w	276	0	0	3	0
Mean (SD)	Sample size		26.3 (7.9)	20.2 (5.0)	20.6 (6.6)	20.7 (6.2)

For EWOC, and EWOC-NETS: Trial stops when a same dose has been recommended to 4 consecutive patient cohorts.

^*: The original trial with standard 3+3 design with dose de-escalation recommended the dose level 6 as MTD and used 13 patient cohorts and a total of 41 eligible patients.

^**: The true MTD suggested by the following Phase II trial.

^#: The maximum possible total dosage is 350 mg/kg.

Table 6 also shows that EWOC-NETS is robust in terms of probability of recommending a dose level as the MTD as β varies. Chen et al. [10] discusses the choice of this parameter based on the results of extensive simulations and conclude that any value in the range of 0.1 to 0.5 should work well in real Phase I clinical trials.

The original trial with the “3+3” design uses large sample size (41) and number of cohorts (13) because it tests all dose levels up to dose level 9 and then down to its recommended MTD (dose level 6). EWOC-NETS uses a smaller sample size (about 21) and fewer cohorts on the average relative to EWOC (sample size = 26.3). We realize that it is hard to make a case here that EWOC-NETS is recommending the correct MTD relative to EWOC. However, the simulations results presented in Section 3.2 and Table 5 suggest that EWOC-NETS recommend the correct MTD more often than EWOC does.

5. DISCUSSION

The limitation of using binary toxicity has been studied by several publications. In 1992, Gordon et al. [19] first proposed a multi-grade toxicity scheme which uses all toxicity grades instead of dichotomizing the results as grades < 3 or ≥ 3 and produces more powerful analyses. In 2000, Wang et al. [20] differentiated grade 3 and 4 toxicities in an extended CRM by giving more impact to grade 4 toxicities, thus reducing the chance of selecting the higher dose level as MTD. Yuan et al. [13] made a significant improvement by using the actual grade of the worst toxicity of each patient instead of a binary toxicity response (DLT). Unfortunately, their method did not consider the fact that patients usually have multiple toxicities and did not fully utilize all toxicities of each patient, which motivated us to propose NETS to overcome their limitation. Our NETS system can take into account all toxicities of each patient and fully utilize them, resulting in substantial improvement in the accuracy of MTD and trial efficiency. Similar to our NETS system, Potthoff et al. [21] also proposed to replace the binary indicator of DLT in the Phase I clinical trial with a mean toxicity ranging from 0 to 1 through mathematical transformation and its feasibility was demonstrated by some simulations. Bekele and Thall [22, 23] considered the commons cases of multiple toxicities per patient by using a total toxicity burden (TTB) to measure qualitatively the severity of multiple toxicities in real trials. But their method is computational intensive and it is time-consuming to perform a thorough investigation of the method’s robustness so that the method is not widely used in practice. Bekele et al. [24] further considered a more complex case of risk group specific dose finding based on an average toxicity score. In their approach, toxicity response is treated as an ordinal variable, but not yet a continuous variable which may fully utilize all toxicity information and achieve maximum trial efficiency.

A toxicity scoring system which calculates an equivalent score measuring the composite severity of multiple toxicities can be a good solution for the common cases of multiple toxicities per patient. In order to fully utilize all toxicity information in a Phase I clinical trial and improve the efficiency of the trial, Chen et al. proposed a novel NTES system to treat toxicity response as a quasi-continuous variable and quantitatively estimate the overall toxicity severity of patients [10]. The NETS scoring system consists of two parts, estimation of NETS for each patient and determination of TNETS based on a detailed target toxicity profile for a Phase I trial. In the estimation of a NETS for each patient, a logistic function is employed to calculate the contribution of additional toxicities besides the “worst” toxicity of the patient because the value range of logistic function (0~1) fits the gap between two consecutive adjusted toxicity grades and a logistic function is commonly used to model the dose-toxicity relationship in Phase I clinical trials. In addition, it provides flexibility and makes more sense from a biological point of view [10]. However, a logistic function is not the only choice for the purpose. There are many possible alternative algorithms, for example, Rogatko et al. proposed an algorithm to calculate a toxicity index (TI) used in an analysis of variance (ANOVA) to identify patient characteristics which compete with dose as predictors of acute treatment toxicity in Phase I and II clinical trials [25]. Even though their purpose was different from the scoring system of Chen et al., their algorithm can be modified to fit into the scoring system of Chen et al. to estimate a NETS for each patient in a Phase I clinical trial.

In this article, we proposed a new Bayesian adaptive design for cancer Phase I clinical trials which takes into account all grades of all toxicities experienced by all patients. The design consists of transforming all toxicity grades into a quasi-continuous score called NETS that was introduced by Chen et al. [10] and adapt it to EWOC [7-9] using a quasi-likelihood approach [11-13, 18]. We demonstrated by simulations under some scenarios that the methodology is superior to some adaptive designs such as EWOC when treating DLT as a binary indicator of toxicity in terms of recommending the correct MTD. In particular, the method seems to perform the best when distribution of the maximum adjusted grade 1, 2, 3, and 4 toxicities is balanced and each is equally likely to occur.

The methodology requires specification of TNETS. This target normalized equivalent toxicity score is elicited by conserving the traditional definition of DLT for a binary indicator of toxicity and adding a toxicity profile based on the expected probabilities of all grades of toxicities when a patient is treated at the MTD. We took TNETS to be a weighted average of the midpoints of NETS range for each maximum adjusted grade of toxicity. Other formulations of toxicity scores are possible, see for example [13] and [25], and each has its own merit. However, for a given practical problem, one has to explore the design operating characteristics under realistic and extreme scenarios and compare the usefulness of the method relative to the available designs treating DLT as a binary indicator of DLT. In our case, we have shown using simulations that the method outperforms the EWOC when different toxicity profiles are used but the traditional definition of DLT is kept the same for all designs. We used the concept of quasi-likelihood to implement the design [11-13, 18] because the EWOC algorithm was readily available from the authors and required minimum efforts to replace the Bernoulli type likelihood in [7-9] by the quasi-likelihood in (8). One can always model the NETS as a function of dose using either parametric or non-parametric distributions.

As mentioned above, there are various other methods for designs that use non-binary scoring and EWOC (or some other design) could be combined with a non-binary system other than NETS. On the other hand, designs other than EWOC, such as CRM, could be combined with NETS and improve their performance substantially. In general, any non-binary design should be better than the corresponding binary design as toxicity data are more fully utilized.

As part of our future work, we are investigating extensions of EWOC-NETS to include patients’ baseline covariates thought to be susceptible to treatment related toxicities as was done in [9, 26, 27] and extending these designs to Phase I/II studies by accounting for patient’s efficacy as well as toxicities. These studies will allow us to target individualized doses based on combination of patients’ characteristics such as clinical factors and genotypes [9, 25]. The number of patients per cohort is also a critical factor to be considered in EWOC-NETS. Multiple-patient cohort has the advantages of less toxicity and its accuracy of estimated MTD is comparable to that of the single-patient cohort, but at the cost of long waiting time and length of trial. However, the problems can be solved by some modification on EWOC-NETS, such as: next dose determination is based on all available completed data without waiting for results for all previous patients and dose allocation is carried whenever a patient is available for treatment.

In summary, we have adopted EWOC to the toxicity scoring system of Chen et al. [10] in order to develop EWOC-NETS design, which treats toxicity response as a quasi-continuous variable instead of a binary indicator of DLT and fully utilizes all toxicity information. Simulation studies and an application to real clinical trial data demonstrate that EWOC-NETS can improve the accuracy of the estimate of the MTD, trial efficiency, therapeutic effect, and overdose control in Phase I clinical trials. A user-friendly software program of EWOC-NETS is under development and will be available in the future.