Abstract
Time-scales of viral evolution and emergence have been studied widely, but are often poorly understood. Molecular analyses of viral evolutionary time-scales generally rely on estimates of rates of nucleotide substitution, which vary by several orders of magnitude depending on the timeframe of measurement. We analysed data from all major groups of viruses and found a strong negative relationship between estimates of nucleotide substitution rate and evolutionary timescale. Strikingly, this relationship was upheld both within and among diverse groups of viruses. A detailed case study of primate lentiviruses revealed that the combined effects of sequence saturation and purifying selection can explain this time-dependent pattern of rate variation. Therefore, our analyses show that studies of evolutionary time-scales in viruses require a reconsideration of substitution rates as a dynamic, rather than as a static, feature of molecular evolution. Improved modelling of viral evolutionary rates has the potential to change our understanding of virus origins.
Keywords: evolutionary rates, virus evolution, phylogenetics, molecular clock
1. Introduction
Determining the time-scale of evolutionary change is central to understanding the patterns and processes of viral emergence. At present, there is little consensus over the time-scale of viral origins and their long-term evolutionary dynamics. For instance, the phylogenetic relationships within some groups of primate lentiviruses (Family Retroviridae), pegiviruses and hepaciviruses (Family Flaviviridae) suggest virus–host codivergence [1] or ancient reservoirs in host species [2,3], which can be explained only by evolutionary timeframes of thousands or millions of years. However, many of the time-scales inferred for these viruses using tip-dated molecular clocks are much shorter, on the order of tens or hundreds of years [4,5].
Obtaining reliable time-scales depends on accurate estimates of evolutionary rate. Although nearly all RNA viruses seem to experience very rapid evolutionary change—usually expressed as rates of nucleotide substitution per site—far lower rates are observed in some large double-stranded DNA (dsDNA) viruses. For example, the nucleotide substitution rates for variola virus and herpes simplex virus (dsDNA) have been reported to be as low as 9.32 × 10–6 and 3 × 10−9 substitutions per site per year, respectively [6,7], and hence between three to six orders of magnitude lower than that of influenza virus A (negative-sense single-stranded RNA; −ssRNA) at 4.1 × 10−3 substitutions per site per year [8]. Overall, most RNA viruses seem to exhibit evolutionary rates of around 10−3 to 10−4 substitutions per site per year [9]. Accordingly, the evolutionary and demographic processes in RNA viruses can be readily observed in a matter of years or even weeks [9,10], and it is unsurprising that many RNA viruses can adapt to escape their host's immune system or to infect different species. The rapid evolution of RNA viruses reflects a high background rate of mutation, itself dependent on a lack of mechanisms for nucleic acid repair and on short generation times [11,12]. By contrast, dsDNA viruses generally have higher replication fidelity compared with their RNA counterparts [10,13], which largely explains their lower substitution rates. The cell type infected can also have an impact on substitution rates in viruses. Indeed, it has recently been shown that the turnover rate of the infected cells is positively associated with the rate of viral evolution [14].
In addition to varying among viral taxa and infected cell type, evolutionary rates appear to scale negatively with the timeframe of observation. Specifically, molecular data sampled over a short timeframe often appear to evolve at higher rates than those sampled over a longer time period [15,16]. Such a time-dependent pattern has been described in a wide range of organisms, including vertebrates [17] and insects [18]. One of the probable causes of this pattern is purifying selection, which acts on the genetic diversity over long timeframes by removing large numbers of transient deleterious mutations that are still present within short timeframes [19,20]. Consequently, rate estimates over long timeframes will be systematically lower than those obtained over short timeframes. The inadequate ‘correction’ of multiple substitutions at single nucleotide sites will also act to reduce evolutionary rates in the long term.
RNA viruses display the largest rate disparities among time-scales [5,20]. An important example is the primate lentiviruses, which include human and simian immunodeficiency viruses (HIV and SIV, respectively). In lentiviruses, nucleotide substitution rates estimated from serial samples collected over a few years within a single patient or host are on the order of 10−3 substitutions per site per year [21]. If this rate is used to calibrate a molecular clock, then the date of the HIV–SIV divergence is estimated at approximately 150 years BP [22]. Some early studies even reported a divergence time for these viruses as recent as 1951, with substitution rates as high as 10−2 substitutions per site per year [4]. However, some phylogenetic relationships among the viruses correspond to those of their primate hosts, indicating some degree of codivergence over thousands or millions of years [1,23–25]. A particularly compelling case is in the lentiviruses that infect Bioko Island drills, which separated around 10 000 years ago from their sister subspecies on the African mainland [25,26]. The SIVs that infect the island and mainland drill subspecies are phylogenetically distinct, such that the initial infection is likely to have occurred before the geographical separation. In this case, a rate of the order of 10−6 nucleotide substitutions per site per year [1] is necessary to explain the evolutionary time-scale of the virus, and hence three orders of magnitude lower than that estimated using virus samples from a single host.
To investigate the evolutionary determinants of these profound temporal rate disparities among viruses, we carried out a range of statistical and phylogenetic analyses. To make our analysis as general as possible, we compiled estimates of nucleotide substitution rates across all virus types in the Baltimore classification in which viruses are grouped according to their nucleic acid type and their method of replication [27]. Our data consisted of 181 rate estimates, including 105 new phylogenetic estimates. A meta-analysis of these data allowed us to determine the main patterns of estimates of rate variation across viral lineages. We conducted more detailed analyses of primate lentiviruses to understand how selective constraints, mutational saturation and phylogenetic model adequacy interact to shape patterns of temporal rate variation.
2. Material and methods
(a). Compilation of rate estimates
We assembled a dataset of 181 estimates of rates of nucleotide substitutions in viruses, including 76 published estimates and 105 newly obtained here. Published rate estimates were included in the dataset if the rate estimation method was fully explained in the original publication. For the rate estimates generated here, we obtained nucleotide sequences from GenBank and analysed them within a Bayesian framework (see below). Our aim was to include estimates from a wide range of virus types within the Baltimore classification. For consistency, we included datasets that corresponded to an individual virus species, or that were published in a single study. We included only sequences from a single gene in each analysis to minimize possible artefacts owing to recombination (or reassortment) or conflicting gene trees (electronic supplementary material, table S1 and data S1).
We aligned the sequences using the Muscle algorithm [28] and then inspected each alignment visually. The rates were estimated using the Bayesian Markov chain Monte Carlo (MCMC) method in Beast v. 1.7.2 [29]. Each dataset was analysed using a constant-size coalescent model [30] with a relaxed uncorrelated log-normal molecular clock [31]. The best-fitting substitution model for each dataset was selected by the Bayesian information criterion in the R package Phangorn v. 1.6-4 [32]. Substitution rate estimates were calibrated using the sampling times of the sequences (i.e. tip dates). Samples from the posterior distribution were drawn every 103 steps from a Markov chain (MCMC) of at least 108 steps. We assessed convergence and sufficient sampling by verifying that the effective sample size for all parameters was at least 200, as estimated in the R package CODA [33]. If the effective sample size was less than 200 for any of the parameters, then we doubled the number of steps in the MCMC and halved the sampling frequency.
We included a set of published rate estimates for our meta-analyses. These included those obtained through mutation experiments, serial sampling of an infected host or group of hosts and phylogenetic estimates assuming codivergence with host species. In our meta-analysis, we distinguish between the estimation methods because they encompass different evolutionary dynamics and timeframes. We refer to the particular method as the ‘sampling level’. In vitro estimates are those obtained through mutation experiments, typically spanning several hours to a few days. ‘Serial sampling’ corresponds to rates estimated by sampling a host or group of hosts through time, with a timeframe of a few months to five years. ‘Tip dating’ refers to the use of sampling times for calibration in phylogenetic analyses, as in the case of our newly reported estimates, with a timeframe ranging from one to around 40 years. ‘Codivergence’ describes the cases in which the internal nodes in the phylogenetic tree are calibrated by assuming codivergence between the virus and the host species, with timeframes of thousands to millions of years. For each rate estimate, we recorded the nucleic acid type (ssRNA, dsRNA, ssDNA or dsDNA), the sampling level and the timespan of the samples.
We note that Bayesian estimates of evolutionary rates with tip dates for calibration can be artificially inflated. This occurs when the sampling period fails to capture sufficient genetic change, so that rate estimates are unduly influenced by the prior for the rate of evolution and by the sampling times, rather than determined by the data [6,13]. To address this problem, we conducted a date-randomization test described by Ramsden et al. [34]. The test consists of analysing the data while randomizing the ages of the samples. The mean rate estimated with the correct sampling times should not be included in the 95% credibility interval of the estimates with the randomized sampling times. We conducted three randomization replicates for all of our 105 newly reported estimates. The estimates that failed this test for at least one replicate were excluded from our subsequent meta-analysis.
(b). Meta-analysis of rate estimates
The first part of our meta-analysis consisted of determining differences in the rate estimates between viruses with different nucleic acid types (i.e. DNA versus RNA viruses). We used a logarithmic transformation (base 10) for the mean rate estimate, and we fitted an ANOVA and performed a Tukey's HSD test. Next, we tested for temporal trends in the rate of evolution. We used a logarithmic transformation for the mean rate and for the sampling timeframe, and we fitted linear regressions to these two variables, with the rate as a function of the timeframe. We used both the complete dataset and some subsets of the data separately. We fitted separate regressions for the DNA and RNA viruses. We also made a distinction between the sampling levels because they may impose different selective constraints. For example, a rate estimate based on serial sampling from a single host will reflect different selective constraints from one that uses samples from several host species, such as under the assumption of virus–host codivergence [35]. In total, we conducted 10 linear regressions, one for each nucleic acid type (DNA and RNA) and one per sampling level (in vitro, serial sampling, tip dating and co-divergence) within each nucleic acid type.
The number of data points for some viruses was disproportionately high with, for example, an overrepresentation of lentiviruses and coronaviruses. This non-random sampling and phylogenetic non-independence can mislead statistical inference. To address this problem in our regressions, we randomly sampled one rate estimate per virus genus, resulting in a reduced dataset. We obtained 1000 reduced datasets, and we fitted a linear regression to each. For our inferences, we report the mean estimates of the slope, and the p-value, with the corresponding 95% quantile range, also known as the confidence interval (CI).
A shortcoming of fitting linear regressions of a quotient as a function of its denominator is that the significance of the slope can be spurious [36]. This risk applies to our analyses, because we fit the rate of evolution, in units of substitutions per time units, as a function of the timespan, in time units. To solve this problem, one can fit the regression while randomizing the denominator. The procedure is repeated a large number of times, and the estimates with the randomized data can be used as a null distribution to assess statistical significance [37]. We used this method for our regressions with 10 000 randomizations each time. It is important to note, however, that posterior estimates from Bayesian analyses are in the form of distributions rather than in the form of point values. For this reason, this analysis has low statistical power and serves only to capture the temporal variation in rates, rather than offering a rigorous significance test.
(c). Lentivirus case study
To investigate the causes of rate variation in detail, we focused on HIV and SIV. This analysis allowed us to control for rate variation among viral taxa, which is expected from differences in life histories [38]. Data were downloaded from the Los Alamos National Laboratory HIV database [39] (accession numbers available in the electronic supplementary material, table S2). We selected sequences for the ENV and POL genes with similar evolutionary time-scales to those of our meta-analysis, ranging from the interspecific divergence of SIV in Bioko island monkeys around 10 000 years ago, to the diversification of HIV strains within a human host over the course of a few months. In total, we had nine datasets for ENV and 11 for POL (electronic supplementary material, table S2). For each dataset, we aligned sequences using Muscle and visually inspected the alignments. We conducted four sets of analyses to evaluate the impact of saturation and purifying selection on these data.
(i). Bayesian estimation of Lentivirus evolutionary rates
We selected substitution models in Phangorn according to the Bayesian information criterion and conducted Bayesian phylogenetic analyses in Beast v. 1.7.2. For each dataset, Bayes factors [40] indicated greater support for the relaxed lognormal clock compared with the strict clock. We also evaluated the posterior distributions of the coefficient of rate variation, which should deviate from zero in the presence of substantial rate variation among branches [31]. We report the results from the relaxed lognormal clock model.
For the datasets corresponding to the deepest divergences, we used the Yule speciation prior and calibrated the analysis by assigning a known age to a single node in the tree (electronic supplementary material, table S2). For the datasets corresponding to more recent time-scales, we compared skyline and constant-size coalescent models using Bayes factors and used the sampling times as calibrations. We report rate estimates only from datasets that passed a date-randomization test with five replicates. To check for convergence and sufficient MCMC sampling, we used the same method described for our phylogenetic estimates in the meta-analysis.
To determine the relationship between rate and time-scale, we fitted a robust regression because there were few data points. We used the same approach for statistical significance as we did for the meta-analysis. In this case, we fit separate regressions for the ENV and POL genes, but we did not make a distinction between sampling levels, because there were fewer data points than in our meta-analysis.
(ii). Analysis of selective constraints
The strength and direction of selection were inferred by estimating the numbers of non-synonymous substitutions (dN) and synonymous substitutions (dS) per site. We inferred a maximum-likelihood tree for each dataset using Garli v. 1.0 [41] and estimated dN and dS for each branch under the MG94 model in HyPhy v. 2.12 [42]. For comparison, we calculated weighted values for these quantities by weighting them by branch length. We carried out linear-regression analyses for dN/dS, dN and dS as functions of time. In the case of dN and dS, the linear model was forced through the origin to reflect the expectation that these values should be negligible at zero time.
(iii). Quantification of saturation
To estimate the degree of mutational saturation, we used the entropy-based I index [43] as implemented in Dambe v. 5.3.00 [44]. This method estimates the realized I and its critical value if the specific alignment were fully saturated (Ic). Because the saturation indices are specific to the data, we used their ratio (I/Ic) for comparison among datasets and then fit a linear regression of the ratio as a function of time. The regression line was forced through the origin, because no saturation is expected at zero time. To approximate synonymous and non-synonymous saturation, we analysed first and second codon sites separately from third codon sites.
(iv). Model adequacy
To evaluate the absolute fit of the time-reversible substitution models that are typically used in phylogenetic analysis, we used a Bayesian approach implemented in MAPPS [45]. The data were first analysed in MrBayes v. 3.2 [46,47] with the model chosen according to the Bayesian information criterion and with the most complex time-reversible model (GTR + I + with six rate categories) to obtain posterior distributions for the model parameters. One thousand datasets of the same size as the original were simulated using parameters sampled from the posterior. A site-pattern statistic (T) is obtained for each simulated dataset, resulting in a null distribution. The T statistic is calculated for the original dataset, known as the realized T, and compared with the null distribution. If the substitution model adequately describes the evolutionary process that produced the dataset, then the realized T should fall in the centre of the null distribution. To assess the performance of the model, we used a Z-score as the normalized distance between the expected and realized T, and we fit a linear regression for the Z-score as a function of time. Results presented here correspond to those with the best-fitting time-reversible model, which was the GTR + I + model for most datasets (electronic supplementary material, table S2).
3. Results and discussion
(a). Meta-analysis of rate estimates and time-dependent evolutionary rates in viruses
We excluded 40 rate estimates from our meta-analysis, because they failed at least one replicate of the date-randomization test, resulting in a total of 141 data points. The datasets lacking temporal structure included dsDNA, ssDNA and ssRNA viruses. Interestingly, dsDNA datasets were disproportionally represented in the unreliable estimates; 32%, compared with 18% and 17% for the ssDNA and ssRNA viruses, respectively. This is consistent with our expectation that sampling timeframes of the order of years are inadequate to estimate substitution rates in slowly evolving viruses.
Our analysis of 141 rate estimates, comprising those from previously published studies and new rate estimates, revealed some important aspects of rate variation among viruses. Rate estimates were significantly different between DNA and RNA viruses (ANOVA p = 2.4 × 10−4). In particular, the Tukey's HSD test revealed that the rates for ssRNA viruses were significantly higher than those of ssDNA viruses (p = 7 × 10−3) and dsDNA viruses (p = 2 × 10−3). This finding was consistent with previous studies that suggested that ssRNA viruses have particularly high evolutionary rates [9,15,48].
The rates estimated for in vitro, serial and tip-date sampling levels largely overlapped with each other. In contrast, the estimates that assumed virus–host codivergence were much lower. A clear example is in the rate estimates for viruses of the family Papillomaviridae (dsDNA). An estimate assuming virus–host co-divergence of non-mammalian papillomaviruses was 9.70 × 10−9 substitutions per site per year [49], which is four orders of magnitude lower than that for human papillomavirus type 31, estimated with tip dating at 4.58 × 10−5 substitutions per site per year.
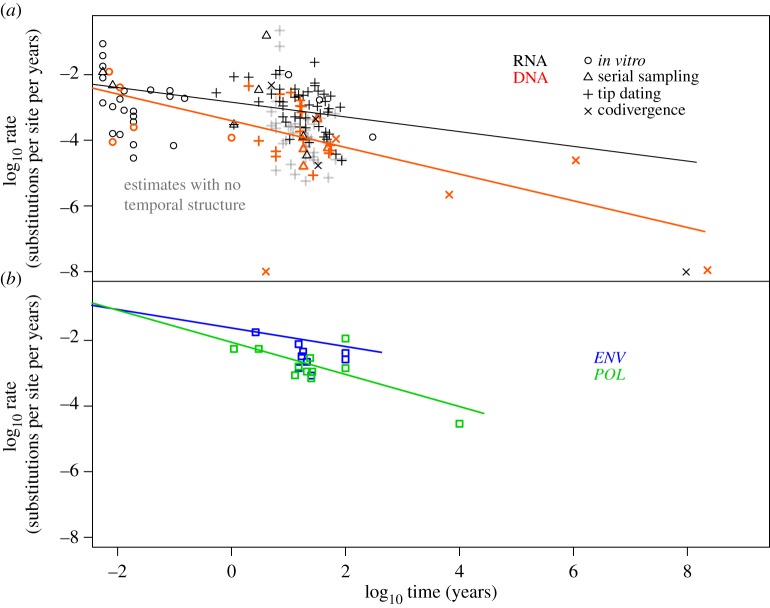
Strikingly, the estimates of rates of evolution were lower for broader sampling levels and longer timeframes in both DNA viruses (mean slope −0.38, CI: −0.48 to −0.16; mean p = 8.8 × 10−4, CI: 0–2.32 × 10−3) and in RNA viruses (mean slope −0.17, CI: −0.27 to 0.08; mean p = 2 × 10−4, CI: 0–3 × 10−4). This time-dependent pattern of rate variation was also sustained within sampling levels, albeit with lower statistical support in some cases (figure 1a and the electronic supplementary material, table S3).
Figure 1.
(a) Meta-analysis of temporal rate variation among viral lineages. Each data point corresponds to a nucleotide rate estimate as reported in this and other studies. The original data are in nucleotide substitutions per site per year and have been log-transformed in this figure. Colours distinguish DNA (red) and all RNA viruses (black), which were analysed separately. (b) Temporal variation in ENV (blue) and POL (green) genes in Lentivirus. Data points are mean rate estimates for different time-scales of primate Lentivirus evolution.
Our meta-analysis of rate estimates across viral lineages allows us to draw a number of general conclusions. First, our regression analyses for DNA and RNA viruses indicate that evolutionary timeframe explains much of the observed rate variation. Although our model lacks the precision to allow substitution rates to be predicted solely on the basis of the evolutionary timeframe, it demonstrates that a time-dependence of substitution rates is ubiquitous among viruses. In particular, studies that assume virus–host codivergence over thousands or millions of years will systematically lead to lower rate estimates than studies of samples collected over a period of years or months, such as in our in vitro, serial sampling or tip-dating estimates. In turn, rate estimates from the latter are likely to reflect a combination of mutation and substitution rates (i.e. they include transient deleterious mutations), whereas those of the former may be affected by extensive site saturation (see below).
(b). A case study in primate lentiviruses
Our meta-analysis of evolutionary rates includes many different virus lineages, preventing us from gaining detailed insights into the underlying causes of time-dependent rate estimates. We, therefore, sought to identify the causes at a molecular level through detailed analyses of HIV and SIV. This group of viruses is of particular interest, because there appears to be general agreement on the time of origin of the human pandemic caused by group M viruses [50]. However, this is not the case for those viruses infecting other primates. In particular, the time-scale of the diversification of the various lineages of SIV has generated considerable debate [51–54].
Our analysis revealed that the slopes for substitution rate as a function of time were negative in both genes analysed (−0.4 in ENV and −0.5 in POL). Although the regression was significant in POL only (p = 0.18 for ENV and p = 0.01 for POL), the overall trend is that rates decline with increasing timeframes (figure 1b).
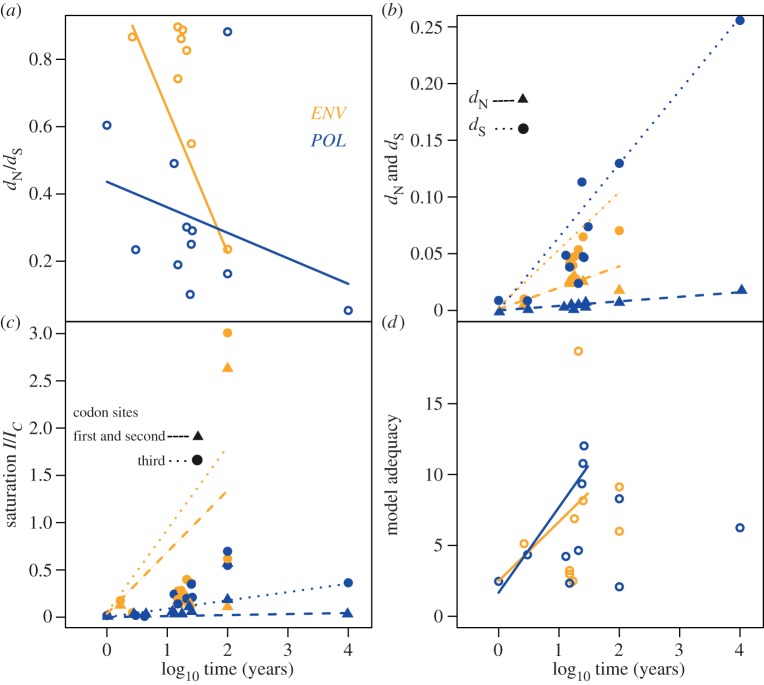
Similarly, our analysis of selective constraints revealed that dN/dS decreased over time, reflecting the action of increasing purifying selection at deeper time-scales. The trend was significant in ENV (slope = −0.40 and p = 0.03) but not POL (slope = −0.11 and p = 0.19; figure 2a). This can be explained by stronger evolutionary constraints acting on POL, which plays a key role in nucleic acid replication [55].
Figure 2.
Temporal variation of (a) selective constraints as the ratio of non-synonymous and synonymous substitutions per site (dN/dS); (b) separate estimation of non-synonymous (dN) and synonymous variation (dS); (c) saturation according to the ratio of observed saturation (I) and full saturation (Ic) and (d) model adequacy, as the Z-score of expected and observed model performance. Note that the x-axis displays time on a logarithmic scale for comparison with figure 1; however, the regression lines correspond to the non-transformed data. The colours correspond to analyses of genes ENV and POL. The symbols represent dN and dS in (b), and first and second, and third codon positions in (c), as indicated in the legends. (Online version in colour.)
The regressions of dS over time were significant for both POL (slope = 2.26 × 10−5, p = 3.00 × 10−3) and ENV (slope = 1.0 × 10−3, p = 0.01), whereas this was not the case for dN (POL slope = 1.53 × 10−6, p = 0.08; ENV slope = 3.9 × 10−4, p = 0.07; figure 2b). Synonymous mutations are fixed at much higher rates than non-synonymous mutations, so that the difference between these two quantities increases over time. These findings point to stronger purifying selection at non-synonymous compared with synonymous sites. As a consequence, the temporal trends in dN/dS are driven by the linear accumulation of synonymous variation over time and the consistent removal of non-synonymous variation.
Mutational saturation can also produce an apparent decline in substitution rates over time by causing the amount of evolutionary change to be underestimated [17]. Our regressions of saturation on time (I/Ic = 1) revealed different patterns for ENV and POL. In ENV, the slope was significant and positive (slope = 0.01, p = 0.01 for first and second codon sites; slope = 0.02, p = 2.00 × 10−3 for third codon sites). By contrast, complete saturation was not reached in POL, and the regression was non-significant (slope = 4.48 × 10−6, p = 0.78 for first and second codon positions; slope = 3.54 × 10−5, p = 0.30 for third codon positions; figure 2c).
Saturation in gene sequence data is typically addressed using models of nucleotide substitution. Maximum-likelihood and Bayesian phylogenetic methods are strongly sensitive to the choice of model, with poorly fitting models potentially leading to biased estimates of evolutionary parameters [56,57]. Some recent developments in molecular clock methods take into account some degree of mutational saturation [58], but the dramatically high levels of saturation we observed in lentiviruses over long timeframes will consistently lead to an underestimation of the evolutionary rate.
The performance of the best-fitting models did not decrease linearly with time, as shown by the non-significant slope coefficients in the regressions of performance as a function of time (p = 0.35 for ENV, p = 0.59 for POL; electronic supplementary material, table S2). However, model performance was highly variable for datasets that represented evolutionary timeframes greater than 100 years, suggesting that substitution patterns become so different among datasets that model fit cannot be assessed reliably. Therefore, we conducted the regression analysis only for timeframes shorter than 100 years using the iteratively reweighted least-squares method, which is robust to small data sizes. In this case, the regression was significant for POL (slope = 0.31, p = 0.02) but not for ENV (slope = 0.21, p = 0.39), suggesting a linear decline in model performance for POL over this timeframe (figure 2d). Beyond temporal trends, these results reveal standard scores considerably above zero for most datasets, reflecting poor overall fit, regardless of the timeframe.
4. Conclusion
Purifying selection and site saturation are strongly associated with temporal variation in rates of nucleotide substitution and can explain the dichotomy between long- and short-term rate estimates in viruses. Sequence data sampled over a short timeframe capture the standing genetic diversity, which is the combined result of non-synonymous and synonymous polymorphisms. A proportion of this comprises slightly deleterious mutations not yet removed by purifying selection. Non-synonymous mutations tend to have greater fitness consequences than those at synonymous sites, so they will be more rapidly removed by purifying selection, delaying the onset of saturation at these sites. By contrast, rapid saturation occurs at synonymous sites, resulting in an apparent decline in the estimated rate of evolution, which is not entirely accounted for by the substitution models that are commonly used. In the case of the lentiviruses, we found a linear decline in model fit across a timeframe of 100 years, at least for one of the two genes analysed.
According to our analysis, rates of evolution almost inevitably appear to decline over time because of the combined effects of natural selection and saturation. Consequently, and critically, estimates of rates are only applicable to the timeframe used to obtain them and cannot readily be extrapolated to other scales of analysis [59]. In particular, short-term rate estimates will lead to underestimates of the timing of ancient divergence events, whereas using long-term rate estimates will cause the timing of recent events to be overestimated. These effects are particularly problematic in viruses, where the ages of many ssRNA virus families are probably orders of magnitude older than suggested by current estimates. Although the evolutionary dynamics of viral emergence over short timeframes can be accurately estimated, their long-term evolution remains elusive. Our lentivirus case study illustrates this finding, and it supports other studies that suggest that the time-scale of these viruses may be thousands of years older than previously estimated [23].
Recently developed methods that attempt to correct for purifying selection have revealed that the time-scale for measles, Ebola and avian influenza viruses might be centuries or millennia older than previously estimated [60]. A prominent example of the application of these methods involves the coronaviruses (Family Coronaviridae), whose emergence was estimated to have occurred millions of years ago rather than around 10 000 years ago [58]. While these methods, and others such as local clocks [61], are an important contribution, we suggest that it is still necessary to develop a molecular clock framework for rapidly evolving viruses that can incorporate all of the factors investigated here, especially site saturation. Importantly, the differences between long- and short-term rate estimates need to be reconsidered, not as conflicting estimates, but as signs of a continuous evolutionary process that can be modelled in terms of increasing levels of saturation and purifying selection over time. This has the potential to change our understanding of the evolution of viruses and the processes behind their current diversity.
Funding statement
S.D. was supported by a Francisco José de Caldas Scholarship from the Colombian government and by a University of Sydney World Scholars Award. E.C.H. was supported by a National Health and Medical Research Council Australia Fellowship. S.Y.W.H. was supported by the Australian Research Council.
References
- 1.Worobey M, et al. 2010. Island biogeography reveals the deep history of SIV. Science 329, 1487 ( 10.1126/science.1193550) [DOI] [PubMed] [Google Scholar]
- 2.Quan P-L, et al. 2013. Bats are a major natural reservoir for hepaciviruses and pegiviruses. Proc. Natl Acad. Sci. USA 110, 7961–7962. ( 10.1073/pnas.1303037110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kapoor A, et al. 2013. Identification of rodent homologs of hepatitis C virus and pegiviruses. MBio 4, e00216–13. ( 10.1128/mBio.00216-13) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Smith TF, Srinivasan A, Schochetman G, Marcus M, Myers G. 1988. The phylogenetic history of immunodeficiency viruses. Nature 333, 573–575. ( 10.1038/333573a0) [DOI] [PubMed] [Google Scholar]
- 5.Simmonds P. 2001. 2000 Fleming lecture. The origin and evolution of hepatitis viruses in humans. J. Gen. Virol. 82, 693–712. [DOI] [PubMed] [Google Scholar]
- 6.Firth C, Kitchen A, Shapiro B, Suchard MA, Holmes EC, Rambaut A. 2010. Using time-structured data to estimate evolutionary rates of double-stranded DNA viruses. Mol. Biol. Evol. 27, 2038–2051. ( 10.1093/molbev/msq088) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McGeoch DJ, Dolan A, Ralph AC. 2000. Toward a comprehensive phylogeny for mammalian and avian herpesviruses. J. Virol. 74, 10 401–10 406. ( 10.1128/JVI.74.22.10401-10406.2000) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fusaro A, et al. 2011. Phylogeography and evolutionary history of reassortant H9N2 viruses with potential human health implications. J. Virol. 85, 8413–8421. ( 10.1128/JVI.00219-11) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Holmes EC. 2009. The evolution and emergence of RNA viruses. New York, NY: Oxford University Press. [Google Scholar]
- 10.Holmes EC, Burch SS. 2000. The causes and consequences of genetic variation in dengue virus. Trends Microbiol. 8, 74–77. ( 10.1016/S0966-842X(99)01669-8) [DOI] [PubMed] [Google Scholar]
- 11.Gojobori T, Moriyama EN, Kimura MOT. 1990. Molecular clock of viral evolution, and the neutral theory. Proc. Natl Acad. Sci. USA 87, 10 015–10 018. ( 10.1073/pnas.87.24.10015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Domingo E, Holland JJ. 1997. RNA virus mutations and fitness for survival. Annu. Rev. Microbiol. 51, 151–178. ( 10.1146/annurev.micro.51.1.151) [DOI] [PubMed] [Google Scholar]
- 13.Ramsden C, Holmes EC, Charleston MA. 2009. Hantavirus evolution in relation to its rodent and insectivore hosts: no evidence for codivergence. Mol. Biol. Evol. 26, 143–153. ( 10.1093/molbev/msn234) [DOI] [PubMed] [Google Scholar]
- 14.Hicks AL, Duffy S. 2014. Cell tropism predicts long-term nucleotide substitution rates of mammalian RNA viruses. PLoS Pathog. 10, e1003838 ( 10.1371/journal.ppat.1003838) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sanjuán R, Nebot MR, Chirico N, Mansky LM, Belshaw R. 2010. Viral mutation rates. J. Virol. 84, 9733–9748. ( 10.1128/JVI.00694-10) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Charrel RN, De Micco P, de Lamballerie X. 1999. Phylogenetic analysis of GB viruses A and C: evidence for cospeciation between virus isolates and their primate hosts. J. Gen. Virol. 80, 2329–2335. [DOI] [PubMed] [Google Scholar]
- 17.Ho SYW, Phillips MJ, Cooper A, Drummond AJ. 2005. Time dependency of molecular rate estimates and systematic overestimation of recent divergence times. Mol. Biol. Evol. 22, 1561–1568. ( 10.1093/molbev/msi145) [DOI] [PubMed] [Google Scholar]
- 18.Papadopoulou A, Anastasiou I, Vogler AP. 2010. Revisiting the insect mitochondrial molecular clock: the mid-Aegean trench calibration. Mol. Biol. Evol. 27, 1659–1672. ( 10.1093/molbev/msq051) [DOI] [PubMed] [Google Scholar]
- 19.Subramanian S, Lambert DM. 2012. Selective constraints determine the time dependency of molecular rates for human nuclear genomes. Genome Biol. Evol. 4, 1127–1132. ( 10.1093/gbe/evs092) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Holmes EC. 2003. Molecular clocks and the puzzle of RNA virus origins. J. Virol. 77, 3893–3897. ( 10.1128/JVI.77.7.3893-3897.2003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jahnke M, Holmes EC, Kerr PJ, Wright JD, Strive T. 2010. Evolution and phylogeography of the nonpathogenic calicivirus RCV-A1 in wild rabbits in Australia. J. Virol. 84, 12 397–12 404. ( 10.1128/JVI.00777-10) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sharp PM, Li WH. 1988. Understanding the origins of AIDS viruses. Nature 336, 315 ( 10.1038/336315a0) [DOI] [PubMed] [Google Scholar]
- 23.Wertheim JO, Worobey M. 2009. Dating the age of the SIV lineages that gave rise to HIV-1 and HIV-2. PLoS Comput. Biol. 5, e1000377 ( 10.1371/journal.pcbi.1000377) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Müller V, De Boer RJ. 2006. The integration hypothesis: an evolutionary pathway to benign SIV infection. PLoS Pathog. 2, e15 ( 10.1371/journal.ppat.0020015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fomsgaard A, Hirsch VM, Allan JS, Johnson PR. 1991. A highly divergent proviral DNA clone of SIV from a distinct species of African green monkey. Virology 182, 397–402. ( 10.1016/0042-6822(91)90689-9) [DOI] [PubMed] [Google Scholar]
- 26.Jones PJ. 1994. Biodiversity in the Gulf of Guinea: an overview. Biodivers. Conserv. 3, 772–784. ( 10.1007/BF00129657) [DOI] [Google Scholar]
- 27.Baltimore D. 1971. Expression of animal virus genomes. Bacteriol. Rev. 35, 235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Edgar RC. 2004. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 32, 1792–1797. ( 10.1093/nar/gkh340) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Drummond AJ, Suchard MA, Xie D, Rambaut A. 2012. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Biol. Evol. 29, 1969–1973. ( 10.1093/molbev/mss075) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Drummond AJ, Rambaut A, Shapiro B, Pybus OG. 2005. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol. Biol. Evol. 22, 1185–1192. ( 10.1093/molbev/msi103) [DOI] [PubMed] [Google Scholar]
- 31.Drummond AJ, Ho SYW, Phillips MJ, Rambaut A. 2006. Relaxed phylogenetics and dating with confidence. PLoS Biol. 4, e88 ( 10.1371/journal.pbio.0040088) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schliep KP. 2011. phangorn: phylogenetic analysis in R. Bioinformatics 27, 592–593. ( 10.1093/bioinformatics/btq706) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Plummer M, Best N, Cowles K, Vines K. 2006. CODA: convergence diagnosis and output analysis for MCMC. R News 6, 7–11. [Google Scholar]
- 34.Ramsden C, Melo FL, Figueiredo LM, Holmes EC, Zanotto PMA. 2008. High rates of molecular evolution in hantaviruses. Mol. Biol. Evol. 25, 1488–1492. ( 10.1093/molbev/msn093) [DOI] [PubMed] [Google Scholar]
- 35.Belshaw R, Sanjuán R, Pybus OG. 2011. Viral mutation and substitution: units and levels. Curr. Opin. Virol. 1, 430–435. ( 10.1016/j.coviro.2011.08.004) [DOI] [PubMed] [Google Scholar]
- 36.Kenney BC. 1982. Beware of spurious self-correlations! Water Resour. Res. 18, 1041–1048. ( 10.1029/WR018i004p01041) [DOI] [Google Scholar]
- 37.Jackson DA, Somers KM. 1991. The spectre of ‘spurious’ correlations. Oecologia 86, 147–151. ( 10.1007/BF00317404) [DOI] [PubMed] [Google Scholar]
- 38.Duffy S, Shackelton LA, Holmes EC. 2008. Rates of evolutionary change in viruses: patterns and determinants. Nat. Rev. Genet. 9, 267–276. ( 10.1038/nrg2323) [DOI] [PubMed] [Google Scholar]
- 39.Kuiken C, et al. 2009. HIV sequence compendium 2009. Los Alamos, NM: Theor. Biol. Biophys. Group, Los Alamos National Laboratory. [Google Scholar]
- 40.Suchard MA, Weiss RE, Sinsheimer JS. 2001. Bayesian selection of continuous-time Markov chain evolutionary models. Mol. Biol. Evol. 18, 1001–1013. ( 10.1093/oxfordjournals.molbev.a003872) [DOI] [PubMed] [Google Scholar]
- 41.Zwickl DJ. 2006. GARLI, vers. 0.951. Genetic algorithm approaches for the phylogenetic analysis of large biological sequence datasets under the maximum likelihood criterion. See http://www.bio.utexas.edu/faculty/antisense/garli/garli.html.
- 42.Pond SLK, Muse SV. 2005. HyPhy: hypothesis testing using phylogenies. In Statistical methods in molecular evolution (ed. Nielsen R.), pp. 125–181. New York, NY: Springer. [Google Scholar]
- 43.Xia X, Xie Z, Salemi M, Chen L, Wang Y. 2003. An index of substitution saturation and its application. Mol. Phylogenet. Evol. 26, 1–7. ( 10.1016/S1055-7903(02)00326-3) [DOI] [PubMed] [Google Scholar]
- 44.Xia X, Xie Z. 2001. DAMBE: software package for data analysis in molecular biology and evolution. J. Hered. 92, 371–373. ( 10.1093/jhered/92.4.371) [DOI] [PubMed] [Google Scholar]
- 45.Bollback JP. 2002. Bayesian model adequacy and choice in phylogenetics. Mol. Biol. Evol. 19, 1171–1180. ( 10.1093/oxfordjournals.molbev.a004175) [DOI] [PubMed] [Google Scholar]
- 46.Huelsenbeck JP, Ronquist F. 2001. MrBayes: Bayesian inference of phylogenetic trees. Bioinformatics 17, 754–755. ( 10.1093/bioinformatics/17.8.754) [DOI] [PubMed] [Google Scholar]
- 47.Ronquist F, et al. 2012. MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 61, 539–542. ( 10.1093/sysbio/sys029) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sanjuán R. 2012. From molecular genetics to phylodynamics: evolutionary relevance of mutation rates across viruses. PLoS Pathog. 8, e1002685 ( 10.1371/journal.ppat.1002685) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Herbst LH, Lenz J, Van Doorslaer K, Chen Z, Stacy BA, Wellehan JFX, Manire CA, Burk RD. 2009. Genomic characterization of two novel reptilian papillomaviruses, Chelonia mydas papillomavirus 1 and Caretta caretta papillomavirus 1. Virology 383, 131–135. ( 10.1016/j.virol.2008.09.022) [DOI] [PubMed] [Google Scholar]
- 50.Worobey M, et al. 2008. Direct evidence of extensive diversity of HIV-1 in Kinshasa by 1960. Nature 455, 661–664. ( 10.1038/nature07390) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sharp PM, Bailes E, Chaudhuri RR, Rodenburg CM, Santiago MO, Hahn BH. 2001. The origins of acquired immune deficiency syndrome viruses: where and when? Phil. Trans. R. Soc. Lond. B 356, 867–876. ( 10.1098/rstb.2001.0863) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Müller MC, et al. 1993. Simian immunodeficiency viruses from central and western Africa: evidence for a new species-specific lentivirus in tantalus monkeys. J. Virol. 67, 1227–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jin MJ, Rogers J, Phillips-Conroy JE, Allan JS, Desrosiers RC, Shaw GM, Sharp PM, Hahn BH. 1994. Infection of a yellow baboon with simian immunodeficiency virus from African green monkeys: evidence for cross-species transmission in the wild. J. Virol. 68, 8454–8460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gao F, et al. 1999. Origin of HIV-1 in the chimpanzee Pan troglodytes troglodytes. Nature 397, 436–440. ( 10.1038/17130) [DOI] [PubMed] [Google Scholar]
- 55.Sanchez-Pescador R, et al. 1985. Nucleotide sequence and expression of an AIDS-associated retrovirus (ARV-2). Science 227, 484 ( 10.1126/science.2578227) [DOI] [PubMed] [Google Scholar]
- 56.Kelchner SA, Thomas MA. 2007. Model use in phylogenetics: nine key questions. Trends Ecol. Evol. 22, 87–94. ( 10.1016/j.tree.2006.10.004) [DOI] [PubMed] [Google Scholar]
- 57.Gatesy J. 2007. A tenth crucial question regarding model use in phylogenetics. Trends Ecol. Evol. 274, 3–14. [DOI] [PubMed] [Google Scholar]
- 58.Wertheim JO, Chu DKW, Peiris JSM, Pond SLK, Poon LLM. 2013. A case for the ancient origin of coronaviruses. J. Virol. 87, 7039–7045. ( 10.1128/JVI.03273-12) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ho SYW, Larson G. 2006. Molecular clocks: when times are a-changin’. Trends Genet. 22, 79–83. ( 10.1016/j.tig.2005.11.006) [DOI] [PubMed] [Google Scholar]
- 60.Wertheim JO, Pond SLK. 2011. Purifying selection can obscure the ancient age of viral lineages. Mol. Biol. Evol. 28, 3355–3365. ( 10.1093/molbev/msr170) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Worobey M, Han G-Z, Rambaut A. 2014. A synchronized global sweep of the internal genes of modern avian influenza virus. Nature 508, 254–257. ( 10.1038/nature13016) [DOI] [PMC free article] [PubMed] [Google Scholar]