Review on measurement techniques of transport properties of nanowires

Physical properties at the nanoscale are novel and different from those in bulk materials.

Abstract

Physical properties at the nanoscale are novel and different from those in bulk materials. Over the last few decades, there has been an ever growing interest in the fabrication of nanowire structures for a wide variety of applications including energy generation purposes. Nevertheless, the study of their transport properties, such as thermal conductivity, electrical conductivity or Seebeck coefficient, remains an experimental challenge. For instance, in the particular case of nanostructured thermoelectrics, theoretical calculations have shown that nanowires offer a promising way of enhancing the hitherto low efficiency of these materials in the conversion of temperature differences into electricity. Therefore, within the thermoelectrical community there has been a great experimental effort in the measurement of these quantities in actual nanowires. The measurements of these properties at the nanoscale are also of interest in fields other than energy, such as electrical components for microchips, field effect transistors, sensors, and other low scale devices. For all these applications, knowing the transport properties is mandatory. This review deals with the latest techniques developed to perform the measurement of these transport properties in nanowires. A thorough overview of the most important and modern techniques used for the characterization of different kinds of nanowires will be shown.

1. Introduction

One of the primary interests of science today is the manipulation of matter at both the atomic and molecular scale. To this end highly multidisciplinary fields have emerged, such as materials and surface sciences, supramolecular chemistry, self-replicating machines and robotics, with the goal of designing and manufacturing nanostructured materials.¹ Therefore, a wide variety of scientific instruments have been developed to process and study those structures at the nanoscale, and different fabrication approaches, such as the “top-bottom” and “bottom-up” techniques, are being used to fabricate nanostructures, devices at the nanoscale and measurement instruments for them. Most of the efforts devoted to study the nanoscale are valuable because of the novel physical phenomena that occur at those small sizes. There are also many challenges that must be overcome in order to implement actual devices, such as making electrical contacts and testing their electric behaviour, that require thorough studies and new technologies.

The effects of reducing the size of the materials can have important consequences on their properties. If one of the dimensions of the sample is comparable to the wavelength of the carriers, the variation of the density-of-states can produce drastic changes in the transport properties compared to the bulk material. This is known as the quantum size regime. In this regime the energy levels available for electrons are different from the traditional continuum of energy levels or bands that can be found in bulk materials.² Moreover, classical effects, which are not usually taken into account in bulk, also come into play when the majority of the atoms are located at the surface, or within grain boundaries. In low dimensions the surface-to-volume ratio dramatically increases as the size is reduced leading to a new collection of physical properties. Among the different structures that can be produced at the nanoscale, nanowires emerge as one of the most interesting ones. They combine low dimensionality due to their small diameters with high aspect ratios, which makes them a good approximation to one dimensional structures. Indeed, their small diameters impose severe constraints on the transport properties. For instance, for very small nanowires, with diameters below the mean-free path of the carriers, electrical or thermal conductivity can be significantly reduced with respect to the corresponding bulk material. Moreover, as the nanowire shrinks in size, surface effects become more important and have a strong influence on its properties because many atoms that lie on the nanowire surface are not fully bonded to neighbouring atoms. These non-bonded atoms are often a source of defects within the nanowire and may cause the nanowire to become less electrically conductive than the same material in bulk.

Currently, there are a wide variety of methods available to produce nanowire structures in different materials, such as template-assisted growth via vacuum melting and pressure injection³ or electrochemical deposition,⁴ or other techniques such as laser assisted growth,⁵ or sono-electrochemistry.⁶ Metallic, semiconducting and insulating nanowires have found applications in logic gates, sensors, and flat-screen displays, among others.

All these effects are of particular importance in the case of thermoelectric (TE) materials, which are able to transform a temperature difference into an electrical current, and vice versa.⁷ These materials have been regarded for a long time as a promising alternative to exploit the waste heat produced in energy conversion or transportation for the generation of electricity. The main drawback of traditional TE materials is their low efficiency, but there has been a renewed interest in the thermoelectricity community since the theoretical prediction of Hicks and Dresselhaus^2,8 that a reduction in size, down to a few nm, would produce an enhancement in thermoelectric efficiency. This efficiency in the heat to electricity conversion is inversely related to the thermal conductivity, so a decrease in this parameter gives rise to more efficient materials.

The enormous progress in the synthesis of new nanostructured materials and nanowires with different shapes and aspect ratios⁹ has been accompanied by progress in the development of new characterization tools to analyse the change in physical properties at the nanoscale. Notwithstanding, probing matter at the nanoscale is a difficult task since higher sensitivity and spatial localization are often required. In this context, a wide variety of techniques able to measure transport by electrons and phonons in single or arrays of nanowires have been developed in recent years. This review provides a comprehensive analysis of the techniques developed to measure transport properties of single and arrays of nanowires. The main advantages and drawbacks of the various techniques, from an experimental point of view and considering their accuracy and sensitivity, are discussed.

The review is divided into two main parts. The first part is described in Section 2, where different techniques to measure the electrical and thermal properties along with the Seebeck coefficient of single nanowires outside or embedded in a matrix are shown. On the one hand, among the different methods explained, microchips have been found to be one of the most powerful and used techniques to measure single nanowires not embedded in a matrix. It is possible to design microchips with different capabilities in order to measure one or several properties of a wider variety of single nanowires with high accuracy. On the other hand, techniques based on Scanning Probe Microscopy (SPM) or optical techniques are powerful tools to measure and analyse properties of single nanowires. Particularly, the SPM technique allows measurements of the properties of single nanowires when they are embedded in a matrix. These values are of vital importance when considering a real device. From these measurements, one can study the changes in the properties of the nanowires due to the effects of quantum confinement or boundaries.

The second part is described in Section 3, where techniques related to nanowire array measurements are explained. This measurement configuration is important because it has been observed that oxidation at the nanowire surface occurs when the nanowire is out of the matrix in certain cases. This effect, or any other that affects the surface, could modify the values of their properties from those corresponding to the nanowires embedded in a matrix. In order to measure the thermal and electrical properties of a whole array inside a matrix, specific setups have been built. Moreover, optical techniques, like the photo-acoustic one, have also been adapted to nanowire arrays in order to study their thermal properties.

2. Characterization techniques of single nanowires

This section will cover some relevant examples of the various devices and methodologies in use to measure electron and phonon transport in single nanowires.

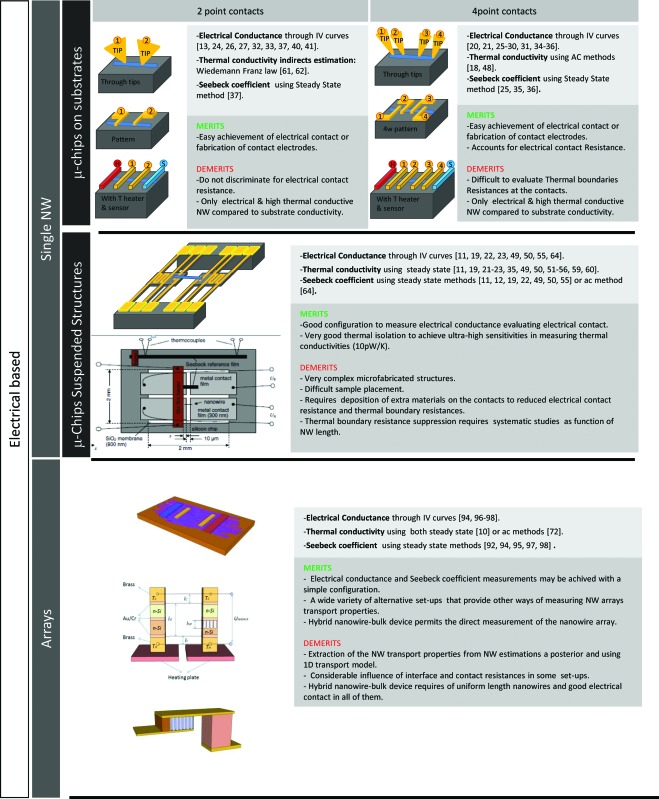
Adapting the measurement techniques currently in use for macroscopic materials to samples with nm dimensions often requires stringent technical demands. For contact techniques, a miniaturization of the electrical contacts and/or the thermometers and heaters is mandatory and micro/nano-fabrication tools are required to build up specific microchips to enable thermoelectrical measurements in 1D structures. Single nanowire properties can also be measured by Scanning Probe Microscopy (SPM) and optical techniques. In the first case, different SPM modes and probes make analysis of the electrical and thermal properties of single nanowires possible thanks to their nanometre resolution. A further advantage of these techniques is the possibility of measuring not only single nanowires but also nanowires embedded in a matrix, as shown in Section 2.2. In the case of optical techniques, electrical and thermal conductivities of single nanowires have been measured with micro-Raman or micro-photoluminescence spectroscopy. In some cases, the use of an appropriate microchip to place the nanowire is required, but in general these optical techniques can be regarded as non-invasive. Table 1 summarizes the main techniques covered in this review.

Table 1. Summary of the different techniques for measuring transport properties presented in this review, for both single and arrays of nanowires.

2.1. Microchips designed to measure single nanowires

The continuous development of the microelectronic industry has provided a broad variety of well-established fabrication methods that have paved the way to miniaturization. This approach has been extensively used and many dedicated microchip devices have been built during the last decade.¹⁰ In many cases, downscaling also permits the development of new measurement techniques that are specific to the nanoscale, as will be shown later.

The measurement of single nanowires using microfabricated probes provides a powerful tool that, with the appropriate design, can deliver not only one specific transport property but also a combination of them. Therefore, microchips with capabilities to measure electrical conductivity, thermal conductivity and/or Seebeck coefficient have been reported in the past years.^11,12

One of the main outcomes of microchip devices is that they provide access to measurements on nanowires with very small diameters down to few nm, where quantum size effects may rule transport properties.^13,14 This size domain, where thermal or thermoelectrical measurements are challenging because of the required sensitivity, offer tremendous prospects for the realization of efficient thermoelectric materials. Additionally, at these very small sizes surface effects become so important that surface absorption of elements can induce variations in electrical transport along the nanowire.¹⁵

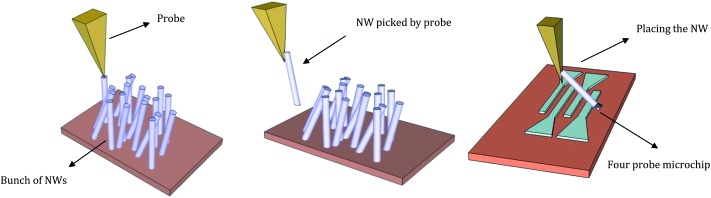
Generally, the fabrication process is one of the main difficulties of these microfabricated devices, because of the need for very specific equipment and installations to implement them. The experimenter faces the challenge of placing the nanowire (NW) at the right position and obtaining low electrical and thermal resistance.¹⁶ When the NW cannot be grown directly in the microchip, there are two main strategies. In the first strategy, single nanowires are placed onto a substrate prior to the microchip fabrication. When nanowires are grown inside a certain matrix, one must first dissolve the matrix that contains the nanowires. In the case of free standing nanowires, this process is not necessary. In both cases, the nanowires are dispersed into a volatile solvent, such as ethanol. Then, a drop of this solution is placed onto the substrate, and the whole set-up is allowed to dry in air. Once the nanowires are placed on the substrate, a lithography process is performed to define the microchip design, followed by the deposition of a certain metal to provide electrical contacts at the ends of the nanowire. These contacts can also act as heaters or thermometers, depending on the requirements of the measuring configuration. These heaters usually consist of two platinum zigzag heating lines which are connected to both ends of the nanowire and which will provide a way of controlling the temperature at the micrometer scale. Finally, in certain cases where further isolation is necessary, in order to have the nanowire suspended between the contacts and avoid leakage to the substrate, removal of the substrate under the nanowire is carried out. This can be achieved via Reactive Ion Etching (RIE), for instance.¹⁶ The second strategy is the fabrication of the microchip with all its features, such as the heaters and contacts, made prior to the positioning of the nanowire. The advantage of this approach is that lithography steps are easily repeatable and a great number of identical microchips can be made at the same time, especially in single silicon wafers. The placement of the nanowires on the chips is made in the same way as mentioned previously, that is, a solution of suspended nanowires in a volatile solvent is dropped onto the wafer. Statistically, some of the nanowires will be placed exactly where they should be, that is between the electrical/thermal contacts.^16,17 In some cases, one can also combine a focused ion beam (FIB) and a nano-manipulator to place the single nanowires on pre-patterned electrodes.¹⁸ With this method, it is possible to select specific nanowires as well as to locate the nanowire accurately on the electrode contacts. For this purpose, the desired nanowire is usually pulled out from the hosting bundle with a tip (see Fig. 1). An electrostatic force at the metal tip can attract a semiconducting nanowire when it is close to the tip. Once the tip touches the end of the nanowire, a platinum deposition is made between the tip and the nanowire for adhesion using an electron beam. Then, a strong “pull-out-force” is applied to extract the nanowire from the bundle. Finally, using a nano-manipulator the “pulled” nanowire is placed on four-point-probe electrodes and an ion beam is used to cut the linkage between the tip and the nanowire. This provides a reliable, selective and highly reproducible way of placing the nanowires in a desired location for certain applications. Nevertheless, it presents a clear disadvantage over the above mentioned procedure, because it is a time consuming process.

Fig. 1. Schematic view of picking and placing a single nanowire for transport property measurements.

2.1.1. Electrical conductivity measurements

Achieving good electrical contacts is the first requirement of any electrical measurement. In this sense strategies mimic those used in the macroscopic domain, but with the need for spatial resolution imposed by the low dimensionality. In cases where quantum confinement plays a role, changes in the electronic density of states and energy levels of the carriers also need to be considered.

For nanowires placed on top of insulating substrates or on substrates covered by thin isolation layers, electrical contacts can be achieved in different ways, as shown in Fig. 2. If the metallic contacts are patterned on the substrate before placement of the NW, the contact can be achieved mechanically, which requires use of sophisticated damped probe stations to minimize distortions due to vibrations, or by deposition of a contacting material, either by Electron Beam Induced Deposition (EBID) or Focus Ion Beam (FIB). In the first case, a hydrocarbon layer is grown by focusing the energetic electron beam of a SEM in the contact area between the NW and the tip. In the second case, platinum can be deposited with high accuracy on the selected region. The NWs can also be dispersed on the substrate and contacted afterwards by a lithographic process of sufficient spatial accuracy to deposit, by standard evaporation methods, the metallic contacts at the ends of the NW. For semiconductor NWs the strategy varies slightly due to the requirement to obtain adequate Ohmic contacts. In all cases, the metal of the electrical contact should be carefully selected, with a work function that permits alignment of the Fermi levels and easy injection of the carriers within the NWs.

Fig. 2. Main types of microchips used for the measurement of transport properties. The design of the microchip and the technique and methodology of choice highly depend on the transport property to be measured (electrical, thermal or thermoelectrical), on the material characteristics (metal, semiconductor or insulating) and on the fabrication of the nanowire.

The most straightforward measurement is the determination of the resistance of the nanowire at a certain temperature, R(T ₀). This can be done by injecting a very low current (in order to avoid self-heating by the Joule effect) into the nanowire via the electrical contacts and measuring the voltage drop¹¹ or plotting I–V curves to obtain the electrical conductance.^19–23 Once the conductance is known, the electrical conductivity can be derived, provided the size and geometry of the nanowire are measured with sufficient accuracy. It is important to note that because of the large impedance associated with individual nanowires, low current precision sources and voltmeters with large input impedances are required for very sensitive and accurate measurements.

I–V curves can be obtained using two probes,²⁴ in which case the influence of the contact resistances may affect the validity of the measurements. Improved accuracy can be achieved by removing the influence of the contacts, probes and spreading resistance using four electrical contacts instead of two.^25,26 The basis of the measurement is the same as that in the case of I–V curves, but the current is passed through the sample with two probes while the voltage drop is measured with the other two probes. Four probe measurements can be carried out with suspended probes^26–28 or with specific designs of the metallic probes on a substrate (see Fig. 2 for a particular example).^29–35 Although the design of this kind of microchips (which we will call four-probe microchips) can be quite complex, a wide variety of nanowires have been fully characterized with them. Moreover, with a slight change in their design, this sort of microchips can measure the dependence of the electrical resistivity with temperature. To that aim, micro-heaters must be placed in one or both ends of the nanowire.^19,36,37 It is also possible to observe semimetal–semiconductor transitions in nanowires while performing those measurements. Models and techniques have been developed to study this phenomenon in nanowires.^38,39 The contact resistance can be evaluated by conducting electrical measurements at different points along the length of the nanowire, such as those performed on 50 nm NiFe/Pt multilayer nanowires.⁴⁰

These types of microchips have also been used to modify the number of charge carriers.⁴¹ In this case, the end contacts of the nanowire serve as source and drain, and the number of carriers flowing through it can be manipulated by the gate voltage, V _g, applied to the back of the substrate. The carrier density induced by the gate voltage can be studied and the mobility of electrons (μ _e) in the nanowires calculated. For this purpose, we must use the equation I _sd = I ₀(V _sd) + (μ _e CV _sd/L ²)V _g where C is the capacitance of the nanowire and I _sd is the current through the nanowire that takes into account two components, the conventional current I ₀, and the current induced by V _g. However, even in the case of Si, there is no consensus if the mobility in NWs is smaller or larger than in bulk Si, since many factors, including NW diameter, crystalline orientation, surface termination or dopant concentration, influence the mobility of the carriers.⁴² It is also possible to obtain the dopant profile along the nanowire length with a similar microchip design. One can carry out capacitance–voltage measurements⁴³ and from low and high frequency capacitance measurements obtain the carrier density profile of the nanowire.

As far as the accuracy and sensitivity of the technique are concerned, when measuring electrical conductivity in metallic and semiconducting single nanowires with the aid of microchips, one can find different values in the literature. For example, Völklein et al. ¹¹ measured transport properties of Pt, Au, Cu and Bi free standing NWs of around 200 nm diameter and 20 μm length with a two probe microchip, obtaining for the Pt NW an electrical conductivity of 4 × 10⁶ (Ω m)^–1 with an error of less than ±0.4 × 10⁶ (Ω m)^–1, and a thermal conductivity of 20 W K^–1 m^–1 with an error of ±4 W K^–1 m^–1 at room temperature. Nowadays, high accuracy measurements have been achieved with other microchips, mainly with four probe ones, that are capable of detecting electrical currents through the NWs of few nano-amperes²⁹ and thermal conductivities of few W K^–1 m^–1.¹⁹

2.1.2. Thermal conductivity measurements

Since effective thermal barriers are not readily available and heat can diffuse through any media, accurate thermal conductivity measurements of single NWs are particularly challenging. In small or medium diameter NWs, where phonon transport is dramatically reduced due to scattering with the boundaries, the energy transfer between the two extremes of a NW held at different temperatures is extremely small and heat losses with the surroundings have to be greatly diminished to carry out reliable measurements. Only in the case of conducting NWs can simpler approaches that benefit from electrical measurements be envisaged.

For conducting nanowires, electrically isolated from the substrate (like those shown in Fig. 2a–c), the nanowire itself can be used as a heater and the thermal conductivity can be derived using the 3ω method, which is well established in the case of bulk materials and thin films.^44–47 It consists of applying an alternating voltage signal to a heater while measuring the third harmonic (3ω) signal response, which is related to the thermal conductivity of the sample. In the four-probe 3ω-method applied for the measurement of single nanowires,^18,48 an alternating current is passed through the nanowire at a frequency ω. Then, the 3ω-voltage response of the nanowire is measured with the other two electrodes. This 3ω-signal correlates with the thermal conductivity of the nanowire according to the equation¹⁸

1

where L, R = R ₀ + R′(T – T ₀) and S are the length, electrical resistance and cross-sectional area of the nanowire, respectively. R′ is the resistance change with temperature at room temperature defined as (∂R/∂T)_T and k is the thermal conductivity of the nanowire.

In general, suspended structures, where the influence of the substrate on the thermal signature is minimized, have to be used for thermal measurements on single nanowires. Fig. 2d shows a SEM micrograph of the central part of a typical suspended structure designed to measure thermal and/or electrical conductivities and the Seebeck coefficient of individual NWs. Although a variety of designs can be found in the literature, most of them consist of 2 suspended platforms, each around 15 μm². Every platform consists of a zigzag heater made of Pt deposited on top of a SiNx membrane and can be used as a heater or temperature sensor.^49,50 Two additional electrodes enable electrical contacts of the NW under study. Both platforms are suspended by long (200 to 400 μm) and narrow (2–4 μm) SiNx arms connected to the Si frame. With this geometry the thermal conductance between the platforms and the Si frame is ∼80 nW K^–1 at 300 K in high vacuum conditions. The nanowire is placed bridging the gap between the heating and the sensing membranes. The measurement is then performed by increasing the temperature of one of the platinum heaters while the temperature change of the opposite electrode is recorded. By a proper analysis of the heat losses through the beams, the thermal conductivity can be obtained through a simple one dimensional analysis.^{16,17,19,23,51–55}

Thermal conductance of the order of 1 nW K^–1 at room temperature is in the lower limit of sensitivity of these devices. Several factors limit the sensitivity of standard four-point measurements on these types of structures, but among them temperature stability of the cryostat and its influence on the electrical measurements are probably the most relevant. It is worth noting that very small diameter nanowires with thermal conductivities of the order of 1 W m^–1 K^–1 will have thermal conductances as low as 10 pW K^–1, and therefore sensitivity improvements are required. In this direction, the use of an on-chip Wheatstone bridge circuit has recently enabled a significant reduction of the noise in conductance to values of ∼10 pW K^–1 at room temperature.⁵⁶ Using this setup, Chen and co-workers⁵⁷ have evidenced the important role of phonon confinement in the reduction of the thermal conductivity in Ge–Si core shell NWs with core diameters below 20 nm. On the contrary, for highly conductive samples bridging the two platforms, such as membranes, carbon nanotubes or graphene, it becomes necessary to consider the modification of the temperature distribution on the platforms. In this case errors around 25% are possible if the standard 1D solution of the heat equation is used. Finite element modelling can be very helpful to provide insights into the modifications of the temperature profile of the suspended platforms. Another source of error in the determination of the thermal conductivity of nanowires can arise from thermal losses by radiation. In this respect, the use of low temperature differences between heater and sensing platforms and the use of appropriate radiation shields should be considered for accurate measurements. The presence of an unknown thermal contact resistance between the nanowire and the heating/sensing platforms is another source of uncertainty. Therefore, a remaining challenge is to reduce or adequately take into consideration this contact resistance. Recently, Yang et al. ⁵⁸ performed measurements of thermal resistance versus the length of multi-walled carbon nanotubes (MWCNTs) and concluded that 50% of the thermal resistance of the nanotube could be due to the contact resistance. Using EBID or FIB to locally grow thermally conducting layers may help improve the contact, but does not reduce it completely.

Suspended structures have been used to measure thermal conductance in a variety of nanowires, with different doping, diameters and roughness,^59,60 including single- (SWCNTs) and multi-walled carbon nano-tubes (MWCNTs),⁵⁸ Si, SiC, Si/SiGe,^29,54,59,60 Bi, Bi₂Te₃,¹⁶ InAs,⁵⁹ PbS, PbSe, PbTe²³ and ZnO³⁵ NWs, among others.

Although theoretically predicted, experimental evidence for clear deviations of classical transport models due to the appearance of quantum confinement effects on the thermal conductivity of single nanowires is still scarce. One example is the measurement of the thermal conductance of Ge–Si core–shell ultrathin NWs, in which the theoretically predicted phonon coherent resonance effect has been experimentally demonstrated.⁵⁷ Further developments of the techniques are necessary to unveil the quantum size regime in nanowires, only few nm in diameter.

In metals, the thermal conductivity can be calculated from the electrical conductivity using the Wiedemann–Franz law. This relationship establishes that in a metal the rate between the electrical and thermal conductivity is proportional to the temperature and a proportionality constant, L, known as the Lorentz number. This expression is written as k _e/σ = LT. Under the assumption of constant temperature and using the thermal and electrical conductivities of a bulk reference sample, it is possible to use the Wiedemann–Franz law to determine the electrical and thermal conductivity of metallic nanowires:

k/k_bulk = σ/σ_bulk 2

This assumption is only valid when the lattice part of the thermal conductivity is negligible in comparison to the electronic term.^61–63 A topic of current interest is whether, when the mean free path of the carriers is comparable to or smaller than the characteristic size of the nanowire, the Lorentz number shows size effects. Recent measurements of electrical conductivity and thermal conductivity on metallic Pt nanowires have found smaller Lorentz numbers than those obtained in the bulk.⁶¹ Further developments of thermal measurements will allow testing these results in other small diameter metallic nanowires.

2.1.3. Seebeck coefficient measurement

To fully characterize the nanowires regarding their thermoelectric capabilities, one needs to measure their Seebeck coefficient, and this can also be made with the aid of different microchip designs. For instance, the suspended structure described in Fig. 2d provides a simple way of performing this measurement by controlling the temperature difference between both ends of the nanowire and measuring the voltage drop across the nanowire.^19,21,22 Given that the Seebeck coefficient is defined as the ratio between the voltage produced and the temperature gradient present in the sample, that is,

S = ΔV/ΔT 3

where ΔV is the voltage variation and ΔT the temperature difference, both measurable in this set-up, the Seebeck coefficient can be obtained. The contribution of the Seebeck coefficient of the wire connected to the sample should be taken into account to obtain accurate values of S _sample.

It is worth mentioning that the measurement of the Seebeck coefficient is associated with at least two experimental challenges in the case of nanowires, namely the generation of a temperature gradient and the exact determination of the temperature at the nanowire contacts. One possible approach to overcome these limitations is described in ref. 11 and 12. The basis of the microchip design used in this case (see Fig. 2e) is the comparison between the nanowire under study and a known reference film. The chip consists of two identical pairs of metallic contacts. A suspended nanowire is placed between two of them, and a film with a known Seebeck coefficient, S _R, between the others. This microchip also holds a thin-film heater, deposited onto the bottom side of the sample, in order to generate the same temperature difference through the film and the nanowire, ΔT. If one takes into account the Seebeck coefficient of the contacts, S _c, from eqn (3) the temperature difference can be determined as ΔT = U _R/(S _R – S _c). Then, the voltage drop across the nanowire, U _N, created by the same temperature difference, can be calculated according to S _N – S _c = U _N/ΔT = U _N/[U _R/(S _R – S _c)].

In ref. 64 the Seebeck coefficient is obtained using the 2ω technique with a four-probe microchip. For this method, an AC current at frequency ω is applied, which produces Joule heating in the microheater with a frequency 2ω. The heat generated causes a temperature oscillation that propagates through to the nanowire. Using the four-probe technique, the temperature difference between both ends of the nanowire can be measured, ΔT(2ω), along with the voltage drop ΔV(2ω), across the nanowire. Thus, the Seebeck coefficient can be obtained from S = ΔV(2ω)/ΔT(2ω). The electrical conductivity of the nanowire in ref. 64 was measured within the same microchip via I–V curves, as it was explained before, obtaining the Power Factor of single nanowires.

Given that the Seebeck coefficient is expected to increase when reducing the diameter of the nanowires due to a higher density of states near the Fermi level,^2,8,38 these microchips have been extensively used to compare nanowire behaviour with bulk.^14,16,19,55 In practice, modification of the electronic density of states is expected to occur for very small diameter NWs. The work of Heath and co-workers shows a substantial Seebeck enhancement with respect to bulk samples for 20 nm doped Si NWs. Shi and coworkers have also observed an enhancement on 50 nm Bi₂Te₃ NWs. The improvement of measurement techniques to characterize nanowires of smaller diameter will undoubtedly stimulate further experimental and theoretical investigation of the influence of quantum size effects on the thermoelectricity of nanowires.

2.2. Single nanowire measurements with scanning probe microscope techniques

An alternative to the measurement of single nanowires with microchips, as presented in the previous section, is their study with the aid of Scanning Probe Microscopy (SPM) techniques, where a tip or probe scans the nanowires with nanometric resolution. These techniques provide some advantages and shortcomings with respect to measurements performed with microchips. Among the first, SPM techniques provide a morphological image of the surface of the sample from the interaction between the probe and the surface. Different physical characteristics can also be measured locally taking advantage of the high spatial resolution of SPM techniques and changing the kind of probe used. To this aim, the use of thermal (for thermal conductivity measurement) and/or conductive probes (for electrical conductivity), which are commercially available, along with slight modifications to the SPM microscope set-up, makes the measurement of the transport properties of single nanowires inside and outside the matrices possible. The nanowires outside the matrix should be placed onto a substrate in a similar way as they are placed in the microchips. In the case of nanowires inside the matrix, it is important that the tips of the nanowires should be touchable by the AFM tip. The fact that the nanowires can be measured inside the matrix is an important advantage versus microchips since no oxidation is produced in the nanowire surface and the nanowire is not exposed to any chemical that can damage the wire.

Among the potential drawbacks of the SPM technique, we note the restriction to measure NWs of diameters smaller than the size of the tip, which vary in the nano-meter scale depending on the kind of measurement, and the need for a very specific expertise to obtain reliable data. This thorough understanding of the particular SPM technique does not only play a role in the performance of the measurement but also in understanding the results. The reason is that in most cases one does not obtain a direct measurement of the property, but it is necessary to use a theoretical model from which the property has to be extracted.

2.2.1. Electrical conductivity measurements

With a standard AFM microscope it is possible to obtain a topographic image of nanowires embedded in a template. After that, the AFM tip can be positioned and contacted on top of a nanowire (see Fig. 3). If the tip is conductive, one can pass current through the nanowire and measure its voltage difference. Several I–V curves of different nanowires provide information on the electrical resistance of the nanowires and, by knowing their geometrical dimensions, it is possible to determine their electrical conductivity.⁶⁵ Like in two probe microchips, the main drawback of this technique is the influence of the contact, probe and spreading resistances on the accuracy of the electrical conductivity measurements. The size of the tip must be properly selected depending on the diameter of the nanowires. Smaller diameters make positioning of the tip on top of the nanowires more difficult.

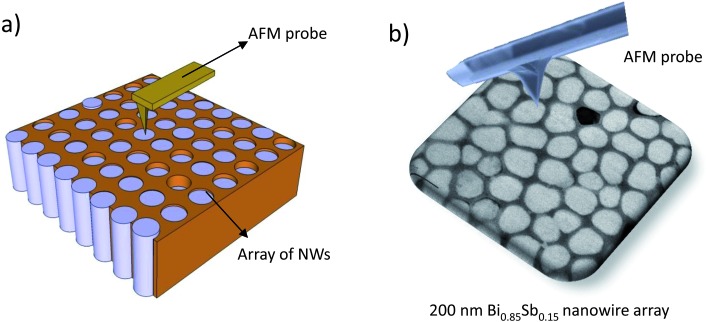
Fig. 3. (a) Schematics of the positioning of the AFM tip on top of an array of NWs to enable electrical conductivity and Seebeck coefficient measurements. (b) Illustration of an AFM probe scanning 200 nm diameter Bi_0.85Sb_0.15 nanowire array.

Another SPM technique that has been modified to be applied to the study of nanowires is Scanning Tunneling Microscopy (STM). This kind of microscope is able to image surfaces at the atomic level based on the concept of quantum tunneling. This effect takes place when a bias is applied between the tip and the surface to be examined (both must be conductive) and they are brought close enough to allow electrons to tunnel through the vacuum between them. The current resulting from those electrons is a function of the tip position, the applied voltage, and the local density of states. With all this information, the electrical conductivity, density of states and Fermi level of silicon oxide nanowires have been obtained via STM measurements. Moreover, if a voltage is applied between the ends of the nanowire, it is possible to observe how the voltage decays along its length by scanning the nanowire with the STM tip.⁶⁶ From this measurement, and using the geometrical dimensions of the nanowire, the electrical conductivity can be determined. Plotting I–V curves with the STM tip when the nanowire is placed between two electrodes is another possibility.⁶⁷

Some disadvantages of the STM technique are the slower scan speed compared to other techniques that are mainly used to analyze conducting materials and that are very sensitive to mechanical and acoustic vibrations, and the requirement of high vacuum conditions which adds complexity to the overall setup.

Kelvin Probe Force Microscopy (KPFM), which maps the surface potential of a sample at atomic or molecular scales in non-contact mode, is another SPM technique that has been used for the measurement of nanowires. In this case, the tip is conductive. The surface potential measured by KPFM is related to the work function of the sample, from which many different surface phenomena can be studied. The work function is measured from the interaction of the electrostatic forces between the conductive AFM tip and the sample surface. A voltage difference, consisting of a DC bias, U _dc, and an AC-voltage, U _AC sin(wt), is applied between the tip and the surface of the sample. Then, an electrostatic force is produced at the tip. This force can be written as

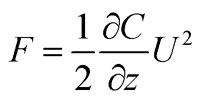4

where U = U _dc + U _ac sin(wt) is the total potential applied and C is the capacitance of the probe–sample system. The capacitance includes geometrical and dielectric properties of the probe–sample system. A local change in the dielectric properties would produce a change in the force signal. The force equation can be split into different terms, when substituting U, according to eqn (4):

F = F_dc + F_w sin(wt) + F_2w sin(2wt) 5

On the one hand, the first term, F _dc, contributes to the topographical surface image. On the other hand, the third term, F _2W, is related to the dielectric properties of the sample. However, in order to measure the surface potential of the sample the second term, F _W, of this equation must be considered. This term depends on the dc voltage and the ac voltage applied. It can be described as

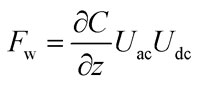6

The dc voltage is composed of two terms, U _dct = U _ext – U _surf where U _ext is the external dc voltage applied while U _surf is the surface potential. Therefore, in order to measure the surface potential, the condition F _w = 0 must be fulfilled. By adjusting the external dc voltage to the surface potential, U _ext = U _surf, it is possible to map the surface potential with a KPFM.⁶⁸

Therefore, the KPFM image gives information about the composition and electronic states of the local structures of the surface and has been used to make electrical analysis of single nanowires.^69–71 This technique can also be applied to the study of the doping of a nanowire, the local voltage drop along the nanowire or the resistance or electrical conductivity of a single nanowire. In order to measure the resistance and electrical conductivity of the nanowire, KPFM measurements of the nanowire are performed with and without an external applied bias and the voltage drop along the nanowire is studied. The subtraction of the data obtained from the unbiased and biased cases allows the deduction of the electrical resistance of the nanowire. If the mobility and the charge of the carriers are known, calculation of the carrier concentration in semiconducting nanowires is possible using the equation, σ = qnμ.^70,71 This technique was employed by Koren et al. ⁶⁹ to measure the non-uniform doping profiles of Si NWs. The dopant distribution along the nanowire length ranged from 1.25 × 10¹⁹(cm^–3) up to 2.25 × 10¹⁹(cm^–3) over a distance of 10 μm.

KPFM requires specialized skills to obtain accurate measurements of the surface potential of the sample. It entails complex probe fittings while measuring, such as fitting of the phase or amplitude of the first and second harmonic signals from the probe. Special care is needed to prevent touching the tip with the surface when doing KPFM measurements, to avoid distortion of the surface potential image. Afterwards, the information given by the KPFM image is related to the work function of the different materials of the sample and must be properly evaluated.

2.2.2. Thermal conductivity measurements

The measurement of thermal properties of single nanowires with SPM techniques has been performed with a combination of Scanning Thermal Microscopy (SThM) and the 3ω method.

SThM uses thermal probes to make a thermal map of a sample surface. Some of the most used tips in SThM are the Wollaston probes, which basically consist of a platinum (Pt) wire. Another kind of probes is constituted of an integrated palladium film on a substrate. In both cases, the electrical resistance of the tip changes with temperature and this makes thermal mapping possible.

SThM could be combined with the 3ω method to determine the thermal conductivity of a sample quantitatively. In this technique, the tip is in contact with the surface of the sample and the application of an alternating signal to the SThM tip causes its warming due to the Joule effect. Then, a heat flux from the tip to the sample is dissipated. The rate of heat flux dissipated to the sample is related to the different thermal conductivities of the composite. This effect will cause a 3ω electrical signal response in the tip that can be measured. From the 3ω voltage measurements and the use of thermal models, the thermal conductivity of nanowires can be calculated.

The thermal conductivity of Si single nanowires, with diameters ranging from 250 nm to 4 μm and embedded in a matrix, has been measured using a Wollaston probe mounted on a nanopositioning stage.⁷² This stage is mounted inside a Scanning Electron Microscope (SEM), and it is used to position the tip on top of the nanowires. The probe is used as both a heating element and thermometer by measuring its electrical 3ω signal response when contacting a nanowire.^73,74 The thermal conductivity shows a decrease for smaller diameter Si nanowires, as previously found by other authors. The uncertainty of these measurements, ∼30%, mainly induced by the small heat impedance of the Wollastone probe, obscures detailed physical analysis of the size dependence.

In ref. 75–77 a probe made of a palladium film that has a spatial resolution under one hundred nanometers has been used. This allows the measurement of nanowires with smaller diameters than the Wollastone probe. Puyoo et al. ⁷⁶ and M.M. Rojo et al. ⁷⁷ carried out thermal imaging of individual Si and Bi₂Te₃ NWs, respectively, with a spatial resolution around 100 nm. Using these tips with a SThM in 3ω mode configuration, the thermal conductivity of single Si and Bi₂Te₃ nanowires of around 200 nm in diameter was determined to be close to that of the bulk material. As outlined in ref. 76 and 77, the thermal contact resistances between the tip and the NW or the NW to the substrate resistance should be properly considered to obtain reliable values of the thermal conductivity of the NW. Theoretical models and the calibration of the probe are an important part of these methods in order to obtain an accurate value of the thermal conductivity of the nanowires.

Thermal conductivity values of around 1.3 W K^–1 m^–1 for 200 nm diameter Bi₂Te₃ NWs and around 128 W K^–1 m^–1 for 200 nm diameter Si NWs have been determined by SThM. The importance of evaluating the NW/matrix influence properly and the right approach to calculate the thermal conductivity of the nanowires accurately could be extremely important.⁷⁷ SPM techniques are non-destructive and therefore allow post-measurements of other properties of the nanowires, like the electrical conductivity or the Seebeck coefficient, using complementary techniques. Further developments in tip design may soon enable sub-100 nm resolution, making these techniques ideally suited to investigate size effects in small diameter single NWs embedded in matrices.

2.3. Single nanowire measurements by optical techniques

Optical measurements in bulk samples are usually characterized as being non-invasive and quite versatile techniques, although their maximal resolution is restricted to sizes comparable to the wavelength of the light used through the Abbe diffraction limit. Nevertheless, this resolution limit was overcome some time ago and nowadays sub-wavelength studies can be carried out with different optical techniques, such as Scanning Near Field Optical Microscopy (SNOM). This is important in the case of aiming directly at single NWs, which would not be detected by optical means otherwise. Nevertheless, classical optical techniques can also be used to measure different properties of single NWs, provided that those isolated NWs are placed onto an appropriate substrate in such a way that they are easily detectable. This is usually achieved with the aid of microchip devices, similar to those presented in Section 2.1. Moreover, the use of microchips combined with optical techniques provides a wider range of measurement possibilities. Then, light can be used to excite carriers in a NW and study the current they create under an external field (photocurrent). This current can be detected and measured with the aid of a microchip (Section 2.3.1.). Light can also be used to heat the sample locally with a focused laser beam or to excite photoluminescence at a certain point of the NW. Optical means can also be used to detect the temperature change of a NW using Raman Thermography or microphotoluminiscence (Section 2.3.2).

Nevertheless, this necessary combination of optical means and microchips is also one of the main drawbacks for the application of optical techniques to the characterization of single NWs. Firstly, the required equipment is more, because not only the appropriate optical equipment (such as lasers, optical microscopes, detectors) has to be available, but it is also imperative to have the facilities and expertise to design and fabricate the microchips. Then, the placement of the NW along with the performance of the electrical contacts at the end of the NW is of paramount importance, as in the case of microchip devices.

2.3.1. Analysis of electrical properties of single nanowires

In order to study transport properties within a NW, light can be used to locally generate an excess of carriers, which induces an electrical current (known as photocurrent). The study of the electrostatic potential through this technique, called Scanning Photocurrent Microscopy (SPCM), has been used for the electrical analysis of single NWs. This is not an exclusively optical technique, because it involves the measurement of the current created along the nanowire under illumination, and thus implies the placement of the single NW in an appropriate microchip with electrical contacts. A laser beam is then focused into the nanowire and a local photocurrent is generated, which is highly sensitive to the electric field. In that way, one can obtain information about interfaces, inhomogeneities, carriers or dopants. For instance, in ref. 78 the potential profiles of phosphorus doped silicon nanowires are quantitatively measured and the effective concentrations of the carriers are determined. For these measurements the silicon NWs were mounted into four-probe microchips, and those on a piezoelectric scanning stage. Then a 532 nm wavelength laser was focused using a confocal microscope. The drift of the free carriers excited by illumination in the presence of an electric field creates the photocurrent. By studying the different photocurrents in as grown and etched NWs, surface doping can be studied. SPCM has also been used to determine the minority carrier mobility of CdS NWs, indicating that the electron transport (μ _e τ _e ≈ 5 × 10^–7 cm² V^–1) was more efficient than the hole transport (μ _h τ _h ≈ 1 × 10^–7 cm² V^–1).⁷⁹ For these measurements, a chopped 457 nm wavelength laser was focused on to a ∼400 nm spot and the NW was placed onto a microchip with contacts at both ends of the NW. Then, a bias voltage was applied between the contacts and the photocurrent created by the illumination was recorded as a function of the position of the beam.

Given that the quantities measured by SCPM can be also measured by Kelvin Probe Force Microscopy (see Section 2.2.1.), these results can be cross-checked with KPFM. Nevertheless, KPFM is a very sensitive technique in which the measured potential can be perturbed if the probe touches the surface of the nanowire. Then, SPCM provides an alternative where the light does not induce any perturbation to the device while supplying a high spatial resolution, which gives insight into the transport processes.⁷⁸

2.3.2. Light-based thermal conductivity measurements

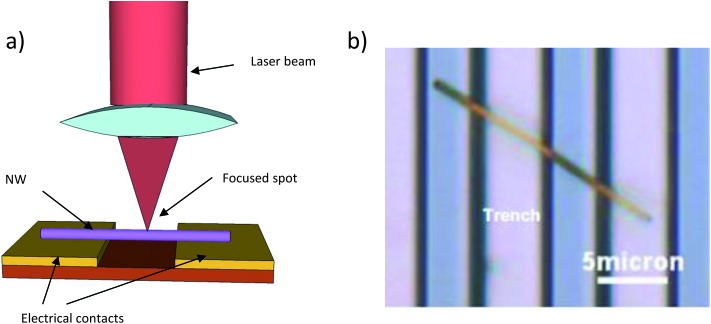
One spectroscopic technique that has been adapted to the measurement of the thermal conductivity of nanowires is photoluminescence. As it was said before, the isolated nanowires have to be easily characterized with classical optical techniques. For example, single CdS NWs with diameters ranging from 200 to 400 nm were partially suspended on a silicon substrate with stripes, and trenches between these stripes.⁸⁰ The NWs were irradiated with a laser beam focused with a confocal configuration (see Fig. 4), causing at the same time local heating and the excitation of the fluorescence of the sample. The actual temperature rise can be determined knowing the laser power and the thermal conduction of the nanowires, which can be characterized through the micro-photoluminescence of the nanowire under the excitation of the laser. Studying different micro-photoluminescence spectra recorded at different temperatures, the temperature at the different positions of the suspended NWs can be extracted.⁸⁰ Thus the thermal conductivity is obtained from the temperature gradient along with the length of the nanowire section between two silicon stripes with the theoretical equation of heat conduction through a solid rod:

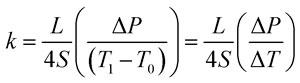7

where L is the length of the nanowire suspended between two stripes, S is the cross-sectional area of the nanowire, x is the position where the laser hits the nanowire and ΔP is the calculated energy absorbed by the nanowire considering the parameters of the laser (spot profile and diameter) and the absorptivity of the surface of the nanowire. Finally, ΔT is the temperature increment caused by the local heating of the laser. From these experiments, a thermal conductivity of 4.9–6.2 W m^–1 K^–1 was obtained for these CdS NWs.

Fig. 4. (a) Schematic view of the experimental set-up used for microphotoluminiscence. (b) Optical image of a suspended CdS nanowire for which microphoto-luminescence spectroscopy was conducted.

Another spectroscopic technique which has been used for obtaining the thermal conductivity of single nanowire measurement is Micro-Raman. The experimental setup is almost the same as the one presented in Fig. 4, with the NW suspended between two contacts or fixed on one side. Then, the excited Raman modes have to be spatially resolved to make a map of the temperature along the nanowire. Some examples of this technique applied to NWs can be found in ref. 81 and 82 where a thermal conductivity of κ ∼ 8–36 W m^–1 K^–1 in GaAs NWs of 150–170 nm in diameter, and κ ∼ 25–75 W m^–1 K^–1 in Si NWs of 80 to 30 nm in diameter was measured. In these studies, a nanowire is locally heated with a focused laser beam and then, the local temperature of the nanowire is determined via the Raman spectra at the micrometric scale. This can be done thanks to the linear relation of the shift of the transverse optical phonon frequency v with temperature, that is, there is a shift in the position of the Raman peaks that depends on the temperature of the sample. Then, from the theoretical model that describes the expected experimental temperature profile of a suspended NW,⁸³ the thermal conductivity can be calculated:

8

where P _abs is the power absorbed inside the nanowire (extracted from simulations), L is the length of the suspended part, A the cross-sectional area, and B ₁ the curvature.

3. Nanowire array measurement techniques

Until now we have discussed different methods to measure the properties of single nanowires, independent of their fabrication process. Nevertheless, it is worth mentioning that the most common way of producing thermoelectric nanowires implies the fabrication of an array of nanowires embedded in a certain matrix or free standing nanowires on a substrate. For instance, anodic alumina templates, or polymeric membranes, are widely used to fabricate nanowires of a variety of materials via electrochemical deposition.^84–88 The realization of efficient thermoelectric devices with sufficient power-output per unit area for a given temperature difference requires assembling a large amount of nanowires electrically connected in parallel within the individual n and p-type legs of the device. This configuration permits enhancing the output current and provides increased mechanical stability. In this sense, nanowire arrays embedded in matrices offer potential prospects for integration into real thermoelectric devices.^89,90 Therefore, it is important to develop techniques that allow measurements of the whole structure, as far as thermoelectric efficiency is concerned. In this section, we present measurement techniques that consider the array of nanowires with the matrix as a whole, and then, if the contribution of the matrix can be independently measured, enable the characterization of the nanowire array.

As previously mentioned in the introduction, these techniques present not only some practical advantages compared to single nanowire measurements, such as easier preparation of the samples, but also prevent the degradation of the nanowires when exposed to air or in the process of dissolving the matrix. In the case of materials in which their surface can easily oxidize, it has been reported that their measurement as single nanowires with the aid of microchips shows the effect of oxidation, modifying their transport properties.⁹¹ Surface oxidation adds complexity to the electrical measurements, and the need to locally remove the oxide layer prior to adding the metallic contacts, in order to obtain reliable data. Furthermore, some disadvantages regarding the measurement of NW arrays include growing a dense array of nanowires to adequately fill the matrix, the possibility of getting good thermal and electrical contacts to reduce the influence of the contact resistances and granting a proper access to the top of the nanowires to assure that the whole array is measured.

3.1. Electrical conductivity and Seebeck coefficient

The electrical conductivity and Seebeck coefficient of a nanowire array can be measured directly in a simple way. The only requirement of the sample is that nanowires must jut out the matrix at both ends of the matrix in order to ensure a good electrical contact. In the case where the nanowires are grown inside a matrix by electrochemical deposition, the electrical contact between what we could call “the bottom side” of the matrix and the nanowires is ensured. Then, the “top side” of the nanowires can be contacted by evaporating or electrochemically growing a gold layer, for instance. In order to measure the Seebeck coefficient, a difference of temperature is applied between both sides of the nanowire template, and at the same time, the Seebeck voltage generated between the top and bottom side is measured. Then, the Seebeck coefficient is calculated using the equation, S = ΔV/ΔT.^65,92–94 A slightly different arrangement is presented in ref. 95, where a set-up consisting of a heater and heat sink sandwiching a nanowire array sample was used to measure the Seebeck coefficient of the array.

Electrical conductivity measurements can also be done taking advantage of the previous measuring configuration. An electrical current is passed through the nanowire array while the voltage drop across the nanowires is measured. The I–V curves obtained are used to calculate the electrical resistance of the nanowire array.⁹³ Two probe measurements can be carried out to obtain I–V curves for several nanowires of the nanowire array but the estimation of the number of nanowires selected is quite complex.⁹⁶ For that purpose, there are several software programs that can help in this estimation to determine it more accurately. As it is a two probe measurement, the influence of the contact and spreading resistances are the main drawback of this technique.

In order to measure the electrical conductivity and Seebeck coefficient of different nanowire arrays, one can use a thin film sample of randomly aligned nanowires on a substrate. Usually this thin film is fabricated by nanowire casting and pressing processes till it gets dense and solid.^97,98 On the one hand, a heater and a heat sink are placed on top of the sides of the thin film. Two thermocouples are in contact with the thin film in order to determine the temperature difference generated by the heaters. On the other hand, two electrodes are pressed on the thin film sample between the heaters for voltage drop measurements. Once the film has been fabricated and the electrical contacts have been done, the sample is ready for electrical conductivity and Seebeck coefficient measurements (see Fig. 5).

Fig. 5. Schematic set-up for electrical conductivity and Seebeck coefficient measurement of thermoelectric nanowires.

The measurement of the electrical conductivity of these nanowire films can be performed with a set-up similar to the four-probe system using the heaters as electrodes, given that they are in close contact with the sample and made of a conductive material. In this case, current is passed along the thin film and the voltage drop is measured. Taking into account the current–voltage curves (I–V curves), scanning electron images for the thin film thickness estimation as well as theoretical transport model considerations for the electrical transport in nanowires, the electrical conductivity of the nanowires can be obtained. To measure the Seebeck coefficient of the nanowires with the same set-up, one can apply a difference of temperature along the thin film sample using the heaters. Then, with the aid of the electrodes, the Seebeck voltage generated in the film as a consequence of such temperature difference can be measured. Thus, the Seebeck coefficient of the nanowires can be obtained from S = ΔV/ΔT.

An advantage of this system is the possibility of fabricating the nanowire thin film and making the electrical contacts with simple processes. Moreover, this technique is based on the four probe method which avoids the contact and spreading resistance of the system. This set-up makes measurements of the electrical conductivity and Seebeck coefficient of the whole film possible, from which later on the properties of single nanowires can be determined. However, one must use a one-dimensional electrical transport model to obtain the properties of the nanowire, which can be complex, as well as the right estimation of the film thickness.

3.2. Thermal conductivity measurements

The measurement of the thermal conductivity of template-embedded arrays of nanowires can, in principle, be accomplished by a variety of methods, ranging from steady state to ac current methods. This very important area of research is still in its infancy and there is room for improvement through the development of new methodologies and/or through modifications of existing tools already in use for thin films or single-nanowires.

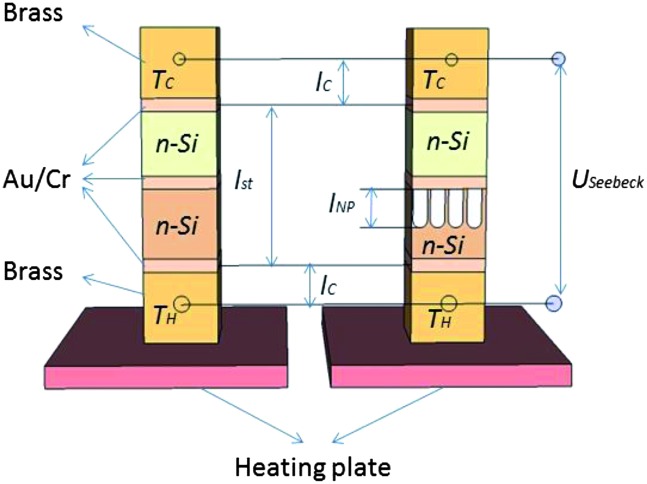
An approach recently used consists in determining the thermal conductivity of an array of Si nanowires from the Seebeck voltage of pressure-joined chip stacks. The device structure consists of two stacks. The first consists of a nanowire array composite pressed between metallic blocks. The other is a bulk Si substrate of similar composition and size in the same configuration⁷² (see Fig. 6).

Fig. 6. Schematic view of the experimental set-up for Seebeck coefficient measurements of NW arrays.

The thermal conductivity of the nanowire array composite is measured by placing both structures on a heating plate, which generates a temperature difference T _H – T _C between the brass blocks of the stacks. When the temperature gradient is constant along the stacks, the Seebeck voltage, U _Seebeck, generated by thermoelectric effects is measured.

A temperature loss is produced due to the brass block and contact layers in the stacks. It causes a decrease in the residual temperature gradient within the stack and thus a reduced Seebeck voltage is expected according to

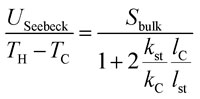9

where S _bulk is the Seebeck coefficient of the bulk sample, k _st and l _st the thermal conductivity and length of the stack, respectively, and k _C and l _C the thermal conductivity and length of the brass, respectively. Neglecting the thermal contact resistances between the blocks of the system and measuring U _Seebeck/(T _H – T _C), the thermal resistance of the nanowire composite stack and bulk stack, l _st/k _st can be calculated.

Under the approximation of no heat conduction through the ambient air and from the well-known bulk thermal conductivity, the thermal resistance of the nanowire array composite stack can be deduced:

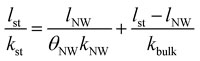10

where l _NW is the length compression of the nano-wires and θ _NW is the coverage of the stack area fraction. From this expression, the thermal conductivity of the nano-wires, k _NW, is calculated. This set-up was used to measure the thermal conductivity and Seebeck coefficient of arrays of silicon nanowires of 250 nm to 4 μm diameter at different temperature ranges. The thermal conductivity obtained for the nanowires was compared with the one measured with the 3ω-technique, made with a Wollastone tip, and a reduction of less than 30% of the thermal conductivity in comparison to bulk silicon was observed in both cases. As a main drawback, evaluating the thermal conductivity of the nanowires is related to eqn (10) that involves the use of different terms that must be evaluated as accurately as possible, like the coverage of the stack area fraction or the compression length of the nanowires.

Another approach, similar to the one described above but using microfabricated structures, was recently developed by Völklein and co-workers¹⁰ to measure the cross-plane thermal conductivity of arrays of Bi nanowires. Electrodeposition was used to grow Bi NWs on top of a highly thermally conductive substrate. On top of the sample a thin dielectric layer is deposited ensuring the isolation to permit the patterning of electrical heaters and thermometers. In steady state conditions, the heaters are used to impose a temperature gradient with respect to the substrate, which is used as a heat sink. The ratio between the temperature difference across the sample and the power released by the heater represents the total thermal resistance which accounts for the thermal resistance of the substrate, the thermal link introduced by the electrical leads used to contact the heaters and thermometers, the thermal boundary resistance between the different interfaces and, of course, the thermal resistance of the sample (both the template and the nanowires filling the pores). Using a suitable reference that contains the empty template (air at atmospheric pressure filling the nano-channels) the thermal conductivity of the nanowires can be evaluated. Complete suppression of the various interface resistances, to evaluate the thermal conductivity of the nanowires with sufficient accuracy, remains a challenge. Although these measurements can also be accomplished with the 3ω method, in general the steady-state method requires much lower electrical power density for the heater/thermometer and a less expensive/complex electrical measuring setup.

3.3. Figure of merit measurements of nanowire arrays

The efficiency of thermoelectric materials is related to their figure of merit, ZT, which is expressed as , where S is the Seebeck coefficient, σ is the electrical conductivity, k is the thermal conductivity and T the absolute temperature.

The figure of merit of nanowire arrays can be measured using the approach developed by Harman.^99,100 The Harman method consists of measuring the ac resistance (R _dc) of the composite and the dc voltage (V _dc) when we pass a low current (I _dc) through the system, and determining the figure of merit through the equation ZT = (V _dc/I _dc – R _ac)/R _ac. For this purpose, a hybrid device, as shown in Fig. 7, can be fabricated.¹⁰¹ The device consists of a sample made of a nanowire array embedded in a matrix connected to a bulk element, of similar size and composition to that of the nanowires, by a metallic tab. To ensure good electrical contact of the nanowires with the tab, it is preferable not to fill the whole length of the matrix with the thermoelectric material under study. Then, some metal on top of the nanowires that fills the matrix completely is deposited to assure better electrical contact. Finally, voltage and current wires are soldered at the top and bottom sides of the metallic pads, which were added to the bulk and nanowire array samples (see Fig. 7). Two thermocouples measure the temperature on the top and bottom of the nanowire array sample. The ac resistance of the composite is obtained from the nanowire composite–bulk ac resistance measurements after being extrapolated from the known properties of the bulk component.¹⁰¹

Fig. 7. Schematic view of the hybrid nanowire–bulk device.

The main disadvantage of this technique is related to the fact that one must accomplish uniform length nanowires, fill most of the pores of the matrix and achieve good electrical contact simultaneously in all nanowires.

3.4. Nanowire array characterization with optical techniques

In contrast to single NW characterization with optical techniques, which required the placement of the NW in an appropriate microchip with electrical contacts at both ends of the NW in most cases, the measurement of NW arrays with optical techniques is more similar to bulk optical techniques, in which the main characteristic is that they provide a non-contact and non-destructive way of gaining information about the material. Moreover, the experimental set-ups necessary for these kinds of measurements are usually the same needed for standard bulk optical measurements without further adaptations. The NW arrays are usually measured without any extra preparation, because no electrical contacts or surface treatments are necessary.

Nevertheless, the main drawback of these optical measurements is that certain characteristics of the nanowire array have to be known, such as the optical absorption, as well as the influence of the containing matrix in the measurement. Usually it is also necessary to study an empty template and then a filled one to take into account the characteristics of the matrix. But in some cases, this is not sufficient, because it is also important to understand the interaction between the NW and the matrix. This results in the need for complex physical models to extract the actual parameters of the NWs, which leads in most cases to complex mathematical systems that have to be solved.

3.4.1. Thermal conductivity measurements

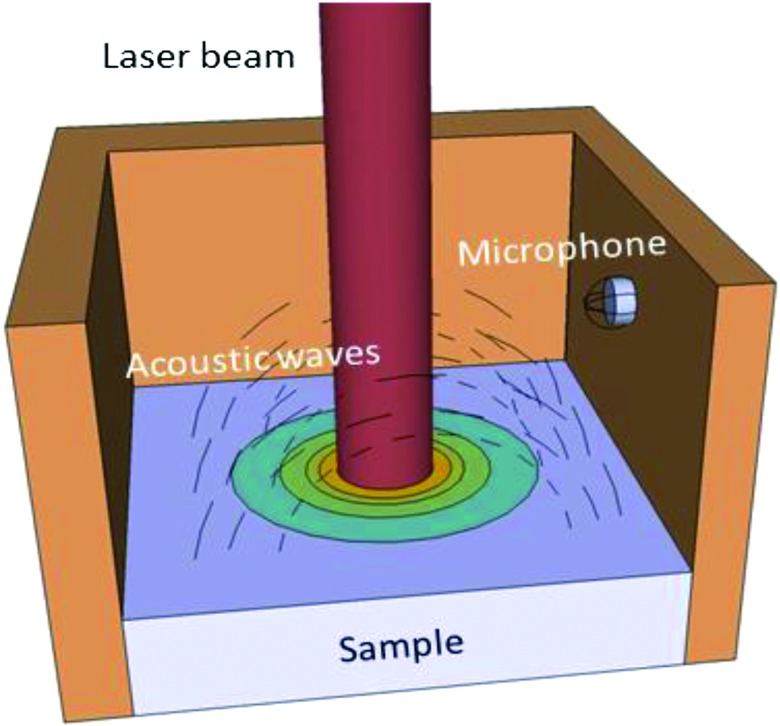
The photo-acoustic technique consists of the generation of acoustic waves in a media caused by the absorption of pulsed or modulated electromagnetic radiation in a material. This absorbed radiation is then transformed into thermal energy, causing the material to warm up and cool down, producing acoustic waves in the surrounding media. From the analysis of the amplitude and phase of this photo-acoustic signal, it is possible to obtain the thermal parameters of the sample. This optical technique is non-invasive or destructive and offers a direct way to measure thermal properties of the sample.

The photo-acoustic technique has been used to measure the thermal conductivity of bulk materials, films, and without any setup modification, nanowire arrays. One of the main problems of the photo-acoustic effect itself when studying the thermal conductivity of films or NW arrays is the mathematical model underlying the physical phenomena. It is important to take into account the geometry of the structure that is being measured, the thermal and optical properties of the components of the sample and the thermal contact resistances between different layers of the structure. This theory can be applied to both bulk and thin film samples, and in the case of NW arrays, one can consider the NW plus the matrix as an effective medium for the mathematical treatment of the data.^102–104

For example, in ref. 89 the sample, which consists of an array of Bi₂Te₃ nanowires embedded into a matrix (SU8 or alumina), is placed inside a sealed acoustic chamber (see Fig. 8). This chamber is filled with a certain gas, such as helium. A modulated laser is in charge of transferring thermal energy to the sample and its heating and cooling cause acoustic waves inside the chamber. The samples can sometimes be coated with a thin metal layer to increase the energy absorption from the laser radiation, but this is not mandatory. In order to measure the thermal conductivity of the sample, the phase shift between the laser heating pulse and the acoustic response of the sample is measured with a microphone mounted in the side of the wall. In order to extract the thermal conductivity of the sample, the amplitude and phase shift of the measured signal have to be analysed using a one dimensional thermal model. In this case, values of 1.4 ± 0.07 W m^–1 K^–1 and 1.1 ± 0.06 W m^–1 K^–1 were obtained for Bi₂Te₃ NW arrays embedded in alumina and SU8, respectively. Then, from the thermal conductivity of the matrix plus NW medium, obtaining the actual value of the thermal conductivity of the Bi₂Te₃ NWs is not straightforward, because one has to take into account the matrix thermal conductivity and its porosity, the filling factor (that is, how many pores are filled with a NW), and then calculate the contribution of the NWs, which in this case results in 1.4 ± 0.1 W m^–1 K^–1.

Fig. 8. Schematic set-up of the photo-acoustic technique.

It is also possible to obtain the thermal diffusivity coefficient of NW arrays embedded in a matrix by using the photo-thermoelectric technique.^105–107 The basis is quite similar to the photo-acoustic technique, that is, a modulated laser heats the surface of a sample and the temperature changes at its backside are recorded (see Fig. 9). In the case of NW arrays measurement, one side of the NW array is hit by the laser and in the other side a thermocouple junction is formed between this surface and a constantan wire. To ensure good temperature measurements at the backside of the NW array, and therefore good thermocouple connection, a metallic layer, such as gold, is deposited on the backside of the sample. Then, the amplitude and phase of the thermocouple voltage are measured.

Fig. 9. Schematic view of the photo-thermoelectric set-up.

To extract the thermal conductivity of the NWs, the experimental data are fitted with a two dimensional heat conduction model and the heat capacity of the specimen is estimated from effective medium theory, that is, taking into account the contribution from the alumina, the pore density, filling factor and so on. Therefore, unfilled alumina templates were also measured to obtain their heat capacity and then the thermal diffusivity of the NWs. Nevertheless, if the thermal diffusivity of the NWs and the matrix are similar, as it is the case for Bi₂Te₃ NWs embedded in alumina templates,¹⁰⁵ this does not lead to reliable measurements and the uncertainty associated with the resulting values is quite high.

4. Conclusions

In this review a thorough revision of the different approaches that have been recently developed for the measurement of transport properties in nanowire structures has been presented. It has been shown that there has been a great effort in a wide variety of fields to obtain reliable data on these structures. This can be understood if one takes into account two of their main characteristics. Firstly, the low dimensionality of these structures, which can be considered almost one dimensional, makes them an ideal bench for testing theoretical models. Secondly, the influence of the quantum confinement effects in the material properties when reducing the nanowire diameters is being extensively studied in condensed physics.

The review is focused on various approaches to measure thermoelectric properties on single and arrays of nanowires. The field of single NW measurements has experienced a remarkable development in the past few years, urged by the need to obtain reliable data to unveil the new physical properties of these low-dimensionality materials. The use of specific microchips or SPM probes permits the determination of the three parameters that enter the figure of merit. In this case a dilemma is observed because the nanowires are usually grown in a matrix and their extraction and posterior exposure to atmosphere may induce surface modifications of the nanowire that can influence the transport properties and affect the accuracy of the properties measured. However, it is also possible to use other methods to measure individual nanowires embedded on a matrix, for instance the Scanning Thermal Microscopy Technique in the 3ω configuration. Finally, the whole nanowire array with the containing matrix can also be measured by certain techniques, extracting the properties of the whole device for further applications. This is important because in actual devices, the most convenient way of arranging the nanowires is having them inside a matrix.

For all those cases, the measurements of the electrical and thermal conductivity, as well as the Seebeck coefficient, have been shown. Proper choice of the techniques lets one measure different properties for a wide variety of nanowires under certain conditions. Comparison of the values of nanowire properties to the bulk material or changes of the nanowire properties with the different diameter ranges, doping or surface roughness are desired to be studied with these experimental measuring configuration.

Modelling and theoretical studies are expected to play an important role in explaining the trend of the nanowire properties at the nanoscale, but they must be supported with experimental data. Reduction of nanowire diameter is becoming possible through different experimental techniques such as electrodeposition or VLS, but measurements of their properties still remain a challenge. Understanding and controlling the properties in general, and thermoelectric materials in particular, are crucial for different fields including of course nano-energy.