Abstract
Many existing cohorts with longitudinal data on environmental exposures, occupational history, lifestyle/behavioral characteristics and health outcomes have collected genetic data in recent years. In this paper, we consider the problem of modeling gene-gene, gene-environment interactions with repeated measures data on a quantitative trait. We review possibilities of using classical models proposed by Tukey (1949) and Mandel (1961) using the cell means of a two-way classification array for such data. Whereas these models are effective for detecting interactions in presence of main effects, they fail miserably if the interaction structure is misspecified. We explore a more robust class of interaction models that are based on a singular value decomposition of the cell means residual matrix after fitting the additive main effect terms. This class of additive main effects and multiplicative interaction (AMMI) models (Gollob, 1968) provide useful summaries for subject-specific and time-varying effects as represented in terms of their contribution to the leading eigenvalues of the interaction matrix. It also makes the interaction structure more amenable to geometric representation. We call this analysis “Principal Interactions Analysis” (PIA). While the paper primarily focusses on a cell-mean based analysis of repeated measures outcome, we also introduce resampling-based methods that appropriately recognize the unbalanced and longitudinal nature of the data instead of reducing the response to cell-means. The proposed methods are illustrated by using data from the Normative Aging Study, a longitudinal cohort study of Boston area veterans since 1963. We carry out simulation studies under an array of classical interaction models and common epistasis models to illustrate the properties of the PIA procedure in comparison to the classical alternatives.
Keywords: biplot, column interaction, eigenvalue, epistasis, intraclass correlation, likelihood-ratio test, non-additivity, permutation tests, pseudo F-test, row interaction, singular vector, Wishart matrix
1 Introduction
Statistical methods for analysis of interactions are receiving considerable attention in the post-genomewide association study (GWAS) era where different consortia are examining gene-gene (G × G) and gene-environment (G × E) interactions [1]. While much of the more recent literature has evolved around case-control association studies, less attention has been devoted to longitudinal cohort studies with rich lifetime exposure data and repeated measures on outcomes. Typically, a naive analysis of repeated measures data attempts to model G × E effects by fitting a regression model to the conditional mean structure of the outcome Y with main effects of G, E and G × E terms after adjusting for other confounders. A random intercept term capturing within subject correlation will commonly be introduced in a standard linear mixed model analysis [2, 3]. However, while incorporating longitudinal effects of time in the model for mean response, one is often confronted with the issue of time varying effects of interaction with a three-way G × E × Time term turning out to be statistically significant in a routine mixed model analysis. It is hard to interpret the interaction parameter in such instances. One can try to model the time varying coefficient corresponding to the interaction term in the generalized additive mixed model framework [4], but tests for such non-parametric, smoothed interaction terms will have little or no power for studies with moderate sample size.
In this paper, we first present an alternate approach to explore interaction structures for cohort studies by first considering the average of repeated measures across subjects as a single observation per subject and then examining the cell-mean structure corresponding to the G = g, E= e in a two-way genotype × environment classification array (G1 = g1, G2 = g2 for a two-way gene × gene array). Due to the two-way repeated measures analysis of variance (ANOVA) formulation, the methods presented are applicable to genotype data on single nucleotide polymorphisms (SNP) and categorical environmental exposures. Though we study the methods in the context of G × E or G × G interactions, they can be used for exploring interactions in any two-way classification array. We then proceed to extend our treatment of the problem to account for individual level repeated measures, beyond the initial cell- means based approach.
The statistical interaction term as described by the inclusion of a product term in a regression model, reflects that the effect of the row variable and the column variable may not be additive in their contribution to the quantitative trait. A variety of models on the structure of this non-additivity have been described. Tukey (1949) proposed his well-known single degree of freedom (df) test for non-additivity where the interaction is modeled as being proportional to the product of the main effects [5]. Mandel (1961) proposed two other more general interaction models where the interaction is proportional to row main effects or column main effects [6]. Along with these classical models, the newer class of models we explore for repeated measures data is the additive main effects and multiplicative interaction model (AMMI) first introduced by Gollob [7] and then developed by several authors [8, 9, 10, 11, 12, 13, 14]. The AMMI models also target towards a sparse representation of interaction terms, but not through main effects. This class of models has been used to analyze data from a balanced experimental design to study genotype × environment in agriculture and crop sciences [15, 16]. Recently, Barhdadi and Dubé applied this class of models to observational studies of gene-gene interaction [17]; Alin and Kurt also contained an overview [18]. All of the work mentioned above were primarily developed for cross-sectional data with fixed effects. The AMMI model was extended to the situation when one of the two factors is fixed, the other is random, again for cross-sectional data [19, 20, 21]. Multiple correlated quantitative traits on the same subject was also considered in a mixed model framework [22].
We first focus on developing simple screening tools for interactions with repeated measures longitudinal data based on cell means where both row and column factors are considered as fixed effects. The fitting of an AMMI model is based on a singular value decomposition of the residual matrix, after removing row and column main effects and retaining the “leading” (in many cases the first) component of this representation. The interaction is then represented by the largest characteristic root and the corresponding right and left singular vectors of the interaction matrix and remainder terms are attributed to residual noise. Thus, by considering a reduced rank approximation (rank one approximation if only the first component is retained) to the interaction matrix, one is able to save degrees of freedom and enhance efficiency when compared to the saturated interaction model. To this end, we call this method “Principal Interactions Analysis” (PIA) due to its similarity with “Principal Components Analysis”. We provide visual/diagnostic tools to isolate subject-specific and time-specific contributions to the principal interaction factors. A comparative simulation study of the AMMI model with the more traditional models proposed by Tukey and Mandel is carried out for repeated measures data which is not present in the literature. The simulation results illustrate that the AMMI models perform well across a spectrum of scenarios and offer far superior protection against model mis-specification than the Tukey/Mandel models. Specifically, for detecting epistasis in absence of main effects of any of the genetic loci, the AMMI model outperform models that attempt to parameterize interaction as a function of main effects.
The primary investigation in this paper is based on averaging the response per subject and per cell, and then applying the Tukey/Mandel/AMMI models. This approach is appealing in terms of its simplicity, fast computation due to closed form analytic expression of the test statistics, and, can be applied based on simple summaries of the data. However, this approach is certainly limited in terms of its applicability and statistical adequacy if there is varying time effect on the response. The cell-mean approach also fails to properly account for unbalanced nature of the data due to the assumed homoscedasticity on the error distribution of cell means. To ameliorate this criticism we propose a more sophisticated analysis that uses individual level data in a mixed-effects regression model setting, followed by a resampling-based test for interaction. Maximum likelihood (ML) and restricted maximum likelihood (REML) estimation under these complex non-linear correlated outcome models is extremely hard, with non-standard asymptotic distribution theory under the null. We adopt two-step procedures and resampling-based tests to circumvent this problem. As expected, the regression approach using individual level data is more powerful than the cell-mean based approach and provides right control of Type 1 error under unbalanced designs. For cross-sectional studies, Barhardi and Dubé [18] note that a standard generalized linear model regression with saturated interaction terms that uses individual level data is more powerful than the reduced df tests based on cell means model. However, they do not propose any alternative to account for unbalanced data or use individual level observations under Tukey/Mandel/AMMI models, even in cross-sectional studies. Thus the paper makes several original contributions.
The example we consider comes from the Normative Aging Study (NAS), a multidisciplinary longitudinal study of aging in Eastern Massachusetts established by the Veterans Administration in 1963. We consider hearing threshold as measured by pure-tone audiometric examinations at every visit until 1996 as our outcome of interest. Up to 8 repeated measures of hearing threshold per subject are available, with 60% subjects having 4 or more measurements. We explore interplay of two genes, Catalase and Heme oxygenase-1, both involved in the oxidative stress pathway and an occupational noise variable that was derived from lifetime history on job titles. This environmental exposure has five ordinal categories. We illustrate both G × G and G × E analysis and investigate changing contribution of the interaction term over time. We compare results of cell-mean based analysis with resampling tests using individual level data.
The rest of the paper is organized as follows. In Section 2, we describe the three classical models, Tukey’s 1-df, Mandel’s Row and Column model. We present the test statistics and the corresponding df/asymptotic null distribution. In Section 3, we discuss the PIA via using AMMI model. We propose diagnostics for follow-up analysis in terms of subject specific and time-window specific contribution to the interaction term. Sections 2 and 3 are based on responses reduced to cell means. In Section 4, we propose analytic approaches that uses individual level data under a mixed-effects regression set-up, followed by a resampling-based test statistic for the interaction term. This strategy accounts for unbalanced repeated measures data. In Section 5, we present the data analysis results from the Normative Aging Study. Section 6 is divided into three parts. Sections 6.1 and 6.2 consider simulation studies on cell-mean based approaches. Section 6.1 presents simulations to study robustness across the classical interaction models for a general I × J table. Section 6.2 specifically considers common epistasis models for studying gene-gene interaction [23]. Section 6.3 presents simulation results corresponding to the resampling tests proposed in Section 4, as compared with the cell means approach. Section 7 concludes with a discussion.
We highlight the new contributions of the paper: (a) application/introduction of PIA to study G × E and G × G effects for repeated measures on quantitative traits, (b) compare with classical interaction models such as Tukey and Mandel’s models as applied to repeated measures data, (c) develop visual and diagnostic tools for a better understanding of interaction structures with longitudinally varying outcomes and (d) introduce novel resampling-based tests for AMMI models (as well as Tukey/Mandel interaction models) that account for unbalanced data structures, uses individual level data under a mixed effects regression modeling framework. The comprehensive simulation studies and the data analyses indicate “PIA” is a promising tool to understand interaction structures and also to trade-off between bias and efficiency in a data-adaptive way under model mis-specification.
2 Classical Models for Interaction
Since the methods are generic to any two-way table, instead of using G and E for the two factors, we use R to denote the row variable with I levels, and C to denote the column variable with J levels. Let Yhijk be the h-th observation corresponding to the k-th subject in the (i, j)-th cell of this (I × J) array. Here k = 1, ⋾, N and h = 1, ⋾, nk, with N denoting the total number of subjects and nk denoting the number of observations corresponding to the k-th subject. We consider the following general model,
| (1) |
Here μ describes the overall mean, Ri and Cj are the row and column main effects and γij describes the interaction between the row and column factors. The standard constraints, ∑i Ri = ∑j Cj = ∑i γij = ∑j γij = 0, are placed on the fixed effects parameters. We assume that the possible random effects associated with components {Sk} (Subject effect), {θik} (Row × Subject), {πjk} (Column × Subject) and {τijk} (Row × Column × Subject) are jointly normal with zero means and covariance matrix ΣS. The random errors {εhijk} are independently and identically distributed with mean zero and variance . A special case of this particular model is the simpler model with only one subject specific random intercept, namely, Sk, normally distributed with mean zero and variance . We consider this simpler model in our simulation studies and data analyses.
We create a two-way cell means array, first averaging all observations corresponding to the k-th subject in the (i, j)-th cell, namely ȳ․ijk, and then averaging ȳ․ijk, over all subjects in the (i, j)-th cell, to obtain {ȳ․ij}, i = 1, ⋾ I and j = 1, ⋾ J. These cell means will have differing degree of variability, depending on the random effects structure specified in (1) and the number of observations per subject as well as number of subjects per cell. In a typical observational study, we will certainly have an unbalanced data structure. In the following, we abuse our notations slightly by dropping the {·} suffixes corresponding to subjects and observations corresponding to a subject, and describe the models in terms of the I × J array of cell means ȳij = ȳ․ij․.
I. A General Saturated Model for Interaction
The implied mean model by (1) for the two-way table in terms of cell means ȳij is,
| (2) |
where interpretation of the fixed effects parameters are as before, but ε̄ij is the mean of the errors of εhijk in (1), by first taking averages over errors associated with observations for the k-th subject and then over all k subjects within the (i, j) th cell. In the following, we denote ȳij by yij, pretending they represent a single observation corresponding to the I × J cell [17]. We assume that ε̄ij ~ N (0, τ2). This assumption does not recognize the non-constant variance in the cell-means due to unbalanced nature of the data. The maximum likelihood estimates of main effects and interaction parameters are then given by:
| (3) |
Let us define the estimated residual contrast after fitting the additive terms as
The df attributed to testing interaction in a saturated model is (I − 1)(J − 1), and, in that case γ̂ij = zij. With more than one replication per cell, one can test for interaction in a saturated model; however, with a single observation or no replication per cell, one exhausts the df for a saturated interaction model, with no df left for errors. Thus a test of non-additivity can not be carried out. In such a situation, several reduced df tests have been proposed by imposing special structures on the interaction parameters. These structures can be used for testing interactions in general regression models for a more powerful test with reduced df [24, 25].
II. One Degree of Freedom Test for Non-Additivity [5]
The essential idea behind this model is to think of interaction as γij = θRiCj +ξij, namely, a leading term and some residual noise ξij that can be absorbed with the error term εij. Thus, of the (I − 1)(J − 1) df attributed to the interaction term, only 1 is used to test H0 : θ = 0 and the rest is attributed to the residual error term, making it possible to test for non-additivity with no replication. Tukey’s model is given by:
| (4) |
where θ is the coefficient for the linear by linear interaction effect. The least square estimate of θ, denoted as θ̂, is given by
Where zij = yij − yi‥ − y․j + y‥ is again the estimated residual contrast after removing additive main effects. This essentially reduces to regressing the cell residuals after fitting the additive terms on the product of estimated row and column main effects [26]. The model is not identifiable if there are no main effects present as any value of θ yields the same likelihood. Tukey’s single df test for non-additivity is obtained by using the test statistic F = MSll/MSE as presented in Table 1 in Appendix that has an F distribution with 1 and (I − 1)(J − 1) − 1 degrees of freedom under the null hypothesis H0 : θ = 0.
III. Column (Row) Regression Model [6]
Mandel (1961) proposed the column regression model and row regression model for testing interactions. In the column-regression model, the interaction effect is a linear function of the column main effects, i.e.,
| (5) |
where λi is the coefficient corresponding to the ith row, and ∑i λi = 0. The maximum likelihood estimate of λi, denoted as λ̂i, is
The MLE of μ and Ri remain unchanged. A test of non-additivity is obtained by constructing an F-statistic for the hypothesis
Under the null hypothesis and normality, this test statistic as described in Table 1 of Appendix, has an F distribution with (I − 1) and (I − 1)(J − 1) − (I − 1) degrees of freedom. Table 2 in the Appendix presents the ANOVA table for this model. By replacing the columns with the rows, one can equivalently posit a row regression model of the following form:
| (6) |
with ∑j ηj = 0 and testing H0 : ηj = 0, j = 1, ⋯, J, with the resultant F statistic having df {J − 1, (I − 1)(J − 1) − (J − 1)}.
Note that models (4)–(6) hierarchically build increasing order of complexity in the interaction structure in a nested manner. For a large two-way array, say a 9 × 5 array [with saturated interaction df (I − 1)(J − 1) = 32], the interaction tests will have 1 (Tukey’s 1-df), 8 (Mandel’s column), 4 (Mandel’s row) for the numerator of the F statistic and 31, 24, and, 28 df for the denominator respectively, thus providing different degrees of efficiency gain and model robustness.
However, all of the above three models have a particular structure of interaction, specified in terms of main effects. Thus when there are no main effects, the models encounter problem with likelihood identifiability. Even in presence of main effects, under any form of mis-specification of this specific structure, all of the above three tests lose tremendous power as discussed in Section 6.
Remark 1: Tukey’s Row-Column Regression Model [26]: Tukey extended Mandel’s column-or row-regression model in his seminal paper in 1962 where he introduced the vacuum cleaner strategy for analyzing two-way arrays where a row regression is followed up with a column regression (or vice versa).
| (7) |
where λi and ηj are the row- and column-specific coefficients, with additional constraints ∑i λi = ∑j ηj = 0 and ∑i λi Ri = ∑j ηjCj = 0. The MLEs of μ, Ri, Cj remain unchanged. The maximum likelihood estimates of θ, λi, and ηj are obtained as:
| (8) |
Table 3 in Appendix presents the ANOVA Table corresponding to this model. The F statistic for testing H0 : θ = λi = ηj = 0, ∀ i, j under the above constraints have numerator df 1 + (I − 2) + (J − 2) = (I + J − 3). The denominator df is thus (I − 1)(J − 1) − (I + J − 3).
For completeness we provide the description of this more general model but refrain from discussing it any further. For a 3 × 3 table for G × G interaction the Tukey row-column model has df 3, offering little power gain over the saturated model which has df 4, another reason for not including this model in our simulation studies.
3 Principal Interactions Analysis via the AMMI model
Gollob (1968) proposed a factor-analysis of variance (FANOVA) model to decompose a two-way table [7]. The essential idea is to represent the I × J rectangular interaction matrix Γ with interaction parameters γij as entries, by the following representation:
Here A = ((αim)) and B = ((βkm)) are I × R and J × R orthonormal matrices (A′A = B′B = I) and D is a R × R diagonal matrix with elements d1 ≥ d2 ⋯ ≥ dR. The maximum rank of Γ is min (I − 1, J − 1) because of the sum-zero constraints on the parameters γij. This makes the matrix Γ doubly centered. Let I ≤ J, thus the maximal rank of Γ is I − 1. Let P = AD1/2 and Q = D1/2 B′, then Γ = PQ′ = ∑m pimqjm, where the pim and qjm satisfy the ortho-normalization constraints ∑i pimpil = ∑j qjmqjl = 0 for m ≠ l and for m = 1, ⋯, R.
By this factor representation, for a saturated model, γij is perfectly reproduced by,
However, one can think of a sparse representation of the interaction matrix by retaining the first M < I − 1 components of this representation, namely,
This representation gives rise to the following general class of additive main effects, multiplicative interaction models (AMMI) [9, 10, 11, 12, 14].
| (9) |
| (10) |
Eckart and Young (1936) shows that for a fixed M, the least square estimates of (A,B,D), equivalently, {αim}, {βjm} and {dm} can be found by expressing the estimated matrix Γ̂ of interaction parameters with entries γ̂ij = yij −yi․ −y․j+y‥ in terms of a singular value decomposition (SVD) as specified by the factor model,
[27]. An alternative interpretation is that the interaction parameter is expressed as a sum of several successive multiplicative contrasts ΨFm = ∑i∑jαimβjmγij such that each contrast is orthogonal to all previous contrasts and accounts for a maximum of the remaining variance. Let Ψ̂Fm denote the estimated normalized orthogonal multiplicative contrast among the interaction parameters {γij} and SSFm denote the sum of squares due to the m-th interaction factor. Then from classical contrast theory we know that . To this end, Ψ̂Fm can be obtained by
Because Γ̂= ÂD̂B̂′, we have D̂ = Â′Γ̂B̂, implying, d̂m = ∑i∑j α̂imβ̂jmγ̂ij. So, Ψ̂Fm and d̂m are equivalent. They both are ∑i∑j α̂im β̂jmγ̂ij. Hence, . Let SSRC denote the total sum of squares due to row-column interaction. The sum of squares corresponding to the residual interaction after M successive interaction factors being extracted from {γij} is therefore
Table 4 in the Appendix contains the ANOVA table corresponding to the AMMI model. The use of pseudo F tests with various prescriptions for the degrees of freedom is based on heuristic approximations [7, 9]. Essentially, corresponding to the m-th interaction factor, there are I + J + 1 parameters αim, βjm, dm, but there are 2m + 2 orthonormality constraints due to orthogonality to prior m −1 contrasts and being normalized to unity. Thus the m-th interaction factor has numerator df: df(m) = (I + J + 1 − (2m + 2)). The set of M factors together have . The remaining interaction df after fitting first M factors is . Since this pseudo F test does not have desirable operating characteristics, we relegate the details to the supplementary Appendix Table 4.
A special case of (9) is of particular interest when M = 1. Namely,
| (11) |
Thus, the test of no interaction is equivalent to testing H0 : d1 = 0. Johnson and Graybill (1972) derived the distributional properties for the likelihood ratio test (LRT) of H0 : d1 = 0 [10]. They show that the maximum likelihood estimate of d1, d̂1 say, is given by the square-root of the largest characteristic root of Γ̂′Γ̂, say l1. The maximum value of the likelihood is attained when {αi} and {βj} are given by the normalized characteristic vector corresponding to l1 in Γ̂′Γ̂ and Γ̂Γ̂′ respectively. Consequently, the LRT for H0 : d1 = 0 vs. Ha : d1 ≠ 0 is given by,
| (12) |
where again is the maximum non-zero (characteristic) root of Γ̂′Γ̂. That is, l1 is the maximum value of (∑i∑j αiβjyij)2 with respect to αi and βj subject to the restriction that ∑iαi =∑j βj = 0 and . The critical region for H0 : d1 = 0 can equivalently be expressed as,
The asymptotic distribution for the LRT statistic is not χ2. Critical points of Λ* for several choices of I and J are provided previously [11, 28]. The theory is based on deriving asymptotic property of the ratio of largest characteristic to the trace of a Wishart matrix. The details of ML estimation are presented in supplementary Appendix.
Remark 2: In general, the number of components M should be chosen in such a way that the residual ϕij represents noise and can again be absorbed with εij leading to a more powerful test with reduced df. Several studies have investigated cross-validation and significance testing approaches for determining M, the appropriate number of multiplicative interaction terms to be retained [29, 30, 31]. When the above model is saturated, M = I − 1. We focus on the model with M = 1 in the remainder of the paper and do not address the issue of data-adaptive selection of M. In our data example including M = 1 component was sufficient.
3.1 Biplot, Subject-specific and Time-specific contribution
In this section, we describe certain graphical diagnostics to provide insight into interaction structures. In particular, we discuss the best rank-two approximation to an interaction matrix as presented by a biplot [32]. We then introduce diagnostics to assess subject-specific contribution and time varying contribution to the leading interaction term.
A. Biplot
The biplot is a graphical planar display of the elements, rows and columns of a matrix. Any matrix of rank two can be displayed as a biplot which is defined through a vector for each row and a vector for each column, such that the inner product represents each matrix element. For a matrix with higher rank, one may use the biplot corresponding to the best rank-two approximation to the original matrix. With the factor analytic representation Γ̂ = ÂD̂B̂′, each entry of the estimated interaction matrix can be approximated by the first two terms of the corresponding factor representation by
For G × G interaction, for example, the matrix of interest is a (I = 3) × (J = 3) matrix with maximal rank I − 1 = 2 and this representation is exact. There are several choices of defining the vectors, we define the points a representing row i and the points describes column j.
Bradu and Gabriel (1978) explained the use of biplots for interaction models [33]. The patterns of the points indicate certain models: additivity (the case of two orthogonal lines), Mandel’s row regression model when Pi are collinear and Qj are scattered or column regression when Qj are collinear and Pi are scattered. The AMMI model typically will give rise to a configuration where Pi, Qj are both scattered. For the special case of AMMI with M = 1 the points are not collinear, but co-planar on the three-dimensional plane. We use this representation for repeated measures data with the cell means residual as described before, to visualize the interaction structure.
B. Measures that summarize subject-specific and time-specific contribution of interaction
The question that we stated at the onset was to capture varying effects of time and subject to the interaction term. We take a very different approach than a standard mixed model regression setting as described in the introduction. We utilize the PIA framework and construct measures which summarize variation due to individual differences in the size of the contribution to the leading interaction factors. Variation due to individual differences can be investigated by defining a contrast using the estimated factor weights (α̂i, β̂j) and the individual person level means for the k-th subject in the (i, j)-th cell, namely, y․ijk, by computing the following N subject-specific regression weights for the m-th interaction factor [7]:
The larger the value {dkm}, for the k-th subject, the larger the absolute contribution of the m-th factor to determine the subject’s mean y․ijk. For the m-th interaction factor, the variation in the contribution of each individual can be calculated by a squared term, (d̂km − d̂․m)2, where d̂․m is . The aggregate measure of squared deviation captures total subject-specific variability in the m-th interaction term around the average regression weight.
Variation of different time contributions can be investigated in a similar manner. We may define T time intervals of a given width w to cover the study period. We calculate ytij․ (t = 1, ⋯, T), which is the averaged score of all observations in the ith row and jth column over the w year follow-up period. Then the variation due to time can be investigated by computing the T quantities for the m-th factor
The relative contribution of each time period can be calculated by a squared term, (d̂tm − d̂․m)2, where d̂․ m is now . The aggregate measure of squared deviation captures time variability in the m-th interaction term around the average regression weight across the study period. We illustrate these diagnostics and graphical representation in the following section through analyzing data from the Normative Aging Study.
4 Resampling-based Interaction Tests using Mixed Models
In Sections 2 and 3 we discussed treatment of the interaction testing problem in terms of reducing the response in a crude way to average per person and per cell and then thinking of the cell mean as a single observation per cell. While this approach is fast and simple, it has many limitations such as ignoring the time variation in response and ignoring the unbalanced nature of the study design. However, due to non-linear structure in the parameters, for example, terms of the form θRiCj for Tukey’s model, λ iCj for Mandel’s column regression model and d1αiβj in AMMI model, ML estimation and establishing asymptotic theory for a general random effects model is hard. There is very little literature for unbalanced data situations with these models and almost nonexistent literature in the repeated measures observational study setting. Maity et al. presents the most general treatment of Tukey’s model but only considers the testing problem [25]. Meyer considers balanced data but correlated multiple response [22]. To solve the testing problem for each of Tukey/Mandel/AMMI model for a general random effects structure and unbalanced data, accompanied with analytical asymptotic theory remains beyond the scope of the paper. In this section we develop a set of novel resampling-based tests for this class of models which have not been proposed in the literature. The permutation tests use individual repeated measures and utilize a general mixed effects analysis of variance/regression framework followed by a permutation-based null distribution of the test statistic.
Two-step regression procedure for Tukey/Mandel models: In step 1, we fit a standard saturated interaction model with γij using all (I − 1)(J − 1) df by including product terms of row and column indicators in the model. For example with a random intercept structure for subject k, we first fit a linear mixed effects model
| (13) |
where . We obtain REML estimates of fixed effects μ̂, R̂i, Ĉj, and variance components under this model. We then construct the marginal residuals:
Recall that even for cross-sectional unbalanced data, there are no closed-form expressions of R̂i and Ĉj as in the two-way balanced ANOVA. Using dummy variable regression model is the best way to express the model estimates in the unbalanced case. In step 2, residuals from Step 1, rhijk, are regressed on R̂iĈj,
At step 2 we have used compound symmetry covariance structure but one can allow for a user-defined covariance structure in , depending on assessment of model fit criterion. Note that one can alternatively use the subject-specific residuals from step 1, namely, , and use them as outcomes in a second stage regression model. Irrespective of the choice of residuals (marginal or subject-specific), that changes the estimation/choice of variance covariance matrix for ε′, the estimate of θ at step 2 appears to remain unbiased under the two-step procedure if the original generating model had the structure γij = θRiCj. Note that we are exploiting the idea that after removing additive term, we are expressing the residual variability attributable to both interaction and random error through a second step correlated outcome model. To test H0 : θ = 0, we used a test statistic that has an analogous form to what we used in the cell-means approach, namely, . To elicit the null distribution under the two-step approach we adopt the following resampling strategy. Note that this exercise of simulating the null can be tricky as one would like to still preserve the main effects and simply eliminate the interaction pattern. Permuting the Y values or subjects across cells will remove the interaction but will destroy the main effects structure as well. To bypass this problem, we generate pseudo data Y* under H0 : θ = 0,
| (14) |
where are REML estimates obtained from step 1 model. We generate 1000 such pseudo datasets reflecting the null. For each such pseudo dataset (containing N individuals, each with number of repeated measures as recorded in the original dataset), we fit a two-step regression approach exactly as our analysis of original data to compute: . We then compare our observed value of based on the original data with the sample percentiles of these 1000 test statistics generated under the null to obtain the P-value corresponding to the test statistic.
Similarly, for Mandel’s column regression model we regress the residuals from step 1 saturated interaction model to obtain a set of I − 1 second step regression coefficients:
Again we consider the familiar form of a multiple of the F-type test statistic to test H0 : λ1 = ⋯ = λI = 0. Compute it for pseudo data Y* as in (14) . We then compare the observed value of the test statistic with the distribution of the test statistics obtained by analyzing the 1000 pseudo datasets generated under the null. The vast literature on choosing appropriate covariance matrices at the step 1 and 2 linear mixed effects model can be applied to a particular data analysis as long as the pseudo datasets are generated and analyzed under the same choices. One could also postulate alternative forms of the test statistics instead of the ones we borrowed from the cell means model.
5 Exploring G × G and G × E in the Normative Aging Study
The Normative Aging Study (NAS) is a multidisciplinary longitudinal study of aging in Eastern Massachusetts established by the Veterans Administration in 1963 [34]. Data were collected every 3–5 years, including extensive physical examination, laboratory, anthropometric, and questionnaire data. The outcome we consider is hearing threshold as measured by pure tone average (PTA) of thresholds at frequencies of 0.5, 1, 2, and 4 kHz. Smaller threshold represents better hearing ability [35]. The dataset contained a total of 662 individuals. Each individual had at least two measurements, and 62% of them had at least 4 measurements over time. Descriptive characteristics of the study population is provided in Table 1. We considered two SNPs on genes related to oxidative stress pathway and one environmental exposure, namely, occupational noise. The two genetic markers were rs2071746 (T/A) on it HMOX-1 (heme-oxygenase 1), a stress response protein which may offer protection against oxidative stress, and rs1001179 (C/T) on CAT (catalase), a gene that decomposes hydrogen peroxide. Both of these SNPs have been studied in NAS as an effect modifier in a recent study of black carbon on blood pressure [36]. However the role of these genetic markers related to oxidative stress defense has not been studied for hearing threshold outcomes. An ordinal measure for lifetime exposure to noise with 5 levels (1 reflecting lowest noise exposure and 5 indicating highest) was created based on prior literature [37].
Table 1.
Descriptive characteristics of 662 study participants in the Normative Aging Study considered in our data analysis. Age, BMI, Health Status and Smoking variables are measured at baseline. PTA hearing threshold is averaged over all repeated measures.
| Variable | Mean | SD |
|---|---|---|
| PTA hearing threshold (dB) (Y) | 10.86 | 6.54 |
| Age (years) | 41.66 | 8.77 |
| Body Mass Index (kg/m2) | 25.71 | 2.76 |
| N | Percent | |
| Race (white) | 645 | 97.43 |
| Education (> 12 years) | 381 | 57.55 |
| Type-2 Diabetes | 13 | 1.96 |
| Hypertension | 28 | 4.23 |
| Pack-Years of Cigarettes | ||
| 0 | 205 | 30.97 |
| < 30 | 336 | 50.76 |
| ≥ 30 | 121 | 18.28 |
| Genes (G) | ||
| CAT(C/T) rs1001179 | ||
| CC | 403 | 65.96 |
| CT | 179 | 29.3 |
| TT | 29 | 4.75 |
| HMOX-1(T/A) rs2071746 | ||
| TT | 171 | 27.67 |
| TA | 320 | 51.78 |
| AA | 127 | 20.55 |
| Environment (E) | ||
| Level of Noise Exposure | ||
| 1 | 120 | 18.13 |
| 2 | 95 | 14.35 |
| 3 | 182 | 27.49 |
| 4 | 153 | 23.11 |
| 5 | 112 | 16.92 |
| Number of Repeated Measures on PTA Per Subject | ||
| 2 | 129 | 19.49 |
| 3 | 122 | 18.43 |
| 4 | 155 | 23.41 |
| 5 | 147 | 22.21 |
| 6 | 85 | 12.84 |
| 7 | 20 | 3.02 |
| 8 | 4 | 0.60 |
The estimated minor allele frequencies (MAF) for the SNPs considered on CAT and HMOX-1 were 0.19 and 0.46, respectively and both SNPs were in Hardy-Weinberg Equilibrium (HWE) (P = 0.30, 0.67 respectively). There can be a maximal number of M = I −1 = 3 − 1 = 2 principal interaction factors here and the biplot representation is exact. The cell means corresponding to the G × G cross-classification, the matrix Γ̂ and the corresponding SVD, along with the corresponding biplot is presented in the upper panel of Figure 1. The plot of cell means suggest evidence for interaction. In the biplot, the points representing the column array appear to be nearly collinear, suggesting possible evidence for Mandel’s column regression model. Table 2 presents the results from the different fitted models along with a random intercept mixed model (under a compound symmetry covariance) with main effects of both SNPs and saturated G × G interaction. The interaction is marginally significant in only Mandel’s column regression model where the interaction is assumed to be proportional to the main effect of rs2071746 on HMOX-1 (P = 0.06) and not significant in any other model. There is evidence of main effect of HMOX-1 as well in the column regression model (P = 0.05) and from the descriptive statistics.
Figure 1.
Cell means, residuals after eliminating additive row and column main effects and the SVD of the estimated Γ̂ matrix for G × G (top panel) and G × E (bottom panel) analyses. The numerical arrays are accompanied by graphical displays of the cell means, entries of Γ̂ and the biplot representation. Results based on the Normative Aging Study data.
Table 2.
Analysis results for gene-gene interaction and gene-environment interaction in the Normative Aging Study. Two SNPs, rs2071746 on HMOX-1 and rs1001179 on CAT gene are considered for G × G analysis. The G × E analysis considers the interaction between the same SNP on HMOX-1 and occupational noise exposure. Results from the four models Tukey’s 1-df, Mandel’s Row, Mandel’s Column, and Principal interaction analysis via AMMI with one component is presented. The last column presents the results of resampling-based tests as discussed in Section 4.
| Model | Hypotheses | Numerator df | F | p-value (cell mean) |
p-value† (resampling) |
|---|---|---|---|---|---|
| Analysis results for CAT(C/T) × HMOX-1(T/A) | |||||
| Tukey’s 1-df for Nonadditivity | H0 : θ=0 | 1 | 0.87 | 0.20 | 0.13 |
| Mandel’s Row(CAT)-Regression | H0 : ηj = 0 | 2 | 0.91 | 0.52 | 0.32 |
| Mandel’s Column(HMOX-1)-Regression | H0 : λi = 0 | 2 | 14.84 | 0.06 | 0.03 |
| AMMI | First PI | 3.57 | F* = 0.11 | 0.61 | 0.41 |
| AMMI | First PI | LRT = 0.9533 | 0.1 < P < 0.2 | ||
| Mixed Model(random intercept, saturated) | CAT×HMOX-1 | 4 | 1.07 | 0.37 | |
| Analysis results for HMOX-1(T/A) × Noise Exposure | |||||
| Tukey’s 1-df for Nonadditivity | H0 : θ = 0 | 1 | 1.06 | 0.34 | 0.25 |
| Mandel’s Row(HMOX-1)-Regression | H0 : ηj = 0 | 4 | 0.19 | 0.93 | 0.85 |
| Mandel’s Column(Noise)-Regression | H0 : λi = 0 | 2 | 0.97 | 0.43 | 0.25 |
| AMMI | First PI | 6.36 | F* = 1.43 | 0.50 | 0.69 |
| AMMI | First PI | LRT = 0.8476 | P >0.40 | ||
| Mixed Model(random intercept, saturated) | HMOX-1×Noise | 8 | 0.61 | 0.77 | |
The AMMI model using the LRT with M = 1 has a P-value between 0.1 and 0.2 for the leading principal factor, whereas the pseudo F-test [9] used in the AMMI Macro in SAS [38] has a much larger P-value of 0.61. The 5% upper critical value of AMMI-LRT [10] for a 3 × 3 array is 0.9994 whereas our observed value is 0.9533. The leading characteristic root of Γ̂′Γ̂, namely, . Since the LRT statistic also represents the fraction of the total variability due to the interaction term explained by the first component, , we note that the first principal interaction component explains 95% of the interaction sum of squares and the second principal interaction component can be attributed to random noise.
We carried the same analysis for G × E model with a 3 × 5 table for HMOX-1 and occupational noise exposure. The maximal number of interaction factors is still 3 − 1 = 2. The lower panel of Figure 1 displays the cell means corresponding to the G × E cross-classification, the matrix Γ̂ and the corresponding biplot. No obvious pattern was observed in the cell means plot and biplot. The results of fitting different models for the interaction between HMOX-1 and noise exposure and fitting a mixed model with random intercepts are also shown in Table 2. No main effects of gene, exposure or G × E interaction was detected in any of the models. The AMMI model using the LRT with M = 1 has a P-value greater than 0.4 for the leading principal factor, whereas the pseudo F-test used in the AMMI Macro in SAS has a larger P-value of 0.50. The 5% upper critical value of AMMI-LRT from Johnson and Graybill for a 3 × 5 array is 0.9648 whereas our observed value is 0.8476. The leading characteristic root of Γ̂′Γ̂, equivalently, . Thus only the first principal interaction component explains 85% of the interaction sum of squares and the second principal interaction component explains the remaining noise. A LRT based on fitting the two nested models also supports the same conclusion.
Subject-specific and time-specific contribution to the principal interaction factors
The left column in Figure 2 displays the contribution of the 662 individuals to the first interaction factor for G × G and G × E analysis as computed by the (d̂k1 − d̂․1)2 term as described in the previous section, for k = 1, ⋯, 662. One can note that there appears to be more subject-specific variability in the G × G analysis than the G × E analysis from this plot. The sum of squared deviations, namely, has value 7663 for G × G analysis and 4524 for G × E analysis. Figure 1 in the supplementary Appendix presents similar plots corresponding to the second interaction factor that reflects much lesser magnitude of subject specific variability.
Figure 2.
Subject-specific contribution and time-specific contribution to the first interaction factor in HMOX-1 × CAT (upper panel) and HMOX-1 × Occupational noise interaction (lower panel). Each point in the plot presents the squared deviations as described in Section 3. Results based on the Normative Aging Study data.
Variation of different time contributions can be investigated in a similar manner. We considered 10 time intervals of 2.5 years each to cover the entire study period of 1963–1996. The last time interval contained all observations after 25 years of follow-up. We then calculated ytij‥ (t = 1, …, 10), which is the averaged score of all observations in the t-th 2.5 year follow-up period for all subjects in that (i, j)-th cell. Due to the width of the time interval there were one observation per individual in each interval. The right column in Figure 2 shows the variation due to different time periods in the contribution of the first interaction factor. For the gene-gene interaction (CAT and HMOX-1), time has less varying contribution to the interaction factor as the curve indicates. On the other hand, time had a substantial effect on the interaction between gene HMOX-1 and occupational noise exposure. It appears that the time window around 10–20 years of follow-up shows strongest contribution than the 0–10 or 20–25 year period. With progressing age, the onset of hearing loss becomes more common and the variation in the quantitative trait is highest in the intervening period. The results suggest that the effect modification of cumulative noise exposure is most relevant in that “window of vulnerability” where average age of the study subjects were in the age-group 55–65. The sum of squared deviations, namely, has value 23.2 for G × G analysis and 49.9 for G × E analysis. Figure 1 in the Appendix presents similar plots corresponding to the second interaction factor, showing almost no time-specific variability.
Though these graphical diagnostics do not establish a “statistical significance” of a G × G × Time or G × E × Time term, they do provide important insight into longitudinal features of the interaction factor. In fact, fitting a mixed effects model with a compound symmetry error structure, fixed main effects of G, E, continuous Time, all pairwise interactions between G, E and Time, and, G × E × Time, the three-way term is highly significant with P < 10−3.
We also used the resampling-based tests described in Section 4 that uses individual observations to explore G × G and G × E effects in the NAS data. The HMOX − 1 × CAT interaction is significant in Mandel’s column regression model (P = 0.03). For G × G analysis, the AMMI (M = 1) model using permutation test with Gollob’s statistic has a P-value 0.41 for the leading principal interaction factor. The observed value of the two characteristic roots of Γ̂′Γ̂, namely, based on the SVD of Γ̂ under a saturated interaction model. Thus the first interaction factor contributes 94% of the total contribution of the interaction term. On the other hand, no significant interaction is detected for G × E interaction analysis for HMOX-1 and occupational noise exposure. The AMMI model using resampling test has a P-value of 0.69 for the leading principal interaction factor. The observed value of Thus the first interaction term explains 89% of variability attributed to interaction term.
6 Simulation Study
We carried out a simulation study to assess the power and Type I error properties of the four tests for interaction (Tukey’s 1-df, Mandel’s row and column, and AMMI-LRT with M = 1). We also considered common epistasis models beyond these four models. We generated individual level data on outcome Y with nk = 4 repeated measures on each subject k for a total of N subjects. The general description of the model, following the notations of Section 2 is given by,
| (15) |
with the error , the subject-specific random intercepts , and {ε, S} are mutually independent. Thus the correlation between any two observations on the same subject is given by . The structure of γij was changed according to the different simulation models. Cell means were first generated and then the vector of observations per individual with given mean and covariance structure were generated from a multivariate normal distribution.
Section 6.1 presents simulation design and results when the data are generated from each of the four interaction models for a general I × J table. We consider a 3 × 3 and a 9 × 5 setting. Section 6.2 specifically focuses on simulation under common epistasis models [39, 40, 23] for studying gene-gene interaction (thus 3 × 3 tables) with repeated measures on quantitative traits. In all analyses in 6.1–6.2, data was summarized by first computing person level average and then by taking average over all individuals in each cell. The four models under consideration were then fitted and tests for interaction were implemented as described in Sections 2 and 3. Under each simulation setting, we generated 1000 datasets, each with N individuals and each individual having 4 repeated measures. We recorded the percentage of rejections for the null hypothesis of no interaction. For evaluating the Type I error we generated data under the additive model. We considered two settings regarding the variance components: , leading to ρ = 0.2 and 0.5 respectively. We considered N = 900, 1800, 3600, 7200, but only present results for N = 3600 in the main text, as the relative performance of the tests remain same across all sample sizes, only the absolute power increases or decreases with increase/decrease in sample size. Results under some additional settings are contained in the supplementary Appendix.
Section 6.3 presents simulation results that compare the cell-mean based models of Sections 2 and 3 with the resampling tests from Section 4. Since the Section 4 resampling tests have more power because of using individual level data, in order to get variation in the power curves we use the same parameter/effect size setting as in Section 6.1 but increase the variance component values to .
6.1 Simulation under the general two-way interaction models
Design and Parameter Setting
We simulated data according to each of the four interaction models with the parameters satisfying the constraints described in Sections 2 and 3: Tukey’s 1-df, Mandel’s row, Mandel’s column, and AMMI (M = 1). Under each of the four models, for a 3 × 3 table, the interaction terms were scaled in such a way that they contributed to 15% of the total variation explained by the model while the remainder is attributed to row and column main effects. Specific details of the parameter setting for 3 × 3 table is described in the Appendix.
While simulating data under the AMMI model, the entire contribution due to interaction effect was assigned to the first interaction factor. We simulated cell frequencies as if we had two unlinked causal loci with allele frequency 0.3 and 0.4 for all 3 × 3 tables. For the larger 9 × 5 table, we pretended as if we are considering combinations of the two loci with allele frequency 0.3 and 0.4 respectively, along with an environmental exposure with five categories with prevalence 0.2 in each category. For the 9 × 5 table, interaction terms were scaled to contribute 20% of the total variability explained by the model while the rest was attributed to main effects. For simulation under the AMMI model 75% of the variation due to interaction was attributed to the first component in the 9 × 5 case. Specific parameter setting for 9 × 5 table is described in the Appendix.
Main Results
The header on each Figure 3 states the true simulation model while all four “test” models are fitted under each simulation scenario. The left panel in Figure 3 shows the simulation results corresponding to four tests for a 3 × 3 table. When the true model is Tukey’s 1-df, surely Tukey’s 1-df is the most powerful test (100% for , 4). Mandel-row, Mandel-column model, being more general than Tukey’s 1-df, can capture the interaction structure as well. AMMI is the worst in this setting, but has a power around 33% for and around 21% for . For simulation under Mandel’s row regression model, Mandel-row model obviously has highest power (98% and 85% for , 4 respectively), whereas Tukey’s 1-df and Mandel’s column model can not detect any interaction and has zero power. Again AMMI is less powerful, with power 25% and 16% for , 4 respectively. Similar feature holds for Mandel-column model where Tukey’s 1-df and Mandel-row fails completely with zero power but AMMI still can capture some certain interactions (AMMI: 18% and 11% for , 4 respectively). With AMMI as the simulation model, all other alternatives fail to capture the interaction in the 3 × 3 setting except the true model. Note that power decreases as increases in all cases.
Figure 3.
Percentage of interactions detected (or null hypotheses of no interaction rejected) by each of the four tests in the simulation settings corresponding to 3 × 3 and 9 × 5 array from 1000 simulated datasets with N = 3600. Details are described in Section 6.1. The top label within each box represents the true simulation model whereas the horizontal axis labels indicate the tests carried out. The error variance is set at 4 in all cases. Results based on cell-means model.
The right panel in Figure 3 presents simulation results for the 9 × 5 array. The same pattern as described for the 3 × 3 remain except for the case of Tukey’s row-column as the simulation model. For this larger array, Tukey 1-df, Mandel-row, Mandel-column can capture interactions that are generated by Tukey’s row-column model, so does AMMI to a lesser extent. All models fail when data is generated under a general pattern under the AMMI model. Tables 4 and 5 in supplementary Appendix presents the numerical percentage of rejected null hypotheses corresponding to Figure 3.
To assess the false positive rates or Type I error in the absence of interaction, we generated data with only additive main effects and no interaction with N = 1800, 3600. Figure 4 presents the percentage of false rejections from 1000 simulated datasets at 5% significance level. All type I error rates are inflated than the nominal 5%, especially Tukey’s 1-df model. This is due to use of the cell-mean based model and ignoring the unbalanced nature of the data. Note that due to asymmetry in genotype frequency, the Type 1 error inflation levels for Mandel’s row and column models are not symmetric.
Figure 4.
Empirical estimates of type I error rates corresponding to the four interaction tests in a 3 × 3 array setting based on cell-means. Data is generated under additive model which has only main effects and the set of tests applied to 1000 simulated datasets under each setting. Simulation settings are described in Section 6.1.
As a summary, AMMI model follows the "mediocrity” principle of not being the best, but perform reasonably across a spectrum of general interaction models, a robustness feature that is desirable in agnostic search for interaction. None of the other four models possess this robustness property according to our simulation study.
6.2 Simulation under common epistasis models
Design and Parameter Setting
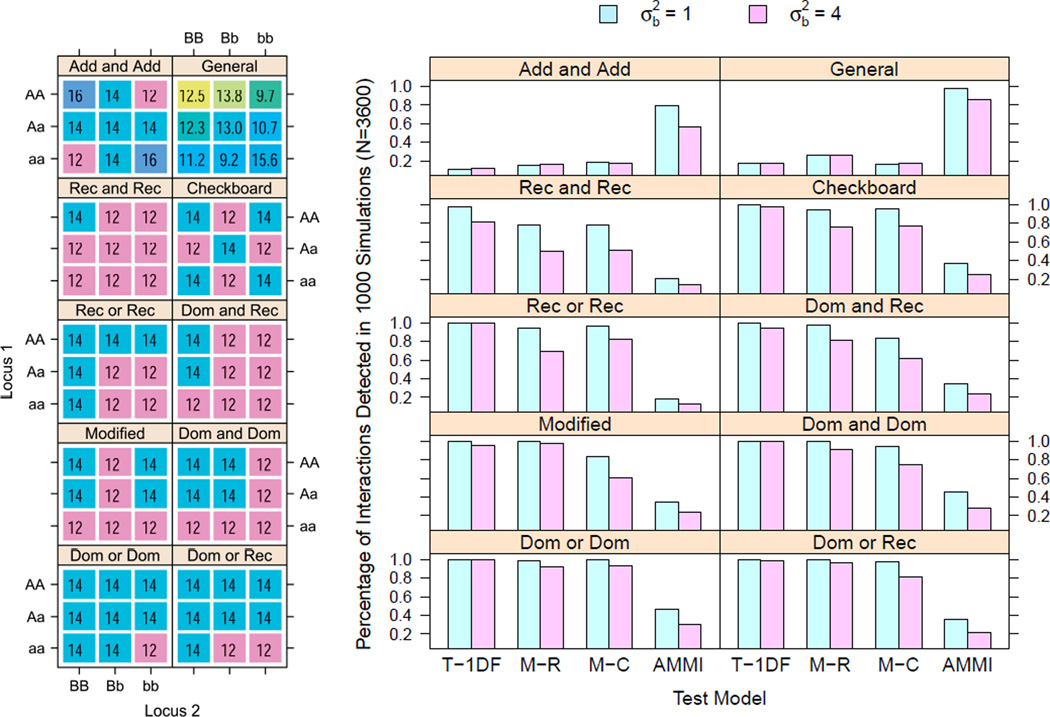
To evaluate the performance of these five models for studying plausible structures of gene-gene interaction in 3 × 3 tables with repeated measures on quantitative traits, data were simulated according to 10 general epistasis models [17]: (1) dominant or dominant (Dom or Dom), (2) dominant or recessive (Dom or Rec), (3) modified model, (4) dominant and dominant (Dom and Dom), (5) recessive or recessive (Rec or Rec), (6) dominant and recessive (Dom and Rec), (7) recessive and recessive (Rec and Rec)[(1)–(7) from Jung et al., 2009], (8) checkerboard, (9) additive and additive (Add and Add) [(8)–(9) from Culverhouse et al., 2004], and (10) a general model. The general model has an arbitrary interaction pattern which was simulated without main effects. The left panel in Figure 5 presents a visual representation of the interaction pattern with true cell means overlayed. In all epistasis models, the grand mean was set to 12. Minor allele frequencies for the two loci are still set at 0.3 and 0.4 respectively.
Figure 5.
Number of interactions detected (or null hypotheses of no interaction rejected) by each of the four tests in 1000 simulated datasets under 10 common epistasis models. The true models with cell means are displayed in different colors on the left hand panel. The top label within each box represents the true simulation model whereas the horizontal axis labels indicate the tests. carried out The error variance is set at 4 in all cases. Simulation settings are described in Section 6.2.
Main Results
Results are displayed in Figure 5. Tukey’s 1-df model and Mandel’s row and column models perform well for epistasis models with main effects (1)–(8). Tukey’s 1-df model and Mandel’s models are substantially more powerful at detecting interactions in model (1)–(8) than AMMI model. When main effects do not exist (models 9 and 10 represented in the first row), the AMMI model is the only model that can detect interaction. Thus, in situations where there may not be any main effect of either loci, AMMI model is able to capture the interaction as it is more flexible than the other four contenders that parameterize interaction in terms of main effects.
Thus to conclude, AMMI model or performing PIA does not appear to be a desirable choice for common epistasis structures when compared to Tukey’s 1-df, Mandel-row and Mandel-column models except for the case when there is no main effects of either loci but epistasis is present.
6.3 Simulation to evaluate the resampling tests
Since the primary goal of the paper is to introduce screening tools in terms of cell means approach, we conducted limited simulations to compare the performance of the resampling based tests introduced in Section 4 with the ones in Sections 2 and 3. We considered N = 1800 and the 3 × 3 parameter settings described in Section 6.1. Since tests of interaction accounting for individual observations have much greater power than the tests using cell means, we increased the magnitude of the variance components so that performances of different models can be distinguished. Data were generated under two settings . The within-subject correlations were still 0.2 and 0.5, respectively. Table 3 shows the power comparison of each of the four interaction models (Tukey’s 1-df, Mandel’s Row, Mandel’s Column, AMMI model) to detect interactions based on cell-mean approach and the resampling-based testing approach using individual data.
Table 3.
Comparison of estimated power (percentage of significant interactions detected in 1000 simulations) of resampling-based tests accounting for repeated measures to that of F statistic-based test using cell means (N = 1800, )
| Cell Means | Repeated Measures | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| True / Test Model | T-1 | M-R | M-C | AMMI | T-1 | M-R | M-C | AMMI | |
| Tukey-1df | 90.8 | 70.7 | 65.0 | 18.8 | 89.0 | 89.0 | 90.2 | 86.1 | |
| Mandel-Row | 0.0 | 65.0 | 0.0 | 12.5 | 17.4 | 93.4 | 18.4 | 91.8 | |
| Mandel-Col | 0.0 | 0.0 | 50.6 | 10.0 | 9.4 | 9.7 | 94.7 | 93.9 | |
| AMMI (M=1) | 0.3 | 0.0 | 0.0 | 12.9 | 28.2 | 49.1 | 62.6 | 89.4 | |
| Additive * | 13.7 | 10.6 | 8.00 | 4.8 | 3.6 | 3.9 | 4.2 | 4.1 | |
| Tukey-1df | 69.8 | 42.7 | 39.5 | 9.9 | 48.8 | 54.5 | 59.0 | 51.0 | |
| Mandel-Row | 1.3 | 39.1 | 0.2 | 7.5 | 10.3 | 55.4 | 14.0 | 51.1 | |
| Mandel-Col | 0.5 | 0.1 | 33.4 | 8.0 | 9.5 | 12.4 | 65.7 | 58.1 | |
| AMMI (M=1) | 2.7 | 1.3 | 1.7 | 10.2 | 11.3 | 25.7 | 29.6 | 53.1 | |
| Additive * | 18.0 | 15.4 | 12.6 | 5.6 | 3.1 | 5.2 | 5.8 | 6.0 | |
Only main effects but no interaction effect
Main Results
As we transition from cell-mean based model to individual data regression models all power values generally tend to increase. Especially the power gain for the AMMI model is quite impressive. When the true model is Tukey’s 1-df, all models perform reasonably well with (over 80% interactions were detected). With increase in , the powers decline and range from 48–60%. For simulation under Mandel’s row regression model, AMMI can detect the interaction; whereas Tukey’s 1-df and Mandel’s column model have low power (17%, 18% and 10%, 14% for , 8 respectively). Similar feature holds for Mandel-column model where Tukey’s 1-df and Mandel-row can hardly detect the interaction but AMMI maintain 94% power for and 58% power for . With AMMI as the simulation model, Tukey’s 1-df model can hardly detect the interaction (28% for ) whereas Mandel’s row and column models have power 49% and 60% respectively with . The AMMI has power 89% in this case, which is expected as it is the true generation model.
To assess the false positive rates or Type I error of the resampling-based tests, we generated data with only additive main effects without interaction. The last row ("Additive") presents the number of false rejections from 1000 simulated datasets at 5% significance level. When , all type I error rates are maintained at the nominal 5% for the resampling-based tests. Note that the Type 1 error for the cell-mean based models again are inflated under the additive null.
We investigated in more detail, the power curve of the AMMI (M = 1) model with repeated measures data to repeated measures with various d1 values. Figure 7 displays the power curve of AMMI where d1 ranges from 0.1 to 2.2 under in a 3 × 3 array setting with 1000 simulated datasets with N = 1800. One can notice that the repeated measures AMMI test is a valid test, maintaining nominal error rate and reasonable power across plausible alternatives.
7 Discussion
In this paper we have made an initial attempt to explore the idea of principal interaction analysis for repeated measures data on quantitative traits. We compared the proposed approach with other alternative reduced df tests for interaction and established robustness properties of the AMMI model for repeated measures data via simulation studies across a spectrum of general interaction models. Our simulation study indicates the AMMI test may not be very powerful for common epistasis models unless epistasis occurs in absence of main effects. In our data analyses we have provided graphical diagnostics to visualize the time and subject-specific contribution to interaction terms.
We have concentrated on the AMMI model with M = 1 and used the LRT [10]. We have downplayed the issue of formal selection of the number of interaction components M given the limited scope and length of the paper. That is an interesting question in itself that requires further research and appropriate strategies for inference.
We have primarily adopted a different and somewhat naive route of summarizing the data in terms of cell means in the I × J configuration and apply classical interaction models for testing non-additivity that are designed for single observations per cell. However, we then have developed new resampling based tests that used a mixed effects regression framework and fully capitalize on the repeated measures data structure, account for unbalanced data structure in Section 4 for all the models we considered. Our simulation study indicates that the resampling-based tests are valid tests maintaining nominal error levels and have substantially increased power over the cell-mean based approach, especially when is large. One can incorporate complex covaraince structures, time varying exposure, longitudinal effects of time, adjust for covariates by extending the first step mixed effects regression model in Section 4. One can explore using generalized estimating equation instead of mixed models in Section 4. We have focussed on testing, estimation related properties of these procedures need to be studied as well.
A proper maximum likelihood approach with repeated measures data and an unbalanced design setting will be more appealing if closed-form expressions for test statistics and their analytic distribution could be obtained instead of the resampling-based approach. Viele and Srinivasan (2000) adopted a Bayesian methodology to bypass the complexities to fit AMMI under complex/unbalanced data structure [41]. One can also fit the AMMI model in a restricted ML framework for mixed models [21, 22]. Model fitting methods and appropriate tests for Tukey’s model under a general regression set-up (including non-linear models) can be extended to the more general Mandel’s row/column and Tukey ’s row-column models [24, 25].
The cell-mean based approach can be viewed as a screening tool or a exploratory/preliminary idea about the interaction structure and longitudinal effects. In that sense, PIA for this problem is not just the AMMI test, but the accompanying simple visuals and diagnostics as well, providing an exploratory analyses of interaction structures. The idea of first fitting additive terms and then representing the residual matrix via a sparse decomposition appears to be a promising approach to study non-additivity. Further development of ML or REML based estimation approaches with proper asymptotic theory are warranted to follow-up the current study.
Supplementary Material
Figure 6.
Estimated power of AMMI (M = 1) resampling tests based on individual repeated measures with d1 ∈ (0.1, 2.2) under array from 1000 simulated datasets with N = 1800. The simulation settings are described in Section 6.3.
ACKNOWLEDGEMENT
This research was partially supported by the Long-Range Research Initiative of the American Chemistry Council and the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health. The research of BM was supported by NSF grant DMS-1007494, NIH grant CA156608-01. The authors will like to thank Dr. Joel Schwartz, Dr. Howard Hu and all NAS participants for sharing the data resources.
References
- 1.Khoury M, Wacholder S. Invited commentary: from genome-wide association studies to gene-environment-wide interaction studies–challenges and opportunities. American journal of epidemiology. 2009;169(2):227. doi: 10.1093/aje/kwn351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Verbeke G, Molenberghs G. Linear mixed models for longitudinal data. Springer Verlag; 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fitzmaurice G, Laird N, Ware J. Applied longitudinal analysis. Wiley-IEEE; 2004. [Google Scholar]
- 4.Lin X, Zhang D. Inference in generalized additive mixed modelsby using smoothing splines. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1999;61(2):381–400. [Google Scholar]
- 5.Tukey J. One degree of freedom for non-additivity. Biometrics. 1949;5(3):232–242. [Google Scholar]
- 6.Mandel J. Non-additivity in two-way analysis of variance. Journal of the American Statistical Association. 1961;56(296):878–888. [Google Scholar]
- 7.Gollob H. A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika. 1968;33(1):73–115. doi: 10.1007/BF02289676. [DOI] [PubMed] [Google Scholar]
- 8.Mandel J. The partitioning of interaction in analysis of variance. J. Res. National Bureau Stand. B. Math. Sc. 1969;73(4):309–328. [Google Scholar]
- 9.Mandel J. A new analysis of variance model for non-additive data. Technometrics. 1971;13(1):1–18. [Google Scholar]
- 10.Johnson D, Graybill F. An analysis of a two-way model with interaction and no replication. Journal of the American Statistical Association. 1972;67(340):862–868. [Google Scholar]
- 11.Johnson D, Graybill F. Estimation of σ 2 in a Two-Way Classification Model with Interaction. Journal of the American Statistical Association. 1972;67(338):388–394. [Google Scholar]
- 12.Corsten L, Eijnsbergen A. Multiplicative effects in two-way analysis of variance. Statistica Neerlandica. 1972;26(3):61–68. [Google Scholar]
- 13.Hegemann V, Johnson D. On analyzing two-way AoV data with interaction. Technometrics. 1976;18(3):273–281. [Google Scholar]
- 14.Marasinghe M, Johnson D. A test of incomplete additivity in the multiplicative interaction model. Journal of the American Statistical Association. 1982;77(380):869–877. [Google Scholar]
- 15.Cornelius P. Statistical tests and retention of terms in the additive main effects and multiplicative interaction model for cultivar trials. Crop science. 1993;33(6):1186–1193. [Google Scholar]
- 16.Piepho H. Robustness of statistical tests for multiplicative terms in the additive main effects and multiplicative interaction model for cultivar trials. TAG Theoretical and Applied Genetics. 1995;90(3):438–443. doi: 10.1007/BF00221987. [DOI] [PubMed] [Google Scholar]
- 17.Barhdadi A, Dubé M. Testing for gene-gene interaction with AMMI models. Statistical Applications in Genetics and Molecular Biology. 2010;9(1) doi: 10.2202/1544-6115.1410. [DOI] [PubMed] [Google Scholar]
- 18.Alin A, Kurt S. Testing non-additivity (interaction) in two-way ANOVA tables with no replication. Statistical methods in medical research. 2006;15(1):63. doi: 10.1191/0962280206sm426oa. [DOI] [PubMed] [Google Scholar]
- 19.Oman S. Multiplicative effects in mixed model analysis of variance. Biometrika. 1991;78(4):729. [Google Scholar]
- 20.Gogel B, Cullis B, Verbyla A. REML Estimation of Multiplicative Effects in Multienvironment Variety Trails. Biometrics. 1995;51(2):744–749. [Google Scholar]
- 21.Piepho H. Analyzing genotype-environment data by mixed models with multiplicative terms. Biometrics. 1997;53(2):761–766. [Google Scholar]
- 22.Meyer K. Factor-analytic models for genotype x environment type problems and structured covariance matrices. Genetics Selection Evolution. 2009;41(1):21. doi: 10.1186/1297-9686-41-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jung J, Sun B, Kwon D, Koller D, Foroud T. Allelic-based gene-gene interaction associated with quantitative traits. Genet Epidemiol. 2009;33(4):332–343. doi: 10.1002/gepi.20385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chatterjee N, Kalaylioglu Z, Moslehi R, Peters U, Wacholder S. Powerful multilocus tests of genetic association in the presence of gene-gene and gene-environment interactions. The American Journal of Human Genetics. 2006;79(6):1002–1016. doi: 10.1086/509704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maity A, Carroll R, Mammen E, Chatterjee N. Testing in semiparametric models with interaction, with applications to gene–environment interactions. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2009;71(1):75–96. doi: 10.1111/j.1467-9868.2008.00671.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tukey J. The future of data analysis. The Annals of Mathematical Statistics. 1962;33(1):1–67. [Google Scholar]
- 27.Eckart C, Young G. The approximation of one matrix by another of lower rank. Psychometrika. 1936;1(3):211–218. [Google Scholar]
- 28.Hanumara R, Thompson W. Percentage points of the extreme roots of a Wishart matrix. Biometrika. 1968;55(3):505. [Google Scholar]
- 29.Gauch H., Jr Model selection and validation for yield trials with interaction. Biometrics. 1988;44(3):705–715. [Google Scholar]
- 30.Gauch H, Zobel R. Predictive and postdictive success of statistical analyses of yield trials. TAG Theoretical and Applied Genetics. 1988;76(1):1–10. doi: 10.1007/BF00288824. [DOI] [PubMed] [Google Scholar]
- 31.Piepho H. On tests for interaction in a nonreplicated two-way layout. Australian & New Zealand Journal of Statistics. 1994;36(3):363–369. [Google Scholar]
- 32.Gabriel K. The biplot graphic display of matrices with application to principal component analysis. Biometrika. 1971;58(3):453. [Google Scholar]
- 33.Bradu D, Gabriel K. The biplot as a diagnostic tool for models of two-way tables. Technometrics. 1978;20(1):47–68. [Google Scholar]
- 34.Bell B, Rose C, Damon A. The Veterans Administration longitudinal study of healthy aging. The Gerontologist. 1966;6(4):179. doi: 10.1093/geront/6.4.179. [DOI] [PubMed] [Google Scholar]
- 35.Cruickshanks K, Wiley T, Tweed T, Klein B, Klein R, Mares-Perlman J, Nondahl D. Prevalence of hearing loss in older adults in Beaver Dam, Wisconsin. American Journal of Epidemiology. 1998;148(9):879. doi: 10.1093/oxfordjournals.aje.a009713. [DOI] [PubMed] [Google Scholar]
- 36.Mordukhovich I, Wilker E, Suh H, Wright R, Sparrow D, Vokonas P, Schwartz J. Black carbon exposure, oxidative stress genes, and blood pressure in a repeated-measures study. Environmental health perspectives. 2009;117(11):1767. doi: 10.1289/ehp.0900591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Park S, Elmarsafawy S, Mukherjee B, Spiro A, III, Vokonas P, Nie H, Weisskopf M, Schwartz J, Hu H. Cumulative lead exposure and age-related hearing loss: The VA normative aging study. Hearing Research. 2010 doi: 10.1016/j.heares.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lee E. Unpublished doctoral dissertation. 2004. Statistical Analysis Software for Multiplicative Interaction Models. [Google Scholar]
- 39.Nothnagel M. Simulation of LD block-structured SNP haplotype data and its use for the analysis of case-control data by supervised learning methods. Am J Hum Genet. 2002;71(suppl 4):A2363. [Google Scholar]
- 40.Culverhouse R, Klein T, Shannon W. Detecting epistatic interactions contributing to quantitative traits. Genetic epidemiology. 2004;27(2):141–152. doi: 10.1002/gepi.20006. [DOI] [PubMed] [Google Scholar]
- 41.Viele K, Srinivasan C. Parsimonious estimation of multiplicative interaction in analysis of variance using Kullback-Leibler Information. Journal of statistical planning and inference. 2000;84(1–2):201–219. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.