Soft-tissue imaging with C-arm cone-beam CT using statistical reconstruction

Abstract

The potential for statistical image reconstruction methods such as penalized-likelihood (PL) to improve C-arm cone-beam CT (CBCT) soft-tissue visualization for intraoperative imaging over conventional filtered backprojection (FBP) is assessed in this work by making a fair comparison in relation to soft-tissue performance. A prototype mobile C-arm was used to scan anthropomorphic head and abdomen phantoms as well as a cadaveric torso at doses substantially lower than typical values in diagnostic CT, and the effects of dose reduction via tube current reduction and sparse sampling were also compared. Matched spatial resolution between PL and FBP was determined by the edge spread function of low-contrast (~40–80 HU) spheres in the phantoms, which were representative of soft-tissue imaging tasks. PL using the non-quadratic Huber penalty was found to substantially reduce noise relative to FBP, especially at lower spatial resolution where PL provides a contrast-to-noise ratio increase up to 1.4–2.2 × over FBP at 50% dose reduction across all objects. Comparison of sampling strategies indicates that soft-tissue imaging benefits from fully sampled acquisitions at dose above ~1.7 mGy and benefits from 50% sparsity at dose below ~1.0 mGy. Therefore, an appropriate sampling strategy along with the improved low-contrast visualization offered by statistical reconstruction demonstrates the potential for extending intraoperative C-arm CBCT to applications in soft-tissue interventions in neurosurgery as well as thoracic and abdominal surgeries by overcoming conventional tradeoffs in noise, spatial resolution, and dose.

1. Introduction

C-arm cone-beam CT (CBCT) is increasingly being used for a growing scope of intraoperative applications, providing surgeons with up-to-date images that reflect anatomic changes within the patient (Siewerdsen et al 2005, Chen et al 2006, Wallace et al 2008, Orth et al 2008, Miracle and Mukherji 2009). While the high spatial resolution typically offered by CBCT is well-suited for imaging applications of high-contrast structures such as the sinuses, skull base, and head-and-neck (Daly et al 2006, Rafferty et al 2006) as well as spine (Schafer et al 2011, Oertel et al 2011) and contrast-enhanced vessels (Fahrig et al 1997, Kamran et al 2010, Patel et al 2011), soft-tissue imaging remains challenging due to inherently low contrast and fairly high levels of noise and artifact in conventional 3D filtered backprojection (FBP) image reconstruction (Struffert et al 2010, King et al 2012). The ability to perform soft-tissue imaging would enable a multitude of improved capabilities and new applications, including localization of soft-tissue tumors, avoidance of adjacent critical anatomy, improved verification of surgical product and visualization of margins, and detection of possible complications such as acute intracranial hemorrhages (ICH). For example, the ability to confidently detect ICH in the operating room (OR) would permit immediate intervention and could avoid the potentially severe morbidity associated with detection hours later in post-operative CT (Qureshi et al 2009, Zrinzo et al 2012). Similarly, soft-tissue imaging in the abdomen would offer expanded capability in applications such as image-guided liver and kidney interventions and perhaps more generally to augment ORs with high-quality 3D imaging employed at the end of a case as a safety check and verification of surgical product.

More widespread utilization of CBCT should additionally ensure that radiation dose is minimized not only in terms of dose to the patient but also to surgical staff. Ideally, patient dose levels would be substantially lower than those in diagnostic CT. For example, typical dose levels of ~40 mGy are used in diagnostic head CT and ~25 mGy in abdominal CT (Tsapaki et al 2006, Sagara et al 2010), while C-arm CBCT dose levels for soft-tissue visualization range from ~5–10 mGy in the head and ~4–6 mGy in the body (Daly et al 2006, Kalender and Kyriakou 2007, Zhang et al 2009, Schafer et al 2011). Among many dose-reduction strategies under development, recent advances in 3D image reconstruction demonstrate the ability to operate at lower dose and/or improved image quality through the use of model-based, statistical reconstruction (Silva et al 2010, Marin et al 2010, Pickhardt et al 2012, Miéville et al 2013). Such advances are similarly promising in C-arm CBCT—for example, penalized-likelihood (PL) reconstruction, which leverages a statistical model of the measured data combined with a priori assumptions on the image such as local smoothness. A growing arsenal of potential iterative reconstruction methods is under development for such purposes, including the simultaneous algebraic reconstruction technique (Mueller and Yagel 2000), total-variation (TV) minimization (Sidky and Pan 2008), penalized weighted least-squares (Wang et al 2008), compressed sensing (Tang et al 2009, Choi et al 2010), and tight-frame regularization (Jia et al 2011).

Methods for low-dose acquisition include x-ray tube current reduction (and/or modulation) and undersampling the number of projections (Bian et al 2010, Tian et al 2011). Undersampling appears in many contexts, including cardiac- or respiratory-gated acquisitions that produce inherently sparse, non-uniform sampling (Nielsen et al 2005, Song et al 2007, Chen et al 2012), faster acquisitions when speed is limited by the source and/or detector readout rate (as opposed to rotational speed), or novel system geometries and trajectories with systems such as robotic C-arms. In the current work, we investigate sparse acquisition simply as a dose-reduction method, comparing dose reduction via tube current reduction in fully sampled acquisitions with so-called ‘sparse acquisitions’ involving a reduction in the number of projection views. When the dose per projection is such that the quantum noise is well above the detector electronics noise (i.e., ‘quantum-limited’), better sampling is expected to enable better image quality. However, the electronic noise floor is a concern for low-dose CBCT (and even diagnostic CT), and splitting dose among too many views may be detrimental.

The image quality in fully sampled and sparsely sampled acquisitions is assessed in this work using FBP as a benchmark in comparison to PL in the context of C-arm CBCT soft-tissue visualization. In each case, an emphasis on fair comparison between reconstruction methods is underscored by enforcing careful matching of 3D spatial resolution, which is similar in spirit to other publications (La Rivière and Billmire 2005, Evans et al 2011, Lauzier et al 2012a). Preliminary results were presented at recent conferences (Wang et al 2013a, 2013b), and this work provides a complete quantitative analysis of image noise and spatial resolution with respect to low-contrast objects representative of soft-tissue imaging tasks in anthropomorphic head and abdomen phantoms and validation in a cadaveric torso, enabling appropriate sampling strategies to be determined and demonstrating the potential for statistical reconstruction methods to improve image quality and/or reduce dose.

2. Methods

2.1. Experimental setup

2.1.1. Mobile C-arm for intraoperative CBCT

CBCT acquisitions were performed with a prototype mobile C-arm (modified PowerMobil, Siemens Healthcare, Erlangen, Germany; see figure 1) equipped with a PaxScan 3030+ flat-panel detector [(1536 × 1536 pixels 194 μm pitch, 2 × 2 binning), Varian Medical Systems, Palo Alto, CA], with a source–axis distance of 60 cm and source–detector distance of 120 cm, providing a ~15 cm volumetric field of view (FOV). A motor drive provided continuous rotation of the C-arm over an orbital range of ~178°, collecting 200 projections during the 64 s orbit. The x-ray source was operated in pulsed-fluoroscopic mode, with the tube potential fixed at 100 kVp while the effective tube current (mA) was varied ranging from {0.31, 0.63, 1.25, and 2.50} mA in the head and {0.23, 0.47, 0.94, 1.88, 3.75, and 7.50} mA in the abdomen, yielding tube current–time products (mAs) ranging from 20–160 mAs in the head and 15–480 mAs in the abdomen. The projections were corrected for detector dark current offset and gain (Schmidgunst et al 2007) with a minimum raw signal value of zero enforced, and a geometric calibration phantom provided projection matrices that captured the source–detector position of each projection relative to the C-arm isocenter (Navab et al 1996, Galigekere et al 2003, Daly et al 2008).

Figure 1.

Mobile C-arm system and anthropomorphic phantom. Axial slices are from diagnostic multidetector CT (MDCT) illustrating plastic spheres contained within. Display windows [–100, 200] HU and [–200, 300] HU for the head and abdomen, respectively.

2.1.2. Phantoms and cadavers

An anthropomorphic head phantom (The Phantom Laboratory, Greenwich NY) included a natural skull and tissue-equivalent plastic (Rando^TM) with 12.7 mm diameter plastic spheres embedded within the cranium to simulate structures ranging in absolute contrast from ~40 to 900 HU (figure 1). The lowest-contrast sphere (9 o'clock position in figure 1) was selected as the target for analysis of image quality, since this size and level of contrast is representative of non-contrast-enhanced acute hemorrhage (typically +50 to +80 HU for fresh blood in the brain) or hypodense chronic hemorrhage/ischemic stroke (typically –15 to –40 HU for coagulated blood) (Naidich et al 2012, Lövblad and Baird 2010, Kidwell and Wintermark 2008, Furlan et al 2009, Gelabert-González et al 2005). The abdominal section of the phantom contained a natural skeleton and a similar arrangement of plastic spheres within a simulated liver. Again, analysis focused on the lowest-contrast insert (80 HU contrast) corresponding to soft-tissue visualization analogous to visualization of tissues such as fat (–82 HU), muscle (+44 HU), kidney (+44 HU), and liver (+54 HU) (Yohannes et al 2012). Analysis in the abdominal phantom identified reconstruction parameters that were in turn applied to a fresh (unfixed) cadaveric torso to visualize these soft-tissue structures in a more realistic abdomen.

Radiation dose in the head was measured with a 0.6 cm³ Farmer ionization chamber (Accu-Pro, RadCal, Monrovia, CA) at the center of a 16 cm diameter acrylic CTDI phantom, giving 0.041 mGy/mAs at 100 kVp. Dose in the abdomen was measured using the same chamber placed at the center and peripheral locations of an oblate abdominal phantom (QRM GmbH, Erlangen, Germany), giving a weighted dose of 0.026 mGy/mAs at 100 kVp (Schafer et al 2011).

2.2. Image reconstruction

All images were reconstructed with isotropic 0.6 × 0.6 × 0.6 mm³ voxels using Matlab (MathWorks, Natick, MA) with calls to custom external libraries for the computationally intensive 3D forward and backprojectors. Specifically, we implemented a modified form of the separable footprints with trapezoid functions (SF-TT) technique (Long et al 2010, Wu and Fessler 2011). Previous experience demonstrated high-frequency aliasing artifacts with ray-driven projectors such as Siddon's method (Siddon 1985) that were resolved by using separable footprints. Additionally, Long et al (2010) demonstrated SF-TT to be more accurate than other state-of-the-art projectors such as the distance-driven method (De Man and Basu 2004) (which in turn was shown to be more accurate than Siddon's method), particularly for larger cone angles and azimuthal angles near odd multiples of π/4. While we selected separable footprints for its improved accuracy, it is recognized that other projectors may also be suitable for low-resolution tasks such as soft-tissue imaging.

Our implementation of SF-TT was written in C/C++ using CUDA libraries for GPU acceleration (GTX 680, nVidia, Santa Clara, CA) and extended the original approach designed for a circular trajectory (five degree of freedom, 5-DOF) to handle an arbitrary 9-DOF geometry represented by the aforementioned projection matrices. The extension changed computation of the ‘amplitude’ (i.e., height of the trapezoid function of the footprint of each voxel) to calculating the intersection length between the voxel and a ray connecting the source and the center of the voxel (Kay and Kajiya 1986), followed by determining the detector pixels intersecting the trapezoidal footprint by projecting the eight vertices of the voxel to compute the trapezoid vertices.

2.2.1. Cone-beam filtered backprojection

Analytic image reconstruction used a variation of the Feldkamp–Davis–Kress (FDK) algorithm for cone-beam FBP (Feldkamp et al 1984). The line integrals l = – log (ỹ/ỹ_air) (where ỹ and ỹ_air represent the detected signal through the object and air, respectively) were capped at 8 (~40 cm water) to avoid potentially severe streak artifacts due to photon starvation resulting from low incident flux and/or large object size. Truncation was handled by extending the edge values in the u-direction with a zero-order hold (as opposed to, for example, zero-padding). The tradeoff between noise and spatial resolution in the axial plane was controlled by a Hann apodization (smoothing) window with adjustable cutoff frequency f_c,u applied to the ramp filter (figure 2). To account for the noise-resolution tradeoff in the longitudinal (z)-direction as well, an additional Hann smoothing filter was included in the v-direction (also illustrated in figure 2) with a cutoff f_c,v = α . f_c,u, where α was a fixed constant empirically chosen to match longitudinal spatial resolution to axial spatial resolution and to limit the noise-resolution parameter space to selection of a single parameter (f_c,u) varied from 10% to 50% of the Nyquist frequency (1.29 mm^–1). Applying smoothing in all directions was necessary for fair comparison between FBP and PL, since the latter employs image regularization in three dimensions, as detailed below. Failure to account for longitudinal spatial resolution would yield overly optimistic contrast-to-noise ratio (CNR) results for PL, since FBP would otherwise not enjoy the same advantage of 3D smoothing. This is an important consideration for CBCT that is sometimes overlooked but is intrinsic to the comparisons reported below.

Figure 2.

Smoothing filters in both the f_u- and f_v-directions provides smoothing in all image directions for FBP reconstruction—an important consideration for comparison to PL reconstruction.

2.2.2. Penalized-likelihood (PL) iterative reconstruction

The PL reconstruction method incorporates a statistical model of the measured data, balancing a data consistency term L(μ; y) with image regularization whose strength is determined by the parameter β applied to the image roughness penalty R(μ):

$$\widehat{\mu }=\underset{\mu }{\arg \max }L(\mu ;y)-\beta R\left(\mu \right).$$ (1)

The data consistency is given by the log-likelihood function and relates the consistency of an image μ to measurements y through the forward-projection operator A. The following Poisson quantum statistics model is applied:

$$y\sim \text{Poisson}\left(I_i\exp (-\mathbf{A}\mu )\right),$$ (2)

where y is the detector signal, ỹ, normalized by the effective detector gain, η, such that y has equal mean and variance, as expected from a Poisson distribution. The effective gain and number of incident quanta I₀ are determined from (a previously acquired) flood-field/gain calibration scan ỹ_air using the relationships:

$$\eta =\frac{\mathrm{Var}\left({\tilde{y}}_{\mathrm{air}}\right)}{\mathrm{E}\left[{\tilde{y}}_{\mathrm{air}}\right]},$$ (3)

$$I_0=\frac{\mathrm{E}\left[{\tilde{y}}_{\mathrm{air}}\right]}{\eta }.$$ (4)

Ignoring constant terms, the log-likelihood is then expressed as:

$$L(\mu ;y)\cong -\sum _i{\left[I_0\exp (-\mathbf{A}\mu )\right]}_i+y_i{\left[\mathbf{A}\mu \right]}_i.$$ (5)

Although the true statistics of the measurements are not necessarily independent and Poisson distributed, this simple model provides basic statistical weighting of the measurements. For example, more heavily attenuated rays have poorer statistics and are therefore down-weighted in the reconstruction.

Regularization was used to reduce image noise by applying a roughness penalty to the image:

$$R\left(\mu \right)=\sum _j\sum _{k\in N}{w}_{ik}\psi ({\mu }_j-{\mu }_k).$$ (6)

A first-order neighborhood $\mathcal{N}$ was used with unity weights w_jk for penalizing differences of the six nearest-neighbors in 3D. Both the basic quadratic penalty function ${\psi }_Q\left(x\right)=\frac{1}{2}{x}^2$ and the edge-preserving Huber penalty function ψ_H were considered:

$${\psi }_H\left(x\right)=\{\begin{array}{cc}\frac{1}{2\delta }{x}^2,\hfill & \mid x\mid \le \delta \hfill \\ \mid x\mid -\frac{\delta }{2},\hfill & \mid x\mid >\delta \hfill \end{array}\phantom{\}}.$$ (7)

For the Huber penalty, the parameter δ controls the width of the region for which a quadratic penalty is applied to differences smaller than δ, while a linear, edge-preserving penalty is applied to differences greater than δ. As δ→0, the Huber penalty approximates TV and favors piecewise-constant images, whereas selecting a large δ effectively provides a quadratic penalty, albeit with an extra factor of 1/δ. While image reconstruction was performed with voxel units of mm^–1, it is convenient to consider δ in HU by applying an approximate conversion factor of 5 × 10⁴ HU/mm^–1. Note that the edge-preservation properties of the Huber penalty are contrast dependent, where δ should be lower than the object contrast since the edge may be spread across more than one voxel. Additionally, the strength of the Huber penalty relative to that of a fully quadratic penalty decreases gradually for larger differences. As a result, we can expect δ to be considerably smaller than the object contrast so that the edge will be less penalized than with a fully quadratic penalty. For example, for the 40 HU target in the head, our initial evaluation of δ selections suggested that δ = {1, 3, 5} HU would span the range of Huber penalty behaviors. The regularization strength β was varied from 10³ to 10⁷ for the quadratic penalty and from 10⁰ to 10⁴ for the Huber penalty to encompass a range extending from under-regularized images (very noisy) to over-regularized images (very smooth).

The PL reconstruction was initialized by FBP and iteratively solved with an ordered subsets (OS), separable quadratic surrogates (SQS) technique (Erdogan and Fessler 1999). All voxels were updated simultaneously at each iteration, requiring 1 forward- and 1 backprojection per iteration to compute the likelihood gradient. While the likelihood curvature also requires a backprojection, it changes slowly and can, for example, be updated every ten iterations. The penalty gradient and curvature were computed directly from the image. Other common initialization strategies include using a zero or uniform image. When PL was run to convergence (as done in this study, for example, using 200 iterations with dynamic OS, described below), we observed only a small root mean square difference of <1 HU in the interior of the C-arm FOV between the different initialization strategies. However, the transient characteristics were observed to vary greatly: FBP initialization provided good edge information and converged in a manner that primarily reduced noise and artifacts, whereas a uniform image initialization filled in low-frequency content more quickly and subsequently converged in a manner that resolved the high-frequency content (edges). Although not studied here, these transient characteristics potentially provide different opportunities for using fewer iterations and is the subject of ongoing work.

Although convergence and monotonicity are no longer guaranteed with OS, its stability has been widely demonstrated, especially with fewer OS (Erdogan and Fessler 1999). Furthermore, while reconstruction is typically accelerated by the number of OS (denoted M), larger selections of M typically cause the reconstruction to approach less optimal limit-cycles looping about the optimum. Therefore, M was dynamically reduced from a large number of subsets toward progressively lower values so that every time M was changed, any potential limit-cycles were disrupted, which is similar to methods investigated by others (Hudson and Larkin 1994, Beekman and Kamphuis 2001, Sheng and Liu 2004). In our data, (rejecting the first two projections due to transient instability in the source and detector) a scan consisted of 198 projections, and a sequence of divisors M = {66, 33, 22, 18, 11, 9, 6, 3, 2, 1} was used for 20 iterations each, yielding a total of 200 iterations with an average of~17 subsets.

Lastly, the reconstruction FOV was chosen to encompass the entire object in the axial plane rather than just the C-arm FOV, since PL—as with other iterative methods—compares line integrals through the entire reconstruction with the measured data and would otherwise pileup the measured attenuation in a bright ring along the edge of the FOV. For example, the reconstruction FOV required expansion to 16.8 × 21.6 × 17.7 cm³ for the head. For large objects with severe truncation, such as the abdomen, the extent of the object may not be well-known, so the support of the object was estimated by fitting an elliptical cylinder (central axis parallel to the axis of the patient) of constant attenuation to the projections. The attenuation, size, and position of the elliptical cylinder were estimated by a least-squares fit of projections of the cylinder to the measured line integrals, as previously reported (Maltz et al 2007, Kolditz et al 2011, Lauzier et al 2012b). The estimated extent of the elliptical cylinder was then used to determine a reconstruction FOV large enough to encompass the cylinder.

2.3. Image quality

Both FBP and PL carry a tradeoff between spatial resolution and noise by way of freely adjustable reconstruction parameters—the cutoff frequency (f_c,u) for FBP and the regularization strength (β) for PL. As detailed below, these parameters were chosen to enable fair comparison—viz., matching spatial resolution (at a specific tissue contrast) for comparison of image noise (evaluated in a homogeneous region in the same tissue and at the same image location)—and image quality characteristics overall were selected with respect to the task of soft-tissue imaging—i.e., detection of a relatively large (~10 mm), low-contrast task(≤100 HU) lesion.

2.3.1. Spatial resolution

In nonlinear reconstruction methods like PL, the dependence of spatial resolution on reconstruction parameters as well as the object itself (i.e., contrast-dependent spatial resolution) requires that spatial resolution be characterized with respect to a structure approximating the task—in our case, a low-contrast structure approximate to soft-tissue (cf, conventional methods utilizing a high-contrast insert, such as a metal wire). Specifically, the low-contrast spheres in the phantoms illustrated in figure 1 were used to provide a measure of spatial resolution associated with soft-tissue structures in terms of the edge spread function (ESF) at the edge of a low-contrast sphere. The ESF width was characterized by fitting an error function (erf):

$$f\left(x\right)=a-\frac{c}{2}\mathrm{eff}\left(\frac{x-r}{\sqrt{2}\sigma }\right),$$ (8)

to oversampled points along the edge, similar to methods used by others (La Rivière and Billmire 2005, Thornton and Flynn 2006, Evans et al 2011, Lauzier et al 2012a, Lauzier and Chen 2013), where

$$\mathrm{erf}\left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{\mathrm{e}}^{-t^2}\mathrm{d}t.$$ (9)

As illustrated in figure 3, the voxel values within a cone whose central axis is normal to the surface of the sphere was plotted against the distance from the center of the sphere, with the voxels binned to the nearest one-tenth voxel distance (0.06 mm) and averaged, providing an oversampled edge spread. The erf fit was computed with Matlab's fit function (MathWorks, Natick, MA) initialized by the average attenuation a = 0.0179 mm^–1 (for the head) or 0.0184 mm^–1 (for the abdomen), contrast c = –0.0008 mm^–1 (for the head) or –0.0016 mm^–1 (for the abdomen), edge location r = 6.35 mm, and edge spread σ = 0.6 mm (1 voxel). For spatial resolution in the axial plane, the average of 12-directional edge spreads was used, where each directional cone had an aperture angle of 60° and its central axis was in the axial plane (figure 3). Directional cones were taken every 30° within the axial plane, and care was taken to exclude regions containing small air bubbles in the plastic spheres. Although spatial resolution is in general directionally dependent, the average directional edge spread parameter σ provided a single metric for spatial resolution of the low-contrast target, allowing comparison of images at ‘matched spatial resolution.’ Spatial resolution in the longitudinal direction was used for determining the FBP v-smoothing scaling parameter α and measured with the cones in the superior and inferior directions. Because the spheres are near the central axial plane (z = 0), cone-beam artifact is minimal, and the sphere ESF has been shown to accurately capture longitudinal-direction spatial resolution as well (Bartolac et al 2009, Baek and Pelc 2011). We note that although spatial resolution could in this way be ‘matched,’ such comparisons pertain to a specific contrast, object, and location (and do not necessarily apply to the entire image).

Figure 3.

The ESF of the low-contrast (9 o'clock) sphere was used to characterize spatial resolution in terms of the width (σ) of an oversampled edge within a 60° cone for each reconstruction type and dose level. The inset shows a magnified region around the sphere, and the ROI adjacent (anterior to) the sphere was used as a relatively artifact-free, uniform region for analysis of noise. The display window of the full FOV is [0.009, 0.028] mm^–1 and of the inset is [0.016, 0.021] mm^–1.

2.3.2. Contrast-to-noise ratio

At matched spatial resolution, a simple metric such as CNR was used for basic comparison of low-contrast imaging performance for large structures (≥10 mm) and rudimentary assessment of potential image quality improvement as a function of dose. Recognizing that CNR is far from a comprehensive metric of image quality, it nonetheless provides a reasonable method for assessing large-area (low-frequency) characteristics pertinent to soft-tissue visualization tasks. The ESF fit was also used to determine the contrast of the sphere (fit parameter c), since high levels of regularization may wash out the low-contrast target. Noise in the anthropomorphic phantoms was measured by taking the standard deviation of a uniform background region adjacent to the sphere (figure 3), while for the cadaver study, noise was determined from the standard deviation in a uniform region of a subtraction image computed between the reconstruction and a high-quality, high-dose reference image (12.5 mGy) to exclude effects of tissue heterogeneity and normalized by $\sqrt{1+d∕12.5}$, where d is the dose (mGy) of the low-dose scan, to account for the noise in the reference image.

2.4. Sparse sampling

The effects of sparse sampling on image quality were also investigated, using comparisons at equal dose and reconstruction time. The fully sampled case with P projections was compared to acquisitions with half and one-quarter the number of projections. To maintain equal dose, the dose per projection was increased by a factor of two and four, respectively, by increasing the tube current. When the number of projections was reduced, the number of subsets was equally reduced, as illustrated in figure 4. In addition to the equal dose, the number of effective iterations—the number of subsets (M) multiplied by the number of iterations (N)—was kept fixed to provide a fair comparison so that although sparse sampling has fewer subsets, it is given more iterations. Since the reconstruction time is directly proportional to this product M · N, the reconstruction time for the different scenarios is also equal. The fully sampled acquisitions were slightly trimmed (P = 192) so the subsets could be easily divided, as indicated in table 1. In this part of the study, the number of subsets was fixed in each case for simplicity, although a dynamic number could be accommodated as described in the previous section.

Figure 4.

Illustration of three sampling strategies with equal dose. The fully sampled case has P projections and M subsets (P = 12 and M = 4 for simple illustration), with dots representing source around the ~180° orbit and subsets labeled { A, B, C, D }. In the fully sampled case, a nominal tube current is used, while in the half- and quarter-sampled cases, the number of projections (and subsets) is reduced by a half and a quarter, respectively, while the tube current is doubled and quadrupled, respectively (illustrated by the size of the dots).

Table 1.

Sparse sampling techniques with equal dose and effective iterations M · N.

Sampling	Projections	Tube current	Subsets M	Iterations N
Full (100% P)	192	I	32	100
Half (50% P)	96	2I	16	200
Quarter (25% P)	48	4I	8	400

Fully-sampled acquisitions were obtained with the x-ray tube operated in pulsed-fluoroscopic mode, and the effective tube current was varied over the range 0.23, 0.47, 0.94, and 1.88 mA (where 0.23 mA was the minimum stable tube current on the C-arm) to form the baseline fully-sampled cases. Additional fully-sampled acquisitions at 3.75 and 7.50 mA were obtained (where 7.50 mA approached the heat load capacity), allowing for sparse acquisitions to be formed by subsampling the higher-technique scans (e.g., the 7.50 mA scan was used to form the case of 25% sparsity and 4 × 1.88 mA). Figure 4 compares the three equal-dose sampling strategies investigated, where sparsity was used to reduce the number of projections and subsets while the dose per projection—as indicated by the size of the dot at each source position—was increased. The sparse sampling comparison was conducted in the abdomen (phantom and cadaver), where electronic noise constitutes a larger part of the total noise at lower tube current.

3. Results

3.1. Anthropomorphic head phantom

For fair comparison of PL image quality to that of FBP, the longitudinal smoothing scaling parameter α was first empirically determined. The ESF of the low-contrast sphere in the head phantom broadens in all directions with PL since regularization is applied in all directions, and a near-linear relationship between the longitudinal direction and average axial-plane ESF was observed when the regularization strength β was varied (in both the quadratic (PL-Q) and Huber (PL-H) penalty cases). Therefore, the FBP cutoff frequency f_c,v for longitudinal smoothing should scale proportionally with the cutoff frequency f_c,u, and a proportionality factor of α = 1.5 was found to be in good agreement with the PL relationship. Using this choice of α, matching the axial-plane spatial resolution between PL and FBP then ensures that the longitudinal spatial resolution is closely matched, and only the average axial-plane spatial resolution will be considered henceforth.

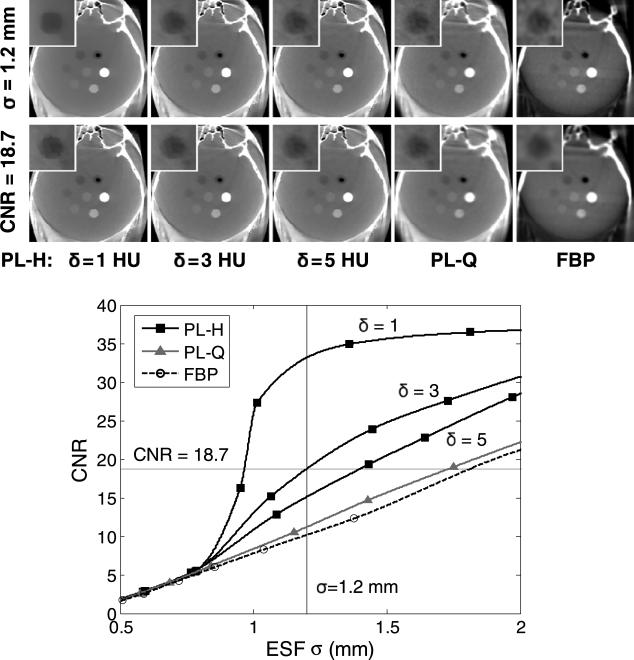
The effect of reconstruction algorithm and parameter selection on image noise and spatial resolution is demonstrated in figure 5 for a fixed dose of 3.3 mGy (1.25 mA × 64 s × 0.041 mGy/mAs), showing the CNR of the low-contrast sphere as a function of ESF. The conventional noise-resolution tradeoff is seen with FBP: as the cutoff frequency is reduced, leading to a smoother edge, the CNR increases accordingly. Perhaps surprisingly, PL-Q follows a tradeoff close to that of FBP due to its uniform application of smoothing, with only a small CNR gain over FBP. In fact, PL only departs from the conventional tradeoff when the Huber penalty is applied with a sufficiently small δ, with a sharp increase in CNR beginning at around σ = 0.8 mm. Therefore, PL-H provides a CNR advantage only at lower spatial resolution for low-contrast edges (e.g., σ > = 0.8 mm for 40 HU contrast in the head), which suggests the visualization of soft-tissue structures is improved by PL-H at lower spatial resolution rather than at higher spatial resolution. For very small δ, such as δ = 1 HU, the sharp increase in CNR becomes especially pronounced, providing a ‘kink’ in the curve that can be attributed to the edge-preservation properties of the Huber penalty. However, over-regularization with such small δ can lead to a blocky appearance of the sphere and patchy texture in uniform regions. Additionally, while larger σ yields a larger relative gain in CNR for PL-H over FBP, excessive image blur should be avoided. For example, the reconstruction methods can be compared at equivalent spatial resolution of σ = 1.2 mm, demonstrating the noise reduction with PL-H at lower δ, but with δ = 3 HU chosen as a reasonable middle-ground for the Huber penalty in terms of a reasonable gain in CNR while avoiding a blocky appearance to low-contrast features. Additionally, although the spatial resolution for low-contrast tissues was reduced in order to improve CNR, PL-H maintains the sharpness of higher contrast features, unlike PL-Q or FBP which apply more uniform smoothing across the object. On the other hand, when the reconstruction methods are compared at equivalent CNR, it is clear that PL-H with larger δ, PL-Q, and FBP require greater image smoothing (in that order), but that δ = 1 HU produces unrealistic, rough edges. Therefore, the apparent gain suggested by metrics such as CNR must be balanced relative to the qualitative acceptability of the images, which may exhibit characteristic blocky or patch textures associated with over-regularization.

Figure 5.

Head phantom showing the noise-resolution tradeoff for different reconstruction methods (3.3 mGy). As β is increased for PL-Q, both CNR and ESF width increase, achieving roughly the same tradeoff as decreasing f_c,u in FBP. The Huber penalty (PL-H), on the other hand, departs from the conventional tradeoff. At fixed spatial resolution (σ = 1.2 mm, top row of images), PL-H offers the lowest image noise, and at fixed CNR = 18.7 (second row of images), PL-H offers the highest spatial resolution, but qualitative assessment indicates that reducing δ too much (e.g., δ = 1 HU) results in a blocky, more piece-wise constant appearance in the image. Display window [0.009, 0.028] mm^–1 for the full FOV and [0.016, 0.021] mm^–1 for the inset.

Other artifacts appear as previously reported with FBP reconstruction (Schafer et al 2011)—e.g., lateral streaks associated with the incomplete orbit (~178° arc) and truncation artifacts (image intensity differences at the edge of the FOV). The quantitative analysis of ESF and CNR avoided the effects of these artifacts by, for example, selecting the noise ROI in a largely artifact-free region. Nonetheless, PL-Q and PL-H are seen to provide the additional benefit of greatly reducing these artifacts in comparison to FBP, with the inherent ability to account for the incomplete orbit (or more generally, an arbitrary orbit) and to diminish the effects of truncation within the C-arm FOV. In particular, we will henceforth focus on PL-H with an appropriately selected δ (viz., δ = 3 HU for the head) due to its improved performance over PL-Q.

At matched spatial resolution (σ 1.2 mm) in PL-H (δ = 3 HU) and FBP across a range of levels, it becomes clear that PL-H provides a boost=in CNR regardless of dose, as shown in figure 6. Although visualization of the low-contrast sphere is reduced at lower dose, PL-H maintains an advantage over FBP for this task, which is representative of the size and level of contrast needed to detect, for example, an ICH. A power-law curve fit (ax^b + c) was applied to the measured CNR in figure 6, and while it is generally an appropriate fit+for FBP, it may be less suitable for PL-H. Nonetheless, it can be seen that PL-H simultaneously offers higher CNR at lower dose. For example, PL-H at 3.3 mGy offers ~50% higher CNR than FBP at 6.6 mGy. As demonstrated above, PL-Q shows little or no improvement over FBP in this regard, and it is the edge-preserving PL-H that departs from the conventional tradeoff. The ability of PL-H to suppress noise appears relatively better at higher dose, where the contrast target is more easily differentiated from the image noise, allowing for stronger noise reduction. The greater relative advantage of PL-H over FBP emerges at doses of 1.7 and 3.3 mGy in this scenario. Despite improvements in CNR, low-dose limits must of course be considered alongside assessment of the clinical acceptability of the images, e.g., noise in the 0.8 mGy images may be too high to be clinically acceptable, even with PL-H.

Figure 6.

Head image reconstructed with PL-H versus FBP over a range of dose levels. At matched spatial resolution, PL-H maintains superior CNR over FBP for the low-contrast target. For example, PL-H at 3.3 mGy yields a 50% higher CNR than FBP at 6.6 mGy.

3.2. Anthropomorphic abdomen phantom

The C-arm FOV was intentionally chosen to be contained entirely within the abdomen phantom, as shown in figure 7, to highlight the interior problem scenario. In this case, the object support size is not immediately known but was instead estimated by fitting an elliptic cylinder to the data. The resulting estimated elliptic support in the axial plane shows fair agreement with the overall extent of the phantom when overlaid on the diagnostic MDCT image and provided the reconstruction FOV relative to the C-arm FOV (30.0 × 24.0 cm² in-plane, with the C-arm FOV offset to the upper left). While the reconstructed image outside the C-arm FOV is not necessarily correct, it improves the accuracy of reconstruction within the C-arm FOV. As an aside, note that the MDCT image is shown only as a reference for visualizing the context of the C-arm FOV, and it is not intended as a comparison of image quality between the two modalities. Such a comparison would warrant a separate study in the future and matching of kVp, dose, reconstruction techniques, etc.

Figure 7.

Axial slice of anthropomorphic phantom from diagnostic MDCT and PL-H reconstruction of CBCT. The C-arm FOV and estimated elliptical object support are overlaid on the MDCT image as an illustration of scale and content outside the C-arm FOV. The grayscale windows for MDCT and CBCT are [–200, 300] HU and [0.015, 0.025] mm^–1, respectively.

Because the lowest-contrast sphere available in the phantom had a slightly higher absolute contrast (~80 HU) than the sphere in the head, a higher value of δ = 5 HU was used for the Huber penalty, and the matched spatial resolution comparison was conducted at a slightly higher spatial resolution of σ = 1.0 mm, where substantial gain in CNR could still be achieved at higher spatial resolution. At such matched spatial resolution, the CNR for PL-H and FBP are shown in figure 8, with PL-H demonstrating that 50% dose reduction can be achieved while maintaining an increase in CNR (by 2.2 × ). Although scatter and beam-hardening contribute to artifacts in both the PL-H and FBP images, the difference in shading across the images is likely due to the different truncation correction methods applied—specifically, an elliptic object support for PL and zero-order extrapolation of the projection data at the edges for FBP. While not the focus of this paper, future work will seek to implement better correction methods and quantify their impact on artifact reduction.

Figure 8.

Image quality comparison at matched spatial resolution (σ = 1.0 mm) for CBCT of the abdomen phantom. PL-H maintains a CNR advantage over FBP—for example, increasing CNR by a factor of 2.2 at 1.6 mGy (0.94 mA × 64 s × 0.026 mGy/mAs) in comparison to FBP at 3.1 mGy. Images are displayed with a grayscale window of [0.015, 0.025] mm^–1.

The comparison of sparse sampling performance in figure 9 was conducted at four levels of equal dose and effective iterations, with CNR evaluated at matched spatial resolution (σ = 1.0 mm). At 3.1 mGy, sparse sampling introduces streak artifacts typically seen in sparse FBP reconstructions that contribute to increased levels of noise, thus discouraging the use of sparsity. However, at 0.4 mGy, the measurement noise (including additive noise sources such as electronic noise) plays a stronger role, and the streak artifacts in FBP at 50% sparsity are mitigated by the benefit of concentrating dose into fewer projections to overcome electronic noise to such an extent that the combined effect is an overall reduction in measured noise and improved visualization of the sphere. At further levels of undersampling (e.g., 25% sparsity), the strong streak artifacts begin outweighing the reduced effects of electronic noise, and image quality is degraded. These results suggest two regimes for a dose-reduction strategy and a crossover point in dose, above which the acquisition should remain fully sampled while reducing the tube current, and below which sparse sampling with higher tube currents becomes advantageous and can be considered the ‘ultra-low’ dose regime. For this particular system, object, and imaging task, the crossover point is ~1 mGy, as determined by the intersection of the power-law curve fits of the fully and half-sampled cases. Note that although the crossover dose level depends on the targeted spatial resolution, with sparse acquisitions performing relatively better at lower spatial resolution due to the lower Nyquist sampling requirement, the overall dose-reduction strategy in the two regimes remains the same. Additionally, larger objects will increase the crossover dose, while smaller objects will reduce the crossover dose.

Figure 9.

Sparse sampling comparison at the low and high end of the dose range considered. Both PL-H and FBP suggest an empirical crossover point of ~1 mGy, below which undersampling can be used to increase CNR for this object and imaging task.

PL-H demonstrates a similar overall trend to FBP except at higher CNR. While it is capable of suppressing the streak artifacts in the undersampled cases, PL-H is equally capable of suppressing noise in the fully sampled case at the higher dose levels considered. However, at ultra-low dose levels (<1.0 mGy in figure 9), a moderate degree of undersampling (e.g., 50% sparsity) reduces image noise by lowering the relative effect of electronic noise in the acquired projections, but low-contrast image quality suffers when too few samples are acquired (e.g., 25% sparsity). Therefore, the PL-H dose-reduction strategy is the same: acquire fully sampled data for dose levels above ~1 mGy, and employ moderate undersampling below ~1 mGy. Note that the fully sampled case here (figure 9) produced similar results to that of figure 8, with the slightly fewer number of projections and fixed number of OS producing only minor differences.

3.3. Cadaveric torso

Because the spatial resolution in the cadaver images could not be easily quantified and verified as in the phantom studies above, the PL-H and FBP reconstruction parameters that generated a matched spatial resolution of σ = 1 mm for the 80 HU contrast sphere in the abdomen phantom were applied to the cadaveric torso. A fair comparison between PL-H and FBP is still expected due to the similarity in size and low-contrast imaging task as well as the identical scanning protocols between the cadaver and abdomen phantom. The fresh cadaver provides realistic soft-tissue imaging with kidney to fat contrast of ~120 HU, which is slightly higher than the sphere considered in the abdomen phantom. The ellipse-fitting initialization method yielded a reconstruction FOV of 30.0 × 21.0 × 18.0 cm³, with 18.0 cm of longitudinal coverage sufficient to prevent longitudinal truncation of any projection ray within the volume.

The multiplanar view of the PL-H reconstruction (figure 10) demonstrate soft-tissue delineation of the liver, kidney, and muscles from surrounding fat, as well as fine, high-contrast details in the spine and the bowel matter containing small pockets of air. The coronal MDCT image illustrates the overall anatomic context in relation to the C-arm FOV (and is not intended as a direct image quality comparison of MDCT and CBCT).

Figure 10.

C-arm setup of cadaver study. Coronal slice of MDCT, showing the greater anatomic context of the C-arm FOV, display window [–200, 300] HU. Multiplanar reformat of PL-H reconstruction for CBCT, display window [0.015, 0.025] mm^–1.

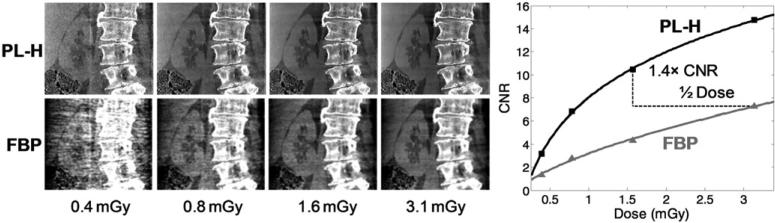
Continuing the focus on soft-tissue imaging, CNR was calculated in the cadaver abdomen using the contrast between the right kidney and surrounding fat, while noise was measured in the somewhat homogeneous liver after subtraction with a high-quality (12.5 mGy) reference image reconstructed with the respective PL-H and FBP algorithms. As shown in figure 11, PL-H once again boosts the CNR relative to FBP, validating the results shown above for the anthropomorphic phantoms. Furthermore, in addition to the improved soft-tissue visualization at approximately matched spatial resolution for soft-tissue, it is easy to appreciate that the Huber penalty preserves the sharpness of high-contrast structures such as the spine and air/tissue interfaces, which for FBP are uniformly smoothed along with the soft-tissue.

Figure 11.

C-arm CBCT images of the cadaver at the same dose levels and reconstruction parameters for σ = 1.0 mm as used in the anthropomorphic abdomen phantom. The results validate a major improvement in image quality (and/or capability for dose reduction) with PL-H. Display window [0.015, 0.025] mm^–1.

The cadaver images also validate the previous results regarding sparse sampling. In particular, the qualitative image appearance and quantitative CNR metric confirm the advantage of sparse sampling at ultra-low dose, as well as the advantage of remaining fully sampled at higher dose, with a crossover at ~1.7 mGy (for simplicity, only the PL-H comparison is shown in figure 12). The crossing point in dose level is slightly higher in the cadaver than the phantom and is possibly attributable to different amounts of the object-specific streak artifacts and potentially inexact matching of spatial resolution after duplicating reconstruction parameters from the phantom to the cadaver, especially in the cases of sparse sampling. Nonetheless, the overall dose regimes appropriate for the fully sampled and half-sampled cases is clear, while the quarter-sampled reconstructions have poor recovery of soft-tissue features.

Figure 12.

Sparse sampling comparison in the cadaver. At low dose levels (below ~ 1.7 mGy in this case), 50% sparsity yields the best image quality, while at higher dose levels, image quality is best when fully sampled. Soft-tissue structures can be difficult to recover when there are too few samples (25% sparsity), regardless of dose level.

4. Discussion and conclusions

Statistical reconstruction methods hold considerable promise for low-dose, soft-tissue imaging capability in C-arm CBCT. The studies reported here emphasized a reasonably fair comparison of basic image quality (CNR) in FBP and PL reconstructions at matched spatial resolution in objects of similar size and contrast. Because of the complex dependencies of image quality on the imaging task, the object itself, and the CBCT acquisition, selection of PL reconstruction parameters β and δ followed an empirical approach. In the context of clinical use, we anticipate task-oriented options for PL such as ‘soft-tissue’ or ‘bone’ driven under the hood by selection of parameters such as β and δ, similar to how diagnostic CT typically offers variants of ‘smooth,’ ‘standard,’ or ‘sharp’ filter kernels for FBP. The parameter selection could be based on empirically derived relationships dependent on the technique, patient size, and size and contrast of the task, or from models built to predict parameters from the data and specified task, including the ability to account for spatially varying resolution and noise seen in PL (Gang et al 2013).

For a quadratically penalized PL reconstruction, we found little or no gain in noise and spatial resolution compared to conventional FBP, while PL with a Huber penalty departed rapidly at lower spatial resolution (e.g., ESF σ > 0.8 mm), with significant gain in CNR achieved via edge-preserving noise reduction. The ESF regime of σ ~1 mm where PL-H excels is well-suited for soft-tissue imaging of large (>10 mm), low-contrast structures. Additionally, the importance of the imaging task is underscored by considering that the high-contrast spheres would have a divergent increase in CNR with little increase in ESF for any δ less than ~100 HU since the edge can be easily preserved even while the uniform regions are arbitrarily smoothed out. This of course would not be appropriate for soft-tissue imaging since it is not representative of the noise-resolution tradeoff seen with the low-contrast objects. In the sparse sampling comparisons, high-contrast features such as bone appear to be well-recovered with PL-H, but sparse sampling should be used judiciously, even in the low-dose regime where electronic noise constitutes a major component in the overall measurement noise. The finding that fully sampled acquisitions provide better image quality in the quantum-noise-limited dose regime is consistent with expectations and as reported by others (Tang et al 2009). Although different choices could be made regarding the number of subsets and iterations, our experience indicates that the overall conclusions hold as long as fair comparison at equal dose and effective iterations (i.e., number of subsets times iterations) are maintained.

Because the objective of this study was to quantify imaging performance achieved by statistical reconstruction, reconstruction time was not a primary concern, although it is recognized that this is an important consideration for practical application, especially in image-guided surgery. However, the image quality improvement and dose reduction enabled by PL-H still allows use of high-quality C-arm CBCT in realistic workflow scenarios in which longer computation times are potentially tolerable (e.g., within 5–10 min), such as a patient safety check acquired at the end of the case (complications or retained foreign bodies) or a quality assurance check to confirm and assess the surgical product. In this study, the computation time for 200 iterations with dynamic OS and the more accurate but slower separable footprints projector was ~4–6 h for full-volume reconstructions, depending on volume size. Methods for speeding up the optimization problem and improved implementation approaches show promise in achieving fully iterative reconstructions estimated to be on the order of minutes. Certainly, substantially fewer iterations can be used, and the reconstruction can run for as many iterations as time permits, especially since most of the image quality improvement typically occurs in the earlier iterations. Since initialization can play an important role when a limited number of iterations is used, an FBP initialization within the C-arm FOV can be combined with ellipse fitting to ensure the reconstruction FOV encompasses the object and the line integrals are approximately matched to the measurements. Moreover, initial experience with acceleration techniques compatible with OS-SQS, such as spatially non-uniform updates and Nesterov's method (Kim and Fessler 2012, Kim et al 2013), indicate the potential for major reduction in reconstruction time. Additionally, while the Matlab implementation of the PL algorithm employed in this work allowed flexible and rapid development in conjunction with GPU-accelerated projection operations, a fully GPU-based implementation of PL would eliminate GPU-CPU memory transfers by keeping all variables in GPU memory and would exploit the inherent parallelism of computing the SQS updates by performing these simple calculations on the GPU. The use of faster, less accurate projectors (e.g., Siddon's method (Siddon 1985) and/or a pixel-driven approach (Peters 1981)) can be considered in lieu of separable footprints for improving reconstruction time, especially when high spatial resolution is not a priority (as may be the case for soft-tissue imaging) and since image regularization offers the potential to mitigate the high-frequency artifacts typically associated with errors arising from forward- and/or back projector sampling effects. Such a comparison in the tradeoff between projector accuracy and reconstruction time is the subject of ongoing work. Lastly, computational hardware is expected to steadily improve in the number of cores and clock speed, and multi-GPU approaches are possible as well.

In summary, statistical image reconstruction methods enable improved low-dose soft-tissue visualization in CBCT, with substantial reduction in noise and artifact, especially when somewhat lower spatial resolution (σ ~ 1 mm) is acceptable as in many soft-tissue imaging scenarios. Although scatter was fairly low due to the extended geometry (Schafer et al 2012), incorporation of scatter-correction as well as beam-hardening correction methods is the subject of ongoing work, with image quality from both analytic and iterative reconstruction methods expected to improve. Furthermore, statistical reconstruction methods have been adapted to include an electronic noise model (La Rivière and Billmire 2005, Xu and Tsui 2009), which may play an important role for improving image quality in the ultra-low dose regime. Incorporation of electronic noise within the model-based reconstruction will also improve identification of the dose below which sparse sampling should be applied, possibly using methods that accurately simulate the effect of dose reduction via tube current reduction and/or undersampling on noise in the projections (Whiting et al 2006, Žabić et al 2013). It is expected that these approaches may be combined to further improve soft-tissue image quality and, along with aforementioned methods for accelerating iterative techniques, highlight the continuing potential of statistical reconstruction methods in C-arm CBCT for image-guided procedures.