Charging the Quantum Capacitance of Graphene with a Single Biological Ion Channel

Abstract

The interaction of cell and organelle membranes (lipid bilayers) with nanoelectronics can enable new technologies to sense and measure electrophysiology in qualitatively new ways. To date, a variety of sensing devices have been demonstrated to measure membrane currents through macroscopic numbers of ion channels. However, nanoelectronic based sensing of single ion channel currents has been a challenge. Here, we report graphene-based field-effect transistors combined with supported lipid bilayers as a platform for measuring, for the first time, individual ion channel activity. We show that the supported lipid bilayers uniformly coat the single layer graphene surface, acting as a biomimetic barrier that insulates (both electrically and chemically) the graphene from the electrolyte environment. Upon introduction of pore-forming membrane proteins such as alamethicin and gramicidin A, current pulses are observed through the lipid bilayers from the graphene to the electrolyte, which charge the quantum capacitance of the graphene. This approach combines nanotechnology with electrophysiology to demonstrate qualitatively new ways of measuring ion channel currents.

Supported lipid bilayers (SLBs) have risen as a robust alternative to the traditional and fragile black membranes for studying ion channel electrophysiology, a key component in biological signaling pathways to passively and selectively transport ions across the impermeable cell membrane. The traditional approach of forming a lipid bilayer across a microscale aperture is extremely flimsy, requiring high level of expertise, which limits throughput. In contrast, SLBs are more robust, easy to make, and potentially applicable toward high throughput.¹⁻⁴ As an atomically thin 2d material, graphene provides an attractive choice as the electrode for such electrophysiology studies, as it adds many additional properties that may be exploited for novel interactions with ion channels. For example, the in plane conductance of graphene is extremely sensitive to the environment, yielding proposals for applications in resistive biosensing.⁵ An additional method of excitation of graphene is capacitive rather than resistive biosensing, which to date has not been exploited, in spite of the known extreme quantum limit of graphene,⁶ where the capacitance is dominated by the finite energy required to add charge to a quantum system, called the quantum capacitance. In order to explore and exploit the unique properties of reduced dimensional materials (such as graphene) for novel applications in electrophysiology, it is necessary first to develop a fundamental understanding of the basics of the interaction between 2d materials such as graphene, lipid bilayers, and ion channels and the effects of the interactions on charge transport in these systems.

In this study, we integrate a supported lipid bilayer (SLB) onto a graphene electrode and demonstrate electrical sensing of the opening and closing of individual ion channels gramicidin A (gA) and alamethicin in the SLBs. The SLB forms an insulating barrier as confirmed by several techniques. The Dirac point of the graphene FETs is not affected by changes in the solution pH or KCl concentration after it is covered by SLBs. By careful measurement and analysis of the appropriate circuit elements in an equivalent circuit model, we confirm that the ion channel current in our setup directly charges the quantum capacitance of the graphene. This is a qualitatively different type of interaction than traditional SLBs with metal electrodes, since metal electrodes do not exhibit quantum capacitance effects. Although we previously showed single ion channel activity with 1d devices,⁷⁻⁹ this is the first time the activity of single ion channels (including gA and alamethicin) has been presented in 2d (specifically graphene) electronic devices.

In this work, the graphene acts as an electrode on one side of the SLB, and current changes observed are due purely to changes in the membrane permeability induced by the opening and closing of ion channels, similar to the case where metal electrodes are used for the same purpose. Qualitatively, the capacitance that is charged is different in this case (the quantum capacitance), as opposed to metal electrodes, in which only the double layer capacitance is charged. As graphene is a new material with many possible opportunities for heterogeneous integration in complex systems, there are many potential advantages of using graphene for this purpose, for example, in printed and flexible electronics on biocompatible polymers for in vivo electrophysiology sensing of neurons (e.g., as a component of the US government BRAIN initiative),^10,11 cardiomyocites, pancreatic beta cells, and other electrophysiologically active cells. The measurement of single ion channels represents the ultimate in sensitivity for such an in vivo measurement. Furthermore, (in contrast to metal electrodes), as the graphene layer is optically transparent (and can even be optically active),⁵ it provides for an opportunity to integrate electrophysiology with optics (both external as well as optically active membrane proteins such as the rhodopsins in both actuation and sensing mode), an exciting frontier area in optogenetics and single ion channel sensing.¹² Finally, as graphene is an active material, this is an important step toward integrating in-plane current sensing of ion channel currents with 2d and 1d⁷⁻⁹ nanoelectronic devices. Thus, this work should be seen as a first step toward integration of nanoelectronics with electrophysiology at the single ion channel level.

While all of these exciting applications are yet to be demonstrated, the novel aspect of this work is the first demonstration of the charging of the quantum capacitance (a nanoelectronic concept) with the ionic currents flowing through biological nanopore (an electrophysiology concept). This general approach thus presents novel and qualitatively new ways that ion channel electrophysiology can be integrated with the quantum properties of reduced dimensional systems such as graphene, paving the way for a new class of devices to probe and assay biological process using the unique quantum and electrical properties of a wide range of nanotechnology based systems where the reduced dimensionality plays a key role.

Results

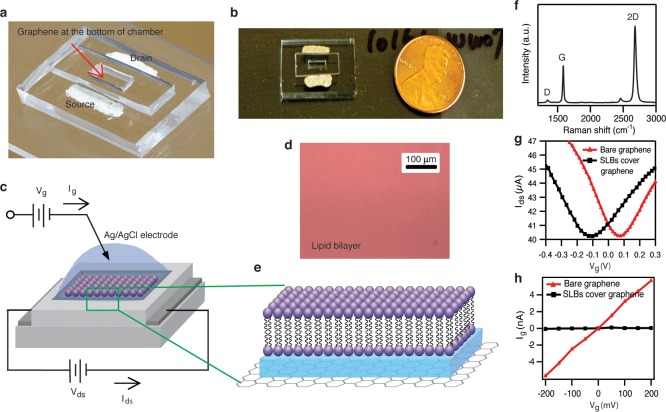
Our integrated system to measure SLBs with graphene FETs is shown in Figure 1a. The scheme consists of a graphene layer on a PDMS substrate serving as the sensing platform. An additional PDMS well on top of the graphene allows convenient deposition of a lipid bilayer and isolates the metal source/drain electrodes from the electrolyte solution. A Ag/AgCl electrode is placed directly in contact with the electrolyte to measure the current from the graphene to the solution. The quality of graphene is examined by Raman spectroscopy (Figure 1f). The graphene film’s two main peaks are G and 2D bands which are located at ∼1568 and ∼2677 cm^–1, respectively. The defect-related peak (the D band) is visible but small at 1332 cm^–1. This result confirms that the graphene is a high quality monolayer.

Figure 1.

(a) Photograph of graphene FET device. (b) Top view photograph of graphene FET device. (c) Schematic illustration of graphene-SLBs platform. (d) Fluorescence image of SLBs on graphene surface (scale bar is 100 μm). (e) High magnification illustration of SLBs on graphene surface. (f) Raman spectrum of monolayer graphene. (g) The drain-source current vs liquid gate voltage characteristics of bare graphene FET and covered by SLBs at 100 mM KCl and V_ds = 100 mV. (h) The liquid gate current vs liquid gate voltage characteristics of FET with bare graphene and covered by SLBs at 100 mM KCl.

Prior to deposition of the lipid bilayer, the electrolyte (0.1 mM phosphate buffer at pH 7 with 100 mM KCl) allows liquid top gating of the graphene in plane conductance. The electrolyte does not contain a redox active species, and so within the voltage window applied by the Ag/AgCl electrode (which we refer to as the gate voltage V_g), we expect no faradaic current; i.e., we expect no electron transport from graphene to solution. Measurements of the graphene to electrolyte current (which we call the “gate current”) confirm this: The current from the graphene to the electrolyte (the background current) is less than 15 nA in the range of applied gate voltage.¹³ The physical origin of this current is likely trace redox active species, or background redox of OH^– and H⁺, both of which are small as expected. (Prior work¹⁴ shows an expected “background” current of less than 5 × 10^–4 A/cm², which would translate into less than 100 nA in our geometry). This confirms that the electrolyte is only capacitively gating the graphene and not allowing a significant amount of direct dc current to flow from graphene to the electrolyte.

Once the basic device was operating without the bilayer, we turned to formation of a lipid bilayer on graphene. Formation of SLBs was performed by the vesicle fusion method. Briefly, lipids in chloroform solvent are evaporated under nitrogen. The dried lipids are solubilized in phosphate buffer solution to form a multilamellar vesicle (MLV) solution. Small unilamellar vesicles (SUVs) are obtained by sonication of the MLV solution. SLBs are deposited on graphene transistors by heating the SUV solution in contact with the graphene surface. This process involves adsorption, deformation, flattening, and rupture of the vesicles on the graphene surface. The lipid bilayers are then rinsed abundantly with deionized water to form continuous SLBs. Formation of SLBs on graphene has also been reported by another group.¹⁵ Typically, continuous and uniform supported lipid bilayers can only form on a surface that is hydrophilic, with a layer of water trapped between the hydrophilic lipid heads and the hydrophilic surface. Although this was not addressed in ref (15), the reason that both that group and our own are able to form continuous, high quality SLBs on graphene is most likely related to the fact that graphene is not entirely hydrophobic, and its surface properties are closely related to the supporting substrate,^16,17 which can even render it hydrophilic in some cases. A key issue for the end result in this experiment is the uniformity, quality, and seal of SLBs. Initially, a simple fluorescence image (using 1 mM of fluorescent dye solution (rhodamine DHPE) added to label lipids hours before evaporation of chloroform) indicates that the bilayer is smooth and continuous (Figure 1d). FRAP and AFM data confirm this interpretation (Supporting Information 9 and 10). However, more comprehensive analysis of the seal was assayed in several ways, discussed in more detail next.

The dc transport data in the presence of the lipid bilayer indicates that the in plane graphene conductance is still gated by the electrolyte through the lipid bilayer, with a small shift of the Dirac point. The interaction of the lipids with the graphene, while not the focus of this work, was studied extensively in ref (15), where the change of the Dirac voltage with lipids of different head charges was studied in detail. Although they did not report the quantitative difference between the Dirac point with pure water vs lipids, and they did not study the pH or electrolyte concentration dependence of the Dirac point as we did (see below), our results are qualitatively consistent with ref (15). For the detection of single ion channel activity, a low-leakage current between the graphene and the electrolyte is necessary, as one generally needs a stable and high electrical resistance of SLBs in the gigaohm range for high quality electrophysiology. In Figure 1h, the effective resistance of the graphene-electrolyte interface is about 35 MΩ. After the graphene is covered by SLBs, the effective resistance between the graphene and the electrolyte increases by over an order of magnitude to about 0.5 GΩ, indicating a high quality, electrically insulating layer has been formed by the lipid bilayer. As our area is 1 mm², this results in a specific resistance of about 10 MΩ-cm², a very high specific resistance for SLBs.^1,18,19 With this GΩ seal, our graphene-SLBs devices are primed to detect single ion channel activity.

The presence of a uniform fluorescence image and high resistance seal does not confirm whether the system is a lipid monolayer, bilayer, or multilayer. Even FRAP is unable to convincingly determine if there is a bilayer or multilayer. Therefore, the one prior claim in the literature of a single bilayer on graphene¹⁵ cannot rule out the possibility that a multilayer was present. Therefore, to date no convincing evidence of a single bilayer on graphene has ever been presented. In order to assay the number of bilayers in our samples, we have used electrochemical impedance spectroscopy (EIS, see Supporting Information 3) to determine the capacitance of SLBs. This is the “gold standard” in electrophysiology to determine the properties of the lipid bilayer, with an expected value of around 0.7 μF/cm². In our experiments, around 30% of devices have a lipid capacitance of 0.6–0.7 μF/cm², which is characteristic of a lipid bilayer. For other devices the capacitance is either around 1–1.3 μF/cm², showing the formation of a lipid monolayer on graphene, or around 0.2 μF/cm², indicating presence of multiple lipid layers on graphene. In order to confirm this interpretation, we performed another test based on fluorescence quenching (Supporting Information 4). The working principle is that QSY-7 amine can quench, via FRET, the fluorescence of the lipid dye reporter TexasRed DHPE (Invitrogen #T1395MP) embedded into the lipid layer. If a supported lipid bilayer is truly a bilayer, only the top layer is accessible to QSY-7 amine, and therefore, adding the quencher will reduce roughly half of the total fluorescence intensity. Similarly, the reduction will be less if the lipid layer is a multilayer. Of all the devices we tested, 30% showed approximately 50% decrease in fluorescence intensity, indicating the formation of a true lipid bilayer. FRAP and AFM data confirm this interpretation (Supporting Information 9 and 10).

In building a sensitive and selective biosensor platform, it is critical for the devices to maintain both graphene’s extreme sensitivity and the SLBs’ chemical and electrical isolation from the electrolyte environment. Once this is demonstrated, the SLBs can be functionalized to specific analyses for selective biosensor applications. Therefore, we next demonstrate the bare graphene transistors’ sensitivity and the SLBs’ seal performance.

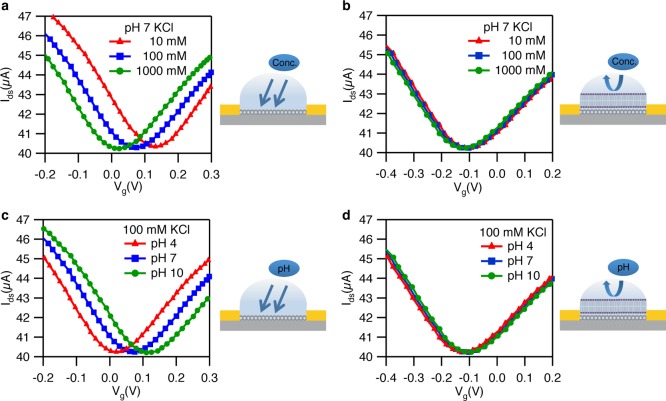
To understand in more detail the effects of SLBs on the graphene surface, we examined bare graphene FETs and those covered with SLBs as a function of electrolyte (KCl) concentration as well as pH. Figure 2a shows depletion curves (drain-source current I_dsvs electrolyte gate voltage V_g) of bare graphene transistors for three different KCl concentrations (10, 100, and 1000 mM), showing the typical V-shaped transfer curves. When the ionic strength is increased, the Dirac point is shifted negative (consistent with previous reports).^20,21Figure 2b demonstrates that this sensitivity of the Dirac point to KCl concentration is completely removed after deposition of SLBs, indicating that SLBs form an effective chemical and electrostatic barrier between the graphene and the electrolyte solution.

Figure 2.

(a) Bare graphene FETs in 0.1 mM PB buffer at pH 7 with 10 mM KCl (red), 100 mM KCl (blue) and 1 M KCl (green). (b) Graphene FETs coating with SLBs in 0.1 mM PB buffer at pH 7 with 10 mM KCl (red), 100 mM KCl (blue) and 1 M KCl (green). (c) Bare graphene FETs in 0.1 mM PB buffer with 100 mM KCl at pH 4 (red), pH 7 (blue), and pH 10 (green). (d) Graphene FETs coating with SLBs in 0.1 mM PB buffer with 100 mM KCl at pH 4 (red), pH 7 (blue), and pH 10 (green). All measurements are conducted at V_ds = 100 mV.

Next, we investigate the sensitivity of the Dirac point to solution pH. Figure 2c presents depletion curves of bare graphene transistors for three different pH values (4, 7, and 10 pH), all showing the typical V-shaped depletion curves. The Dirac point has shifted positive with an increase in pH value from pH 4 to pH 10.^22,23 Similarly to the electrolyte case, we show that the Dirac point is completely unaffected by the electrolyte pH after deposition of SLBs (Figure 2d). This provides further indication that the graphene is chemically isolated from the electrolyte after deposition of SLBs.

Taken collectively, by measuring the electrical current directly through SLBs, as well as the sensitivity of the Dirac point to changes in the electrolyte pH and concentration before and after deposition of SLBs, in addition to the bilayer capacitance and fluorescence, we provide strong evidence that the graphene is insulated from the electrolyte environment by SLBs. We next turn our attention to the behavior of this system upon introduction of pore forming membrane proteins gA and alamethicin.

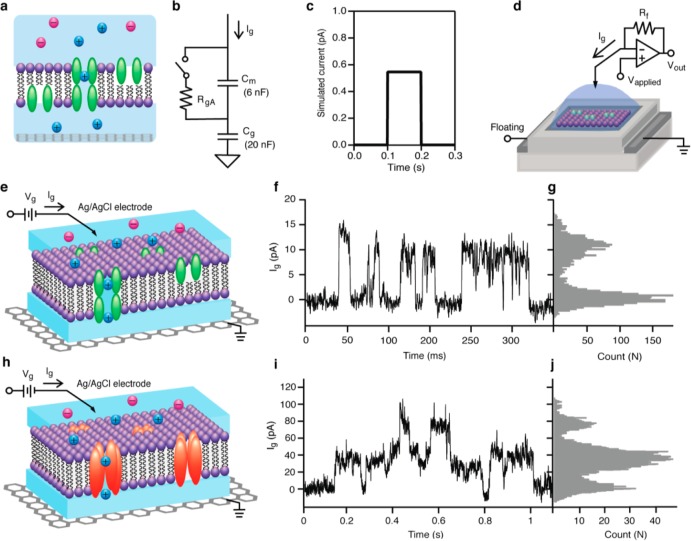
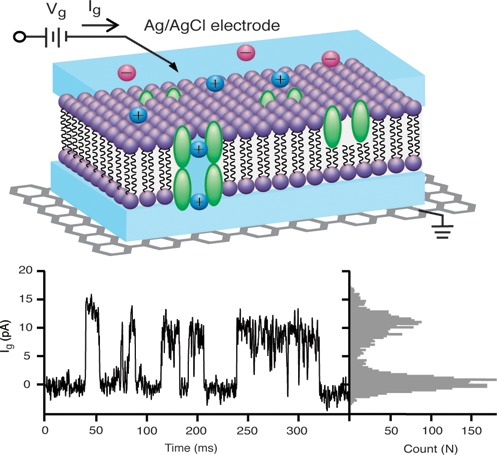
Gramicidin A (gA) is a canonical (model) ion channel protein for demonstration of electrophysiology because of its simple behavior: It displays linear conductance with membrane voltage (i.e., it is a voltage-independent channel), is permeable to monovalent cations, is stable at different chemical environments, and is easy to be modified to obtain various sensing applications.^24,25 Gramicidin A monomers (which diffuse laterally on both sides of the bilayer) occasionally dimerize (with a lifetime of the order of 1 s), forming a 4 Å wide and 25 Å long water channel for the conduction of monovalent cation current, with a conductance of the order of 10 pS (100 GΩ). In suspended lipid bilayer experiments, this results in a step function current vs time trace with heights of the order of a few pA, and widths of the order of seconds. In order to investigate this for our lipid bilayer geometry, we introduce gA monomers into the SLBs prior to formation (Figure 3e) and then measure the current through the SLB with a high resolution patch clamp amplifier system vs time (see Methods).

Figure 3.

(a) Schematic diagram of SLBs with gA on graphene surface. (b) Circuit diagram of graphene-SLBs. R_gA represents a single ion channel gA that is either open (R_gA ∼ 100 GΩ) or closed (R_gA an open). C_membrane is the capacitance of SLBs, measured to be 0.6 μF/cm² and scaled to the 1 mm² area of our system. C_quantum is the capacitance of graphene, measured to be 2 μF/cm² and scaled to the 1 mm² area of our system. (c) Simulation result of current detected by patch clamp system. (d) Schematic diagram of SLBs on graphene FETs connected with patch clamp system. (e) Schematic diagram of SLBs with gA on graphene surface for ion channel activity detection. (f) Current trace for ion channel activity of gA at V_g = 100 mV in 1 M CsCl. (g) Histogram of current trace f. (h) Schematic diagram of SLBs with alamethicin on graphene surface for ion channel activity detection. (i) Current trace for ion channel activity of alamethicin at V_g = 100 mV in 100 mM KCl. (j) Histogram of current trace i.

Figure 3f presents the current (between the graphene and the electrolyte, through the SLB) vs time at 100 mV positive applied voltages between the electrolyte and the graphene. Clear, step function behavior is observed with the approximate expected amplitude (12 pA) and width (10s of ms) of the opening and closing of a single gA channel. From the histogram of the current trace (Figure 3g), open and close events are apparent. At 50 mV positive applied voltage, the current step magnitude is 6 pA (Supporting Information 5), about half of the 100 mV step height, indicating a linear current voltage curve, as expected for gA. In order to further support our interpretation that the current steps are due to the opening and closing of individual ion channels, we decided to vary the type of membrane protein ion channel, while keeping all of the other procedures essentially identical. Our next ion channel to study is alamethicin.

Alamethicin is a voltage-gated channel-forming peptide:²⁵ when the membrane surface has sufficiently negative potential, the ion channel will form in the SLBs. Depending on the number of monomeric units forming the channel, different conductance levels are typically observed. The selectivity for ions is minimal, but cations are somewhat preferred over anions (Figure 3h). Thus, the key features of alamethicin (in particular, as compared to gA) are (A) an asymmetric current–voltage relationship, (B) multiple conductance values, and (C) much larger conductance (∼100 pS vs ∼10 pS) than gA.

Figure 3i presents a representative time trace for the same experimental conditions as Figure 3f but with the only substantial difference that we use alamethicin instead of gA. A histogram of the currents clearly indicates multiple current values, typical of alamethicin, which displays multiple conductance values (Figure 3j). Alamethicin is known to have 5 conductance values in suspended lipid bilayers (which are not uniformly spaced), but of these the largest conductance state is rarely observed, and the smallest is very close to zero conductance compared to the other 4 states. This is completely consistent with our measurement, where we do not have enough signal-to-noise to resolve the first (lowest) conductance state, and the highest conductance state is not observed in our measurement time. (A more detailed analysis in the Supporting Information 6 shows that the steps that we do observe are completely consistent with the multiple conductance states observed in the literature.) Similarly, the open dwell times are of the order of 100 ms, also characteristic of alamethicin. Finally, the current values (∼100 pA) are about an order of magnitude larger for the alamethicin channels than the gA channels, as expected. These observations (higher current, multiple conductance states, and asymmetric current–voltage characteristics) are in agreement with well-known properties of alamethicin ion channels.²⁵ The yields of observing ion channel activity are about 20 and 40% for alamethicin and gA, respectively. Although we have not done a systematic study, this yield seems to improve with lower applied voltages across the lipid bilayer. At voltages larger than 0.5 V, this yield drops to zero. This is consistent with the known properties of both suspended and supported lipid bilayers.

Discussion

We now turn to a circuit interpretation of our results. Figure 3b presents a simplified equivalent circuit model. (A more detailed circuit model is presented in the Supporting Information 1.) We are mostly interested in the pulse shape and height, i.e., transients in response to opening and closing of ion channels. Therefore, the capacitances are of primary interest here. We model the system as two capacitors in series: The first is the well-known lipid bilayer membrane capacitance C_membrane (from prior studies as well as our own measurements described in the Supporting Information 3 to be ∼0.6 μF/cm²). The second capacitance is the graphene capacitance, which consists of two components in series: The electrochemical double layer capacitance and the quantum capacitance are in series, together forming C_g. We now discuss the quantum capacitance and the double layer capacitance in more detail.

The physical origin of the quantum capacitance is due to the following effect:²⁶ Adding electrons to a quantum system (e.g., a gas of many electrons, such as the electrons in a sheet of graphene) increases the Fermi energy of that system. Because of the Pauli exclusion principle, the lowest occupied quantum states are already filled, and only the next available quantum states in the system can be filled with the addition of additional electrons. Adding N electrons increases the Fermi energy by the density of states times the number of electrons added, and one can equate this increase in energy with a capacitance (called the quantum capacitance), given by ΔE = Q²/2C_quantum. In general, unless the dimensions of the system are small, the spacing between each energy level in the system is very small compared to kT, and therefore, the discreteness of the energy levels (i.e., the quantization of the energy levels) is not observed. (In other experiments where all 3 dimensions are small, the discrete quantum states can be observed, and these are called quantum dots. Our system is much too large in size to see quantum dot effects.) Therefore, the term quantum capacitance does not indicate a capacitance that is quantized. Rather, the quantum capacitance is a finite density of states effect. Normally in metals, the density of states is extremely large (due to the large electron density and Fermi energy), so that the quantum capacitance is also much larger than any other capacitance in the system, and hence does not appear in electrical measurements. In 2d and 1d systems with large geometric capacitances (due to ultrathin and high K dielectrics or intimate physical contact with a gating electrolyte as in our system), the quantum capacitance is a significant component of the total capacitance of the system. How large is the quantum capacitance compared to the double layer capacitance in an electrolyte gated system? We now address that question for our particular system.

We first discuss the numerical value of the double layer capacitance C_DL. This consists of two physical capacitors in series: The Helmholtz capacitance C_Helmholtz, due to ions adsorbed directly on the surface, and the diffuse layer capacitance C_diffuse, due to a higher local ionic concentration of one charge species within a Debye length of the interface. The Helmholtz capacitance is typically independent of applied bias and around 10–20 μF/cm². Numerically, the diffuse capacitance can be estimated (at zero applied bias) as (ref (27), eq 13.3.21b) C_diffuse = 228 C^1/2 μF/cm², where C is the electrolyte concentration in mol/L. At 0.1 and 1 M, the prediction is C_diffuse = 72 and 228 μF/cm², respectively. C_diffuse has a mild bias dependence. Since the Helmholtz capacitance is much smaller than the diffuse layer capacitance, it dominates at the electrolyte concentrations used in this experiment, and the total double layer capacitance should be around 10–20 μF/cm², dominated by the Helmholtz capacitance, and only weakly dependent on applied bias. (See, e.g., Figure 13.3.1 of ref (27), which shows 16–20 μF/cm² for 0.1 to 1 M NaF in contact with Hg, with very weak dependence on electrolyte concentration.) Note that the value of 0.1 mM to 1 mM used in ref (6) is in a different regime, where the diffuse layer is the dominant capacitance, and hence the total interfacial capacitance is strongly dependent on the electrolyte concentration. (See again, e.g., Figure 13.3.1 of ref (27), which shows a strong dependence of the differential capacitance for NaF concentrations between 1 and 10 mM.) We next discuss the value of the quantum capacitance. Prior measurements of the quantum capacitance⁶ put this value at between 2 and 4 μF/cm² at the Dirac point, for impurity induced densities between 0.5 and 2 × 10¹² cm^–2. Note that varying the electrolyte concentration can change the screening of impurities and hence the quantum capacitance. By this analysis, the literature seems to indicate that the quantum capacitance is significantly smaller than the double layer capacitance (2–4 vs 10–20 μF/cm² at the electrolyte concentrations used in our experiments). This was not the case in ref (6), where at low electrolyte concentrations the double layer capacitance would be predicted to be dominated by the diffuse capacitance, and be numerically comparable to the quantum capacitance.

Instead of relying on the literature, we have measured the total capacitance of graphene with no SLB using EIS (Supporting Information 2). We find a total value (including the quantum capacitance in series with the double layer capacitance) of between 2 and 5 μF/cm² at the Dirac point at the electrolyte concentrations used in these experiments. In the Supporting Information, we discuss in further detail the dependence of this measured capacitance on electrolyte concentration and composition, and compare to the only other measurement in the literature.⁶ Although the detailed dependence on electrolyte concentration is not explained by existing theories, taken together our reasoning and data seem consistent with the consideration that the quantum capacitance is the dominant (smallest) capacitance compared to the double layer capacitance (specifically, C_quantum ∼ 2–5 μF/cm² and C_DL ∼ 10–20 μF/cm²), although current experimental techniques do not allow a separate measurement of each. Furthermore, as discussed further in the Supporting Information, the measured quantum capacitance vs gate voltage for graphene with no SLB behaves as expected by the theory presented in ref (6) for an impurity concentration of ∼10¹² cm^–2, a reasonable value consistent with the literature of graphene properties. Regardless of the relative contribution of each component, the measured capacitance is larger than the membrane capacitance (measured separately, see Supporting Information 2), and this allows us to develop the simple circuit model in Figure 3b to analyze the electrical properties of our system.

The model in Figure 3b is intended to give a qualitative description of the pulse heights that confirms our interpretation of measurements of the opening and closing of ion channels. Because the graphene capacitance is larger than SLB capacitance, the system forms a voltage divider, and most of the applied voltage drop is across SLB. In the case where there is a dc conductance across the bilayer, and from the solution to the graphene, the ratio of the conductances sets the dc voltages. As discussed in the Supporting Information, this does not qualitatively change the dc bias in our case. Thus, a 100 mV bias from graphene to counter electrode provides a ∼90 mV voltage across the lipid bilayer membrane.

We next discuss what happens when the channel opens. When the ion channel opens, the resistance in the model R_gA changes from an open circuit to 100 GΩ. As the initial voltage is 90 mV, an initial current of ∼0.9 pA flows through the ion channel (the resistor R_gA in the model). As this initial current flow, it charges the two capacitors. A simple model shows that in the limit where C_g ≫ C_m (which is approximately true in this case), the current through the entire loop (which is measured by the current amplifier in our setup) is approximately equal to the current flowing through the ion channel. The exact expression is I_measured = (C_g/(C_g + C_m)) I_gA, where I_gA is the current flowing through gA ion channel. Thus, when the ion channel opens, most of the current is used to directly charge the quantum and interfacial capacitance of the graphene.

How long does the current flow and how does the amplitude change with time during the open period of the ion channel? As the charges on the capacitors change, so does the voltage across the lipid bilayer and the current flowing through the ion channel I_gA. However, the change in voltage is very small for times of the order of 1 s or less, which is the time scale that the ion channel is open in our experiments. As the initial current flowing through the ion channel is approximately 90 mV/R_gA ∼ 1 pA, this would change the voltage by the capacitors at a rate of 10^–3 V/s or less. Within the one second time constant of the channel open or close time, this corresponds to a negligible change in the lipid bilayer voltage, and hence a negligible change in the current through the channel. Thus, the current vs time is expected to be a step function, as is observed in our experiments. Note that we do not see any evidence of local changes in the ionic concentration in the water layer between the graphene and SLBs. Such a change might, for example, through various mechanisms cause a drop in the current while the ion channel was open; in contrast we observe a constant current during the open period. A more detailed model that includes the resistances of the membrane, the electrolyte resistance, and also any faradaic current between the graphene and the solution does not alter this conclusion (Supporting Information 1). Note that this is in sharp contrast to our comparable nanotube ion channel experiments,⁷⁻⁹ which has shown spikes in the current under identical experimental conditions, due to the small intrinsic capacitance of the nanotubes in a similar setup.

There are two physical effects that we next consider. The first is the dependence of the capacitance on the concentration of ions and voltages in the circuit, which both depend on time. The second is the possibility of nonuniform charging of the capacitances, which are distributed spatially. We discuss these both in turn.

First, the circuit model in Figure 3b assumes the capacitances are all independent of time. However, in principle this is not true. For the simple case of an electrolyte in contact with a metal electrode, it is by now well established that the double layer capacitance depends on the dc potential applied between the electrolyte and the metal electrode.²⁷ Therefore, if this dc potential changes with time, the capacitance will also change with time. In addition, the quantum capacitance of graphene depends on both the electron Fermi energy, i.e., electron density (which is also related to the applied dc potential, which will change in time as the various capacitors in the circuit are charged up), and the impurity density (which may change with time if the local ion concentration of the water layer between the graphene and the SLB changes). Prior to opening of the ion channel, our estimates above indicate that 90% of the voltage applied between the counter electrode (i.e., Ag/AgCl electrode in the electrolyte) and the graphene is dropped across the lipid bilayer membrane. Therefore, for an applied voltage of 100 mV, only 10 mV is applied between the water in contact with the graphene and the graphene itself. When the ion channel opens, this changes the applied voltage by an amount of roughly 10^–3 V/s across the membrane, and 10^–4 V/s between the water and the graphene. This would mean a change of less than 0.1% of the quantum capacitance during the 1 s time the ion channel is open, and an even smaller change in the double layer capacitance during the same time (Supporting Information Figure S2). Because the ionic strength of the electrolyte in contact with the graphene can change the graphene to electrolyte capacitance (Supporting Information 2), it is also possible that this changes with time. Although we do not know the exact ion concentration vs time for the aqueous layer between the graphene and the bilayer, we can estimate that it is roughly comparable to the concentration of the bulk electrolyte. Using our data in Supporting Information Figure S5 to estimate the change in capacitance with changes in the electrolyte concentration, we estimate that the percentage change in the graphene quantum capacitance due to the change in ionic strength is negligible during the measurement time. Thus, none of the physical effects that cause time dependence of the capacitances in our system is significant enough to change the measured ion channel current within the resolution of our system. Finally, the in plane conductance of graphene will change with time because of the changes in the ionic concentration and voltages with time. However, since the graphene is highly conductive in plane compared to the impedance of the capacitors and the resistance of the bilayer and ion channel, the change in the in plane conductance will have a negligible effect on the ion channel current.

An important question is the effect of local ionic buildup. Our circuit model assumes the charge spreads quickly over the entire area. However, this is likely not the case, as there is bound to be significant spreading resistance in the lateral direction in the region between the SLB and the graphene electrode.²⁸ In our case, this would result in a smaller effective area that is charged. Thus, the ion channel current may not be charging the entire ∼ mm² area in ∼100 ms. However, as long as the spreading resistance is less than the individual ion channel resistance when it is open (approximately 100 GΩ for gA), this will not significantly change the shape of the current pulse.

Because at present we do not have a reliable way to measure the ion concentration in the water layer between the SLB and the graphene, we do not know the exact value of this quantity. In fact the exact thickness of the water layer is not certain in our measurements. However, it is clear from the electrical data that the magnitude and the time of the current spikes is consistent with a water layer that is thick enough to sustain an ionic current through the ion channel protein for the period of time that it is open, i.e., 10s of milliseconds. In the future, additional experimental techniques such as X-ray or neutron scattering will be required to quantify the exact distance between the SLB and the graphene in our system, a project that is currently underway in our laboratories.

Although a simple model of a uniform lipid bilayer is consistent with the time constant and magnitude of the current spikes, the frequency of current spikes is much less than would be expected given prior literature on gA incorporation into large area SLBs and the resultant change in the net resistance of the bilayer (i.e., the time average).²⁹ This could be due to one of several factors. First, the incorporation efficiency of the ion channels could be very low in this system. Second, it is possible that there are patches of multilayer and bilayers simultaneously present; when an ion channel is incorporated into a bilayer, current spikes are registered, but when an ion channel is incorporated into a multilayer, no current spikes are registered. This is consistent with the EIS measurements which indicate, in some cases, the presence of predominant multilayers, as measured by the capacitance of the membrane in our circuit model (Figure 3b). Finally, although we consider this unlikely, it is possible that the channels are denatured somehow by the graphene itself. We note that none of these interpretations would change the conclusion that each individual ion channel is charging predominantly the quantum and interfacial capacitance of the graphene, as it is still the dominant capacitance in the circuit.

We now compare these results to those obtained in the literature on comparable systems using metal electrodes in place of the graphene used in our experiments. The group of Duran has measured single ion channel currents through gA using lipid bilayers covalently tethered to Au.³⁰ There, they observed approximately the correct current, but the lifetime was 100× smaller than our measured lifetime of gA and that of suspended bilayer measurements of gA, with no explanation given. Following on measurements by the same group gave a measurement of M2δ,³¹BK,³¹MscL³² with 3–10× lower conductance, but comparable lifetimes to those same ion channel proteins in suspended lipid bilayers. Guidelli has measured single ion channel alamethicin on metal electrodes and compared two different methods to form the bilayers: drop spilling and vesicle fusion.^33,34 He found a lower conductance but comparable lifetime to suspended bilayers using vesicle fusion method, but a conductance as in suspended but a smaller lifetime with drop spilling, indicating that the lipid preparation has a significant impact on the measured electrical properties, and possibly unfused vesicles forming local liposomes with incorporated ion channels complicating the measurement and blocking the measured current so that the conductance measured is not that of a suspended membrane ion channel. In our measurements, as we do not have a covalent tether, we speculate that this allows our ion channels to more freely diffuse in the plane, and allows us to more closely measure both the lifetime and conductance level that is comparable to the values of these ion channels in suspended membranes, in contrast to the metal electrode measurements published to date. However, this issue deserves further research, as the lipid bilayer deposition chemistry can most likely be tuned and optimized much further than our initial proof of concept demonstration of single ion channel sensing with graphene.

In the experiments presented here, the graphene acts as an electrode, whose conductance is large compared to the individual ion channel. Therefore, the change in the in plane conductance of the graphene layer due to the ionic currents flowing through the membrane protein is not registered in our setup; the graphene acts as an atomically thin electrode. In addition, as we are limited in bias range to protect the fragile lipid bilayer (typically to p/m 100 mV), the Dirac point of the graphene does not always fall within the bias range of the ion channel experiments. However, local capacitive charging of the graphene at the nanoscale may change its plane transport characteristics, an exciting area to extend our work to future sensing modalities. In the future, it would be interesting to extend these measurements to include the measurements of the source-drain current in response to the ion channel currents.

Conclusions

Taken collectively, this is strong evidence that we are indeed measuring the opening and closing of individual ion channels with graphene based electrodes. This represents a major milestone, as it demonstrates integration of nanoelectronics with electrophysiology, and opens many opportunities for integration of the two different disciplines. We anticipate that this general technique can be applied to any class of nanoelectronic device (top down or bottom up nanowires, nanotubes, other 2d materials, etc.). A long-term dream of electrophysiologists has been to measure individual ions one by one as they pass through an ion channel. While this is not possible with traditional electrophysiology measurements, we speculate that approaches such as those demonstrated here, which combine advances in nanotechnology with qualitatively new measurements modalities of electrophysiology, may be the key to this holey grail of electrophysiology, opening new ways of unraveling ion channel currents with unprecedented levels of detail.

Methods

Chemicals

Iron(III) nitrate nonahydrate (ACS reagent, ≥98%), potassium chloride (bioXtra, ≥99%), cesium chloride (optical grade, ≥99.5%), phosphate buffer solution, and alamethicin were purchased from Sigma-Aldrich. Gramicidin A was from Enzo Life Sciences. Polydimethysiloxane (PDMS) was made by sylgard 184 silicone elastomer kit. 1,2-Diphytanoyl-sn-glycero-3-phosphocholine (DPhPC) in chloroform was obtained from Avanti Polar Lipids. 1,2-Dihexadecanoyl-sn-glycero-3-phosphoethanolamine, triethylammonium salt (rhodamine DHPE) was from Life Technologies. CVD-grown single layer of graphene on copper foil was obtained from ACS Material.

Fabrication and Measurement of Graphene FETs

The graphene device was transferred and fabricated by polydimethysiloxane (PDMS) block as described in our previous publication.¹³ The second layer of PDMS with a 1 mm × 1 mm well was attached on top of the graphene to insulate the solution from the two electrodes for the liquid-gating effect and ion channel measurements. The electrolyte is a 0.1 mM phosphate buffer at pH 7 in 100 mM KCl. The gate voltage is applied by a Ag/AgCl reference electrode. The drain-source current vs gate voltage was measured by Agilent 34401A multimeter.

Formation of Supported Lipid Bilayers with Ion Channels Alamethicin and Gramicidin A on Graphene Devices

The supported lipid bilayers (SLBs) were prepared by evaporating 160 μL of DPhPC (25 mg/mL) in chloroform under nitrogen flow. After the dried lipid films were obtained, 5 mL of 10 mM phosphate buffer was added to rehydrate at 55 °C for 1 h. Then the lipid suspension was sonicated for 1 h to form small unilamellar vesicles (SUVs). In order to get homogeneous SUVs, the suspension was filtered by a 0.2 μm nylon filter. For the deposition of the SLBs on graphene, the lipid suspension was dropped on the graphene device with PDMS well as described above. This was followed by incubation of lipid vesicles on the graphene devices for 3 h at 60 °C to form supported lipid bilayers on the graphene surface. Then the device was cooled for 30 min. The unbounded lipid bilayers were removed by rising with distilled water for 10 times. As in ref (15), we found the best results when the graphene device was soaked by distilled water overnight prior to depositing the SLBs on graphene surface. In order to prevent disintegration of SLBs, the solution must be maintained on the devices all the time. For the fluorescence study, 1 mM of fluorescent dye solution (rhodamine DHPE) was added to label lipids for 2 h before evaporation of chloroform. For the study of ion channel alamethicin, a solution of 10 μg/mL of alamethicin in 100 mM KCl was added into the graphene-supported lipid bilayers devices. For the formation of ion channel gA with SLBs, 0.1 mM of gA was mixed with DPhPC suspension in chloroform for 2 h before solvent evaporation. If desired, the lipid bilayer can be dissolved by adding detergents.

Characterization

For Raman spectroscopy, a 532 nm excitation laser and a 50× objective lens were used for graphene film investigation. The graphene film was prepared by transfer-printing from PDMS onto SiO₂/Si substrate in order to reduce the noise peaks that are generated by the PDMS substrate. For observing SLBs, the fluorescent dyes (rhodamine DHPE) were mixed with DPhPC at 0.1% molar ratio. Images were obtained using an inverted microscope (Olympus IX-71) with a digital monochrome CCD camera.

Ion Channel Activity Measurement

Ion channel activity was measured by a patch clamp amplifier (Axopatch 200B, Axon Instruments), which was placed on a vibration isolation table with a Faraday cage shield. The electrolyte voltage was applied by a Ag/AgCl electrode, and ground was connected to the source terminal of the graphene device, with the drain terminal floating. The signal was acquired and digitized by Digidata 1440A (Axon Instrument) and passed through a 1 kHz filter and digitized at a 10 kHz sampling rate. Data collection was performed by electrophysiology software (pClamp10).

Supporting Information Available

Supporting Information 1–11 and Figures S1–S13. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States