Abstract
The temperature increase inside mesoporous silica nanoparticles induced by encapsulated smaller superparamagnetic nanocrystals in an oscillating magnetic field is measured using a crystalline optical nanothermometer. The detection mechanism is based on the temperature-dependent intensity ratio of two luminescence bands in the upconversion emission spectrum of NaYF4:Yb3+, Er3+. A facile stepwise phase transfer method is developed to construct a dual-core mesoporous silica nanoparticle that contains both a nanoheater and a nanothermometer in its interior. The magnetically induced heating inside the nanoparticles varies with different experimental conditions, including the magnetic field induction power, the exposure time to the magnetic field, and the magnetic nanocrystal size. The temperature increase of the immediate nanoenvironment around the magnetic nanocrystals is monitored continuously during the magnetic oscillating field exposure. The interior of the nanoparticles becomes much hotter than the macroscopic solution and cools to the temperature of the ambient fluid on a time scale of seconds after the magnetic field is turned off. This continuous absolute temperature detection method offers quantitative insight into the nanoenvironment around magnetic materials and opens a path for optimizing local temperature controls for physical and biomedical applications.
Keywords: nanoscale temperature sensing, dual-core nanoparticle, mesoporous silica nanoparticle, optical temperature measurement, upconversion nanocrystal, superparamagnetic nanocrystal
Ferromagnetic compositions generate heat under a high-frequency oscillating magnetic field (OMF) as a result of hysteresis energy loss and Neel or Brown relaxation.1−3 Numerous magnetic materials have been designed to conduct hyperthermia therapy for cancer treatment, benefiting from the higher sensitivity of lesions to raised temperatures compared to normal tissues.4−7 With the advance of nanomedicines, hypotheses have suggested single cell heating, termed “intracellular hyperthermia”, based on the idea that magnetic nanoparticles are able to raise the temperature of their immediate surroundings more efficiently than that of the overall volume.8 It was proposed to provide a more selective heating to targeted cells, which is thus superior to the intercellular hyperthermia method. However, several theoretical thermal studies analyzed the heat generation and heat flow by nanoparticles and argued that the temperature rise localized in the magnetic particle surroundings is negligible and that the entire occupied volume should have a homogeneous temperature distribution.9,10
In an effort to solve the puzzle by experimental methods, researchers have examined chemical and biological evidence of local heating in the vicinity of magnetic nanoparticles.11−13 Either thermal-sensitive chemical bond breaking or temperature-regulated protein activity has been monitored after applying the OMF, and the results indicated that a higher local temperature was achieved compared to the macroscopic temperature. However, indirect temperature characterizations do not carry quantitative information with high sensitivity and could not distinguish between events that happened during the exposure or afterward. Given the fast heat processing on the nanoscale, a continuous direct measurement method is required for accurate understanding. To date, the nanoenvironment temperature change induced by magnetic materials during the oscillating magnetic field exposure has not been quantified and remains crucial in the efficiency evaluation and development of nano-hyperthermia therapy.
A facile, direct, and sensitive detection method is needed for the nanoscale experimental measurement. Instead of the temperature-dependent properties that are used in bulk analyses, such as density and resistance change, a temperature-sensitive optical signal is more accessible and offers enhanced spatial and temporal resolution. Previously, Polo-Corrales etal. observed a larger fluorescence intensity increase of a copolymer when placed in the oscillating magnetic field compared to that when the field was off, even though the monitored solution temperature was the same, suggesting a different local temperature environment in the vicinity of magnetic nanoparticles.14 Later on, Freddi etal. used the excited-state lifetime of rhodamine B electrostatically absorbed in a polymer matrix to monitor the surface temperature of gold nanoparticles with different shapes.15 Compared to other spectral changes such as fluorescence intensity quenching,16 a thermal responsive intensity ratio variation in the spectra has the advantages of absolute measurement, high sensitivity, and simpler equipment requirements and is less subject to environmental perturbations. The ratiometric method of temperature detection has been achieved either by incorporating two fluorophores with one of them showing a strong thermal response, such as a semiconducting polymer particle with organic dye molecules,17 or, for some fluorophores, by intrinsic thermally coupled excited states, as demonstrated by Vetrone etal. in their work of cell temperature mapping.18 The upconversion fluorescence spectra of Yb3+- and Er3+-doped NaYF4 nanocrystals have two green emission bands, from which the intensity ratio is a function of temperature, independent of the total luminescence intensity changes caused by experimental variations.18−23
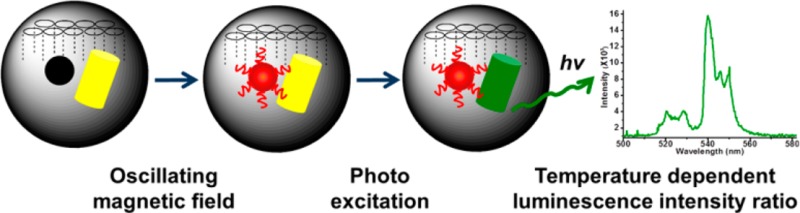
To measure the local nanoenvironment temperature change around magnetic nanocrystals, a hybrid dual-core mesoporous silica nanoparticle (MSN) is synthesized. MSNs were chosen as the container because they are studied extensively as a biocompatible platform for drug delivery,24−26 catalysis,27,28 and hyperthermia.29,30 A detailed interior temperature examination of MSNs would provide quantitative guidelines for optimizing designs for magnetically induced on-demand drug delivery and hyperthermia. The controlled synthesis of an organized mesoporous silica scaffold embedded with two types of nanocrystals is much more difficult than that of a solid silica shell structure,31,32 due to the sensitivity of the self-assembling of the templating surfactants to perturbations. In this study, by using a stepwise phase transfer method, the NaYF4:Yb3+, Er3+ optical thermometer nanocrystal (UCNC) and the superparamagnetic Fe3O4 nanocrystal (MNC) are encapsulated in the same mesoporous silica nanoparticle that provides the rigid structure support. The construction is designed to immobilize the thermometer next to the nanoheater in a nanoenvironment that is distinct from the bulk surroundings. Upon the exposure to a high-frequency oscillating magnetic field, the superparamagnetic iron oxide nanocrystals generate heat inside the MSNs. The upconversion nanocrystal encapsulated in the same MSN senses the temperature change and gives a direct luminescence read-out of this nanoenvironment temperature.
In this paper, we describe the synthesis of the dual-core mesoporous silica nanoparticles, quantify the nanoparticle interior temperature changes initiated by nanoheaters during an oscillating magnetic field exposure, and measure the temperature gradient between the nano- and macroenvironment as it evolves.
Results and Discussion
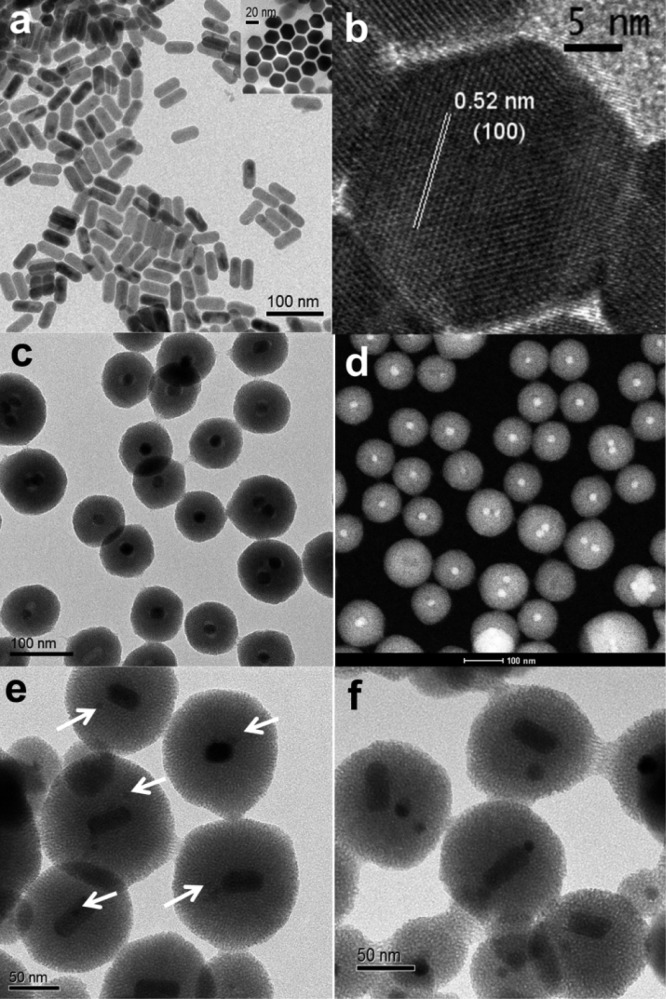
The UCNCs were synthesized by a modified thermolysis approach using lanthanide chlorides as the precursors and oleic acid as the stabilizing surfactant.33,34 These single crystalline nanorods have a narrow size distribution (49 ± 2 nm long and 23 ± 1 nm wide, Figure 1a). The hexagonal lattice structure of β-NaYF4 is confirmed by high-resolution transmission electron microscopy images (HRTEM, Figure 1b) and X-ray power diffraction (XRD, Supplementary Figure S1). The MNCs of two different sizes were obtained from a commercial source, and the average size is 6.4 ± 1.0 nm for MNC5 and 17 ± 2 nm for MNC20 (Supplementary Figure S2).
Figure 1.
Transmission electron microscopy (TEM), high-resolution transmission electron microscopy (HRTEM), and scanning transmission electron microscopy (STEM) images of nanoparticles. (a) TEM image of UCNCs with an average crystal size of 49 ± 2 nm long and 23 ± 1 nm wide. The inset shows the hexagonal side of the nanocrystals. (b) HRTEM of UCNCs, confirming the hexagonal lattice structure. (c, d) TEM and STEM image of control group UCNC@MS. (e) TEM images of dual-core nanoparticles UCNC:MNC5@MS (arrows point to the MNCs). (f) TEM images of dual-core silica nanoparticles UCNC:MNC20@MS, with both the UCNCs and the 20 nm MNCs. Scale bars, 100 nm (a, c, d), 50 nm (e, f), 20 nm (a inset), 5 nm (b).
We developed a synthetic method to assemble a mesoporous silica nanoparticle system that encapsulates simultaneously both the superparamagnetic nanocrystals and the temperature-sensitive upconversion nanocrystals. This approach starts with the stepwise phase transfers of the hydrophobic nanocrystals into the aqueous solutions, featuring a thorough mix of two types of nanocrystals and a facile preparation for the construction of MSNs later on. The as-synthesized UCNCs were first transferred from chloroform to water by coating them with the surfactant hexadecyltrimethylammonium bromide (CTAB) and then evaporating the organic solvent. The aqueous solution dispersed with UCNCs was then mixed with the MNCs in chloroform. The CTAB-stabilized UCNCs help the MNCs to transfer from the hydrophobic phase to the hydrophilic phase and promote the mixing of the MNCs into their coating matrix. Compared to the direct blending of two types of nanocrystals in the same phase, this stepwise phase transfer method uses the surface-coated surfactants on one nanocrystal to extract a different nanocrystal over the phase boundary, reduces the surface tension, offers more control of a homogeneous distribution, and prevents the aggregation of nanocrystals. The aqueous solution containing both nanocrystals was introduced into the sol–gel reaction solution, followed by adding the silica precursor to construct the dual-core mesoporous silica nanoparticles. The nanocrystal ratio and the surfactant amount were carefully tuned to facilitate the formation of a one-to-one composition in MSNs. To further enhance the homogeneity, a magnet was used to separate particles that contain the MNCs, so that the temperature of only the silica nanoparticles that encapsulate both the MNCs and the UCNCs is studied. The measurement is the sum of all mesoporous silica nanoparticles under detection. A control sample of MSNs with only the UCNCs (UCNC@MS) was also synthesized (Figure 1c,d). Both 5 and 20 nm spherical Fe3O4 MNCs are used in this study for size comparison (Supplementary Figure S2). UCNC:MNC5@MS contains both the UCNCs and the 5 nm MNCs (Figure 1e), and UCNC:MNC20@MS has both the UCNCs and the 20 nm MNCs (Figure 1f, Figure 2a).
Figure 2.
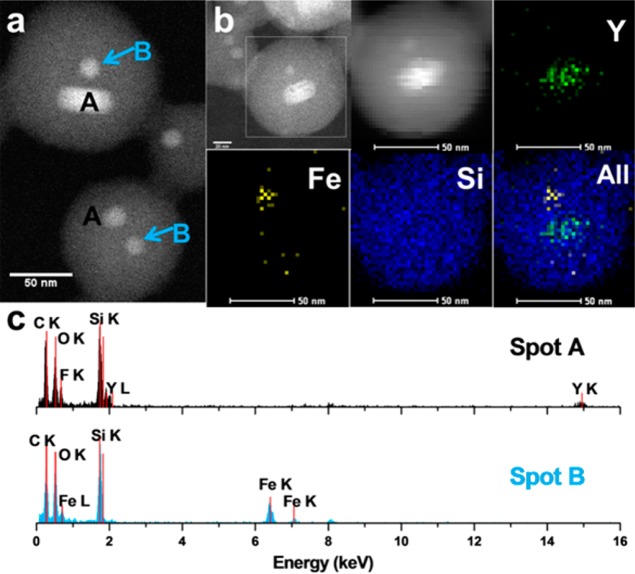
STEM image and elemental analysis of UCNC:MNC20@MS. (a) STEM image, scale bar: 50 nm. The spots A and B have different EDX spectra as shown in (c). (b) EDX element mappings of Y, Fe, and Si in the same nanoparticle and their merged picture. The first STEM image circles the detected particle (scale bar: 20 nm), and the second STEM image was obtained with an element mapping process (scale bar: 50 nm). (c) EDX spectra of spots A and B in (a), verifying that the two different types of nanocrystals are both embedded in the same MSNs.
The energy-dispersive X-ray (EDX) spectra and element mappings confirm that both MNC and UCNC are embedded in the same UCNC:MNC20@MS nanoparticles (Figure 2). The average distance between the UCNC and the MNC is about 8 and 9 nm (Supplementary Table S1). After the magnet separation, the population of nanoparticles with a 1:1 ratio between UCNC and MNC is about 70 percent by statistical analyses (Supplementary Table S1). Another 10 percent of nanoparticles contain two heating nanocrystals. A portion of particles have only MNCs embedded, but they do not give an optical signal. The mesoporosity of the two samples was analyzed by N2 adsorption–desorption, and the calculated pore volume is 0.792 cm3/g for UCNC&MNC5@MS and 0.631 cm3/g for UCNC&MNC20@MS (Supplementary Figure S3).
The upconversion luminescence spectra of UCNCs were collected at different bulk temperatures, and the emission peak intensity ratios were plotted as a function of the temperature to generate a working curve (Figure 3 and Supplementary Figure S4). After two sequential energy transfers from Yb3+ ions to Er3+ ions, the excited Er3+ ions undergo nonradiative relaxations to the thermally coupled 2H11/2 and 4S3/2 states and radiatively transfer back to the ground state, giving rise to two green emission bands (Figure 3a).23 The fine peak structures in the bands are due to the energy level splittings in the crystal field.35 The relative populations respond to the temperature: as the temperature increases, the higher level gains more population, while that of the lower level decreases. The natural log of this intensity ratio is linearly related to the inverse of the temperature according to the Boltzmann distribution (see eq 1), where I520 and I540 are the peak intensities, ΔE is the energy gap between the two excited states, k is the Boltzmann constant, and T is the absolute temperature. The thermal sensitivity of intensity ratio is about 28.8 × 10–4/K for the nanocrystals (see the Supporting Information). After collecting the emission spectra, they were fitted by a multipeak fitting program with fixed peak positions (Figure 3b). The reason for the peak fitting calculation instead of direct integration of peak areas is that the 520 nm and the 540 nm peak overlap around 535 nm. To distinguish the contribution from the two peaks in this area, the peak fitting procedure is necessary. The spectra collected at different temperatures and the corresponding working curve are shown in Figure 3c and d.
| 1 |
Figure 3.
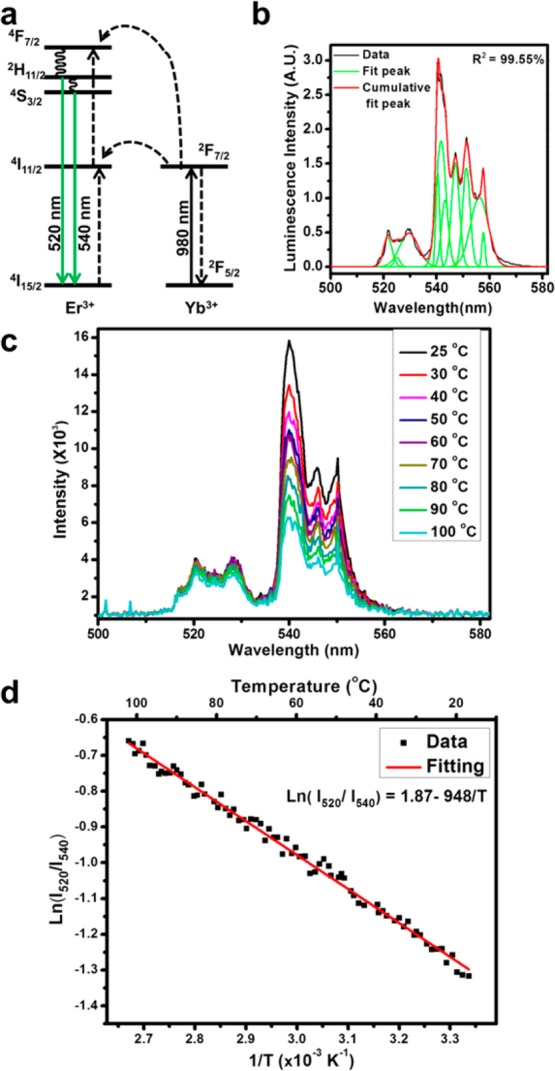
Upconversion luminescence mechanism and the temperature conversion working curve. (a) Illustration of the upconversion mechanism. The Yb3+ ions absorb the 980 nm photons and transfer the energy to the Er3+ ions. After two sequential energy transfers, the excited Er3+ ions relax to the thermally coupled states 2H11/2 and 4S3/2 (via nonradiative decays) and transit back to the ground state, corresponding to the green emissions centered at 520 and 540 nm. (b) Illustration of peak fitting process in calculating the emission band intensities. The black curve is the collected spectrum, the green curves are the fitting peaks, and the red curve is the sum of all fitting peaks. The coefficient of determination for this fitting is 99.55%. (c) Emission spectra of UCNCs collected at different temperatures. (d) Linear working curve correlating the emission intensity ratios and the inverse temperatures for UCNC. I520 and I540 stand for the peak intensities in the luminescence spectra. The populations of states 2H11/2 and 4S3/2 follow the Boltzmann distribution. As the temperature increases, the 2H11/2 level gains more population, while the 4S3/2 level loses population, resulting in the increase in emission intensity ratio.
The magnetically induced heating is examined by comparing the spectra of UCNCs before and after the OMF exposure (Supplementary Figure S5). The oscillating magnetic field was generated using a five-turn induction coil and an oscillation frequency of 375 kHz (see the Supporting Information). The following paragraphs discuss the impact of the magnetic nanoparticle size, the magnetic field induction power, and the OMF exposure length.
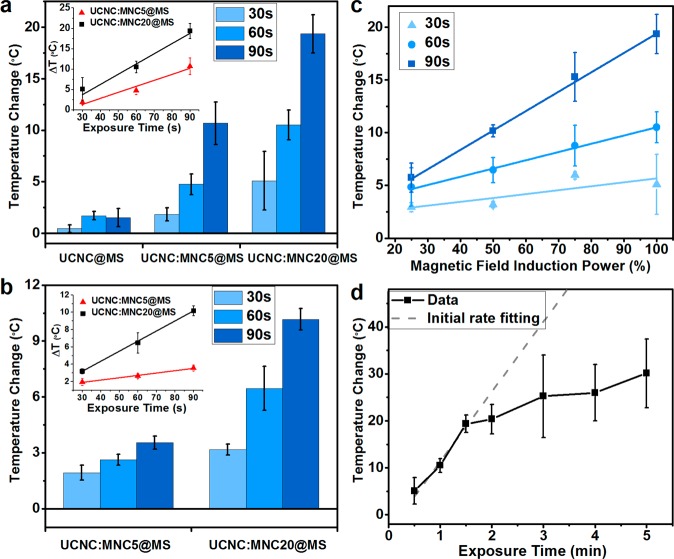
The heating rate is faster for the 20 nm MNCs than for the 5 nm MNCs at a constant magnetic field induction power. The temperature increase in the UCNC:MNC20@MS is almost double that of the UCNC:MNC5@MS (Figure 4a), and the same trend is observed for different exposure times. UCNC:MNC20@MS (Figure 4a inset black squares) shows a higher rate increase in the exposure time dependency plot as a result of higher specific loss power expected for larger single domain superparamagnetic particles.2 Similar trends are observed when the magnetic field induction power is reduced by half (Figure 4b).
Figure 4.
Nanoparticle temperature change under various experimental conditions. (a) Nanothermometer-detected temperature changes of UCNC@MS, UCNC:MNC5@MS, and UCNC:MNC20@MS with a 30, 60, and 90 s OMF exposure. The UCNC:MNC20@MS experiences more heating than the UCNC:MNC5@MS. The control sample UCNC@MS shows neither a significant temperature increase nor an exposure time dependency. The inset shows the temperature change in response to the exposure time for UCNC:MNC5@MS (red triangles) and UCNC:MNC20@MS (black squares) and their linear fittings. A proportional increase is observed as the exposure time increases. (b) Parallel study to (a), when the magnetic field induction power is reduced to half. (c) UCNC:MNC20@MS temperature change under variable OMF induction power. The 30 s (light blue triangles), 60 s (blue dots), and 90 s (dark blue squares) indicate the exposure time. A linear dependency is present because the magnetic field induction power is proportional to the heat dissipation power of the nanocrystals. (d) UCNC:MNC20@MS heating effect as a function of OMF exposure time. The temperature increase is linearly related to the exposure time initially (gray dashed line) and eventually saturates as the length approaches 5 min, as a result of the greater temperature gradient with the environment and the faster heat dissipation rate. Error bars are experimental standard deviations. See Supporting Information for error propagation analysis.
The possible heating from the Yb3+ and the Er3+ ions in an OMF, both of which are paramagnetic in their ground and excited states, was also examined. UCNC@MS were studied as the control group. As shown in Figure 4a (left columns), with a 30, 60, and 90 s OMF exposure, their temperature increases are much smaller than those of the MNC-embedded samples.
The heating is directly proportional to the induction power of the oscillating magnetic field. For UCNC:MNC20@MS, a linear dependency of temperature increase on the magnetic field induction power is observed for various exposure times (Figure 4c). The linear relation can be explained by the correlation between the induction power and the MNC heat dissipation power. The magnetic field induction power (Pi) is proportional to the square of electrical current, and thus proportional to the square of the magnetic amplitude (H), Pi ∝ H2. The dissipation power (Pd) from a MNC under an OMF is also proportional to the square of the magnetic amplitude, Pd = μ0πχfH2.1 Thus, the MNC dissipation power is linearly related to the field induction power, Pi ∝ Pd. Assuming that the thermal conductivity and heat capacity of the nanoenvironment are not strongly temperature dependent, the temperature increase inside the nanoparticle depends only on the dissipation power of the MNCs and thus the induction power of the magnetic field. A similar linear dependency of the temperature increase on the input energy has been observed previously in polymer capsules with gold nanoparticles in optical heating systems.36
The temperature increase is proportional to the OMF exposure time. Proportional correlations are preserved for both the UCNC:MNC20@MS and UCNC:MNC5@MS under full magnetic field induction power (Figure 4a inset) and reduced power (Figure 4b inset). However, we observed an eventual saturation as the exposure time approaches 5 min (Figure 4d and Supplementary Figure S6). The UCNC:MNC20@MS temperature increase grows with the longer exposure time, but the rate decreases at times longer than 90 s. The longer exposure time leads to a higher temperature gradient and thus more efficient heat dissipation. The balance between the heating and the dissipation results in the leveling off of the temperature change rate as the exposure time increases.
The magnitude of the temperature difference (if any) between the interiors of the silica particles and the surrounding liquid is monitored using a “field on” experiment where the temperatures were recorded during the OMF exposure. (A control study was carried out to confirm that the OMF did not affect the intensity ratio in the emission spectrum of the UCNCs, Supplementary Figure S7.) The in situ nanoparticle interior temperature change was recorded at different time intervals during the exposure period. In a parallel experiment, the UCNCs were suspended directly in the solution, but the MNCs were embedded in the MSNs, forming the single-core nanoparticles (MNC20@MS, Supplementary Figure S8), such that the nanoheaters are separated from the nanothermometers and the nanothermometers measure the bulk solution temperature. The mesoporous nanoparticles in the two cases have similar particle sizes, and the same silica surfaces are exposed to the solution. Thus, they do not have any differences between the heating center distances.37Figure 5a shows the “field on” temperature evolution for both the nanoparticles and the bulk solution for a 90 s exposure, and Figure 5b is that for a 5 min exposure. In both cases, the nanoparticle interior temperature (red dots) rises much faster than that of the bulk solution (black squares). For a 5 min exposure, the temperature change inside the nanoparticles is 42 °C compared to 19 °C for that of the bulk solution. Immediately after the exposure, the heating stops and the nanoparticle interior temperature quickly decreases. The solution continues to absorb heat from nanoparticles until its temperature equilibrates with the nanoparticles. The system gradually dissipates heat to the ambient environment and recovers to room temperature in 15 to 20 min after the exposure. In order to reduce the heat dissipated from the nanoparticles and examine the temperature change, we lowered the magnetic field induction power to the point that the solution temperature was almost constant over the exposure time. In this case, we still observed the temperature increase inside the dual-core nanoparticles, confirming that the temperature gradient exists between the nano and bulk environment (Supplementary Figure S9).
Figure 5.
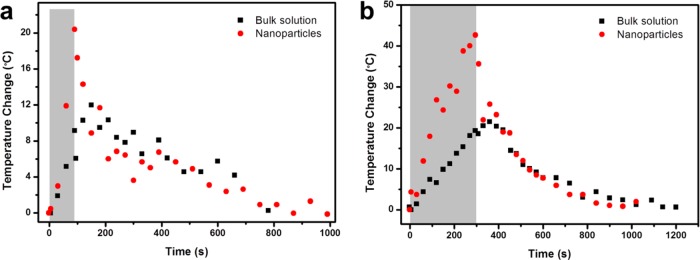
In situ nanoparticle temperature detection during and after exposure to the oscillating magnetic field. (a) Nanoparticle (red dots) and bulk solution (black squares) temperature changes during and after a 90 s OMF exposure. (b) Nanoparticle and bulk solution temperature changes during and after a 5 min OMF exposure. During the OMF exposure (gray area), the nanoparticle inside has a much higher heating rate than the bulk solution and the temperature gradient grows with time. At the end of the exposure, the nanoparticle temperature is about twice that of the solution. After the exposure, the nanoparticle temperature quickly decreases while the bulk solution slightly increased to equilibrate with the nanoparticles. Then the system gradually dissipates heat and recovers its initial state.
The specific absorption rate (SAR) of the iron oxide nanoparticles, calculated from the measured nanoparticle and solution temperature changes, is about 500 W/g under our experimental conditions (see Supporting Information). This value is in close agreement with experimental results and theoretical calculations previously reported for iron oxide nanocrystals under similar magnetic field conditions.2,3
Conclusion
We have developed a method of measuring the interior temperature of dual-core silica nanoparticles based on the luminescence intensity ratios in the spectra of NaYF4:Yb3+, Er3+ nanocrystals and have quantified the nanoenvironment temperature change induced by the superparamagnetic nanocrystals. A novel synthetic approach was developed to incorporate two types of nanocrystals with a one-to-one ratio in the same mesoporous silica nanoparticle. The UCNC nanothermometer detected the MSN temperature changes initiated by the superparamagnetic nanocrystals. The nanoparticle interior temperatures were studied under variable OMF exposure times and induction powers and also with different magnetic nanocrystal sizes. The temperature increase is proportional to the magnetic field induction power and initially increases linearly with the exposure time. During the OMF exposure, a temperature gradient between the nanoparticles and the bulk solution was observed, and it increased over the exposure period. To our knowledge, this is the first study of ratiometric optical measurement of the nanoenvironment temperature with temporal resolution. This unique nanothermometer technique opens a path for experimental quantification of both the temperature in nanoenvironments and heat transfer on the nanoscale, and it provides a novel method for small-scale temperature characterization in biomedical hyperthermia applications.
Methods
Materials
Cetyltrimethylammonium bromide (CTAB) (95%, Aldrich), tetraethyl orthosilicate (TEOS) (98%, Aldrich), hexane (98.5%, Fisher), 1-octadecene (95.0% Aldrich), toluene (99.5%, Aldrich), methanol (99.9%, Firsher), oleic acid (90%, Aldrich), yttrium(III) chloride (99.99%, Aldrich), ytterbium(III) chloride hexahydrate (99.9%, Aldrich), erbium(III) chloride hexahydrate (99.9%, Aldrich), chloroform (99.8%, Fisher), ethanol (99.5%, Fisher), ammonium fluoride (98.0%, Aldrich), and iron oxide(II, III) magnetic nanoparticles (Aldrich) were used. All chemicals were reagent grade and used without further purification or modification.
Characterization
Transmission electron microscopy (TEM) was carried out on a JEM1200-EX (JEOL) instrument. High-resolution transmission electron microscopy (HRTEM), scanning transmission electron microscopy (STEM), and energy disperse X-ray (EDX) analysis were performed using a Titan S/TEM (FEI, 300 kV). Powder X-ray diffraction (XRD) spectra were collected using a Philips X’Pert Pro diffractometer equipped with Cu Kr radiation. A TechnicaLaser MLL-III-980-2w laser emitting 2 W at 980 nm was utilized as the exciting source. An Instrument SA HR 320 spectrograph/monochromator together with a PI-MAX intensified CCD camera from Princeton Instruments was used to record the luminescence spectra. The oscillating magnetic field was provided by a Magnetic Hyperthermia System manufactured by MSI Automation, Inc. The five-turn coil diameter was 50 mm, and the depth was about 50 mm. The oscillation frequency was 375 kHz, and the full induction power was 5 kW. A 700 nm cut-on filter from Newport (10SWF-700-B) was employed to filter out the exciting light at the detector window.
Synthesis of UCNC
The upconversion nanocrystals were synthesized by a modified thermolysis method using lanthanide chlorides as the precursors.33,34 A 156 mg amount of YCl3, 70 mg of YbCl3, and 8 mg of ErCl3 were mixed with 15 mL of 1-octadecene and 12 mL of oleic acid and heated to 120 °C for half an hour. In a separate container, 100 mg of NaOH and 149 mg of NH4F were dissolved in 10 mL of methanol. After the lanthanide solution was cooled to 50 °C, the NH4F methanol solution was added into the lanthanide solution and slowly heated to 80 °C to remove the methanol. The mixed solution was then purged with argon gas and reacted at 300 °C for an hour. After the solution was cooled to room temperature, an excess amount of ethanol was added to precipitate the UCNCs. The nanocrystals were washed several times with hexane and ethanol and then suspended in chloroform at a concentration of 20 mg/mL.
Synthesis of UCNC@MS
The synthesis of upconversion nanocrystal embedded core–shell mesoporous silica nanoparticles (UCNC@MS) started with changing the hydrophobicity of the nanocrystals with the help of CTAB.24,29 A 2 mL amount of UCNC chloroform solution was added into 20 mL of H2O containing 400 mg of CTAB. The solution was sonicated thoroughly and slowly heated to 65 °C to evaporate the chloroform. A 1.5 mL portion of this UCNC aqueous solution was added into 13.5 mL of H2O and heated to 80 °C. After the temperature was stabilized, 110 μL of 2 M NaOH and 150 μL of TEOS were added. The reaction was maintained at 80 °C for 2 h before further centrifugation and washing with H2O and methanol.
Synthesis of UCNC:MNC5@MS
The incorporation of two types of nanocrystals into the MSNPs was based on stepwise phase transfers of the nanocrystals. UCNCs and the 5 nm MNCs were both suspended in chloroform at a concentration of 20 mg/mL prior to this experiment. A 2 mL sample of UCNC chloroform solution was added into 20 mL of H2O containing 400 mg of CTAB. The mixture was sonicated thoroughly and slowly heated to 65 °C to evaporate the chloroform. A 1.5 mL amount of this solution was mixed with 18.8 μL of MNC chloroform solution. Again, it was sonicated thoroughly and slowly heated to 65 °C to evaporate the chloroform. This aqueous solution was stirred overnight and added into 13.5 mL of H2O. From there, the reaction followed the same procedure as that for the UCNC@MS. A magnet was used to make sure all collected particles contain Fe3O4 nanocrystals.
Synthesis of UCNC:MNC20@MS
A similar experiment was carried out to that for UCNC:MNC5@MS to make the 20 nm MNC embedded MSNPs. Instead of adding the 5 nm MNC chloroform solutions, 37.5 μL of a 20 nm MNC chloroform solution was used. All other procedures were the same.
Synthesis of MNC20@MS
Similar to the synthesis of UCNC@MS, 37.5 μL of a 20 nm MNC solution was added into 15 mL of H2O with 30 mg of CTAB and sonicated thoroughly. The chloroform was evaporated. The solution was heated to 80 °C, and 110 μL of 2 M NaOH was added followed by 150 μL of TEOS. The reaction was continued for 2 h before further washing.
Working Curve
Upconversion luminescence spectra were collected to generate the working curve between temperature and peak intensity ratios. All samples were dispersed in toluene at a concentration of ∼10 mg/mL and placed on a stir heater plate. The hot plate was turned on to heat the solution slowly while stirring, and the temperature was monitored by a K-type thermocouple immersed in the solution. The whole setup was placed in front of the monochromator and the CCD camera. A 980 nm infrared laser was used as the exciting source. After the temperature reached a recording point, the laser was turned on briefly and a spectrum of the sample was collected. A luminescence background baseline was also collected under the same conditions when the excitation laser was off.
The luminescence spectra were analyzed to calculate the intensity ratios between the 520 and 540 nm emission peaks. After subtracting the baseline, the spectra were fitted by a multipeak fitting program with the peak positions fixed. An example of a peak fitting result is shown in Figure 3b. The reason for the peak fitting calculation instead of direct integration of peak areas is that the 520 and 540 nm peaks overlap around 535 nm. To distinguish the contribution from the two peaks in this area, the peak fitting procedure is necessary. The fitted peak areas were then summed up, and the area ratios between the two peaks were calculated. For each sample, the ratios were plotted against the inverse of absolute temperature and then fitted with a linear function. The working curve graphs and luminescence spectra for UCNC, UCNC@MS, UCNC:MNC5@MS, and UCNC:MNC20@MS are illustrated in Figure S2.
In Situ Luminescence Detection Setup
The exciting beam (cross section is about 8 mm × 4 mm) was focused with an 80 cm focal length plano-convex lens. The coil of the magnetic hyperthermia system was placed horizontally in front of the CCD detector. A polystyrene foam frame was placed inside the coil to secure the sample and to prevent direct heat conduction. The nanoparticle sample was contained in a 2 mL glass vial placed in the polystyrene foam in the center of the coil. The emitted light was collected with a 10 cm focal length convex lens placed between the CCD detector and the coil. A 6 cm plano-convex lens was in front of the monochromator slit to focus the light. The coil was tilted about 30 °C from the axis that connected the CCD detector and the collecting lens, due to the position limitations. A 700 nm cut-on filter was placed in front of the CCD detector window to filter out the excitation light (Supplementary Figure S11). For the pure UCNC luminescence detection, the detector slit size was 0.5 um and spectrum integration time is 0.5 s. For all other nanoparticles, a slit size of 1 μm and an integration time of 1 s were used. The CCD camera gain was set as zero for all experiments.
The sample was placed inside the current coil of a magnetic hyperthermia system to characterize the induced heating effect. A background spectrum without the excitation laser was used for data processing. The IR laser was on for 1 s to record the luminescence spectra of the nanoparticles at the initial state. The OMF was turned on for a defined exposure time, and the luminescence spectra of the sample under the OMF influence were collected at regular intervals, depending on the experiment. The same multipeak fitting program used in generating the working curves was then applied to calculate the peak area ratios for the spectra, and the ratios were then converted to temperatures according to the working curve. The experiment was repeated three to five times to generate the experimental deviations. The induction power of the magnetic field was tunable on the magnetic hyperthermia system for the induction power dependent study.
Acknowledgments
This work was supported by U.S. National Institutes of Health NIH R01 CA133697 and Department of Defense HDTRA-1-13-1-0046. We thank Dr. B. C. Regan for helpful discussions. We also thank Dr. M. Xue and A. A. Hwang for their assistance with experiments.
The authors declare no competing financial interest.
Supporting Information Available
Additional material characterizations and figures. This material is available free of charge via the Internet at http://pubs.acs.org.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Rosensweig R. E. Heating Magnetic Fluid with Alternating Magnetic Field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar]
- Hergt R.; Dutz S.; Mueller R.; Zeisberger M. Magnetic Particle Hyperthermia: Nanoparticle Magnetism and Materials Development for Cancer Therapy. J. Phys.: Condens. Matter 2006, 18, S2919–S2934. [Google Scholar]
- Etheridge M. L.; Bischof J. C. Optimizing Magnetic Nanoparticle Based Thermal Therapies within the Physical Limits of Heating. Ann. Biomed. Eng. 2013, 41, 78–88. [DOI] [PubMed] [Google Scholar]
- Kim J.; Kim H. S.; Lee N.; Kim T.; Kim H.; Yu T.; Song I. C.; Moon W. K.; Hyeon T. Multifunctional Uniform Nanoparticles Composed of a Magnetite Nanocrystal Core and a Mesoporous Silica Shell for Magnetic Resonance and Fluorescence Imaging and for Drug Delivery. Angew. Chem., Int. Ed. 2008, 47, 8438–8441. [DOI] [PubMed] [Google Scholar]
- Lu A.-H.; Salabas E. L.; Schueth F. Magnetic Nanoparticles: Synthesis, Protection, Functionalization, and Application. Angew. Chem., Int. Ed. 2007, 46, 1222–1244. [DOI] [PubMed] [Google Scholar]
- Hao R.; Xing R.; Xu Z.; Hou Y.; Gao S.; Sun S. Synthesis, Functionalization, and Biomedical Applications of Multifunctional Magnetic Nanoparticles. Adv. Mater. 2010, 22, 2729–2742. [DOI] [PubMed] [Google Scholar]
- Veiseh O.; Gunn J. W.; Zhang M. Design and Fabrication of Magnetic Nanoparticles for Targeted Drug Delivery and Imaging. Adv. Drug Delivery Rev. 2010, 62, 284–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon R. T.; Hines J. R.; Gordon D. Intracellular Hyperthermia - Biophysical Approach to Cancer-Treatment via Intracellular Temperature and Biophysical Alterations. Med. Hypotheses 1979, 5, 83–102. [DOI] [PubMed] [Google Scholar]
- Rabin Y. Is Intracellular Hyperthermia Superior to Extracellular Hyperthermia in the Thermal Sense?. Int. J. Hyperthermia 2002, 18, 194–202. [DOI] [PubMed] [Google Scholar]
- Keblinski P.; Cahill D. G.; Bodapati A.; Sullivan C. R.; Taton T. A. Limits of Localized Heating by Electromagnetically Excited Nanoparticles. J. Appl. Phys. 2006, 100, 054305. [Google Scholar]
- Stanley S. A.; Gagner J. E.; Damanpour S.; Yoshida M.; Dordick J. S.; Friedman J. M. Radio-Wave Heating of Iron Oxide Nanoparticles Can Regulate Plasma Glucose in Mice. Science 2012, 336, 604–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedinger A.; Guardia P.; Curcio A.; Garcia M. A.; Cingolani R.; Manna L.; Pellegrino T. Subnanometer Local Temperature Probing and Remotely Controlled Drug Release Based on Azo-Functionalized Iron Oxide Nanoparticles. Nano Lett. 2013, 13, 2399–2406. [DOI] [PubMed] [Google Scholar]
- Hamad-Schifferli K.; Schwartz J. J.; Santos A. T.; Zhang S. G.; Jacobson J. M. Remote Electronic Control of DNA Hybridization through Inductive Coupling to an Attached Metal Nanocrystal Antenna. Nature 2002, 415, 152–155. [DOI] [PubMed] [Google Scholar]
- Polo-Corrales L.; Rinaldi C. Monitoring Iron Oxide Nanoparticle Surface Temperature in an Alternating Magnetic Field Using Thermoresponsive Fluorescent Polymers. J. Appl. Phys. 2012, 111, 07B334. [Google Scholar]
- Freddi S.; Sironi L.; D’Antuono R.; Morone D.; Dona A.; Cabrini E.; D’Alfonso L.; Collini M.; Pallavicini P.; Baldi G.; etal. A Molecular Thermometer for Nanoparticles for Optical Hyperthermia. Nano Lett. 2013, 13, 2004–2010. [DOI] [PubMed] [Google Scholar]
- Huang H.; Delikanli S.; Zeng H.; Ferkey D. M.; Pralle A. Remote Control of Ion Channels and Neurons through Magnetic-Field Heating of Nanoparticles. Nat. Nanotechnol. 2010, 5, 602–606. [DOI] [PubMed] [Google Scholar]
- Ye F. M.; Wu C. F.; Jin Y. H.; Chan Y. H.; Zhang X. J.; Chiu D. T. Ratiometric Temperature Sensing with Semiconducting Polymer Dots. J. Am. Chem. Soc. 2011, 133, 8146–8149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetrone F.; Naccache R.; Zamarron A.; Juarranz de la Fuente A.; Sanz-Rodriguez F.; Martinez Maestro L.; Martin Rodriguez E.; Jaque D.; Garcia Sole J.; Capobianco J. A. Temperature Sensing Using Fluorescent Nanothermometers. ACS Nano 2010, 4, 3254–3258. [DOI] [PubMed] [Google Scholar]
- Chatterjee D. K.; Gnanasammandhan M. K.; Zhang Y. Small Upconverting Fluorescent Nanoparticles for Biomedical Applications. Small 2010, 6, 2781–2795. [DOI] [PubMed] [Google Scholar]
- Wang G.; Peng Q.; Li Y. Lanthanide-Doped Nanocrystals: Synthesis, Optical-Magnetic Properties, and Applications. Acc. Chem. Res. 2011, 44, 322–332. [DOI] [PubMed] [Google Scholar]
- Wade S. A.; Collins S. F.; Baxter G. W. Fluorescence Intensity Ratio Technique for Optical Fiber Point Temperature Sensing. J. Appl. Phys. 2003, 94, 4743–4756. [Google Scholar]
- Berthou H.; Jorgensen C. K. Optical-Fiber Temperature Sensor Based on Upconversion-Excited Fluorescence. Opt. Lett. 1990, 15, 1100–1102. [DOI] [PubMed] [Google Scholar]
- Rakov N.; Maciel G. S. Three-Photon Upconversion and Optical Thermometry Characterization of Er3+:Yb3+ Co-Doped Yttrium Silicate Powders. Sens. Actuators B: Chem. 2012, 164, 96–100. [Google Scholar]
- Liong M.; Lu J.; Kovochich M.; Xia T.; Ruehm S. G.; Nel A. E.; Tamanoi F.; Zink J. I. Multifunctional Inorganic Nanoparticles for Imaging, Targeting, and Drug Delivery. ACS Nano 2008, 2, 889–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Q.; Zhang Z.; Gao F.; Li Y.; Shi J. In Vivo Biodistribution and Urinary Excretion of Mesoporous Silica Nanoparticles: Effects of Particle Size and Pegylation. Small 2011, 7, 271–280. [DOI] [PubMed] [Google Scholar]
- Dong J.; Xue M.; Zink J. I. Functioning of Nanovalves on Polymer Coated Mesoporous Silica Nanoparticles. Nanoscale 2013, 5, 10300–10306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng Y.; Cai Y.; Sun Z.; Liu J.; Liu C.; Wei J.; Li W.; Liu C.; Wang Y.; Zhao D. Multifunctional Mesoporous Composite Microspheres with Well-Designed Nanostructure: A Highly Integrated Catalyst System. J. Am. Chem. Soc. 2010, 132, 8466–8473. [DOI] [PubMed] [Google Scholar]
- Rioux R. M.; Song H.; Hoefelmeyer J. D.; Yang P.; Somorjai G. A. High-Surface-Area Catalyst Design: Synthesis, Characterization, and Reaction Studies of Platinum Nanoparticles in Mesoporous SBA-15 Silica. J. Phys. Chem. B 2005, 109, 2192–2202. [DOI] [PubMed] [Google Scholar]
- Thomas C. R.; Ferris D. P.; Lee J.-H.; Choi E.; Cho M. H.; Kim E. S.; Stoddart J. F.; Shin J.-S.; Cheon J.; Zink J. I. Noninvasive Remote-Controlled Release of Drug Molecules in Vitro Using Magnetic Actuation of Mechanized Nanoparticles. J. Am. Chem. Soc. 2010, 132, 10623–10625. [DOI] [PubMed] [Google Scholar]
- Lin Y.-S.; Wu S.-H.; Hung Y.; Chou Y.-H.; Chang C.; Lin M.-L.; Tsai C.-P.; Mou C.-Y. Multifunctional Composite Nanoparticles: Magnetic, Luminescent, and Mesoporous. Chem. Mater. 2006, 18, 5170–5172. [Google Scholar]
- Yi D. K.; Selvan S. T.; Lee S. S.; Papaefthymiou G. C.; Kundaliya D.; Ying J. Y. Silica-Coated Nanocomposites of Magnetic Nanoparticles and Quantum Dots. J. Am. Chem. Soc. 2005, 127, 4990–4991. [DOI] [PubMed] [Google Scholar]
- Insin N.; Tracy J. B.; Lee H.; Zimmer J. P.; Westervelt R. M.; Bawendi M. G. Incorporation of Iron Oxide Nanoplarticles and Quantum Dots into Silica Microspheres. ACS Nano 2008, 2, 197–202. [DOI] [PubMed] [Google Scholar]
- Liu C.; Wang H.; Li X.; Chen D. Monodisperse, Size-Tunable and Highly Efficient Beta-NaYF4:Yb,Er(Tm) Up-Conversion Luminescent Nanospheres: Controllable Synthesis and Their Surface Modifications. J. Mater. Chem. 2009, 19, 3546–3553. [Google Scholar]
- Li Z.; Zhang Y.; Jiang S. Multicolor Core/Shell-Structured Upconversion Fluorescent Nanoparticles. Adv. Mater. 2008, 20, 4765–4769. [Google Scholar]
- Carnall W. T.; Goodman G. L.; Rajnak K.; Rana R. S. A Systematic Analysis of the Spectra of the Lanthanides Doped into Single-Crystal LaF3. J. Chem. Phys. 1989, 90, 3443–3457. [Google Scholar]
- Skirtach A. G.; Dejugnat C.; Braun D.; Susha A. S.; Rogach A. L.; Parak W. J.; Mohwald H.; Sukhorukov G. B. The Role of Metal Nanoparticles in Remote Release of Encapsulated Materials. Nano Lett. 2005, 5, 1371–1377. [DOI] [PubMed] [Google Scholar]
- Bedard M. F.; Braun D.; Sukhorukov G. B.; Skirtach A. G. Toward Self-Assembly of Nanoparticles on Polymeric Microshells: Near-IR Release and Permeability. ACS Nano 2008, 2, 1807–1816. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.