Evolution in a genetically heritable social environment

Nearly 40 years ago W. D. Hamilton (1) published his classic paper on the genetic evolution of social behavior. His mathematical theory of kin selection and the related concept of inclusive fitness played a major role in redirecting the evolutionary study of social behavior and accounting for apparently altruistic phenotypes observed in nature. Since that time, and especially after publication of E. O. Wilson's book on sociobiology (2), the evolution of social behavior in animals has been studied as the balance between the fitness costs of behavior performed relative to the fitness benefits accrued by kin. This balance is summarized in Hamilton's rule, altruism will increase in a population when the genetic correlation among interacting individuals (r) exceeds the ratio of costs to benefits (|c|/b). The development of sociobiology has been seen as a triumph for the application of the principles of Darwinian evolution to the understanding of social behavior. Darwinian evolutionary theory states that evolutionary change occurs through the natural selection of heritable variation. However, there remains a difficulty with traditional kin selection theory as a model of Darwinian evolution. Most models of kin selection fail to adequately account for the nature of heritable variation in systems of interacting individuals (3) and heritable variation is a key partner with selection in the evolutionary process.

In this issue of PNAS, Wolf (4) provides an explicit, general model and an experimental system in which it is possible to fully define and measure heritable variation in systems of interacting individuals. The key concept in this model is that an individual's characteristics are influenced by two kinds of genetic effects; direct genetic effects (DGEs) of the genes carried by that individual on its own traits and indirect genetic effects (IGEs) of genes carried by others. These indirect genetic effects are the effects of genes carried by an individual on the developmental environment of their social partners. A key and truly innovative element of Hamilton's (1) kin selection model was to explicitly consider these indirect effects. However, in doing so, the potential direct effects of these genes on an individual's characteristics were ignored.

The approach taken by Wolf (4) has a long history that until recently has had little impact on studies of the evolution of social behavior. Given its origins, I will refer to it as the quantitative genetic kin selection model. Agricultural geneticists are faced with practical problems in scientific breeding and develop models to address these problems and guide their stock improvement plans. A particularly important and difficult problem involved selection for neonatal and early postnatal growth traits. These traits were sometimes refractory to artificial selection pressures. Geneticists realized that neonatal and preweaning postnatal growth was critically tied to the environment provided by the mother for her offspring and that variation in this environment could be affected by variation in maternal genes. Nearly 20 years before Hamilton's paper, Dickerson (5) produced the standard quantitative genetic maternal effects model describing the measurement of heritable variation and expected selection response when there is heritable variation in the environment a mother provides for her offspring. The environment a mother provides her offspring was conceptualized as maternal performance encompassing all maternal traits, behavioral and otherwise, that had environmental effects on her offspring. Dickerson's model (5) and its consequences for animal improvement was further developed and expanded by Willham (6, 7) and Hanrahan (8, 9). Most importantly, these models showed that the heritable variation component (V_a) of Darwinian response to selection models is not simply the heritable variance caused by the direct effects of genes (V_ao), as is common in quantitative evolutionary theory. Rather, the heritable variance is composed of that produced by the direct effects of genes, the heritable variance in maternal performance for the offspring trait (V_am; indirect genetic effects) and the heritable covariance between the direct and maternal genetic effects [cov(A_o, A_m)],

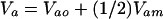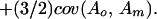Unlike the traditional kin selection model, this model encompasses the effects of both direct and indirect genetic effects on a trait.

The genes that influence an individual's characteristics are that individual's genes along with those carried by others.

Quantitative genetic kin selection models did not come to the attention of evolutionary geneticists until the 1980s (3, 10–13). Cheverud (3) generalized the earlier agricultural maternal effects models to situations in which any kind of kin provides an environment that affects an individual's characteristics. Kirkpatrick and Lande (10) took this model further, breaking the composite maternal performance character into its component maternal features and analyzing their coevolution with offspring traits. One striking and counterintuitive peculiarity of this model is that when the heritable covariance between direct and maternal effects [cov(A_o, A_m)] is strongly negative and maternal performance is relatively important, selection for increased offspring growth can actually lead to a predicted response in the opposite direction (3, 5–10). Surprisingly, in this case natural selection leads to maladaptation. Under even less restrictive conditions, selection for increased offspring growth can result in expected decreases in the quality of maternal performance and constrain the rate of phenotypic response to selection. Features of heritable variation for characters affected by social environment are clearly important and can lead to outcomes not ordinarily considered in optimization-based evolutionary models.

Examination of traditional kin selection models in light of this analysis of heritable variation shows that the only genetic effect considered was the indirect effect of the altruistic relative. It is implicitly assumed that there are no direct effects of genes on the recipient's own traits and that the heritable covariance between direct and indirect effects is zero. If these assumptions are off the mark, the models they produce will not be descriptive of evolution in nature or especially useful in interpreting the evolution of social behavior. A restatement of Hamilton's rule allowing for direct effects and direct-indirect covariances indicates that altruism will increase in a population when

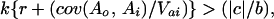where k is the proportion of variance in the recipient's trait caused by the kin effect (assumed equal to 1.0 in Hamilton's rule beacuse there are no direct effects), r is the genetic correlation among interacting individuals, cov(A_o, A_i) is the heritable covariance between direct and indirect effects, and V_ai is the heritable variance of indirect effects (3). Because 0 and 1 usually bound the genetic correlation between interacting individuals, clearly, the opportunities for altruistic evolution can be dominated by the heritable covariance between direct and indirect effects. If it is strong and positive, altruism may evolve even in the face of massive costs and minimal benefits. On the other hand, if the covariance is strong and negative, altruism will not evolve despite minimal costs and massive benefits. However, if the covariance is nil, we return to the standard Hamilton's rule with the left side of the inequality decremented by the presence of direct effects.

Unfortunately, there is very little empirical evidence for the relative influence of direct and kin effects on trait variation and even less on the possibility of direct-indirect heritable covariances. The only well known system is the agricultural one in which maternal effects have been evaluated. In general, the findings for early mammalian growth (see ref. 3) confirm that maternal effects are indeed a very important source of variation in preweaning growth (≈50% of the variance) and that variations in maternal effects are moderately heritable (≈40% of the variance in maternal performance). These heritable effects are similar in importance to the direct effects of genes carried by offspring on their own traits (≈30% of the variance). Furthermore, a very common finding was that there was a strong negative heritable correlation between the direct and maternal effects on preweaning growth (3). This means that the same genes promoting faster than average growth when expressed in offspring provide an unfavorable growth environment for offspring when expressed in the mother. This strong negative correlation was, perhaps, responsible for the observed lack of progress in artificial selection for preweaning growth. However, the strong negative correlation also has important consequences for parent–offspring conflict theory and other aspects of social evolution. Even with strong contrasting selection operating on the mother's behavior and her offspring's growth, a negative direct-maternal genetic covariance may result in complementary rather than contrasting evolutionary responses to selection.

A major difference between traditional and quantitative genetic kin selection models is in their accounting for fitness. The difference arises as a consequence of differences in definitions of heritable variation. In quantitative genetic kin selection models that incorporate both direct and indirect genetic effects, fitness is directly assigned to individuals carrying the phenotype selected, not to others who may provide an environment affecting that individual's phenotype. The evolution of the social environment is treated, in part, as a correlated response to selection on the affected individual's characteristics. This starkly contrasts with traditional kin selection models where the only genetic effect on a trait arises from the social environment and thus any selection on that trait is assigned to the individual expressing that social environment. This leads to the concept of inclusive fitness. The altruist accumulates all of the fitness effects, both directly on their own survivorship and reproduction and also the survival and reproduction of those it provides an environment for. It was this view of inclusive fitness that reconciled observations of altruism in nature with standard views of individual selection and discounted the concept of group selection. However, an inclusive fitness accounting requires that there are no direct effects of genes on fitness. This is a patently false assumption. Quantitative genetic kin selection models specify the role of both direct and indirect effects in social evolution and are clearly richer and more complete in their accounting of heritable variation and are therefore to be preferred.

Wolf and colleagues (14) have made further explorations of quantitative genetic kin selection models generalizing them to encompass interacting sets of both related and unrelated individuals. This theoretical work has led to a growing number of research programs considering the role of complex heritable variation in behavioral evolution (e.g., refs. 15–20). These studies consistently demonstrate the importance of the heritable social environment in determining heritable variation and evolution of social behaviors.

Wolf (4) provides a particularly interesting example and one of the first empirical studies of the evolutionary effects of social environment outside of the parent–offspring paradigm. In a very ambitious experiment, he shows that an appreciable portion (18%) of the variation in Drosophila melanogaster pupae size can be attributed to genetic effects of sibling–sibling interaction. This is about half the relative magnitude of direct effects (34%). The heritable covariance between direct and indirect effects is strong and negative (genetic correlation = −0.85). This indicates either that loci affecting both individual growth and the environment provided for growth of siblings do so in opposite directions or that loci with separate but opposite effects on these traits are in strong linkage disequilibrium. Furthermore, altruistic evolution in this population is prohibited by the strong negative direct–indirect genetic correlation regardless of potentially minimal costs and maximal benefits.

The interplay between individuals is what makes social behavior evolution an exciting part of evolutionary biology.

Most studies to date have focused on estimating the components of heritable environmental effects and their significance for response to selection. Recently, a few studies have begun to map quantitative trait loci (QTLs) for indirect effects (18, 21, 22) shedding light on the genetic architecture underlying indirect effects. Wolf and colleagues (21) found several direct and maternal effect QTLs for offspring preweaning growth in a cross of LG/J and SM/J inbred mouse strains. Although the number of direct and maternal effect loci detected were nearly the same, maternal effect loci contributed much more strongly to the genetic variance in offspring growth. Maternal effect loci displayed over- or underdominance, only one in four loci displaying an additive effect. Epistatic interactions were also stronger among maternal effect than among direct effect QTLs. Unlike many other populations, the direct–indirect genetic covariance was low and positive in the LG/J by SM/J intercross. Correspondingly, the direct and maternal effect loci mapped to distinct portions of the genome.

In the future, I hope that the perspective provided by quantitative genetic kin selection models can be expanded, especially to specifically accommodate two-way interactions between individuals. Agrawal and colleagues (16) have made a beginning in this direction in their consideration of feedback in parental–offspring interactions. The interplay between individuals is what makes social behavior evolution a unique and exciting part of evolutionary biology. The development of kin selection theory has played a major role in the growth in interest in behavior ecology. Now, with the development of models capable of more fully expressing behavioral interactions, accurately accounting for their heritable variation, and predicting their evolutionary consequences, we can hope for a new renaissance in this field.