Localization of denaturation bubbles in random DNA sequences

Abstract

We study the thermodynamic and dynamic behaviors of twist-induced denaturation bubbles in a long, stretched random sequence of DNA. The small bubbles associated with weak twist are delocalized. Above a threshold torque, the bubbles of several tens of bases or larger become preferentially localized to AT-rich segments. In the localized regime, the bubbles exhibit “aging” and move around subdiffusively with continuously varying dynamic exponents. These properties are derived by using results of large-deviation theory together with scaling arguments and are verified by Monte Carlo simulations.

Localized opening of double-stranded DNA is essential in a number of cellular processes such as the initiations of gene transcription and DNA replication (1). Although thermal denaturation is highly unlikely under physiological conditions, in vitro experiments show that local denaturation can be readily induced by underwinding the DNA double-helix by an amount that is physiologically reasonable (2–4). The basic physical effect is simple: An underwound double-helix suffers a reduction in binding free energy (5–7). Local openings of the double-helix (referred to as “denaturation bubbles”) relieve the twist experienced by the remainder of the double-helix and are thus energetically favorable. The denaturation bubbles may be recruited to a specific location of the genome by a designed (e.g., AT-rich) sequence, since AT pairs bind more weakly than GC pairs (8). On the other hand, entropic effect that favors bubble delocalization is non-negligible for long sequences. Also significant is the kinetic trapping of the bubbles due to statistical agglomeration of AT-rich segments in long heterogenous sequences.

To gain some quantitative understanding on the competing effects of entropy and sequence heterogeneity, we characterize in this study the thermodynamic and dynamic properties of denaturation bubbles in a long, stretched random DNA sequence with no special sequence design. Previously, there have been a number of experimental and theoretical studies (9–12) on the effect of sequence heterogeneity on DNA melting and unzipping transitions. Our study is along this general direction. The specific behaviors exhibited by the denaturation bubbles are rather complex and are typical of those observed in systems dominated by quenched disorders (13): The bubbles are localized upon increase of the applied torque beyond a certain threshold. In the localized regime, their dynamics exhibits “aging” (14, 15) and is subdiffusive with continuously varying exponents.

Interestingly, twist-induced denaturation presents a rare physical example of the celebrated random-energy model (REM) of a disordered system (16). Consequently, detailed analysis of both the thermodynamics and dynamic properties can be made by applying the well-developed theory of disordered systems (13), together with exact results from large-deviation theory familiar in the related sequence alignment problem (17, 18). We will draw on detailed experimental knowledge of thermal denaturation (19–21) throughout the analysis and make our results quantitative whenever possible.

Thermodynamics

Let us consider the application of a torque that underwinds a long, stretched** piece of double-stranded DNA. We are interested in the regime where the applied torque 𝒯 is below the threshold 𝒯_d for bulk denaturation, but sufficiently strong so that denaturation bubbles appear in the system. Due to the highly cooperative nature of the denaturation process, the typical distance N_× between the large bubbles is large, in which case treating the bubbles as a dilute gas of particles is appropriate. Our strategy will be to first characterize analytically the thermodynamic behavior of a single bubble, and then use this knowledge to determine the length scale N_× and the many-bubble states for N ≫ N_×. We will find that N_× > 𝒪(10³) bp as long as we are not very close to the threshold 𝒯_d, so that the dilute gas approximation is reasonable for a large range of parameters.

The Single-Bubble Model.

Consider a denaturation bubble confined in a DNA double-helix between two complementary DNA strands of N bases each. The double-strand is denoted by the base sequence b₁b₂ … b_N [with b_k ∈ {A, C, G, T}] of one of the strands, ordered from the 5′ to 3′ end.

To simplify the notation, we assume that the two ends of the helix are sealed, so that the bubble is always contained in the segment b₁ … b_N. Let the index of the first and last open pairs of the open bubble be m and n, with 1 ≤ m ≤ n ≤ N. We denote the total free energy of the bubble (defined with respect to the helical state) by ΔG_L(m), where L ≡ n − m + 1 is the number of open bases and referred to as the bubble length. Then the partition function of the single-bubble system is given by

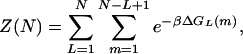where β⁻¹ ≡ k_BT ≃ 0.62 kcal/mol at 37°C.

In the absence of the external torque, the bubble energy ΔG_L(m) has two components. First, there is the loss of stacking energy δG_b,b′ between two successive bases b and b′. These stacking energies are in the range of 0.5 to 2.5 k_BTs at 37°C, with the AT stacks weaker than the GC stacks. Their values have been measured carefully (19–21). Second, assuming that there is no secondary pairing between bases in the bubble so that the open configuration can be regarded as a polymer loop, there is a well-known polymeric loop entropy cost

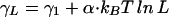for a bubble of length L, with α ≈ 1.8 (22) for a linearly extended†† DNA chain. The bubble initiation cost γ₁ depends on the base composition at opening and closing ends, ionic strength, etc., and generally lies‡‡ in the range of 3 to 5 k_BT. For relevant bubble sizes of few tens of bases in length (see below), the total entropic cost is γ_L = 8 ∼ 12 k_BT. This large cost justifies the single bubble approximation (at least to the length scale N_× ∼ e^βγ_L≳ 5 × 10³ bp) and contributes significantly to the sharpness of the observed thermal denaturation transition (21).

An applied negative torque 𝒯 reduces the thermodynamic stability of the helical state relative to the denatured one by an amount equal to the work done to unwind the helix. This effect is simply modeled here by a linear decrease in the stacking energy in the relevant parameter range (6), i.e., δG_b,b′ → δG_b,b′ − θ₀𝒯, where θ₀ = 2π/10.35 is the twist angle per base of the double-helix. Putting the above together, we have

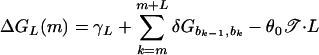as the single-bubble energy, which can be computed once the DNA sequence b₁ … b_N is given. Note that although Eq. 3 is formulated specifically for twist-induced denaturation, the general form can be used to describe a number of destabilizing effects, e.g., due to changes in temperature, ionic concentration, etc.

Sequence Heterogeneity.

As the torque 𝒯 increases from zero toward the denaturation point 𝒯_d, denaturation bubbles appear in the double-strand and grow in size. We want to know whether the bubbles are free to diffuse along the double-strand, or are they localized in the high AT regions of the DNA where binding is the weakest. For simplicity, we will characterize the typical behavior of an ensemble of random (i.e., independent and identically distributed) sequences described by the single-nucleotide frequencies p_b, although our approach and qualitative findings are also applicable to sequences with short-range correlations.

For a given sequence of bases, the partition function Z can, of course, be efficiently evaluated numerically (including all the multiple-bubble states) by using available programs such as meltsim (21). All thermodynamic quantities can subsequently be evaluated from the free energy F = −k_BT ln Z. To obtain the typical behavior of the ensemble, we ideally want to compute the ensemble average of the free energy, F̄ ≡ −k_BT 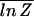. [We use the overline to denote average over the ensemble of random sequences, i.e., X̄ ≡ ∑_{b1, … ,bN} X_{b1, … ,bN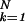} ∏ p_bk; this is also known as the “disorder average.”] Computing F̄ numerically, however, will require explicit generation of a large number of random sequences and can be very time consuming for large Ns. Fortunately, we can apply a large body of knowledge accumulated from the statistical mechanics of random systems (13) and provide a detailed characterization of the typical behavior of our system without the need of exhaustive simulation. To introduce notation and concepts in this approach, we examine first the simplified problem of a single bubble with a fixed length.

Bubble with Fixed Length.

Let us consider a bubble with a fixed length L (with 1 ≪ L ≪ N) embedded in a long, random sequence b₁ … b_N. The partition function reads

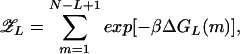where the scripted variables refer to properties of the fixed-length bubble. For a random sequence, the energies of the different states labeled by m are uncorrelated with each other beyond the distance L. Such systems belong§§ to the class of REM and was solved exactly in the 1980s by Derrida (16) for a Gaussian distribution of ΔGs. Discrete distribution of ΔGs was studied in the closely related system involving protein–DNA interaction (26). Below, we will briefly review the salient properties of REM by using the present example.

The REM has a “high-temperature” phase where many (of order N) bubble configurations contribute significantly to the partition sum, and a “low-temperature” phase dominated by only one or a few lowest energy states. It follows that, in the former case, the bubble is delocalized and can freely diffuse along the sequence, whereas in the latter case, the bubble is localized to the lowest energy position. Transition between the two phases is driven by competition between the energetic (variation in ΔG) and entropic (ln N) effects. In the present problem, the magnitude of terms in the partition sum 4 can be tuned not only by varying the temperature, but also by varying the bubble size L. Hence, at a fixed β, whether a bubble is free or localized depends both on the bubble size L and the sequence length N.

An interesting property of the REM is that, in the high-temperature phase, 𝒵_L/N tends to a finite limit given by the annealed average Z̄_L/N as N → ∞, independent of the particular realization of the random sequence. This allows us to replace the average free energy F̄ ≡ −k_BT 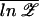by its annealed approximation F̃ ≡ −k_BT ln Z̄, which is much easier to calculate. [We will use the tilde to denote all quantities computed in the annealed approximation.] Introducing a 4 × 4 matrix M(β) with components M_b,b′ = 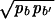exp[−βδG_b,b′], and let the largest eigenvalue of M(β) be Λ(β), then the disorder average of terms in 4 can be written as

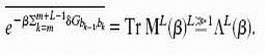It is convenient to introduce the quantity

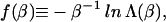with which we have (for N ≫ L)

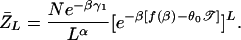Hence, in the delocalized phase,

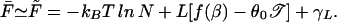The annealed entropy can be calculated from F̃, with¶¶

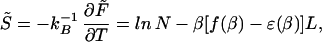where ɛ(β) ≡ −(∂/∂β) ln Λ. It will also be useful to introduce the relative entropy per base for the fixed-length bubble,

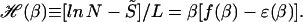Note that being the difference between f and ɛ, the quantity ℋ is a measure of the intrinsic variation in the binding energies δGs for a random sequence with nucleotide frequency p_b and is independent of the average binding energy 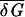, which external environments such as the temperature or solvent conditions most directly affect.

Derrida's solution of REM (16) shows that the annealed entropy S̃ vanishes at the transition to the low-temperature phase, beyond which the annealed approximation is no longer applicable. Using Eqs. 8 and 9, we can write the condition for phase transition as

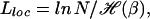which gives the minimal bubble size for localization at a given N. With the values of δGs obtained from ref. 19 at [Na⁺] = 1 M and 37°C, and assuming an equal nucleotide distribution (i.e., p_b = 1/4 for all bases), we find f ≈ 1.83 k_BT, ɛ ≈ 1.50 k_BT, so that ℋ ≈ 0.33 and L_loc ≈ 20 bp for N ∼ 10³ bp. From Eq. 10, it is clear that as N → ∞ any fixed-length bubble remains delocalized.

Bubble Without Length Constraint.

The full partition function Z is obtained simply by summing 𝒵_L for different Ls. We will again approach the problem by first applying the annealed approximation and then determining where it breaks down.

Annealed approximation.

The annealed partition function Z̄(N) ≡ ∑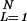Z̄_L has a transition at 𝒯_a = f(β)/θ₀, where the exponential factor in 7 reaches one: The sum over L is finite and Z̄ ∝ N only if 𝒯 < 𝒯_a. In this regime, the annealed free energy is simply F̃ ≈ −k_BT ln N + γ₁. The annealed energy Ẽ ≡ −(∂/∂β) ln Z̄(β) is also readily computed; it can be expressed as Ẽ = γ₁ + [ɛ(β) − θ₀𝒯]⋅L̃ where L̃(𝒯) ≡ ∑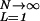LZ̄_L/Z̄ is the average bubble length in the annealed approximation. As 𝒯 approaches 𝒯_a, L̃(𝒯) diverges, and the annealed entropy

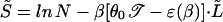becomes negative.

In the limit N → ∞, the annealed free energy F̃ is actually identical to F̄ for all 𝒯 ≤ 𝒯_a. This can be seen from the inequalities 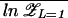≤ ≤ 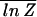ln Z̄, and 𝒵_L=1 > N min{exp[−βΔG₁],1}. Since both the lower and upper bounds grow as ln N,

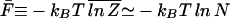for all 𝒯 ≤ 𝒯_a.

Ground-state properties.

To find the ground state of the unconstrained bubble in a long random sequence, we need to study the statistics of stretches of exceptionally high AT content. If we neglect the polymeric contribution γ_L to the bubble energy (to be justified shortly), then the ground-state energy E* expected in a sequence of length N can be computed exactly from large-deviation theory (17, 27), with

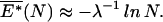The constant λ in Eq. 13 can be expressed as the unique positive root of the equation

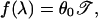where f is defined by the δGs through Eqs. 5 and 6. Note that, at 𝒯 = 𝒯_a, Eq. 14 is satisfied with λ = β. In this case, 13 coincides with 12.

The length of the minimal energy bubble is also known from large-deviation theory (18, 27), with

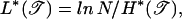where the relative entropy H* is given exactly by

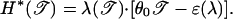From the logarithmic dependence of the bubble length L* on N, it is clear that the corresponding polymeric contribution γ_L* ∼ ln(ln N) can indeed be treated as a constant shift of bubble energy.

Phase transitions.

Based on the above discussion, a phase transition can be formally established in the limit N → ∞. This is seen by comparing the expressions 12 and 13. For 𝒯 > 𝒯_a, solution to 14 satisfies λ < β. Consequently, 12 must break down there, yielding a phase transition at 𝒯 = 𝒯_a. Since F̄ ≤ 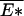in general (e.g., for all 𝒯 > 𝒯_a), and at the phase transition point 𝒯 = 𝒯_a the equality F̄ = 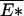already holds, i.e., the ground state already dominates, then we must have the ground state dominating throughout the localized phase. This is exactly the behavior of the REM (16).

A physical understanding of the transition can be obtained by examining the importance of the ground-state contribution exp(−βE*) ∼ N^β/λ to the partition sum Z as the applied twist 𝒯 is varied. For 𝒯 < 𝒯_a, the ratio β/λ(𝒯) is <1. In this case, the energy gain 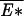(N) of placing the bubble at the site of the lowest energy is insufficient to overcome the entropy ln N of placing the bubble in different positions, hence the bubble is typically small and delocalized. When 𝒯 exceeds 𝒯_a, the ground-state contribution grows faster than N, signaling dominance of one or a few low-energy states where the bubble typically resides. The transition is thus identified as the localization transition of the bubble at 𝒯_loc = 𝒯_a.

The onset of the zero entropy point can be obtained from Eq. 11 and written as

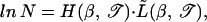where

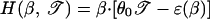is the relative entropy of the unconstrained bubble. These equations are analogous to the expressions 15 and 16 for the ground-state bubble. In fact, both L*(𝒯) and H*(𝒯) are reproduced through the substitution β → λ(𝒯), e.g., L*(𝒯) = L̃(λ(𝒯), 𝒯). This turns out to be true also for other thermodynamic variables. Thus the localized phase at different 𝒯s can be viewed as the phase-transition points of systems with different effective temperatures λ⁻¹(𝒯); this will be clearly manifested in the bubble dynamics discussed below.

Next, we observe that since H* ∝ λ (see Eq. 16), the bubble length diverges (or approaches N) as λ → 0. This defines the point of bulk denaturation∥∥ 𝒯_d, i.e.,

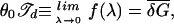where the second equality is obtained from manipulating Eqs. 5 and 6. Using 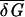≈ 1.40 k_BT (derived from the δGs in ref. 19), we find 𝒯_d ≈ 10 pN⋅nm. The dependence of λ on 𝒯 close to 𝒯_d can be obtained from the expansion

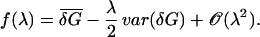Inverting the above for λ by using 14 and 19, we find

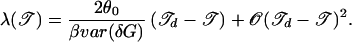It turns out that the term linear in 𝒯_d − 𝒯 in 21 already gives a very good approximation (to within 1%) of λ throughout the localized phase where λ/β < 1. The localization transition point 𝒯_loc can be thus obtained by solving Eq. 21 with λ(𝒯_loc) = β. Using β²var(δG) ≈ 0.565 (derived from ref. 19), we find 𝒯_d − 𝒯_loc ≈ 2 pN⋅nm. Unlike the value of 𝒯_d that is derived from the average stacking energy 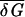and hence is sensitive to temperature, ionic strength, etc., the difference 𝒯_d − 𝒯_loc is set by the variance of δG_b,b′ and should be much less sensitive to experimental conditions. The same is expected for the relative entropy, which has the form

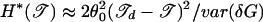throughout the localized phase.

Multiple Bubbles.

The localization transition discussed above occurs only as N → ∞. However, for large N, the single-bubble approximation will break down regardless of the large (but finite) bubble cost γ_L. When multiple bubbles are localized, each bubble is effectively in a finite-length system, thereby blurring the localization transition.

We first analyze the delocalized phase for which the annealed approximation is valid. Once multiple bubbles are allowed in the system, we expect a broad range of bubble lengths, as described by the distribution 7. Qualitatively, we expect only the largest bubbles, of size L̃(𝒯) to be localized as 𝒯 → 𝒯_loc, while the smaller ones remain delocalized. We shall thus focus on these large bubbles. It is the average separation distance N_× between these large bubbles that sets the effective system size of the single-bubble localization problem.

The Boltzmann weight of one such large bubble in a sequence of length N ≫ L̃ is W̃(N) = e^−βγ₁N/L̃^α in the vicinity of the localization transition. Setting W̃(N) = 1 yields the typical spacing between the large bubbles on the delocalized side,

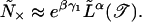Note that for bubbles of size 10 bp, the crossover length is already of the order of 10³ bp. A similar estimate can be made on the localized phase by using the exact expression (28) for the lowest energy for multiple bubbles. We find

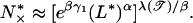as the average distance between large bubbles of size L*.

For N ≫ N_×, the system consists of N/N_× effective number of single-bubble subsystems, each of length N_×. At the localization “transition” of an infinite system then we have ln Ñ_× = H(β, 𝒯_loc)L̃(𝒯_loc) (see Eq. 17). Together with Eq. 23 (or 24 with λ = β), we find L̃(𝒯_loc) ≈ 25 bp at the onset of localization (using γ₁ ≈ 3 k_BT and H ≈ 0.33), with the crossover length Ñ_× ≈ 6,500 bp. Thus we expect there to be typically one bubble of ∼ 25 bp in a random DNA double-strand of length ∼ 6,500 bp at the localization transition.

Bubble Dynamics

The localization of bubbles is reflected ultimately in their slow dynamics. We expect bubbles to diffuse freely along the DNA double-helix in the delocalized phase, but become trapped in low-energy positions in the localized phase. Details of the bubble movement in the latter case, however, can be rather complicated with nontrivial memory (or aging) effects typical of glassy states (14, 15) as will be described below.

Model.

For simplicity, we will restrict ourselves to the description of the movement of a single bubble over its lifetime, which can be rather long in the localized phase. For reasons discussed above, interaction with other bubbles can be neglected when the bubble displacement is within a distance of order N_× ∼ 10³ bp. We will also neglect the polymeric loop entropy γ_L, which provides essentially a constant shift to the bubble energy as shown in the single-bubble section.

In addition to the drift and breathing motion, a bubble may shrink to zero size and disappear from the system. To our knowledge, the time scale involved for the spontaneous collapse of a bubble, particularly under an applied twist, has not been documented so far. Zipping the bubble requires not only pairing of the bases in the open segment, but also rewinding of the helix against the applied undertwist, both of which contribute to the energy barrier to the no-bubble state. This suggests a long lifetime for a bubble, which can be enforced by setting a lower bound (e.g., 10 bp) in the allowed bubble length. However, as we will see, the longtime behavior of bubble dynamics is determined crucially by the occurrence of the large bubble states, and insensitive to the value of the lower bound on L, as long as the L = 0 state is excluded. Once accurate estimates of bubble lifetime become available, one may supplement the discussion below with such a cutoff.

Scaling Theory.

Eq. 13 gives the lowest energy of an unconstrained bubble in a sequence of length N, while a bubble with its position (but not size) fixed typically has an energy of the order λ⁻¹. For small λ, the energy variation ΔE(N) ≃ λ⁻¹ ln N is large, hence the bubble dynamics is dominated by the thermal escape from the deepest trap. The escape time is thus t_e(N) ≃ e^βΔE(N) ∼ N^β/λ, i.e., the dynamics is subdiffusive deep in the localized phase (where β ≫ λ).

To investigate the dynamical behavior in more detail, especially close to the localization transition where λ ≈ β, we need to include also the random motion of the bubble along the double-strand. Toward this end, it is useful to describe the bubble dynamics as a single point moving in the 2D space spanned by the bubble's only two degrees of freedom, its instantaneous length L and the position of one of its ends, say m. The statistics of the 2D energy landscape ΔG_L(m) is well characterized by the large-deviation theory (18). It consists of a number of valleys, whose depths (denoted by ΔĜs) are given by the Poisson distribution

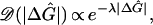where λ is the constant defined through 14. The typical valley length is L̂ ∼ 1/H*, where H* is given by 16. The valleys are spread out along the corridor at L ≲ L̂, separated by a typical distance M, which is also calculable from the large-deviation theory. For much larger Ls, the bubble energy becomes prohibitively high.

Clearly, the dynamics consists of two parts: At short times, it is dominated by the escape of the bubble out of an individual valley and is analogous to the (biased) Sinai problem (29). At longer time scales, the bubble “hops” from one valley to another along the corridor of valleys. This dynamics, which is essentially that of a particle traversing a series of exponentially distributed energy valleys (see Eq. 25), has been extensively investigated previously in the context of the one-dimensional trap model (30, 31). Here we review some key results and refer the reader to ref. 32 for details.

The basic dynamic quantity is the time τ(ΔĜ) ∝ e^β|ΔĜ| to escape each valley of depth ΔĜ. The average time to traverse K valleys over a length scale N = K⋅M by random walk is then given by

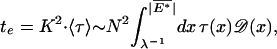where 〈τ〉 is the average of the trap time τ(ΔĜ), and the limits of integration in 26 are from the magnitude of the typical valley depth λ⁻¹ to that of the deepest valley 13 expected for a segment of length N. The total time according to Eq. 26 can be written as t_e(N) ∝ N^z, with the dynamic exponent z given by

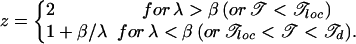The anomalous exponent z > 2 in the glass phase shows explicitly that the dynamics is slow, i.e., subdiffusive.

Glassy Dynamics.

We next report the result of a Monte Carlo simulation of the bubble dynamics on predefined random nucleotide sequences. We impose local dynamics in which the bubble can only change its length L or shift its end position m by a single base, as long as L ≥ 1. To remove edge effects and probe the asymptotic dynamics, we use a very large sequence length (>10⁴ bp) so that the bubble never reaches the boundary of the sequence given the duration of our numerical study. All disorder-averaged quantities reported are performed over 10⁴ random sequences.

Anomalous diffusion.

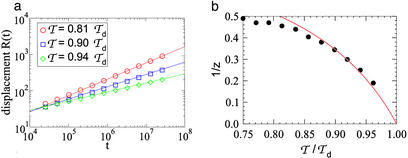
To characterize the slow dynamics quantitatively, we show in Fig. 1a the time evolution of the average displacement R(t) = |m(t) − m(0)| of the bubble position for a few selected values of 𝒯s in the glass phase. Clearly, the displacement can be described by a power law of the form R(t) ∝ t^ν, where we expect ν = 1/z. In Fig. 1b, we plot the extracted exponents for different values of 𝒯s in the range 𝒯_loc ≤ 𝒯 < 𝒯_d. The expected values 1/z according to Eq. 27 (using the linear expression in ref. 21 for λ) is shown as the solid line for comparison. We note that the observed exponents follow the general trend predicted, changing continuously from 1/z = 0.5, close to the expected location of the glass transition (𝒯_loc ≈ 0.8 𝒯_d), toward zero as 𝒯 → 𝒯_d. For 𝒯 close to 𝒯_d, the dynamics becomes exceedingly slow, making it difficult to access the asymptotic region. For 𝒯 ≈ 𝒯_loc, we also observed some finite-size effect. The overall agreement between the scaling theory and numerical results is within 5 ∼ 10% over the range tested.

Fig 1.

(a) Average bubble position vs. time for various values of 𝒯s in the glass phase: the solid lines are power law fits. (b) The extracted exponents vs. 𝒯: the solid line is the prediction of the scaling theory, Eq. 27.

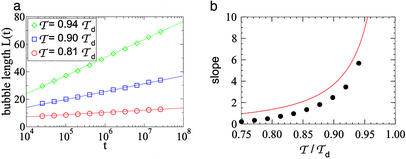
In Fig. 2a, we show the dependence of the average bubble length on time for different 𝒯s. The data depict the slow, logarithmic growth of the bubble length. Logarithmic growth is one of the signatures of glassy dynamics. Its occurrence in this particular system can be understood quantitatively as follows: The optimal bubble size L*(N) in a segment of length N depends logarithmically on N; see Eq. 15. On the other hand, for a bubble placed at an arbitrary position in a long sequence, the effective sequence length is the distance the bubble can explore within a time t, i.e., N ∼ t^1/z for the subdiffusive dynamics expected in the glassy regime. Hence,

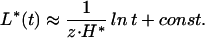is the expected length of the optimal bubble within a time t. Generally, we expect L*(t) to be the upper bound of the observed bubble length L(t), with L(t) ≈ L*(t) for large t deep in the glass phase. However, outside the glass phase, L(t) must be finite even for t → ∞.

Fig 2.

(a) Average bubble length vs. time for several 𝒯s; the solid lines are fits to the form L(t) = a + b ln t. (b) Slope b of the logarithmic time dependence of L(t) for various 𝒯s. The solid line is the corresponding quantity for the upper bound of the bubble length L*(t); see text.

In Fig. 2b, we show the coefficients of the observed logarithmic time dependence of L(t) for 𝒯s throughout the range 𝒯_loc < 𝒯 < 𝒯_d. Also shown is the upper bound 1/(z⋅H*) (solid line) according to 28, using the expression 22 for H*. We note that the difference between the data and the upper bound is nearly constant (≈1) for the range studied.

Aging.

Perhaps the most characteristic feature of glassy dynamics is that the system ages, e.g., the temporal fluctuation of the system depends on how long the system has evolved from some (arbitrary) initial condition (14, 15): the longer it has evolved, the slower it fluctuates. This is easy to understand in the context of a rough energy landscape with deep valleys and high barriers, since the longer the system evolves, the deeper the energy valley it finds, and hence the higher the barrier it will have to overcome to travel farther. This feature is in marked contrast to subdiffusive hydrodynamic systems that are time-translationally invariant.

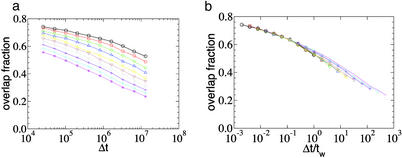
Quantitatively, we can define the aging phenomenon via the time-dependent correlation function C(t_w, Δt), which measures how much the system changes in time Δt, after first evolving for a waiting period t_w from the initial condition. Let us define a binary variable η_i(t) ∈ {0, 1}, for each base i of the nucleotide sequence. η_i(t) takes on the value 1 if base i is open and belongs to the bubble at time t, and the value 0 if base i is paired. The correlation function, defined as C(t_w, Δt) ≡ ∑_i η_i(t_w)η_i(t_w+ Δt) after averaging >10,000 random sequences, is a measure of the average self-overlap of the bubble at time t_w and t_w + Δt. A more convenient quantity to characterize is the fraction of overlap, C(t_w, Δt)/L(t_w), where L(t) = ∑_i η_i(t) is the instantaneous bubble length.

In Fig. 3a, we show the overlap fraction, parameterized by the different waiting time t_ws for the system biased deep in the glass phase with 𝒯 = 0.9 𝒯_d. The overlap fraction clearly depends on the waiting time, illustrating the glassy nature of the dynamics. In contrast, the same quantity computed for 𝒯 < 𝒯_d (data not shown) gives no statistically significant dependence on t_w. To characterize more quantitatively the behavior, we replot in Fig. 3b the curves in Fig. 3a with Δt normalized by t_w. We find these curves to collapse reasonably onto a single master curve that exhibits a weak kink at Δt/t_w ∼ 1. A naive explanation of this behavior is that for Δt ≪ t_w, the bubble stays approximately within the energy valley found at time t_w, whereas for Δt ≫ t_w, the bubble makes an excursion faraway from the valley. For the one-dimensional trap model, it was shown rigorously (33) that C(t_w, Δt) indeed scales as a function of Δt/t_w, even though the largest trap time actually scales sublinearly with t_w. This behavior can be understood in terms of the particle making multiple returns to the original valley after escaping it (32), as manifested by the slow decay shown in Fig. 3b for Δt ≫ t_w.

Fig 3.

Aging plot. (a) Average overlap fraction C(t_w, Δt)/L(t_w) for different t_ws (from 1× to 512× 25,600 Monte Carlo steps) deep in the glass phase, with 𝒯 = 0.9 𝒯_d > 𝒯_loc. (b) Scaling plot of a with Δt normalized by t_w.

Discussion

In this study we investigated the thermodynamic and dynamic behaviors of twist-induced denaturation bubbles in a long, random sequence of DNA. The small bubbles associated with weak twist are delocalized, e.g., they flicker in and out of existence according to the Boltzmann distribution and are independent of the DNA sequence. The bubbles increase in lengths upon increase in the applied torque. When the largest bubbles reach a critical size L_loc which is of the order of a few tens of bases, the bubbles become localized to AT-rich segments which occur statistically in a long random sequence. According to the parameters (19) taken at 37°C with [Na⁺] = 1 M, the localization “transition” occurs at 𝒯_loc ≈ 8 pN⋅nm, which is ∼80% of the torque needed for bulk denaturation 𝒯_d. In the localized regime, the bubbles exhibit aging and move along the double-helix subdiffusively, with continuously varying dynamic exponents.

All of the results are obtained under the single-bubble approximation. Thermodynamically, we expect this approximation to be valid for DNA sequences of several thousand bases or less. This is due to the strongly cooperative nature of bubble formation, as manifested in the large initiation energy γ₁. The single-bubble description of dynamics is further restricted by the finite life time of the bubble: Even at length scales where the single-bubble approximation is appropriate thermodynamically, the bubble may annihilate and reappear elsewhere in the sequence, effectively performing long-distance hops. Experimental knowledge of the bubble lifetime in the presence of an applied twist is needed to estimate the crossover time to the long-distance hopping regime. Qualitatively, we expect these bubbles to have much longer lifetimes than the thermally denatured bubbles, since the applied twist plays the role of an energy barrier preventing bubble annihilation.

Finally, we note that bubble localization characterized in this study is a reflection of the statistical background present in long random nucleotide sequences. This background traps the bubble kinetically if the bubble size becomes sufficiently large. Thus, to localize denaturation bubbles at appropriate locations specified by designed sequences (e.g., promoters or replication origins) for biological functions, it is necessary to operate away from the localized regime, i.e., below the onset of localization.

Abbreviations

• REM, random-energy model