Site-specific contributions to the pH dependence of protein stability

Abstract

Understanding protein stability is a significant challenge requiring characterization of interactions within both folded and unfolded states. Of these, electrostatic interactions influence ionization equilibria of acidic and basic groups and diversify their pK_a values. The pH dependence of the thermodynamic stability (ΔG_FU) of a protein arises as a consequence of differential pK_a values between folded and unfolded states. Previous attempts to calculate pH-dependent contributions to stability have been limited by the lack of experimental unfolded state pK_a values. Using recently developed NMR spectroscopic methods, we have determined residue-specific pK_a values for a thermodynamically unstable Src homology 3 domain in both states, enabling the calculation of the pH dependence of stability based on simple analytical expressions. The calculated pH stability profile obtained agrees very well with experiment, unlike profiles derived from two current models of electrostatic interactions within unfolded states. Most importantly, per-residue contributions to the pH dependence of ΔG_FU derived from the data provide insights into specific electrostatic interactions in both the folded and unfolded states and their roles in protein stability. These interactions include a hydrogen bond between the Asp-8 side-chain and the Lys-21 backbone amide group in the folded state, which represents a highly conserved interaction in Src homology 3 domains.

The thermodynamic stability of a protein is defined as its unfolding free energy and is therefore determined by the differential stability of its folded and its unfolded states. Hence, knowledge of structural and dynamic parameters that contribute to the stability of unfolded states is critical for understanding the complex interplay of enthalpic and entropic contributions to protein stability. Recent experimental data suggest that unfolded states of proteins are ensembles of rapidly interconverting, structurally and dynamically diverse conformers that may be fairly compact and exhibit considerable amounts of nonrandom structure. Residual secondary and tertiary structure can be retained in unfolded states, involving specific local and long-range interactions, some of which are native-like and some of which are not observed in the native (folded) structure (1–5).

The extent to which electrostatic interactions are present in unfolded states and their role in stabilizing residual structure are important issues (6, 7). Electrostatic interactions manifest themselves in deviations of pK_a values of ionizable groups from those of unstructured standard compounds. Unlike pK_a values for folded proteins, which are routinely measured employing standard NMR spectroscopic approaches, pK_a values for unfolded proteins (of Asp and Glu residues, in particular) were not determined experimentally until very recently because of the small chemical shift dispersion of nuclei in unfolded states. In the simplest approach, the unfolded state of a protein has been treated as a state where all ionizable groups titrate independently with their standard pK_a values (“zero interaction model”). Such neglect of interactions between individual ionizable or polarizable groups has proved to be useful in studies involving chemical denaturants, which are known to have a profound effect on pK_a values due to a reduction of the amount of residual structure. More recently, however, general shifts of Asp and Glu side-chain pK_a values in unfolded states to lower than standard pK_a values (by 0.3−0.4 pH units on average) have been predicted, pointing toward the presence of stabilizing electrostatic interactions within unfolded states of proteins under nondenaturing conditions (8–19).

To test these models, we have applied a recently developed triple-resonance NMR pulse scheme (20) to experimentally determine residue-specific pK_a values of Asp and Glu side-chain carboxyl groups in the N-terminal Src homology 3 (SH3) domain (residues 1–59) of the Drosophila protein drk (drkN SH3). This protein domain is thermodynamically unstable and exists in equilibrium between a folded state (F_exch) and a highly populated unfolded state (U_exch) at ambient temperature under nondenaturing conditions (21). The interconversion between the two states is slow on the NMR chemical shift time scale, giving rise to separate sets of resonances for the F_exch and the U_exch states. Determination of the relative intensities of these sets of resonances in NMR spectra enables calculation of the fractional populations and, therefore, the unfolding free energy ΔG_FU. Within the pH range of pH 1 to pH 7, both states are sufficiently populated to be experimentally observable, with the folded:unfolded ratio varying between a maximum ≈5:1 and a minimum of ≈0.3:1, allowing for the experimental determination of residue-specific pK_a values for both protein states under identical, nondenaturing conditions.

Methods

Sample Preparation and NMR Experiments.

Wild-type drkN SH3 domain was expressed and purified as described (22). Site-directed mutations (His-7 → Ala, Asp-8 → Asn, Arg-20 → Ala, and Lys-21 → Ala) were introduced by using a QuikChange mutagenesis kit (Stratagene). Expression and purification of mutant proteins were identical to the wild-type protein. NMR experiments were performed on 0.6–1.1 mM samples of the drkN SH3 domain (wild-type and mutants) containing 50 mM sodium phosphate, 92% H₂O/8% D₂O, at a temperature of 278 K. The pH of each sample was measured in the NMR tube. Values were not corrected for the isotope effect on the pH electrode because of the consistent cancellation of isotope effects on the pK_a values of ionizable groups and on the electrode (23, 24). Asp and Glu side-chain pK_a values were determined experimentally for the folded and unfolded states of the wild-type and the His-7 → Ala mutant by monitoring side-chain carboxyl carbon chemical shifts in a pH titration experiment as described (20), with the exception of the C-terminal residue Asp-59, for which an HB(CB)CO type experiment was used (25). For the wild-type, His side-chain imidazole pK_a values based on ¹⁵Nδ chemical shifts were measured by using heteronuclear multiple bond correlation experiments (26). pH profiles of chemical shifts were fit to the Henderson-Hasselbach equation, leaving the pK_a value and the plateau values in the acidic (δ_A) and basic (δ_B) limits as floating parameters. For Asp-8 (F_exch) in the wild-type and His-7 → Ala mutant, the acidic branch of the titration curve could not be sampled due to the low population of the F_exch state at low pH, and the difference between chemical shifts in the acidic and basic limits, Δδ = δ_B − δ_A, was set to the average value of Δδ that was determined for all other Asp residues (F_exch and U_exch states), 3.28 ± 0.15 ppm, and normally distributed within its standard deviation in a Monte Carlo fitting procedure.

Fractional populations of the F_exch and the U_exch states (p_F and p_U) in wild-type and all mutant drkN SH3 domains as a function of pH were approximated by ratios of peak volumes of backbone amide ¹H^N—¹⁵N correlations in heteronuclear single quantum coherence spectra. This method was verified by employing a longitudinal exchange experiment (27) analyzed as described (28). Average values for residues that are not overlapped in either state and do not exhibit additional line-broadening due to intermediate conformational exchange were used to extract values of ΔG_FU.

Calculation of the pH Dependence of ΔG_FU.

The unfolding free energy, ΔG_FU, can be calculated at any pH as (29)

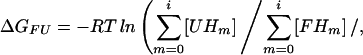where [UH_m] and [FH_m] represent sums of concentrations corresponding to the binding of m protons to i binding sites for protons (ionizable groups) in the unfolded and folded states, respectively, R is the universal gas constant, and T is the temperature. ΔG_FU can be separated into a pH-independent term, ΔG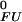 (representing nonelectrostatic contributions to ΔG_FU, as well as electrostatic contributions at a pH where all ionizable sites i are protonated in both states), and terms related to protonation/deprotonation equilibria involving individual ionizable groups, ΔG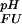(i) (representing the pH dependence of the contribution of proton binding at site i to the overall ΔG_FU) as

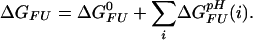Assuming an equilibrium between four species (folded and unfolded state, protonated, and deprotonated) at each site i, individual, pH-dependent values of ΔG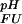(i) can be calculated for each group as

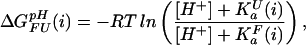where K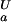(i) and K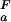(i) are the ionization constants for group i in the unfolded and folded state, respectively. The maximum of ΔG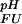(i) between very high pH where both states are fully deprotonated and very low pH where both states are fully protonated is given by ΔG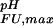(i) = 2.303RT⋅{pK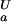(i) − pK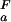(i)}. Irrespective of the pH independent term ΔG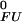, relative values of the pH dependence of the thermodynamic stability for a system containing multiple (i) ionizable groups can be calculated by summation as ∑_iΔG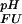(i), leaving the baseline of the stability curve undetermined. The analytical description presented here is numerically equivalent to a commonly used approach that relates stability changes to the pH-dependent difference in net charge between the two states (30), but provides a simple means to dissect the pH dependence of ΔG_FU into additive contributions due to individual ionizable groups. Changes in stability as a function of pH due to other effects, such as conformational adaptations in response to changes in the ionization state, are not taken into account.

For the calculation of ∑_i ΔG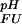(i), it is to a good approximation possible to exclude ionizable groups whose pK_a values are far from the pH range of interest (31). For the pH range between pH 1 and pH 7, only pK_a values for Asp, Glu, and His side-chains and the C terminus are of relevance. Standard pK_a values of Asp and Glu (as determined for the peptides AlaAspAla and AlaGluAla with N- and C-terminal blocking groups) are 4.0 and 4.4, respectively (32). For the side-chain carboxyl of Asp-59 (U_exch state) and C terminus of the protein (i.e., the backbone carboxyl of Asp-59, standard pK_a = 3.8), experimental pK_a values could not be measured for either folded or unfolded states due to resonance overlap. Because backbone amide resonances for the C-terminal residue Asp-59 titrate with identical apparent pK_a values in the unfolded and folded states, indicating that the C termini of the two ensembles are electrostatically very similar, Asp-59 was assumed not to contribute to ∑_iΔG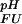(i).

For the His-7 → Ala mutant, experimental pK_a values were used for the calculation of ∑_i ΔG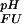(i). For Arg-20 → Ala, Lys-21 → Ala, and Asp-8 → Asn, experimental pK_a values were not determined, but wild-type pK_a values were used for the calculation of ∑_i ΔG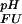(i). For all mutant proteins, calculations were performed as for the wild-type, with the following exceptions: for the Asp-8 → Asn mutant, Asp-8 and His-7 pK_a values were removed from ∑_i ΔG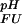(i); and for the His-7 → Ala mutant, His-7 pK_a values were removed from ∑_i ΔG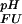(i). In this analysis, it is assumed that the structure of the protein is not significantly disrupted by the mutation and that the pK_a values of residues other than Asp-8 are unperturbed, as justified by NMR data on the mutant proteins, which indicate that chemical shift changes relative to the wild-type protein are small and restricted to the local environment of the mutation site. Moreover, Asp-8 and its possible interaction partners are isolated from other Asp and Glu residues.

Results

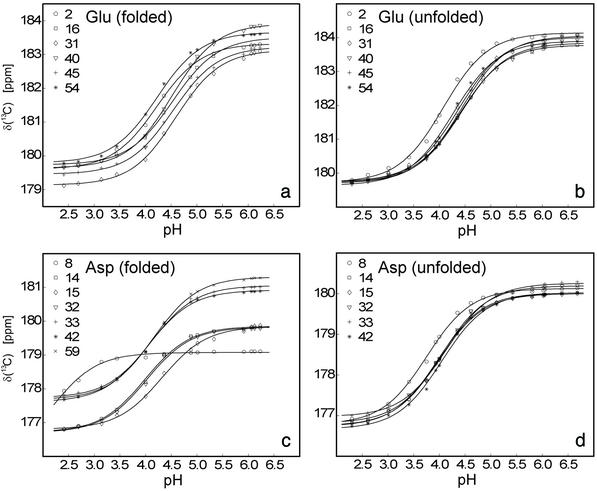
An almost complete set of experimental, residue-specific pK_a values for Asp and Glu residues for the unfolded and folded states of the wild-type drkN SH3 domain was obtained based on pH titration data (Fig. 1). In total, 25 (of 26, U_exch and F_exch) pK_a values for Asp and Glu carboxyls could be determined experimentally. Fig. 2c lists the experimental pK_a values for Asp and Glu in both F_exch and U_exch states of the wild-type drkN SH3 domain. Titration curves for the Asp-59 side-chain in the unfolded state and the C terminus (the Asp-59 backbone carboxyl) of either state could not be obtained because of resonance overlap. Apparent backbone NH pK_a values for the C-terminal residue Asp-59 for folded and unfolded states are identical within experimental uncertainty (pK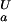 = 3.88 ± 0.06, pK 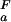= 3.96 ± 0.05), indicating that the highly dynamic C termini of the two ensembles are electrostatically very similar. In addition, all four (U_exch and F_exch) pK_a values for His imidazoles were determined. Experimental pK_a values for His side-chains are: pK 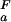= 6.98 ± 0.04 and pK 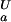= 7.07 ± 0.05 for His-7, pK 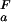= 7.72 ± 0.07 and pK 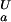= 7.83 ± 0.07 for His-58.

Fig 1.

Experimental titration curves (carboxyl carbon chemical shifts vs. pH) obtained for glutamate and aspartate side-chain acidic groups in the folded (a and c) and unfolded (b and d) states of the drkN SH3 domain, including best-fit lines (see Methods). Best-fit pK_a values are given in Fig. 2c.

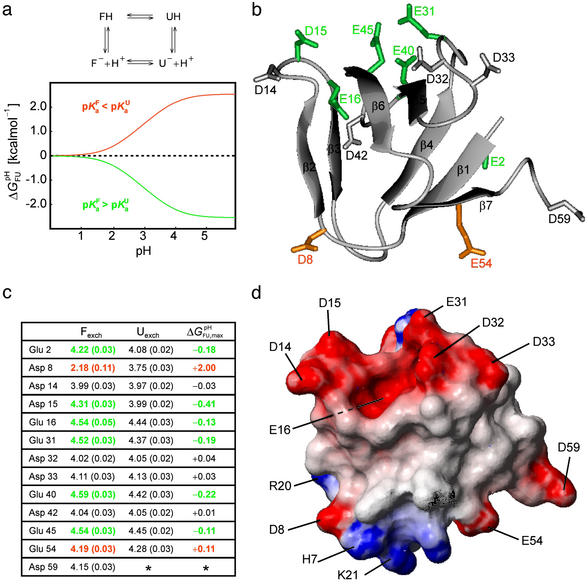
Fig 2.

Analysis of the pH dependence of ΔG_FU. (a) Simulation of ΔG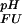(i) for a single ionizable group that titrates with (i) pK 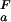= 2.0 and pK 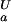= 4.0, orange line, (ii) pK 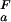= 4.0 and pK 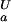= 2.0, green line, and (iii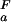) pK = pK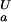, dashed black line, at 278 K. (b) The folded state structure of the drkN SH3 domain. Asp and Glu side-chains are color-coded (if |ΔG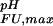(i)| > 0.1 kcal⋅mol⁻¹) according to whether 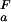pK < pK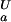 (orange) or 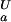pK < pK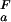 (green). (c) Experimental side-chain carboxyl pK_a values and error estimates (in parentheses) for Asp and Glu in the F_exch and U_exch states and ΔG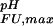(i) values. The pK_a values for the side-chain of Asp-59 in the unfolded state (*) could not be obtained due to resonance overlap. (d) Surface electrostatic potential of the drkN SH3 domain at neutral pH, identical view as b. Red represents negative electrostatic potential, white is neutral, and blue represents positive electrostatic potential. (b and d) Diagrams were generated by using the program MOLMOL (38).

The pH dependence of the thermodynamic stability of a protein arises due to differential electrostatic interactions in its folded and unfolded states. It can be calculated and analyzed in terms of contributions from individual ionizable groups. Assuming an equilibrium between four species for each ionizable group i (the folded and unfolded states with the ionizable group i being either protonated or deprotonated; Fig. 2a), the contribution of the protonation/deprotonation equilibrium involving site i to the unfolding free energy can be calculated as ΔG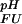(i) = −RT ln[([H⁺] + K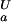(i))/([H⁺] + K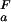(i))] at any proton concentration if residue-specific ionization constants for the folded and unfolded states (K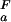(i) and K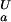(i), respectively) are known (see Methods). The pH dependence of the stability of a protein containing multiple ionizable groups can be calculated by summation of the contributions of individual groups as ∑_i ΔG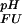(i). An ionizable group for which pK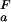(i) < pK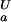(i) contributes to the pH dependence of the unfolding free energy by increasing ΔG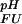(i) with increasing pH, as shown in Fig. 2a. The further a pK_a value in the folded state is lowered relative to the unfolded state, the more the conjugate base stabilizes the folded state structure relative to the unfolded state structure at pH values where group i is present in its deprotonated form in both states (the maximum stabilizing contribution, ΔG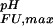(i), scales linearly with the pK_a difference). Conversely, if for a particular ionizable group pK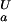(i) < pK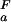(i), the opposite behavior is observed and ΔG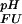(i) decreases with increasing pH. The trivial case of a flat pH stability profile is encountered if pK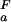(i) = pK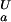(i). Maxima in the pH stability profile do not necessarily coincide with the isoelectric point, pI, of a folded protein, as suggested by the Linderstrom-Lang model, which predicts the stability of a protein to be decreased due to unfavorable electrostatic interactions introduced by positive (at pH < pI) or negative (at pH > pI) overall charges on a protein (33). Rather, differences in net charges between the folded and the unfolded state of a protein, as reflected by differential pK_a values for the two states, determine the pH dependence of protein stability (30).

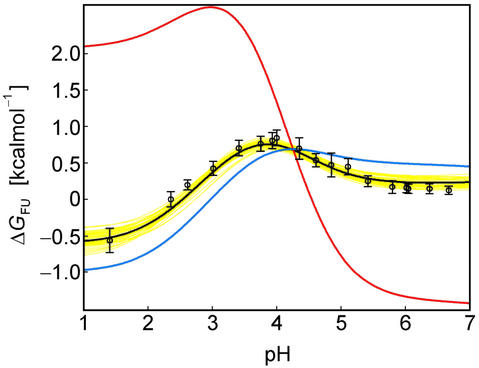
A complete set of residue-specific pK_a values for the folded and unfolded states enables the analytical calculation of the pH dependence of ΔG_FU. Fig. 3 demonstrates that the pH stability profile determined on the basis of the measured, residue-specific pK_a values for the F_exch and U_exch states (black/yellow curves) agrees very well with the experimental pH stability profile derived from relative populations (circles). In contrast, the profile derived assuming general downward shifts for all Asp and Glu pK_a values in the unfolded state relative to standard compound values (Fig. 3, red curve) is very different from that observed experimentally. Likewise, the profile derived on the basis of the “zero interaction model” assuming standard pK_a values for the unfolded state also does not agree with the experimental pH stability profile of the drkN SH3 domain (Fig. 3, blue curve).

Fig 3.

The pH dependence of protein stability of the drkN SH3 domain between pH 1 and pH 7. Experimentally determined values of ΔG_FU (black circles) were determined as ΔG_FU = −RT ln(p_U/p_F), where p_U and p_F are fractional populations as measured from peak volumes of the U_exch and F_exch states in heteronuclear single quantum coherence experiments and error bars represent SD. The calculated pH dependence of ΔG_FU (black line) was derived by using experimental, residue-specific pK_a values for both states employing Eqs. 2 and 3. The vertical offset of the calculated curve, ΔG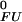, was determined by minimizing the χ² with the experimental data. A Monte Carlo simulation was performed by normally distributing pK_a values within their SD as estimated from experimental uncertainties (yellow lines). For comparison, pH stability profiles representing simplified models for the unfolded state are plotted assuming (i) standard pK_a values (blue line) and (ii) general downward shifted pK_a values (by 0.3 pH units from standard values, red line) for the unfolded state but by using experimental pK_a values for the folded state.

A salient feature of the pH stability profile of this SH3 domain is the stability maximum at pH ≈ 3.9. The reason for this maximum is the distribution of Asp and Glu pK_a values for the F_exch state around the rather uniform pK_a values for the U_exch state. Note that the pI for the folded SH3 domain is 4.60. In detail, for a number of residues (Glu-2, Asp-15, Glu-16, Glu-31, Glu-40, and Glu-45) indicated in green in Fig. 2, the pK_a values for the F_exch state are higher than for the U_exch state, and those residues consequently contribute to the stability profile of the protein by destabilizing the F_exch state relative to the U_exch state as the pH increases (by ΔG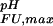(i) values of up to −0.4 kcal⋅mol⁻¹, Asp-15). The majority of these residues participate in a negatively charged cluster (at neutral pH) on the surface of the folded SH3 domain (Fig. 2d). Repulsive electrostatic interactions in such an arrangement, which is involved in binding the positively charged target region of Sos (22), increase the proton affinity, corresponding to the observed increase of pK_a values relative to standard values. In contrast, the steep pH dependence of ΔG_FU at pH < 3.9 is dominated by a single residue, Asp-8, which exhibits a significantly lower pK_a value in the F_exch state relative to the U_exch state, by 1.6 pH units (corresponding to ΔG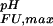(i) = +2.0 kcal⋅mol⁻¹), reflecting more favorable electrostatic interactions involving the conjugate base of Asp-8 in the folded than in the unfolded state. The unusually upfield shifted resonance of the deprotonated form of Asp-8 in the folded state is indicative of a hydrogen-bonded carboxylate (34). Indeed, by replacing the ionizable side-chain with an amide group, the steep dependence of ΔG_FU at pH < 3.9 is removed, and the mutant protein is most stable at low pH (Asp-8 → Asn mutant, Fig. 4).

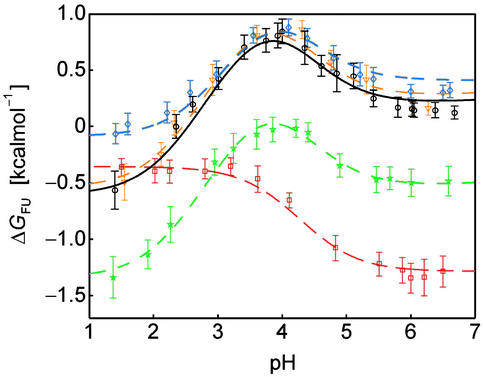
Fig 4.

Comparison of the pH stability profiles of the wild-type drkN SH3 domain (black) and mutant proteins His-7 → Ala (blue), Asp-8 → Asn (red), Arg-20 → Ala (green), and Lys-21 → Ala (orange). Values of ΔG_FU were determined from peak volumes of the U_exch and F_exch states in heteronuclear single quantum coherence experiments for the wild-type and each mutant, and curves were calculated as described in Methods.

To further investigate the electrostatic interactions contributing to the markedly low pK_a value of Asp-8 in the F_exch state, a number of other amino acid substitutions were made. Fig. 2d shows that, in the folded state, the side-chain acidic group of Asp-8 is located at the surface of the SH3 domain, surrounded by positively charged potential salt bridge interaction partners, including the sequentially proximate residue His-7 and residues Arg-20 and Lys-21, which are located in the “diverging” type II β-turn connecting strands β3 and β4. Because the pH dependencies of ΔG_FU for the mutant proteins Arg-20 → Ala and Lys-21 → Ala (Fig. 4) are identical to that of the wild-type protein (irrespective of absolute values of ΔG_FU), it is evident that the side-chains of Arg-20 and Lys-21 do not interact with the carboxylate of Asp-8. The pH-independent stability differences of ΔG_FU, such as that between the Arg-20 → Ala mutant and wild-type protein, reflect changes of enthalpic or entropic contributions to the thermodynamic stability of either the folded and/or the unfolded state on modification of the side-chain. The contribution of solvent-exposed charges (Arg-20, Lys-21) to the thermodynamic stability of a protein can exhibit considerable variability (35).

The experimental pH stability profile for His-7 → Ala, however, is notably different from that for the wild-type protein. For the His-7 → Ala mutant, residue-specific pK_a values for Asp and Glu side-chain carboxyls were determined experimentally and were found to be identical to wild-type pK_a values, with the exception of Asp-8, for which pK_a values were determined as pK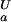 = 3.98 + 0.03 and pK 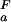= 2.66 + 0.06, corresponding to ΔG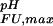(i) = +1.6 kcal⋅mol⁻¹. This value, which compares with the wild-type value of ΔG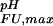(i) = +2.0 kcal⋅mol⁻¹ (Fig. 2c), indicates that, although His-7 does interact with Asp-8 in the F_exch state, somewhat reminiscent of a His−Asp salt bridge observed in T4 lysozyme (36), the main interaction(s) involving Asp-8 are retained in this mutant. In the folded state of the wild-type protein, the side-chain of Asp-8 forms a hydrogen bond to the backbone amide group of residue Lys-21, an interaction that seems to be conserved in SH3 domains (37). This interaction is corroborated by NMR chemical shift data showing that the backbone amide group of Lys-21 titrates with an apparent pK_a value that coincides with the side-chain pK_a of Asp-8. Presumably, this side-chain/backbone interaction is preserved in the His-7 → Ala mutant and constitutes the major electrostatic interaction of Asp-8 in the folded state.

Our experimental data on the drkN SH3 domain show that pK_a values of Glu and Asp residues in the unfolded state exhibit a much smaller distribution than those in the folded state. With two exceptions, experimental unfolded state pK_a values of Glu (average pK_a = 4.39 ± 0.07) and Asp (4.04 ± 0.06) residues compare well with standard values. Notable deviations were found for only two residues: Glu-2 displays a downward shifted pK_a of 4.08, which can most likely be attributed to a local electrostatic interaction with the positively charged N terminus of the protein, whereas the pK_a of Asp-8 (pK_a = 3.75) is probably downward shifted due to local interaction with the side-chain imidazole moiety of residue His-7. As noted above, the His-7 → Ala mutant has an Asp-8 pK_a value of 3.98 (near standard) in the unfolded state, confirming the presence of the His-7–Asp-8 local interaction in the wild-type protein. This interaction is further supported by the pK_a values of the His-7 imidazole in the wild-type protein, which are shifted to above standard pK_a values (by 0.5 pH units) in both states. Hence, although the local sequence does have an effect on pK_a values, a general trend toward lower than standard pK_a values for residues in the unfolded state of the drkN SH3 domain is not found.

These results are consistent with a view of the U_exch state as an ensemble of interconverting conformers, the majority of which contain a hydrophobically collapsed core with polar and charged groups on the surface protruding into the solvent water as in the folded state. Because, however, electrostatic interactions even in the folded SH3 domain are weak (with the exception of the side-chain/backbone interaction involving residue Asp-8), electrostatic interactions are likely to be even weaker in the less compact and more hydrated unfolded state of the protein. The conformationally less restrained and more dynamic U_exch state, with its increased surface area, allows for a wider spatial distribution of charged residues and a concomitant attenuation of electrostatic interactions due to distance, screening effects of counterions and the high dielectric constant of the solvent water. The fact that local electrostatic interactions seem to be sufficient to account for the (few) shifted pK_a values in the unfolded drkN SH3 domain contrasts data on other proteins, which indicate the presence of generally stabilizing electrostatic interactions in unfolded states (8–11). Unlike the SH3 domain studied here, all proteins for which such trends were proposed exhibit significantly downward shifted pK_a values for Asp and Glu residues in their folded states. Presumably, residual native-like electrostatic interactions are preserved in these unfolded states that would lead to significant effects on specific pK_a values, potentially in combination with nonnative interactions.

The experimental data for the drkN SH3 domain show that there are no general trends for electrostatic interactions in unfolded states. Rather, unfolded proteins are as diverse as folded proteins in terms of the factors that contribute to their stability. Although electrostatic interactions within unfolded states can be weak, knowledge of accurate, residue-specific pK_a values is vital for analyzing the pH dependence of protein stability. The existing methodology enables experimental determination of unfolded state pK_a values, providing the tools to probe the contribution of electrostatic interactions to the thermodynamic stability of proteins.

Abbreviations

• SH3, Src homology 3