The hydration structure of guanidinium and thiocyanate ions: Implications for protein stability in aqueous solution

Abstract

Neutron diffraction experiments were carried out on aqueous solutions containing either guanidinium or thiocyanate ions. The first-order difference method of neutron diffraction and isotopic substitution was applied, and the hydration structures of two of nature's strongest denaturant ions were determined. Each ion is shown to interact weakly with water: Guanidinium has no recognizable hydration shell and is one of the most weakly hydrated cations yet characterized. Hydration of thiocyanate is characterized by a low coordination number involving around one hydrogen-bonded water molecule and approximately two water molecules weakly interacting through “hydration bonds.” The weak hydration of these denaturant ions strongly supports suggestions that a major contribution to the denaturant effect is the preferential interaction of the denaturant with the protein surface. By contrast, solute species such as many sugars and related polyols that stabilize proteins are strongly hydrated and are thus preferentially retained in the bulk solvent and excluded from the protein surface.

Just over a century ago, Hofmeister (1) arranged ions into a series based on their ability to salt out proteins. Since then, others have extended this approach and have used it to characterize the ability of particular ions to nature or denature biological material (2–5). In this article we provide convincing evidence from neutron diffraction and isotopic substitution experiments that, we believe, goes a significant way to rationalizing the differing behavior of certain ions in biological solution. We came to this conclusion by focusing on two of nature's strongest denaturant ions [guanidinium (Gdm⁺) and thiocyanate (SCN⁻)] and by referring to previously published results derived from neutron diffraction and isotopic substitution. The method was first introduced in the 1970s and has been used to obtain structural information at the atomic level around specific atoms and ions in solution (6). In contrast to other methods, it is formally exact and does not require sophisticated modeling procedures for the determination of properties, such as nearest-neighbor coordination numbers and ion-water geometry.

Specifically, the article addresses the question of what the differences are, if any, in the hydration structure of ions whose denaturation properties have been arranged in a series according to their ability to denature or stabilize proteins. The results we present below on the hydration structure of Gdm⁺ and SCN⁻ have relevance to the mechanics of ion denaturation of biologically active material in aqueous electrolyte solution. The Gdm⁺ cation is the most powerful protein denaturant commonly used in studies of protein stability and folding (5), despite the fact that the detailed mechanism of its denaturation properties remains unresolved. Gdm⁺ ions bind to polypeptides, and this binding is expected to provide a significant contribution to protein denaturation because, on unfolding, many buried peptide backbone amides, hydrogen-bonded within the folded structure, become available for denaturant binding (7, 8). In contrast, the effect of denaturants on increasing the aqueous solubility of hydrophobic side chains exposed on unfolding has been rationalized in terms of an effect on the hydrogen-bond network of water (e.g., ref. 9); this situation is observed in Gdm⁺- and urea-promoted increases in the aqueous solubility of small hydrophobic molecules (10). There is also some evidence that denaturants may increase solubility by binding directly to nonpolar surfaces (11).

It is also found that the SCN⁻ anion greatly promotes salting out of proteins (e.g., lysozymes; ref. 12), caused, in part, by the SCN⁻ neutralization of excess positive charge on the lysozyme molecule. Moreover, SCN⁻ is a powerful protein denaturant; of the commonly used Gdm⁺ salts, GdmSCN is the most powerful protein denaturant (5). A notable property of the SCN⁻ ion in aqueous solution is its considerable effect on the number density of water. Water has an unusually high number density (0.10 atoms per ų), and all primitive aqueous electrolytes lower the number density of the solution. The ability of the SCN⁻ ion to lower the number density of an aqueous solution is about twice that of a comparable primitive electrolyte, an observation that we believe is a consequence of the hydration properties of the ion as described in the following sections.

Structural information on both these ions will, as we show, provide a key to the reasons why some ions are more effective denaturants than others.

Experimental Methods

The difference methods of neutron diffraction and isotopic substitution are well established in the literature (13); we reproduce only those parts that are relevant to the work undertaken here. The main tenet of the method is that there is complete isomorphism between isotopically labeled samples of the same chemical compound. In the present case, labeled GdmCl and NaSCN containing either ¹⁵N or ^natN were purchased from Aldrich Chem (Metuchen, NJ). The atomic concentration of ¹⁵N in both (¹⁵N₃) GdmCl and NaSC¹⁵N was >99%. Aqueous solutions of 3.33 mol of GdmCl and 5.00 mol of NaSCN per 55.55 mol of D₂O were prepared by using standard procedures (14).

All neutron-scattering data were recorded on the SANDALS diffractometer at the ISIS spallation source of the Rutherford Appleton Laboratory (Didcot, U.K.). In all cases, the samples were loaded into flat-plate null coherent scattering Ti/Zr containers with a sample thickness of 1 mm and then into the SANDALS sample changer. These containers provide a flat background and enable the identification of structure in the data to be attributed solely to the sample contained. The raw intensity data were analyzed by standard methods and normalized to a vanadium plate standard to give total structure factors F(Q) for all four solutions (15). These functions are given in units of barns⋅str⁻¹ (1 barn = 10⁻²⁸ m², which is the approximate cross-sectional area of a proton) and contain all of the pair correlations of the atomic species in the liquid. In mathematical terms we write

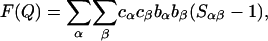where the sum is over all independent species in the solution. c_α is the atomic concentration of atomic species α, whose coherent neutron scattering length is b_α; S_αβ(Q) is known as the partial structure factor of the pairs of atoms α and β and is related through Fourier transformation to the real space pair radial distribution function g_αβ(r), i.e.,

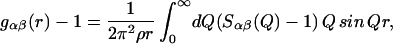where p is the atomic number density of the solution. The interpretation of these functions, either individually or as linear combinations, provides direct information on the local structure in solutions.

The first-order difference method is based on the determination of the F(Q)s of two solutions, which are identical except for the isotopic composition of one particular atomic species α; a difference function Δ_α(Q) can then be calculated, which contains only terms relevant to the substituted species. For the two aqueous solutions referred to in this article, the method was applied to the nitrogen atoms of the Gdm⁺ and SCN⁻ ions. The difference function Δ_N(Q) for each solution is written in terms of a summation of weighted S_αβ(Q)s, which relate to the pairwise structure around the substituted nitrogen nucleus, i.e., the nitrogen atom in both cases. Specifically for the GdmCl ion in 3.33 molal Gdm⁺ chloride solution,

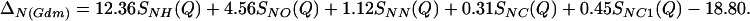Fourier transformation of this difference function gives the corresponding atom specific total pair radial distribution functions G_N(r) in dimensions of millibarns·str⁻¹.

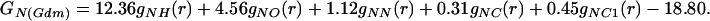Similarly for SCN⁻ in 5.00 molal NaSCN solution,

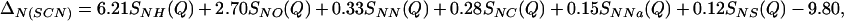which on Fourier transformation yields

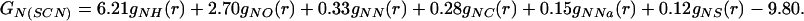It is worth noting, at this point, that although similar functions can be set up in Q space and r space in x-ray scattering experiments, the fact that x-rays interact with atomic electrons means that the scattering parameters corresponding to b_α (i.e., the x-ray atomic form factors of atom α) are Q dependent, and the Fourier transformation procedure involves a convolution of the partial structure factors. As a result, the real space information is at an inherently poorer resolution than the neutron diffraction. Moreover, there is no equivalent procedure to isotopic substitution, although the technique of isomorphic replacement can be used in some favorable cases (16).

Results and Discussion

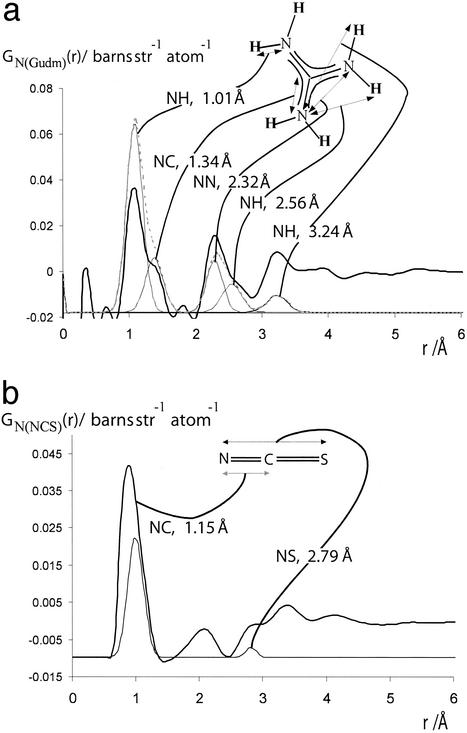
Fig. 1 a and b show, respectively, the G_N(r)s for the Gdm⁺ and SCN⁻ ions. It is clear that G_N(r)s for both ions contain several well defined molecular correlations. These correlations are in good general agreement with those predicted for the molecular ion and also provide a useful internal consistency check of data normalization. They do, however, show an increased error at lower r, especially below ≈1 Å. This observation is symptomatic of the relatively minor long-term instability observed in the data from the SANDALS instrument over Q ranges >10 Å⁻¹.

Fig 1.

(a) The thick-lined curve is the total nitrogen atom pair distribution function G_N(Gdm)(r) of the Gdm⁺ cation in 3.33 mol of GdmCl and 55.55 mol of heavy water. [G_N(Gdm) = 12.36g_NH(r) + 4.56g_NO(r) + 1.12(r) + 0.31g_NC(r) + 0.45g_NCl(r) − 18.80.] The dashed-line curve represents the corresponding intramolecular part of G_N(Gdm)(r) calculated on the assumption that correlations between the nitrogen atom and other atoms in the molecule can be represented by a spread function of the form exp(−(r²/w)/r) (shown as a thin solid line, labeled with the correlation they represent) where w₀ is the full width at half height of the peak. (b) The thick-lined curve is the total nitrogen atom pair distribution function G_N(SCN)(r) of the SCN⁻ anion in 5.00 mol of NaSCN and 55.55 mol of heavy water. [G_N(SCN) = 6.21g_NH(r) + 2.70g_NO(r) + 0.33g_NN(r) + 0.28g_NC(r)+ 0.15g_NNa(r) + 0.12g_NS(r) − 9.80.] The thin-lined curve represents the corresponding intramolecular part of G_N(SCN)(r) calculated by assuming that correlations between the nitrogen atom and other atoms in the molecule can be represented by a spread function of a form similar to that in a.

In the first instance, it is convenient to discuss the hydration structure of each ion separately.

The Gdm⁺ Cation.

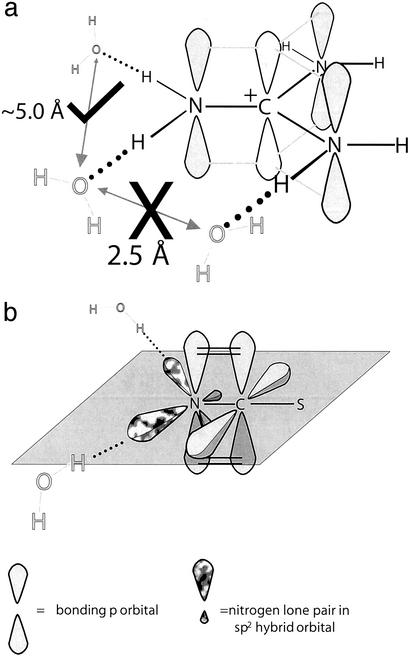
In the analysis of the G_N(Gdm)(r) we first note that the ion is planar and contains a carbon atom, surrounded by three nitrogens in a trigonal form, with all of the atoms in question being sp² hybridized (Fig. 2a). Within the accuracy of the results we observe no intermolecular correlations between the nitrogen atoms of the Gdm⁺ ion and other atoms <2.8 Å. Furthermore, when the intramolecular N–H correlation at 3.2 Å is subtracted from G_N(Gdm)(r), we note only a slight enhancement of structure in the region 3.2–4.0 Å. We thus conclude that the hydration of the Gdm⁺ ions is much weaker than any other cation (or indeed anion) we have yet investigated and the concept of a well defined coordination number cannot be applied to Gdm⁺.

Fig 2.

(a) The known geometry and dimensions of the Gdm⁺ ion. Probable positions of water molecules are shown in gray and the expected distances are given. If two adjacent hydrogen atoms attached to different nitrogen atoms are involved in hydrogen bonds, it would be necessary for the two oxygen atoms to have an improbably close separation of ≈2.5 Å, as indicated by the large X. The large check mark indicates an acceptable separation of hydrated water molecules. (b) The SCN⁻ anion with its two sp² orbitals containing the lone pairs of electrons of the nitrogen atom highlighted in mottled gray. The remaining 2p_z orbital forms a π bond with the 2p_z of the C atom. From our data we conclude that the nitrogen atom forms ≈1.2 hydrogen bonds with the lone pairs in the sp² orbitals of the nitrogen.

In specific terms, whether it is assumed that there are radial H bonds from the Gdm⁺ ion (Fig. 2a), it is expected that, given that the N–H ⋅ ⋅ ⋅ O optimum bond angle is 180°, the N–O correlation will be at ≈3 Å. Unfortunately, there is a molecular NH correlation at this same distance, and the data are not well enough resolved to separate these two correlations. In fact, G_N(Gdm)(r) can be represented to good approximation by a sum of the known molecular structure plus a relatively featureless function that begins at ≈3.2 Å. The data are, however, robust enough to support the conclusion that G_N(Gdm)(r) in the region 3.2–4.0 Å from the nitrogen atom has a slight but significantly higher number density than the bulk solution (r > 4 Å). This slight enhancement over the mean density of G_N(Gdm)(r) corresponds to the hydration of the Gdm⁺ ion. This result demonstrates that the Gdm⁺ ion does not compete effectively for hydrogen-bonding interactions with water and allows water molecules to maximize their interaction with each other (2). The form of G_N(Gdm)(r) also provides a good match (both in position and in magnitude) for the two N–H intramolecular correlations at 2.56 and 3.24 Å. Whereas numerous crystal structures of molecular complexes containing Gdm⁺ demonstrate that the ion crystallizes in a planar configuration (e.g., ref. 17), our results provide, to our knowledge, the first structural experimental evidence that the Gdm⁺ ion in solution is flat and rigid. If this were not the case, the two peaks at 2.56 and 3.24 Å would remain unresolved because of rotation around the N–C covalent bond.

Comparison of these results with similar studies on hydration of other cations confirms that the Gdm⁺ cation exhibits one of the weakest hydration structures determined so far. For example, the hydration of many cations consists of at least one well defined hydration shell, and these cations are known to have only limited effects on denaturation in solution (13, 18). We rationalize this lack of hydration structure by the following. The hydration of primitive electrolytes is dominated by charge density: The higher the charge density the more structuring around the ion (see ref. 19 and references therein for a recent theoretical analysis of ion hydration). Gdm⁺ has a relatively low charge density, considerably less than Cl⁻, which is held to be weakly hydrated. It is, therefore, expected that on charge-density grounds, Gdm⁺ will be weakly hydrated. A further cause of the hydration structure is in the nature of the hydrogen bond. The Gdm⁺ ion can form up to six such bonds (although only a maximum of three undistorted bonds can be formed; see Fig. 2a). However, the NH ⋅ ⋅ ⋅ O hydrogen bond has half the energy of the OH ⋅ ⋅ ⋅ O hydrogen bond [≈10 and 25 kJ⋅mol⁻¹, respectively (20§)]. It is therefore expected that any hydrogen bonds formed in the hydration of Gdm⁺ will be weaker and less structured than hydrogen bonds observed in the OH–O correlation of pure water (which is itself a broad structural feature). Finally, the local structure being hydrated comprises sp² NH₂ groups with an H–N–H bond angle of 120°, which is incompatible with the short-range tetrahedral structure of water.

The SCN⁻ Anion.

Analysis of the SCN⁻ ion proceeds along similar lines to that of the Gdm⁺ ion. The SCN⁻ ion is known to be linear, with the nitrogen being sp²-hybridized. The known molecular correlations give a measure of the quality of the data. It is found that the N–C correlation (known from gas phase and crystallographic data to be at 1.15 Å; ref. 21) is ≈50% too large in our results, a significant error. The N–C–S correlation is not useful for assessment of the data as its contribution to G_N(r) is too small and is mixed in with another correlation that occurs at the N–S distance. We can dismiss this first peak at 1 Å because of instrumental instability. One of the checks of internal consistency that can be applied to the data is to confirm that in regions where there are no atomic correlations expected, the function G_N(SCN) gives a value of zero. If this is not the case, then the data are demonstrably of poor quality. Although it is true that we do not know exactly where these values are for SCN⁻, experience, combined with the observed data themselves, leads us to believe that in the SCN⁻ case G_N(SCN) should be equal to zero at 1.5 and 2.5 Å. The data here do indeed drop to zero in a convincing fashion. We therefore take this as a measure that the data are of good quality. Moreover, the data in the region of 1.5–2.5 Å comply with the low r limit that is determined by the physical parameters of the system, a result that confirms the high quality of the data. Our results are also in good agreement with those of a previous study (22) performed on NaSCN at 6.1 molal and unpublished results of our own.

We assign the peak at 2.05 Å to the hydration between the nitrogen and a hydrogen of a nearest-neighbor water molecule. On this assumption, the coordination number of this first hydration shell is calculated to be 1.2 ± 0.2. Given the fact that the bond length here is comparable with that of a hydrogen bond, and that the peak width is similar to that of a hydrogen bond, we conclude that this peak represents a hydrogen bond between water molecules and the lone pairs in the sp² orbitals of the nitrogen. The bonding is not ionic as is found between ions such as Cl⁻ and water molecules. This assertion is strengthened by the fact that ion hydration starts, in the case of Cl⁻, at ≈0.2 Å from its ion surface, whereas for the SCN⁻ ion the hydration starts ≈1 Å from the ion surface [estimated from the ionic radius of Cl⁻ and the van der Waals size of the molecular ion (SCN⁻)]. Moreover, given that the OH ⋅ ⋅ ⋅ N bond is somewhat weaker than the OH ⋅ ⋅ ⋅ O hydrogen bond, (OH ⋅ ⋅ ⋅ N ≈ 20 kJ⋅mol⁻¹, OH ⋅ ⋅ ⋅ O ≈ 25 k⋅mol⁻¹), and the coordination number of an oxygen atom to a hydrogen atom in water is ≈1.8, then our assertion that water molecules are hydrogen bonded to the SCN⁻ ion is consistent with the lower coordination number of 1.2 ± 0.2 (Fig. 2b). We note again that the structure being hydrated is an sp² nitrogen atom, which is not easily accommodated in the locally tetrahedral structure of water.

The peak at 2.8 Å is too close and too large to arise from the oxygen atom associated with the hydrogen atom bonded to the N. We therefore attribute this peak to water molecules hydration-bonded to the ion, because water molecules hydrate anions with their electron-poor hydrogen atom directed toward the anion. Given this assumption, a coordination number of 2.1 is calculated after taking account of the correlations N–C–S and N ⋅ ⋅ ⋅ H–O, which also occur in the same region.

Our data therefore show that around the nitrogen of the SCN⁻ ion there are two types of hydration. The first arises from hydrogen atoms of the water molecules bonding by means of sp² orbitals to the nitrogen atom of the SCN⁻ ion at ≈2.1 Å, and the second we assign to a hydration bond, presumably primarily coulombic in nature, at ≈2.8 Å. Besides the obvious biological significance of this weakly hydrated and strongly denaturing anion, these results provide a natural explanation for the SCN⁻ to dramatically lower the number density of aqueous solutions.¶

In summary, the results above show the following:

1. The Gdm⁺ ion is flat and rigid in solution with no freely rotating C–N bonds.

2. The Gdm⁺ ion is relatively weakly hydrated. The reason for this is probably twofold. First, the NH ⋅ ⋅ ⋅ O hydrogen bond is about half the strength of the OH ⋅ ⋅ ⋅ O hydrogen bond, with the latter known to be quite weakly structured. Second, the Gdm⁺ ion has a low charge density, about a third of that of Cl⁻, which is also known to be relatively weakly hydrated.

3. The SCN⁻ ion is weakly hydrated. We conclude that there are two types of hydration bond to the SCN⁻ ion. The first is a hydrogen bond-type interaction between the hydrogen atoms of water molecules and the lone pairs of the sp² hybridized orbitals of the nitrogen; this occurs at 2.1 Å and has a coordination number of 1.2 ± 0.2. The second hydration bond is to a hydrogen at 2.8 Å and has a coordination number of 2.1. Further, we attribute the low number density of solutions containing SCN⁻ to the low coordination number of the SCN⁻ ion combined with the fact that this hydration of the anion starts at an unusually high r and is of the same order as that for O—O in water (23).

We find it significant that both Gdm⁺ and SCN⁻ are only weakly hydrated, and we believe that this property is crucial to their function as strong denaturants as described below. Comparisons with the hydration structure of other anions in the Hofmeister series are particularly edifying, as follows: G_I(r)s for Cl⁻ (24); ClO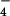 (25); NO 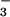(26); and SCN⁻ (this work) confirm the trend toward stronger denaturation with weak hydration as suggested by the series S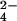O, HPO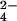 > F⁻ > Cl⁻ > I⁻ ≈ Cl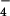O ≈ NO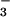 > SCN⁻ (3), where > expresses the idea that ions to the left of the series are strong naturants, which stabilize proteins, and those to the right destabilize proteins. Our results also help explain the structural origins of Jones–Dole viscosity B coefficients, which show a crossover from positive to negative values between F⁻ and Cl⁻ (27).

Our results enable us to predict that stabilizing anions such as HPO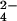 and SO 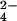will have strong hydration shells. Neutron diffraction and isotopic substitution results of Leberman and Soper (28) on solutions of sulfate ions imply that SO 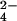is indeed strongly hydrated, as do our results for the phosphate ions HPO 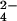and PO 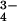(P.E.M., G.W.N., and A.C.B., unpublished work). These ideas also help explain why the neutral weakly hydrated molecule urea is a strong denaturant (30, 31) and why many divalent and trivalent cations with relatively strong hydration shells are relatively ineffective in denaturation processes (18).

Implications for the Properties of Gdm⁺ and SCN⁻ as Protein Denaturants.

Weak hydration of Gdm⁺ and SCN⁻ is expected to manifest itself in two ways that are relevant to current thinking about the denaturation mechanism(s) of these molecules. First, weak hydration promotes the partial dehydration required for these ions to interact with poorly hydrated regions of the protein, particularly those exposed on protein unfolding. These ions are “sticky” in the manner described by Collins (32) for the “pushing” of weakly hydrated ions (chaotropes) onto weakly hydrated surfaces by relatively stronger water–water interactions. Denaturation results to a greater or lesser extent from the favorable interaction with the polypeptide backbone exposed on unfolding as described for Gdm⁺ and urea (7, 8, 33, 34). In contrast, a large class of sugars and other polyols (osmolytes), which stabilize proteins, interacts unfavorably with the peptide backbone and is preferentially excluded from the protein surface (35–37). The binding of SCN⁻ to discrete sites on folded proteins (often involving electrostatic interactions with the weakly hydrated lysine amino and arginine guanidinyl groups) has been characterized in crystal structures (38, 39), but binding to the peptide backbone and hydrophobic side chains of unfolded proteins has not been described. However, analysis of crystal structures of small molecular complexes (40, 41) shows that SCN⁻ is a prodigious hydrogen-bonding ion, with both the S and N atoms acting as hydrogen bond acceptors; in many cases hydrogen bonding by both acceptors occurs simultaneously, with the SCN⁻ acting as a bridge between molecular fragments. It is therefore possible that SCN⁻ may form weak hydrogen bond interactions with the N–H of the peptide amide exposed on protein unfolding.

The second potential contribution to the denaturation properties of these molecules that relates to their weak hydration is their ability to promote the solubility of nonpolar groups (10, 34). Weak hydration necessarily results in reduced local water density (consistent with the large decrease in the number density of water, which is a feature of SCN⁻ solutions). According to the model of Muller (42), this may aid hydrophobic side-chain solubility by preempting space in the solvation shell around the nonpolar solute that could otherwise accommodate water molecules. The observation in crystal structures of planar stacking interactions of aromatic side chains with the side chain of arginine (structurally homologous with Gdm⁺) is suggestive of this possibility (43).

Finally, it is worth considering the implications of the weak hydration of Gdm⁺ for the structurally homologous side chain of the amino acid arginine. In proteins, the guanidinyl group of arginine often participates in inter- and intramolecular interactions, often involving anions, especially carboxylates (44–46). In general, the arginine side chain is overrepresented at protein–protein interfaces (hot spots; ref. 47) and is more buried (lower solvent-accessible surface area) in protein crystal structures than expected on the basis of its hydrophobicity (48). This burial is likely to be facilitated by the weak hydration of the guanidinyl group. There are a number of examples of hydrogen bonding of the arginine guanidinyl group with defined water molecules in protein crystal structures (29). In the context of the present study, it is significant that defined waters “hydrating” arginine guanidinyl groups in proteins are almost exclusively distributed so that water–guanidinyl hydrogen bonding is within the plane of the guanidinyl group (29). As indicated in Fig. 2a, analysis of the data presented here leads to a similar interpretation of the hydration of Gdm⁺ in water, namely that hydration is limited to the few water molecules able to form hydrogen bonds within the molecular plane of Gdm⁺.

Abbreviations

• Gdm⁺, guanidinium