Abstract
Most of our knowledge about transmission at central synapses has been obtained by studying populations of synapses, but some important properties of synapses can be determined only by studying them individually. An important issue is whether a presynaptic action potential causes, at most, a single vesicle to be released, or whether multiquantal transmission is possible. Previous work in the CA1 region has shown that the response to stimulation of a single axon can be highly variable, apparently because it is composed of a variable number of quantal elements (≈5 pA in amplitude). These quantal events have a low coefficient of variation (CV). Because the number of synaptic contacts involved is not known, the response could be because of uniquantal transmission at a varying number of synapses, or to multliquantal transmission at a single synapse. The former predicts that the CV at individual synapses should be small. We have used optical methods to measure the N-methyl-d-aspartate receptor-mediated Ca2+ elevation at single active synapses. Our main finding is that the amplitude of nonfailure responses could be highly variable, having a CV as large as 0.63. In one fortuitous experiment, the optically studied synapse was the only active synapse, and we could therefore measure both its N-methyl-d-aspartate (NMDA) receptor- and α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor-mediated signals. At this synapse, both signals varied over a 10-fold range and were highly correlated. These results strongly suggest that transmission at single CA1 synapses can be multiquantal. Furthermore, the individual quantal response is very far from saturation, allowing the effective summation of many quanta. The existence of multiquantal release has important implications for defining synaptic strength and understanding the mechanisms of synaptic plasticity.
Although there has been rapid progress in understanding the properties of central synapses, most experiments have been done on populations of synapses. Such studies can answer many types of questions, but provide little direct evidence regarding the stochastic properties of individual synapses. Recently, individual central synapses have begun to be studied (reviewed in ref. 1). An important question relates to the number of vesicles that are released and the interaction between them. There are indications that transmission can be uniquantal at some synapses, but multiquantal at others (2–4).
The most extensively studied central synapse is the Schaffer collateral synapse onto CA1 hippocampal pyramidal cells. However, even for this synapse, there remain substantial questions about the properties of quantal transmission. A minimal stimulation method has been extensively used to study the “unitary” responses generated by single axonal inputs. There are now reports from seven independent laboratories indicating that the amplitude distribution of the excitatory postsynaptic potential (EPSP) can have evenly spaced peaks (5–12), the signature of quantal transmission. Statistical analysis shows that the peaks cannot be attributed to sampling artifacts. The separation of the peaks is ≈5 pA, in the same range as the average value of miniature (m) excitatory postsynaptic currents (EPSCs) in these cells (11). The interpretation of these results is that the overall response is because of the linear summation of the responses to an integral number of vesicles. Furthermore, because the histograms peaks are fairly narrow, the variability of quantal size must be low. This variability is defined by the coefficient of variation (CV) and is calculated to be <0.2 (5). Although these results indicate that multiple vesicles contribute to the unitary response, it is unclear as to how many synapses are involved, because axons can often make multiple synapses with their targets (13). Thus, two very different interpretations of the response histograms are possible. According to the uniquantal model, there are multiple synapses, each of which releases at most a single vesicle and generates a stereotyped response with low CV. In this case, the overall response variation is because of variation in the number of synapses that release a single vesicle. According to the multiquantal model, a single synapse can release multiple vesicles, each of which produces a stereotyped response (CV < 0.2). In this case, the overall response at the single synapse will vary with the number of vesicles released and will have a high CV.
To distinguish between these models, we used optical and electrical methods to measure the CV at individual CA1 synapses. Previous work has shown that highly localized Ca2+ signals can be detected at individual spines when the synapse on that spine is active (14–17). Such signals can be generated by stimuli that evoke subthreshold EPSPs. Biophysical and pharmacological analysis has demonstrated that under these conditions, the spine Ca2+ signal is due primarily to Ca2+ entry through the small-fraction N-methyl-d aspartate (NMDA) channels that are opened when the membrane voltage is near resting membrane potential (14). Specifically, it has been shown that the signal has the voltage-dependence of NMDA channels and is completely blocked by NMDA receptor (NMDAR) antagonists. In contrast, the signals are nearly unaffected by depleting intracellular stores (but see ref. 15), by blocking voltage-gated Ca2+ channels or by blocking the EPSP with α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) channel blockers (see also ref. 18), indicating that other mechanisms make little contribution to these Ca2+ signals. The question we set out to answer is whether the Ca2+ signal at single synapses has a low CV (<0.2), as would be predicted by the uniquantal model, or whether it has high CV, as would be predicted by the multiquantal model.
Methods
Electrophysiological Methods.
Acute hippocampal slices were prepared from 17- to 21-day-old Long–Evans rats according to the methods described by Otmakhov et al. (19). Rats were decapitated under anesthesia (5% isoflurane) and their brains were rapidly removed and placed in ice-cold cutting solution. Brain slices (350–400 μm thick) were cut on a Vibratome. The CA3 region was surgically removed with the sharp edge of a razor blade. The slices were then incubated in artificial cerebrospinal fluid (aCSF) buffer containing 2 mM Ca2+ and 6 mM Mg2+) in a chamber to which humidified oxygen was continuously supplied (95% O2/5% CO2). Slices were incubated at room temperature for at least 2 h before they were transferred to the recording chamber. The chamber was attached to the movable stage of an Olympus (Tokyo) upright microscope (BX50WI). During recordings, slices were continuously superfused with aCSF composed of the following (in mM): 124 NaCl, 26 NaHCO3, 1.25 NaH2PO4, 2.5 CaCl2, 1.3 MgSO4, 20 d-glucose, and 0.05 picrotoxin; pH 7.4, bubbled with 95% O2/5%CO2. The neurons were visualized through a high-numerical-aperture water-immersion objective (×60 lens, 0.92 numerical aperture, 2.0-mm working distance) with near infrared (IR) oblique illumination. The image was visualized on a video monitor by means of a charge-coupled device (CCD) camera (KP-160, Hitachi, Tokyo).
Tight-seal whole-cell recordings were obtained under visual control with patch pipettes pulled from glass capillaries having a resistance of 4–6 MΩ when filled with intracellular solution containing the following (in mM): 120 K-gluconate, 10 KCl, 10 Hepes, 8 NaCl, 2 MgATP, 0.3 NaGTP, 10 Phosphocreatine, and 100–250 μM Oregon green 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA)-1 (Molecular Probes); pH 7.3, adjusted with KOH, with an osmolarity of 290–300 mOsM. Electrical whole-cell measurements were obtained through an Axopatch 1-D (Axon Instruments, Foster City, CA). Voltages are given without correction for junction potential. The analog signal was filtered at 1 kHz and then digitized by an analog–digital converter (ADC) board (Digidata 1200B, Axon Instruments) and collected on a Pentium PC by custom-made software in the AXOBASIC 1.2 programming environment. The stimulation patterns were generated by the program and sent through the ADC Digidata 1200B board to stimulus isolation units. Series resistance and input resistance were monitored every 6 sec by measuring the peak and steady-state currents in response to 2-mV, 35-μsec hyperpolarizing steps. The holding current was also recorded throughout the experiment. The stimulating electrode was positioned in the brain slice under visual control. The solution in the electrode was the same as the bath solution. The stimulation was achieved by sending current pulses of 100-μsec duration, generated by either of two stimulating units (constant current stimulus isolators, WPI Instruments, Sarasota, FL).
Fluorescence Optical Recordings.
The neuron was filled with Ca2+-sensitive fluorescent dye through the recording electrode. A confocal laser scanning system (Oz, Noran Instruments, Middleton, WI) was used for the illumination of the sample and detection of the optical signal. A Silicon Graphics (Mountain View, CA) O2 workstation, with intervision software (Noran Instruments) was used to control the operation of the entire Oz confocal system. A trigger sent out from the imaging program was used to synchronize the optical and electrical acquisition systems. The frame rate was either 30 or 60 frames per sec depending on the size of the image (115 × 256 or 49 × 256 pixels at 0.2 μm per pixel).
Image Analysis.
The images were converted from SGI movie file format to the TIFF format. Several regions of interest were selected, including a region far from the filled neuron, which was used to calculate the background signal. Once the background was subtracted, the average optical signal F within the regions of interest was calculated for every frame. ΔF/F(t) in the regions of interest was then calculated as
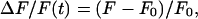 |
where F0 is the average fluorescence before the stimulus onset and F is the fluorescence at time t. All data analysis was done by using a custom-made program in the IGOR pro (Version π, Wavemetrics, Lake Oswego, OR) programming environment. Responses were quantified by averaging the optical signal over a 250-msec period. To distinguish successful transmission from failures, we adopted a conservative method for setting a threshold: we computed the maximal deviation of ΔF/F from zero for 250-msec periods before the stimulus onset in 10 trials. A response to the stimulus was identified as a “nonfailure” if the optical signal exceeded this threshold for more than two consecutive data points. The CV of successful responses was calculated as follows:
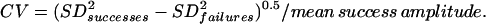 |
The error made on the evaluation of the CV for each experiment was calculated as follows: the error in the evaluation of the standard deviation from a limited number of samples is given by
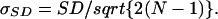 |
From error propagation theory, the standard deviation of the CV is
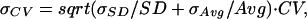 |
from which:
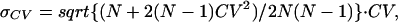 |
where N is the number of successes and Avg is the mean success amplitude.
In the bootstrap method (20), for the significance of the difference in CVs the CVs were calculated for N = 50,000 runs and the value of the probability given is the cumulative probability of CV being less than 0.22 (this is a worst-case assumption assuming ±10% error in the 0.2 value). The spine data where the number of responses was <10 were not considered.
Results
Dendrites and spines of hippocampal CA1 pyramidal neurons in acute brain slices were imaged after obtaining whole-cell recordings in the voltage-clamp mode (Vhold = −55 mV). The intracellular electrode contained K+-based solution and the calcium indicator dye Oregon green BAPTA-1 (100–200 μM). The tip of an extracellular stimulating electrode was positioned ≈20–50 μm from the visualized dendrite. To find active spines, bursts of three stimuli were given (60–140 Hz) because such bursts make transmission probability at active synapses close to 1. Stimulus current was adjusted to evoke an EPSC in the 30- to 200-pA range and no effort was made to obtain minimal stimulation.
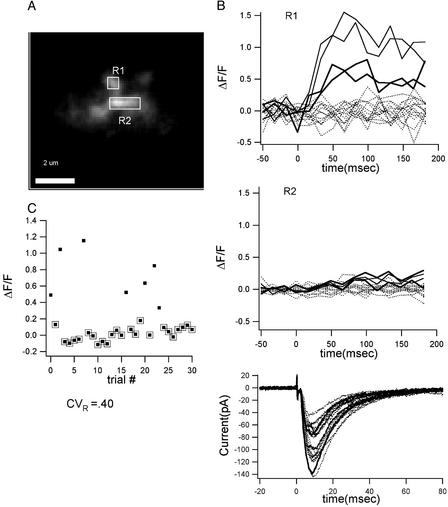
Once an active spine was found, the responses to single stimuli were measured (Fig. 1). Under these conditions the optical response was probabilistic; the probability of successful transmission at different spines ranged from 0.1 to 0.9, as reported (14–17). The optical response in a spine for 18 consecutive trials is plotted in Fig. 1B Top showing 4 successes and 14 failures (no optical response). The Ca2+ signals were highly localized within the visualized spine, with little spread to the dendrite and neighboring spines (Fig. 1B Middle). During stimulation, we also recorded the EPSC (Fig. 1B Bottom). In this and six other experiments, a large EPSC still occurred when the local optical signal failed. This result was expected because we did not use minimal stimulation and therefore, there were other active synapses outside of the visual field.
Fig 1.
Variable size of local Ca2+ signals evoked by single presynaptic action potentials. (A) Spine (region 1) and nearby dendrite (region 2) from which measurements were made. (B Top) Ca2+ signals (ΔF/F) in the spine (R1) from 18 consecutive trials show both successes and failures (dotted lines) of neurotransmitter release. The CV at this spine was 0.40. The probability of release was 0.4 (n = 20). (Middle) Ca2+ signals do not spread into the nearby dendrite (R2). (Bottom) Whole-cell voltage-clamp measurements of evoked EPSCs. (C) Plot of (ΔF/F) vs. trial number. Points surrounded by a box are failures (see Methods).
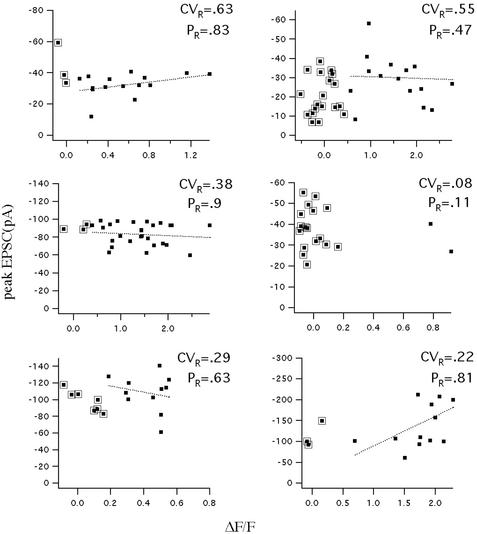
The key question we sought to answer is whether the amplitude of nonfailure optical responses at the identified spine showed large trial-to-trial variation or the whether the responses were stereotyped (CV < 0.2). Stimuli were given repetitively at a frequency of 0.06–1.6 Hz. The amplitude of the optical signal was averaged over a time window of 250 msec after the stimulus onset to minimize measurement noise. As shown in Fig. 1C, the response amplitude in this spine varied dramatically. We calculated the CV of the optical signal after subtracting the variation because of measurement noise (see Methods); the CV for the experiment in Fig. 1 is 0.40 ± 0.13. The results from six other experiments are shown in Fig. 2. The CVs for these recordings in seven experiments were as follows: 0.40 ± 0.13, 0.63 ± 0.16, 0.55 ± 0.12, 0.38 ± 0.06, 0.08 ± 0.06, 0.29 ± 0.07, and 0.22 ± 0.05. The bootstrap method was used to calculate the statistical difference between the measured CV and the 0.2 value for quantal variance (ref. 5; see Methods). Of five experiments in which there was a sufficient number of successes, three had a CV that was significantly larger than the 0.2 value (P = 0.005, 0.0001, and 0.009, respectively). It is also clear that the CV is not the same at all synapses, but the CV itself shows variation from synapse to synapse. It should also be noted that we found no correlation between the probability of response and the CV.
Fig 2.
The CV of the Ca2+ signal at individual spines can be large. Plots show the amplitude of all of the optical responses (ΔF/F) from an individual spine plotted against the simultaneous EPSC. Results from six different spines are shown. The CV and the probability of response (PR) are indicated for each spine. Points surrounded by a box are failures of the optical response (see Methods). There is little relationship between the optical and electrical signals because the latter arises from many synapses.
One possible explanation for the variability of the NMDAR-mediated response at individual spines would be that larger AMPA receptor (AMPAR)-mediated currents (generated by all of the active synapses) produced a greater depolarization (assuming imperfect clamp), allowing for more opening of NMDA channels. If this were the case, the magnitude of Ca2+ signals should have a positive correlation with the magnitude of the EPSC. Contrary to this prediction, we found a poor correlation of the optical and electrical signals (0.04 < | correlation coefficient ρ | < 0.48) and either a slightly positive or a slightly negative slope for the linear fit [(y = ax + b, with −71 < a < 39 pA/(ΔF/F), average = 0.16 × 10−3 pA/(ΔF/F)] (Figs. 1C and 2). This lack of correlation makes it unlikely that variability in the optical signal was caused by variations in the AMPAR-mediated depolarization. A second concern is that variability might result from rundown or damage, especially because the period of cell viability with optical recording is generally less than normal. However, there was no significant difference between the average amplitude of the first and second half of the responses in most cases; in those cases in which some small rundown was seen, the CVs for the first and second half of the experiment were calculated separately, and were found to give values similar to the total CV. We conclude that the CV of the NMDAR-mediated responses at individual synapses can often be substantially >0.2.
Optical and Electrical Measurements from a Single Spine.
As noted above, there were generally many active synapses, only one of which was monitored optically. Under these conditions, no relationship between the local optical signal and the electrical signal generated by the ensemble is expected and none was found (Fig. 2). However, in principle, it might be possible to stimulate only a single axon, and this axon might make only a single synapse with the target cell. In this case, the optical and electrical signal would be generated by the same synapse and a relationship between the two signals would be expected. Because the peak of the EPSC is primarily due to the AMPA component of transmission (21), such measurements would yield information about the evoked AMPA-mediated response at the identified synapse. Thus, this recording situation would allow simultaneous monitoring of the AMPAR-mediated electrical signal and the NMDAR-mediated Ca2+ signal from the same synapse. In one experiment, we fortuitously achieved this recording situation. This experiment is the first case, to our knowledge, where it has been possible to measure both components of evoked transmission at an identified spine in the slice preparation and it complements a single previous study in which it was possible to measure both the evoked AMPA and NMDA electrical response at an identified synapse in culture (22).
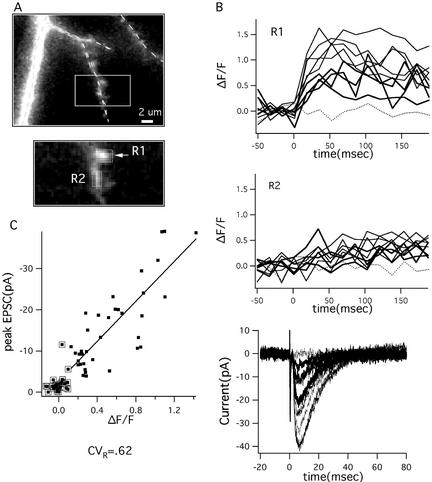
In this experiment, the cell body from which we recorded was located at a depth of 45 μm from the slice surface. The stimulating electrode was positioned 100 μm from the cell body along the direction of the primary apical dendrite and 60 μm away from it, ≈20 μm from two tertiary branches. We identified a single spine that showed an increase in fluorescence due to axonal stimulation (Fig. 3). Fig. 3A shows the region where the branch was located together with the image of the branch and spine. No other region in the same or nearby branch showed detectable fluorescence increases.
Fig 3.
In one experiment, the optical signal recorded from an active spine had a strong correlation with the total EPSC, indicating that the EPSC is generated at the optically identified spine. (A) Image of the dendritic location of the active spine and close-up of regions where optical measurements were made showing spine (R1) and parent dendrite (R2). (B Top and Middle) The optical responses in the two regions for 10 consecutive trials are plotted as a function of time and divided into failures (dotted line), medium (thick line), and large (thin line). (Bottom) The corresponding electrical responses are plotted as a function of time with the same line coding. (C) There is a high correlation (P = 0.9) between the amplitude of the optical response and that of the electrical response. Optical failures are points surrounded by a box; all but one optical failure corresponds to a failure in the electrical responses. A second “failure” at −5 pA falls directly on the regression line, which can be most likely interpreted that there is a small optical response that is below our conservative threshold (see Methods). Both electrical and optical signal are highly variable (CV = 0.71 and 0.62, respectively). It cannot be excluded that the measured optical response is the superposition of the responses in two neighboring active spines that cannot be optically resolved. However, even in this case, the computed CV in each of these spines would be >0.4.
After identification of this active spine, the stimulation protocol was changed to single shocks. Failures and successes in inducing Ca2+ entry on stimulation were detected. The probability of an optical response for this spine was 0.6. The current during successful responses averaged 16 pA. Fig. 3B shows a few sample traces of the electrical response and the corresponding optical signals in the spine and neighboring regions. If only a single spine were active, whenever that spine failed to produce an optical response, there should also be a failure of the electrical response. The optical failures are marked by points surrounded by boxes in Fig. 3C (see Methods for criterion for optical failure). It can be seen that almost all of the failures in the optical response were accompanied by failures in the electrical response. In one case, a small (10-pA) response was observed during an optical failure. Because characterization of the electrical noise indicated that 91% of the peak current is <2 pA, it is unlikely that the 10-pA value can be attributed to noise. It could have been because of evoked release at another synapse or to a spontaneous event at any of the cell's synapses. It is also possible that there was an optical response at the monitored spine, but that it fell below the detection threshold. In any case, if another synapse was involved, it would have a low probability (<0.04; 1 of 24 failures) to be activated together with the spine being imaged and would not influence the statistics of the results. We conclude that all or nearly all of the recorded EPSCs are from the optically identified spine.
In this spine, the CV for the nonfailure NMDAR-mediated responses was 0.6 ± 0.1, similar to the highest values of CV obtained in our other experiments (the difference from 0.2 was significant; P < 0.0001). The CV of the peak electrical response had a similarly high value (0.71 ± 0.09). Both the optical and electrical signals varied over nearly a 10-fold range. Fig. 3C further shows that the amplitude of the optical and electrical signals were highly correlated, as would be expected if they were from the same spine (correlation coefficient = 0.9). This finding indicates that there are common factors that underlie the large variability of the AMPAR- and NMDAR-mediated signals.
Discussion
Our principal finding is that the response at individual CA1 synapses can be highly variable, extending over a 10-fold range. This variability was observed in the local Ca2+ signal that results from entry of Ca2+ through NMDA channels. In four of eight experiments, this CV was >0.4, the highest value being 0.62. In one fortuitous experiment, it was possible to measure both the CV of the NMDAR-mediated optical signal and the CV of the AMPAR-mediated EPSC generated by the same synapse. Both signals varied over a very wide range (CV > 0.6) and were highly correlated. The interpretation of these high CV values is strongly constrained by previous work on CA1 synapses showing that quantal responses have a low CV (<0.2; see Introduction). Thus, if release is uniquantal, responses at single synapses should have a low CV. Our finding of a high CV at single identified spines therefore argues that release is multiquantal. An additional finding is that the maximum AMPA-mediated response can be very large (>40 pA), much larger than measurements of quantal size (5–11) or the average mEPSCs generated by synapses with a comparable distance from the soma (≈5 pA; ref. 11). The large responses can be simply explained in terms of the summation of multiple quanta.
However, before accepting the multiquantal interpretation, several alternative interpretations need to be discussed. With regard to the interpretation of the NMDA-mediated signals, it might be argued that the variability arises from voltage fluctuations generated by the synaptically induced depolarization. Although our measurements were made under voltage clamp, there could be depolarization because of voltage escape. Two arguments indicate that such escape is unlikely to be important. First, when experiments are done under current clamp, eliminating subthreshold EPSPs with 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) has little effect on the Ca2+ signal (14, 18), indicating that small depolarizations have little effect on NMDA channels. Furthermore, in our experiments where multiple axons were stimulated, we found little or no correlation between the local NMDA-mediated Ca2+ signal and the EPSC (Fig. 2). Such a correlation would be expected if optical signals were dependent on voltage escape.
A second possible source of trial-to-trial variation could be in the number of NMDA channels present or fluctuations in the number that open. However, it has been shown that when NMDA is applied to a single synaptic region, the saturated response shows very little variability (CV = 0.18), as does the response when it is only 10% maximal (23). This lack of variability is not unexpected, given the large number of NMDA channels at synapses (24). It might be argued that variability in the NMDA response arises from fluctuation in the position of release of a single vesicle at the synapse or the rate at which transmitter is released from that vesicle. Recent experiments specifically manipulated these parameters during direct glutamate application. The results show that whereas spatial and temporal factors may be important in determining the amplitude of the AMPA response, they are relatively unimportant for the NMDA response (25). This finding is understandable because the high affinity of NMDA receptors for glutamate makes them sensitive to glutamate even after the transmitter becomes diluted in the cleft as it spreads away from the site of vesicle fusion. Therefore, variability in the NMDAR-mediated response (Figs. 1–3) cannot be attributed to fluctuations in the rate or position of glutamate exit from the vesicle. Finally, it might be argued that release is uniquantal, but that vesicle glutamate concentration is highly variable and possibly quantally distributed. This hypothesis predicts that the average size of nonfailure responses should be unaffected by changing the probability of release, contrary to recent findings (26).
We conclude that the only straightforward interpretation of our results is that multiquantal releases occur at single synapses and that the single quantal event is very far from saturation, allowing effective quantal summation. It should be emphasized that our experiments were done preferentially on larger spines because these are easiest to detect optically. Because synapse size varies over a 100-fold area at Schaffer collateral synapses (27, 28), it is quite possible that release is uniquantal at small synapses, but multiquantal at large ones. This possibility may explain instances where evoked release has a unimodal amplitude distribution and where changing the probability of release does not affect the average amplitude of successful responses, results that imply uniquantal transmission (29, 30). Finally, it is important to clarify that CA1 synapses do not have multiple active zones (27). Thus, what we are proposing here is the release of multiple quanta at a single active zone.
There have been previous indications that multiquantal transmission can occur at CA1 synapses. A study of population responses in the CA1 region showed that low-affinity NMDA antagonists were less effective under high-release conditions, a result that was interpreted to imply multiquantal release (31). Importantly, this finding was not based on optical methods, which are biased toward large spines, and thus suggests that multiquantal release is not a property only of the large spines used in optical studies. Recent work (26) on CA1 synapses shows that facilitation increases the amplitude of nonfailure NMDA-mediated Ca2+signals in spines, a result that is easiest to interpret in terms of multiquantal release. Our work provides a direct observation of the large variability in response attributable to the summation of a variable number of quanta. The largest responses were up to 10 times larger than the smallest response, implying a wide dynamic range for multiquantal transmission. In the case where we were able to study the AMPA-mediated response, the maximal response was 40 pA, much larger than quantal size (5–11). This large maximal current is in line with recent experiments showing that direct application of glutamate to synapses in culture (23, 32) and in brain slices (33) can produce currents up ≈100 pA. It thus appears that a quantal response involves the opening of only a small fraction of the channels at large synapses, and that multiple quanta summate to produce a wide range of currents.
Recent work begins to shed light on events in the cleft during a quantal event. Dendritic recordings (11, 34) of mEPSCs evoked by sucrose application near the site of recording indicates that the rise time (<70 μsec) is much faster than previously thought. Analysis of glutamate diffusion and channel activation indicates that the channels that are rapidly opened occur in a hotspot near the site of vesicle fusion (S. Raghavachari and J.L., unpublished data). This finding means that each vesicle release preferentially activates different regions of the synapse and explains why quantal summation can be linear.
A previous investigation of the responses evoked by minimal stimulation has noted that multiquantal release does not obey binomial statistics (5). This discovery is also evident in our results, which are as follows: if the average number of vesicles released is 4 in the experiment of Fig. 3 (see below), then the number of failures should be 3 in 60 trials, which is much lower than the 22 that were observed. The key requirement for binomial release is that each stimulus produce the same Ca2+ elevation in the presynaptic terminal. There are many reasons to doubt that this requirement is met. These include (i) failures to stimulate the axon, (ii) all-or-none Ca2+ signals in boutons (35), (iii) changes in Ca2+ amplification in the terminal by internal release (36, 37), and perhaps most importantly, (iv) stochastic variation in the number of Ca2+ channels that open (4, 38).
Our findings have implications for defining synapse strength and plasticity. To generate multiquantal release, there must be a large pool of docked vesicles. Because synapses have 250 docked vesicles per μm2 (39), a moderately large synapse (0.1 μm2) would have 25 vesicles, more than enough to allow the release of 10 vesicles and the production of the largest observed responses (40 pA). These considerations also provide a potential solution to a puzzling aspect of paired-pulse depression (40, 41), a form of short-term synaptic plasticity. It has been generally thought that this depression arises from the fact that vesicles released by the first stimulus deplete the pool of docked vesicles. However, if this pool consists of 25 vesicles, uniquantal release would have little effect. Multiquantal release, in contrast, could potentially reduce the pool enough to account for paired-pulse depression.
The existence of multiquantal release changes the way synaptic strength must be measured. Synaptic strength is defined by the average response (including failures and nonfailures) of the EPSC at a single synapse. It is often assumed that synaptic strength can be measured by the size of a mEPSC, but this method depends on the assumption of uniquantal release. A further common interpretation has been to assume that changes in the quantal parameter, N, imply changes in the number of synaptic contacts. Again, this interpretation is based on the assumption of uniquantal release. It now appears that N would be more accurately described as the number of effective sites for the release of vesicles at a single synapse. These considerations emphasize the importance of understanding the microphysiology of synaptic transmission to properly interpret the changes in quantal properties that occur as a function of synapse position (11), development (42), and plasticity (43).
Acknowledgments
We thank O. Moran for his contribution in setting up the analysis software; N. Otmakhov, S. Raghavachari, A. Kepecs, and Eric Hanse for useful discussions; and N. Otmakhov and R. Malinow for comments on the manuscript. This work was supported by National Institutes of Health/National Institute of Neurological Disorders and Stroke Grants R01 NS35083 and R01 NS27337 and National Institutes of Health/National Institute of Neurological Disorders and Stroke Grant 1 P50 MH60450. We also acknowledge the support of the W. M. Keck Foundation.
Abbreviations
CV, coefficient of variation
AMPA, α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid
AMPAR, AMPA receptor
NMDA, N-methyl-d-aspartate
NMDAR, NMDA receptor
EPSP, excitatory postsynaptic potential
EPSC, excitatory postsynaptic current
mEPSC, miniature EPSC
References
- 1.Auger C. & Marty, A. (2000) J. Physiol. 526, 3-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Auger C., Kondo, S. & Marty, A. (1998) J. Neurosci. 18, 4532-4547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wadiche J. I. & Jahr, C. E. (2001) Neuron 32, 301-313. [DOI] [PubMed] [Google Scholar]
- 4.Wall M. J., Robert, A., Howe, J. R. & Usowicz, M. M. (2002) Eur. J. Neurosci. 15, 785-797. [DOI] [PubMed] [Google Scholar]
- 5.Stricker C., Field, A. C. & Redman, S. J. (1996) J. Physiol. 490, 419-441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Malinow R. (1991) Science 252, 722-724. [DOI] [PubMed] [Google Scholar]
- 7.Larkman A., Stratford, K. & Jack, J. (1991) Nature 350, 344-347. [DOI] [PubMed] [Google Scholar]
- 8.Liao D., Jones, A. & Malinow, R. (1992) Neuron 9, 1089-1097. [DOI] [PubMed] [Google Scholar]
- 9.Kullmann D. M. & Nicoll, R. A. (1992) Nature 357, 240-244. [DOI] [PubMed] [Google Scholar]
- 10.Foster T. C. & McNaughton, B. L. (1991) Hippocampus 1, 79-91. [DOI] [PubMed] [Google Scholar]
- 11.Magee J. C. & Cook, E. P. (2000) Nat. Neurosci. 3, 895-903. [DOI] [PubMed] [Google Scholar]
- 12.Voronin L. L., Kuhnt, U., Gusev, A. G. & Hess, G. (1992) Exp. Brain Res. 89, 275-287. [DOI] [PubMed] [Google Scholar]
- 13.Sorra K. E. & Harris, K. M. (1993) J. Neurosci. 13, 3736-3748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kovalchuk Y., Eilers, J., Lisman, J. & Konnerth, A. (2000) J. Neurosci. 20, 1791-1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Emptage N., Bliss, T. V. & Fine, A. (1999) Neuron 22, 115-124. [DOI] [PubMed] [Google Scholar]
- 16.Malinow R., Otmakhov, N., Blum, K. I. & Lisman, J. (1994) Proc. Natl. Acad. Sci. USA 91, 8170-8174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yuste R., Majewska, A., Cash, S. S. & Denk, W. (1999) J. Neurosci. 19, 1976-1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Koester H. J. & Sakmann, B. (1998) Proc. Natl. Acad. Sci. USA 95, 9596-9601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Otmakhov N., Griffith, L. C. & Lisman, J. E. (1997) J. Neurosci. 17, 5357-5365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Efron B. & Tibshirani, R. J., (1993) An Introduction to the Bootstrap (Chapman & Hall, New York).
- 21.Hestrin S., Sah, P. & Nicoll, R. A. (1990) Neuron 5, 247-253. [DOI] [PubMed] [Google Scholar]
- 22.Renger J. J., Egles, C. & Liu, G. (2001) Neuron 29, 469-484. [DOI] [PubMed] [Google Scholar]
- 23.McAllister A. K. & Stevens, C. F. (2000) Proc. Natl. Acad. Sci. USA 97, 6173-6178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cottrell J. R., Dube, G. R., Egles, C. & Liu, G. (2000) J. Neurophysiol. 84, 1573-1587. [DOI] [PubMed] [Google Scholar]
- 25.Murnick J. G., Dube, G., Krupa, B. & Liu, G. (2002) J. Neurosci. Methods 116, 65-75. [DOI] [PubMed] [Google Scholar]
- 26.Oertner T. G., Sabatini, B. L., Nimchinsky, E. A. & Svoboda, K. (2002) Nat. Neurosci. 5, 657-664. [DOI] [PubMed] [Google Scholar]
- 27.Harris K. M. & Stevens, J. K. (1989) J. Neurosci. 9, 2982-2997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lisman J. E. & Harris, K. M. (1993) Trends Neurosci. 16, 141-147. [DOI] [PubMed] [Google Scholar]
- 29.Stevens C. F. & Wang, Y. (1994) Nature 371, 704-707. [DOI] [PubMed] [Google Scholar]
- 30.Hanse E. & Gustafsson, B. (2001) J. Physiol. 531, 467-480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tong G. & Jahr, C. E. (1994) Neuron 12, 51-59. [DOI] [PubMed] [Google Scholar]
- 32.Liu G., Choi, S. & Tsien, R. W. (1999) Neuron 22, 395-409. [DOI] [PubMed] [Google Scholar]
- 33.Matsuzaki M., Ellis-Davies, G. C., Nemoto, T., Miyashita, Y., Iino, M. & Kasai, H. (2001) Nat. Neurosci. 4, 1086-1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Diamond J. S. & Jahr, C. E. (1997) J. Neurosci. 17, 4672-4687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Frenguelli B. G. & Malinow, R. (1996) Learn. Mem. 3, 150-159. [DOI] [PubMed] [Google Scholar]
- 36.Emptage N. J., Reid, C. A. & Fine, A. (2001) Neuron 29, 197-208. [DOI] [PubMed] [Google Scholar]
- 37.Llano I., Gonzalez, J., Caputo, C., Lai, F. A., Blayney, L. M., Tan, Y. P. & Marty, A. (2000) Nat. Neurosci. 3, 1256-1265. [DOI] [PubMed] [Google Scholar]
- 38.Mackenzie P. J., Umemiya, M. & Murphy, T. H. (1996) Neuron 16, 783-795. [DOI] [PubMed] [Google Scholar]
- 39.Schikorski T. & Stevens, C. F. (1997) J. Neurosci. 17, 5858-5867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zucker R. S. (1989) Annu. Rev. Neurosci. 12, 13-31. [DOI] [PubMed] [Google Scholar]
- 41.Matveev V. & Wang, X. J. (2000) J. Neurosci. 20, 1575-1588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hsia A. Y., Malenka, R. C. & Nicoll, R. A. (1998) J. Neurophysiol. 79, 2013-2024. [DOI] [PubMed] [Google Scholar]
- 43.Oliet S. H., Malenka, R. C. & Nicoll, R. A. (1996) Science 271, 1294-1297. [DOI] [PubMed] [Google Scholar]