Abstract
We illustrate the application of the Bayesian Adjustment for Confounding (BAC) algorithm when the treatment covariate is binary. Using data from the Multi-Ethnic Study of Atherosclerosis, we estimate the effect of ever smoking on common carotid artery intimal medial thickness (CCA IMT) among adult Caucasian participants (n = 1378). Our novel implementation of the BAC algorithm is performed first from an outcome model perspective and secondly from a treatment model perspective with both inverse-probability-weighting (IPW) and doubly-robust (DR) estimation techniques. The BAC results are compared to the results obtained using standard model averaging and full model strategies, giving a range of adjusted estimates between 45.50 μm and 65.30 μm for increased CCA IMT among ever smokers. For both perspectives, we observe that BAC offers similar performance to using the fully specified outcome and/or treatment model (the full outcome model ever smoking effect is 48.61 μm; 95% CI: (0.62, 96.60)). We then redo the analyses for the African American, Hispanic and Chinese adult participants to study the robustness of these findings with reduced sample size. For the Chinese subcohort, which corresponds to the smallest sample size (n = 436), we find that, from a treatment model perspective, BAC reduces the variability of the estimates in comparison to using a full model approach. This suggests that the use of BAC in conjunction with IPW and DR estimation can be advantageous when applied to relatively small sample sizes. This conjecture is subsequently verified on the basis of three simulated experiments.
Keywords: Bayesian Adjustment for Confounding, binary treatment variable, Multi-Ethnic Study of Atherosclerosis, smoking, common carotid artery intimal medial thickness
1. Introduction
The process by which a researcher selects a model for a given estimation procedure is important but most often neglected when reporting the results. By not taking into account the issue of model uncertainty, that is by ignoring the process by which one model is selected among the set of all possible models, a study overstates confidence in the chosen model and corresponding conclusions. A common way of surmounting the problems associated with selecting a few explanatory covariates out of a long list of available covariates is to use Bayesian model averaging [1]. The idea behind this technique is that the estimate of a quantity of interest (e.g., parameter, future observation) is averaged over multiple models according to the posterior probability given to each model under consideration. Model averaging stands in contrast to the more common approach of model selection, whereby an estimate is obtained from a single model. The statistical properties of Bayesian model averaging are well-known and it has been demonstrated that it increases predictive ability [1, 2]. While model averaging is recognized to be successful to account for model uncertainty in prediction problems, its potential benefits in the causal inference framework were cast into doubt in past years [3, 4]. Indeed, when applied in the context of a conventional regression strategy for causal treatment effect estimation, model averaging is recognized to attribute large posterior probabilities to outcome models that may not appropriately adjust for confounding, thus having sub-optimal properties for such usage.
Recently, Wang et al. [4] introduced the Bayesian Adjustment for Confounding (BAC) algorithm as an alternative to model averaging in causal problems. Similarly to model averaging, BAC considers unknown nuisance indicators for the inclusion of each potential confounding covariate in the adjusted outcome model and an average effect estimate is obtained by weighting the model-specific estimates by the posterior probabilities of the outcome models. However, BAC differs from model averaging in that it shifts the bulk of adjusted outcome models’ posterior weights to models for which the treatment effect is believed to be unconfoundedly estimated. Indeed BAC is devised to take into account model uncertainty while ensuring a common interpretation of the coefficient associated to the treatment covariate in high posterior probability outcome models. This functioning of BAC is made possible by considering both an outcome and a treatment model and the use of a prior distribution that controls the probability of inclusion of the potential confounding covariates in these models. Specifically, the prior is such that a covariate included in the treatment model is given increased probability to be included in the outcome model. BAC is this way designed to give larger posterior probabilities to outcome models that are appropriately adjusted for confounding.
Wang et al. [4] introduced BAC from a fully Bayesian perspective and illustrated the technique with continuous treatment variables only. In this paper, we illustrate how one can apply BAC when the treatment covariate is binary and assess the effect of ever smoking on carotid intima-media thickness using data from the Multi-Ethnic Study of Atherosclerosis (MESA). To do so, we rely on Lefebvre et al.’s [5] perspective on BAC and take an approximate Bayesian approach that facilitates the implementation of the algorithm. Adjusted estimates are then reported using different estimation strategies from an outcome regression modeling perspective. We begin by comparing the results obtained from 1) adjustment for the full set of potential confounding covariates, 2) a model averaging strategy and 3) BAC. With this set of results, we aim to provide a comprehensive and real-data based example of the differences between standard implementations of model averaging and BAC for causal effect estimation.
With binary treatment covariates, causal treatment effect estimation is often performed through the modeling of the treatment (propensity score) model. While propensity score methods have become common to estimate treatment effects in non-experimental health studies [6], the construction of the treatment model remains a challenging aspect of their application [7]. In a recent paper that criticizes a common treatment model-building practice - that is the selection of the most predictive model - Westreich et al. [8] state that : “as no method for variable selection is foolproof, the epidemiologist should consider reporting various results under different, sensible, and transparently explained model specifications”. We agree with this point of view and encourage the development of propensity score methods that formally but adequately take into account model uncertainty. We thus additionally investigate the use of BAC within an inverse-probability-weighting and doubly-robust estimation frameworks. The extension of BAC to such frequentist causal estimators was identified by Vansteelandt [9] as an interesting line of research. Moreover, theoretical and empirical examinations of model averaging (and adapted versions) in doubly-robust estimation have recently started to emerge and results have shown promise [10]. Therefore our work continues the investigation of such inferential strategies for causal effect estimation.
The paper is structured as follows. The method is described in Section 2 and is divided in three parts. We present MESA and the data considered in Subsection 2.1. In Subsection 2.2, we introduce BAC and its implementation to estimate the effect of ever smoking on carotid intima-media thickness from an outcome regression approach. In Subsection 2.3, we examine the application of BAC from a treatment model perspective and present different inference strategies investigated within the inverse-probability and doubly-robust frameworks. The MESA results are presented in Section 3. In Section 4, we present a simulation study whose goal is to verify the findings of Section 3. We conclude by a discussion in Section 5.
2. Methods
2.1. Data description
MESA is a population-based, prospective cohort study designed to determine risk factors for the development and progression of subclinical and clinical cardiovascular diseases [11, 12]. All MESA participants were free of clinical cardiovascular diseases at study entry. For the primary analyses, participants were restricted to adult (< 65 years old) Caucasian, for a total of n = 1436 participants out of 6814. This subcohort was chosen in order to investigate the statistical techniques on a moderately large sample size and for reasons of clinical relevance as individuals under 65 years old are most viable targets for smoking cessation. The outcome of interest was common carotid artery intimal medial thickness (CCA IMT) measured by ultrasonography; CCA IMT has been used in many studies to assess factors contributing to levels of sub-clinical atherosclerosis. The treatment of interest was “ever smoking”, where, for ever smoking, a person must have reported smoking at least 100 cigarettes in his/her lifetime. The covariates we considered were age, sex, body mass index, physical activity, cholesterol (total, HDL, triglycerides), levels of the inflammatory markers Interleukin 6 (IL6) and C-reactive protein (CRP), diabetes, use of antidiabetic drugs, use of lipid lowering medications, level of hemostatic marker, alcohol consumption, education and income. These covariates were identified by prior papers in the literature as either possible predictors of CCA IMT or candidate confounding covariates for the relationship between smoking and CCA IMT [12–20]. We omitted blood pressure (systolic, diastolic) and use of antihypertensive drugs from the list of candidate confounders since it can be argued that they are on the causal pathway between smoking and CCA IMT, and therefore should not be adjusted for [13, 14, 5]. We dropped all participants of the subcohort who had any missing information on the selected covariates, for a total of 58 participants removed out of 1436 (4%). Of the remaining 1378 participants, 774 (56.2%) were ever smokers. Individual characteristics are presented for ever smoker and never smoker separately in Table 1. Three covariates (inflammatory marker IL6, alcohol consumption, education) significantly differed by smoking status at a 5% level of significance.
Table 1.
Participant characteristics for adult Caucasian ever smokers (n = 774) and never smokers (n = 604)
| Ever smoker | Never smoker | P-value* | |
|---|---|---|---|
| CCA IMT (μm) | 99.30 (47.27) | 90.42 (44.59) | <0.01 |
| Age (year) | 54.86 (5.56) | 54.39 (5.65) | 0.12 |
| Male | 373 (48.19) | 275 (45.53) | 0.35 |
| Body mass index (kg/m2) | 28.01 (5.48) | 28.05 (5.55) | 0.89 |
| Physical activity (MET-hours/week) | 2440.0 (2624.9) | 2697.3 (2882.1) | 0.09 |
| Total cholesterol (mg/dl) | 196.01 (36.42) | 198.79 (36.62) | 0.16 |
| HDL cholesterol (mg/dl) | 52.20 (16.27) | 51.92 (14.98) | 0.74 |
| Triglycerides (10 mg/dl) | 135.74 (91.42) | 135.69 (118.54) | 0.99 |
| Inflammatory marker IL6 (pg/ml) | 1.40 (1.25) | 1.23 (1.13) | <0.01 |
| Inflammatory marker CRP (mg/l) | 3.25 (4.39) | 3.42 (6.10) | 0.57 |
| Diabetes | 38 (4.91) | 25 (4.14) | 0.58 |
| Use of anti-diabetic drugs | 27 (3.49) | 19 (3.15) | 0.84 |
| Use of lipid lowering medications | 115 (14.86) | 84 (13.91) | 0.67 |
| Hemostatic marker fibrinogen | 323.38 (68.08) | 325.60 (66.85) | 0.54 |
| Alcohol consumption (drinks/week) | 7.21 (10.81) | 3.83 (7.87) | <0.01 |
| Education | <0.01 | ||
| Low | 26 (3.36) | 11 (1.82) | |
| High-school | 375 (48.45) | 198 (32.78) | |
| College | 172 (22.22) | 166 (27.48) | |
| Graduate | 201 (25.97) | 229 (37.91) | |
| Income ($) | 0.15 | ||
| < 25K | 82 (10.59) | 51 (8.44) | |
| 25 – 50K | 179 (23.13) | 139 (23.01) | |
| 50 – 100K | 296 (38.24) | 214 (35.43) | |
| > 100K | 217 (28.04) | 200 (33.11) |
Continuous covariates: mean presented with standard deviation in parentheses; Binary or polytomous covariates: total (n) presented with percentage (%) in parentheses.
P-values obtained from t-tests for continuous covariates and from chi-squared tests for binary or polytomous covariates.
Previous epidemiological studies have shown a difference of the order of 20 μm and 100 μm between smokers and non-smokers [15–19]. These studies have occurred among diverse populations including Caucasian [15–17], Chinese [18], and HIV infected [19] populations, with the largest differences being seen in the cohorts with the highest baseline age [15, 16] as opposed to younger cohorts [17, 19]. However, inference about the size of CCA IMT between cohorts remains tricky in the absence of calibration as reader effects on estimates of CCA IMT can be larger than the observed size of the smoking effect [20].
2.2. The Bayesian Adjustment for Confounding algorithm and its implementation from an outcome regression approach
We first introduce the BAC algorithm for both continuous outcome and treatment covariates, as in Wang et al. [4]. Then, relying on the novel perspective on BAC studied in Lefebvre et al. [5], we describe how BAC can be easily extended when the treatment covariate is binary. Finally, we describe our specific implementation of the algorithm to estimate the BAC effect of ever smoking on CCA IMT. Since the difference between BAC and a standard implementation of model averaging only comes from setting a hyperparameter in the prior distribution of the covariate inclusion indicators in the outcome and treatment models to different values, we thereby also present our implementation of model averaging for the MESA data.
Let Y be the continuous outcome variable, X be the continuous treatment variable, and U = {U1, …, UM} be the set of available potential confounding covariates. The outcome and treatment models are normal main effect models, which we assume are correctly specified. Specifically, the outcome model is a linear regression of Y as a function of X and U, while the treatment model is a linear regression of X as function of U. Let the inclusion vector αY be an unknown vector of size M with component value if covariate Um is (is not) in the outcome model. Similarly, αX is an unknown inclusion vector for the U covariates in the treatment model. Let y = (y1, …, yn), x = (x1, …, xn) and um = (u1,m, …, un,m) (m = 1, …, M) be respectively the outcome, treatment, and covariate data. The outcome and treatment model specifications yield the following likelihoods
| (1) |
and
| (2) |
where are unknown regression parameters and i indexes the sampled units. The conditioning on the covariates U is implicit in the LHS of Equations (1) and (2). Strictly speaking, αY only refers to the inclusion of the U covariates in the outcome model. However, since every outcome model includes an intercept and the treatment covariate X, there exists a one-to-one relationship between the outcome model and αY. In the sequel, we therefore refer to the outcome model and αY interchangeably (and similarly for the treatment model). In any outcome model αY, β refers to the effect of the treatment X whether or not this effect can be interpreted causally. For the purpose of inference, the goal is to target the αY models for which β can indeed be interpreted as the true (causal) effect of X on Y.
The key to BAC is the specification of the prior distribution P(αY, αX) such that, conditional on a predictor’s inclusion in the treatment model, the same predictor has a higher probability to be included in the outcome model. The prior P(αY, αX) is defined as
| (3) |
where
| (4) |
for ω ∈ [1, ∞]. The two endpoint values of ω are of particular interest. When ω = 1 the outcome and treatment model indicators ( ) are a priori independent and BAC gives marginally 0.5 probability for each covariate Um (m = 1, …, M) to appear in the outcome and treatment models. The strongest dependency between the outcome and treatment models is obtained when ω = ∞. In this case, forces covariate Um to be included in the outcome model if it is included in the treatment model. As confounding covariates are often conceptualized as common causes of both treatment and outcome (other than through treatment) [21], this prior intuitively favors the inclusion of confounding covariates in the outcome model. Finally, the priors P(θY |αY) and P (θX|αX) are standard normal gamma conjugate priors with hyperparameters selected as in Raftery et al. [22] (see Wang et al. [4] for details).
Recall that our interest lies in the inference for the treatment effect β. Wang et al. [4] perform inference on β through an MCMC algorithm that targets the joint posterior distribution of (β, αY, αX). Lefebvre et al. [5] take a different route which first requires writing the posterior distribution of β as
| (5) |
Then, using assumptions made in BAC [4, 24], P(β|y, x) is simplified to
| (6) |
| (7) |
where P(β|αY, y, x) is simply the posterior distribution of β conditional on outcome model αY. Examining (7), we thus realize that the difference between model averaging and BAC arise through the posterior distribution P(αY |y, x). Put differently, the effect of the BAC hyperparameter ω is solely expressed through the marginal posterior probabilities of the outcome models. BAC with ω = 1 is such that the corresponding probabilities P(αY |y, x) are the same than those that would be obtained with a model averaging algorithm on the outcome model with a uniform prior on αY, which, recall, completely ignores the specification of a treatment model. When ω > 1, these two sets of marginal posterior probabilities of the outcome models generally differ.
Given the convenient representation of the posterior distribution of β in (6) and (7), Lefebvre et al. [5] analytically study the effect of the BAC prior (3) on the posterior distributions of (αY, αX) and αY. One advantage of targeting P(αY, αX|y, x), which we exploit in this work, is that an MCMC algorithm that samples from this distribution can be easily implemented using the following approximation
| (8) |
where BICY (BICX) is the BIC value of the outcome (treatment) model. Approximation (8) is obtained by expressing the joint integrated likelihood P(y, x|αY, αX) as the product of the integrated likelihoods P(y|x, αY) and P(x|αX) (see Lefebvre et al. [5] for full details). The integrated likelihoods are then approximated with the well-known BIC approximation, approximation which bypasses the need to explicitly define the prior distribution of the models’ parameters [23]. From this point, implementing BAC with a binary treatment covariate is straightforward. This can be done by replacing likelihood (2) by
where , and the consequence is that we now compute the BIC value of a logistic model rather than a normal model in (8).
We now present our specific implementation of BAC for the MESA data based on the 16 potential confounding covariates presented in Section 2.1, with the alcohol consumption covariate parametrized as (log(drinks/week+1)). First, our implementation easily permits the consideration of factor covariates if one is willing to consider models that contain either all or none of the corresponding dummy variables. We used single indicator variables to indicate the inclusion of all dummies associated to the education and income covariates in the outcome and treatment models. Therefore, αY and αX are vectors of length 16 (instead of 20). The BIC values appearing in (8) are however calculated on the basis that these factor covariates are transformed into an appropriate number of dummies in the models.
As mentioned in Section 1, we used an approximate Bayesian perspective which facilitated the implementation. To simplify the notation introduced earlier, let outcome model Mk,y refers to configuration k of αY where k = 1, …, K and K = 216. The BAC estimate of the effect of ever smoking on CCA IMT, β̂BAC, was taken to be the weighted average of all K model-specific estimates:
| (9) |
with β̂k being the maximum likelihood estimate of β under model Mk,y and P̂(Mk,y|y, x) the proportion of times model Mk,y was visited over the MCMC iterations. The corresponding estimated variance was computed as
| (10) |
where V̂ (β̂k) is the estimated variance of β̂k. Expressions (9) and (10) are analogs to the model averaged posterior mean and variance, respectively (see Hoeting et al. [1]). We remark that V̂ (β̂BAC) takes into account both the within and between-model variability of the estimations.
The BAC effect estimate (9) was obtained for the most conservative ω value, that is ω = ∞. This choice is well justified since ω = ∞ targets unbiased causal treatment effect estimation, although this value may not translate into smallest mean square error for the corresponding estimator [5]. In general, the choice of ω remains a challenging aspect of BAC [24, 5 ]. A model averaged estimate of the effect of ever smoking on CCA IMT was also obtained using expression (9) since BAC with ω = 1 amounts to model averaging. The BAC and model averaged estimates were computed using the R programming language along approximation (8) for sampling from the posterior distribution of (αY, αX) when ω = ∞ and ω = 1. The R functions glm and extract AIC were used to obtain the treatment effect estimates and the BIC values. For both BAC and model averaging, we used three MCMC chains of 50 000 post burn-in iterations for a total of 150 000 draws from P(αY, αX|y, x). Note that for these MESA data, there are 22×16 = 4 294 967 296 possible combinations of joint outcome and treatment models.
2.3. Implementing BAC from treatment model approaches
We now describe our implementation of BAC within treatment model approaches, more precisely through inverse-probability-weighting (IPW) and doubly-robust (DR) estimations.
The causal effect of ever smoking on CCA IMT was estimated by IPW under different BAC and model averaged strategies. Using a specified treatment model, recall that IPW requires first computing the propensity of the treatment received given covariates for every individual. Then the outcomes under the two levels of treatment are compared while weighting by the inverse of the propensities calculated in the first step. Specifically, we used the following stabilized IPW estimator [26] to estimate the treatment effect
| (11) |
where êi = P̂(Xi = 1|Ui) is the estimated propensity score value for the ith individual. As for the outcome regression approach, IPW requires including all necessary confounding covariates in the (treatment) model in order to achieve unbiased estimation (e.g., [27]).
We investigated five IPW strategies which differed in the way the propensity score values êi, i = 1, …, n, were computed:
include all the available covariates in the treatment model to calculate the propensity score values;
use the treatment models αX sampled by model averaging to calculate weighted averaged propensity score values, where the weights are the posterior probabilities of the treatment models;
same as IPW Strategy 2 but using the treatment models sampled by BAC;
use the outcome models αY sampled by model averaging to calculate weighted averaged propensity score values, where the weights are the posterior probabilities of the outcome models. In other words, propensity score models are fitted (and subsequently averaged) by including covariates indicated by the vectors αY obtained through model averaging;
same as IPW Strategy 4 but using the outcome models sampled by BAC.
IPW Strategy 2 is based on targeting the potential confounding covariates that are the most strongly associated with the treatment (irrespectively of their association with the outcome), thus we anticipate that this strategy exhibits the same difficulties than model averaging on the outcome model for causal effect estimation. IPW Strategies 4 and 5 are based on the inclusion of risk factors for the outcome in the propensity score models, which is an increasingly accepted practice when constructing such models. Note however that IPW Strategy 5 is hypothesized to be a better approach since it attemps to include both confounders and risk factors for the outcome in the propensity score, practice that can be considered as the current gold-standard when building propensity score models [7, 8].
The ever smoking effect on CCA IMT was also estimated using a DR approach under five different strategies. The DR estimator considered was
where m̂xi = Ê[Yi|X = x, Ui], x = 0, 1. This estimator is said to have the double-robustness property in that Δ̂DR remains consistent if either i) the propensity e is correctly specified but the outcome model mx (x = 0, 1) is not or ii) mx (x = 0, 1) is correctly specified but e is not [26].
Similarly to the IPW case, the DR strategies investigated differed in the way the treatment and outcome models were used to calculate the propensity score êi and predicted outcome m̂xi values, x = 0, 1 and i = 1, …, n:
include all the available covariates in the treatment and outcome models to calculate the propensity score and the predicted outcome values;
use the treatment models αX and the outcome models αY sampled by model averaging to respectively calculate weighted averaged propensity score and predicted outcome values, where the weights are the probabilities given to the models αX and αY a posteriori;
same as DR Strategy 2 but using the treatment and outcome models sampled by BAC;
use the outcome models αY sampled by model averaging to calculate both weighted averaged propensity score and predicted outcome values, where the weights are the posterior probabilities of the outcome models;
same as DR Strategy 4 but using the outcome models sampled by BAC.
The DR Strategies 2–5 are analogous to the DR model averaged strategies investigated in Cefalu et al. [10], but differ in the following aspects. First, in DR Strategies 2–5, the different treatment and outcome models are used to provide individual average propensity score and predicted outcomes. In Cefalu et al. [10], the authors instead investigate the process of averaging model-specific treatment effect estimates based on models’ probabilities. Moreover, while Cefalu et al. [10] explore DR model averaged strategies with different priors on the space of models, they did not implement a DR model averaged strategy using the BAC prior (3), although this is identified as an obvious alternative in their conclusion.
We implemented the IPW and DR Strategies 2–5 on the MESA data using the treatment and outcome models that were initially sampled from P(αY, αX|y, x) (with ω = ∞ and ω = 1) and subsequently used to compute the BAC and model averaged estimates based on (9). Let αY,O and αX,O refer to these outcome and treatment models for given value ω. The standard errors were computed by bootstrap using 1000 bootstrap samples from the original data. More precisely, we did not sample 150 000 new (αY, αX) (with ω = ∞ and ω = 1) to be used in Strategies 2–5 for each bootstrap sample although we did reestimate the parameters of the αY,O and αX,O models for each bootstrap sample (similarly to IPW/DR Strategy 1 where we refitted the full outcome and treatment models for each bootstrap sample).
3. MESA results
3.1. Results from the outcome regression approach
We report the results under the conventional outcome model (OM) regression approach. The crude (unadjusted) effect of ever smoking on CCA IMT was 88.78 μm (standard error (se): 25.04; 95% confidence interval (CI): (39.66, 137.89)). The outcome model adjusted for all 16 covariates (the full model) yielded a barely significant ever smoking effect of 48.61 μm (se: 24.48; 95% CI: (0.62, 96.60); p-value: 0.047). This estimate corresponds to the traditional regression estimate using the full set of clinically relevant covariates, and thus forms the basis of comparison for the more complex approaches presented herein. The model averaged (i.e. BAC with ω = 1) estimate of the ever smoking effect was 64.82 μm with a standard error of 25.75. The BAC (with ω = ∞) estimate of the ever smoking effect was 49.66 μm with a standard error of 24.45. We next investigated the model averaging and BAC results.
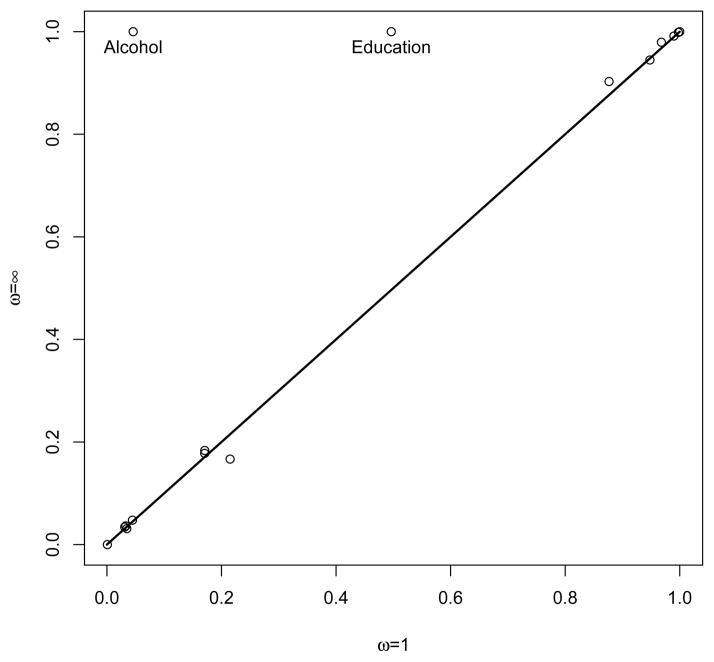
The posterior probabilities of inclusion of the covariates in the outcome model were close for both model averaging and BAC (see Figure 1), except for the education and alcohol consumption covariates that were given greater marginal posterior probability of inclusion under BAC. Two outcome models were given higher posterior probabilities under model averaging. The most probable model (posterior probability (pp) equal to 18.4%) included age, sex, total cholesterol, HDL cholesterol, use of lipid lowering medications and inflammatory marker IL6 as covariates. The second most probable outcome model under model averaging (pp = 18.2%) included the same covariates as the most probable model, but additionally included the education covariate. Three outcome models were given higher posterior probabilities under BAC. Unsurprisingly, the most probable outcome model (pp = 40.9%) selected by BAC included the same covariates as the most probable model under model averaging, but additionally included education and alcohol consumption. The second and third most probable outcome models under BAC included the same covariates than the best BAC model, but respectively additionally included diabetes and use of anti-diabetic drugs (pp = 11.4% and pp = 10.4%, respectively).
Figure 1.
Posterior probability of inclusion of each covariate in the outcome model for both model averaging (ω = 1) and BAC (ω = ∞).
We also examined the treatment models αX sampled by model averaging and BAC. Most covariates were observed to have small marginal posterior probability of inclusion in the treatment model under both model averaging and BAC, for the exception of education and alcohol consumption which both had an estimated marginal posterior probability of 1. Both model averaging and BAC gave high posterior probability to the same treatment models. The most probable model according to these two techniques was the one only including the education and alcohol consumption covariates (pp = 36.3% for model averaging and 48.6% for BAC). The second most probable treatment model was the one also including the inflammatory marker IL6 covariate (pp = 19.7% for model averaging and 25.4% for BAC).
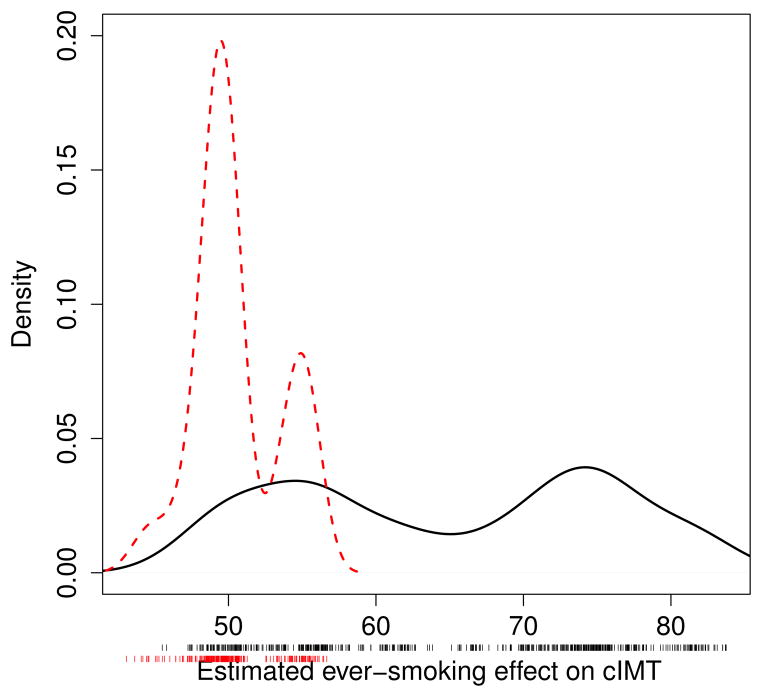
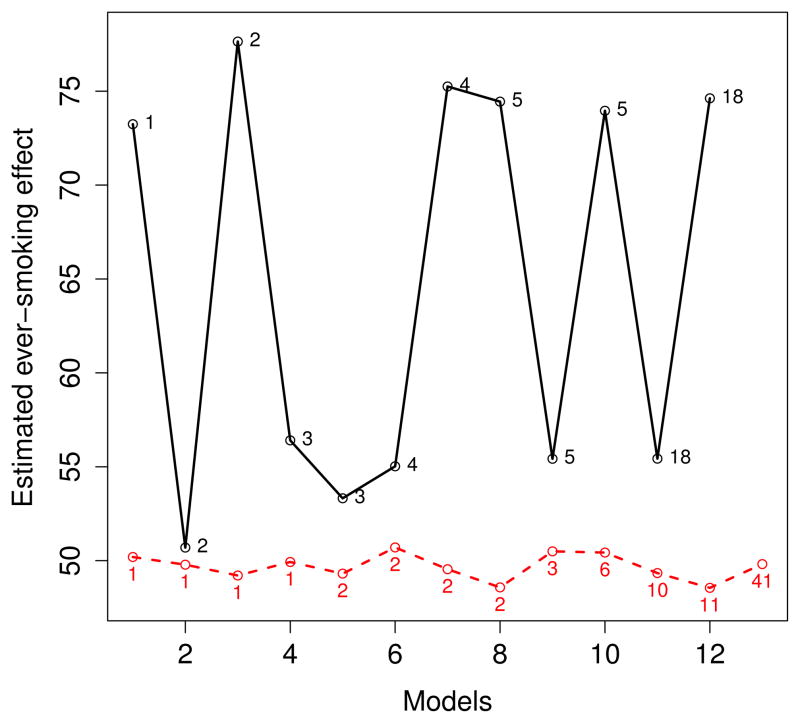
We next looked at the range of estimated ever smoking effects (that is, the maximum likelihood estimates of β) for the outcome models obtained through model averaging and BAC. Over 150 000 iterations each, 530 and 243 distinct outcome models were sampled by model averaging and BAC, respectively. Smooth histograms were obtained for the corresponding estimated treatment effects (see Figure 2), irrespectively of the posterior probabilities associated to the models. The curve associated to the BAC estimates is bimodal with one mode around 49 μm and another one around 55 μm for the ever smoking effect on CCA IMT. A closer examination of the covariates included in the outcome models associated to each of these modes indicates that the inflammatory marker IL6 covariate is such that its inclusion/exclusion causes the change in the estimation. More precisely, this covariate is included in almost all outcome models associated to the 49 μm mode while it is excluded from all models associated to the 55 μm mode. Figure 3 shows the estimated ever smoking effects for the most likely outcome models (with posterior probability greater than or equal to 0.01) according to model averaging and BAC. We see from this figure that the estimated effects are very similar across the best models selected by BAC and close to the estimated effect under the fully adjusted outcome model. In fact, Figure 3 shows that the most probable outcome models according to BAC are all associated to the first mode of the curve for the BAC estimates appearing in Figure 2.
Figure 2.
Smooth histograms of estimated ever smoking effect on CCA IMT (in μm) associated to distinct (unique) post burn-in sampled outcome models for model averaging (solid line) and BAC (slashed line).
Figure 3.
Estimated ever smoking effect on CCA IMT (in μm) for the most likely outcome models according to model averaging (solid line) and BAC (slashed line). Numbers in the central part of the graph represent posterior probabilities (pp) in %. Estimated ever smoking effect are presented by model in increasing order of pp (only models with pp > 0.01 are shown).
As seen, the model averaged, BAC and full model estimators exhibited similar standard error for the effect of ever smoking on CCA IMT (respectively 25.75, 24.45 and 24.48 μm). We gave a closer look at the variance of these estimators by evaluating the contribution of the within and between-model variability (first and second terms on the RHS of (10), respectively) to the total variability of the model averaged and BAC estimators. First we observed that the sizes of the best models according to model averaging were smaller than the sizes of the best models according to BAC. The estimated variances of the best models according to model averaging were overall also slightly smaller than the estimated variances of the best models according to BAC. These results are not surprising since 1) recall that when ω = ∞, the BAC prior (3) forces a covariate included in the treatment model to be included in the outcome model, whether or not this covariate is truly associated with the outcome and 2) including strong predictors of the treatment in an adjusted outcome model inflates the variance of the corresponding treatment effect estimator [25]. Over all models, the square root of the estimated within model variability was computed to be 23.70 for model averaging and 24.43 for BAC. BAC’s within model variability is essentially equal to the variability of the full outcome model (24.48). The square root of the estimated between model variability was equal to 10.09 for model averaging and 1.04 for BAC. These results nicely illustrate a potential pitfall, that is inflated variance due to large between-model variability, of model averaging for causal effect estimation (seen when it averages over high posterior probability models yielding dissimilar treatment effects) [3]. Moreover, these results are in accordance with BAC’s objective of small between-model variability, but are somewhat disappointing with respect to the anticipated reduction in within-model variability (as compared to the full outcome model). Indeed, recall that the rationale behind BAC is to obtain unbiased estimation, as in the full model, but with potentially smaller standard error for the effect of the treatment since averaging over models generally smaller than the full one [4].
3.2. Results from the treatment model approaches
Table 2 displays the results under the five IPW strategies presented in subsection 2.3. All strategies, except IPW Strategy 4, gave similar point estimates for the ever smoking effect on CCA IMT. Using averaged propensity score values based on the treatment models sampled by model averaging and BAC (IPW Strategies 2 and 3) produced the largest standard errors. Using propensity score values based on the full treatment model (IPW Strategy 1) and using averaged propensity score values based on the outcome models sampled by BAC (IPW Strategy 5) produced similar results.
Table 2.
Ever smoking effect on CCA IMT from inverse-probability-weighting (IPW) estimation with five strategies for computing the propensity scores
| Strategies | Δ̂ |
|
95% CI* | |
|---|---|---|---|---|
| 1: Full** | 45.50 | 28.60 | (−10.56, 101.55) | |
| 2: MA with αX*** | 49.71 | 31.25 | (−11.54, 110.97) | |
| 3: BAC with αX | 49.97 | 31.28 | (−11.34, 111.29) | |
| 4: MA with αY | 65.30 | 24.02 | (18.22, 112.39) | |
| 5: BAC with αY | 46.16 | 28.75 | (−10.20, 102.53) |
Δ̂: ever smoking effect estimate (μm); : associated standard error;
( );
all covariates used for computing the propensity scores.
For strategies 2–5, the labels refer to the technique (model averaging (MA) or BAC) and model (αX or αY) used for the calculation of the propensity scores.
Table 3 displays the DR results under the five strategies investigated (also as described in Subsection 2.3). The DR results were similar to those obtained with IPW, with a decrease in variance for all strategies but DR Strategy 4.
Table 3.
Ever smoking effect on CCA IMT from doubly-robust (DR) estimation with five strategies for computing the propensity scores and the predicted outcome values
| Strategies | Δ̂ |
|
95% CI* | |
|---|---|---|---|---|
| 1: Full** | 49.83 | 28.36 | (−5.76, 105.42) | |
| 2: MA with (αX, αY)*** | 47.02 | 29.05 | (−9.92, 103.95) | |
| 3: BAC with (αX, αY) | 47.07 | 29.02 | (−9.81, 103.95) | |
| 4: MA with (αY, αY) | 60.95 | 24.27 | (13.37, 108.52) | |
| 5: BAC with (αY, αY) | 50.03 | 28.37 | (−5.58, 105.64) |
Δ̂: ever smoking effect estimate (μm); : associated standard error;
( );
all covariates used for computing both the propensity scores and the predicted outcome values;
the first argument of the parentheses indicates the model used for the calculation of the propensity scores and the second argument indicates the model used for the calculation of the predicted outcome values.
3.3. Additional analyses
In order to examine the sensitivity of all techniques investigated to diminishing sample sizes, we further estimated the ever smoking effect on CCA IMT for the three other ethnic subcohorts: the adult African American (n = 963), Hispanic (n = 842) and Chinese (n = 436). The results for the Chinese subcohort are presented in Table 4 (other results not shown). Two remarks can be made based on these additional analyses. For the three smaller subcohorts, there was less consistency in the pattern of the full, model averaged and BAC point estimates across strategies (OM, IPW and DR), compared to the Caucasian subcohort. However, the results indicated that model selection was generally beneficial to reduce the variability of estimates, especially for the estimation approaches that rely on the treatment model (IPW, DR). This was most notable for the Chinese subcohort where the use of the full model within IPW and DR yielded a standard error approximately twice the size of the other strategies.
Table 4.
Ever smoking effect on CCA IMT for the adult Chinese (n = 436) subcohort based on an outcome modeling (OM), an inverse-probability-weighting (IPW) and a doubly-robust (DR) approach (with different strategies)
| Strategies | Estimate | Standard error | 95% CI |
|---|---|---|---|
| OM, Crude | 76.40 | 38.41 | (0.90, 151.89) |
| OM, Full | −13.66 | 40.69 | (−93.40, 66.08) |
| OM, MA | 7.43 | 42.59 | (−76.04, 90.91) |
| OM, BAC | 2.60 | 40.10 | (−76.00, 81.20) |
|
| |||
| IPW, 1: Full | −70.06 | 71.86 | (−210.91, 70.79) |
| IPW, 2: MA with αX | −5.59 | 39.27 | (−82.56, 71.39) |
| IPW, 3: BAC with αX | −2.68 | 38.85 | (−78.81, 73.46) |
| IPW, 4: MA with αY | 4.40 | 36.63 | (−67.39, 76.20) |
| IPW, 5: BAC with αY | −10.94 | 39.51 | (−88.37, 66.50) |
|
| |||
| DR, 1: Full | −36.24 | 81.82 | (−196.60, 124.12) |
| DR, 2: MA with (αX, αY) | −24.22 | 39.10 | (−100.86, 52.43) |
| DR, 3: BAC with (αX, αY) | −23.59 | 39.37 | (−100.75, 53.57) |
| DR, 4: MA with (αY, αY) | −10.09 | 37.89 | (−84.36, 64.17) |
| DR, 5: BAC with (αY, αY) | −17.45 | 39.10 | (−94.09, 59.20) |
In order to provide additional insight on the results, we analyzed the IPW weights given to each individual in the Chinese subcohort. In relation to IPW estimator (11), we define the weight of a treated individual as the inverse of its propensity score; the weight of an untreated individual is the inverse of one minus its propensity score. We compared the full treatment model (IPW Strategy 1) weights to those obtained from IPW Strategy 5 which, recall, consists in using in (11) a weighted average propensity score based on the outcome models sampled by BAC with ω = ∞. We focused on these two strategies since they were observed to provide very similar results for all subcohorts except the Chinese. For IPW Strategy 1, the weights ranged from 1.01 to 67.61 while the weights ranged from 1.04 to 27.67 for IPW Strategy 5. The IPW Strategy 1 weights were on average larger and more variable than the IPW Strategy 5 weights ((mean=2.08, sd=4.97) vs (mean=1.97, sd=3.32), resp.). Moreover, the two outlier weights in IPW Strategy 1 (64.63, 67.61) were more than half reduced in IPW Strategy 5 (26.82, 27.67). These results suggest that IPW Strategy 5 could be seen here as a principled way to control the magnitude and variability of IPW weights, as opposed, for example, to ad-hoc weight truncation [28].
4. Simulation study
In order to better understand the differences between estimators, we ran three simulated experiments on which the performance of all inference strategies considered was assessed.
Scenario 1
Our first scenario shares some similarities with the illustrative example in Wang et al. [4]. The causal links between covariates are as follows
where U1, U2, U3, U4, εY are independent N (0, 1) random variables. The set of available potential confounding covariates is U = {U1, U2, U3, U4}. In this scenario, the true outcome model is the full model although only U1 to U3 need to be included in the outcome model to unconfoundedly estimate the true effect of X on Y (here equal to 0.1).
Scenario 2
For the second scenario, the data generating process satisfies the following relationships
with U1, U2, U4, ε3, ε5, εY ~ N (0, 1) all independent. The set of available covariates is U = {U1, U2, …, U5}. The true effect of X on Y is 0.1.
Scenario 3
The third scenario is slightly more complicated and features an indirect effect of X on Y
where U4, ε1, ε2, ε3, ε5, ε6, εY ~ N (0, 1) all independent. The set of available covariates is U = {U1, U2, …, U5, U7, U8}, where U7 and U8 are independent N (0, 1). Covariate U6 is excluded from U since it is in the causal pathway from X to Y. The true effect of X on Y (both direct and indirect) is 0.1.
For each scenario, we estimated the bias, the standard deviation, the root-mean-squared error (RMSE) and the percentage coverage (nominal coverage rate of 95%) of all estimators investigated. This was done using 1000 datasets of various sizes generated from each of the three data mechanisms considered (for Scenarios 1 and 2 the sample sizes were n = 200, 500, 1000, 2000 and for Scenario 3 the sample sizes were n = 200, 500). The calculation of the coverage rates was done as follows. For each estimator, we computed the number of times (out of 1000) where the absolute difference between the treatment effect estimate and the true treatment effect (0.1 in all three scenarios) was no more than 1.96 times the standard error, where the standard error was obtained differently according to the estimators. For the full outcome model estimator, the standard error was the one directly obtained from the regression output. For the model averaged and BAC estimators from an outcome regression approach, the standard error was computed using expression (10). For each IPW and DR estimators, the standard error was taken to be the standard deviation of 1000 bootstrap estimates based on a single generated dataset (as described in Section 2.3).
The results are presented in Tables 5–7. We first discuss the results from an OM perspective (first part of the tables). In all three scenarios, the model averaged estimator based on (9) is biased, with largest amounts of bias showing when n = 200. The RMSE of the MA estimator can however be smaller than the RMSE of the full model or BAC estimator, especially if the sample size is small. The results for the full model and BAC estimators are very comparable in all scenarios and sample sizes (in Scenarios 1 and 2, BAC attributes very large posterior weight to the full model at all sample sizes). We secondly focus on the IPW and DR results (second and third parts of the tables). Overall, only few differences are observed in the results between IPW Strategies 2 and 3, which use the treatment models αX sampled by either model averaging or BAC to calculate weighted averaged propensity score values. IPW Strategy 5, which uses outcome models sampled by BAC, but implicitly includes treatment models in its definition, is often showing the least amount of bias after the full model strategy (IPW Strategy 1). The IPW estimators also sometimes show some undercoverage. In general, the IPW and DR estimators based on model averaging are those observed to be the most biased and least variable, although no significant bias is observed for DR Strategy 2 (recall that this strategy uses the outcome and treatment models sampled by model averaging to respectively calculate weighted averaged propensity score and predicted outcome values). In more complex Scenario 3, we see a clear evidence for the usefulness of BAC or model averaging strategies for reducing the variability and RMSE of the IPW/DR estimators when the sample size is small. In this scenario, the largest reduction in RMSE is observed between DR Strategy 1 (full model) and DR Strategy 3 (which uses the outcome models αY sampled by model averaging to compute both average propensity scores and predicted outcomes) when n = 200, where DR Strategy 3 has 37% less RMSE than DR Strategy 1.
Table 5.
Scenario 1: Estimated Bias (B), standard error (SE), root-mean-square error (RMSE) and percentage (%) coverage (COV) of causal effect estimators based on an outcome modeling (OM), an inverse-probability-weighting (IPW) and a doubly-robust (DR) approach (with different strategies)
| n = 2000 | n = 1000 | n = 500 | n = 200 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||
| Strategies | B | SE | RMSE | COV | B | SE | RMSE | COV | B | SE | RMSE | COV | B | SE | RMSE | COV |
| OM, Full | .001 | .052 | .052 | 94.6 | −.001 | .070 | .070 | 95.1 | .003 | .099 | .099 | 94.7 | −.005 | .160 | .160 | 94.7 |
| OM, MA | .004 | .054 | .054 | 94.0 | .015 | .075 | .076 | 93.7 | .032 | .102 | .106 | 93.3 | .032 | .157 | .160 | 95.1 |
| OM, BAC | .001 | .052 | .052 | 94.6 | −.001 | .070 | .070 | 95.1 | .003 | .099 | .099 | 94.7 | −.003 | .160 | .160 | 94.8 |
|
| ||||||||||||||||
| IPW, 1: Full | .001 | .064 | .064 | 93.5 | −.000 | .093 | .093 | 94.7 | .010 | .125 | .125 | 94.3 | .005 | .215 | .215 | 94.1 |
| IPW, 2: MA with αX | .027 | .082 | .087 | 93.2 | .067 | .118 | .135 | 89.5 | .109 | .154 | .188 | 90.9 | .134 | .250 | .284 | 92.6 |
| IPW, 3: BAC with αX | .027 | .083 | .087 | 93.6 | .067 | .117 | .135 | 89.4 | .109 | .154 | .189 | 90.3 | .138 | .249 | .285 | 92.5 |
| IPW, 4: MA with αY | .014 | .068 | .070 | 88.1 | .035 | .093 | .100 | 88.1 | .059 | .114 | .128 | 89.4 | .060 | .174 | .184 | 93.1 |
| IPW, 5: BAC with αY | .001 | .064 | .064 | 93.5 | −.000 | .093 | .093 | 94.7 | .010 | .125 | .125 | 94.2 | .012 | .213 | .213 | 93.9 |
|
| ||||||||||||||||
| DR, 1: Full | .001 | .053 | .053 | 93.8 | −.001 | .074 | .074 | 94.8 | .004 | .105 | .105 | 94.3 | −.006 | .168 | .168 | 95.1 |
| DR, 2: MA with (αX, αY) | .001 | .053 | .053 | 93.8 | −.001 | .074 | .074 | 95.1 | .004 | .105 | .105 | 94.1 | −.005 | .166 | .166 | 95.0 |
| DR, 3: BAC with (αX, αY) | .001 | .053 | .053 | 93.8 | −.001 | .074 | .074 | 95.1 | .004 | .104 | .104 | 93.9 | −.006 | .166 | .166 | 95.2 |
| DR, 4: MA with (αY, αY) | .003 | .054 | .054 | 93.4 | .008 | .076 | .076 | 93.2 | .024 | .104 | .107 | 92.5 | .023 | .160 | .161 | 94.5 |
| DR, 5: BAC with (αY, αY) | .001 | .053 | .053 | 93.8 | −.001 | .074 | .074 | 94.8 | .004 | .105 | .105 | 94.3 | −.005 | .168 | .168 | 95.1 |
Table 7.
Scenario 3: Estimated Bias (B), standard error (SE), root-mean-square error (RMSE) and percentage (%) coverage (COV) of causal effect estimators based on an outcome modeling (OM), an inverse-probability-weighting (IPW) and a doubly-robust (DR) approach (with different strategies)
| n = 500 | n = 200 | |||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Strategies | B | SE | RMSE | COV | B | SE | RMSE | COV |
| OM, Full | .000 | .121 | .121 | 93.9 | .016 | .187 | .188 | 95.8 |
| OM, MA | .037 | .121 | .126 | 93.0 | .085 | .188 | .206 | 92.5 |
| OM, BAC | .000 | .121 | .121 | 93.5 | .020 | .186 | .188 | 95.2 |
|
| ||||||||
| IPW, 1: Full | .025 | .212 | .214 | 89.5 | .062 | .280 | .287 | 91.9 |
| IPW, 2: MA with αX | .025 | .209 | .211 | 88.6 | .077 | .261 | .272 | 88.7 |
| IPW, 3: BAC with αX | .024 | .209 | .210 | 89.2 | .085 | .250 | .264 | 88.2 |
| IPW, 4: MA with αY | .095 | .138 | .168 | 79.3 | .165 | .186 | .249 | 76.5 |
| IPW, 5: BAC with αY | .025 | .209 | .211 | 88.9 | .076 | .254 | .265 | 88.7 |
|
| ||||||||
| DR, 1: Full | .003 | .232 | .232 | 94.3 | .001 | .319 | .319 | 97.6 |
| DR, 2: MA with (αX, αY) | .000 | .225 | .225 | 93.7 | .013 | .285 | .285 | 94.1 |
| DR, 3: BAC with (αX, αY) | −.003 | .229 | .229 | 93.9 | .005 | .266 | .266 | 95.0 |
| DR, 4: MA with (αY, αY) | .013 | .131 | .132 | 92.1 | .051 | .195 | .201 | 88.8 |
| DR, 5: BAC with (αY, αY) | −.002 | .229 | .229 | 93.9 | .003 | .271 | .271 | 95.1 |
5. Discussion
The purpose of this paper was to extend the application of the Bayesian Adjustment for Confounding (BAC) algorithm to binary treatment covariates and thereby continue the investigations on BAC. We showed how a simple approximate Bayesian approach, which makes use of standard regression outputs, can be used to implement BAC in this case. Our illustration was done using data from the Multi-Ethnic Study of Atherosclerosis and the analyses aimed at estimating the ever smoking effect on common carotid artery intimal medial thickness primarily for the Caucasian adult subpopulation. We also investigated the use of BAC from a treatment modeling perspective, that is within both a standard inverse-probability-weighting and a doubly-robust framework. Here, different model averaged and BAC strategies were adopted for constructing the propensity score and predicted outcome values required for using these estimators. We subsequently investigated these strategies in three simulated experiments.
The main findings of this work are the following. First, from the perspective of the conventional outcome model regression approach, we found that model averaging should not be used if one desires to unbiasedly estimate the causal treatment effect, especially when the size of the sample is small. Moreover, we observed that the model averaged treatment effect estimator could possess larger variance than the estimator based on the full outcome model (as seen for the adult Caucasian subcohort and for some sample sizes in Scenarios 1 and 3). Our results thus reinforce the documented inappropriateness of standard model averaging as a way to account for model uncertainty in causal problems. Secondly, and again from the perspective of the conventional outcome model regression approach, we found that BAC behaved similarly to the full outcome model approach, and thus did not yield the anticipated reduction in variability. This result should not be overgeneralized as it was reached, in part, on the basis of a limited set of simulation scenarios of small or moderate complexity. In particular, additional simulations for Scenarios 2 and 3 indicated that around 7% and 4.5% of reduction in root-mean-squared error could be achieved by using the true outcome model instead of the full model, respectively. Third, our results from MESA and the simulation study hinted however for BAC to be advantageous when used along with inverse-probability-weighting and doubly-robust estimation techniques, techniques for which the control of variance is a critical aspect of their implementation (most notably with relatively small sample sizes) [28, 29].
Another interesting result seen from the simulation study was that our standard model averaging strategy in doubly-robust estimation yielded an unbiased (or close to an unbiased) estimator in the finite sample sets-up considered here. Our simulation results did not point out to a BAC or model averaging strategy uniformly superior to the other for all combinations of scenarios and sample sizes, with respect to the variance or the mean-square-error of the doubly-robust estimator. Albeit found to show some amount of bias, the doubly-robust estimation strategy that use the outcome models αY sampled by model averaging to calculate both weighted averaged propensity score and predicted outcome values nonetheless often exhibited markedly smaller variance and mean-square-error than the other strategies. Further work will be required to better understand the impact of different nuances of estimation strategies in this new class of doubly-robust estimators.
Table 6.
Scenario 2: Estimated Bias (B), standard error (SE), root-mean-square error (RMSE) and percentage (%) coverage (COV) of causal effect estimators based on an outcome modeling (OM), an inverse-probability-weighting (IPW) and a doubly-robust (DR) approach (with different strategies)
| n = 2000 | n = 1000 | n = 500 | n = 200 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||
| Strategies | B | SE | RMSE | COV | B | SE | RMSE | COV | B | SE | RMSE | COV | B | SE | RMSE | COV |
| OM, Full | .002 | .049 | .049 | 95.7 | −.002 | .073 | .073 | 95.2 | .000 | .102 | .102 | 94.6 | −.002 | .152 | .152 | 96.6 |
| OM, MA | .010 | .047 | .048 | 95.0 | .013 | .070 | .071 | 94.6 | .017 | .096 | .097 | 94.7 | .018 | .141 | .142 | 96.6 |
|
| ||||||||||||||||
| OM, BAC | .002 | .049 | .049 | 95.7 | −.002 | .073 | .073 | 95.2 | .001 | .102 | .102 | 94.5 | .001 | .151 | .151 | 96.5 |
| IPW, 1: Full | .002 | .087 | .087 | 94.6 | .007 | .115 | .116 | 94.5 | .008 | .174 | .174 | 95.1 | .011 | .267 | .268 | 96.3 |
| IPW, 2: MA with αX | .001 | .109 | .109 | 94.1 | .006 | .142 | .142 | 95.3 | .006 | .207 | .207 | 95.3 | .046 | .301 | .305 | 95.9 |
| IPW, 3: BAC with αX | .001 | .109 | .109 | 94.1 | .006 | .142 | .142 | 95.4 | .003 | .205 | .205 | 95.5 | .104 | .276 | .295 | 93.4 |
| IPW, 4: MA with αY | .035 | .057 | .067 | 86.7 | .044 | .077 | .089 | 89.5 | .054 | .107 | .119 | 90.8 | .059 | .166 | .176 | 94.8 |
| IPW, 5: BAC with αY | .002 | .087 | .087 | 94.6 | .007 | .115 | .116 | 94.5 | .010 | .174 | .174 | 94.9 | .045 | .239 | .244 | 95.2 |
|
| ||||||||||||||||
| DR, 1: Full | .003 | .053 | .053 | 95.3 | .000 | .079 | .079 | 95.4 | .000 | .114 | .114 | 94.4 | .003 | .173 | .173 | 96.8 |
| DR, 2: MA with (αX, αY) | .003 | .053 | .053 | 95.2 | .000 | .079 | .079 | 95.3 | .000 | .114 | .114 | 94.3 | .005 | .167 | .167 | 95.8 |
| DR, 3: BAC with (αX, αY) | .003 | .053 | .053 | 95.3 | .000 | .079 | .079 | 95.4 | .000 | .113 | .113 | 94.3 | .003 | .162 | .162 | 96.0 |
| DR, 4: MA with (αY, αY) | .007 | .048 | .048 | 94.7 | .009 | .070 | .071 | 93.4 | .013 | .098 | .098 | 93.6 | .015 | .144 | .145 | 95.4 |
| DR, 5: BAC with (αY, αY) | .003 | .053 | .053 | 95.3 | .000 | .079 | .079 | 95.4 | .000 | .113 | .113 | 94.5 | .004 | .165 | .165 | 96.1 |
Acknowledgments
The authors thank the other investigators, the staff, and the participants of the MESA study for their valuable contributions. A full list of participating MESA investigators and institutions can be found at http://www.mesa-nhlbi.org. The authors would also thank the Editorial team for useful comments that have substantially improved the article.
References
- 1.Hoeting JA, Madigan D, Raftery AE, Volinsky CT. Bayesian model averaging: a tutorial (with discussion) Statistical Science. 1999;14:382–401. [Google Scholar]
- 2.Raftery AE, Zheng Y. Discussion: Performance of Bayesian model averaging. Journal of the American Statistical Association. 2003;98:931–938. [Google Scholar]
- 3.Crainiceanu CM, Parmigiani G, Dominici F. Adjustment uncertainty in effect estimation. Biometrika. 2008;95(3):635–651. [Google Scholar]
- 4.Wang C, Parmigiani G, Dominici F. Bayesian effect estimation accounting for adjustment uncertainty. Biometrics. 2012;68(3):661–671. doi: 10.1111/j.1541-0420.2011.01731.x. [DOI] [PubMed] [Google Scholar]
- 5.Lefebvre G, Atherton J, Talbot D. The effect of the prior distribution in the Bayesian Adjustment for Confounding algorithm. Computational Statistics and Data Analysis. 2013 doi: 10.1016/j.csda.2013.09.011. [DOI] [Google Scholar]
- 6.Stürmer T, Joshi M, Glynn RJ, Avorn J, Rothman KJ, Schneeweiss S. A review of the application of propensity score methods yielded increasing use, advantages in specific settings, but not substantially different estimates compared with conventional multivariable methods. Journal of Clinical Epidemiology. 2006;59(5):437–447. doi: 10.1016/j.jclinepi.2005.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Patrick AR, Schneeweiss S, Brookhart MA, Glynn RJ, Rothman KJ, Avorn J, Stürmer T. The implications of propensity score variable selection strategies in pharmacoepidemiology: an empirical illustration. Pharmacoepidemiology and Drug Safety. 2011;20(6):551–559. doi: 10.1002/pds.2098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Westreich D, Cole SR, Funk MJ, Brookhart MA, Stürmer T. The role of the c-statistic in variable selection for propensity score models. Pharmacoepidemiology and Drug Safety. 2011;20(3):317–320. doi: 10.1002/pds.2074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vansteelandt S. Discussions. Biometrics. 2012;68(3):675–678. doi: 10.1111/j.1541-0420.2011.01734.x. [DOI] [PubMed] [Google Scholar]
- 10.Cefalu M, Dominici F, Parmigiani G. Harvard University Biostatistics Working Paper Series. Feb, 2013. Model averaged double robust estimation. working Paper 149. [Google Scholar]
- 11.Bild DE, Bluemke DA, Burke GL, Detrano R, Diez Roux AV, Folsom AR, Greenland P, Jacobs DR, Kronmal R, Liu K, Nelson JC, O’Leary D, Saad MF, Shea S, Szklo M, Tracy RP. Multi-ethnic study of atherosclerosis: objectives and design. Am J Epidemiol. 2002;156:871–881. doi: 10.1093/aje/kwf113. [DOI] [PubMed] [Google Scholar]
- 12.Folsom AR, Kronmal RA, Detrano RC, O’Leary DH, Bild DE, Bluemke DA, Budoff MJ, Liu K, Shea S, Szklo M, Tracy RP, Watson KE, Burke GL. Coronary artery calcification compared with carotid intima-media thickness in the prediction of cardiovascular disease incidence: the Multi-Ethnic Study of Atherosclerosis (MESA) Arch Intern Med. 2008;168(12):1333–1339. doi: 10.1001/archinte.168.12.1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bowman TS, Gaziano JM, Buring JE, Sesso HD. A prospective study of cigarette smoking and risk of incident hypertension in women. J Am Coll Cardiol. 2007;50(21):2085–92. doi: 10.1016/j.jacc.2007.08.017. [DOI] [PubMed] [Google Scholar]
- 14.Niskanen L, Laaksonen DE, Nyyssönen K, Punnonen K, Valkonen VP, Fuentes R, Tuomainen TP, Salonen R, Salonen JT. Inflammation, abdominal obesity, and smoking as predictors of hypertension. Hypertension. 2004;44(6):859–65. doi: 10.1161/01.HYP.0000146691.51307.84. [DOI] [PubMed] [Google Scholar]
- 15.Tell GS, Polak JF, Ward BJ, Kittner SJ, Savage PJ, Robbins J. Relation of smoking with carotid artery wall thickness and stenosis in older adults. The Cardiovascular Health Study. The Cardiovascular Health Study (CHS) Collaborative Research Group. Circulation. 1994;90(6):2905–2908. doi: 10.1161/01.cir.90.6.2905. [DOI] [PubMed] [Google Scholar]
- 16.Diez-Roux AV, Nieto FJ, Comstock GW, Howard G, Szklo M. The relationship of active and passive smoking to carotid atherosclerosis 12–14 years later. Prev Med. 1995;24(1):48–55. doi: 10.1006/pmed.1995.1007. [DOI] [PubMed] [Google Scholar]
- 17.Polak JF, Person SD, Wei GS, Godreau A, Jacobs DR, Jr, Harrington A, Sidney S, O’Leary DH. Segment-specific associations of carotid intima-media thickness with cardiovascular risk factors: the Coronary Artery Risk Development in Young Adults (CARDIA) study. Stroke. 2010;41(1):9–15. doi: 10.1161/STROKEAHA.109.566596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Thomas GN, Chook P, Yip TW, Kwong SK, Chan TY, Qiao M, Huang XS, Guo DS, Feng JZ, Chan SW, Leong HC, Celermajer DS, Woo KS. Smoking without exception adversely affects vascular structure and function in apparently healthy Chinese: Implications in global atherosclerosis prevention. Int J Cardiol. 2008;128:172–177. doi: 10.1016/j.ijcard.2007.11.065. [DOI] [PubMed] [Google Scholar]
- 19.Grunfeld C, Delaney JA, Wanke C, Currier JS, Scherzer R, Biggs ML, Tien PC, Shlipak MG, Sidney S, Polak JF, O’leary D, Bacchetti P, Kronmal RA for the study of Fat Redistribution and Metabolic Change in HIV Infection (FRAM) Preclinical atherosclerosis due to HIV infection: carotid intima-medial thickness measurements from the FRAM study. AIDS. 2009;23(14):1841–1849. doi: 10.1097/QAD.0b013e32832d3b85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Delaney JAC, Scherzer R, Polak J, Biggs ML, Kronmal R, Sidney S, Bacchetti P, Grunfeld C. Measurement error due to reader effects in studies using carotid intimal medial thickness (cIMT) quantified by carotid ultrasonography: the Study of Fat Redistribution and Metabolic Change in HIV Infection and the Multi-Ethnic Study of Atherosclerosis. Eur J of Epidemiol. 2010;25(6):385–92. doi: 10.1007/s10654-010-9442-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.VanderWeele TJ, Shpitser I. A new criterion for confounder selection. Biometrics. 2011;67(4):1406–1413. doi: 10.1111/j.1541-0420.2011.01619.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Raftery AE, Madigan D, Hoeting JA. Bayesian model averaging for linear regression models. Journal of the American Statistical Association. 1997;92:179–191. [Google Scholar]
- 23.Clyde M. In Subjective and Objective Bayesian Statistics. 2. S. James Press: Wiley-Interscience; 2003. Model averaging. [Google Scholar]
- 24.Wang C, Parmigiani G, Dominici F. Rejoinder: Bayesian effect estimation accounting for adjustment uncertainty. Biometrics. 2012;68(3):680–686. doi: 10.1111/j.1541-0420.2011.01731.x. [DOI] [PubMed] [Google Scholar]
- 25.O’Brien RM. A caution regarding rules of thumb for variance inflation factors. Quality & Quantity. 2007;41:673–690. [Google Scholar]
- 26.Lunceford JK, Davidian M. Stratification and weighting via the propensity score in estimation of causal treatment effects: a comparative study. Statistics in Medicine. 2004;23(19):2937–2960. doi: 10.1002/sim.1903. [DOI] [PubMed] [Google Scholar]
- 27.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 28.Cole SR, Hernán MA. Constructing inverse probability weights for marginal structural models. American Journal of Epidemiology. 2008;168(6):656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lefebvre G, Gustafson P. Impact of outcome model misspecification on regression and doubly-robust inverse-probability-weighting to estimate causal effects. The International Journal of Biostatistics. 2010;6(2):Article 15. doi: 10.2202/1557-4679.1207. [DOI] [PubMed] [Google Scholar]