Beyond slots and resources: Grounding cognitive concepts in neural dynamics

Abstract

Research over the past decade has suggested that the ability to hold information in visual working memory (VWM) may be limited to as few as 3-4 items. However, the precise nature and source of these capacity limits remains hotly debated. Most commonly, capacity limits have been inferred from studies of visual change detection, in which performance declines systematically as a function of the number of items participants must remember. According to one view, such declines indicate that a limited number of fixed-resolution representations are held in independent memory ‘slots’. Another view suggests that capacity limits are more apparent than real, emerging as limited memory resources are distributed across more to-be-remembered items. Here we argue that, although both perspectives have merit and have generated and explained an impressive amount of empirical data, their central focus on the representations—rather than processes—underlying VWM may ultimately limit continuing progress in this area. As an alternative, we describe a neurally-grounded, process-based approach to VWM: the dynamic field theory. Simulations demonstrate that this model can account for key aspects of behavioral performance in change detection, in addition to generating novel behavioral predictions that have been confirmed experimentally. Furthermore, we describe extensions of the model to recall tasks, the integration of visual features, cognitive development, individual differences, and functional imaging studies of VWM. We conclude by discussing the importance of grounding psychological concepts in neural dynamics as a first step toward understanding the link between brain and behavior.

1. Introduction

Working memory refers to the cognitive and neural processes underlying our ability to hold information in mind when it is no longer present in the environment, to mentally manipulate this information, and to use it in the service of cognition and behavior (Baddeley, 1986; Postle, 2006). Over the past several decades, a growing body of research has revealed that the amount of information that may be held in working memory, known as working memory capacity, is severely limited to as few as 3-5 items (Cowan, 2001; Luck & Vogel, 1997; Sperling, 1960). Individual differences in working memory capacity are predictive of other important cognitive abilities including language comprehension, learning, planning, reasoning, general fluid intelligence, and scholastic achievement (Baddeley, 1986; Cowan et al., 2005; Engle, Kane, & Tuholski, 1999; Jonides, 1995; Just & Carpenter, 1992). Additionally, impaired working memory function has been implicated in the constellation of cognitive deficits that accompany psychiatric and neurological conditions, including schizophrenia (Keefe, 2000). Given its central importance, significant efforts within the neural and behavioral sciences have focused on characterizing the limits of working memory and elucidating the processes that underlie this critical aspect of cognition.

Capacity limits in working memory have been probed using a variety of tasks across verbal and visual domains (Cowan, 2001; Miyake & Shah, 1999). Much of the evidence suggesting the existence of capacity limits in the visual domain stems from studies employing some variant of the change detection task depicted in Figure 1A (Luck & Vogel, 1997). In this task, participants view briefly-presented memory arrays consisting of one or more simple objects to remember. After a short delay, a test array is presented, and the participant must compare the test array with the memory array to identify whether the arrays are the same or different. In most experiments, the memory and test arrays are identical on 50% of trials, and differ by one item on the other 50% of trials; however, some variants of the task probe memory for a single item at test, either through a cue or by presenting only one item in the test array. Figure 1B shows an example of adults’ performance in an experiment where each memory array contained between one and six colored squares (see Appendix for methodological details). As shown by the dashed line, accuracy was near perfect for arrays with small numbers of items and decreased systematically as the number of items increased. This decline in performance with increasing numbers of to-be-remembered items, referred to as the set size, provides the primary evidence for the limited capacity of visual working memory (VWM).

Figure 1.

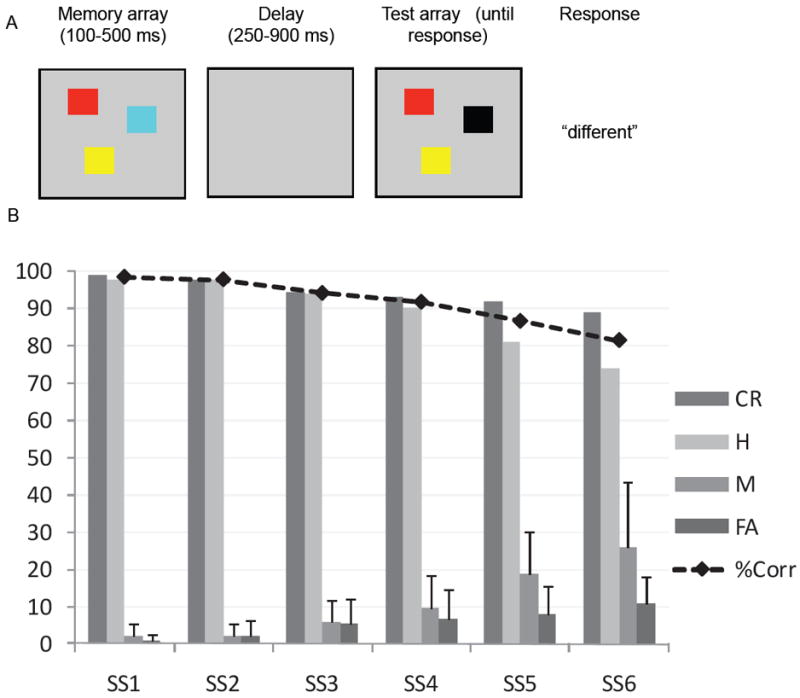
(A) Schematic of the change detection task. (B) Behavioral results from change detection: across set sizes one through six, line shows percent correct, bars show proportion separated by response type. Error bars show one standard deviation. SS = set size, CR = correct rejections, H = hits, M = misses, FA = false alarms; note that CR and FA sum to 100, and H and M sum to 100.

A topic of considerable debate over the past 5-10 years has been how best to characterize and explain the apparent capacity limits suggested by studies of visual change detection; Table 1 summarizes the primary contrasts between the dominant theories. According to one prominent perspective, the observed decline in performance with increasing set size reflects the functioning of a working memory system that stores a limited number of fixed resolution representations in discrete memory ‘slots’ (Cowan, 2001; Luck & Vogel, 1997; Zhang & Luck, 2008). By this view, errors primarily arise when the item probed at test is not stored in memory, which occurs when set size exceeds the number of available memory slots¹. That is, performance declines are caused by a structural limit in the number of items that can be stored in VWM. More recently, an alternative view that does not rely on the notion of a capacity limited working memory store has been put forth (Bays & Husain, 2008; Wilken & Ma, 2004). This approach conceives of VWM as a continuous resource that is flexibly allocated to each of the items in memory. As set size increases, less and less of this resource is available for each item, and as a result, each item is stored with lower fidelity (i.e., with greater amounts of variability or noise). The increase in noise as more items are encoded in VWM makes it difficult to discriminate familiar from novel inputs at test (i.e. to detect the signal in the noise), giving rise to the appearance of a capacity limit at higher set sizes when in fact there is none.

Table 1.

Comparison of slot, resource, and DFT accounts of change detection performance

	“Classic” Slots1	“Modern” Slots2	Resources3	DFT
Encoding:	discrete, all-or-none	discrete, all-or-none	continuous, partial	discrete, all-or-none
Maintenance:
Capacity	fixed, small	fixed, small	unlimited	variable, small
Resolution	fixed, high	fixed, high	variable (inversely related to number)	variable (depends on metrics and noise)
Comparison process:	unspecified	unspecified	unspecified	inhibitory feedback from WM to input layer
Same/different decision:	unspecified	decision rule (process unspecified)	decision rule (process unspecified)	competition between activation related to items in WM vs. new inputs
Source of errors:	items not in VWM, guessing	items not in VWM, guessing, insufficient resolution, attention lapse	insufficient resolution	failure of consolidation, maintenance, comparison, or decision

¹e.g., Pashler, 1998; Cowan, 2001; Luck & Vogel, 1997

²e.g., Zhang & Luck (2008); Rouder, Morey, Morey, & Cowan, 2011

³e.g., Bays & Husain, 2009; Wilken & Ma, 2004

These two perspectives have generated and explained an impressive amount of empirical data and have largely dominated the discourse in VWM research over the last several years. Despite their successes, however, an increasing number of researchers have begun to develop approaches that attempt to move beyond the slots vs. resources dichotomy. The most prominent among these are the so called “hybrid” views, in which an upper bound on capacity is proposed to coexist with a variable limit on the total amount of information that can be stored about each object (Alvarez & Cavanagh, 2004; Xu & Chun, 2006). In the present paper, we describe an alternative account based on the dynamic field theory, a neurally-grounded, process-based approach to working memory that has been used to capture performance in change detection and recall tasks that probe VWM (Johnson & Simmering, in press). As Table 1 shows, this theory incorporates some characteristics of both slot and resource accounts, as well as providing more specificity in the processes underlying performance in the change detection task.

Through a series of simulations, we will illustrate how the model can capture performance in change detection. Additionally, we highlight novel behavioral predictions that have been derived from the model, and consider how the model addresses issues relevant to the proposed neural systems underlying VWM, the integration of visual features, and VWM development. We show that, although our model overlaps to some extent with both slot and resource approaches, it violates key assumptions of both views of the nature of VWM (see Table 1). We conclude by arguing that moving in the direction of neurally-plausible, process-based approaches to working memory is critical if we are to move the debate in this area forward and begin to understand the link between brain and behavior.

2. The Dynamic Field Theory of visual working memory and change detection

In this section, we describe a formal theory of VWM and change detection that builds on the Dynamic Field Theory (DFT) of visuospatial cognition (Johnson & Simmering, in press; Spencer, Perone, & Johnson, 2009; Spencer, Simmering, Schutte, & Schöner, 2007), and how it embodies the characteristics listed in Table 1. Performance in the change detection task can be conceptualized as involving four cognitive processes: encoding items from the memory array into VWM, maintenance of these items over the memory delay, comparison of the items in VWM to the test array, and generating a “same” or “different” decision. The two types of trials, change and no change, combined with the two possible responses lead to four response types. In the parlance of Signal Detection Theory (Green & Swets, 1966), correct responses are referred to as “correct rejections” (on no change trials) and “hits” (on change trials), and errors are referred to as “false alarms” (on no change trials) and “misses” (on change trials). Through a series of simulations, we illustrate how the model encodes, maintains, and compares visual inputs, and generates same/different decisions in the context of change detection. We also show how each of these response types come about in the model, highlighting how the model’s explanation of errors, in particular, diverges from common assumptions in the literature. Later sections describe how the model can be used to account for performance in cued recall tasks, recent work using the DFT to capture neuroimaging results, extensions of the model architecture, and the development of working memory across domains.

The DFT is in a class of continuous-attractor neural network models originally developed to capture the dynamics of neural activation in visual cortex (Amari, 1977; Wilson & Cowan, 1972). The general form of models in this class consists of a layer of feature-selective excitatory neurons reciprocally coupled to a layer of inhibitory interneurons. Neurons within the excitatory layer interact via short-range excitatory connections and project to similarly-tuned neurons in the inhibitory layer. The inhibitory layer, in turn, projects broad inhibition back to the excitatory layer. The resulting locally excitatory and laterally inhibitory, or “Mexican Hat,” pattern of connections allows localized peaks of activation to form in response to input. The center of mass of such peaks provides an estimate of the particular stimulus value (e.g. hue, orientation, spatial location) represented by the neural system at a particular moment in time. Additionally, with strong excitatory and inhibitory projections, peaks of activation can be sustained in the absence of continuing input. This property of dynamic neural fields forms the basis for the sustained activation purported to underlie working memory (Compte, Brunel, Goldman-Rakic, & Wang, 2000; Edin et al., 2009; Tegner, Compte, & Wang, 2002; Trappenberg & Standage, 2005; Wang, 2001).

To apply this neural framework to change detection performance, Johnson and colleagues (Johnson, Spencer, Luck, & Schöner, 2009; Johnson, Spencer, & Schöner, 2009) proposed the three-layer model depicted in Figure 2. The model consists of an excitatory contrast field (CF), an excitatory working memory field (WM), and a shared inhibitory layer (Inhib). In each cortical field, the x-axis consists of a collection of neurons with receptive fields tuned to particular color values, the y-axis shows each neuron’s activation level, and the z-axis captures the time within a trial; interactions within and between layers are shown as green (excitatory) and red (inhibitory) arrows (equations and parameter values can be found in the Appendix). In addition, to capture the decision required in the change detection task, a simple competitive neural accumulator model (Standage, You, Wang, & Dorris, 2011; Usher & McClelland, 2001), comprised of two self-excitatory and mutually-inhibitory neurons, was coupled to the three-layer architecture. One neuron receives summed excitatory activation from CF to generate different responses, while the other receives summed activation from WM to generate same responses (see Simmering & Spencer, 2008, for a similar process in position discrimination). Activation autonomously projects to these neurons when a decision is required in the task: a “gating” neuron receives projections from WM as well as the stimulus input; when activation of this gate neuron rises above threshold (at the presentation of the test array), its activation combines with specific projections (i.e., CF and WM) to the response neurons (described further in section 2.2.1; see Appendix for complete details). The response neurons are coupled in a “winner-takes-all” fashion such that only one neuron will attain above-threshold activation, thereby generating a response. Thus, the model’s response is the result of competition between activation projected from CF, which preferentially represents novel perceptual inputs (i.e., items that are not currently being held in memory), and WM, which represents the current contents of memory.

Figure 2.

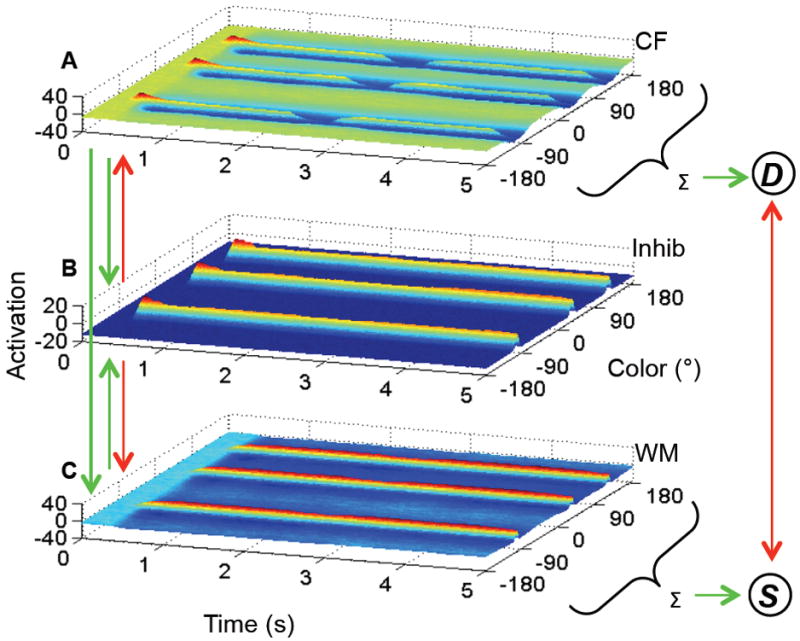
The Dynamic Field Theory consisting of three layers: (A) an excitatory contrast field (CF), (B) an inhibitory layer (Inhib) and (C) an excitatory working memory field (WM). In each panel, time is across the x-axis, activation on the y-axis, and color value on the z-axis. Arrows indicate excitatory (green) and inhibitory (red) projections between layers. The excitatory fields are coupled to two self-excitatory, mutually-inhibitory neurons: one for different (D) decisions receives activation projected from CF; one for same (S) decisions receives activation projected from WM.

Note that while variants of this architecture have been closely linked to neurophysiology (e.g., Bastian, Riehle, Erlhagen, & Schöner, 1998; Erlhagen, Bastian, Jancke, Riehle, & Schöner, 1999; Erlhagen & Schöner, 2002; see Schöner & Spencer, in press, for review), the specific model described here was not derived directly from neurophysiological studies of WM and change detection. Instead, the model was designed to provide a functional neural account of behavior in the change detection task by linking a particular neural implementation of encoding and maintenance in WM to plausible comparison and decision processes. We contend that models of this sort can make an important contribution to our understanding of the neural bases of cognitive processes by showing how the functionality required to support behavior in tasks such as change detection can arise within relatively simple neural circuits organized according to known neural principles. Below we discuss current work aimed at connecting this model more directly to neural data (see Sections 3.2 and 3.5).

2.1. Quantitative model simulations

To demonstrate that the DFT provides a plausible neural mechanism for change detection performance, we conducted a set of quantitative simulations to fit the model’s performance to behavioral data collected in our lab. Full details of the behavioral method and results (shown in Figure 1B) can be found in the Appendix. In brief, we conducted a change detection study using colored squares as stimuli; the memory array was presented for 500 ms, followed by a 1 s delay. Next, the test array was presented in which all of the items were identical to the memory array (50% of trials) or one item had changed (50% of trials). The test array remained visible until the participant entered a response on the keyboard (cf. Figure 1A). Set size varied randomly across trials between one and six items, with no colors repeated within an array. Our results replicate the general finding of a monotonic decrease in accuracy as set size increased, as shown in Figure 1B. We estimated capacity by computing Pashler’s k (Pashler, 1988) separately for each participant at each set size, and then taking the highest value across set sizes as the participant’s capacity (e.g., Olsson & Poom, 2005; Todd & Marois, 2005). Mean capacity across 19 participants was estimated to be 4.58 items (SD = 0.78, range = 3.00-5.68). This mean estimate of capacity is somewhat higher than the 3-4 item capacity reported by some investigators (e.g., Luck & Vogel, 1997), although the range of performance is comparable to other reports in the literature using similar methodology (e.g., Alvarez & Cavanagh, 2004; Cowan, Fristoe, Elliott, Brunner, & Saults, 2006; Gold et al., 2006; Ross-Sheehy, Oakes, & Luck, 2003).

Table 2 shows results from our model simulations along with participants’ data, demonstrating the close fit of the model across both change and no change trials (see Appendix for full details; parameter values are shown in Table A1). Note that each mean from the simulations fell within one standard deviation of the means from the behavioral data, and the mean absolute error between the model’s performance and our behavioral data was 2.26%, less than one half the overall standard deviation observed for the behavioral data (7.11%). As with the behavioral data, we used Pashler’s k to compute the model’s capacity separately for each “participant” (simulation run) by taking the highest estimate across set sizes, then averaging across runs; this resulted in an estimate of 4.64 items. Thus, the DFT can provide a close fit of adults’ performance in the change detection task across set sizes one through six.

Table 2.

Comparison of Results from Simulations and Behavioral Experiment

	Simulations		Behavioral Data
	CR Rate	H Rate	CR Rate	H Rate
SS1	99.00 (2.05)	99.00 (2.05)	99.21 (1.87)	97.89 (3.46)
SS2	99.75 (1.12)	96.50 (3.66)	97.89 (4.19)	97.89 (3.46)
SS3	99.50 (1.54)	94.75 (6.38)	94.47 (6.43)	93.95 (5.67)
SS4	99.25 (1.83)	87.25 (4.13)	93.16 (7.68)	90.53 (8.96)
SS5	94.50 (4.56)	76.75 (8.63)	92.11 (7.51)	81.32 (11.28)
SS6	85.75 (6.93)	72.25 (8.50)	89.21 (7.31)	73.95 (17.45)

2.2. Decision-making, errors, and capacity limits in the DFT

In addition to providing robust quantitative fits to adults’ change detection performance, a key strength of the proposed framework is the opportunity it provides to explore the dynamic processes underlying performance on a trial-by-trial basis. This opportunity is lacking in other, non-process based accounts of VWM capacity limits that may capture overall performance, but fail to specify a response on each trial (see Table 1). Here we probe how change detection decisions arise in the DFT to account for capacity limits observed in behavioral experiments. We begin by considering how correct responses (i.e., correct rejections and hits) arise. Next, we examine the factors contributing to errors (i.e., misses and false alarms). Finally, we consider the origin of capacity limits by exploring the number of unique neural representations that can be maintained concurrently in WM.

2.2.1. Correct rejections and hits

Figure 3 shows a trial in which the DNF model makes a correct rejection, correctly responding same when the display colors were identical between the memory and test arrays. This figure shows time-slices through all three layers at critical points in the trial: at the end of memory array presentation following encoding (Figure 3A); at the end of the delay when the colors are being maintained in memory (Figure 3B); and when the decision is generated during presentation of the test array (Figure 3C). To show the time course of the decision process, activation of the decision neurons is shown across time in the trial. Note that, although separate task “stages” are highlighted for simplicity in each simulation, patterns of activation evolve continuously throughout the trial, and the stage-like character of performance arises as a result of the timing of specific task events together with dynamic interactions within and between the model’s layers, rather than different processes corresponding to different stages.

Figure 3.

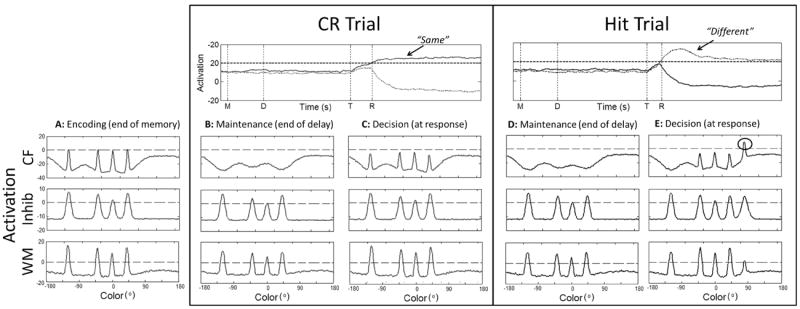
Simulations of the DFT illustrating correct performance in the model, with time slices through the three layers of the model during key points in the trial: (A) after encoding, which did not differ across trial types, (B) during the delay and (C) at test on a no-change trial, and (D) during the delay and (E) at test on a change trial. Activation of the decision neurons over the course of the trial is shown above the delay and test panels, with lines indicating the onset of the memory array (M), beginning of the delay (D) onset of the test array (T), and response time (R). Dashed horizontal lines in each panel indicate zero. CR = correct rejection.

The trial begins with the presentation of the memory array for 500 ms. This event is captured as localized excitatory input projected strongly into CF and weakly into WM (see Appendix for details). As shown in Figure 3A, by the end of the stimulus presentation period, multiple peaks of activation have formed in WM, reflecting the consolidation of each of the memory array colors in memory. At this time, bumps of activation have also formed in Inhib, as a result of excitatory input from WM and CF. Activation from Inhib is projected back to both WM and CF. Inhibitory input to WM together with local excitatory recurrence among neurons allows self-sustained peaks to remain active in WM throughout the delay interval (Figure 3B). In contrast, inhibitory input to CF produces regions of inhibition centered at field sites representing the colors being held in WM. Thus, when the test array colors match the colors being held in memory, excitatory stimulus-related input to CF is met with strong inhibitory input (resulting from the reciprocal connection between Inhib and both CF and WM) at the same color values. This prevents peaks of activation from forming at those locations in CF (see Figure 3C), and the model “recognizes” that the test array colors are the same as the items currently held in memory. When the test array is presented, the stimulus input combines with an excitatory projection from WM to drive the activation of a “gate” neuron. When the gate neuron’s activation exceeds threshold (zero), this autonomously enables the projection from CF and WM to the different and same neurons, respectively. In this trial, the presence of four peaks in WM results in strong activation of the same neuron, whereas the inhibitory troughs in CF prevent this layer from sending activation to the different neuron. Thus, the same neuron rises above threshold, producing a correct rejection.

Figure 3 also shows how the model generates a hit response, correctly responding different when one item has changed at test. In this trial, following the encoding and delay (Figure 3A, 3D), the test array appears with a change in one of the colors (from -120° to 80°; Figure 3E). This new input projects to a relatively uninhibited region of CF, allowing an input-driven peak to form (see circle in Figure 3E); note that a peak also begins to form in WM, although activation builds more slowly in WM than in CF at this new color value. Because above-threshold peaks are present in WM and CF at test, strong activation is projected to both the same and different neurons, resulting in competition for response output. In the model, the projection from CF to the decision system is stronger than the associated projection from WM (see Appendix). Consequently, the different neuron pierces threshold first and is able to suppress the same neuron, generating a correct different response (see dashed line in Figure 3).

2.2.2. Misses and false alarms

The previous simulations show how the model performs the encoding, maintenance, comparison, and decision processes necessary for correct performance in the change detection task. These two response types are the most frequent responses observed in adults’ change detection performance (see Figure 1B and Table 2). As set size increases, however, performance begins to decline. In particular, the proportion of hits begins to decrease as participants make more misses. The failure to detect changes when they occur is the most common type of error seen in change detection tasks, typically occurring about two to three times more frequently than false alarms (e.g., Vogel, Woodman, & Luck, 2001).

Figure 4 shows the DFT performing a set size four miss trial. As before, the trial begins with the presentation of four inputs to the model (Figure 4A), and this event produces peaks in WM that sustain throughout the delay (Figure 4B). At test, one of the colors is changed to a new value (i.e., -120° changes to -80°). However, unlike the hit trial described above, on this trial the new color falls between two colors already held in WM (Figure 4C). Because inhibition spreads laterally around the two remembered items, activation at the changed value in CF is still relatively inhibited compared to other field sites during the delay (e.g., compare activation at the location of the change in Figure 3D versus Figure 4D). Thus, the test array input to CF is unable to rise to above-threshold levels of activation at the color value of the new item (see circle in Figure 4C). As a result, the activation projecting from WM to the same neuron is stronger than the input from CF to the different neuron, and the model incorrectly makes a same response (see solid line in Figure 4). In general, misses become more likely as inhibition spreads more broadly in CF at higher set sizes. Moreover, the present simulation highlights that the likelihood of missing a change may depend on the metric relationship between the changed item and the items in WM. We return to this issue in Section 2.2.4.

Figure 4.

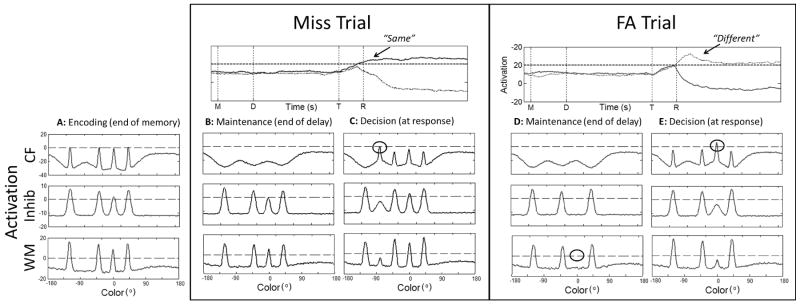
Simulations of the DFT illustrating errors in the model, with time slices through the three layers of the model during key points in the trial, plus activation of the response neurons over the course of the trial, as in Figure 3. FA = false alarm.

An example of the final response type—false alarms—is also shown in Figure 4. This trial begins with the four inputs projecting to CF and WM, building peaks in WM (Figure 4A). However, during the delay on this trial (Figure 4D), activation for one color value is not maintained (see circle in Figure 4D). Without a peak in WM, there is no corresponding inhibition in CF at this field location. Consequently, an input-driven peak builds in CF at the location of the forgotten item even though the same four colors are present in the test array (see circle in Figure 4E). The presence of an above-threshold peak in CF strongly activates the different neuron in the decision system, which generates an incorrect response (see dashed line in Figure 4). Thus, even though the model is capable of holding four (or more) items in WM at one time, competition between neighboring peaks prevented one item from being consolidated in WM (discussed further in the following section), which produced a false alarm.

The DFT contrasts with other prominent approaches to change detection in that guessing does not explicitly factor into our account of errors. For example, many models assume that, on trials where no change is detected and the set size exceeds capacity, participants generate a response by randomly guessing (e.g., Pashler, 1988; Rouder, Morey, Morey, & Cowan, 2011; Wei, Wang, & Wang, 2012). By contrast, responses in our model are always driven by activation of the same and different neurons, which results from the dynamic interactions between the neurons as they receive projections from WM and CF, respectively. Although the notion of guessing has intuitive appeal, and participants’ confidence in their responses surely varies across trials, the current implementation of decisions in the DFT avoids the need to posit metacognitive processes that would be necessary to generate a guess. For example, to implement guessing in the model, some component would be needed to monitor WM to determine whether all of the items were present, and then select a response at random at test if any items were missing. Including such a mechanism in the model would be possible in principle, but the close correspondence between the model simulations and behavioral data suggests that this is not necessary. We are not arguing guessing never occurs in the behavioral task. To the best of our knowledge, there exists no definitive evidence regarding the prevalence of guessing and/or the normative form that guessing takes. Thus, whether some form of guessing needs to be added to the model is, at present, an open question.

2.2.3. Capacity limits in the DFT

A critical component of the debate between slot and resource accounts of VWM is whether there is truly a limit on the number of representations that can be held in VWM, or whether insufficient resolution merely gives the appearance of capacity limits at higher set sizes (see Table 1). On this particular issue, the DFT provides an alternative to these two views, in that the total number of items is limited but not fixed. This can be seen in Figure 5, which shows the number of peaks that were present in WM at the end of the delay in each trial of the quantitative simulations described above. Two important points should be noted. First, the number of items being held in WM was somewhat higher than the capacity estimated using Pashler’s (1988) formula for calculating k, with an average of 5.79 peaks at SS6 producing an estimated k of just 4.64 items. Thus, the model must hold 5-6 items in memory in order to generate a capacity estimate between 4 and 5 items. This result highlights the importance of considering the processes underlying VWM, not just the representations: errors may still arise on trials in which all of the items were held in memory.

Figure 5.

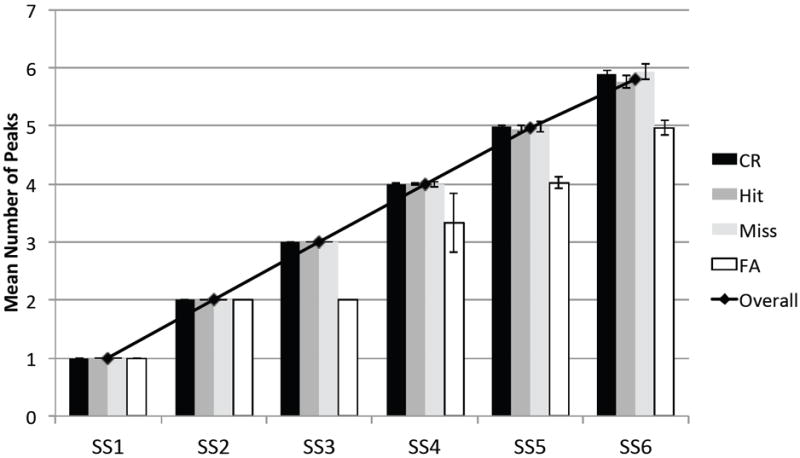
Mean number of peaks sustaining in WM at the end of the delay, averaged across all trails: line shows overall mean, bars show means separated by response type. Error bars show one standard deviation. SS = set size, CR = correct rejections, FA = false alarms.

This leads to the second notable point from our simulations, that the number of peaks maintained across trials varied systematically by response type (see separate bars in Figure 5). For set sizes three and above, we found that fewer peaks were present in WM at the end of the delay on false alarm trials—that is, on trials in which the model incorrectly generated a different response. By contrast, the highest average number of peaks was present on miss trials, in which the model incorrectly generated a same response. This contrasts with the assumptions underlying commonly-used approaches to estimating capacity (see Table 1). As can be seen in Figure 5, for set sizes one and two, all of the array items were held in memory for each response type, demonstrating that errors can arise even when all items have been successfully stored. At higher set sizes, the number of items maintained was frequently less than the set size. A clearer picture of the effect of forgetting on performance can be seen in Table 3, which shows the frequency of each response type when either all of the items were remembered, or when the number of peaks present at the end of the delay was either one or two items lower than the set size. As can be seen, misses (and correct rejections) were most likely when all of the items were held in memory, whereas false alarms (and hits) were most likely to occur when at least one of the items failed to be consolidated and maintained in WM. This suggests that errors in change detection do not arise solely from the number or resolution of items held in memory, but also through the comparison and decision processes (as previously suggested by Mitroff, Simons, & Levin, 2004).

Table 3.

Number of Trials of Each Response Type based on the Number of Items Held in WM

	Correct Rejection	Hit	Miss	False Alarm	Total
All items
SS1	396	396	4	4	800 (100%)
SS2	399	386	14	1	800 (100%)
SS3	398	377	21	0	796 (99.50%)
SS4	386	331	51	0	769 (96.13%)
SS5	351	269	91	3	714 (89.25%)
SS6	294	188	99	1	582 (72.75%)
One item below set size
SS3	0	2	0	2	4 (0.50%)
SS4	11	17	0	3	31 (3.88%)
SS5	27	37	2	19	85 (10.63%)
SS6	47	91	11	51	200 (25.00%)
Two items below set size
SS5	0	1	0	0	1 (0.03%)
SS6	1	10	1	5	17 (2.13%)
Three items below set size
SS6	1	0	0	0	1 (0.03%)

Note. Across all simulations, 400 trials were conducted per trial type (i.e., no-change versus change trials) per set size; thus, the proportion of the respective trial types corresponds to the number of trials divided by 400. SS = set size.

The simulations described above suggest that, although the number of items in WM at the end of the delay was less than set size on some trials, in many cases, nearly all of the items were maintained. A critical question is whether this holds true for set sizes greater than six. To explore capacity limits in the model further, we assessed the model’s performance at higher set sizes across a series of 250 separate simulations, corresponding to 20 participants in a change detection task. Overall, these simulations revealed that, as the set-size was increased beyond 6 items, the model’s performance declined from 78.8% correct in SS6 to 71.88% in SS7 and 63.75% in SS8. To illustrate the role that forgetting may have played in increasing the occurrence of errors, Figure 6 shows the pattern of activation in the WM layer at different points in a set of representative trials when five, six, seven, or eight inputs were presented.

Figure 6.

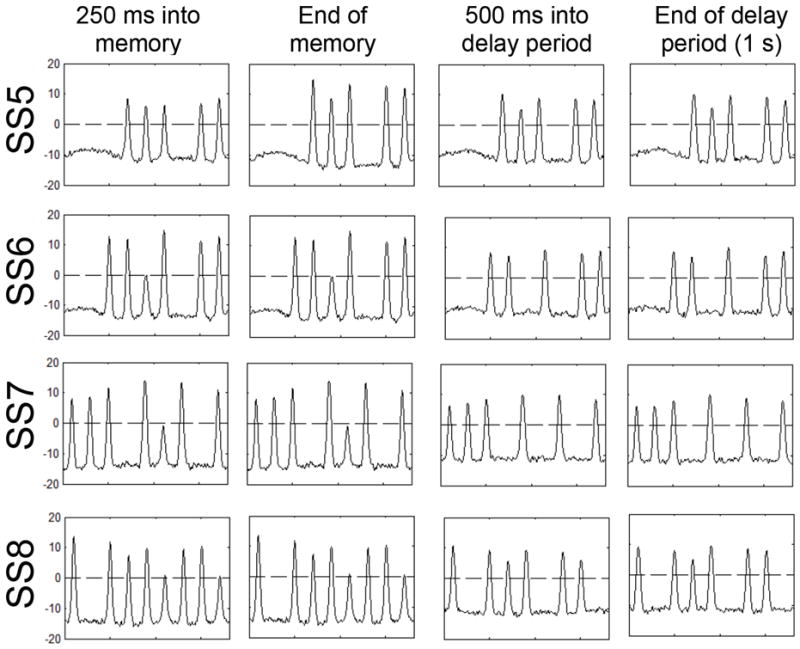
Time slice through WM demonstrating how many peaks can be built and maintained simultaneously. Color values are shown on x-axes and activation on y-axes.

As can be seen in Figure 6, when five items were presented (top row), four peaks were formed and a fifth had begun to form within ~250 ms; although this fifth peak remained relatively weak, all five peaks were sustained throughout the delay. The next row of Figure 6 shows a set size six trial. In this case, only five peaks were able to build in WM and sustain throughout the delay—one item was forgotten. When seven items were presented (third row), peaks for six items built within the first 250 ms of the memory array, and a seventh peak reached threshold by the end of the memory array. However, because this peak was relatively weak, it was suppressed by inhibition associated with the other items in WM. As a result, only six peaks remained in WM at the end of the delay. Finally, when eight items were presented (bottom row), six peaks were formed by the end of the memory array and were maintained throughout the delay, whereas two items failed to consolidate in WM. Our simulations demonstrate how the capacity of the DFT is limited to, at most, 5-6 items, but that the number of peaks maintained is not fixed (for complementary analysis of capacity in a model with similar dynamics, see Edin et al., 2009). The time-dependent nature of peak formation may seem to suggest that capacity can be increased arbitrarily by lengthening the memory array duration. This is not the case: at some point, inhibition from the other items in WM makes it impossible to maintain more than 5-6 items in WM once input is removed, regardless of how long the items were presented.

As this figure demonstrates, the relative strength of excitation and inhibition between layers provides an upper limit on the number of peaks that can be maintained simultaneously in WM. Thus, capacity limits in the DFT can be attributed to the strength and width of the Mexican hat function. With weaker interactions, the capacity of the model is decreased (see Section 3.3 below for discussion of how this type of parameter change can capture developmental improvements in VWM). Critically, however, the performance of the model is not influenced solely by the number of items in WM, as described in the following section.

2.2.4. Other contributions to errors in the DFT

To conclude this subsection, we revisit the question of where errors come from in the model. In our analysis of this issue (see Section 2.2.2), we suggested that errors are most likely to occur when either a) one or more items have failed to be consolidated or maintained in WM throughout the delay interval, increasing the likelihood of a false alarm, or b) WM is full, and as a result, inhibition projects broadly back to CF, making it difficult for a peak to build in that layer when a change occurs at test and increasing the likelihood of a miss. Note that these two explanations align roughly with slots and resource accounts, respectively; this is how the DFT is able to capture many of the same empirical phenomena that support one or the other of those theories within a single framework (see further discussion in Section 3.1). The exact number of peaks held in WM on a given trial is partly influenced by random fluctuations of activation (i.e., noise). Noise within the fields may increase the excitation or inhibition at a given color value, which can bias nearby peaks toward an on or off state, respectively. In addition to noise, there are more systematic influences on activation and inhibition related to the items being held in WM. Specifically, our simulations revealed that errors could occur on trials in which no items were forgotten and WM was not full to capacity. For example, in Section 2.2.2 we described a set size four trial that resulted in a miss response even though all of the items were successfully remembered throughout the delay, and set size was below the maximum number of peaks that can be simultaneously maintained in WM. In this case, one item changed to a color that fell in-between the colors of two other items that were being held in WM. Because these colors were relatively close together in color space, the inhibition associated with each peak in WM was overlapping, producing a region of relatively strong inhibition between these two color values in CF (see pattern of inhibition in CF in Figure 4). As a consequence, the test input failed to generate a peak of sufficient strength in CF to drive a different response.

The false alarm trial shown in Figure 4 illustrated another potential consequence of metric interactions in WM, in which a peak “died out” during the delay due to strong inhibition from neighboring peaks. These simulations lead to a novel prediction that we can evaluate with our own behavioral data—that the metric relationship between the items in WM will influence which items are stored, and by extension, will have a measureable effect on performance. Although our task was not specifically designed to test this prediction, we evaluated it by calculating an approximate similarity metric between the items in the memory array on each trial, and comparing response types based on item similarity.² To do this, we ordered the stimuli in each memory array by similarity and calculated the number of “steps” between nearest neighboring items, such that two neighboring colors (e.g., cyan and blue) would have one step between them, colors separated by one other color would have two steps, and so on for each additional color. We then computed the mean distance between items for set sizes two through six. Note that the minimum mean distance score for any set size is one, corresponding to a trial where all colors are no more than one color step away from their nearest neighbor. Given that there were nine possible colors used in behavioral experiments, the maximum possible distance between two colors is 4, but with each additional item added to the array, the mean distance score necessarily decreases. Collapsing across trial types, the mean distance scores across set sizes two through six were, respectively, 2.53, 1.95, 1.65, 1.41, and 1.25 steps.

Figure 7 shows the proportion of correct versus incorrect responses on no-change (Figure 7A) and change (Figure 7B) trials as a function of the mean distance between items in the memory array, collapsed across set sizes two through six. Because stimuli were selected randomly on every trial, and higher mean distances were only possible at lower set sizes, there were large variations in the numbers of trials that yielded each possible mean; as such, we combined roughly equal numbers of trials to arrive at the bins specified along the x-axis (note that 1900 trials contributed to each panel—19 participants each completed 20 no-change trials and 20 change trials in each of these 5 set sizes). As this figure shows, errors were more likely when the mean distance was small, that is, when items in the memory array were more similar to one another. We also considered how the similarity between the memory array items and the novel test color on change trials influenced performance. Figure 7C shows the percent of change trials that resulted in hits or misses, this time as a function of the mean distance between the changed color and the items in the memory array. Again, smaller distances (more similarity) led to more errors, as predicted by the DFT. Although these results are consistent with the model’s performance, this prediction warrants further testing because it was not an explicit goal of the current experiment, but rather was tested post hoc.

Figure 7.

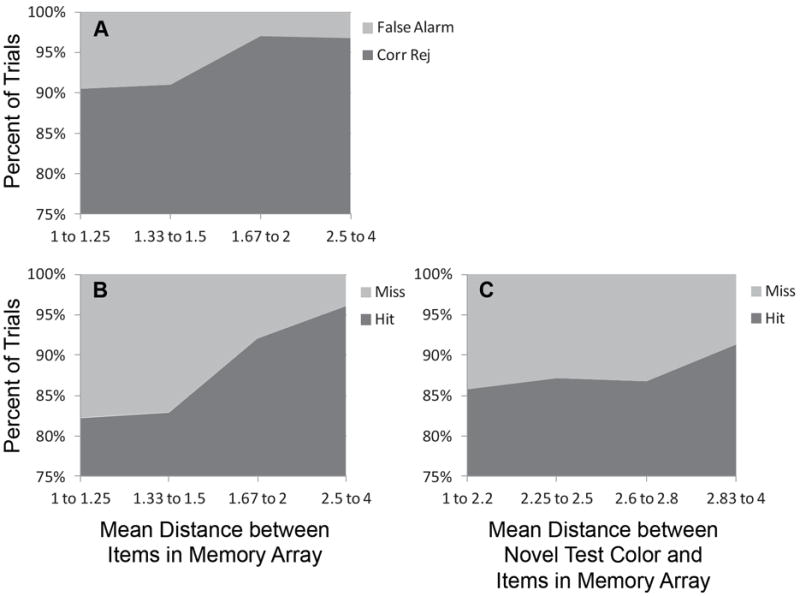
Percent of (A) no-change and (B) change trials that resulted in errors (false alarm, miss) or correct responses (corr rej, hit) as a function of the similarity of items in the memory array. (C) Percent of change trials that resulted in errors or correct responses as a function of the similarity between the test item and the items in the memory array.

Note that these results contrast with the findings of Johnson and colleagues (Johnson, Spencer, Luck, et al., 2009; Lin & Luck, 2009), who observed a similarity-based enhancement of change detection performance in two separate experiments exploring memory for colors and memory for orientation. In contrast to the present study, in which we derived the prediction of a similarity-based increase in false alarms from the model’s performance after fitting it to our behavioral data, the enhancement effect observed by Johnson et al. was an a priori prediction derived from a systematic exploration of the effects on change detection of different metric separations between inputs (Johnson & Spencer, unpublished observations). Specifically, at very close separations, two peaks in WM nearly always fused (combining into a single peak at an average color) or one peak “killed” the other. At slightly larger separations, mutual inhibition produces a sharpening and a reduction in the amplitude of each peak, weakening and narrowing the inhibitory projection to CF, and allowing relatively small changes to be detected more readily. With even larger separations, the peaks are less affected by the metrically-specific lateral inhibition associated with the other peak and more influence comes from global inhibition (see Appendix). Global inhibition limits the total number of peaks that can be held in WM, and combined effects of lateral inhibition will make some peaks more likely to “die out” than others (cf. Figure 4). Thus, metric interactions between nearby items may enhance or disrupt performance under different circumstances in the DFT.

In a related model, Wei, Wang, and Wang (2012) proposed a form of primarily excitatory interaction as one of the main causes of errors in change detection. Our view differs from theirs in that merging in our model only occurs at very close separations (i.e., at separations smaller than those used in most change detection experiments), with primarily inhibitory interactions predominating at larger separations. For example, at the intermediate separations shown to produce sharpening of peaks, overlap between the lateral inhibition profiles of nearby peaks leads to an asymmetry in inhibition, with stronger inhibition in-between the peaks than on the “outside”. As a consequence, the peaks move away from each other over the delay period—they are “repelled” from each other. Importantly, this postulated form of neural interaction leaves a behavioral signature that can be detected using recall working memory tasks (see Johnson, Dineva, & Spencer, 2013, and Section 3.1).

Taken together, the results and simulations described in this section highlight that, although individual items are represented as discrete peaks in WM, they are not stored independently but rather interact in systematic ways that can impact performance. This unique feature of the DFT contrasts with the assumption underlying the discrete slots perspective, that items are stored independently in working memory (see Table 1); similarly, no such provisions for neural interactions of this sort are provided by the resource perspective, although high item similarity could be expected to produce interference by this view (Wilken & Ma, 2004). Furthermore, several of the consequences arising from high item similarity considered here only become evident through the comparison and decision processes in the DFT—other theories and models do not explicitly address these processes.

As with slot and resource models, failures in the encoding or consolidation processes contribute to errors in the DFT. Behavioral studies of the rate of consolidation in VWM have suggested that encoding occurs more slowly as set size increases (Vogel, Woodman, & Luck, 2006), which can result in the failure to encode one or more items when the display duration is relatively short. We examined this characteristic of the model by plotting the mean above-threshold activation (averaged across trials and runs of the model) in WM during the presentation of the memory array. Figure 8 shows the mean activation across set sizes during encoding (8A) and the delay period (8B). As Figure 8A shows, the rise time of activation per item increased as additional items were added to the memory display, but only to a point: the total amount of activation was similar for SS3 and above, despite the increased number of items. Thus, consolidation occurred more slowly per item with more items, as seen in behavioral studies (Vogel et al., 2006). In the DFT this occurs as a result of increasing inhibition with greater numbers of inputs, which slows down the overall increase in excitatory activation necessary to sustain peaks.

Figure 8.

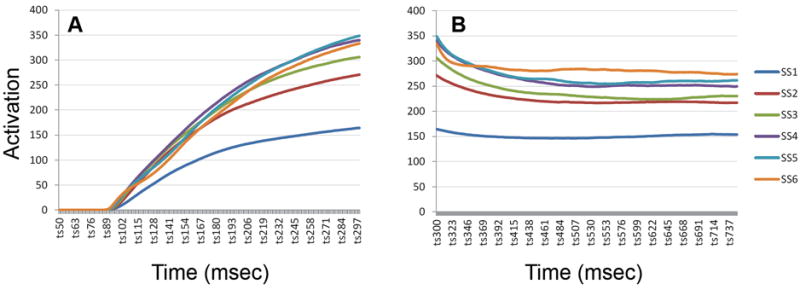
Above-threshold activation in WM during encoding (A) and during the delay period (B) as a function set size.

The same pattern can be seen in activation in WM during the delay period: the amount of activation increased as the number of items increased, but not linearly (Figure 8B). Although there is not a direct correspondence between activation in the WM field of the DFT and specific neural measures, this pattern is generally consistent with fMRI and EEG data showing a correspondence between neural activity and capacity limits in change detection (e.g., Todd & Marois, 2004, 2005; Vogel, McCollough, & Machizawa, 2005). This feature of the model contrasts with other recent approaches that attempt to reconcile slots and resource views of working memory, by positing that the total amount of above- threshold excitatory activation is akin to a continuous resource that remains roughly constant across set size (see, e.g., Wei et al., 2012, and discussion below).

2.3. Comparison to slot- and resource-based approaches to change detection

We conclude this section by considering the similarities and differences between our approach and the discrete slot and continuous resource models. Table 1 summarized the contrasts between approaches; we will briefly discuss each in turn here. A central contrast between approaches is in how items are encoded: slots theories posit discrete, all-or-none encoding whereas resource models assume continuous encoding, with a gradual accumulation of information over time, allowing for the partial representation of a potentially very large number of items. In the DFT, encoding occurs when input is sufficiently strong and enduring to produce a self-sustaining peak in the WM layer (for further discussion, see Johnson, Spencer, & Schöner, 2009). This involves a discrete transition—known as a bifurcation in Dynamic Systems Theory (Braun, 1994)—from an “off” state, characterized by graded subthreshold patterns of activation, to an “on” state in which locally excitatory interactions among similarly-tuned neurons are engaged. Thus, peaks are either stabilized in an above-threshold activation state or they relax back to the neuronal resting level. They do, in fact, have a discrete, all-or-nothing character.

According to slots theories, the capacity of VWM is limited to a small number of high resolution representations, which is more or less fixed within a given participant (but see Kundu, Sutterer, Emrich, & Postle, 2013, for evidence that capacity can be increased through particular types of training). Resource models, by contrast, posit that the number of representations that can be maintained is essentially unlimited, although only a small number can be represented with high precision. In the DFT, there is an upper limit on the number of peaks that can be sustained in WM; however, the total number of peaks maintained is not fixed, but varies from trial to trial depending on stochastic processes (i.e., noise), and more systematic influences, such as the metric separation between maintained items.

The DFT differs from the classic form of the slots view in that items are not encoded and maintained with perfect fidelity (see Table 1). Instead, each item is represented as a noisy population vector of activation occupying a unique position within a continuous feature space. In this sense, the DFT is more similar to resource models; although such models have not been explicitly implemented in a neural framework, the underlying assumption is that individual items are represented as noisy population codes, with the amount of noise (i.e., variance) associated with each item increasing as limited resources are spread out among larger numbers of items (Bays, Catalao, & Husain, 2009; Bays & Husain, 2008, 2009). However, we are unaware of any implemented population coding model that captures multi-item VWM in the manner described by proponents of the resource view (Ma & Huang, 2009). Indeed, until quite recently, the majority of models in this class that have addressed working memory have focused on memory for single spatial locations (Camperi & Wang, 1998; Compte et al., 2000). Achieving multi-item working memory in such models has proven to be a challenge because this requires a delicate balance between excitation and inhibition (Trappenberg, 2003). With too little inhibition (or when excitation is too broad), peaks have a strong tendency to merge, making it difficult for unique peaks of activation to be formed and maintained (discussed above; see also Wei et al., 2012). Conversely, if inhibition is too strong, only a single peak can be maintained at a time, which is inconsistent with capacity estimates obtained from behavioral experiments. Thus, the same neural dynamics that make it possible to maintain multiple neural representations at one time in these models (locally excitatory recurrence together with broad inhibition) also give rise to capacity limits at higher set sizes. As a result, a plausible neural basis for the unlimited capacity WM proposed by proponents of the resource view remains unclear.

This difficulty is demonstrated in a recent model developed by Wei and colleagues (2012), which attempts to reconcile the slots and resource views of WM. In their model, the strength of excitatory and inhibitory interactions among neurons supporting maintenance are tuned such that the total number of activated neurons during the delay remains more or less constant (i.e., continuous) across set sizes. This mode of functioning is in keeping with the conceptualization of WM as a continuous resource that is divided up evenly among the items in memory, with less and less resource available for each item as set size increases. However, they also show that the capacity of the model is strictly limited as peaks of activation representing items in WM either fade out (as a result of increased competition) or merge together (due to overlapping excitation) as set size increases. Thus, although some aspects of the model’s functioning are consistent with the resource view, others are not. Additionally, it is difficult to see how this model, or the resource view more generally, could capture findings from neural recording studies of WM showing that, rather than remaining constant, activation during the delay interval steadily increases with increasing set size, leveling off at an individual’s capacity (e.g., Todd & Marois, 2004, 2005; Vogel et al., 2005).

Proponents of slots theories have proposed an alternate neural implementation of a limited capacity working memory system to the one described here. In this model, each item is actively stored by a separate cell assembly that fires synchronously in the gamma band frequency range and out of phase with cell assemblies representing other items (Lisman & Idiart, 1995; Raffone & Wolters, 2001). Capacity limits arise when the number of items to be maintained exceeds the number of distinct phases available. In addition, the ability to maintain separate sustained oscillatory states can be influenced by noise, item similarity, and other factors that have been shown to influence performance in the DFT and neural population coding models more generally. Although this is a promising explanation, to date there is little direct evidence supporting this proposal (see discussion in Fukuda, Awh, & Vogel, 2010). Additionally, though maintaining multiple highly similar items might produce interference among representations, it is unclear whether such a temporal coding model could accommodate the various kinds of metric interactions our work has uncovered.

The most notable difference between the DFT and slot and resource accounts is that only the DFT includes specific mechanisms underlying the comparison and decision processes required in change detection. Even in neural implementations of slot models (e.g., Raffone & Wolters, 2001), or in what could be considered hybrid slot/resource models (e.g., Edin et al., 2009; Wei et al., 2012), the comparison and decision processes are not explicitly implemented. As our simulations demonstrated, however, the process of translating a memory representation into a behavioral response introduces the potential for errors, which brings us to the final contrast among theories: the source of errors in the change detection task. The “classic” slots accounts were admittedly simple, attributing all errors to items not being held in memory. More recent variations of slot models, however, provide a richer set of hypotheses to account for performance in change detection, including insufficient resolution to detect small changes (see discussion in Awh, Barton, & Vogel, 2007), or lapses in attention (Rouder et al., 2008, 2011), in addition to failures of encoding or maintenance. The primary source of errors in the resource models, by contrast, is limited resolution, which makes decisions more prone to error as set size increases (Wilken & Ma, 2004). In the DFT, errors can arise through any of the processes involved in the change detection task, and are not solely, or even primarily, attributable to failures of memory (cf. Mitroff et al., 2004). Adopting a process-oriented approach to VWM, in which the proposed mechanisms underlying performance are explicitly implemented in a formal model, affords the opportunity to explore additional sources of errors that may not be evident in other approaches that focus primarily on characterizing the representations underlying VWM. Importantly, the potential sources of errors suggested by our model are not simply theoretical curiosities, but have led to testable predictions that have been confirmed in behavioral and neuroimaging experiments, as we describe in the next section.

3. Beyond change detection

Thus far, our discussion has focused exclusively on modeling the change detection task in adults. In this section, we consider how the model can be used to address performance in other tasks used to measure VWM in the laboratory, and in age groups other than adults. First, we describe a DFT approach to modeling cued recall, which has overtaken the change detection task as the primary paradigm used to study VWM. Next, we describe recent extensions of this architecture that incorporate higher dimensional representations, attention, and sequence learning. These additions make it possible to capture performance in several other tasks that are widely used to measure VWM. In a final section, we consider how the model can account for the development of visuospatial working memory.

3.1. Recall tasks probing VWM

Much of the current debate between proponents of slots and resource views focuses on performance in recall, rather than change detection, VWM tasks. The recall task is identical to the change detection task, with the exception that, instead of making a same/different decision in response to a test array, observers are cued to report a particular attribute of a remembered stimulus (e.g., its color) by, for example, clicking on the region of a color wheel that matches the remembered attribute. Although the primary focus of the present paper has been change detection, the majority of previous work applying the DFT to working memory has addressed spatial recall (Simmering, Schutte, & Spencer, 2008; Spencer et al., 2007). As a result, adapting the model described in Section 2 to recall studies of VWM is fairly straightforward. Recall that the basic units of representation within the DFT are localized peaks of activation, whose center of mass can be taken as an estimate of the particular stimulus value(s) (e.g. hue, orientation, spatial location) represented by the neural system at a particular moment in time. Thus, a simple means of deriving simulated recall data from the model is to present it with one or more inputs followed by an unfilled delay, as in change detection, and then read out the position of each distinct peak that is present in WM at a specified point in time after the end of the delay. The simulated response distributions can then be used to estimate the capacity, accuracy and precision of peaks in WM in the same way that recall responses are used to estimate these parameters from behavioral data (as in, e.g., Bays, Catalao, & Husain, 2009; Zhang & Luck, 2008).

Using this method, Johnson and colleagues (Johnson et al., 2013; Johnson, 2008) used the DFT to derive a novel prediction that was confirmed behaviorally: that neural interactions between nearby peaks in WM would produce similarity-based feature repulsion (see discussion in Section 2.2.4). Additionally, model simulations and behavioral data revealed a decrease in precision when one item versus three items were retained in WM, in keeping with previous findings (see, e.g., Zhang & Luck, 2008). Note that the method of deriving recall data from the model simplifies the generation of responses in the recall task, in which participants are typically required to map the color they are holding in memory onto a spatially distributed representation of the color space. That is, generating the response requires the integration of spatial and non-spatial dimensions. One means of achieving this is to couple the one-dimensional color WM field to a two-dimensional colorspace response field (spanning, e.g., 360° of color and 360° of polar angle), which makes it possible to map activation in WM onto a feature-space representation of the color wheel (see Section 3.3 for further discussion of the use of higher dimensional fields to represent conjunctions of features and spatial locations). In principle, the DFT is in a position to capture all of the necessary processes required to perform the recall task, from the encoding and maintenance of individual colors, to the generation of a spatially localized recall response. Formally implementing the processes underlying both recall and change detection in the same architecture may provide a more direct means of assessing the connection between performance in these tasks than is possible with current slots and resource models.

3.2. Expanded model architecture

Although the three-layer architecture described in Section 2 has been used to capture performance in spatial cognition and VWM tasks in children and adults (see Johnson & Simmering, in press; Simmering & Schutte, in press, for review), it is still limited in the extent to which it has been applied to many of the well-documented empirical phenomena in VWM research. To remedy this, we have been working with a group of colleagues to expand the model architecture to incorporate a wider array of cognitive processes (see Schöner & Spencer, in press, for review). The full range of applications of this expanded architecture is beyond the scope of this paper, but we will briefly highlight the examples that apply most directly to VWM research here.

One limitation of the three-layer architecture described above is that it only captures WM for single features (i.e. the colors of the items), not their locations or other visual attributes; similarly, spatial versions of the model only capture the spatial locations of objects and no other visual features. The expanded DFT architecture addresses this limitation by incorporating higher dimensional representations in which activation in a single field can span different dimensions, such as a spatial dimension and a metric feature like orientation, direction of motion, or hue. Representations of this sort are ubiquitous throughout many cortical areas. Most notably, neurons in the early visual system are known to form a population code over the two dimensional space of stimulus positions on the retina. Importantly, many of these neurons also respond to particular visual features, like edge orientation, spatial frequency, movement direction, or hue (see, e.g., Blasdel, 1992; Hubel & Wiesel, 1959; Issa, Trepel, & Stryker, 2000; Livingstone & Hubel, 1988). The DFT uses these kinds of visual representations to capture the integration of spatial and non-spatial dimensions in VWM. For instance, using a simplified one-dimensional representation of space (capturing, e,g., the position of a stimulus relative to fixation in polar coordinates), Johnson, Spencer, and Schöner (2008) showed how feature-location integration could be realized by combining separate one-dimensional architectures for individual features (color, space, etc.), and two-dimensional fields that localize features in space. In this type of architecture, the two-dimensional color-space WM field receives input from color WM along one dimension and spatial WM along the second dimension; where these inputs intersect specifies the spatial location of the color in the visual scene (see Schneegans, Spencer, & Schöner, in press, for further details).

To represent multi-feature objects, individual feature dimensions (orientation, hue, etc.) are represented in separate two-dimensional feature-space fields. The separate feature dimensions can then be bound across the shared spatial dimension through reciprocal connectivity with a single field representing the spatial locations of a limited number of encoded objects (see Simmering, Miller, & Bohache, 2013, for further discussion in the context of change detection). In the simplest case, in which one multi-featured object is present in the visual field, input from the one-dimensional feature and space fields would uniquely specify the location of the object and each of its associated features. However, in more realistic situations, in which multiple objects are simultaneously present in the visual field, a problem can arise in which the features of different objects are incorrectly combined; a variant of the well-known “binding problem” (Treisman, 1996; von der Malsburg, 1981). One proposed solution to this problem is to process individual items in a sequential fashion (Treisman & Gelade, 1980). To achieve this, another component needed to be added to the model: visuospatial attention. Specifically, in addition to the two-dimensional WM fields and their associated Contrast Fields, this architecture includes both one- and two-dimensional Attention Fields. These fields include local excitatory interactions paired with global inhibition such that peaks are self-stabilized but not self-sustaining (i.e., activation returns to resting level when input is removed), and only a single peak can rise above-threshold at any given time. Attention Fields are reciprocally coupled with both CF and WM in the respective architectures (i.e., one- versus two-dimensional). The function of these fields is to serially attend to items within the visual scene, thereby reducing the likelihood of mis-binding features across different objects. The addition of an explicit attentional mechanism to the DFT architecture allows for further comparison with other models of VWM that emphasize the role of attention in capacity limits (e.g., Cowan & Rouder, 2009). Additionally, as discussed further below, reciprocal coupling between WM, CF, and the Attention Fields makes it possible to capture behavioral performance in tasks other than change detection.

Before considering the application of the expanded model to other WM tasks, we briefly consider its ability to capture findings related to the storage of multi-feature objects in VWM. Behavioral studies have shown that both children (Riggs, Simpson, & Potts, 2011; Simmering et al., 2013) and adults (e.g., Luck & Vogel, 1997) have comparable capacity estimates for single- versus multi-feature objects, suggesting that VWM capacity is limited by the number of objects rather than the number of features (for important qualifications of these findings, see Oberauer & Eichenberger, 2013; Olson & Jiang, 2002; Wheeler & Treisman, 2002). In the expanded DFT, this limited number of objects would arise through similar mechanisms as those that limit capacity in the three-layer DFT (described in section 2.2.3). In particular, the balance between excitation and inhibition would limit the number of peaks that could be maintained in each of the WM fields—not only in the onedimensional fields (e.g., hue, orientation, space) but also in the two-dimensional fields (e.g., color-space, orientation-space, etc.). Within the expanded architecture, capacity would ultimately be limited by the number of distinct peaks that could be maintained in the spatial field that each of the 2D feature-space fields is coupled with. Thus, although it would be possible to represent 3-5 multi-feature objects (e.g., 4 colored oriented bars at different locations), it would not be possible to maintain four colors and four orientations at different locations (i.e., eight single-feature objects) because this would exceed the capacity of the spatial field. Thus, it seems plausible that the extended model could accommodate the “object benefits” observed in studies of VWM. However, the implementation of feature binding in the DFT architecture described here has only been tested qualitatively; further tests will be needed to see if this mechanism can quantitatively capture behavioral data requiring memory for multi-feature objects and generate novel predictions.

The expanded model was designed, in part, to account for the proposed close relationship between the storage function of VWM and the control of visual attention (Desimone & Duncan, 1995; Desimone, 1996). One piece of evidence supporting this proposal is the observation that saccadic eye movements to visual targets can be modulated by the relationship between the target stimuli and the contents of VWM. Specifically, Hollingworth, Matsukura, and Luck (2013) showed that saccades to targets matching the contents of VWM were generated more rapidly and landed closer to the center of the target than saccades to non-matching objects. In the model, the proposed interaction between WM and perceptual processes arises as a result of excitatory coupling between the WM field and the Attention Field, which biases attention (and thereby the oculomotor system) towards targets that share features with items being maintained in WM. A similar mechanism could be used to capture performance in other tasks that require the selection of targets that match the contents of VWM (as opposed to detecting nonmatching items, as in change detection), such as visual search, a widely used measure of attention, or the delayed match-to-sample task, a widely used measure of VWM in humans and non-human primates. A full consideration of how the model can be applied to each of these tasks is beyond the scope of the present work. For in-depth discussion of these issues, including the use of dynamic neural fields to capture multi-feature objects, attention, performance in visual search and other tasks used to probe the relationship between attention and working memory, the reader is directed to Schneegans, Lins, and Spencer (in press), and Schneegans, Spencer, and Schöner (in press).

To conclude this section, we briefly consider additional extensions of the DFT that make it possible to capture performance in more complex tasks than have been considered thus far. One important goal within working memory research more generally is to understand how it relates to higher-level cognitive abilities, such as general fluid intelligence. Many studies that demonstrate links between working memory and such highlevel skills use more complex tasks than the visual change detection paradigm discussed here. As an example, consider the n-back task: in this task, participants are required to monitor a sequence of stimuli and press a response key when the current stimulus matches the item that appeared n items previously in the sequence. This task is reliably correlated with fluid intelligence, and some studies have shown that training on n-back improves performance on measures of intelligence (Jaeggi, Buschkeuhl, Jonides, & Perrig, 2008; but see Chooi & Thompson, 2012; Redick et al., 2013), suggesting it is an important task to understand.

In order to perform the n-back task, a few additional modifications to the extended model described above would be needed. Most importantly, the model would need to incorporate information about the order of item presentation: to evaluate whether the appropriate two stimuli match, knowing the number of intervening items in the sequence is vital. More generally, the ability to represent sequential information and to generate sequentially ordered actions plays a critical role in even the simplest activities. To address this important issue, Sandamirskaya and colleagues (Sandamirskaya & Schöner, 2010; Sandamirskaya, Zibner, Schneegans, & Schöner, 2013; Sandamirskaya, in press) developed a system for sequence learning and generation. Briefly, the proposed system includes three separate components: a neural representation of seriality itself in which activation is defined over an abstract dimension, the “ordinal” axis along which the serial order of actions is represented; an intention field, in which activation is defined over relevant motor, perceptual, or cognitive dimensions (akin to the continuous neural fields described above); and a neural representation of the condition-of-satisfaction, whose activity reflects the match between the state that corresponds to the fulfillment of the current intention and the perceived state of the environment or the agent. With these additions, Sandamirskaya and Schöner demonstrated that a robotic agent could learn to perform a sequence of actions (e.g., visiting a series of colored blocks in a specific order).

The robotic implementation of the model described above provides a compelling proof of concept, demonstrating the feasibility of representing ordinal position in the DFT framework, a key requirement of capturing performance in more complex working memory tasks such as n-back. With the sequential information encoded, the next step in modeling behavior in this task would be to compare the current item to the item from the appropriate ordinal position in the sequence. This could be done in the same manner in which the three-layer DFT compares the memory and test arrays in the change detection task and generates a same/different decision (described in section 2.2). The comparison and decision required in n-back tasks is essentially a single-item change detection trial: does the current item match the item at the appropriate ordinal position in memory or not? The response nodes could be modified such that a response is only generated for a same decision by, for example, decreasing the resting level of the different neuron from the change detection model. Although this application to the n-back task is only hypothetical at this point, and would need to be tested to determine whether it could indeed capture behavioral results from that task, this section demonstrates the utility of a process-based model in extrapolating to other cognitive tasks.

3.3. Cognitive development

A final component that separates the DFT from most other accounts of VWM is that it focuses on developmental change in memory and performance (see Simmering & Schutte, in press, for review). The developmental mechanism implemented in the DFT—the Spatial Precision Hypothesis—extends from previous work in spatial cognition, which has captured developmental changes in spatial recall and position discrimination, including the influences of reference frames and long-term memory. According to this hypothesis, neural interactions strengthen over development (Perone, Simmering, & Spencer, 2011; Perone & Spencer, in press, 2013; Schutte, Spencer, & Schöner, 2003; Schutte & Spencer, 2009; Simmering et al., 2013, 2008; Simmering & Patterson, 2012; Simmering, 2013; Spencer et al., 2007; cf. Edin, Macoveanu, Olesen, Tegner, & Klingberg, 2007). This increase in excitation and inhibition leads to peaks that increase in strength, stability, and precision over development.

The spatial precision hypothesis can account for increased capacity estimates from change detection observed between 3 and 7 years of age (Simmering et al., 2013; Simmering, 2013). Simulations showed that the number of peaks held in WM increases over development, but this change alone is not sufficient to account for children’s performance. In addition, quantitative fits required changes in the decision system, such that younger children were more likely to respond “same” in the task. The same underlying memory system has also been linked with a fixation system to capture infants’ and young children’s performance in a preferential looking paradigm developed to measure VWM capacity (Perone et al., 2011; Simmering, 2008, 2013).

Using the parameters that captured the developmental trajectory in both change detection and preferential looking tasks between 3 and 5 years, Simmering and Patterson (2012) generated novel predictions of developmental improvements in the precision of VWM, which were supported by children’s performance in a color discrimination task. Compared to other models of VWM capacity in adults, the DFT has generalized across a wider range of behavioral tasks, and has accounted for developmental changes in these tasks through improvements in the underlying memory system and the behavioral response systems. These applications of the DFT to VWM follow extensive work showing how this developmental process captures multiple types of change in spatial cognition, including the A-not-B error (Simmering et al., 2008), position discrimination (Simmering & Spencer, 2008), and recall biases arising from long-term memory (Schutte et al., 2003) and reference frames (Schutte & Spencer, 2009).

Beyond visuospatial memory tasks, similar dynamic neural field architectures have also been used to account for a variety of cognitive development processes. For example, Buss and Spencer (in press) developed a multi-layered architecture of dynamic neural fields to perform the dimensional change card sort task, in which young children (typically 3-year-olds) have difficulty shifting rules used to sort cards. In their model, Buss and Spencer approximated executive control through the process of boosting the resting levels in the neural fields that represent the different dimensions of the cards (e.g., shape versus color) used to generate the sorting rules. Through simple, quantitative changes in the magnitude of these boosts over development, they successfully captured performance across a variety of different conditions in this task. Samuelson, Schutte, and Horst (2009) applied a dynamic neural field architecture to word learning tasks, and showed that changing input strength for different object characteristics (e.g., shape versus material) captured children’s performance on multiple novel noun generalization tasks. Finally, Perone and Spencer (in press, 2013) have shown how a dynamic neural field architecture can explain developmental changes in infants’ looking behavior in both habituation and paired comparison tasks through changes in neural interactions in memory and looking dynamics. As these examples demonstrate, a model like the DFT has broad application across behavioral tasks, cognitive domains, and developmental periods.

3.4 Remaining challenges

Although the DFT framework has been applied to a wide variety of phenomena related to VWM, a number of important challenges remain. In this final section, we discuss two such challenges, which we view as especially important: the development of a DFT approach to individual differences in working memory, and clarification of the relationship between the model’s behavior and the neural processes underlying performance. Ongoing efforts to address each of these challenges are discussed in the sections that follow.

3.4.1 Individual differences in working memory

As noted above, working memory capacity has been closely related to other important cognitive functions and to general fluid intelligence (Baddeley, 1986; Cowan et al., 2005; Engle et al., 1999; Jonides, 1995; Just & Carpenter, 1992) in addition to deficits observed in psychiatric populations (Keefe, 2000). This relationship provides a compelling motivation for the study of working memory in general, and the underlying factors influencing capacity in particular. Thus, one important goal for future work within the DFT framework is the development of an explicit account of individual differences in working memory. There are a number of ways in which individual differences could be implemented in the DFT. In the simulations presented here, average performance and variation were captured across separate runs of the model, which served as a proxy for individual subjects. However, the parameters of the model were identical across each run; thus any variation in the model’s performance across runs arose solely through noise. Specifically, two forms of noise were used here: spatially-correlated noise within the fields, and colored noise that influences the resting levels of the fields. Each of these noise sources impacts performance on a trial-by-trail basis, but variation in resting levels does not carry over from one trial to the next within a given run of the model (i.e., for a given “participant”). That is, variation in resting levels in each of the fields is random across trials and runs. Thus, a first step toward capturing individual differences would be to modify the model such that small differences in the effective resting levels in the fields carried over from trial to trial for a given run (see Buss & Spencer, in press, for this type of change implemented in a similar DFT architecture). Changes in the resting level can have an important influence on the model’s behavior. Generally speaking, with a lower resting level stronger input is required to form and maintain stable peaks, whereas with a higher resting level, the overall activity level within a field is increased. Each of these changes would have consequences for patterns of activation within a field as well as projections to other fields.

Another approach to individual differences could build from the DFT approach to development. As described in section 3.3, developmental changes in spatial and visual working memory have been modeled using the Spatial Precision Hypothesis, in which the strength of excitatory and inhibitory neural interactions become stronger and more precise over development. These variations in parameter strengths have previously been used to simulate relatively large differences in performance between children and adults, but Simmering (2013) showed that relatively small changes in these parameters produced enough variation across runs of the model to capture correlations in performance across VWM tasks. Additionally, Spencer, Perone, and Johnson (2009) described another consequence of increasing the strength of neural interactions in the model that could factor into a DFT account of individual differences: greater resistance to noise and the impact of task-irrelevant distractors on performance. Thus, variation in parameters of this sort could provide an account of individual differences in capacity, and performance in working memory tasks more generally.

3.4.2. Relationship between the model and neural processes

As noted above, the DFT model described here provides a functional neural account of phenomena related to VWM and change detection. Specifically, we implemented a neurally plausible form of encoding and maintenance through the sustained activation of feature selective neurons, and we showed how these can be linked to a plausible comparison and decision process. As demonstrated in section 2, the resulting model captures behavioral performance in change detection tasks, and suggests specific sources for errors. An important remaining challenge for this framework is to clarify the relationship between the model’s behavior and the neural processes underlying each response type (see Schöner & Spencer, in press, for discussion). As a first step in this direction, Buss, Magnotta, Schöner, and Spencer (2013) adopted a model-based approach to fMRI data (Ashby & Waldschmidt, 2008; Davis, Love, & Preston, 2012; Deco, Rolls, & Horwitz, 2004; White & Poldrack, 2013). A critical component of a model-based approach to fMRI is to specify a linking hypothesis that states how the processes in a model map onto the neural process driving the blood-oxygen level dependent (BOLD) signal. Recent biophysical work has demonstrated that the local field potential (LFP) is most strongly correlated with the BOLD response (Logothetis, Pauls, Augath, Trinath, & Oeltermann, 2001). An LFP is a measure of dendritic activity within a local neural population that accounts for both inhibitory and excitatory ion channels. This provides a measure of the input to, and local processing within, a given neural region. Further, a BOLD response can be reconstructed by convolving the LFP with a general impulse response function that specifies the time-course of the slow changes in blood flow that occur in response to neural activity. Deco and colleagues (2004) built off of this work to simulate the neural dynamics of VWM using an integrate-and-fire neural network. Specifically, they simulated an LFP by summing the absolute value of all ionic channels in the model that contribute to the rate of change in neural activation.

Buss and colleagues (2013) showed that this same mapping could be used with the DFT by tracking the absolute value of all excitatory and inhibitory neural interactions over the course of an experiment. Using a variant of the model architecture described in Section 2, they clarified the neural processes underlying the four different kinds of responses in the change detection task. Specifically, Buss and colleagues used the same model to quantitatively simulate behavioral performance as well as make quantitative predictions about the BOLD signal. Assessing the data across the four different response types, their results showed a close correspondence between different components of the model and particular cortical regions of interest. In particular, the ‘different’ neuron hemodynamics corresponded to the pattern of data reported from frontal eye field (FEF), the ‘same’ neuron hemodynamics corresponded to the data reported from parietal cortex, and CF layer hemodynamics corresponded to the data reported from fusiform cortex. This mapping of model dynamics to cortical areas suggests that the frontal eye fields (FEF) are involved in detecting changes when they occur, parietal cortex is involved with spatially orienting to the changed item, and fusiform cortex is involved with maintaining active representations of colors in the array.

Thus, although DFT is implemented at the fairly abstract level of neural population dynamics, this work demonstrates that the DFT can provide a neurally plausible account of both behavioral and neural imaging data related to change detection. Nonetheless, directly linking particular components of the proposed model to specific neural processes remains a central challenge for this perspective going forward.

4. Conclusions

The goal of this paper was to present a process-based neural model of VWM, the DFT, and to illustrate how it captures key characteristics of capacity limits, while also contributing to our understanding of the processes underlying change detection performance. The dominant models of VWM for the past decade have debated whether representations are best characterized as ‘slots’ or ‘resources’; although these perspectives have generated and explained an impressive amount of empirical data, we contend that the field is at a point where it can benefit from the development of formal process-based approaches to VWM that can capture behavioral and neuroimaging data using neurally plausible mechanisms. Far from representing a mere “implementation” of cognitive concepts, such endeavors can provide rich insights into the processes underlying cognitive phenomena, and can lead to novel predictions that can be tested behaviorally and using neuroimaging methods such as fMRI and EEG. In addition to our own work, other models in the same class of neurally-grounded process models have recently been proposed as a means of reconciling, and potentially moving beyond, the slots versus resources stalemate (see, e.g., Edin et al., 2009; Wei et al., 2012). To date, these models have been used to generate novel behavioral predictions and have been supported by neuroimaging data, suggesting they are poised to make continued contributions to our understanding of VWM.

Most importantly, and in contrast to these other models, the model we present here is grounded in a broader context—the DFT has already been applied across a wide range of behavioral tasks, age groups, and cognitive domains, and it continues to be developed to incorporate our expanding knowledge of the neural bases of cognition. Linking specific models within the domain of VWM to broader neurocognitive architectures is critical if we are to understand the relationship between VWM and the wider perception-cognitionaction system within which it is embedded.

Appendix

Change Detection Experiment

Method

Participants

Nineteen University of Iowa undergraduates (12 females) participated in exchange for course credit. Participants received course credit for their participation. All reported normal or corrected-to-normal visual acuity and normal color vision.

Apparatus

Stimulus presentation was controlled by a Macintosh G4 computer running Matlab 5.2 using the Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997). Stimuli were presented against a gray background (28.73 cd/m²; R = 150, G = 150, B = 150) at a viewing distance of approximately 60 cm. They consisted of small colored squares (1 in. × 1 in., subtending approximately 2° × 2°. Nine colors were used for the squares: black (0, 0, 0), brown (164, 42, 42), green (0, 255, 0), cyan (0, 255, 255), blue (0, 0, 255), red (255, 0, 0), violet (238, 130, 238), yellow (255, 0, 0), and white (255, 255, 255). On each trial, the positions of the squares were randomly determined for the memory array with the constraint that none could appear within 1.5 in. of the edges of the monitor or other squares (for set sizes greater than one). The positions of the squares within the test array were identical to the memory array for each trial. Colors were selected randomly without replacement on every trial.

Procedure

Each trial began with a blank gray screen for 500 ms, followed by the memory array presented for 500 ms, a blank delay of 1 s, and the test array, which remained visible until a response was generated. Participants were instructed to indicate whether the color(s) within the test array were the same as the memory array, or if one color had changed; they entered their response on the computer keyboard by pressing “a” for “different” and “l” for “same” (keys were marked with stickers to help participants remember the mapping). Accuracy was emphasized over speed, and a short buzz sound was played following incorrect responses. Participants completed 12 practice trials followed by 240 test trials, 40 each at set sizes one through six, with breaks offered every 24 trials. On half of the trials (no-change trials), the test array matched the memory array; on the other half of trials (change trials), one item within the test array had changed to a new color, selected without replacement from the nine possible colors. Both set size and change type varied randomly across all trials. To prevent verbal recoding of the memory array colors, participants were instructed to repeat a randomly-generated three digit number throughout the experiment. A new number was generated to begin each block.

Results

Participants’ responses were classified as correct rejections, hits, misses, and false alarms across trials within each set size, as shown with bars in Figure 1B. We also computed overall percent correct for each set size, shown with the line in Figure 1B. Performance was near ceiling for small set sizes, with performance declining as set size increased and misses becoming more common than false alarms. To analyze performance, we conducted a one-way ANOVA with Set Size (one, two, three, four, five, six) as a within-subjects factor. This analysis revealed a significant effect of Set Size, F5, 90 = 27.24, p < .001, η2 = .52; follow-up Tukey HSD tests (p < .05) showed that performance was significantly lower in set size five than set sizes one and two, and in set size six compared to set sizes one through four; all other differences were not significant. We also computed capacity (K) for each participant using Pashler’s (1988) formula, K = SS * (H – FA) / (1 – FA), based on the hit (H) and false alarm (FA) rates for each set size (SS). Figure A1 shows each participant’s K estimates across set sizes, along with the mean K across participants. Because K can equal, at most, the set size for each block, we then selected each participant’s maximum estimate across set sizes (cf. Olsson & Poom, 2005; Simmering, 2012; Todd & Marois, 2005), to derive K_max for each participant. The mean K_max estimate across participants was 4.58 (SD = .078).

Figure A1.

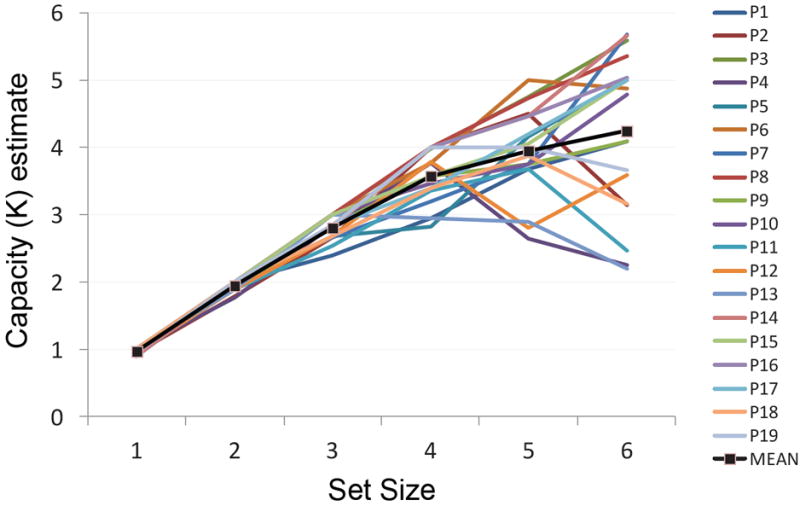
Capacity estimates (K) across set sizes (SS) for each participant (colored lines), as well as the mean across participants (black line).

Model Equations

Activation in the contrast field, CF(u), is captured by:

$$\begin{array}{c}\tau \dot{u}(x,t)=-u(x,t)+h_u+\int c_{\mathit{uu}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{uu}}(u(x^{\prime },t))d{x}^{\prime }-\int c_{\mathit{uv}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{uv}}(v(x^{\prime },t))d{x}^{\prime }\\ +a_{\mathit{uc}}{\mathrm{\Lambda }}_{\mathit{uc}}(r_c(t))+S(x,t)+(C_{\mathit{ud}}\ast r_d)+\mathit{noise}\end{array}$$ (1)

where u̇(x,t) is the rate of change of the activation level for each neuron across the spatial dimension, x, as a function of time, t. The constant τ determines the time scale of the dynamics (Erlhagen & Schöner, 2002). The first factor that contributes to the rate of change of activation in CF(u) is the current activation in the field, -u(x,t), at each site x. This component is negative so that activation changes in the direction of the resting level h_u. The resting level included colored noise, which was determined by the equation τ_h ḣ(t) = −h(t)+q_h *noise, in which the current resting state is increased or decreased by a random amount (q_h* noise) at each time step; q_h was set to 6 and τ_h was 80. This is termed colored noise because the value at each time step is partially determined by the value at the previous time step; this contrasts with white noise, which is independent across time steps.

Next, activation in CF(u) is influenced by the local excitation / lateral inhibition interaction profile, defined by self-excitatory projections, ∫ c_uu (x − x′) Λ_uu (u (x′, t))dx′, and inhibitory projections from Inhib(v), ∫ c_uv (x − x′) Λ_uv (v (x′, t))dx′. These projections are defined by the convolution of a Gaussian kernel with a sigmoidal threshold function. In particular, the Gaussian kernel is specified by:

$$c(x-x\prime )=c\exp \left[-\frac{{(x-x\prime )}^2}{2{\sigma }^2}\right]-k,$$ (2)

with strength, c, width, σ, and resting level, k. The sigmoidal function is given by:

$$\mathrm{\Lambda }(u)=\frac{1}{1+\exp [-\beta u]},$$ (3)

where β is the slope of the sigmoid, that is, the degree to which neurons close to threshold (i.e., 0) contribute to the activation dynamics. Lower slope values permit graded activation near threshold to influence performance, while higher slope values ensure that only above-threshold activation contributes to the activation dynamics. At extreme slope values, the sigmoid function approaches a step function. For all simulations presented here, β = 0.5.

Inputs to the model take the form of a Gaussian:

$$S(x,t)=c\exp \left[-\frac{{(x-x_{\mathit{center}})}^2}{2{\sigma }^2}\right]{\chi }^{(t)},$$ (4)

centered at x_center, with width, σ, and strength, c. These inputs can be turned on and off through time (e.g., as items appear and then disappear). This time interval is specified by the pulse function χ^(t).

Next, a global input to the field is projected from the different response node (r_d) when the activation of the node is above zero. Lastly, activation within the field is influenced by the addition of a stochastic component consisting of spatially correlated noise:

$$\mathit{noise}=q\int d{x}^{\prime }{g}_{\mathit{noise}}(x-x^{\prime })\xi (x^{\prime },t).$$ (5)

Noise was added to the simulations by convolving a noise field composed of independent noise sources with a Gaussian kernel specified by:

$$g_{\mathit{noise}}(x-x^{\prime })=\frac{1}{\sqrt{2{\sigma }_{\mathit{noise}}}}\exp \left[-\frac{{(x-x^{\prime })}^2}{2{\sigma }_{\mathit{noise}}^2}\right],$$ (6)

where σ_noise is the spatial spread of the noise kernel (set to 10 in all simulations). (For discussion of the differences between spatially correlated noise and Gaussian white noise, see Schutte et al., 2003).

The second layer of the model, Inhib(v), is specified by the following equation:

$$\begin{array}{c}\tau \dot{v}(x,t)=-v(x,t)+h_v+\int c_{\mathit{vu}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{vu}}(u(x^{\prime },t))d{x}^{\prime }\\ +\int c_{\mathit{vw}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{vw}}(w(x^{\prime },t))d{x}^{\prime }+\mathit{noise}.\end{array}$$ (7)

As before, v̇(x, t) specifies the rate of change of activation across the population of feature-selective neurons, x, as a function of time, t; the constant τ sets the time scale (note that the time scale for inhibition is faster than for the excitatory layers, i.e., τ_v < τ_u); v(x, t) captures the current activation of the field; and h_v sets the resting level of neurons in the field. As with CF(u), colored noise was added to the resting level. Inhib(v) receives activation from two projections: one from CF(u), ∫ c_vu (x − x′) Λ_vu (u(x′, t))dx′; and one from WM(w), ∫ c_vw (x − x′) Λ_vw (w(x′, t))dx′.

As described above, projections are defined by the convolution of a Gaussian kernel (Equation 2) with a sigmoidal threshold function (Equation 3). Finally, this field also receives spatially-correlated noise, as described above. This noise is independent from the noise sources in the other layers of the model.

The third layer of the model, WM(w), is governed by the following equation:

$$\begin{array}{ll}\tau \dot{w}(x,t)& =-w(x,t)+h_w+\int c_{\mathit{ww}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{ww}}(w(x^{\prime },t))d{x}^{\prime }-\int c_{\mathit{wv}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{wv}}(v(x^{\prime },t))d{x}^{\prime }\\ & +a_{\mathit{wn}}{\mathrm{\Lambda }}_{\mathit{wn}}(r_n(t))+\int c_{\mathit{wu}}(x-x^{\prime }){\mathrm{\Lambda }}_{\mathit{wu}}(u(x^{\prime },t))d{x}^{\prime }+c_{s}S(x,t)+\mathit{noise}.\end{array}$$ (8)

Again, ẇ(x, t) is the rate of change of activation across the population of feature-tuned neurons, x, as a function of time, t; the constant τ sets the time scale; w(x,t) captures the current activation of the field; and h_w sets the resting level. As with CF(u), colored noise was added to the resting level. WM(w) receives self excitation, ∫ c_ww (x − x′) Λ_ww (w(x′, t))dx′, lateral inhibition from Inhib(v), ∫ c_wv (x − x′) Λ_wv (v (x′, t))dx′, and excitatory input from CF(u), ∫ c_wu (x − x′) Λ_wu (u(x′, t))dx′.

This field also receives direct target inputs, S(x,t), scaled by c_s to be weaker (i.e., c_s < 1), and includes spatially-correlated noise as described above. Again, this noise is independent from the noise sources in the other layers of the model.

The neurons in the response layer are governed by the following equations:

$$\tau {\dot{r}}_d(t)=-r_d+h_d+c_{\mathit{dd}}{\mathrm{\Lambda }}_d(r_d)-c_{\mathit{sd}}{\mathrm{\Lambda }}_s(r_s)+a_{\mathit{dg}}{\mathrm{\Lambda }}_{\mathit{dg}}(g(t))+{\mathrm{\Lambda }}_{\mathit{dg}}(g(t))\int c_{\mathit{du}}{\mathrm{\Lambda }}_u(u(x^{\prime },t))d{x}^{\prime }+\mathit{noise}$$ (9)

$$\tau {\dot{r}}_s(t)=-r_s+h_s+c_{\mathit{ss}}{\mathrm{\Lambda }}_s(r_s)-c_{\mathit{sd}}{\mathrm{\Lambda }}_d(r_d)+a_{\mathit{sg}}{\mathrm{\Lambda }}_{\mathit{sg}}(g(t))+{\mathrm{\Lambda }}_{\mathit{sg}}(g(t))\int c_{\mathit{sw}}{\mathrm{\Lambda }}_w(w(x^{\prime },t))d{x}^{\prime }+\mathit{noise}$$ (10)

The rate of change of each neuron’s activation, ṙ (where the constant τ determines the timescale and the subscripts d and s denote the different and same neurons, respectively), is determined by the current activation level, -r, and the resting level of the neuron activation, h_r. Each neuron has a self-excitatory connection, c_ddΛ_d(r_d) or c_ssΛ_s(r_s), and receives inhibition from the other neuron, c_dsΛ_ds(r_s) or c_sdΛ_sd(r_d). Additionally, the different neuron receives summed excitatory input from CF(u), ∫c_du Λ_u (u(x′, t))dx′, and the same neuron receives summed excitatory input from WM(w), ∫c_sw Λ_w (w(x′, t))dx′.

Activation to the neurons was controlled by a gating system, given by the following equation, which served as an indication of when a response was required in the task.

$$\tau {\dot{r}}_g(t)=-r_g+h_g+c_{\mathit{gg}}{\mathrm{\Lambda }}_g(r_g)+\int c_{\mathit{gw}}{\mathrm{\Lambda }}_w(w(x^{\prime },t))d{x}^{\prime }+c_{\mathit{tar}}+c_{\mathit{trans}}+\mathit{noise}$$ (11)

This system consisted of a single neuron that received input from the stimulus presentation and WM(w); as such, activation of this neuron only passed threshold when one or more items (peaks) was held in WM(w) and the stimulus was present. The stimulus presentation consisted of both a constant input while the arrays were present (c_tar), as well as a transient input (c_trans, for 30 ms) at the onset of the stimulus. These combined inputs, combined with input from WM(w) drove activation of the gate neuron above threshold; throughout each trial, this neuron’s activation was sigmoided and multiplied by the activation from CF(u) and WM(w) to the decision nodes. In this case, activation from the fields to the decision nodes was only robust when the gate node was activated above threshold.

Lastly, noise represents white noise added to the activation of the two decision neurons and gate neuron at each time step. The noise sources are independent for each neuron.

Model Parameters and Fits

We began with parameters from Johnson et al. (2009)³, with the exception of the gating neuron, which was not used in Johnson et al.’s model. Our behavioral task differed from theirs in three ways. First, Johnson et al. tested only set size three, whereas we tested set sizes one through six. Second, Johnson et al. used a single-item test array rather than the whole-array test we used. Third, our stimuli were selected randomly on each trial from a pre-determined set of nine colors; Johnson et al. selected from a continuous color space with 180 possible colors equally distributed in CIELAB 1976 color space with some constraints on their separations (see Johnson et al., 2009, for details). These changes were straight-forward to implement in the model, first by changing how many stimuli were presented to the model in the memory and test arrays, and then by defining the colors as equally distributed through the 360° color space.

Despite these changes in the task, the parameters from Johnson et al. (2009) provided a relatively good fit to our data. We chose to modify the parameters slightly to achieve a closer fit, eventually producing means for each trial type at each set size that were within one standard deviation of the behavioral means (see Table 2). The mean absolute error of the model relative to the behavioral data was 2.26%, which is about one-third the overall standard deviation of 10.73%. Thus, the performance of the model was well within the range of typical participants in this task.

To accomplish this fit, we began with the parameters from Johnson et al. (2009) and modified three parameters within the fields: increasing the resting level of CF(u) from -7 to -6.75, decreasing the resting level of WM(w) from -4 to -4.5, and increasing self-excitation in the WM layer from 1.5 to 1.6; these changes were necessary to accommodate the range of set sizes used and the whole-array test, as opposed to all set size three trials with single-item test in Johnson et al. We also added excitatory projections from the decision neurons to their associated neural layer. These were used to help stabilize activation within the system once a decision was made. For the decision system, we added the gate neuron to control the projections to the decision neurons. We also changed the following parameters within the decision neurons: increased the resting level of the same node from -5 to -4.35; made the projections from CF(u) to the different node stronger, from 1 to 1.4 and made the projection from the WM (w) to the same neuron stronger, from 0.01 to 0.025; and decreased the strength of noise on the decision neurons from 0.1 to 0.065. The complete parameter set is shown in Table A1.