Desolvation Costs of Salt Bridges across Protein Binding Interfaces: Similarities and Differences between Implicit and Explicit Solvent Models

Abstract

The prevalence of salt bridges across protein binding interfaces is surprising given the significant costs of desolvating the two charged groups upon binding. These desolvation costs, which are difficult to examine using laboratory experiments, have been computed in previous studies using the Poisson−Boltzmann (PB) implicit solvent model. Here, for the first time, we directly compare the PB implicit solvent model with several explicit water models in computing the desolvation penalties of salt bridges across protein−protein interfaces. We report both overall agreement as well as significant differences between the implicit and explicit solvent results. These differences highlight challenges to be faced in the application of implicit solvent methods.

Protein binding interactions often involve salt bridges, that is, pairs of oppositely charged residues that are within hydrogen-bonding distance. On the basis of theoretical studies, salt bridges are thought to make surprisingly little (or even no) favorable contribution to protein folding or binding due to the significant cost of desolvating the two charged salt bridge partners.¹⁻⁵ For efficient computations, these previous studies all used a dielectric continuum solvent model based on the Poisson−Boltzmann (PB) equation. This model, which is the gold standard of implicit solvent models, has been successfully parametrized to reproduce solvation free energies of small molecules determined by either experiment⁶ or simulations^7,8 with explicit water molecules. However, the PB model lacks important molecular details of the first solvation shell and a description of nonpolar contributions to solvation.⁹ Valuable insights about modeling solvation can therefore be obtained by comparing explicit and implicit solvent calculations.⁹⁻¹³

Here, for the first time, we directly compare the PB implicit solvent model with several explicit water models in computing the desolvation penalties of salt bridges across protein−protein binding interfaces. We performed both implicit and explicit solvent calculations on all 14 salt bridges across the binding interfaces of four protein−protein complexes (Figure S1, Supporting Information) that were identified by a previous study as having a wide range of desolvation penalties.⁵ We computed the desolvation penalty for each salt bridge upon binding relative to its hydrophobic isostere, that is, a hypothetical mutant version that has all partial charges on the salt bridge side chains set to 0; this desolvation penalty is reported as ΔΔG_solv. In the explicit solvent calculations, this desolvation penalty was computed using thermodynamic integration techniques (see Methods). As done in previous theoretical studies, we focused on rigid binding, with the unbound conformations of the proteins being identical to the corresponding bound conformations. To circumvent convergence problems associated with net-charged systems in explicit solvent calculations,¹⁴ we represented the unbound state, in both the implicit and explicit solvent calculations, with proteins separated by 30 Å (between their centers of mass) and simultaneously turned off the charges of the oppositely charged side chains of the salt bridge; this was done in both the unbound and bound states of the proteins.

In order to directly compare the solvation thermodynamics of the implicit and explicit water models, it was essential to keep the proteins completely rigid, even in the explicit solvent molecular dynamics (MD) simulations. A direct comparison also required that we fix all other parameters common to the two approaches to ensure that they remained absolutely identical, that is, protein coordinates, atomic charges and radii (OPLS-AA/L force field),¹⁵ box volume, and temperature. MD simulations were performed with periodic boundary conditions and a PME treatment of long-range electrostatics.¹⁶ Periodic boundary conditions were also employed in the PB calculations, implicitly including long-range electrostatic interactions with all periodic images. Implicit and explicit solvent calculations were performed using the DelPhi¹⁷ and GROMACS¹⁸ software packages, respectively. Three different water models were explored in the explicit solvent calculations, TIP3P,¹⁹ TIP4P,¹⁹ and SPC/E.²⁰ To represent the boundary between the low-dielectric protein region and high-dielectric solvent region in the implicit solvent calculations, we focused primarily on the molecular surface of the protein,²¹ which is the standard representation; calculations were also performed using the van der Waals surface, which has been proposed as an alternative^22,23 but led to comparable results (see below).

As shown in Figure 1A, the desolvation penalties estimated by implicit solvent calculations are strongly correlated with those from explicit solvent calculations with the TIP3P water model (R² = 0.996). An equally strong correlation results when the TIP4P and SPC/E water models are used (R² of 0.993 and 0.992, respectively; Figure S2, Supporting Information). The overall agreement between the results from implicit and explicit water models is surprisingly good, given the dramatic differences in their representations of solvent and given the large range of the desolvation penalties (∼10 to ∼210 kcal/mol). These results provide important reinforcement, therefore, of the widely appreciated utility of Poisson-based calculations for modeling solvation effects in charged, biomolecular systems.

Figure 1.

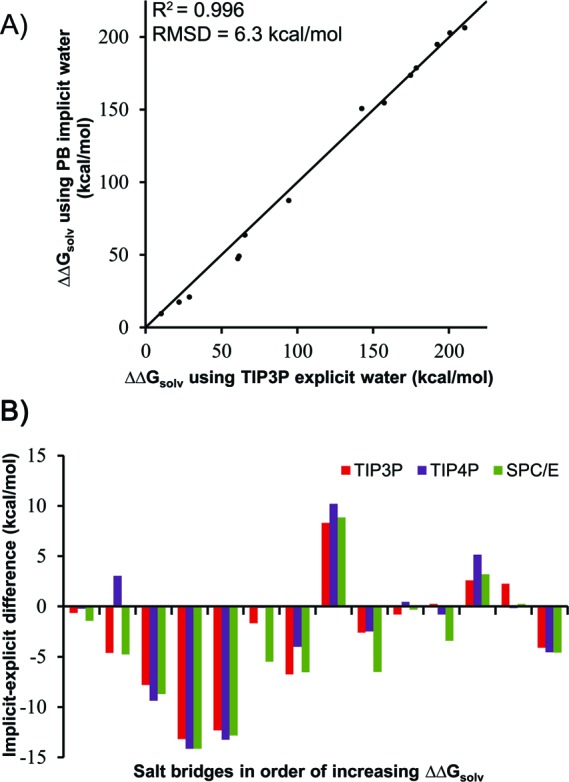
(A) Comparison of implicit and explicit solvent models for computing desolvation penalties of salt bridges upon protein binding (ΔΔG_solv). The dielectric boundary in the implicit solvent calculations was represented by the molecular surface of the protein. The diagonal line represents perfect agreement. Error bars are included but difficult to see since they are small (<2 kcal/mol). (B) Implicit−explicit differences for each salt bridge.

That said, a closer examination of the results reveals significant discrepancies between the implicit and explicit solvent predictions; the rms deviations between the predictions for all salt bridges are 6.3, 6.8, and 7.1 kcal/mol for the TIP3P, TIP4P, and SPC/E water models, respectively, which correspond to relative rms deviations of 5.5, 6.0, and 6.2%, respectively (absolute rms deviation divided by the average ΔΔG_solv of the explicit water model). Notably, the implicit−explicit discrepancies for individual salt bridges are largely independent of the explicit water model (Figure 1B). Results among the three explicit solvent models are comparable, with rms deviations of 2.6, 1.9, and 3.0 kcal/mol for TIP4P versus TIP3P, SPC/E versus TIP3P, and SPC/E versus TIP4P, respectively (Figure 2). These findings not only provide further confidence in the explicit solvent calculations, they also strongly suggest that the discrepancies reflect key differences between implicit and explicit models of solvation.

Figure 2.

Comparison of explicit solvent models for computing desolvation penalties of salt bridges upon protein binding (ΔΔG_solv). Diagonal lines represent perfect agreement. Error bars are included but difficult to see since they are small.

To investigate the source of the discrepancies between the implicit and explicit solvent results, we also performed calculations on the same 14 salt bridges in the absence of the protein environment, that is, with the same geometries, but in solution and with the residues capped with acetyl and N-methyl groups at the N- and C-termini, respectively. In this second set of explicit solvent calculations, only the TIP3P water model was used. The rms deviation between the implicit and explicit solvent results is significantly reduced from 6.3 to 1.8 kcal/mol when the protein environment is replaced by solvent (Figure 3). It appears, therefore, that the protein environment, and the solvent’s response to it, is the primary source of the deviations observed between implicit and explicit solvent calculations.

Figure 3.

Comparison of implicit and explicit solvent models for computing desolvation penalties of salt bridges upon association in the absence of the protein environment (ΔΔG_solv). The dielectric boundary in the implicit solvent calculations was represented by the molecular surface of the protein. The diagonal line represents perfect agreement. Error bars are included but difficult to see since they are small.

Representation of the protein environment in the implicit solvent calculations is influenced not only by the protein dielectric constant but also by the dielectric boundary between the protein and solvent regions. In addition to using the molecular surface of the protein to represent the dielectric boundary, which is traced out by a spherical “water” probe with a radius of 1.4 Å, we also tested the van der Waals surface. However, the resulting (implicit) desolvation penalties were found to be comparable to those associated with the molecular surface, with rms deviations of 5.9 kcal/mol from the TIP3P explicit solvent calculations, for example (Figure S2, Supporting Information). Interestingly, although the molecular surface with the current set of atomic radii underestimates the solvation free energies of the salt bridges relative to their hydrophobic isosteres (ΔG_solv^(un)bound) in the unbound and bound states (Figure S3, Supporting Information), the differences between the two states (ΔΔG_solv) are underestimated for some of the salt bridges and overestimated for others when compared to explicit solvent calculations (Figure 1A).

To determine why certain salt bridges have larger implicit−explicit differences than others, we plotted these differences versus (a) ΔΔG_solv and (b) the percent burial upon binding; both van der Waals and molecular surface implicit solvent results were considered. Only the plot involving the van der Waals surface and percent burial resulted in any correlation (R² of 0.320; Figure S4, Supporting Information). We also looked for a correlation between implicit−explicit differences and the involvement of the salt bridge in a “network” where at least one of the charged partners forms another salt bridge;^5,24 however, no correlation was found (Table S2, Supporting Information). We did find a significant correlation between the magnitude of implicit−explicit differences in the solvation free energy of the salt bridge in its bound state relative to its hydrophobic isostere, ΔG_solv^bound, and the probability of observing “bridging” water molecules in the explicit solvent simulations when the molecular surface was used (Figure 4); no correlation was found when the van der Waals surface was used (Figure S5, Supporting Information). We tried reducing implicit−explicit differences by using a lower solvent dielectric constant for the implicit solvent calculations that is more representative of the explicit solvent models (i.e., 52, the dielectric constant of TIP4P, since this value is the lowest among the explicit solvent models tested),²⁵ but this lower value had no effect (Table S3, Supporting Information). Finally, we considered reducing implicit−explicit differences by either increasing the protein dielectric constant or scaling the atomic radii in the implicit solvent calculations. However, these approaches would underestimate the desolvation penalties for some salt bridges and overestimate those for others, even in the absence of their protein environments (as is evident in Figure 3).

Figure 4.

Correlation of the magnitude of implicit−explicit differences in ΔG_solv^bound versus the probability of observing bridging water molecules during simulations in TIP3P explicit water when the dielectric boundary in the implicit solvent calculations is represented by the molecular surface of the protein. Probabilities were computed from conformations sampled every ps during the 1 ns simulations. Water molecules were defined as bridging if they form hydrogen bonds with both salt bridge partners in their bound state. A hydrogen bond was defined as having a hydrogen−acceptor length of 2.5 Å and a donor−hydrogen−acceptor angle of more than 90°. The diagonal line represents perfect agreement.

In closing, we have performed the first direct comparison of implicit and explicit solvent models for use in evaluating free-energy contributions of salt bridges to protein−protein binding. We have demonstrated that the desolvation penalties of salt bridges upon protein binding are of similar magnitudes when estimated using implicit and explicit solvent models. Nonetheless, significant discrepancies exist for particular salt bridges. Given that bridging water molecules have been shown to be a source of discrepancies in other studies,^10,11 hybrid implicit−explicit solvent models might be an attractive alternative approach.²⁶ Since the set of salt bridges⁵ studied here highlights challenges to be faced in the application of implicit solvent methods, it might also provide valuable test cases for the development of improved fast solvation models.

Methods

To directly compare the solvation thermodynamics of the implicit and explicit solvent approaches, we kept the proteins rigid and fixed all parameters common to the approaches to be identical, that is, protein coordinates, atomic charges and radii (OPLS/AA-L force field),¹⁵ box volume, and temperature. To enable a consistent treatment of long-range electrostatics, periodic boundary conditions were employed in both approaches, enabling the use of the PME method¹⁶ for the explicit solvent calculations; all systems were electrically neutral. Details of the protein models are provided in Supporting Information. Desolvation penalties of salt bridges upon protein binding (ΔΔG_solv) were computed according to the thermodynamic cycle shown in Figure S6 (Supporting Information).

Implicit Solvent Calculations. Implicit solvent calculations were performed using finite difference methods, as implemented in the DelPhi 4.0 software package,¹⁷ to solve the linearized form of the PB equation (which reduces to the Poisson equation in the absence of salt, as in our calculations). In particular, electrostatic contributions to solvation free energies were computed for each wild-type salt bridge and its hydrophobic isostere in the unbound and bound protein states; these contributions were determined by first directly calculating the induced polarization charges and then calculating the interaction between the protein charges and the reaction field due to the polarization charges.²³ The electrostatic contribution to the solvation free energy of the salt bridge relative to its hydrophobic isostere in the unbound or bound state yielded the solvation free energies ΔG_solv^unbound or ΔG_solv, respectively. The desolvation penalty of each salt bridge upon protein binding relative to its hydrophobic isostere was computed using ΔΔG_solv = ΔG_solv^unbound − ΔG_solv (see Figure S6, Supporting Information).

Calculations of each state of the system were performed 14 separate times, with systematic molecular translations on the grid at 25 °C. Results reported are averages of 14 calculations, with uncertainties represented by the standard deviation. Each calculation was carried out for 10000 steps to satisfy a convergence criterion of 0.001 kT/e in the potential. To avoid errors in the dielectric boundary, the OPLS/AA-L radii of polar hydrogen atoms were converted from 0 to the default value of 1.0 Å. To represent the dielectric boundary, we tested both the molecular (default)²¹ and van der Waals surfaces of the protein. Consistent with keeping the proteins rigid, a dielectric constant of 1 was used for the protein region; to represent the dielectric properties of water at 25 °C, a dielectric constant of 78.4 was used for the solvent region. A grid resolution of 0.33 Å/(grid units) was used for all protein systems, except for the neuraminidase−antibody complex, which was limited to a slightly lower resolution of 0.37 Å/(grid units) due to its large size. Grid dimensions for the barnase−barstar, growth hormone−receptor, neuraminidase−antibody, and RafRBD−Rap1A complexes were 343 × 343 × 343, 403 × 403 × 403, 479 × 479 × 479, and 361 × 361 × 361, respectively. Each calculation required 1.5−4 CPU hours on a single core of a dual-core 2.6 GHz Opteron node.

Explicit Solvent Calculations. Explicit solvent calculations were performed using the thermodynamic integration approach²⁷ with explicit solvent MD simulations, as implemented in the GROMACS 4.0.4 software package.¹⁸ In particular, we first computed differences in the overall free energy of each salt bridge relative to its hydrophobic isostere in its unbound and bound states ΔG^(un)bound, which is the sum of contributions from both nonbonded protein−protein and protein−solvent interactions, ΔG_protein^(un)bound and ΔG_solv, respectively. Next, to obtain differences in solely the solvation free energies, all nonbonded protein−protein interactions were subtracted from differences in the overall free energies. Finally, the desolvation penalty of each salt bridge upon protein binding relative to its hydrophobic isostere was computed using ΔΔG_solv = ΔG_solv^unbound − ΔG_solv.

Differences in the overall free energies of each salt bridge relative to its hydrophobic isostere in its unbound and bound states were computed using the following

1

where H(λ) is the system Hamiltonian as a function of the coupling parameter λ and the brackets represent ensemble averaging at a given λ value; the λ values of 0 and 1 represent the wild-type and hydrophobic isostere versions of the salt bridge, respectively. Separate MD simulations of the proteins (unbound and bound states) were performed at each of the following eight λ values, linearly discharging the side chains of the salt bridge: 0, 0.15, 0.3, 0.45, 0.6, 0.75, 0.9, and 1. The trapezoidal method was then used to numerically solve the thermodynamic integral to obtain ΔG^(un)bound. Uncertainties in the free energies were derived from sampling errors in ⟨∂H(λ)/∂λ⟩_λ; errors at each λ value were estimated using block averaging,²⁸ as implemented in the g_analyze utility of GROMACS.¹⁸

MD simulations were performed with explicit solvent (TIP3P,¹⁹ TIP4P,¹⁹ or SPC/E)²⁰ in the NVT ensemble, with the number of atoms in the unbound and bound states of each system enforced to be exactly the same (see Supporting Information). Proteins were kept rigid throughout the simulations using the GROMACS “frozen” option, setting velocities of all protein atoms to 0. Real space electrostatic interactions were truncated at 10 Å, while the long-range components of these interactions were calculated using the PME method¹⁶ with periodic boundary conditions, a spline order of 6, Fourier spacing of 1.0 Å, and relative tolerance of 10⁻⁶ between long- and short-range energies. van der Waals interactions were switched off smoothly between 8 and 9 Å. Each λ simulation was performed for 1 ns at constant temperature (25 °C) and volume. Prior to each λ simulation, the solvent was equilibrated in two stages, (1) 10 ps at constant temperature (25 °C) and volume and (2) 100 ps at constant temperature (25 °C) and pressure (1 atm). The Langevin thermostat (frictional constant of 1 ps⁻¹) and a weak Berendsen barostat²⁹ (coupling time constant of 5 ps) were used to maintain constant temperature and pressure, respectively. A 2 fs time step was used for all simulations. Each λ simulation required 1−6 CPU days on a dual-quad core 2.66 GHz Xeon node.

Supporting Information Available

Full details of protein models; Figures S1−S6; and Tables S1−S3. This material is available free of charge via the Internet at http://pubs.acs.org.