Skip to main content
PMC home page
Taylor & Francis Open Select logoLink to Taylor & Francis Open Select
. 2014 May 1;17(13):1502–1517. doi: 10.1080/10255842.2014.899588

Development and validation of a computational model of the knee joint for the evaluation of surgical treatments for osteoarthritis

R Mootanah a,b,*, CW Imhauser c, F Reisse a, D Carpanen a, RW Walker a, MF Koff d, MW Lenhoff b, SR Rozbruch e, AT Fragomen e, Z Dewan b, YM Kirane e, Pamela A Cheah a,f, JK Dowell a,f,g, HJ Hillstrom a,b
PMCID: PMC4047624  PMID: 24786914

Abstract

A three-dimensional (3D) knee joint computational model was developed and validated to predict knee joint contact forces and pressures for different degrees of malalignment. A 3D computational knee model was created from high-resolution radiological images to emulate passive sagittal rotation (full-extension to 65°-flexion) and weight acceptance. A cadaveric knee mounted on a six-degree-of-freedom robot was subjected to matching boundary and loading conditions. A ligament-tuning process minimised kinematic differences between the robotically loaded cadaver specimen and the finite element (FE) model. The model was validated by measured intra-articular force and pressure measurements. Percent full scale error between EE-predicted and in vitro-measured values in the medial and lateral compartments were 6.67% and 5.94%, respectively, for normalised peak pressure values, and 7.56% and 4.48%, respectively, for normalised force values. The knee model can accurately predict normalised intra-articular pressure and forces for different loading conditions and could be further developed for subject-specific surgical planning.

Keywords: subject-specific finite element knee model, knee joint contact mechanics, osteoarthritis, model validation, in vitro cadaveric test, lower limb malalignment

Introduction

Osteoarthritis (OA) is a degenerative disease that often leads to significant pain, loss of joint function and is the leading cause of physical disability in the elderly (Cooper et al. 2013). The World Health Organization reported that OA accounted for 1 % of total deaths in 2002 worldwide and was projected to be the tenth leading cause of disability adjusted life years (2.5 %) in high-income countries by 2015 (Mathers and Loncar 2006). About 14% of men and 23% of women over 45 years of age in the USA and Europe show radiographic signs of knee OA (Valkenburg 1980). The total annual cost of OA to the UK economy is estimated at £12 billion (1% of the annual gross national product) and $185.5 billion to the USA (Mathers and Loncar 2006).

Joint malalignment is a strong predictor of the development and progression of OA (Petersson and Jacobsson 2002). Absent a cure, current therapeutic approaches cannot arrest or reverse disease progression for OA. As little as 5° of varus malalignment increases the compressive forces in the medial compartment from 70% to 90% of the total knee joint load (Tetsworth and Paley 1994). A slight malalignment may initiate a vicious cycle where the increased compartment pressures produce more laxity and joint deformity, thereby increasing malalignment perpetuating the process (Coventry 1965, 2001). A prospective study by Sharma et al. (2001) suggested that knee OA can progress in as little as 18 months if treated in a palliative manner (Sharma et al. 2001).

Excessive joint pressure is considered the common pathway that damages tissues within the diarthrodial joint. The effect of different treatment strategies on the magnitude of knee joint contact loading and compartmental distribution is not well understood. Furthermore, planning surgical procedures to relieve damaged tissues from excessive loading is limited.

High tibial osteotomy (HTO) is a surgical technique used to correct lower limb malalignment in mild to moderate knee OA patients (Coventry 1965). The clinical standard of care is for surgeons to use a two-dimensional (2D) frontal plane radiograph to plan alignment correction, based on reducing the deviation from the knee centre to the mechanical axis (a line connecting the centres of the hip to the ankle). This procedure has met with inconsistent results and differing 10-year survivorships (Rinonapoli et al. 1998; Virolainen and Aro 2004; Dowd et al. 2006). However, given that the HTO does not violate the joint, it may be considered a conservative procedure for treating knee OA.

Computer modelling (Specogna et al. 2007; Bhatnagar and Jenkyn 2010), cadaveric and gait (Johnson et al. 1980; Andriacchi et al. 2000; Hurwitz et al. 2002) studies have contributed some basic understanding (Andriacchi et al. 2000; Chao 2003; Zhim et al. 2005; Agneskirchner et al. 2006) of the procedure but no method currently exists to plan malalignment correction to minimise excessive knee joint pressure (Dorsey et al. 2006; Esenkaya et al. 2007; Bhatnagar and Jenkyn 2010). The 2D model implemented in the OASIS software by Chao et al., although capable of estimating contact forces, cannot predict contact stress (Chao and Sim 1995; Chao 2003). Furthermore, Chao's model is constrained to the frontal plane and is limited in its capability to evaluate loading response at different sagittal knee flexion angles to simulate peak loading during the gait cycle.

The specific aims of this study were to develop and validate a three-dimensional (3D) computational knee joint model. Model validation was carried out by comparing the predicted knee joint contact mechanics with those obtained from in vitro experiments, using the same cadaveric knee from which the model was built and identical loading conditions.

We hypothesise that tibio-femoral contact mechanics (normalised peak pressure, force and compartmental force distribution) of the cadaver specimen and corresponding finite element (FE) model predictions will agree within 10% for the same boundary conditions.

Methods

A subject-specific FE model of a cadaveric knee joint was created and compared with in vitro testing that emulated the end of weight acceptance during the stance phase of gait, when the knee is subjected to high loads. This model is an implicit quasi-static model. Loading levels were changed very slowly in the cadaver testing. Discrete loads were applied to the FE model (axial force and bending moments) and the resulting joint contact forces and stress were computed.

Model specimen

The left lower extremity of an anonymous 50-year-old male was obtained from a tissue bank, screened negative for blood-borne pathogens, truncated to 15 cm above and below the knee joint, secured in a sealed plastic bag and taken to the Hospital for Special Surgery (HSS) Radiology Department for magnetic resonance imaging (MRI).

3D imaging protocol of the knee

MRI data of the knee joint were generated with different contrast mechanisms. Scanning was carried out on a clinical 3.0 T system (GE Healthcare, Waukesha, WI, USA), using an eight-channel transit-receive phased array knee coil (Invivo, Orlando, FL, USA). Two scanning sequences (3D T1-weighted frequency selective fat-suppressed spoiled gradient recalled echo (SPGR) and 3D CUBE) were acquired to generate a volumetric data-set for segmentation of cartilage, bone, meniscus, and ligament structures to visualise each tissue (Figure 1).

Figure 1.

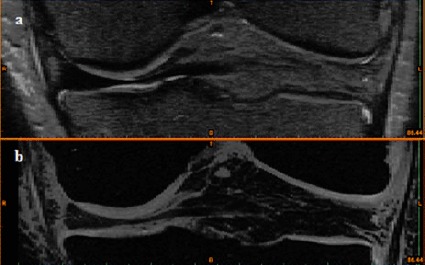
Figure 1.

Open in a new tab

MRI images of the frontal view of the knee joint in (a) CUBE sequence for representation of meniscus and ligament and (b) SPGR sequence for representation of cartilage and bone.

Acquisition parameters for the 3D SPGR sequence were as follows: TE, 3 ms; TR, 14.6 ms; acquisition matrix, 512 × 512; number of excitations, 2; field-of-view, 15 cm; slice thickness, 0.6 mm; receiver BW, ± 41.7 kHz. Parameters for the 3D CUBE sequence were as follows: TE, 33 ms; TR, 2500 ms; acquisition matrix, 512 × 512; number of excitations, 0.5; field-of-view, 15 cm; slice thickness, 0.6 mm; echo train length, 42; receiver BW, ±41.7 kHz. The in-plane resolution for both series was 0.29 mm × 0.29 mm.

Dicom images of the MRI data-sets were imported into Mimics V14.2 (Materialise, Leuven, Belgium). The CUBE sequence was used to create 3D representations of the menisci and ligaments. The SPGR sequence was used to create representations of the bones and cartilage. Tissue segmentation was carried out using the interactive 3D LiveWire tool, which is particularly suitable for low contrast images (Figure 2) to create 3D masks of the different tissues. The masks were then used to create individual 3D models of the different knee structures.

Figure 2.

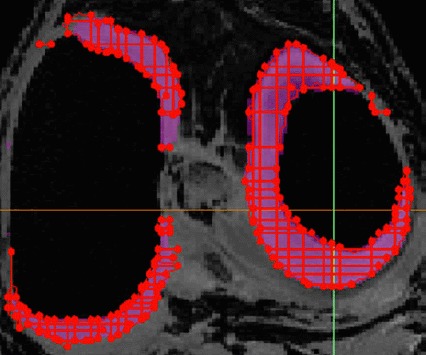
Figure 2.

Open in a new tab

3D LiveWire algorithm used to create geometries of the different tissues.

Surfaces defining ligament attachment on bones were created, using the computer-aided design (CAD) and primitive modules of Mimics in preparation for loading and boundary conditions in the FE model. The surface mesh was smoothed and re-meshed, using the three-matic module of Mimics to minimise the surface irregularities, number of tiny elements and unnecessary computational burden.

3D assembly of the knee joint model

The creation of adjacent anatomical structures in any CAD package inevitably results in gaps or overlaps at surfaces in contact. To avoid contact boundary gaps or overlaps when creating the FE model, common borders between adjacent masks were created using the ‘non-manifold assembly’ algorithm, a useful tool in Mimics for structures with complex and irregular geometries.

As an illustration, to create the cartilage–femur non-manifold assembly, the femur surface geometry was used to identify the femur–cartilage common boundary. The inner cartilage surface was made to penetrate the distal femur to eliminate any gap at the interface (Figure 3(a)). The non-manifold assembly tool was then used to superimpose the femur boundary on the femoral cartilage to eliminate the cartilage region that overlapped into the femur (Figure 3(b)). This process ensured a matching contact boundary and subsequent convergence of computational analyses. It was repeated until all anatomical structures comprising the knee joint were included. A 3D surface assembly model of the knee joint was created and exported to CATIA V5R18 CAD package (Dassault Systèmes, Vélizy-Villacoublay, France), where solid geometries of the different tissues were created to generate a 3D solid FE knee joint assembly model (Figure 4).

Figure 3.

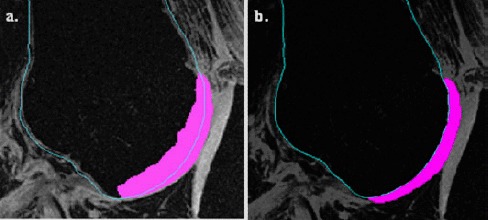
Figure 3.

Open in a new tab

The use of the ‘non-manifold algorithm’ to create common contact areas between adjacent tissue, such as the distal femur and femoral cartilage. (a) The inner geometry of the cartilage was overestimated to protrude into the femur and eliminate any gap at the femur-cartliage boundary. (b) The non-manifold assembly technique superimposed the accurately identified femur with the overestimated cartilage image to remove overlaps between the femur and cartilage, creating a common boundary between the adjacent femur and cartilage surfaces.

Figure 4.

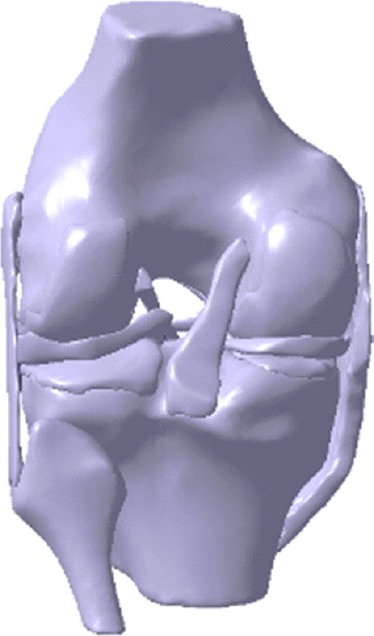
Figure 4.

Open in a new tab

3D solid geometry of the knee joint assembly created in CATIA CAD package.

FE model of the knee joint

Geometry

The solid 3D knee joint assembly model (Figure 4) was exported to ABAQUS V6.11–2 (Dassault Systèmes) where the osseous and soft tissues were meshed with linear tetrahedral and eight-noded hexagonal elements, respectively, to predict joint contact mechanics. To accommodate hexahedral elements, a special 3D spline function in CATIA was used to truncate edges with very thin thicknesses (Figure 5(a),(b)).

Figure 5.

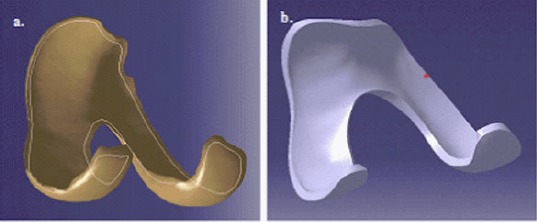
Figure 5.

Open in a new tab

Model preparation for hexagonal meshing. (a) A 3D spline was created near the edge of the cartilage surface. (b) The 3D spline was used to truncate the very thin edge to produce a finite thickness that would accommodate hexahedral elements.

Following the application of boundary and loading conditions, sensitivity analyses were conducted on element size for the different anatomical geometries to ensure that peak joint pressures did not change by over 5% (Tables 1 and 2). Case 3 was selected because it required less computational time to solve while maintaining an error of less than 5% compared with the reference model. Coarser meshes gave unacceptable errors.

Table 1.

Mesh sensitivity analysis on element size.

Number of elements (element size)
Femoral cartilage Tibial cartilage Menisci Change in maximum contact pressure (%)
Reference 29,547 (0.75 mm) 36,026 (0.5 mm) 38,034 (0.5 mm) –
Case 1 29,547 (0.75 mm) 36,026 (0.5 mm) 4314 (1mm) 2.92
Case 2 29,547 (0.75 mm) 4988 (1mm) 4314 (1mm) 3.63
Case 3 11,044 (1 mm) 4988 (1mm) 4314 (1mm) 4.56
Case 4 2558 (1.5 mm) 1994 (1.5 mm) 1224 (1.5 mm) 15.68
Case 5 1455 (2 mm) 674 (2 mm) 936 (2 mm) 20.5
Open in a new tab

Note: Case 3 is 95% accurate compared with the reference case.

Table 2.

Mesh sensitivity analysis on element types (4-noded and 10-noded tetrahedral elements) for bone meshing.

Force(N)
 Contact pressure (MPa)
Lateral Medial Lateral Medial
RMSE (4-noded vs 10-noded tetrahedral elements) 3.4372 9.02428 0.02763 0.05916
Maximum value 237.515 631.984 2.22 3.9
%FSE 1.4% 1.4% 1.2% 1.5%
Open in a new tab

Note: There was a maximum of 1.5% full-scale error (FSE) in force and contact pressure between the two element types.

Given the thinness of the articular cartilage and inner periphery of the menisci, aspect ratios of up to 3.0 were used for these tissues (femoral cartilage: 1.70; medial tibial cartilage: 1.53; lateral tibial cartilage: 1.44; meniscus: 2.96). A sensitivity analysis was carried out to investigate whether the four-noded tetrahedral elements (linear) gave similar results to 10-noded tetrahedral elements (quadratic) for the bones. The forces and contact pressures were compared between the two models. Percent full-scale error (FSE) for force and peak pressure between the two element types was 1.5%. The bony tissues were therefore modelled using four-noded tetrahedral elements.

The knee joint assembly FE model (Figure 6) included 3D representations of the tibia (57,546 elements), femur (86,207 elements), fibula (14,985 elements), femoral cartilage (11,044 elements), lateral tibial cartilage (2982 elements), medial tibial cartilage (2006 elements), menisci (4314 elements), anterior cruciate ligament (ACL; 597 elements), posterior cruciate ligament (PCL; 688 elements), medial collateral ligament (MCL; 10,810 elements) and lateral collateral ligament (LCL; 1386 elements).

Figure 6.

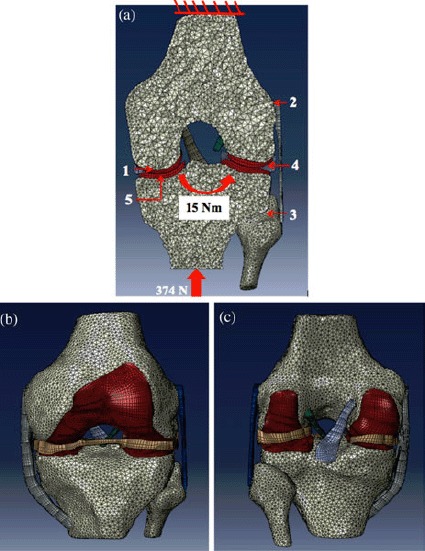
Figure 6.

Open in a new tab

(a) Boundary and loading conditions on the FE knee joint model: tied contact pair between (1) cartilage–bone, (2) ligament–bone and (3) tibia–fibula; contact pairs between (4) cartilage–meniscus and (5) cartilage–cartilage. The proximal femur was fixed in 6 degrees of freedom. A 374-N axial load was applied along the tibia, and varus/valgus bending moments, ranging from 0 to 15 Nm, were applied about the knee joint centre. (b) Anterior and (c) posterior views and of the knee joint FE model, displaying the hexagonal and tetrahedral mesh elements for the soft tissues and bones, respectively.

Boundary conditions

Attachment of each ligament and cartilage to bone was modelled by merging the nodes on the corresponding surfaces that were previously created, using the three-matic routine in the Mimics software. Cartilage–cartilage and cartilage–meniscus contact surfaces were simulated by zero-friction sliding contact elements (Figure 6). Each meniscal horn was fixed to the tibial plateau to simulate anatomical attachment. The peripheral rim of the meniscus was attached to the tibial plateau using spring elements to simulate attachment to the joint capsule. The proximal femur was mechanically grounded in all six degrees of freedom to replicate in vitro testing. The distal tibia was free in five degrees of freedom and fixed in 20° of sagittal plane knee flexion to simulate the end of weight acceptance during the stance phase of gait, when the knee joint is subjected to higher loading.

Loading conditions

The loading conditions of the FE knee simulated those of the in vitro tests. A 374-N axial load was applied along the tibia to the knee centre, as defined by the Grood and Suntay joint coordinate system (Grood and Suntay 1983). Varus and valgus bending moments, ranging from 0 to 15 Nm, were then applied about the knee joint centre to simulate different degrees of malalignment (Figure 6(a)).

Coordinate system

A Grood and Suntay coordinate system (Grood and Suntay 1983) was created for both the FE model (Figure 6(a)–(c)) and experimental specimen (Figure 7(a)–(e)), using the tibial condyles, femoral epicondyles and the most distal posterior location on the tibia as bony landmarks. This allowed computation of the relative position of the tibia with respect to the femur for both the experimental and FE models so that kinematic data could be compared.

Figure 7.

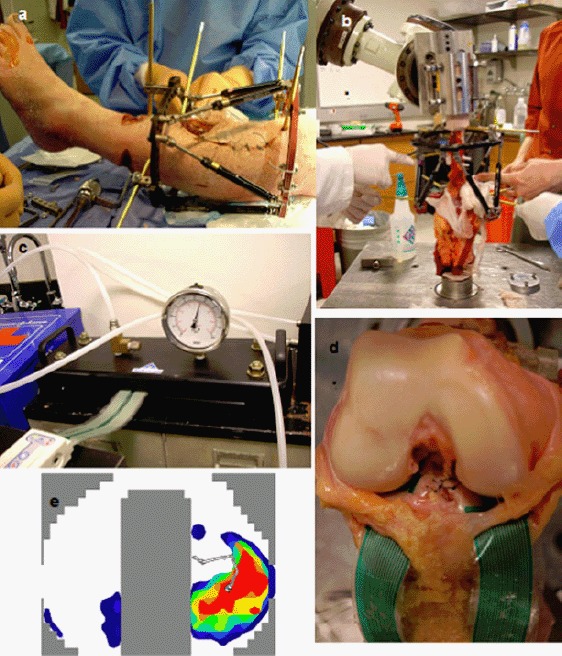
Figure 7.

Open in a new tab

(a) Taylor Spatial Frame fixed to cadaveric leg for subsequent simulations of lower limb malalignments and corrections by HTO; (b) cadaveric knee, mounted on a 6-degree-of-freedom robot for controlled loading; (c) TekScan IScan sensor equilibration before calibration; (d) sensors fixed in vitro to the cruciate ligaments between the tibial cartilage and the femur; (e) pressure distribution in the knee joint during in vitro loading.

Ligament tuning

Soft-tissue material properties depend on factors, such as synovial fluid, age and level of activity, and vary among individuals. Moreover, ligaments engage (exhibit tensile loading) at different knee positions. In order to match the FE model ligament material properties to those of the cadaver, a two-stage ligament tuning process was developed. Initial material properties of the ligaments were obtained from the literature.

First, the cadaveric specimen was moved by the robot actuator, in a minimum load path, from full extension to 65° flexion. The FE model ligament properties were adjusted iteratively until the kinematics of the tibia relative to the femur closely matched those in vitro in all six degrees of freedom (Figure 8(a),(b)). Secondly, a 374-N axial load and varus/valgus bending moments, spanning from 0 to 15 Nm, were applied to the distal tibia; the model ligament properties were further adjusted until knee model kinematics matched those in vitro in all six degrees of freedom (Figure 8(c),(d)).

Figure 8.

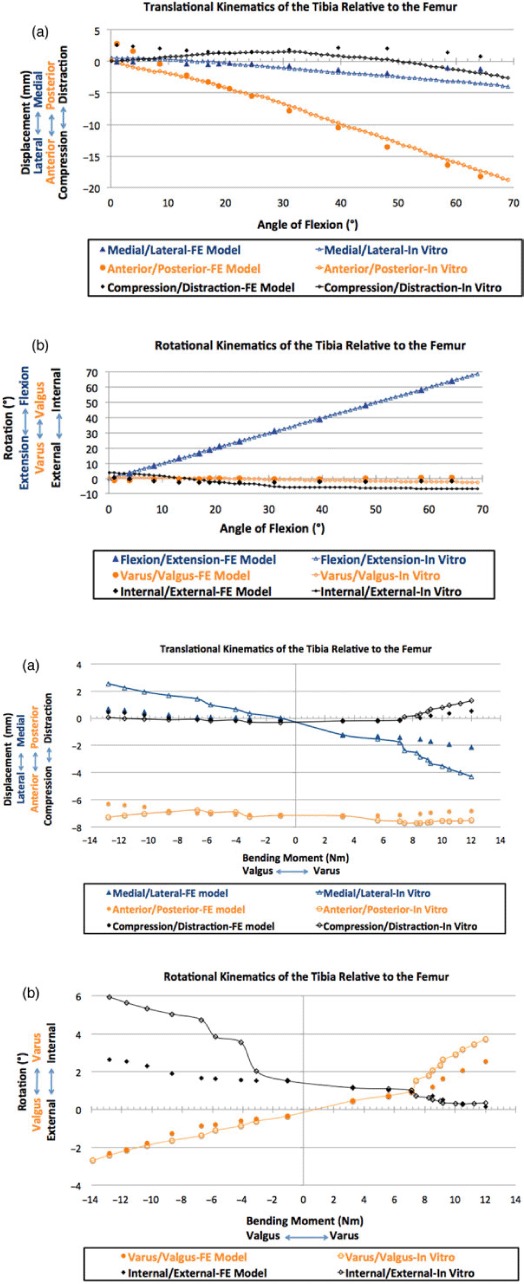
Figure 8.

Open in a new tab

The ligament tuning process: the ligament properties were adjusted in an iterative process until the kinematics of the tibia relative to the femur in the model closely matched those in vitro in all six degrees of freedom for (a) translational and (b) rotational kinematics during a sagittal rotation from full extension to 65° flexion, and (c) translational and (d) rotational kinematics during a 374-N axial load and a 0–15-Nm valgus/varus bending moment.

Material properties

Table 3 presents the material properties assigned to each anatomical structure within the knee joint (Schreppers et al. 1990; Shepherd and Seedhom 1997, 1999; Perie and Hobatho 1998; Weiss and Gardiner 2001). The meniscus was modelled as a linear elastic, transversely isotropic material. Neo-Hookean hyperelastic material properties were used to represent the cruciate and collateral ligaments. Young's modulus values (E) for each ligament, from full extension to 65° flexion and with an axial load of 374 N and a bending moment spanning – 15 Nm (valgus) to 15 Nm (varus) were obtained after the ligament tuning process described above (Figure 8(a)–(d)).

Table 3.

Material properties assigned to the different tissues comprising the knee joint.

Components Modulus (MPa) Poisson's ratio v
Bone Young's: 1000 0.3
Cartilage Young's: 25 0.45
Meniscus Circumferential E1: 120 Out-of-plane: v12 = v13 = 0.3
Axial and radial: E2, E3: 20 In-plane (circumferential) v23 = 0.2
Shear G12, G13: 57.7
Shear G23: 8.33
Open in a new tab

Linear increments in ligament Young's moduli were applied in the FE model as bending moments increased from 0 to 15 Nm varus and valgus. The shear (µ0) and bulk (K0) moduli were obtained from the modulus of elasticity E and Poisson's ratio v.

graphic file with name gcmb17_1502_eq1.jpg (1)
graphic file with name gcmb17_1502_eq2.jpg (2)

Neo-Hookean coefficients, D1 and C10, were calculated, using the bulk and shear moduli, respectively, and input to the strain energy density function within Abaqus to define the soft-tissue properties.

graphic file with name gcmb17_1502_eq3.jpg (3)
graphic file with name gcmb17_1502_eq4.jpg (4)

The material properties for each ligament at different angles of flexion are presented in Figure 9. The LCL, MCL, ACL and PCL material properties at normal alignment and varus and valgus malalignment at the end of weight acceptance are summarised in Table 4. Our ligaments properties were consistent with values reported in the literature (Butler et al. 1986; Quapp and Weiss 1998).

Figure 9.

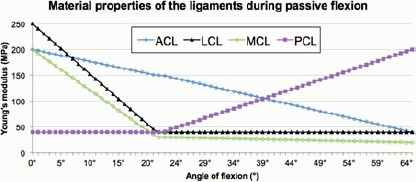
Figure 9.

Open in a new tab

Material properties for the LCL, MCL, ACL and PCL at every angle of flexion, following the ligament tuning process.

Table 4.

Young's modulus values of the MCL, LCL, ACL and PCL before and after application of varus and valgus bending moments.

Young's modulus(MPa)
Bending moment MCL LCL ACL PCL
15 Nm varus 10 60 250 40
ONm 43 56 154 40
15 Nm valgus 60 5 150 40
Open in a new tab

Note: Linear increments in ligament Young's moduli were applied in the model as bending moments increased from 0 to 15 Nm varus and 15 Nm valgus.

In vitro investigation on the cadaveric knee

A Taylor Spatial Frame (TSF) was fixed to the prepared cadaveric knee for subsequent simulations of lower limb malalignments and HTO corrections (Figure 7(a)). The knee was then positioned upside down in a six-degree-of-freedom Kawasaki robot with the proximal femur mechanically grounded to a floor-mounted fixture and the distal tibia affixed to the robot gripper and load cell (Delta, ATI, Inc, Apex, NC, USA) (Figure 7(b)). The robot used force feedback to determine the kinematic pathway to achieve the desired loading conditions within a prescribed tolerance of less than 5 N force and less than 0.5 Nm moment.

The specimen was oriented in accordance with normative movement data (obtained from the Leon Root Motion Analysis Laboratory at HSS) in a position emulating weight acceptance during stance (20° flexion), which occurs during maximum varus thrust just after the diagonal weight shift following heel strike. The applied axial load and bending moments were within the limits of the six-degree-of-freedom load cell.

Pressure at the tibial plateau was recorded using a 0.2-mm-thick Kscan 4010 sensor (Tekscan, Inc., South Boston, MA, USA). This sensor consists of two separate measurement areas, each with a total matrix width and height of 68.1 and 43.9 mm, respectively. The transducer resolution was 25 sensels/cm2. Following equilibration and calibration (Figure 7(c)), the pressure sensor was positioned on the tibial plateau and sutured to the base of the ACL and the posterior capsule (Figure 7(d)) to record contact pressures in the tibio-femoral joint. Medial and lateral compartment pressures and forces were measured in response to the externally applied forces and moments by the robot (Figure 7(e)).

Sensitivity analyses were carried out on material properties of bones and soft tissues to identify those that were critical to joint contact mechanics. A custom analysis program was developed in Matlab (MathWorks, Natick, MA, USA) to evaluate the cadaveric knee loading in the medial and lateral compartments. To compare the trends of FE-predicted and in vitro-measured peak pressure and compartmental force values, these loading parameters were normalised to the corresponding maximum compartmental value. The normalised FE-predicted and in vitro-measured values were compared for model validation. The percentage load acting in the medial and lateral compartment of the knee were computed and compared with published data and a static equilibrium numerical approximation.

Results and analysis

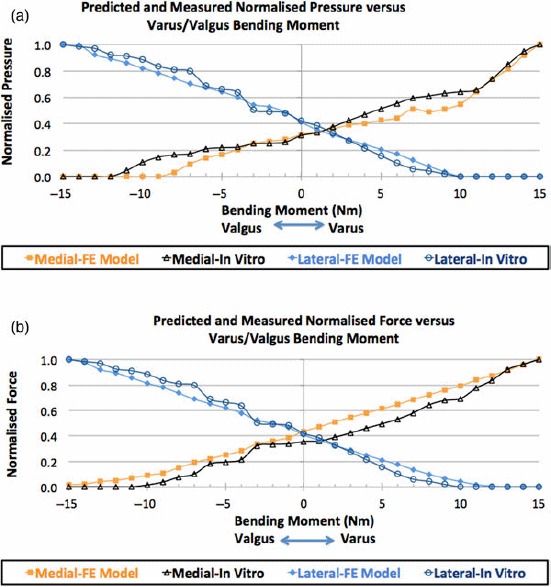
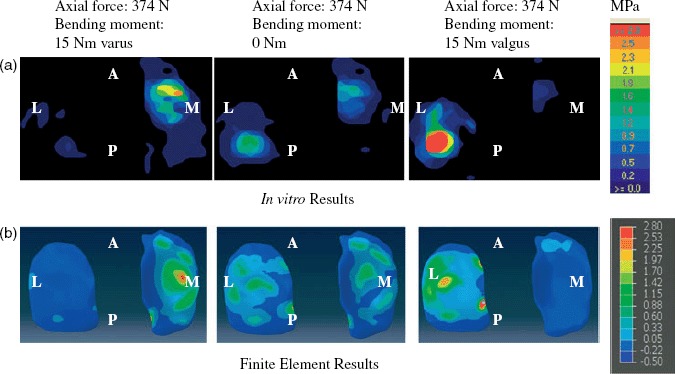
Figure 10(a),(b) illustrates the pressure distributions on the tibial cartilage for the loading conditions of a 374-N axial force with (i) a 15-Nm varus bending moment, (ii) no bending moment and (iii) a 15-Nm valgus bending moment. The experimentally measured intra-articular compartmental pressure distribution is shown in Figure 10(a) and the corresponding FE-predicted results are shown in Figure 10(b). Figure 11(a),(b) shows graphs of the in vitro and computer-simulated normalised medial and lateral compartmental pressures and forces, respectively, during loading.

Figure 10.

Figure 10.

Open in a new tab

Evaluation of FE model. Pressure distributions in the tibio-femoral joint in response to a 374-N axial load and a 15-Nm varus/valgus bending moment for (a) in vitro testing and (b) FE model predictions. A, anterior; P, posterior; L, lateral; M, medial.

Figure 11.

Figure 11.

Open in a new tab

In vitro and FE-predicted medial and lateral compartment loading in response to a 374-N axial load and 0–15 Nm varus and valgus bending moments for (a) normalised peak pressure and (b) normalised force.

Table 5 presents the absolute and normalised in vitro and FE results of (1) the medial and lateral force, (2) the medial and lateral peak pressures, (3) the corresponding root mean square error (RMSE), in bold, (4) the percentage fall scale error (% FSE) for peak pressure and force in the medial and lateral compartments and (5) the percentage of force acting in the medial and lateral compartments.

Table 5.

RMSE and percentage FSE in medial and lateral force and peak pressure values between in vitro and FE results for axial load of 374 N and varus/valgus bending moments ranging from 0 to 15 Nm.

Medial compartment
 Lateral compartment
 Medial compartment
 Lateral compartment
 Force ratio
Absolute force (N)
 Normalised force
 Absolute force (N)
 Normalised force
 Absolute pressure (MPa)
 Normalised pressure
 Absolute pressure (MPa)
 Normalied pressure
 Medial compartment
 Lateral compartment
Bending moment (Nm) Exp FE Exp FE Exp FE Exp FE Exp FE Exp FE Exp FE Exp FE Exp FE Exp FE
15 267 494 1.00 1.00 0 0 0 0 2.26 2.21 1 1 0 0 0 0 100 100 0 0
14 257 474 0.96 0.96 0 0 0 0 2.14 2.03 0.95 0.92 0 0 0 0 100 100 0 0
13 246 451 0.92 0.91 0 0 0 0 1.92 1.8 0.85 0.81 0 0 0 0 100 100 0 0
12 223 432 0.84 0.87 0 3 0 0.01 1.67 1.62 0.74 0.73 0 0 0 0 100 99 0 1
11 207 414 0.78 0.84 0 8 0 0.02 1.48 1.42 0.65 0.64 0 0 0 0 100 98 0 2
10 185 392 0.69 0.79 0 18 0 0.04 1.45 1.21 0.64 0.55 0 0 0 0 100 96 0 4
9 181 375 0.68 0.76 6 29 0.02 0.07 1.42 1.13 0.63 0.51 0.09 0.07 0.02 0.04 97 93 3 7
8 172 357 0.64 0.72 13 43 0.04 0.1 1.38 1.08 0.61 0.49 0.17 0.15 0.04 0.08 93 89 7 11
7 155 339 0.58 0.69 18 59 0.06 0.14 1.34 1.13 0.59 0.51 0.22 0.24 0.05 0.12 90 85 10 15
6 142 320 0.53 0.65 31 76 0.1 0.17 1.25 0.98 0.55 0.44 0.34 0.33 0.07 0.17 82 81 18 19
5 132 303 0.49 0.61 48 92 0.16 0.21 1.16 0.94 0.51 0.43 0.51 0.4 0.11 0.21 73 77 27 23
4 123 286 0.46 0.58 65 108 0.21 0.25 1.06 0.89 0.47 0.4 0.7 0.47 0.15 0.24 65 73 35 27
3 113 270 0.42 0.55 83 125 0.27 0.29 0.96 0.86 0.42 0.39 0.9 0.54 0.19 0.28 58 68 42 32
2 104 252 0.39 0.51 100 141 0.33 0.32 0.85 0.8 0.38 0.36 1.1 0.61 0.23 0.31 51 64 49 36
1 96 233 0.36 0.47 117 159 0.38 0.36 0.75 0.75 0.33 0.34 1.3 0.69 0.27 0.35 45 59 55 41
0 95 215 0.36 0.44 128 177 0.42 0.41 0.7 0.7 0.31 0.32 1.5 0.8 0.32 0.41 43 55 57 45
− 1 90 190 0.34 0.38 147 203 0.48 0.47 0.59 0.62 0.26 0.28 1.8 0.95 0.38 0.49 38 48 62 52
− 2 89 178 0.33 0.36 150 217 0.49 0.5 0.57 0.59 0.25 0.27 1.94 1.03 0.41 0.53 37 45 63 55
− 3 86 166 0.32 0.34 154 228 0.5 0.52 0.56 0.55 0.25 0.25 2.1 1.06 0.44 0.54 36 42 64 58
− 4 57 140 0.21 0.28 194 253 0.64 0.58 0.5 0.45 0.22 0.2 2.72 1.17 0.57 0.6 23 36 77 64
− 5 52 124 0.19 0.25 202 270 0.66 0.62 0.49 0.37 0.22 0.17 2.93 1.25 0.62 0.64 20 31 80 69
− 6 48 109 0.18 0.22 210 285 0.69 0.65 0.47 0.31 0.21 0.14 3.12 1.31 0.66 0.67 19 28 81 72
− 7 27 94 0.1 0.19 243 300 0.8 0.69 0.39 0.21 0.17 0.1 3.54 1.37 0.75 0.7 10 24 90 76
− 8 20 74 0.07 0.15 247 321 0.81 0.74 0.37 0.07 0.16 0.03 3.66 1.45 0.77 0.74 7 19 93 81
− 9 10 54 0.04 0.11 255 340 0.84 0.78 0.33 0 0.15 0 3.8 1.53 0.8 0.78 4 14 96 86
− 10 4 45 0.01 0.09 270 355 0.89 0.81 0.24 0 0.11 0 4.03 1.6 0.85 0.82 1 11 99 89
− 11 0 34 0 0.07 278 373 0.91 0.86 0.1 0 0.04 0 4.2 1.68 0.88 0.86 0 8 100 92
− 12 0 25 0 0.05 282 390 0.92 0.89 0 0 0 0 4.35 1.74 0.92 0.89 0 6 100 94
− 13 0 20 0 0.04 296 401 0.97 0.92 0 0 0 0 4.52 1.8 0.95 0.92 0 5 100 95
− 14 0 11 0 0.02 300 426 0.98 0.98 0 0 0 0 4.6 1.94 0.97 0.99 0 3 100 97
− 15 0 8 0 0.02 305 436 1 1 0 0 0 0 4.75 1.95 1 1 0 2 100 98
RMSE 138.71 0.08 65.18 0.04 0.16 0.07 1.49 0.06 8.05 8.05
FSE (%) 28.08 7.56 14.59 4.48 0.07 6.67 0.31 5.04
Open in a new tab

Note: Percentage FSE was obtained by expressing the RMSE as a percentage of the maximum corresponding value.

Peak pressure in the tibial cartilage

A 15-Nm varus bending moment increased pressure in the medial tibial cartilage and decreased pressure in the lateral tibial cartilage for both the in vitro (Figure 10(a)) and FE (Figure 10(b)) studies. When a valgus bending moment was applied, lateral compartment pressure increased and medial compartment pressure decreased, as expected. Peak pressure locations were in quantitative agreement between in vitro-measured and FE-predicted pressure values (Figure 10(a),(b)).

Figure 11(a) shows that for both the FE model and the in vitro investigations, normalised peak pressure increased monotonically in the medial (lateral) compartment and decreased in the lateral (medial) compartment as varus (valgus) bending moment increased from 0 to 15 Nm (Figure 11(a)). Peak pressure was normalised to the corresponding maximum compartmental peak pressure. After normalisation, the FSE (%) between FE-predicted and in vitro-measured peak pressures was 6.67% in the medial and 5.94% in the lateral compartments.

Compartmental forces in the tibial cartilage

Figure 11(b) shows that for both the FE model and the in vitro investigations, normalised force increased monotonically in the medial (lateral) compartment and decreased in the lateral (medial) compartment as varus (valgus) bending moment increased from 0 to 15 Nm (Figure 11(b)). Force values were normalised to the corresponding maximum compartmental force. After normalisation with the corresponding maximum compartmental forces, the FSE (%) between FE-predicted and in vitro-measured forces was 7.56% in the medial compartment and 4.48% in the lateral.

As varus bending moment increased, the ratio of the force in the medial compartment to the total force acting in the knee joint also increased, while the ratio of the force in the lateral compartment to the total force decreased for both in vitro and FE studies. The reverse occurred during a 0–15 Nm valgus bending moment (Table 5, Figure 12).

Figure 12.

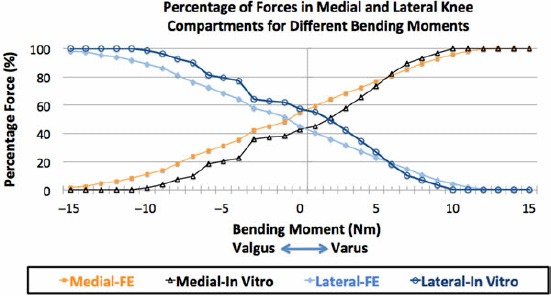
Figure 12.

Open in a new tab

In vitro and FE-predicted forces in the medial and lateral compartments as a percentage of the total axial force during 0–15 Nm varus and valgus bending moments.

The model was also verified by a simple frontal plane static equilibrium calculation for varus and valgus bending moments at lift off (Figure 13). The distances from the knee joint centre, measured from MRI scans, were 40 mm to the medial and lateral ends of the tibial plateau and 45 mm to the LCL and MCL. Given the cylindrical shape of the femoral condyles, the points of contact between the distal femur and the proximal tibia were approximated to be in the middle of each compartment (20 mm from knee centre) throughout the bending moments. LCL force was ignored at valgus lift off and MCL force was ignored at varus lift off due to slack. Bending moments resulting from forces in the ACL and PCL were ignored due to the close proximity of the line of force from the joint centre.

Figure 13.

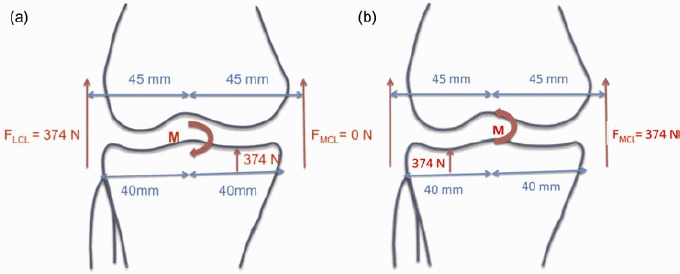
Figure 13.

Open in a new tab

Static equilibrium diagrams showing forces and bending moment acting on the knee joint during (a) varus and (b) valgus lift off. FMCL = internal force in the MCL; FMCL = internal force in the LCL; M = bending moment.

Lift off occurs when the total 374-N axial force shifts to one compartment. From Figure 13, the bending moment M causing lift off in either compartment was estimated as 9.35 Nm, calculated as (374 × 0.045)–(374 × 0.02)Nm. Table 5 and Figure 12 show that the normalised in vitro-measured force in the medial compartment was more than 92% of the axial total force when the varus bending moment reached 9 Nm. Lateral compartment loading reached 92% when an 11-Nm bending moment was applied. The FSE (%) between normalised FE-predicted and in vitro-measured forces was 8.05% for both medial and lateral compartments.

Discussion

A method for the development and validation of a subject-specific FE model of the tibio-femoral compartment of the knee joint is presented. The FE knee model used tissue-specific MRI-scanning sequences and Mimics-based image processing to represent the 3D geometry of knee joint tissues. The geometries of bone, meniscus, cartilage and ligaments influence the force and pressure values in the knee joint. Hence, the subject-specific FE knee model was created from 3D MRI data-sets of the same knee that was used for the experimental validation. The same loading conditions were applied to the FE model and the cadaveric specimen to assess model performance. The magnitudes of the absolute medial and lateral force and pressure values are influenced by soft-tissue material properties. We ensured that the correct tissue properties were used in the FE model by tuning the collateral and cruciate ligaments to obtain matching computational and experimental kinematics of the tibia relative to the femur.

In the process of building this model, we needed to consider that ligament properties were nonlinear, varied as a function of angular position, engaged as a function of angular position or loading, and were hence important for the estimation of contact loading. Material properties from the literature served as a starting point but they did not describe the precise properties of this specimen's ligaments nor did they specify when the ligaments became engaged. Model ligament properties were ‘tuned’ (adjusted) such that the knee kinematics matched those of the cadaveric specimen. Our intention was not to validate the kinematics, but use these measures as a tool to tune the ligaments. The purpose of this study was to validate the joint contact force and stress prediction of our computational model. The model was designed to predict contact mechanics; the ligament properties were only one of the components that contributed to the knee joint stress prediction.

Knee joint contact mechanics are influenced by bone and soft-tissue geometries, as well as pathologic states. Our validated FE model can be virtually modified to simulate the arthritic joint and other pathologic states, as well as treatment methods to further understanding of these parameters.

FE-predicted normalised forces and peak joint pressures in the medial and lateral tibial cartilage agreed with those obtained from in vitro tests for every loading condition. Absolute FE-predicted force values were higher than in vitro-measured values (normalised medial and lateral force FSE (%): 7.56% and 4.48%, respectively). This was expected because some of the load-bearing anatomical structures could have been physically outside the force transducer sensel areas and not recorded by the sensor matrix. Moreover, the numerical approximation of bending moment at lift off agreed closely with in vitro-measured and FE-predicted values. These results (< 7.6% FSE) confirmed our hypothesis that tibio-femoral contact mechanics of the cadaver specimen and corresponding FE model predictions agreed within 10%. These results serve as a benchmark for improvement in modelling nonlinear properties of irregular geometry in our future work.

Other investigators have validated their models by comparing their results with subject-specific cadaveric knee kinematics, kinematics of a different specimen or published kinematics, subject-specific in vitro results, in vitro results of different cadavers, or experimental results published by other investigators (Table 6). Outside of our work, no in vitro experiments using an intact knee have been carried out to validate the contact force and stress in a subject-specific knee model. The bottom three references in Table 6 did evaluate joint contact stress, but not in a subject-specific manner. This manuscript provides a methodology for developing a 3D subject-specific joint stress model and a procedure for independent validation. The model is subject-specific in terms of tissue geometries. Cartilage and meniscal properties were included from the literature. Initial ligament properties were obtained from the literature and then tuned such that model and cadaver kinematics were matched for the same angular excursions and loading levels.

Table 6.

Previously published validated or verified computational knee models.

Authors and date Parameters validated Type of specimen
Guess et al. (2010) Kinematics of a multibody knee model Identically loaded cadaveric knee
Baldwin et al. (2011) Kinematics of three subject-specific FE total knee replacement models In vitro dynamic tests from three cadaveric specimens
Blankevoort, and Huiskes (1996) Kinematics of the knee soft tissue FE model In vitro tests from other cadaveric knee specimens
Beillas et al. (2004) Kinematics of an FE knee model In vitro tests from other cadaveric knee specimens
Halloran, Petrella and Rullkoetter (2005) Kinematics of an FE knee model Previously published experimental kinematic data
Perillo-Marcone, Taylor (2007) Kinematics of an FE knee model Previously published experimental kinematic data
Godest et al. (2002) Kinematics of an FE knee model Previously published experimental kinematic data
Yosibash, Trabelsi and Milgrom (2007); Yosibash, Tal and Trabelsi (2010) Strain and displacement of an FE femur model In vitro tests from subject-specific cadaveric femur
Kiapour et al. (2012) Kinematics of an FE knee model In vitro tests from 19 different cadaveric leg specimens
Tuncer et al. (2013) Strain in tibia and femur of an FE knee model with a unilateral knee replacement (UKR) In vitro tests from 10 different cadaveric knee specimens
Miller et al. (2009) Total load, peak load and peak load location for axial, varus and valgus loading conditions of a 2D discrete element analysis model In vitro study from four human cadaveric knees
Mononen, Juvelin and Korhonen (2013) Knee joint stresses and strains – musculoskeletal multibody dynamics Experimental findings from other investigators
Shirazi and Shirazi-Adl (2009) Joint contact pressures of an FE knee model In vitro results from other cadavers
Pena et al. (2006) Joint contact pressures of an FE knee model Experimental findings from other investigators
Open in a new tab

Our results for compartmental forces agree with the experimental measurements of other investigators. These results, as shown in Table 5 and Figure 12, illustrate that a typical 4-Nm varus bending moment in a well-aligned knee yield an in vitro-measured medial-to-lateral force ratio of 65:35 and an FE-predicted force ratio of 73:27. Medial compartmental loading of 60%–70% has been reported by a number of investigators (Schipplein and Andriacchi 1991; Tetsworth and Paley 1994; Agneskirchner et al. 2004; Thambyah 2007). This is because the mechanical axis passes slightly medially to the healthy knee joint centre resulting in an adduction moment. Figure 11(b) shows that as the varus bending moment was increased, medial compartmental force increased and lateral compartmental force decreased. In particular, our FE results in Table 5 show that an increase in varus bending moment from 4 to 8 Nm resulted in an increase in medial compartmental force percentage from 73% to 89%. This agrees with the work of Tetsworth and Paley (1994), who reported that 5° of varus malalignment increases medial compressive loading from 70% to 90% (Tetsworth and Paley 1994). Medial load transfer resulting from an increase in adduction moment, or varus malalignment, has also been reported (Tetsworth and Paley 1994; Zhao et al. 2007; Kutzner et al. 2010).

FE model predictions for peak pressure values in the medial and lateral compartments in this study ranged from 0 to 2.51 MPa with a 381-N axial force and 15-Nm maximum bending moment. This is in line with other experimental and FE studies, in which corresponding contact pressures between 2.4 and 34 MPa have been reported for higher axial loads of 700–2000 N on simulated intact and injured or reconstructed knee joints (Donahue et al. 2002; Marzo and Gurske-DePerio 2009; Morimoto et al. 2009; Adouni et al. 2012; Mononen and others 2012).

Compartment normalised force and peak pressures predicted by computer simulation in this study were consistent with those obtained experimentally. The subject-specific FE knee model will be enhanced in future versions by: evaluating knee joint contact mechanics throughout sagittal angles spanning the full range of motion during functional activities; including the patella and quadriceps musculo-tendinous forces, as well as hamstrings and gastrocnemius muscles; simulating different knee joint alignments to evaluate surgical realignment; and using more physiological tissue material properties.

Although the tissue geometries of the FE knee model were subject-specific, the material properties were acquired from the literature. Cartilage material properties can substantially influence knee joint contact mechanics (Shirazi et al. 2008). However, our previous sensitivity analyses showed that a change in the material properties (meniscus, cartilage and ligament) affected the absolute compartmental force and pressure values, but not the relative values where loading was normalised to the peak values in each respective compartment (Mootanah et al. 2012).

The ultimate aim of this investigational team was to use this approach for subject-specific HTO planning to improve surgical outcomes. Following further development and testing, the model will be applied to in vivo test subjects to assess its utility in obtaining improved outcomes. Such a model could form the basis of a subject-specific tool to guide orthopaedic surgeons towards obtaining realignment of a malaligned knee that minimises peak pressure within the joint.

Based on results of their OASIS surgical planning tool for malalignment correction, Chao et al. found that patients with medial compartment force ratios between 40 and 60% achieved a 100% 10-year survivorship (Chao and Sim 1995; Chao 2003). OASIS, although limited to a 2D static standing posture, linear elastic elements for cartilage and ligaments, and a uniplanar osteotomy wedge angle, has increased HTO success rate (Chao and Sim 1995; Chao 2003).

Our study adds to the sparse validation available in the knee modelling literature. Given the complex geometry and role of stabilising structures within the femoral–tibial joint, the investigators postulate that a 3D model, capable of predicting joint pressure, will yield further improvements in predicting alignment correction and clinical outcomes. Additional steps are required before this model may be applied clinically. However, this study represents the first step towards this important application, which is to validate the capability of a subject specific model for predicting joint forces and pressures experienced under load.

Acknowledgements

We gratefully acknowledge the support of the Chelmsford Medical Education and Research Trust for funding the research. We acknowledge receipt of the 2012 Medical Innovation Award from Materialise, developer of Mimics for this project.

References

  1. Adouni M, Shirazi-Adl A, Shirazi R. Computational biodynamics of human knee joint in gait: from muscle forces to cartilage stresses. J Biomech. 2012;45(12):2149–2156. doi: 10.1016/j.jbiomech.2012.05.040. [DOI] [PubMed] [Google Scholar]
  2. Agneskirchner JD, Freiling D, Hurschler C, Lobenhoffer P. Primary stability of four different implants for opening wedge high tibial osteotomy. Knee Surg Sports Traumatol Arthrosc. 2006;14(3):291–300. doi: 10.1007/s00167-005-0690-1. [DOI] [PubMed] [Google Scholar]
  3. Agneskirchner JD, Hurschler C, Stukenborg-Colsman C, Imhoff AB, Lobenhoffer P. Effect of high tibial flexion osteotomy on cartilage pressure and joint kinematics: a biomechanical study in human cadaveric knees. Winner of the AGA-DonJoy award 2004. Arch Orthop Trauma Surg. 2004;124(9):575–584. doi: 10.1007/s00402-004-0728-8. [DOI] [PubMed] [Google Scholar]
  4. Andriacchi TP, Lang PL, Alexander EJ, Hurwitz DE. Methods for evaluating the progression of osteoarthritis. J Rehabil Res Dev. 2000;37(2):163–170. [PubMed] [Google Scholar]
  5. Baldwin MA, Clary CW, Fitzpatrick CK, Deacy JS, Maletsky LP, Rullkoetter PJ. Dynamic finite element knee simulation for evaluation of knee replacement mechanics. J Biomech. 2011;45(3):474–483. doi: 10.1016/j.jbiomech.2011.11.052. [DOI] [PubMed] [Google Scholar]
  6. Beillas P, Papaioannou G, Tashman S, Yang KH. A new method to investigate in vivo knee behavior using a finite element model of the lower limb. J Biomech. 2004;37(7):1019–1030. doi: 10.1016/j.jbiomech.2003.11.022. [DOI] [PubMed] [Google Scholar]
  7. Bhatnagar T, Jenkyn TR. Internal kinetic changes in the knee due to high tibial osteotomy are well-correlated with change in external adduction moment: an osteoarthritic knee model. J Biomech. 2010;43(12):2261–2266. doi: 10.1016/j.jbiomech.2010.05.001. [DOI] [PubMed] [Google Scholar]
  8. Blankevoort L, Huiskes R. Validation of a three-dimensional model of the knee. J Biomech. 1996;29(7):955–961. doi: 10.1016/0021-9290(95)00149-2. [DOI] [PubMed] [Google Scholar]
  9. Butler DL, Kay MD, Stouffer DC. Comparison of material properties in fascicle-bone units from human patellar tendon and knee ligaments. J Biomech. 1986;19(6):425–432. doi: 10.1016/0021-9290(86)90019-9. [DOI] [PubMed] [Google Scholar]
  10. Chao EY. Graphic-based musculoskeletal model for biomechanical analyses and animation. Med Eng Phys. 2003;25(3):201–212. doi: 10.1016/s1350-4533(02)00181-9. [DOI] [PubMed] [Google Scholar]
  11. Chao EY, Sim FH. Computer-aided preoperative planning in knee osteotomy. Iowa Orthop J. 1995;15:4–18. [PMC free article] [PubMed] [Google Scholar]
  12. Cooper C, Dennison E, Edwards M, Litwic A. Epidemiology of osteoarthritis. Medicographia. 2013;35:145–151. [Google Scholar]
  13. Coventry MB. Osteotomy of the upper portion of the tibia for degenerative arthritis of the knee. A preliminary report. J Bone Joint Surg Am. 1965;47:984–990. [PubMed] [Google Scholar]
  14. Coventry MB. Osteotomy of the upper portion of the tibia for degenerative arthritis of the knee. 2001. A preliminary report by Mark B. Coventry, MD. From the section of orthopedic surgery, Mayo Clinic and Mayo Foundation, Rochester, Minnesota. 1965. Bone Joint Surg Am. 83-A(9):1426. [PubMed]
  15. Donahue TL, Hull ML, Rashid MM, Jacobs CR. A FE model of the human knee joint for the study of tibio-femoral contact. J Biomech Eng. 2002;124(3):273–280. doi: 10.1115/1.1470171. [DOI] [PubMed] [Google Scholar]
  16. Dorsey WO, Miller BS, Tadje JP, Bryant CR. The stability of three commercially available implants used in medial opening wedge high tibial osteotomy. J Knee Surg. 2006;19(2):95–98. doi: 10.1055/s-0030-1248086. [DOI] [PubMed] [Google Scholar]
  17. Dowd GS, Somayaji HS, Uthukuri M. High tibial osteotomy for medial compartment osteoarthritis. Knee. 2006;13(2):87–92. doi: 10.1016/j.knee.2005.08.002. [DOI] [PubMed] [Google Scholar]
  18. Esenkaya I, Misirlioglu M, Kelestemur MH, Elmali N, Fadillioglu E. Biomechanical evaluation of different fixation plates in medial opening upper tibial osteotomy. Knee. 2007;14(1):46–50. doi: 10.1016/j.knee.2006.10.003. [DOI] [PubMed] [Google Scholar]
  19. Godest A, Beaugonin M, Haug E, Taylor M, Gregson P. Simulation of a knee joint replacement during a gait cycle using explicit finite element analysis. J Biomech. 2002;35(2):267–275. doi: 10.1016/s0021-9290(01)00179-8. [DOI] [PubMed] [Google Scholar]
  20. Grood ES, Suntay WJ. A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. J Biomech Eng. 1983;105(2):136–144. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
  21. Guess TM, Thiagarajan G, Kia M, Mishra M. A subject specific multibody model of the knee with menisci. Med Eng Phys. 2010;32(5):505–515. doi: 10.1016/j.medengphy.2010.02.020. [DOI] [PubMed] [Google Scholar]
  22. Halloran JP, Petrella AJ, Rullkoetter PJ. Explicit finite element modeling of total knee replacement mechanics. J Biomech. 2005;38(2):323–331. doi: 10.1016/j.jbiomech.2004.02.046. [DOI] [PubMed] [Google Scholar]
  23. Hurwitz DE, Ryals AB, Case JP, Block JA, Andriacchi TP. The knee adduction moment during gait in subjects with knee osteoarthritis is more closely correlated with static alignment than radiographic disease severity, toe out angle and pain. J Orthop Res. 2002;20(1):101–107. doi: 10.1016/S0736-0266(01)00081-X. [DOI] [PubMed] [Google Scholar]
  24. Johnson F, Leitl S, Waugh W. The distribution of load across the knee. A comparison of static and dynamic measurements. J Bone Joint Surg Br. 1980;62(3):346–349. doi: 10.1302/0301-620X.62B3.7410467. [DOI] [PubMed] [Google Scholar]
  25. Kiapour A, Kiapour AM, Kaul V, Quatman CE, Ditto RC, Levine JW, Worderman S, Hewett TE, Demetropoulos CK, Goel VK. Finite element model of the knee for investigation of high rate injury mechanism: development and validation. 2012. Proceedings of ORS 2012 Annual Meeting 36; Paper No. 0101. [DOI] [PMC free article] [PubMed]
  26. Kutzner I, Heinlein B, Graichen F, Bender A, Rohlmann A, Halder A, Beier A, Bergmann G. Loading of the knee joint during activities of daily living measured in vivo in five subjects. J Biomech. 2010;43(11):2164–2173. doi: 10.1016/j.jbiomech.2010.03.046. [DOI] [PubMed] [Google Scholar]
  27. Marzo JM, Gurske-DePerio J. Effects of medial meniscus posterior horn avulsion and repair on tibiofemoral contact area and peak contact pressure with clinical implications. Am J Sports Med. 2009;37(1):124–129. doi: 10.1177/0363546508323254. [DOI] [PubMed] [Google Scholar]
  28. Mathers CD, Loncar D. Projections of global mortality and burden of disease from 2002 to 2030. PLoS Med. 2006;3(11):e442. doi: 10.1371/journal.pmed.0030442. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Miller EJ, Riemer RF, Donahue TL Haut, Kaufman KR. Experimental validation of a tibiofemoral model for analyzing joint force distribution. J Biomech. 2009;42(9):1355–1359. doi: 10.1016/j.jbiomech.2009.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Mononen ME, Mikkola MT, Julkunen P, Ojala R, Nieminen MT, Jurvelin JS, Korhonen RK. Effect of superficial collagen patterns and fibrillation of femoral articular cartilage on knee joint mechanics – a 3D finite element analysis. J Biomech. 2012;45(3):579–587. doi: 10.1016/j.jbiomech.2011.11.003. [DOI] [PubMed] [Google Scholar]
  31. Mononen ME, Jurvelin JS, Korhonen RK. Implementation of a gait cycle loading into healthy and meniscectomised knee joint models with fibril-reinforced articular cartilage. Comput Methods Biomech Biomed Engin. 2013. pp. 1–12. [Epub ahead-of-print] [DOI] [PubMed]
  32. Mootanah R, Reisse F, Carpanen D, Walker R, Hillstrom HJ. The effects of the material properties of bones and soft tissues on knee joint contact stress. 2012. 10th international symposium on Biomechanics and Biomedical Engineering; Berlin, April, 10–14; ARUP, Solihull.
  33. Morimoto Y, Ferretti M, Ekdahl M, Smolinski P, Fu FH. Tibiofemoral joint contact area and pressure after single- and double-bundle anterior cruciate ligament reconstruction. Arthroscopy. 2009;25(1):62–69. doi: 10.1016/j.arthro.2008.08.014. [DOI] [PubMed] [Google Scholar]
  34. Pena E, Calvo B, Martinez M, Doblare M. A three-dimensional finite element analysis of the combined behavior of ligaments and menisci in the healthy human knee joint. J Biomech. 2006;39(9):1686–1701. doi: 10.1016/j.jbiomech.2005.04.030. [DOI] [PubMed] [Google Scholar]
  35. Perie D, Hobatho MC. In vivo determination of contact areas and pressure of the femorotibial joint using non-linear FE analysis. Clin Biomech (Bristol, Avon) 1998;13(6):394–402. doi: 10.1016/s0268-0033(98)00091-6. [DOI] [PubMed] [Google Scholar]
  36. Perillo-Marcone A, Taylor M. Effect of varus/valgus malalignment on bone strains in the proximal tibia after TKR: an explicit finite element study. J Biomech Eng. 2007;129(1):1–11. doi: 10.1115/1.2401177. [DOI] [PubMed] [Google Scholar]
  37. Petersson IF, Jacobsson LT. Osteoarthritis of the peripheral joints. Best Pract Res Clin Rheumatol. 2002;16(5):741–760. doi: 10.1053/berh.2002.0266. [DOI] [PubMed] [Google Scholar]
  38. Quapp KM, Weiss JA. Material characterization of human medial collateral ligament. J Biomech Eng. 1998;120(6):757–763. doi: 10.1115/1.2834890. [DOI] [PubMed] [Google Scholar]
  39. Rinonapoli E, Mancini GB, Corvaglia A, Musiello S. Tibial osteotomy for varus gonarthrosis. A 10–21-year followup study. Clin Orthop Relat Res. 1998. pp. 185–193. [PubMed]
  40. Schipplein OD, Andriacchi TP. Interaction between active and passive knee stabilizers during level walking. J Orthop Res. 1991;9(1):113–119. doi: 10.1002/jor.1100090114. [DOI] [PubMed] [Google Scholar]
  41. Schreppers GJ, Sauren AA, Huson A. A numerical model of the load transmission in the tibio-femoral contact area. Proc Inst Mech Eng H. 1990;204(1):53–59. doi: 10.1243/PIME_PROC_1990_204_228_02. [DOI] [PubMed] [Google Scholar]
  42. Sharma L, Song J, Felson DT, Cahue S, Shamiyeh E, Dunlop DD. The role of knee alignment in disease progression and functional decline in knee osteoarthritis. JAMA. 2001;286(2):188–195. doi: 10.1001/jama.286.2.188. [DOI] [PubMed] [Google Scholar]
  43. Shepherd DE, Seedhom BB. A technique for measuring the compressive modulus of articular cartilage under physiological loading rates with preliminary results. Proc Inst Mech Eng H. 1997;211(2):155–165. doi: 10.1243/0954411971534278. [DOI] [PubMed] [Google Scholar]
  44. Shepherd DE, Seedhom BB. Thickness of human articular cartilage in joints of the lower limb. Ann Rheum Dis. 1999;58(1):27–34. doi: 10.1136/ard.58.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Shirazi R, Shirazi-Adl A, Hurtig M. Role of cartilage collagen fibrils networks in knee joint biomechanics under compression. J Biomech. 2008;41(16):3340–3348. doi: 10.1016/j.jbiomech.2008.09.033. [DOI] [PubMed] [Google Scholar]
  46. Shirazi R, Shirazi-Adl A. Computational biomechanics of articular cartilage of human knee joint: effect of osteochondral defects. J Biomech. 2009;42(15):2458–2465. doi: 10.1016/j.jbiomech.2009.07.022. [DOI] [PubMed] [Google Scholar]
  47. Specogna AV, Birmingham TB, Hunt MA, Jones IC, Jenkyn TR, Fowler PJ, Giffin JR. Radiographic measures of knee alignment in patients with varus gonarthrosis: effect of weightbearing status and associations with dynamic joint load. Am J Sports Med. 2007;35(1):65–70. doi: 10.1177/0363546506293024. [DOI] [PubMed] [Google Scholar]
  48. Tetsworth K, Paley D. Malalignment and degenerative arthropathy. Orthop Clin North Am. 1994;25(3):367–377. [PubMed] [Google Scholar]
  49. Thambyah A. Contact stresses in both compartments of the tibiofemoral joint are similar even when larger forces are applied to the medial compartment. Knee. 2007;14(4):336–338. doi: 10.1016/j.knee.2007.05.002. [DOI] [PubMed] [Google Scholar]
  50. Tuncer M, Cobb JP, Hansen UN, Amis AA. Validation of multiple subject-specific finite element models of unicompartmental knee replacement. Med Eng Phys. 2013;35(10):1457–1464. doi: 10.1016/j.medengphy.2013.03.020. [DOI] [PubMed] [Google Scholar]
  51. Valkenburg H. Clinical versus radiological osteoarthritis in the general population. In: Peyron J, editor. Epidemiology of osteoarthritis. Paris: Ciba-Geigy; 1980. p. 53. [Google Scholar]
  52. Virolainen P, Aro HT. High tibial osteotomy for the treatment of osteoarthritis of the knee: a review of the literature and a meta-analysis of follow-up studies. Arch Orthop Trauma Surg. 2004;124(4):258–261. doi: 10.1007/s00402-003-0545-5. [DOI] [PubMed] [Google Scholar]
  53. Weiss JA, Gardiner JC. Computational modeling of ligament mechanics. Crit Rev Biomed Eng. 2001;29(3):303–371. doi: 10.1615/critrevbiomedeng.v29.i3.20. [DOI] [PubMed] [Google Scholar]
  54. Yosibash Z, Trabelsi N, Milgrom C. Reliable simulations of the human proximal femur by high-order finite element analysis validated by experimental observations. J Biomech. 2007;40(16):3688–3699. doi: 10.1016/j.jbiomech.2007.06.017. [DOI] [PubMed] [Google Scholar]
  55. Yosibash Z, Tal D, Trabelsi N. Predicting the yield of the proximal femur using high-order finite-element analysis with inhomogeneous orthotropic material properties. Philos T Roy Soc A. 2010;368(1920):2707. doi: 10.1098/rsta.2010.0074. [DOI] [PubMed] [Google Scholar]
  56. Zhao D, Banks SA, Mitchell KH, D'Lima DD, Colwell CW, Jr, Fregly BJ. Correlation between the knee adduction torque and medial contact force for a variety of gait patterns. J Orthop Res. 2007;25(6):789–797. doi: 10.1002/jor.20379. [DOI] [PubMed] [Google Scholar]
  57. Zhim F, Laflamme GY, Viens H, Saidane K, Yahia L. Biomechanical stability of high tibial opening wedge osteotomy: internal fixation versus external fixation. Clin Biomech (Bristol, Avon) 2005;20(8):871–876. doi: 10.1016/j.clinbiomech.2005.04.008. [DOI] [PubMed] [Google Scholar]

Articles from Computer Methods in Biomechanics and Biomedical Engineering are provided here courtesy of Taylor & Francis

RESOURCES