Assessing and improving acoustic radiation force image quality using a 1.5D transducer design

Abstract

A 1.5D transducer array was developed to improve acoustic radiation force impulse (ARFI) imaging signal-to-noise ratio (SNR_ARFI) and image contrast relative to a conventional 1D array. To predict performance gains from the proposed 1.5D transducer array, an analytical model for SNR_ARFI upper bound was derived. The analytical model and 1.5D ARFI array were validated using a finite element model-based numerical simulation framework. The analytical model demonstrated good agreement with numerical results (correlation coefficient = 0.995), and simulated lesion images yielded a significant (2.92 dB; p < 0.001) improvement in contrast-to-noise ratio when rendered using the 1.5D ARFI array.

Introduction

Acoustic radiation force imaging is a classification of ultrasound imaging that uses tissue displacement, rather than acoustic reflectivity, as the source of image contrast. In general, these techniques produce images by using acoustic radiation force to push tissue, followed by a series of tracking pulses to measure displacement. This displacement can then be used to calculate relative or absolute stiffness. Radiation force imaging techniques, such as acoustic radiation force impulse (ARFI) imaging [1], shear wave imaging [2–7], and monitored steady-state excitation and recovery imaging [8], have shown promise in detecting lesions in a variety of organs including the abdomen [9], [10], heart [11], liver [12], breast [13], and prostate [15] as well as measuring blood coagulation ex vivo [16], [17]. Since contrast is derived from stiffness, and stiffness is derived from displacement, the mean and variance of the displacement estimates have a large impact on lesion detection.

A major limiting factor in displacement estimation performance during ARFI imaging is echo decorrelation. While larger acoustic output, and thus larger acoustic radiation force, can increase ARFI image signal (i.e. displacement magnitude), displacement variance is also increased due to echo decorrelation from increased scatterer shearing [18], [19]. Additionally, increasing displacement magnitude is further limited by tissue ultrasound absorption and heating considerations (e.g. < 15 μm for < 1°C tissue heating [20]). In addition to increasing displacement variance, decorrelation derived from scatterer shearing is also associated with an underestimation of the peak displacement magnitude [19]. Therefore, displacement estimate improvements (i.e. high mean displacements and lower variance) are strongly dependent on the ability to reduce decorrelation between the reference and subsequent tracking echo signals. While signal processing methods, including principle component analysis [21], [22], can reduce decorrelation, it is also recognized that transducer design and imaging parameters effect the degree of differential motion across the point spread function, and thus, the observed levels of echo decorrelation [18]. In this paper, a new 1.5D ARFI transducer design is proposed for reduced echo decorrelation, and improved ARFI image signal-to-noise ratio (SNR_ARFI), compared with a conventional 1D array. Echo decorrelation improvements are achieved using the 1.5D design because it enables electronic focusing in elevation and dedicated elements for each of the pushing and tracking functions. To investigate the relationship between echo decorrelation, transducer design, and image quality, we first develop an analytical model that relates the properties of a transducer to a radiation force image quality metric, SNR_ARFI. While we focus on ARFI imaging, this analysis can be generalized to any radiation force imaging technique that share the common feature of deriving image contrast from displacement estimates. Using this new analytical model, an upper bound for SNR_ARFI is derived as a function of tissue properties, transducer geometry, and imaging parameters. This model is validated using a numerical simulation framework and used, along with finite element model (FEM) simulations, to assess the performance of the proposed 1.5D array design compared with a convention 1D array in terms of SNR_ARFI and contrast-to-noise ratio.

II Theory and Methods

A. Derivation of ARFI Image SNR upper bound

Image contrast in ARFI imaging is derived from differences in tissue stiffness, which are manifest in different displacement responses assuming constant acoustic radiation force excitation – i.e. assuming constant attenuation and tissue within a small distance of the transmit focus. With application of the same acoustic radiation force, stiffer tissue exhibits less displacement than more compliant tissue. Images are typically formed as maps of displacement estimates computed from locations within the 2D imaging region. To quantify image quality and assess the performance of the proposed 1.5D ARFI transducer design (described further below), an upper bound for SNR_ARFI was derived. We start by defining SNR_ARFI as follows:

$${\mathit{SNR}}_{\mathit{ARFI}}=\frac{\mu }{\sigma }$$ (1)

where μ and σ are the mean and standard deviation (or “jitter”) of the estimated displacement, respectively. The standard deviation of ultrasound motion estimation depends on electronic signal-to-noise (SNR_E), echo correlation (ρ), center frequency (f_o), motion estimator window length (T), and fractional bandwidth (B). An expression for the minimum jitter (σ̂) achievable from an unbiased time delay estimator was previously derived by Walker and Trahey [23]:

$$\widehat{\sigma }\ge \sqrt{\frac{3}{2f_0^3{\pi }^{2}T(B^3+12B)}\left(\frac{1}{{\rho }^2}{\left(1+\frac{1}{{\mathit{SNR}}_E^2}\right)}^2-1\right)}$$ (2)

While there are several parameters in (2), echo correlation is an important factor dictating estimator performance since small increments result in large gains [23]. Under typical imaging conditions – 30 dB SNR_E and 80% BW – improving ρ by just 0.009, from 0.99 to 0.999, reduces jitter by 64%.

The physical source of decorrelation (1-ρ) between successive echoes result from either of two phenomena – out of beam motion or differential motion across the point spread function [21]. Both phenomena result in shifted and decorrelated versions of the reference echo, rather than perfectly shifted replicas, following displacement. As a result, bias and variance of the displacement estimate increase. Out of beam decorrelation typically occurs when scatterers move into and out of the point spread function between subsequent received echoes and is most common in imaging techniques with large displacements (e.g. elastography or Doppler) or in regions of the anatomy exhibiting large physiological motion (e.g. cardiac imaging). Differential motion decorrelation occurs when scatterers are differentially displaced within the pushing beam. Since displacements in ARFI and other radiation force imaging techniques are small (~10 μm [24]), the contribution of out of beam motion to decorrelation is often viewed as insignificant and ignored in further theoretical or FEM analysis [18], [19], [25], [26]. However, as evidenced by the work of several groups to implement physiological motion filters [11], [27], [28], out of beam motion in ARFI imaging can occur due to physiological motion. Nevertheless, the present work continues as in previous work with contributions from out of beam decorrelation assumed to be negligible. This assumption is valid in nearly all physiological environments with the exceptions of cardiac imaging. Even in this environment, the source of out of beam decorrelation (i.e. cardiac motion) occurs on a time scale that is slower than the source of differential motion decorrelation (i.e. radiation force-induced displacements).

McAleavey et al [18] derived an expression for the magnitude of differential motion decorrelation in ARFI imaging that is a function of motion amplitude and the ratio of pushing beam width to tracking beam width. A major assumption of this derivation is that tissue displacement width is equal to the width of the two way response of the pushing beam and that displacement only occurs in the axial direction. Tissue, and other linearly elastic materials, however, exhibit mechanical coupling effects that result in tissue displacement widths that are wider than the pushing beam width and occur in all three directions (Fig 1b) [25], [29]. To correct for this effect, echo correlation is described using the expression from McAleavey [18], but accounting for mechanical coupling through parameters, L_X and L_Y:

$$\rho =1-\frac{1}{c^2}4A^2{f}_0^2{\pi }^2{L}_x{L}_y\left(\frac{1}{\sqrt{(1+L_x^2)(1+L_y^2)}}-\frac{4L_x{L}_y}{(1+2L_x^2)(1+2L_y^2)}\right)$$ (3)

$$L_x=\frac{D_x}{T_x},L_y=\frac{D_y}{T_y}$$ (4)

where A is the maximum scatterer displacement, c is the speed of sound, and D_x, T_x, D_y, T_y, are displacement and tracking beam widths in the lateral and elevational dimensions, respectively. The parameters relating displacement to tracking beam widths in (3) and (4), L_X and L_Y, replace the W_X and W_Y parameters relating pushing to tracking beam widths from McAleavey [18]. Substituting (3) into (2) results in a new expression for the jitter lower bound in ARFI imaging:

$$\widehat{\sigma }\ge \sqrt{\frac{3}{2f_0^3{\pi }^{2}T(B^3+12B)}\left(\frac{1}{{\left(1-\frac{1}{c^2}4A^2{f}_0^2{\pi }^2{L}_x{L}_y\left(\frac{1}{\sqrt{(1+L_x^2)(1+L_y^2)}}-\frac{4L_x{L}_y}{(1+2L_x^2)(1+2L_y^2)}\right)\right)}^2}{\left(1+\frac{1}{{\mathit{SNR}}_E^2}\right)}^2-1\right)}$$ (5)

where σ̂ is in units of seconds. McAleavey et al [18] further derived an expression for ARFI imaging signal (i.e. the expectation value of the displacement estimate). Replacing the assumption of equal displacement and pushing beam widths with the updated expression in (4) results in a new expression for ARFI image signal:

$$\mu =\frac{2{\mathit{AWL}}_x{L}_y}{\sqrt{\left(2L_x^2+1\right)\left(2L_y^2+1\right)}}$$ (6)

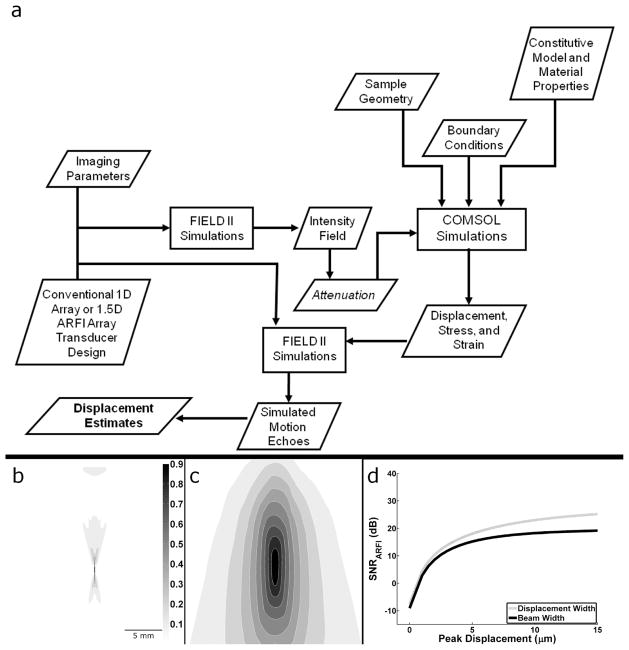
Fig. 1.

a) Block diagram of the numerical simulation framework. b) Intensity field output from FIELD II c) Displacement output from tissue FEM. Scale bar and color map of relative intensity apply to both images. d) Acoustic radiation force impulse SNR upper bound from (7) when using the actual displacement width parameter or the beam width proxy as in McAleavey et al [18].

Substituting (5) and (6) into (1) and scaling by c/2 to maintain consistent units results in a final expression for the upper bound of SNR_ARFI:

$${\widehat{\mathit{SNR}}}_{\mathit{ARFI}}\le \frac{\mu }{\left(\widehat{\sigma }\frac{c}{2}\right)}$$ (7)

The upper bound in (7) results in larger SNR_ARFI values when compared with an upper bound derived using McAleavey’s pushing beam width as a proxy for displacement width (Fig 1).

B. Numerical Simulation Framework

A numerical simulation framework (Fig 1a) was developed based on previously described FEM simulation methods [19], [25], [26] to validate the derived analytical model in (7). Transducer design and relevant imaging parameters were selected and the intensity field was calculated using FIELD II [30]. Since intensity is proportional to the acoustic radiation force [31], [32], FIELD II results provided the body force input parameters for the FEM (COMSOL Multiphysics, COMSOL Inc. Burlington MA) simulations. FEM simulations were performed using a 50 mm × 50 mm × 50 mm block and a free tetrahedral mesh. Mesh element size was optimized to adequately sample displacement while minimizing the total number of elements. A maximum element size of 0.5 mm was used in regions where displacement estimates were extracted. To mimic human tissue using linear elastic assumptions, a Poisson’s ratio (ν) of 0.49 [1] was used. Three-dimensional displacement fields were calculated from FEM simulations using a linear GMRES (generalized minimal residual) iterative solver [33] and a geometric multigrid preconditioner [34]. The displacement results were then imported into MATLAB and scaled to achieve the desired peak displacement value. FEM simulations were conducted using static analysis where displacement fields represented immediate deformation responses to an impulsive acoustic radiation force. This time point is of greatest interest in ARFI imaging as images are typically formed using the maximum displacement parameter. Additionally, it is this time point where the proposed 1.5D array is anticipated to make the greatest contribution as later time points yield less differential motion decorrelation due to lower displacements and shear wave propagation [19]. Using these FEM methods, the mechanical coupling effects were incorporated into the proposed analytical model, D_X and D_Y described above, by measuring the lateral FWHM displacement at the focus.

Received echo data from the proposed transducer array were simulated by first building a 20 mm × 40 mm × 25 mm volume comprising 2.5 × 10⁵ uniformly distributed point scatterers with Gaussian distributed amplitudes. Reference, pre-motion, echoes were calculated using the FIELD II function calc_scat. A second echo, representing received echo data from the ARFI “tracking” pulse, was then simulated by displacing scatterers according to the FEM displacement field results and then repeating the calc_scat computation. Electronic noise was modeled as additive Gaussian white noise. Displacements were calculated using the Loupas autocorrelation method [35] and a sliding window length of 1.5 periods of the tracking center frequency.

SNR_ARFI was calculated from displacement results as the ratio of the sample mean to the standard deviation of the calculated displacement. Mean and standard deviation for SNR_ARFI values were computed by repeating the simulation over multiple (n = 30) independent realizations of scatterer positions, amplitudes, and electronic noise.

C. 1.5D ARFI Transducer Design and Comparison

A 1.5D transducer array for ARFI imaging was designed for the purpose of increasing SNR_ARFI using insights from the analytical model, while taking hardware complexity into consideration (i.e. 1.5D is less complex than a 1.75D or 2D array solution). SNR_ARFI improvements using the 1.5D array is derived from mitigation of echo decorrelation through two primary mechanisms. First, the additional rows of elements enable electronic focusing in elevation, thus reducing the tracking beam width in this dimension. Second, the functions of pushing and tracking pulses can be assigned to different rows (Fig 2). This allows pushing rows to use lower frequency elements than the tracking rows, thus widening the pushing beam width relative to the tracking beam width. The parameters describing the 1.5D array and a conventional 1D array are given in Table I.

Fig. 2.

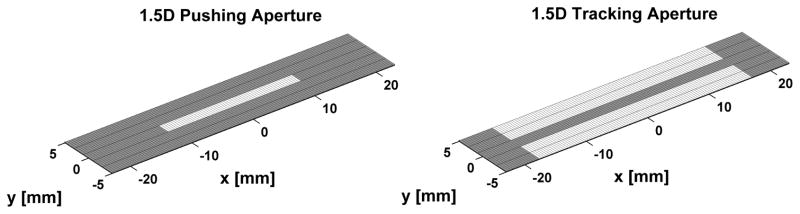
Pushing and tracking array geometry for the proposed 1.5D ARFI imaging transducer. White denotes active elements in the array.

Table I.

Simulation parameters for the conventional 1D array and 1.5D ARFI array. With the exception of number of elements and center frequency, all other values were constant between the two designs in order to better compare the improvement in SNR_ARFI due to increased pushing to tracking beam width ratios.

	Conventional 1D		1.5D ARFI
	Pushing	Tracking	Pushing	Tracking
Elements	60	96	60	4 × 96
Center Frequency (MHz)	4.21	6.15	2	7
Bandwidth (%)	50	80	50	80
Lateral Pitch (μm)	350
Elevation Pitch (mm)	1

SNR_ARFI for the 1.5D ARFI array and a conventional 1D array were computed over a range of peak displacements, using the numerical framework outlined above. In addition, a 4 mm diameter soft lesion [36] at a depth of 20 mm within a stiffer homogeneous background tissue, representing breast tissue [37], was simulated. All parameters were the same as above except the maximum element size of the tissue block, transducer focal area, and lesion were 2 mm, 0.5 mm, and 0.25 mm, respectively. Images of the lesion produced with the 1.5D ARFI or the conventional 1D array were produced. Elastic modulus contrast between the simulated lesion and background tissue was 1:10 (e.g. 10 kPa lesion in a 100 kPa background) with peak displacement inside the lesion of 12 μm. Image contrast-to-noise ratio (CNR) was calculated as [38]:

$$\mathit{CNR}=20{log}_{10}\left(\frac{\mid {\mu }_i-{\mu }_o\mid }{{\sigma }_o}\right)$$ (8)

on median filtered images, where μ_l and μ_o are the mean displacements within equal area regions inside and outside the lesion, respectively, and σ_o is the standard deviation of displacement outside the lesion.

III. Results and Discussion

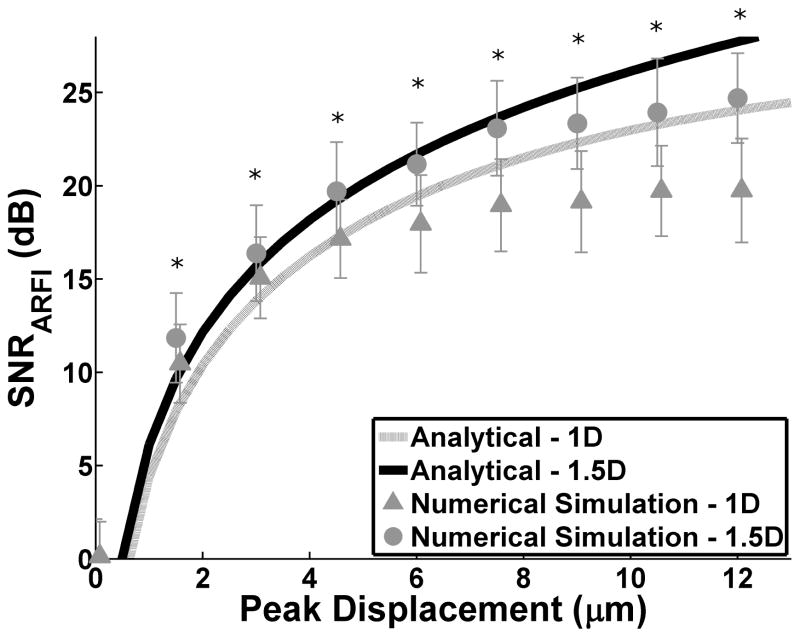
To validate the analytical model (7), SNR_ARFI was calculated for independent realizations of scatterers with increasing peak displacement for both the conventional 1D array and 1.5D ARFI array (Fig 3). The solid lines denote the derived SNR_ARFI upper bound and the symbols represent numerical simulation results. Excellent agreement was observed between numerical simulation results and the proposed SNR_ARFI analytical upper bounds – correlation coefficients of 0.995 and 0.998 for the 1D and 1.5D arrays respectively. In addition, the 1.5D ARFI array had an increased SNR_ARFI for all normalized displacements as compared to the 1D array (p < 0.05). Finally, when SNR_ARFI was calculated for increasing SNR_E, it was found to plateau above 30 dB. This trend substantiates the importance of improving SNR_ARFI through reductions in echo decorrelation as corresponding SNR_ARFI gains achieved via higher SNR_E are negligible.

Fig. 3.

SNR_ARFI as a function of peak displacement. Solid lines represent the derived analytical model and the symbols with error bars are numerical simulation results for the 1D and 1.5D arrays. SNR_E = 30 dB. Mean and standard deviations for SNR_ARFI were calculated over 30 independent runs. * indicates significant difference between 1.5D and 1D numerical simulation (two sided t-test p < 0.05)

Pushing and tracking beam widths for the conventional 1D and 1.5D ARFI imaging arrays were calculated using FIELD II (Table II). By enabling electronic focusing in the elevational dimension, the 1.5D ARFI array possessed a significantly wider pushing beam and narrower tracking beam width as compared to the conventional 1D array. Additionally, due to an ability to use dedicated elements for pushing and tracking functions, different center frequency ceramics were used for different rows of the 1.5D array (e.g. 2 MHz and 7 MHz for the 1.5 D array versus 4.21 MHz and 6.15 MHz for the conventional 1 D array as described in Table I). Thus, while more substantial gains in displacement to tracking beam widths were observed in the elevational dimension, gains were also achieved in the lateral dimension due to a larger range of center frequencies.

Table II.

Tissue displacement width, tracking beam width and the ratio of displacement width to tracking width (Disp, Track, Displ:Track, respectively) for the 1.5D ARFI and the conventional 1D array. The 1.5D ARFI array has a 9 fold increase in D_y and a 1.2 fold increase in D_x as compared to the conventional 1D array. For comparison, the ratio of pushing beam width to tracking beam width is also included.

Transducer	Direction	Displ (mm)	Track (mm)	Displ: Track (Di)	Push:Track
Conventional 1D	Lateral	6.4	0.25	25.9	1.5
	Elevation	10.3	5.4	1.9	1.2
1.5D ARFI	Lateral	8.1	0.25	32.9	2.9
	Elevation	17.7	1.0	17.8	13.2

Lesion simulations were performed with independent realizations of scatterers for the purpose of illustrating the effects of transducer geometries and parameters on image quality (Fig 4). The lesion was better delineated – a 2.92 dB improvement (two-sided t-test, p < 0.0001) – when imaged using the 1.5D ARFI array over the conventional 1D array (Table III).

Fig. 4.

Simulated image of a compliant lesion embedded in stiffer surrounding tissue (1:10 ratio in Young’s Modulus) imaged using either the (b) 1D or the (c) 1.5D array. The 1.5D array exhibited a 2.92 dB average improvement in CNR over the conventional 1D array (n=30). The (a) black and white image illustrates the location and size of the lesion (4 mm diameter, 20 mm depth) and the dotted lines indicate regions of interest (ROI) used for CNR and SNR calculations. Media-Color 1

Table III.

CNR and SNR values of the simulated lesion when imaged with the conventional 1D and the 1.5D ARFI array (n = 30). A 2.92 dB average improvement in CNR was achieved with the 1.5D ARFI array (two-sided t-test, p < 0.0001). The average SNR values inside and outside the lesion were also significantly improved with the 1.5D ARFI array (p < 0.0001).

Transducer	CNR (dB)	SNRlesion (dB)	SNRtissue (dB)
Conventional 1D	6.91±1.21	7.29±0.62	14.48±0.97
1.5D ARFI	9.82±0.83	11.02±0.68	23.26±1.64

IV. Conclusion

An analytical model for the upper bound of ARFI image SNR, a metric for comparing ARFI image quality, has been derived as a function of tissue properties, imaging parameters, and transducer geometry. The analytical model was validated using a numerical simulation framework that coupled FIELD II to a finite element tissue model. By accounting for tissue displacement, there was excellent agreement between the analytical model and the numerical simulations. Using insight gained from the analytical model, a novel 1.5D array for ARFI imaging was designed. The 1.5D ARFI array increased displacement to tracking beam width ratio by allowing electronic focusing in the elevation and by allowing the pushing elements to be at a lower center frequency than the tracking elements. These improvements, impossible in a 1D array, resulted in an overall increase in echo correlation and improved SNR_ARFI as predicted by the analytical model. When compared to a conventional 1D array, the 1.5D ARFI array provided significantly improved displacement estimation, ARFI image SNR, and image CNR. Finally, the coupling of transducer design to an accurate analytical model of ARFI image SNR highlights the potential utility of this new tool. By using the analytical model to develop more sophisticated transducers that improve image quality, the clinical utility of ARFI can be improved for more accurate assessments of tissue material properties or better delineation of different tissue structures, such as lesions or arterial plaques.