Biophysical constraints on the evolution of tissue structure and function

Abstract

Phylogenetic analyses based on models of molecular sequence evolution have driven to industrial scale the generation, cataloguing and modelling of nucleic acid and polypeptide structure. The recent application of these techniques to study the evolution of protein interaction networks extends this analytical rigour to the study of nucleic acid and protein function. Can we further extend phylogenetic analysis of protein networks to the study of tissue structure and function? If the study of tissue phylogeny is to join up with mainstream efforts in the molecular evolution domain, the continuum field description of tissue biophysics must be linked to discrete descriptions of molecular biochemistry. In support of this goal we discuss tissue units, and biophysical constraints to molecular function associated with these units, to present a rationale with which to model tissue evolution. Our rationale combines a multiscale hierarchy of functional tissue units (FTUs) with the corresponding application of physical laws to describe molecular interaction networks and flow processes over continuum fields within these units. Non-dimensional numbers, derived from the equations governing biophysical processes in FTUs, are proposed as metrics for comparative studies across individuals, species or evolutionary time. We also outline the challenges inherent to the systematic cataloguing and phylogenetic analysis of tissue features relevant to the maintenance and regulation of molecular interaction networks. These features are key to understanding the core biophysical constraints on tissue evolution.

Key points

• We outline an extension of phylogenetic studies of protein interaction networks to take into account biophysical constraints to interaction imposed by tissues regulating these networks and we define these constraints explicitly as a means to track the evolution of tissue structure and function objectively.

• For biophysical constraints that are associated at the lowest spatial scales with molecular diffusion within and between cells that are less than 100 μm apart, we define a cylinder of 40 μm radius centred on a small vessel as the primary functional tissue unit (pFTU).

• Molecular transport and communication between distributed or contiguous pFTUs via the endothelial or epithelial vessels is characterised at the level of secondary functional tissue units (sFTUs). sFTUs represent units of physiological function that are replicated multiple times in a whole organ.

• Non-dimensional analysis, which expresses the relative importance of biophysical processes, provides the metrics to quantify and compare the function of FTUs for phylogenetic analysis.

• We lay the ground for a systematic approach to the measurement of tissue structure and function, based on biophysical principles, at the level of primary and secondary FTUs.

Introduction

The cladistic approach to phylogeny infers ancestry by taking into account the sharing of comparable features (Telford & Budd, 2003). To ensure reliability of inference, a mathematical model of feature change is applied to predict the phylogenetic tree that best explains feature transitions between ancestors and known taxa (Kelchner & Thomas, 2007).

For example, to trace the evolution of organisms, phylogenetic analysis combines: (i) a set of measurements of putatively homologous structural or functional features across a set of known organisms, as well as (ii) a mathematical model that quantifies the transitional probability of these measurements (i.e. a computationally readable representation of how measurements of these features are expected to change). A classical example of this approach is drawn from phylogenetic analysis of nucleic acid or polypeptide sequences. In this case, the features under study are sites within a sequence, and the measurement of these features generates (nucleic or amino acid) characters occupying these sites. The development of mathematical models about transitions between characters of these features (e.g. models based on amino acid substitution matrices: Henikoff & Henikoff, 1992; Eddy, 2004), and the interpretation of the resultant phylogenetic trees, constitute a substantial contribution to evolutionary study in molecular biology.

In this work, we address the challenge of extending the above phylogenetic methods to comparative mammalian physiology. In particular, we draw upon methods developed in the field of molecular phylogeny to develop a compatible rationale for the study of evolution of mammalian tissues. Specifically, this rationale focuses on:

1. Identifying and defining the biochemical and biophysical features of tissue that are central to the maintenance and regulation of molecular interactions, with particular reference to control of flow (i) along the lumen of endothelial and epithelial vessels and (ii) across the walls of these vessels;

2. Generating measurements about the above features from different organisms;

3. The development of multiscale models, based on non-dimensional analysis, that take into account the biophysical constraints to molecular interaction and fluid flow that are to be satisfied by the above tissue features over the course of evolution.

The first section of this paper builds the qualitative rationale for the application of biophysical constraints to study tissue evolution, in terms of the maintenance and regulation of molecular interaction and flow across scales. We then propose a set of features that are applicable to molecular interaction and transport at the tissue scale, and consider the mathematical modelling of these features in terms of geometric and biophysical constraints on molecular interaction and fluid flow. The final section concludes with an outline of the challenges ahead in the collection and cataloguing of measurement data for the above features by the community, in support of the systematic phylogenetic study of different tissue and organ systems.

Biophysical constraints on the evolution of structure and function: regulation of molecular interaction over multiple scales

The focus of this section is on: (i) the biophysical relationship between structural and functional features across scales, and (ii) the central role of this relationship in identifying putatively homologous features for phylogenetic analysis. In view of the direct emphasis on phylogenetic study, we primarily address structure–function relationships for genome encoded entites, and proteins in particular.

In this work, we apportion biological structure–function relationships over four major levels of organisational complexity. These levels, numbered I to IV, are outlined in Fig. 1.

Figure 1. Four levels of structure–function relationships.

For each level, labels ‘X’ and ‘Y’ (in red) highlight the interacting entites, namely: (I) amino acid residues, (II) protein domains, (III) well-mixed compartments, bound by phospholipid membrane, bearing PIN modules, and (IV) PINs contained by whole pFTUs. Left: protein domain architecture diagrams, in the style of Bateman & Chothia, 1995 and Fig. 3, illustrating amino acid interaction for both backbone and side-chains. The two identical immunoglobulin superfamily domains shown in level II are a duplication of the one in level I. Right: level III shows schematic bisection of a pFTU bearing two cells: X, an endothelial cell and Y, a hypoblast. The PIN diagram represents the secretion (dashed red arrow) of paracrine FGF from a hypoblast cell to interact with receptors on either cell type within the same pFTU. Level IV depicts the transit of endocrine FGF (e.g. FGF15 or FGF23, Itoh, 2010) from one part of a sFTU to another via an advective system, which is also part of the same sFTU. The advective tubing is diagrammatically positioned between the two pFTUs (labelled X and Y). In this case, the dashed red arrow represents the transition of the FGF hormone either entering (right) or leaving (left) plasma.

Levels I and II: evolution of protein domain structure and protein domain function

The study of the relationship between protein structure (level I) and function (level II) gave rise to a significant cataloguing of evidence by the community (e.g. Dessailly et al. 2009; Perkins et al. 2010; Bertolazzi et al. 2013). Despite the considerable range and heterogeneity of this evidence, four key data sets stand out on the basis of (i) their extensive breadth of coverage or depth of detail, as well as (ii) the substantial community collaboration invested in their generation. These data sets are numbered 1 to 4 and described below. Generally applicable principles governing the relationship between biological structure and function emerge from the study, both in isolation or combination, of these data sets. Here, we outline and document three core principles emerging from these studies, in preparation for their further application to tissues in levels III and IV.

(1) Function is defined in terms of structural change caused by direct interaction

Data Set 1 includes the GO (Blake et al. 2013), GOA (Barrell et al. 2009), and Reactome (Matthews et al. 2009) databases. The ‘Molecular Function’ section in the Gene Ontology (GO_MF), and associated pathway databases annotated by these terms, are the result of a large scale community effort in cataloguing the function of gene products – predominantly that of proteins. In particular, a few thousand GO_MF terms are applied in annotating over half a billion protein gene products (GOA stats, 2014), either directly (e.g. GOA) or via association with mechanistic descriptions of molecular reactions in pathway databases (e.g. http://www.reactome.org). Of the 17 top-level terms in the GO_MF hierarchy, 16 represent functions in which a protein carrying out such a function must effect a change in molecular structure over the course of direct physical interaction with other molecules (Fig. 2). Detailed examples of molecular change may be found in pathway databases, which explicitly depict structural alteration in terms of reaction substrates prior to, and products subsequent to, the execution of protein function (e.g. IRS-mediated signalling).

Figure 2. Measuring molecular function.

Screenshot detail from the OBOEdit software tool (Blake et al. 2013) showing the top-level hierarchy of the Molecular Function portion of the Jan 2014 version of the Gene Ontology.

Data Set 2 includes the Intact (Orchard et al. 2014) and STRING (Franceschini et al. 2013) databases. While the bookkeeping of Data Set 1 provides a crucial overview of protein function, its generation depends on a widespread annotation effort that curates and subjectively interprets results published in the primary literature. Conversely, the experimental high-throughput verification of interaction (e.g. using techniques such as TAP-MS or Y2H) in Data Set 2 provides objective and consistent first-hand evidence of direct interaction for large sets of proteins under tightly controlled conditions. As a coherent depiction of protein binding that is necessary for the execution of function, the generation of protein interaction networks (PINs) directly from this high-throughput effort represents a second major data set central to the study of the evolution of protein structure and function.

(2) Structure at one scale is the result of a set of functions at a lower scale

Protein function is defined in terms of the ability to continuously engage in, and disengage from, binding with other molecules. Conversely, tertiary protein structure is the result of a constantly ongoing conformational change (i.e. folding and unfolding) through interactions between amino acid residues in the same primary structure (i.e. the protein binding with itself). The chain of amino acids residues, therefore, has the function of folding into a three-dimensional (3D) protein domain. The order of residues on the linear chain (i.e. the primary structure of the protein) is critical to the kind of fold that is achieved as the polypeptide backbone constrains and controls which residues can interact.

Data Set 3 includes the RCSB (Rose et al. 2013) database. The production of geometric models of proteins, through techniques such as X-ray crystallography and NMR, has generated a classified repertoire of independently folding domains (e.g. SCOP: Fox et al. 2014; CATH: Cuff et al. 2009) showing explicitly the physical interaction between residues in the resulting structure. In biophysical terms, these domains satisfy the energetic constraints for the maintenance of a small set of stable conformations. These conformations can be directly correlated to the network of amino acid interactions that are causal to the fold (Figs 1 and 3). In that sense, protein structure is the outcome of amino acid-level interaction.

Figure 3. Protein conformation.

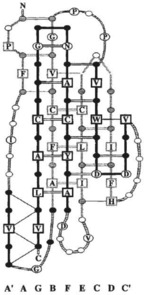
Backbone-and-side-chain schematic for an immunoglobulin superfamily protein domain from smooth muscle telokin (reproduced from Bateman & Chothia, 1995).

Data Set 4 includes the UniProt (Magrane & Consortium, 2011) database. Similarly to PINs, the concerted effort to generate and catalogue geometric models of protein domains is a major experimentally intensive achievement by the biomedical community. In parallel to this effort, the generation of primary structures inferred from genomic sequencing has provided very large volumes of surrogate knowledge about the 3D structure of protein domains (i.e. the tertiary structure). On a protein-by-protein comparison, this sequence dataset outstrips Data Set 3 by about two orders of magnitude in terms of protein coverage, and this disparity is likely to widen further (Fig. 4). Primary sequence data does not provide explicit information about specific residue-to-residue interaction. However, the combination of residue substitution models and techniques such as dynamic programming provides the means to align homologous sequences from different organisms and to identify residues that are conserved over the course of evolution. In particular, a sequence alignment on a set of homologous proteins (Supplemental Fig. S1) predicts that each column on the alignment represents a geometrically equivalent site throughout the tertiary structures corresponding to that set. While the availability of a geometric model is not necessary for the interpretation of an alignment, having at least one such model provides the means to interpret more accurately the biophysical role of the conserved residues in the context of the folded domain (Supplemental Movie S2).

Figure 4. Protein sequence content vs geometric protein models.

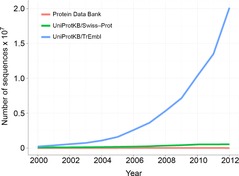
Graph showing the growth of UniProt protein sequence content compared to Protein Data Bank holdings of geometric protein models. Census of by Ruder Boskovic Institute, Croatia (Creative Commons Attribution-Non-Commercial-Share Alike 3.0 Croatia License).

(3) Evolution is traced primarily by comparing homologous interaction networks across organisms

Phylogenetic analysis on a set of homologous sequences that fold into protein domains of the same class is based on the premise that the very similar biophysical folding constraints are applicable across this set of proteins (e.g. the beta-trefoil fold discussed in Venkataraman et al. 1999; Beenken & Mohammadi, 2009 and illustrated in Supplemental Fig. S1 and Movie S2). On that basis, individual residue columns in a protein sequence alignment provide a tabulation of the types of amino acid that satisfy the biophysical constraints exerted on a particular site involved in an interaction. Sites corresponding to highly conserved columns bear critical residues that ensure the stability of the 3D fold by either (i) sterically preventing interactions that trap the nascent fold in a less stable energetic local minimum, or (ii) sustaining precisely positioned attachments that secure different parts of the backbone together. Therefore, phylogenetic analysis of protein domains tracks the evolution of interaction networks of amino acid residues that accommodate the biophysical constraints imposed to attain the requisite fold. In practice, however, the sequence data supplied for this type of study are only a partial description of this network (Russell & Barton, 1993; Pearson & Sierk, 2005), a limitation partially overcome through the availability of geometrical models of corresponding domain structures.

Phylogenetic analysis on a set of homologous whole-organism PINs is based on the premise that the biophysical constraints imposed on the evolution of protein domain structure are also imposed on physical interaction between domains. On that basis, the results of protein sequence phylogenetic analysis is a key input to the study of PIN evolution that tracks protein-coding gene duplication and sequence divergence as a key source of PIN growth and diversification (Zinman et al. 2011). Results from these studies report that, even between close species, similarity of sequence is no guarantee of similarity of interaction, and that preservation of interactions is particularly poor. However, the set of interactions of a protein is more likely to be conserved if it is involved in a high number of diverse interactions (i.e. it is an interacting hub) and/or it is a component of well-established protein complexes (Jin et al. 2013). Seeking these interaction properties within whole-organism PIN graphs has identified functional modules with significantly higher conservation rates compared to baseline. Compared to phylogenetic analyses of protein sequence discussed above, studies of PIN evolution (i) analyse a more explicit representation of the network under investigation, in terms of both participants and the interactions they are involved in, but (ii) lack an independent explicit representation of the sites in which protein-to-protein interaction takes place. In that sense, while it is possible to develop a coherent understanding of the implication of residue conservation on the structural integrity of a protein domain, the objective determination of the physiological implication of conserved PIN modules is more challenging due to lack of models of tissue structure onto which such interactions can be sited.

Levels III and IV: evolution of tissue unit structure and tissue unit function

In their current form, therefore, large-scale analyses of whole-organism PIN evolution do not take into account the topological mapping of PINs onto cellular and tissue compartments. Therefore, unlike the combination of sequence analysis and protein geometry modelling, studies of whole-organism PINs lack crucial physiological context in terms of location of interaction. Given that a significant aspect of protein interaction regulation depends on controlling the co-location of interactors in the same compartment, it is difficult to factor in the regulatory impact of one interaction on another without consistently mapping PINS to compartments. Interpreting evolutionary change in PINs without this key information is, therefore, a formidable obstacle to bridging molecular biology to comparative physiology.

Overcoming the above obstacle entails the construction of a multiscale compartmental hierarchy onto which to map PIN topology. This map would support the coherent interpretation of molecular interaction progressively at protein, subcellular, cellular, tissue and organ level. This compartmental hierarchy would provide a scaffold onto which biophysical constraints to interaction may be matched with the appropriate mathematical models appropriate for each scale. In this section we develop a hierarchical scale of constraints from protein to tissue level, in terms of control of molecular interaction, as follows:

• Level I – protein domain structure: interaction between amino acid residues is constrained to occur over a volume corresponding to a protein domain, such that control over which side-chains interact resides with the linear ordering of the residues along the backbone of the primary structure.

• Level II – protein domain function: the same biophysical considerations governing protein domain folding in level I are applicable to the study of amino acid residue interaction across domains. At this scale, however, regulation of interaction has to contend with a larger well-mixed space compared to level I. This space is bound by phospholipid membrane, for example: the cytosol of a cell, or the volume of tissue fluid bound by cells in a primary functional tissue unit (see level II below). Regulating the probability of PIN interaction at this level takes the form of controlling the rates of addition/removal of interactors through (i) gene expression/protein ubiquitination, or (ii) conformational changes that sterically allow/inhibit interaction.

• Level III – pFTU structure: primary functional tissue units (pFTUs, described in de Bono et al. 2013) represent generic tissue spaces in which any two points within a pFTU are within diffusion distance. pFTUs are centred around a small advective channel, such as a capillary, in preparation for higher-order assemblies of pFTUs known as secondary FTUs (sFTUs; see below). pFTUs provide a first compartmental organisation onto which to map PINs that require the representation of molecular transit across phospholipid membranes, such as the export of proteins from a cell to the immediate tissue fluid surroundings (e.g. secretion of FGF1 to the surrounding extracellular matrix; see Fig. 1, Level III). At this level, regulation of interaction depends on regulations at level II, as well as controlling the permeability of phospholipid membranes and extracellular matrix to the relevant interactors in the PIN.

• Level IV – pFTU function: this level takes into account the interaction of PINs spanning pFTUs. Level IV caters for constraints of distance beyond diffusive limits requiring advective transit to co-locate interactors. Apart from absolute distance, a second constraint controlling interactor co-location is the permeability of basement membranes (as distinct from phospholipid membranes) associated with advective tubes (e.g. the capillary basement membrane). Assemblies of pFTUs are anticipated to be of two types: (i) contiguous sFTUs, such as nephron or intestinal crypt, in which a PIN is mapped onto a contiguous set of pFTUs assembled along a continuous advective tube, or (ii) distributed sFTUs, in which pFTUs in different organs act, for example, as a scaffold for endocrine PINs (e.g. small intestinal mucosa and liver regulating biliary secretion via FGF15 portal feedback; see Fig. 1, Level IV). Regulation of interaction at level IV, therefore, takes into account all considerations for the previous levels together with control of total volumes for advected fluid and associated pFTUs, permeability across relevant (endothelial or epithelial) vessel walls, as well as regulation of advective flows along these vessels.

The four levels outlined above describe mechanisms regulating molecular interaction operating at different scales. The requirement to regulate molecular interaction is common to all scales. This requirement imposes biophysical constraints that have to be satsified over the course of evolution. Modelling an explicit relationship between PINs and the tissue compartments that site and regulate such interactions is, therefore, a requisite step to understand the evolutionary constraints imposed on primary and secondary FTUs. Modelling this relationship in terms of biophysical constraints on diffusive and advective flow in levels III and IV is the objective of the next section.

Tissue scale biophysical features applicable to molecular interaction and transport

In the previous section we summarised methods used to study the evolution of proteins and protein networks, and identified protein domains (level I in Fig. 1) and the well-mixed compartments of protein networks (level II in Fig. 1) as protein-level canonical volumes. We associated protein structure, determined by amino acid interactions, with the protein domain and protein function, determined by protein domain interactions, with the well-mixed compartment. A key point, used later for tissue units, is that functional interactions (such as amino acid interactions) at one level determine the structure at a higher level (i.e. that of the protein domain). We also concluded that environmental constraints operating on the evolution of PINs are characterised by three biophysical quantities (compartment volume, permeability and fluid flow) that are a consequence of the structure and function of the tissue in which these networks are sited.

In this section we lay the ground for a quantitative biophysical description of pFTUs and sFTUs. The rationale for this description is that pFTUs and sFTUs are stable (i.e. evolutionarily conserved) units. Just as stable protein domains can be combined in multiple ways to form higher levels of protein structure that are selected to achieve functional roles in protein-protein or protein-ligand interactions, so too pFTUs are combined in diverse ways to form the higher level sFTUs that are themselves stable and conserved.

The primary functional tissue unit (pFTU)

The transport of nutrients and waste between cells and the endothelial vascular system, and the communication between adjacent cells via paracrine signalling, are governed by molecular diffusion at a scale where diffusion can be treated as the average movement of large numbers of molecules. Analysis of this thermally driven Brownian motion (Nelson, 2004) shows that the mean-square displacement increases linearly in time, with a proportionality constant for three dimensional diffusion of 6D, where D (with units m² s⁻¹) is the diffusion constant. Thus, the time taken to transport a molecule by diffusion varies as the square of distance. To keep the diffusion time within acceptable limits, all cells in mammalian tissues are within 50 μm of a capillary (Renkin & Crone, 1996). We have previously defined the primary functional tissue unit (pFTU) as a cylinder of diameter 80 μm centred on a capillary so that every point within the pFTU is within 40 μm of the blood supply (de Bono et al. 2013). pFTUs encapsulate behaviour at the molecular scale but the analysis of their function can use equations that represent the transition between molecular mechanisms and continuum properties (see below).

The secondary functional tissue unit (sFTU)

The physiological function of many organs is achieved via multiple (in some cases millions) of similar FTUs that operate in parallel and independently throughout the organ, supplied with advective vessels that have bifurcated 20–30 times from the main parent vessel. Examples of contiguous sFTUs are well established in functional histology, for instance, in the human: (i) a liver contains approximately one million lobule sFTUs, each containing about one thousand pFTUs centred around sinusoids; (ii) a kidney has approximately one million nephron sFTUs (containing a glomerulus and a loop of Henle), and (iii) a lung has approximately 30,000 acinii sFTUs (each containing about 10,000 alveoli). Other examples include exocrine glands in the pancreas, osteons in bone, muscle bundles in the heart and skeletal muscles, cortical columns in the brain, villi in the small intestine and crypts in the colon. Examples of distributed sFTUs may be generated from any combination of pFTUs that participate in a PIN – the following two instances are drawn from FGF physiology (from Itoh, 2010):

1. PIN involving the secretion of FGF23 from bone into the systemic blood stream in response to active vitamin D in systemic blood, with FGF23 directly influencing vitamin D activation by the kidneys. This distributed sFTU consists of: pFTU (bone), pFTU(kidney), as well as the intervening advective vessels for blood;

2. PIN involving the secretion of FGF15 into the portal blood stream in response to bile acids in the intestinal lumen, with FGF15 directly influencing bile acid production by the liver. In this case, the sFTU consists of: pFTU(small intestinal mucosa), pFTU(liver) together with the intervening advective vessels for portal blood, bile and chyme.

The comparative physiology of some contiguous sFTUs is well documented. Mammalian nephrons, for instance, are very similar in structure and function: the differences between kidneys in mouse, human and elephant lie primarily in the number of nephrons – about 3 × 10³ for a 25 g mouse with (resting) cardiac output of 0.2 ml s⁻¹, 1.5 × 10⁶ for a 75 kg man with cardiac output of 100 ml s⁻¹, and 15 × 10⁶ for a 5000 kg African elephant with cardiac output of 1000 ml s⁻¹. These differences in number of nephrons correspond well with the 1:500:5000-fold difference in cardiac output (and hence filtration load; Moffat, 1975). This strongly suggests that nephrons evolved within biophysical constraints to an optimal design prior to subsequent Eutherian developments, and that the filtration requirements for different sized mammals are catered for by repetition of these basic sFTUs operating in parallel, supplied by a variable length branching blood vascular tree. Similar arguments hold for sFTUs in other organs, although the primate brain, with its highly developed cortex and cortical column sFTU, is an obvious late-comer to Eutherian evolution.

We tabulate and classify a range of sFTUs that exist in mammalian organs, together with their corresponding pFTUs and their constituent cells, in Supplemental Table S3. In the next section we consider the types of biophysical constraint that govern level III and IV regulation of PINS in these FTUs, and use non-dimensional analysis of the relevant biophysical processes to identify non-dimensional numbers that can be used as metrics for comparative studies.

Modelling geometric and biophysical constraints on molecular interaction and fluid flow

Biophysical constraints imposed on the evolution of protein network interactions by their tissue environments may be understood by considering, first, the pFTU that allows communication locally via molecular diffusion but with access to more distant communication via the vessel on which it is centred and, second, the sFTU that supports physiological function with larger, higher level structures that contain contiguous or distributed pFTUs. We have listed putative primary and secondary FTUs for mammalian organ systems in Supplemental Table S3. In this section we discuss the physical processes that support their function and propose the use of non-dimensional numbers based on an analysis of the equations representing these biophysical processes as a means to derive appropriate metrics with which to compare the variation of FTUs across individuals, species or evolutionary time. While availability of data required to formulate appropriate models is somewhat limited, the framework proposed below can be used to guide the development of new types of instrumentation and experiment needed to generate relevant data. Although we focus on axial and transmural flows in a conduit and the movement of solutes, the examples of biophysical process elaborated here can be feasibly extended to other types of primary and secondary FTUs.

Molecular processes, continuum fields and physical laws

The Brownian motion of individual molecules has energy k_BT joules (J), where the Boltzmann constant k_B is approximately 1.38 × 10⁻²³ J K⁻¹. At 25°C, or 298K, k_BT ≈ 4.11 × 10⁻²¹ J, the minimum amount of energy to contain a ‘bit’ of information at that temperature. Physiological processes at higher length scales, on the other hand, rely on physical processes for which governing equations can be derived from the statistically average behaviour of large numbers of molecules. Avogadro's number N_A (6.022 × 10²³ mol⁻¹) is the scaling factor between molecular and macroscopic processes. A mole of atoms at temperature T has energy k_BN_AT, or RT J mol⁻¹, where the ‘universal gas constant’ R = k_BN_A = 1.38 × 10⁻²³ × 6.022 × 10²³ ≈ 8.31 J mol⁻¹ K⁻¹. At 25°C, or 298K, RT ≈ 2.5 kJ mol⁻¹.

A material made up of molecules with energy k_BT can be said to have an intensive property T at any point in the material, where a ‘material’ here implies a continuous substance (a ‘continuum’) that has properties imparted by the molecules, and ‘intensive’ means that it is a physical property of the material that is not dependent on the amount of material. The continuous property, such as temperature or the concentration of a particular molecule, is a ‘continuum field’ and is one of the ‘state’ variables describing the state of the material. The density ρ or mass per unit volume (kg m⁻³) of the material is also an intensive property described by a continuum field. Equations representing the physical laws that all materials must obey, are expressed in terms of these macroscopic continuum quantities.

The physical processes and their expression as continuum equations fall under four general categories: (i) momentum and mass balance in fluid flow are expressed by the Navier–Stokes equations, (ii) solute transport processes by the advective Nernst–Planck equation, (iii) momentum and mass balance in solid tissue mechanics by large deformation stress equilibrium equations, and (iv) electro-magnetic processes by Maxwell's equations. Here we consider only the first two of these. We summarise the key physical concepts behind transport in physiological systems and focus on the flow of fluid (e.g. blood, plasma filtrate, air) along the axis and across the walls of a conduit that represents a section of blood vessel, kidney tubule, lung airway and many other sFTUs.

Axial and transmural flow from hydrostatic and osmotic forces

The energy per unit volume of a collection of molecules (n moles or nN_A molecules in V m³) is represented by a macroscopic continuum quantity called the pressure p (J m⁻³). Thus:

This equation links the energy at temperature T of one molecule, k_BT (J) to the macroscopic field property p (J m⁻³) via the molecular density 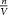(mol m⁻³) and Avogadro's number N_A (mol⁻¹).

The energy density (in J m⁻³), represented by p, exerts a force p × A (J m⁻¹ or N) on a surface of area A (m²) on which the molecules are impacting (essentially exchanging momentum across the surface). In this context p is a force per unit area (N m⁻²) and is called a stress. For viscous fluids such as blood the mechanical concept of stress must be extended to include shear stress and for solid materials, such as soft tissues, the ‘stress tensor’ includes six independent quantities, three ‘normal stresses’ (corresponding to the three components of force that act orthogonally to the three orthogonal surfaces that can be drawn at a point) and three shear stresses that represent forces acting tangentially on those surfaces.

For steady flow Q (m³ s⁻¹) down a tube of radius r, momentum balance in an incompressible fluid (the Navier–Stokes equations) reduces to Poiseulle's pressure–flow relation (Nichols & ORourke, 2005):

(1)

where μ (Pa s) is the dynamic viscosity (water at 20°C has 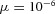kPa s) and the gradient operator ∇ reduces to for one-dimensional gradients in the (axial) x-direction. For constant tube radius r, the axial flux gradient from eqn (1) is:

(2)

where 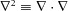is the Laplacian operator which reduces to 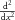for one-dimensional flow. The water flux per unit area (i.e. the fluid velocity) produced by a pressure difference 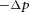across a permeable membrane is 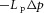, where L_p (units m s⁻¹ Pa⁻¹ or m⁴ s⁻¹ J⁻¹) is the filtration coefficient of the membrane.

For a membrane that is impermeable to a molecular species α but permeable to water, the concentration difference across the membrane, 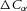, exerts an osmotic pressure difference of 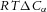that drives water flow through the membrane. The transmural flow per unit area from the combined effects of hydraulic pressure (Darcy flow) and osmotic pressure is therefore:

(3)

where sums the osmotic effects of solute concentration differences for all species α.

Now consider a cylindrical conduit (see Fig. 5) with radius r, length L, axial flow Q and transmural flow J per unit length of tube (m² s⁻¹). Mass balance requires

Figure 5. Illustration of a generic tissue conduit.

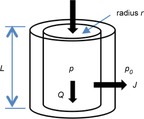
r, inner tube radius; L, length; p, internal pressure; p₀, external pressure; Q, axial flow; J, transmural flow.

(4)

where, from (3),

(5)

Substituting eqns (2) and (5) into the mass balance eqn (4) with (for steady state) gives:

or, rearranging:

(6)

Note that, as well as generating fluid flow along the axis and across the wall of a conduit, the hydrostatic pressure p generates tensile stress in the wall. To a first approximation this is a circumferential or ‘hoop’ stress σ. A simple stress balance (the ‘Law of Laplace’) gives:

(7)

where the hoop stress σ is related to the hoop strain e_rr by 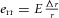, where E is the elastic modulus of the wall (the Young's modulus) in the circumferential direction. Equation (7) is relevant when considering the pulsatile flow that occurs in larger arteries, but will not be considered further here.

Movement of solutes

The driving force (an increase in entropy) for the diffusion of a solute such as an ion is the energy difference across a semipermeable membrane or an energy gradient in a solvent. The energy density for concentration 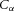(mol m⁻³) of a solute species α is 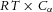(J m⁻³). The energy density difference across a membrane separating a solute difference 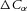(mol m⁻³) is 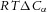(J m⁻³) and the energy density gradient for a solute gradient 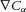(mol m⁻⁴) is (J m⁻⁴).

To move an electron of charge e (≈1.6 × 10⁻¹⁹ C) through a voltage change of 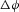(V or J C⁻¹) requires energy 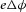(J). The energy needed to move an ion species α of valence 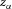through a voltage change of 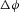is therefore 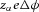(J ion⁻¹) or 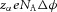(J mol⁻¹). For a voltage gradient of this is, correspondingly, 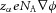(J m⁻¹ mol⁻¹) to move a mole of species α, or (J m⁻⁴) to move ions at concentration 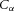(mol m⁻³). Using the Faraday constant 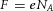≈ 96.4 × 10³ C mol⁻¹, this gradient of energy density is 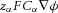(J m⁻⁴), or 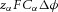(J m⁻³) for a transmural voltage difference .

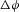Now, a gradient in energy density (J m⁻³ m⁻¹) provides a driving ‘force/volume’ (J m⁻¹ m⁻³ or N m⁻³) and the ability of a force to produce a flux (the rate of transport of the energy associated with ion movement) depends on the medium, whether solvent or membrane, through which the ions move. The ‘resistance’ experienced by a solute can sometimes be calculated from first principles but usually we can use experimental observation to bypass a detailed atomic calculation. Moreover, it is often observed that a linear approximation is valid, in which case ‘energy density flux’ is D_α × ‘force/volume’, where 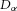(m² s⁻¹) is the experimentally observed ‘diffusibility’ of the solute. Energy density flux is an energy density (J m⁻³) times a velocity (m s⁻¹) and therefore has units of (J m⁻² s⁻¹), or:

The energy density flux for electro-diffusion of an ion species α is therefore:

for the flux generated by the gradients in spatial field concentration (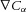) and voltage (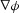), or:

for the transmural flux per unit length of tube in our cylindrical tube example (see Fig. 5), driven by differences in concentration (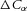) and voltage (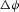). Note that a positive energy density flux results from a negative gradient in ion concentration. Here we only consider the second of these two expressions for flux, i.e. solute flux in the transmural direction.

The energy density flux 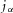can also be expressed as an equivalent ion concentration flux by dividing by 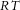(J mol⁻¹) to give the Nernst–Planck flux:

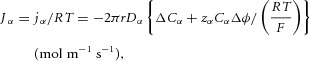(8)

where 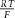(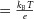) at T = 300K is approximately 25 mV and is a useful way of non-dimensionalising the voltage difference 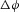to compare its influence with the normalised concentration difference .

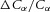If the solvent containing the ion concentration 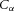(mol m⁻³) itself has a bulk velocity J (m² s⁻¹) in the transmural direction (eqn (5), then an additional energy flux 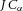(mol m⁻¹ s⁻¹) arises from the transport of the solute by the bulk flow of the solvent – called ‘advective’ transport.

Adding this term to the flux in eqn (8) gives the advective–Nernst–Planck fluxes:

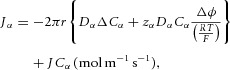Or, substituting for J from eqn (5):

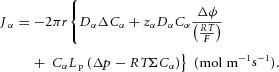(9)

Equation (9) gives the transmural solute flux driven by diffusive and electrostatic forces (the first two terms) and the solute flux associated with transmural solvent (water) flow driven by hydrostatic and osmotic forces (the second two terms). The pressure p is found by solving eqn (6), which balances the driving forces in the axial direction for solvent flow. Together these equations govern transport of solutes in a cylindrical tube – a primary or secondary FTU that could be either an endothelial conduit or an epithelial conduit. The actual solution of these equations, which depends both on particular values of the physical parameters and on the boundary conditions, is not our focus here. Rather we wish to use the equations to derive non-dimensional numbers, representing the relative contribution of the various physical processes, which can be used as metrics for comparing FTUs across individuals, species or evolutionary time.

Non-dimensional numbers

The most convenient way of comparing the relative contribution of various physical processes to the physiological function of an FTU is to derive appropriate non-dimensional numbers. The best known example of a non-dimensional number is the Reynolds number 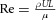, where U (m s⁻¹) is the flow velocity, L (m) is a characteristic length, ρ (kg m⁻³) is fluid density and μ (kg m⁻¹s⁻¹) is fluid viscosity. This represents the ratio of inertial forces to viscous forces in a fluid flow. When Re << 1, inertial forces are negligible and the viscous flow is called Stokes flow. When Re >> 1, inertial forces dominate and at a sufficiently high Re (at least 2300 for flow in a tube), the flow may become turbulent. At intermediate values of Re other considerations may come into consideration. Steady state, fully developed flow in a straight tube, for example, can be represented by the Poiseulle flow pressure–flow relation (eqn (1) above). Note that the implications of Re for animals living at the micrometre scale are discussed in (Dusenbery, 2009).

A further useful characterisation of flow in larger arteries (radius R) is the Womersley number 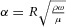, which gives the ratio of transient or oscillatory inertial forces to shear forces in linear pulsatile flow of frequency ω. Another example is the Péclet number 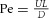, which gives the ratio of advective to diffusive transport (Pe > 1 implies the dominance of advective transport).

The first of the non-dimensional numbers relevant to the physics of the cylindrical tube FTU example we are considering here (Fig. 5) comes from eqn (6). For a cylindrical segment of length L the ratio of the two fluxes, one axial and one transmural, is governed by the product of the dynamic viscosity and the filtration coefficient scaled by r and L to give the non-dimensional number (ndn1 below). The second non-dimensional number comes from eqn (9) by comparing the ratio of diffusive and hydrostatically driven transmural solute fluxes (ndn2). The third comes from eqn (9) by comparing the ratio of electrostatically and hydrostatically driven transmural solute fluxes (ndn3), and the fourth comes from eqn (9) by comparing the ratio of osmotically and hydrostatically driven transmural solute fluxes (ndn4).

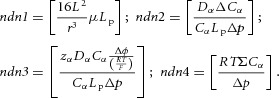(10)

These non-dimensional numbers, calculated for an FTU, quantify the biophysical constraints imposed by that FTU on its protein interaction networks and therefore provide metrics for comparing the evolution of that FTU. In the next section we propose a strategy to measure the parameters and solution variables needed to evaluate these non-dimensional numbers.

A case for systematic biophysical measurements

Defining FTUs at the scale of molecular diffusion (pFTUs) and transport processes based on biophysical continuum models (sFTUs) is a first step to build a quantitative means of comparing tissue structure and function objectively. This approach facilitates the systematic comparison of tissues, across evolutionary time, in terms of protein network evolution. Since PINs are constrained by their tissue environments, this FTU biophysical approach extends the phylogenetic study of PINs to take into account the variability of immediate environmental factors. We quantify the nature of these environmental factors by introducing non-dimensional numbers that provide a measure of the relative importance of the biophysical processes operating within the FTUs and illustrate the approach by analysing the transport of fluids and solutes relevant to PINs. The challenge we now face, however, is the limited availability of data to build statistical correlations. There is, therefore, a strong case for coordinated and sustained efforts in the development of instrumentation and measurements for the characterisation of primary and secondary FTUs in the biophysical terms described above (e.g. to acquire data for the generation of tissue-specific non-dimensional numbers as exemplified above). To that end, Supplemental Table S3 serves as a preliminary scaffold for the organisation of tissue-specific characterisation of both pFTUs and sFTUs:

1. pFTUs: the tandem generation, for the same tissue region, of (i) population atlases of same-tissue pFTUs derived from 3D image reconstruction of serial histology sections, and annotation of this data (as demonstrated in de Bono et al. 2013) for cell boundary segmentation and 3D layout architecture of cells around the advective vessel, and (ii) proteomic data for the reconstruction of tissue region specific PINs.

2. sFTUs: pFTU-specific characterisations described above, as well as vessel- and fluid-related measurements relevant to flow across and along the wall. In particular, (i) fluid viscosity, (ii) wall permeability for the range of solutes that are relevant to the interaction network, (iii) solute diffusibility, (iv) electric charge on key solutes, (v) transmural electrical potential, (vi) transmural pressure differences, (vii) axial and transmural flow, and (viii) geometric measurements such as radius and length. The biophysical significance of these terms has been shown above in the derivation of the four non-dimensional numbers given in eqn (10) from eqns (6) and (9).

Conclusion

Developing standardised metrics over which to compare tissue structure and function is a crucial prerequisite for the systematic modelling and physiological interpretation of changes in tissue. It could, for example, help to provide a deeper understanding of the role of functional tissue units in fields as diverse as drug discovery, tissue engineering and evolutionary pressure. Such modelling would be applicable to two neighbouring domains of study – that of ontogenesis (i.e. comparison of different tissue units within the same type of organisms over its lifespan) and evolution (i.e. comparison of the same tissue unit across different organisms over evolutionary time). The development of models of sequence evolution led to significant advances in the study of protein structure. More recently, the development of models of PIN evolution have begun to study the complexity of protein function. This complexity requires careful dissection to build a biophysically realistic account of molecular networks that occur at tissue level, and to quantify the role of these networks in moulding tissue evolution. In this paper, we provide an organisational scaffold for a community-led cataloguing and classification of tissue-specific measurements that are required for this dissection of PINs. A critical goal for such an effort is to describe evolution as a set of functions causing structural change in response to prevailing environmental biophysical constraints.

The development of standardised metrics for studying ontogenesis and evolution builds on a long tradition, notable contributions being D'Arcy Thompson's Growth and Form (Thompson, 1942), Julian Huxley's Problems of Relative Growth (Huxley, 1972), Rupert Riedl's Order in Living Organisms (Riedl, 1978) and Stuart Kauffman's The Origins of Order (Kauffman, 1993). Riedl, for example, discusses the selection of ‘standard parts’, which matches our concept of a functional tissue unit. As Riedl pointed out, the existence of ‘standard parts’ (or sFTUs) makes it possible to understand how organisms can respond so smoothly to size selection and provides a setting for addressing questions about existing allometric relationship between organs.

In this paper we argue for the use of metrics based on non-dimensional numbers to describe the biophysical constraints and illustrate this concept with four such non-dimensional numbers that characterise the biophysical processes for one particular FTU – solute transport in a cylindrical tube. It is worth noting that a biophysical approach to this particular problem was first presented by the Danish physiologist August Krogh in the early part of the 20th century in this very journal (Krogh, 1919). The use of biophysical principles to study physiological processes clearly also has a fine pedigree. It is time to merge biophysical approaches with the power of high-throughput molecular techniques. The challenge now is to design instrumentation to measure the parameters for specific tissues and to evaluate these non-dimensional numbers under controlled physiological conditions for a wide variety of species.

Glossary

pFTU

primary functional tissue unit

PIN

protein interaction network

sFTU

secondary functional tissue unit

Additional information

Competing interests

None declared.

Funding

P.J.H. gratefully acknowledges grants from the NZ Marsden Fund, the NZ Maurice Wilkins Centre and the Virtual Physiological Rat project funded by the NIH. B.d.B. gratefully acknowledges grants from the Innovative Medicines Initiative (IMI) grants 115156 -2 (DDMoRe) and 115568 (AETIONOMY), as well as European Union FP7 grant agreement 600841 (CHIC).

Supporting Information

The following supporting information is available in the online version of this article.

Figure S1. Clustal X multiple sequence alignment for human FGF 1–23 (except FGF 15, which is only found in the mouse), showing underneath (in grey) a bar graph of relative site conservation. (Reproduced with kind permission from Dr Larry Taylor, University of Michigan.)

Movie S2. The first ten seconds of this movie show the beta-trefoil fold cartoon structure of FGF1 (PDB code 3UD7) in green. The display then overlays ten amino acid residues with high conservation in the alignment shown in S1, namely: LEU14, LEU23, VAL54, ILE56, GLY71, LEU73, CYS83, PHE85, GLU87, SER99.

Table S3. A tabulation of cell types and their role within pFTUs, together with a corresponding set of contiguous sFTUs, for 12 mammalian organ systems.