Transfer Entropy Reconstruction and Labeling of Neuronal Connections from Simulated Calcium Imaging

Abstract

Neuronal dynamics are fundamentally constrained by the underlying structural network architecture, yet much of the details of this synaptic connectivity are still unknown even in neuronal cultures in vitro. Here we extend a previous approach based on information theory, the Generalized Transfer Entropy, to the reconstruction of connectivity of simulated neuronal networks of both excitatory and inhibitory neurons. We show that, due to the model-free nature of the developed measure, both kinds of connections can be reliably inferred if the average firing rate between synchronous burst events exceeds a small minimum frequency. Furthermore, we suggest, based on systematic simulations, that even lower spontaneous inter-burst rates could be raised to meet the requirements of our reconstruction algorithm by applying a weak spatially homogeneous stimulation to the entire network. By combining multiple recordings of the same in silico network before and after pharmacologically blocking inhibitory synaptic transmission, we show then how it becomes possible to infer with high confidence the excitatory or inhibitory nature of each individual neuron.

Introduction

Important advances in the last decade have provided unprecedented detail on the structure and function of brain circuits [1], [2] and even programs aiming at an exhaustive mapping of the brain connectome(s) have been announced [3]–[6]. First, the combination of invasive and non-invasive techniques such as high-resolution optical imagery and diffusion-based tractography have revealed the major architectural traits of brain circuitry [7]. Second, functional imaging has provided non-invasive measures of brain activity, both at rest [8] and during the realization of specific tasks [2]. These efforts have opened new perspectives in neuroscience and psychiatry, for instance to identify general principles underlying interactions between multi-scale brain circuits [9], [10], to probe the implementation of complex cognitive processes [11], [12], and to design novel clinical prognosis tools by linking brain pathologies with specific alterations of connectivity and function [13]–[15]. At the same time, tremendous technological advancements in serial-section electron microscopy are making the systematic investigation of synaptic connectivity at the level of detail of cortical microcircuits accessible [16].

Despite continuous progresses, the understanding of inter-relations between the observed functional couplings and the underlying neuronal dynamics and circuit structure is still a major open problem. Several works have shown that functional connectivity [17] at multiple scales is reminiscent of the underlying structural architecture [8], [18], [19]. This structure-to-function correspondence is, however, not direct and is rather mediated by interaction dynamics. On one side (“functional multiplicity”), structural networks generating a large reservoir of possible dynamical states can give rise to flexible switching between multiple functional connectivity networks [20], [21]. On the other (“structural degeneracy”), very different structural networks giving rise to analogous dynamical regimes may generate qualitatively similar functional networks [22]. Therefore, particular care is required when interpreting data originating from non-invasive functional data-gathering approaches such as fMRI [23]. Altogether, these arguments call for highly controllable experimental frameworks in which the results and predictions of different functional connectivity analysis techniques can be reliably tested in different dynamic regimes.

A first step in this endeavor consists in simplifying the neuronal system under investigation. For this reason, different studies have focused on in vitro neuronal cultures of dissociated neurons [24], [25]. Neuronal cultures are highly versatile and easily accessible in the laboratory. Unlike in naturally formed neuronal tissues, the structural connectivity in cultures can be dictated to some extent [25], and even neuronal dynamical processes can be regulated using pharmacological agents or optical or electrical stimulation. These features have made neuronal cultures particularly attractive for unveiling the processes shaping spontaneous activity, including its initiation [26], [27], synchronization [28] and plasticity [29], [30], as well as self-organization [31] and criticality [32]. Moreover, some studies also showed that spontaneous activity in in vitro preparations shares several dynamical traits with the native, naturally formed neuronal tissues [33].

A second step consists in developing and testing the analysis tools that identify directed functional interactions between the elements in the network. Information theoretic measures such as Transfer Entropy (TE) [34], [35] can capture linear and non-linear interactions between any pair of neurons in the network. TE does not require any specific interaction model between the elements, and therefore it is attracting a growing interest as a tool for investigating functional connectivity in imaging or electrophysiological studies [36]–[39]. The independence of TE on assumptions about interaction models has made it adequate to deal with different neuronal data, typically spike trains from simulated networks [40], multi-electrode recordings [41]–[44] or calcium imaging fluorescence data [22]. TE proved to be successful in describing topological features of functional cortical cultures [41], [42], [44], and in reconstructing structural network connectivity from activity [22], [43].

In a previous work [22], we investigated the assessment of excitatory-only structural connectivity from neuronal activity data (with inhibitory synaptic transmission blocked). For this purpose we developed an extension of TE, termed Generalized Transfer Entropy (GTE). To test the accuracy of our connectivity reconstruction method, we considered realistic computational models that mimicked the characteristically bursting dynamics of spontaneously active neuronal cultures. Comparing diverse reconstruction approaches, we concluded that GTE performed superiorly, even when systematic artifacts such as light scattering were explicitly added to our surrogate data. Besides the inclusion of corrections coping with the poor temporal resolution of typical calcium fluorescence recordings, a key ingredient making GTE successful was dynamical state selection, i.e. the restriction of the analysis to a dynamical regime in which functional interactions were largely determined by the underlying hidden structural connectivity. In particular we showed that it was necessary to restrict the analysis to inter-burst regimes, while consideration of bursting epochs led to inference of exceedingly clustered structural topologies [22].

Here we extend our previous work, by attempting the inference of both excitatory and inhibitory connectivity. Inhibition is a major player in regulating neuronal network dynamics, and the regulation of the excitatory-inhibitory balance is crucial for optimal circuit function [45], [46]. In the brain, inhibition shapes cortical activity [47], dominates sensory responses [48], and regulates motor behavior [49]. Severe behavioral deficits in psychiatric diseases such as autism and schizophrenia have been ascribed to an imbalance of the excitatory and inhibitory circuitry [50]. Despite the importance of inhibition, functional connectivity studies often disregard it because of the difficulty in its identification. Hence, unraveling inhibitory connections, and their interplay with the excitatory ones in shaping network dynamics, is of major interest. We show here that the TE-based approach that we previously used for the inference of excitatory connectivity can be extended with virtually no modifications to networks including as well inhibitory interaction, whose dynamics is once again reproduced by realistic computational models for which the ground-truth connectivity is known. We reveal that the most difficult inference problem is not the identification of a link, be it excitatory or inhibitory, but rather the correct labeling of its type. We show that an elevated accuracy of labeling of both excitatory and inhibitory links can be obtained by combining the analysis of network activity in two conditions, a first one where both excitation and inhibition are active, and a second one where inhibition is pharmacologically removed. We show as well, however, that the inference of link types remain extremely uncertain with current experimental protocols. As a perspective solution, we foresee, based on extensive simulations, that significant improvements in both reconstruction and labeling performance could be achieved by enhancing the spontaneous firing of a culture through a weak external stimulation.

Results

Dynamics of biological and simulated networks

Dissociated neurons grown in vitro self-organize and connect to one another, giving rise to a spontaneously active neuronal network within a week (see Figure 1A) [24], [30], [51], [52]. About 70–80% of the grown connections are excitatory, while the remaining 20–30% are inhibitory [51]. Activity in neuronal cultures is characterized by a bursting dynamics, where the whole network is active and displays quasi-synchronous, high frequency firing within 100–200 ms windows [30]. The timing of the bursts themselves is irregular, with average inter-burst intervals on the order of 10 s in a typical preparation. Between different bursts, firing across the network has a low-frequency and can be described as asynchronous.

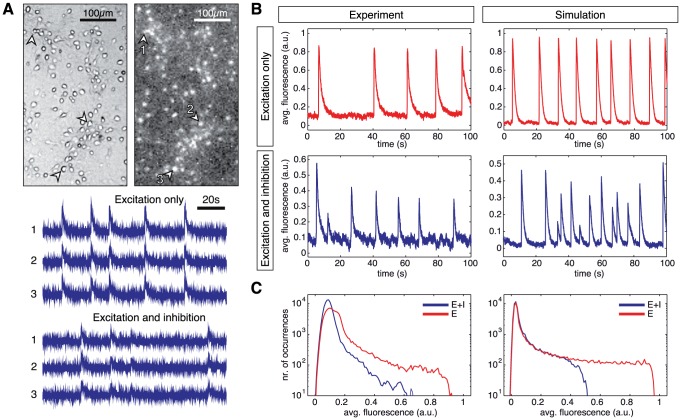
Figure 1. Neuronal network dynamics.

A Top: Bright field and fluorescence images of a small region of a neuronal culture at day in vitro 12. Bright spots correspond to firing neurons. Bottom: Representative time traces of recorded fluorescence signals of 3 individual neurons. The numbers beside each trace identify the neurons on the images. Data shows, for the same neurons, the signal in recordings with only excitation active (“E”) and the signal with both excitation and inhibition active (“E+I”). B Population-averaged fluorescence signals in experiments (left) and simulations (right), illustrating the semi-quantitative matching between in vitro and in silico data. Top: excitatory-only traces (“E–only” data). For the experiments, inhibition was silenced through application of saturating concentrations of bicuculline. For the simulations, inhibitory synapses were silenced by setting their efficacy to zero. Bottom: traces for both excitation and inhibition active (“E+I” data). Network bursts appear as a fast increase of the fluorescence signal followed by a slow decay. Bursts are more frequent and display lower and more heterogeneous amplitudes in the presence of inhibitory connections. C Histogram of population-averaged fluorescence intensity for a 1 h recordings in experiments (left) and simulations (right). Data is shown in semilogarithmic scale for clarity. Red curves correspond to the “E–only” condition, and the blue curves to the “E+I” one.

Neuronal dynamics in cultures may be monitored using calcium fluorescence imaging (see Methods)[24], [53], which enables the recording of the activity of thousands of individual neurons simultaneously. Figure 1A shows example traces illustrating the characteristic fluorescence signal of individual neurons in vitro. The fluorescence signal is characterized by a fast onset as a result of neuronal activation and the binding of 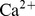ions to the fluorescence probe, followed by a slow decay back to the baseline due to the slow unbinding rate. This behavior is apparent in the population average of the signal, as shown in Fig. 1B, where bursts are clearly identified by the fast rise of the fluorescence signal.

To appraise the role of inhibition on dynamics, we monitor neuronal network activity in two different conditions: A first one, with only excitatory connections active, where inhibitory connections have been completely blocked (denoted as “E–only” networks); and a second one, where both excitatory and inhibitory connections are functionally active (herein after denoted as “E+I” networks). In experiments, inhibitory synapses are silenced through the application of saturating levels of bicuculline, a GABA_A receptor antagonist (see Methods). An example trace of the population average signal of such an excitatory-only system is shown in the top left panel of Fig. 1B, whereas the dynamic behavior in presence of inhibition is shown in the bottom left panel of Fig. 1B. In the “E–only” condition, bursts are more pronounced and more regular in amplitude than in the “E+I” condition, an effect also seen in other studies [30], [54], [55].

These recordings in neuronal cultures provide a comparison reference for our simulated networks of model neurons. We build a computational model of a culture whose dynamics capture its major qualitative features. These include a high variability in the inter-burst intervals, a low 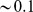Hz inter-burst firing rate, and, in presence of inhibition, an increase in bursting frequency as well as a general decay in the amplitudes of the fluorescence signal, paired by an increase in their heterogeneity. More specifically, we consider a network of 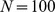leaky integrate-and-fire nodes with depressive synapses in combination with a model for the calcium fluorescence. Network connectivity is random and sparse, with links rewired in order to reach an above-chance level of clustering (see Methods). Each node receives inputs from its pre-synaptic neighbors as well as from independent external sources to mimic spontaneous single neuron activity due to noise fluctuations in the ionic current through its membrane. Free model parameters, such as the homogeneous conductance weights of recurrent connections, were calibrated such as to yield dynamics comparable to the biological recordings, with a bursting rate of 0.1 Hz and realistic decay time constants of the calcium fluorescence (see the bottom right panels of Figure 1B). The blocking of inhibitory connections (top right panel of Figure 1B) is simulated by setting the synaptic weight of all inhibitory connections to zero (note, therefore, that the firing itself of inhibitory neurons is not suppressed, but just its postsynaptic effects).

As discussed more in depth in [22], a hallmark of bursting dynamics is the right-skewed histogram of the population average of the calcium fluorescence signal (see Figure 1C). Low fluorescence amplitudes are associated to the non-bursting regime, which is noise dominated, and the right tail of the distribution reflects bursting events. The range spanned by this right tail is distinctly shortened in presence of inhibition. This difference in the large fluorescence amplitude distribution can be ascribed to the dynamics at the synapse level: For purely excitatory networks, the neurotransmitters resources of a given synapse are depleted during a bursting event [56]. Neurons experience high frequency discharge, but require a longer time to recover, giving rise to long inter-burst intervals. Inhibition lowers this release of neurotransmitters by suppressing neuronal firing before complete depletion, therefore providing a faster recovery, shorter inter-burst periods and lower firing activity inside the bursts.

Reconstructing structural connectivity from directed functional links

Based on simulations of the calcium dynamics in the network, a network of (directed) functional connectivity is reconstructed by computing the Generalized Transfer Entropy (GTE) for each (directed) pair of links (see Methods). GTE is an extension of Transfer Entropy, a measure that quantifies predictive information flow between stationary systems evolving in time [35]. As an information theoretical implementation of the Granger Causality concept [57], a positive TE score assigned to a directed link from a neuron to a neuron 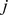indicates that the future fluorescence of 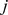can be better predicted when considering as well the past fluorescence of in addition to the past of 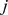itself. We previously introduced GTE to study the reconstructed topology of purely excitatory networks under diverse network dynamical states and signal artifacts [22]. Here we extend its applicability to data that includes inhibitory action.

Conditioning as state selection

A central observation that motivated the definition of GTE was the existence of different dynamical states in the switching behavior from asynchronous firing to synchronous bursting activity. The distribution of fluorescence amplitudes (see Figure 1C) provides a visual guide to the relative weight of the single activity events and the bursting episodes. A functional reconstruction in this bursting regime shows a very clustered connectivity due to the tightly synchronized firing of large communities of neurons. We can understand intuitively this finding, by considering that, in the bursting regime, the network is over-excitable and the firing of a single neuron can trigger the firing of a large number of other neurons not necessarily linked to it by a direct synaptic link. On the other hand, the neuronal activity in the non-bursting regime is sparse and dominated by pairwise interactions, and thus, a reconstruction in this regime identifies directed functional interactions that more closely match the structural connectivity (i.e. high GTE might signal direct pre- to post-synaptic coupling in this regime), as previously discussed thoroughly for “E–only” networks [22].

A rough segmentation of the population signal into time sequences of bursting and non-bursting events is simply achieved by defining a fixed conditioning level on the population average fluorescence. This simple modification with respect to the original TE formulation, makes GTE suitable for an analysis of functional interactions which distinguish different dynamical regimes, as illustrated for purely excitatory networks in the left panel of Figure 2A. The network is indeed considered to be in a bursting regime when the network-averaged fluorescence exceeds the chosen conditioning level (dotted line in Figure 2A), and in an inter-burst regime otherwise. The value of the conditioning level itself is obtained through the analysis of the fluorescence signal histogram and set close to the transition from the Gaussian-like profile shown for low fluorescence values to the long tail characteristic of the population bursts.

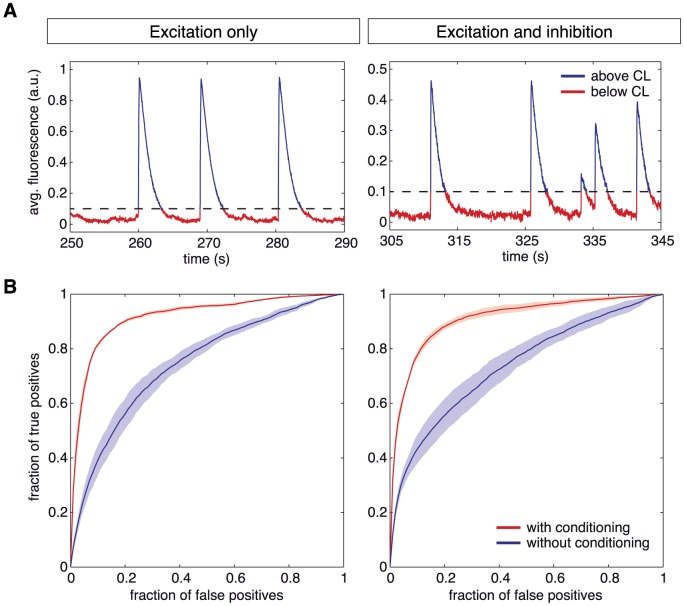
Figure 2. Signal conditioning.

A Separation of the signal in two regimes according to the conditioning level (dotted line), a first one that encompasses the low activity events (red curves), and a second one that includes the bursting regimes only (blue). The same conditioning procedure is applied in both “E–only” networks (left) and in “E+I” ones (right). B Receiver Operating Characteristic (ROC) curves quantify the accuracy of reconstruction and its sensitivity on conditioning. Functional networks are generated by including links with a calculated GTE score exceeding an arbitrary threshold. ROC curves plot then the fraction of true and false positives in the functional networks inferred for every possible threshold. For “E–only” networks (left) and “E+I” networks (right), the red curves show the goodness of the reconstruction after applying the conditioning procedure. Blue curves illustrate the reconstruction performance without conditioning. The ROC curves show that the conditioning procedure significantly improves reconstruction performance. ROC curves were averaged over different network realizations (95% confidence intervals shown).

Note that, while our approach works by restricting the analysis to epochs of inter-burst activity only, other complementary methods exploit detailed information about typical burst build-up sequences in order to infer structure, with potentially superior results when the required time resolution is accessible (e.g. [58]).

Connectivity reconstruction of simulated “E–only” networks

Reconstruction performances from the GTE computation are quantified in the form of receiver operating characteristic (ROC) curves. These curves are obtained as follows: GTE assigns a score to every possible link in the network, and only scores above a given threshold are considered as putative links. These accepted links are then systematically compared with the ground truth topology of the network, and for gradually lower threshold levels. The ROC curves finally plot the fraction of true positives, i.e., inferred connections which really exist, as a function of the fraction of false positives, i.e., wrongly inferred connections.

The ROC curves of the reconstruction performance, with and without conditioning, for the case of simulated “E–only” networks are shown in the left panel of Figure 2B. Without conditioning (blue ROC curves), the reconstruction quality of excitatory connections — to both excitatory and inhibitory neurons confounded — is significantly better than a random choice (which would correspond to a diagonal line in the ROC curve). The reconstruction is, however, hindered by the fact that the analysis effectively averages over data from multiple dynamical regimes as described above. The reconstruction performance thus significantly increases by applying a conditioning (red ROC curves) which selects uniquely the inter-burst regime.

It was also shown for simulations comparable to the ones generated as described above, that the reconstructed networks using GTE are approximately unbiased regarding bulk network properties, such as the mean clustering coefficient, or the average length of connections in the network [22].

Connectivity reconstruction of simulated “E+I” networks

An important aspect of Transfer Entropy, and by extension of GTE, is its model-free nature. Thus, during the process of identifying causal influences between neurons, there is no need to define a generative model for neuronal firing or calcium dynamics, as in the case, e.g., of Bayesian inference approaches [59]. It follows that we can apply GTE without modifications to the case in which both excitatory and inhibitory links are active, provided that the inter-burst network state can be identified in an analogous way. Indeed we observe that while the presence of inhibition does change the dynamics of the system to some extent, the switching behavior remains robustly present (see the right panel of Figure 2A), allowing the straightforward identification of a performing conditioning level.

Remarkably, the reconstruction performance of “E+I” networks remains at high levels after conditioning, of about 80% true positives at 10% false positives, as shown in the right panel of Figure 2B. Thus the model-independence of GTE allows the reconstruction of both excitatory and inhibitory links. As a further self-consistency check, we have simulated the dynamics of a neuronal culture with a topology identical to the inferred one and compared it with the dynamics of the network with the original ground-truth topology. The resulting bursting and firing rates, for both the “E-only” and the “E+I” cases, are not statistically significantly different from the case of perfect reconstruction, while they markedly differ from the case of a randomized topology (not shown). Nevertheless, given the phenomenon of structural degeneracy, a large number of even very different structural circuits could give rise to equivalent dynamical regimes [22]. Therefore, passing this self-consistency check is not a sufficient condition to prove high reconstruction quality, though it is a necessary one.

Note, finally, that we have disregarded, until now, the identification of the specific type, i.e. excitatory or inhibitory, of each link, focusing uniquely on whether a link is present or absent in the ground-truth structural network, whatever is its nature. As previously mentioned, correctly labeling a link turns out to be a more elaborated task than just inferring its existence.

Distinguishing excitatory and inhibitory links

GTE probes the existence of unspecified influences between signals, but cannot identify the type of occurring interaction a priori. Its versatility also means that very different types of interactions can give the same GTE score if their influence in terms of predictability is the same. Hence, to separate between excitatory and inhibitory connections we have to either introduce ad hoc information on neuronal types or combine different reconstructions together to single out the different connectivity types.

Such ad hoc information might come from dye impregnation, fluorescence labeling or immunostaining [60]. These techniques identify cell bodies and processes according to some specific traits, for instance membrane proteins or neurotransmitters' receptors. According to Dale's principle [61], a neuron shows the same distribution of neurotransmitters along its presynaptic terminals. Hence, if a neuron is labeled as either excitatory or inhibitory, we can assume that all its output connections are of the same matching type. Thus by combining the type of information provided by some extrinsic labeling technique with the unspecific causal information provided by GTE, the overall set of inferred links can be separated into two non–overlapping subsets of excitatory and inhibitory links.

Being able to identify the type of a neuron — even with perfect accuracy — does not guarantee a priori that excitatory and inhibitory links can be inferred equally well. On the contrary, different reconstruction performances have to be expected in general, since the interaction mechanism of excitatory links is inherently different from the inhibitory ones, the former promoting the activity of the target neuron, whereas the latter restrain it. We have tested the accuracy of this ad hoc approach through numerical simulations. GTE is applied to the “E+I” data, and the reconstruction quality is assessed separately for the connections originating from neurons of different types (see Methods). Non trivially, the results of this analysis indicate that both types of connections are reconstructed with high accuracy (see Figure 3A). At a fraction of 10% of false positives, excitatory links are detected at a true positive rate of 80%. Inhibitory links show a lesser but still high detection accuracy, of about 60% of true positives.

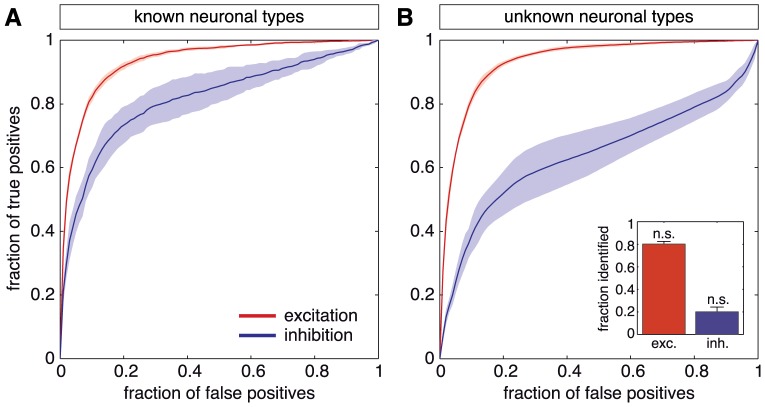
Figure 3. Optimal network reconstruction.

A ROC curves for the reconstruction of a network with both excitatory and inhibitory connections active, supposing to know a priori information about neuronal type. GTE is first applied to the “E+I” data. Next, following Dale's principle and exploiting the available information on neuronal type, links are classified according to their excitatory (red) or inhibitory (blue) nature. B ROC curves for the best possible identification of excitatory and inhibitory connections, when information on neuronal type is unaccessible. Excitatory links (red) are identified by adding together the Transfer Entropy scores of simulations run in “E–only” and “E+I” conditions, and later thresholding them. Inhibitory links (blue) are identified by computing the difference in Transfer Entropy scores between the runs with inhibition present and blocked. Inset: fraction of excitatory and inhibitory neurons correctly identified from these ROC curves. Results were not significantly different from random guess (see Methods). All the results were averaged over different network realizations. The shaded areas in the main plots, as well as the error bars in the inset, correspond to 95% confidence intervals.

Reconstructing and labeling connections from spontaneous dynamics

In the absence of information on neuronal types, an alternative approach consists in a direct combination of the reconstructions procured by the “E–only” and “E+I” data on the same neurons. By adding together the GTE scores from the two reconstructions we can assume that the higher scores come from links that show a high score in both reconstructions. This procedure is thus expected to highlight the pool of excitatory connections, since they are the only ones present in both network conditions. Similarly, we can subtract the “E–only” scores from the “E+I” ones. High scores will then now highlight those links that are present in the “E+I” but not in the “E–only” network, i.e. the pool of inhibitory connections.

The performance of this first two-step reconstruction approach is shown in Figure 3B. The reconstruction of excitatory connections has a quality as good as the one obtained with a priori knowledge of neuronal type based on extrinsic labeling (see Figure 3A). However, the performance markedly deteriorates for the reconstruction of inhibitory links, since only 40% of the inhibitory connections are correctly identified at 10% of false positives.

Note that an additional complication arises with the described two-steps pipeline. A given link might be attributed a combined score above the inclusion threshold, both when considering the sum and the difference of original GTE scores. In this case, the link would be labeled as “both excitatory and inhibitory”, a fact which is excluded by Dale's principle. Despite this problem, we might still try to combine the “E–only” and “E+I” reconstructions to infer the nature of each neuron. To test the accuracy of such identification we try to label neurons as excitatory or inhibitory based on a highly “pure” structural network reconstruction. To do so, we select a very high GTE threshold for link, in such a way that in the inferred subnetwork —including, correspondingly, very few links only— the fraction of false positives remains small (with a maximally tolerable ratio of 5%). We first sum and subtract “E–only” and “E+I” scores to obtain putative excitatory and inhibitory links, as just discussed. We next compute the output degrees of the neurons for each subnetwork, 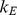and 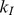, respectively. Finally, we rank each neuron according to the difference 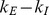. Following Dale's principle, the set of neurons with the highest (positive) ranking would be labeled as excitatory, and those with the lowest (negative) ranking as inhibitory. The results, however, as shown in the inset of Figure 3B, indicate that this approach does not provide better results than a random guessing of neuronal type (see Methods for details on significance testing) and a different approach is required.

Reconstructing and labeling connections from stimulated dynamics

As a matter of fact, the major challenge for an accurate reconstruction and precise labeling of neuronal types is the identification of inhibitory links, and this for the following reason. To estimate GTE, we need to evaluate the probability of each given neuron to be active in a short time window of a duration 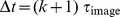, where 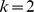is the order of an assumed Markov approximation (see Methods) and 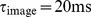is the image acquisition interval. With these parameter choices, we obtain then 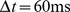. Neurons in a culture spike with an average inter-burst frequency of 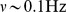, resulting in a low firing probability within each time bin. Continuing this reasoning, the probability that two unconnected neurons spike at random in the same time window is given by 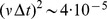. The number of coinciding events 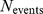expected in a recording is thus:

(1)

where 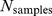is the number of independent samples in a recording. In a typical recording session lasting 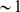h, one gets 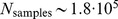independent samples and therefore 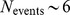. Hence, one can expect to observe, on average, just six concurrent spikes between any pair of unconnected neurons. If an excitatory link exists between two neurons, the conditional probability of firing rises above this random level and more coincidence events are observed, turning into an appreciable contribution to the GTE calculation. However, if an inhibitory link is present, the number of simultaneous spikes gets further reduced with respect to the already very small chance level, making any accurate statistical assessment very difficult. Nevertheless, we note that the number of detected events scales as 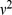with the frequency of firing, and even a slight increase in spiking frequency would enhance considerably the reconstruction performance.

A promising approach to increase neuronal firing consists in forcing the neuronal network through external stimulation. Several studies on neuronal cultures have used external drives, typically in the form of electrical stimulation, to act on neuronal network activity, for instance to investigate connectivity traits [51], [62], modify or control activity patterns [63], [64], or explore network plasticity [65], [66]. Such in vitro approaches are reminiscent of in vivo clinically relevant techniques such as deep brain stimulation, used in the treatment of epilepsy and movement disorders [67], [68].

External stimulation in neuronal cultures has been reported to increase neuronal firing [64] and to reduce network bursting [63], [65], a combination of factors that, in the GTE reconstruction context, improve the accuracy in the identification of the network architecture. To explore potential improvements in reconstruction, we simulate the effect of an applied external drive in a purely phenomenological way by increasing the frequency parameter of the Poisson process that drives spontaneous activity. This additional drive never increases the spontaneous firing frequency beyond 3 Hz, being meant to represent the effects of a rather weak external stimulation. Due to this contained increase of firing rate, the collective bursting activity of the simulated network continues to be shaped dominantly by network interactions, rather than by the drive itself.

The performance of our GTE algorithm combined with a weak network stimulation is illustrated in Fig. 4A, where we show the fraction of true positives in the reconstruction of “E–only” networks at 5% false positives. The presence of even very small external drives substantially enhances reconstruction based on GTE. For higher drives, reconstruction performance reaches a plateau that quantifies the range of optimum stimulation. Performance later decays due to the excess of stimulation, which substantially perturbs spontaneous activity and alters qualitatively the global network dynamics. We incidentally remark that the incorporation of the external drive makes unnecessary — actually, even deleterious — the instantaneous feedback term correction (IFT, see Methods), i.e., an ad hoc modification to the original formulation of TE which was introduced in [22] to cope with the poor frame rate of calcium fluorescence recordings, definitely slower than the time-scale of monosynaptic interaction delays. The IFT correction allows to encompass interactions occurring in the same temporal bin of the recording for TE estimation, a feature useful to enhance reconstruction results when the time-scale of pre-postsynaptic neuron interactions is fast relative to the time resolution of the recording. However, same–bin interactions also result in an overestimation of bidirectional connections, since one cannot establish directionality within a single time bin. When the firing rate is enhanced with respect to spontaneous conditions these negative effects of the IFT corrections become predominant.

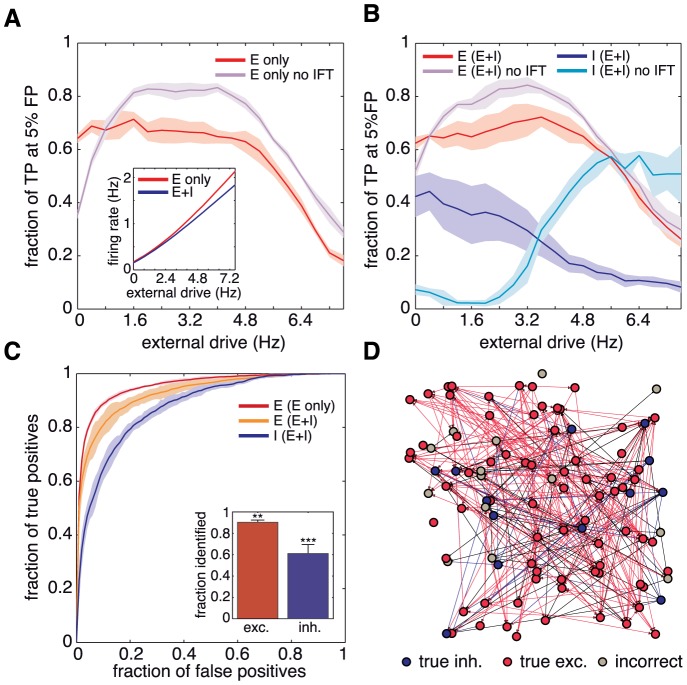
Figure 4. Reconstruction improvement through external stimulation.

A and B, fraction of true positives from the reconstructions at the 5% false positive mark for the studied networks. “E–only” networks are shown in A; “E+I” networks in B. Inset: dependence of the spontaneous firing rate on the applied external drive, emulated here by increasing the rate of the background drive to the culture in silico. All the excitatory reconstructions reach a stable plateau in the reconstruction after removal of the instantaneous feedback term (IFT) correction (see Methods). The inhibitory reconstruction is accurate only for higher values of the external drive. C ROC curves extracted from A and B with an external stimulation of 4 Hz. Inset: fraction of excitatory and inhibitory neurons correctly identified from these reconstructions. Identification was statistically significant compared to random guessing. For excitatory neurons, 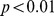(**); for inhibitory neurons, 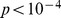(***). D Example of an actual reconstruction after identification of neuronal type. Identified excitatory neurons are shown in red and inhibitory ones in blue. Incorrectly identified neurons are shown in grey. Correctly identified excitatory and inhibitory links are shown in red and blue, respectively, and wrongly identified links are shown in black. For clarity in the representation of the links, a threshold value lower than the optimal has been applied.

The same reconstruction analysis for “E+I” networks is shown in Fig. 4B, for excitatory and inhibitory links separately. The identification of excitatory links greatly improves with moderate drives and, again, IFT becomes unnecessary. For inhibitory links, performance is optimum at low drives, when IFT is used. Without IFT, however, performance is better at relatively high drives, and one can observe the existence of an optimal stimulation range (leading to a firing rate of 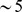Hz) that maximizes inhibition reconstruction while preserving a relatively good excitatory identification.

We note as well that, for “E+I” networks, bursts disappear in general at higher values of the external drive. In general, as depicted in the inset of Fig. 4A, the dependence of the spontaneous firing frequency on the external drive is quantitatively different from “E–only” networks, requiring typically a stronger drive to achieve a comparable firing rate.

With the external drive the overall ROC curves are also improved. In Figure 4C we show the reconstruction performance for medium values of stimulation. In this new regime, we can again try to determine the neuronal type based on the labeling procedure used in the previous section (inset of Figure 4C). Now excitatory neurons are correctly identified with 90% accuracy, whereas the fraction of inhibitory neurons correctly identified rises conspicuously to 60%. This marked improvement is now statistically significant (see Methods).

In Figure 4D we show an actual reconstruction of a portion of the original network with this procedure. Correctly inferred excitatory and inhibitory neurons are shown in red and blue respectively, and mismatches in yellow. Correctly identified excitatory and inhibitory links are also shown in red and blue respectively, and false positives are shown in black. It is visually evident that for this thresholding level a very high purity is achieved, and only a small fraction of the reconstructed links are false positives.

We conclude that the addition of a weak external stimulation to the “bare” network dynamics results in an overall improvement on the reconstruction of both excitatory and inhibitory links. Moreover, by combining the reconstructions of “E–only” and “E+I” networks, we also become able to infer the neuronal type by just analyzing the dynamics, with no a priori knowledge of the system and without resorting to extrinsic information of any sort.

Discussion

Living neuronal networks contain both excitatory and inhibitory neurons. Although the interplay between excitation and inhibition gives rise to the rich dynamical traits and operational modes of brain circuits, inhibition is often neglected when analyzing functional characteristics of neuronal circuits, mostly because of its difficult identification and treatment. In this work we have made a first step towards filling this gap, and introduced a new algorithmic approach to infer inhibitory synaptic interactions from multivariate activity time-series. In the framework of a realistically simulated neuronal network that mimics in a semi-quantitative way key features of the behavior of neuronal cultures, we applied Generalized Transfer Entropy (and Dale's principle) to identify excitatory as well as inhibitory connections and neurons.

In a previous work [22], we developed the GTE framework and applied it to extract topological information from the dynamics of purely excitatory networks, but left as an open question the treatment of inhibition. Here we have shown that GTE has the potential to be applied without substantial modifications to recordings relative to cultures with active inhibition (“E+I” cultures). This data is characterized by an irregular bursting dynamics with overall lower — but distinctly fluctuating — fluorescence amplitudes as well as higher bursting frequencies than purely excitatory (“E–only”) signals. In general, GTE provided an overall good reconstruction of the “E+I” simulated data, hinting at the robustness and general applicability of the algorithm. This is a highly non trivial achievement of the algorithm, given the profoundly different functional profile of inhibitory actions. The GTE reconstruction alone performed well in identifying the existence of links between pairs of neurons, however, it was not sufficient to resolve their excitatory or inhibitory nature. Yet, we provided evidence through numerical experiments that this additional goal could be fulfilled by retrieving a priori information about the types of different neurons (e.g. through immunostaining or selective fluorescent dyes), or by combining the reconstructions obtained from both “E+I” and “E–only” recordings from a same network (thus, again relying uniquely on time-series analysis).

When a priori information about the type of each neuron is available, Dale's principle proves to be, at least in our simulations, a solid yet simple approach that allows the identification of the major connectivity traits of the neuronal network. However, when applying Dale's principle to actual, living neuronal networks recordings (see later), one has to consider its possible limitations, like the existence of (rare) exceptions to it [69]. We also remark that, in a more realistic context, other types of a priori information beyond the nature of the neurons and their processes could be considered, like, e.g. information about their spatial distribution. Although in this work we have considered only purely random distance-independent topologies, neuronal cultures grow on a bi-dimensional domain, and excitatory connections are typically of shorter range than inhibitory ones. This kind of information could be integrated in the analysis of network models that include metric properties and accounts for spatial embedding (such as [27], [70], [71]), as well as different connectivity rules for the generation of excitatory and inhibitory sub-networks.

A systematic extrinsic labeling of neuronal types might be difficult to achieve in large culture experiments. When a priori information is unavailable, our results show that the combination of the reconstructions for “E–only” and “E+I” spontaneous activity data fails at identifying robustly the inhibitory interactions. Nevertheless, we find that the reconstruction performance of excitatory links remains almost unchanged when inhibition is present, despite the fact that inhibition may substantially alter excitatory interactions, and in turn network dynamics, for instance through feedback and feedforward inhibitory loops. The observation that excitatory links are still correctly reconstructed in “E+I” data shows the robustness of the algorithm to the presence of different interactions in the system. We remark that the main factor determining the poor identification of inhibitory links is the weak firing rate during inter-burst epochs. Since, in a nearly asynchronous regime of inter-burst firing, the action of a direct inhibitory link manifests itself by reducing below the already small chance level the probability of firing coincidence between the two connected neurons, the recording of a larger amount of inhibitory firing would be required to improve the reconstruction of inhibitory couplings. Although the recording duration can be increased at will in numeric simulations, this is not the case for real experimental recordings, to which our algorithm aims at being applied.

In our simulations, we naturally achieved to increase single neuronal firing activity, and therefore reconstruction statistics through a weak external stimulation of the network, with neither a significant disturbance in neuronal network dynamics nor the need for substantially longer recordings. In many previous works resorting to external drives to stimulate network activity, both experimental and theoretical, the applied stimulation was supra-threshold, i.e. the stimulation triggered directly neuronal firing [51], [54], [62], [72], [73]. Our approach raises instead network excitability by a weak external drive that effectively increases activity without modifying the network intrinsic behavior, in the direction of other experimental studies that stimulated multiple sites of a neuronal culture via a multi-electrodes array, to either increase network firing, reduce the occurrence of bursting episodes, or investigate plasticity [64], [66]. Interestingly, these works observed that a weak stimulation along few hours did not induce plastic effects, i.e. did not change network behavior, thus making our reconstruction strategy of immediate applicability in experimental recordings.

In the present work we have exhibited experimental data only for qualitative comparison with fluorescence traces obtained from the numerical model. The experimental data could be analyzed in principle without need of any modification to the GTE formulation, but we found our present knowledge of the experimental recordings insufficient to get reliable reconstructions. In particular, we are lacking good estimates of the neuronal firing rate during the inter-burst periods, as well as the amount of fluorescence change caused by an action potential. The former does not allow to determine whether we expect enough events to make the reconstruction of inhibitory links feasible (see Eq. (1)), while the latter prevents the application of an optimal data discretization strategy that would reduce the minimal recording length needed for accurate results. Our study intends therefore to foster the future application of the workaround strategies here explored in experiments in silico, i.e., most notably: (i) a weak external stimulation to increase spontaneous activity; and (ii) the extrinsic labeling of excitatory and inhibitory neuronal cell bodies after the recording (to provide at least a partial source of a priori information) to be used in synergy with our algorithmic approach.

Finally, our reconstruction algorithm has the potential to be immediately applied to the analysis of fluorescence data in experimental recordings that are not affected by the aforementioned limitations. In particular, in vivo recordings and brain slice measurements [74]–[76] display a much richer activity at the individual neuron level than in the in vitro counterparts. Recent works have highlighted the ability of high speed multi-neuron calcium imaging to access neuronal circuits in vivo [77]–[79]. Our methodology can thus be directly applied to these data, particularly in those investigations that target the role of inhibition [80], [81], although systematic verification of the inferred connectivity (in absence of a known ground-truth structure) remains currently out of reach and validation is only possible at the statistical level.

Methods

All procedures were approved by the Ethical Committee for Animal Experimentation of the University of Barcelona, under order DMAH-5461.

Calcium traces from in vitro cultures

Experimental traces of fluorescence calcium signals were obtained from rat cortical cultures at day in vitro 12, following the procedures described in our previous work [22] and in other studies [27], [51], [82]. Briefly, rat cortical neurons from 18–19-day-old Sprague-Dawley embryos were dissected, dissociated and cultured on glass coverslips previously coated with poly–l–lysine. Cultures were incubated at 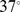C, 95% humidity, and 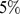CO₂. Each culture gave rise to a highly connected network within days that contained on the order of 500 neurons/mm². Sustained spontaneous bursting activity appeared by day in vitro . Prior to imaging, cultures were incubated for 40 min in recording medium containing the cell–permeant calcium sensitive dye Fluo-4-AM. The culture was washed with fresh medium after incubation and finally placed in a recording chamber for observation. The recording chamber was mounted on a Zeiss inverted microscope equipped with a Hamamatsu Orca Flash 2.8 CMOS camera. Fluorescence images were acquired with a speed of 50 frames per second and a spatial resolution of 3.4 µm/pixel.

In a typical measurement, we first recorded spontaneous activity as a long image sequence 60 min long. Both excitatory and inhibitory synapses were active in this first measurement (“E+I” network). We next fully blocked inhibitory synapses with 40 µM bicuculline, a GABA_A antagonist, so that activity was solely driven by excitatory neurons (“E–only” network). Activity was next measured again for another 60 min. At the end of the measurements, images were analyzed to to retrieve the evolution of the fluorescence signal for each neuron as a function of time.

Note once again that, in this study, experimental fluorescence traces were used only as a guiding reference for the design of synthetic data in “E–only' and “E+I” conditions, and were not analyzed to provide network reconstructions, given the limitations of current experimental protocols, highlighted in the Results and Discussion section.

In silico model

Network generation

We randomly distributed 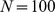neurons over a square area of 1 mm². Neurons were labeled as either excitatory with probability 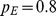or inhibitory with 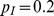. A directed connection (link) was created between any pair of neurons with fixed probability 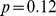, giving rise to a directed Erdős-Rényi network[83]. The resulting network is defined by the adjacency matrix 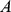, whose entries 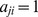denote a connection from neuron 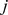to neuron (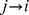). The average full clustering coefficient of the network [84] is given by

(2)

where 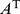is the transpose of 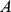and 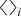denotes average over index . 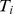is defined as

(3)

where 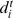is the total degree of node (the sum of its in– and out–degree) and 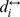is the number of bidirectional links of node . The clustering coefficient of the network after its construction was 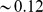, a value that was then raised up to a target one of 0.5 by following the Bansal et al. construction [85], as follows. Two existing links 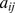and 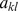were first chosen at random, with 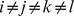. These links were then replaced by 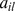and 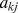. This step was repeated until the desired clustering coefficient was finally reached within a tolerance of 0.1%.

This above-chance clustering level was generated to account for experimental observations of clustered connections in neuronal local circuits [86]. We do not perform here a systematic study of the impact of CC on reconstruction performance, referring the reader to Ref. [22] for this issue, in which CC-independent performance is demonstrated.

Network dynamics

Neurons in the simulated culture were modeled as integrate-and-fire units, of the form

(4)

where 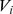is -th neuron's membrane potential and 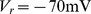its resting value, 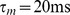is the membrane time constant, 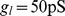is the leak conductance, 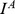and 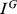the excitatory (AMPA) and inhibitory (GABA_A) input currents respectively, and 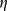a noise term. When the membrane potential reaches the threshold value 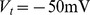the neuron fires and its membrane potential is reset to a value 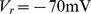, which is maintained for a refractory time 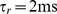during which the neuron is prevented from firing.

Neurotransmitters were released as a response to a presynaptic action potential fired at time 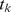, binding to the corresponding receptors at the postsynaptic side of its output neurons. The binding of neurotransmitters at the receptors triggered the generation of postsynaptic currents 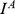or 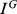, depending on the presynaptic neuronal type. The total input current received by a given neuron was described by

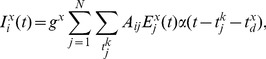(5)

where 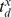is a transmission delay (mimicking axonal conduction), with 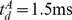and 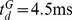. 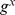is the synaptic strength, which was adjusted to obtain the desired burst rate. The value of 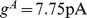in a network with inhibition silenced provided a bursting rate of 0.1 Hz. When inhibition was active, a comparable bursting rate of of 0.12 Hz was obtained by setting 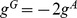. 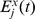is a term accounting for short–term synaptic depression, and 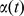is an alpha shaped function of the form

(6)

where 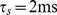represents the synaptic rise time and 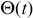is the Heaviside step function.

Short–term synaptic depression accounts for the depletion of available neurotransmitters at the presynaptic terminals due to repeated activity [87]. The neurotransmitters dynamics at the synapses of neuron was described by the set of equations [88]:

(7)

where 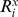and 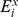are the fraction of available neurotransmitters in the recovered and active states, respectively. 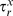is the characteristic recovery time with 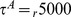ms and 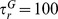ms. 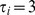ms is the inactivation time and 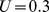describes the fraction of activated synaptic resources after an action potential.

Simulating calcium fluorescence signals

Based on the simulated spike data, synthetic calcium fluorescence signals were generated according to a model that incorporates the calcium dynamics in the neurons and experimental artifacts. The former describes the saturating nature of calcium concentration bound to the calcium dye inside the cells, while the latter treats the noise of the recording camera as well as light scattering due to anisotropies in the recording medium [22].

Each action potential of a neuron at time leads to the intake of 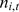calcium ions through the cell membrane, raising the calcium concentration inside the cell. A number 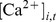of the Calcium ions bind the fluorescence dye by a fixed amount 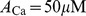, and are slowly freed with a time scale 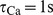. This process is described by the equation

(8)

where 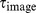is the simulated image acquisition frame rate.

The level of calcium fluorescence 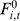emitted by a cell was modeled by a Hill function of the bound calcium concentration (with saturation level 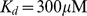) together with an additive Gaussian noise term 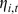characterized with a standard deviation 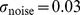[59], i.e.

(9)

The level of fluorescence recorded by the camera at a given neuron was not independent of neighboring cells due to the introduction of simulated light scattering. We incorporated this artifact by adding to the monitored cell a fraction 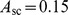of the fluorescence from neighboring cells, which was weighted according to their mutual distance 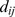by a Gaussian kernel of width 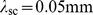. The total fluorescence captured in a neuron was then given by:

(10)

Generalized Transfer Entropy

Generalized Transfer Entropy (GTE) was introduced in [22] as an extension of the original Transfer Entropy notion [35]. It is given by the Kullback-Leibler divergence between two probabilistic transition models for a given time series 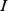, conditioned on the system visiting a specified target dynamical state. In the case of fluorescence signals, this state selection is achieved by conditioning the analysis to the regime where the population average of the time series 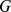is lower than a given threshold 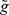, i.e.

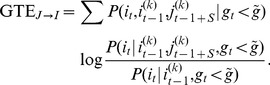(11)

Here, vectors in time are denoted by their length in brackets, which is equal to the order of Markov order approximation assumed for the underlying process, 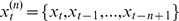. The sum is defined over all possible values of 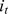and the vectors 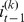and 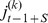. The shift variable 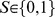denotes the inclusion of same-bin (instantaneous) interactions for 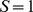. This adjustment was introduced in [22] to cope with the limited time-resolution of calcium fluorescence signals and is dubbed in the text as Instantaneous Feedback Term (IFT) correction. Furthermore, the time-series of calcium fluorescence were high-pass filtered by mean of a discrete difference operator, as a straightforward attempt to enhance the visibility of firing events drowned in noise. Note that GTE reduces to conventional Transfer Entropy for 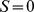and 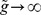, i.e. when same-bin interactions are excluded and when the selected state encompasses the whole observed dynamics. The Markov order of the underlying process is here somewhat arbitrarily set to 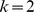, following on [22] where we extensively checked its effect on the reconstructions: in our previous study, 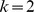resulted to be the lowest dimensionality in the probability distribution allowing to separate actual interactions from signal artifacts like light scattering.

Note that we did not perform any delay embedding of the time-series, because we did not find it here necessary to reach satisfying performance levels, or leading to noticeable improvements. Methodological developments along the lines of [38], [39] would be however desirable for future applications to real experimental data.

Code for our Generalized Transfer Entropy method is publicly available at https://github.com/olavolav/TE-Causality.

Optimal binning

The probability distributions in GTE as defined in Eq. (11) were estimated based on discretized values of the temporal difference signal of the observed fluorescence. To cope with potential undersampling artifacts —since the probability distributions to estimate have an elevated dimensionality, as large as 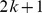— we symbolized the signals into a binary sequence, by applying a sharp threshold. The optimal threshold value 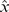for this conversion was obtained from the following analysis. We first ignored the exponential decay of the fluorescence signal since it has a small influence on discretely differentiated signals, and assumed a sufficiently low firing rate so that the occurrence of more than one spike per frame of a given neuron is negligible. Under these simplification hypotheses, the probability distribution of the signal can be cast as a combination of Gaussian functions, with mean values given by the offset associated to the number of action potentials encountered in the current time bin. Additionally, to preserve information about spiking events when projecting the time-series into a binary representation, we computed the optimal mapping by determining the probability 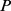that the mapping is correct at any given time step (provided the parameters of the model and a threshold value ), i.e.:

where 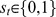denotes the occurrence of a firing event at time frame , and refers to unspecified but frozen parameters of the analyzed system, which have a potential influence on the estimated probability. In particular, the probability that a neuron fires at a given image frame is a function of the firing rate and the length of the image frame, 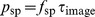. For a normally distributed camera noise with standard deviation 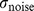and an expected variation 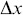in fluorescence due to a single spike, a straightforward solution for the optimal separation value 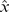that yields the maximum of the correct mapping probability can be derived:

(12)

GTE scores were robust against the selection of a separation value above the optimal 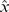. Indeed, for 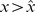the total number of samples above the separating value is reduced, but the fraction of samples that correspond to real spikes is actually increased. The resulting network reconstructions did not show any notable decrease of quality for values of up to a 30% above the optimal value.

Network reconstruction

In order to reconstruct a whole network, GTE was computed for each directed pair of neurons 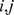from Eq. (11), resulting in a matrix 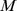of directed causal influences where 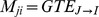. A new binary matrix 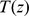was created from the GTE scores, where 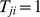if 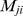is amongst the fraction of links with the highest GTE score.

The quality of the reconstruction was quantified through a Receiver Operating Characteristic (ROC) analysis. The ROC is a parametric curve that establishes a relationship between the true and the false positive links found in 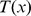for the different thresholded levels. If 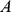denotes the binary connectivity matrix of the real network, then the true positive ratio (TPR) is defined as the number of links in 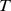that are present in 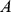respect to the total number of existing links. The false positive ratio (FPR) is the fraction of links in 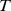that do not match original links, i.e.,

(13)

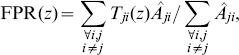(14)

where 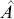is the negation of the binary connectivity matrix 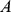(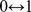). Thus 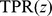and 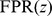constitute, respectively, finite-size estimates of the probabilities 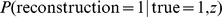and 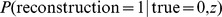, for any given link across the network. Confidence intervals for ROC curves were estimated based on 5 different network realizations.

Combining two reconstruction results

To distinguish between excitatory and inhibitory neurons, we combined the information of the reconstructions obtained from the “E+I” and “E–only” data, namely 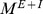and 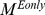. We assumed that excitatory links are present in both datasets, while inhibitory ones appear only in the “E+I” reconstruction, and proceeded by defining new matrices of putative excitatory 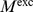and putative inhibitory influences 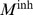, of the form:

(15)

(16)

To obtain the effective connectivity reconstruction only the rank ordering of GTE values is relevant. Therefore no rescaling of these matrices is necessary, and the final set of links could be obtained by thresholding the matrices as described above.

To label the neurons as either excitatory or inhibitory, we first removed all links that were present in both reconstructions, and then ranked the neurons according to the difference between excitatory and inhibitory links, 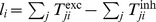. We next used the prior information that a fraction 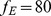% of the neuronal population is excitatory, therefore identifying as excitatory neurons the 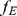fraction with the highest score, and labeling the rest as inhibitory.

Statistical tests

Statistical significance on the inference of excitatory and inhibitory neuronal types was performed as follows. Assuming that the fraction of excitatory and inhibitory neurons (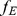 and 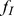respectively) is known with good precision in a population of 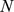cells, the probability to correctly identify by chance a given set of neurons 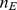and 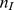in a given trial 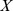follows a binomial distribution:

(17)

Let suppose that a labeling method provides a fraction 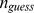of correctly labeled links. We considered this labeling result as statistically significant if the probability of outperforming by chance this success rate was 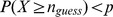, with a standard choice of .

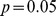Funding Statement

JO and JS received financial support from Ministerio de Ciencia e Innovacion (Spain) under projects FIS2009-07523, and FIS2010-21924-C02-02, FIS2011-28820-C02-01 and from the Generalitat de Catalunya under project 2009-SGR-00014. OS, TG and DB were supported by the German Ministry for Education and Science (BMBF) via the Bernstein Center for Computational Neuroscience (BCCN) Goettingen (Grant No. 01GQ0430). OS and DB acknowledge in addition, respectively, the Minerva Foundation (Muenchen, Germany) and funding from the FP7 Marie Curie career development fellowship IEF 330792 (DynViB). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.