Nonuniform temporal weighting of interaural time differences in 500 Hz tones

Abstract

The discrimination and lateralization of interaural time differences (ITD) in rapidly modulated high-frequency sounds is dominated by cues present in the initial portion of the sound (i.e., at sound onset). The importance of initial ITD at low frequencies is, however, less clear. Here, ITD discrimination thresholds were measured in 500 Hz pure tones with diotic envelopes and static or dynamic fine-structure ITD. Static-ITD thresholds improved as tone duration increased from 40 to 640 ms but by an amount less than expected from uniform temporal weighting of binaural information. Dynamic conditions eliminated ITD from either the beginning or end of the sound by presenting slightly different frequencies to the two ears. While overall thresholds were lower when ITD was available at sound onset than when it was not, listeners differed appreciably in that regard. The results demonstrate that weighting of ITD is not temporally uniform. Instead, for many listeners, ITD discrimination at 500 Hz appears dominated by ITD cues present in the initial part of the sound. To a variable degree, other listeners rely more equally on ITD cues occurring near sound onsets and offsets, although no listeners appear to utilize such cues uniformly throughout the sound's duration.

INTRODUCTION

This paper concerns the temporal weighting of interaural time differences (ITD) by listeners asked to discriminate the lateral positions of low-frequency pure tones. That is, we are interested in whether listeners' discrimination is equally sensitive to ITD cues throughout the sound's entire duration, and if not, whether discrimination is more strongly influenced by ITD cues carried early or late in the sound.

For periodic high-frequency sounds (e.g., centered at 4000 Hz) that are amplitude modulated faster than 200–300 Hz, lateralization depends almost entirely on the ITD present at onset and is not strongly influenced by ITD cues appearing later in the sound (Hafter and Dye, 1983; Brown and Stecker, 2010). It has been suggested that this result follows from listeners' reduced ability to access ongoing envelope ITD cues at high modulation rates (Bernstein and Trahiotis, 2002). As a consequence, listeners may rely more heavily on other cues, such as ILD (Stecker, 2010) and onset ITD (Stecker and Brown, 2010), as modulation rates increase.

Hafter and Dye (1983) studied listeners' ability to utilize ITD cues in modulated high-frequency sounds by measuring how ITD thresholds improved with duration. Their approach followed earlier work by Houtgast and Plomp (1968), who measured the lateralization of narrowband noises centered at 500 Hz, also as a function of duration. If equal information is derived from each successive portion of a stimulus, then uniform averaging of those samples reduces the variance of the average proportionally to the number of samples (i.e., the duration) and defines the “optimal” rate of threshold improvement with duration (see, e.g., Hafter and Dye, 1983, for a more detailed discussion). Both studies described thresholds that improved with increasing duration, but at less than this optimal rate.

Hafter and Dye observed optimal threshold-ITD improvements when modulation rates were slow (less than about 100 Hz), but increasingly suboptimal improvement with duration at successively higher rates. Houtgast and Plomp (1968) observed suboptimal threshold improvements as well, for ITD carried by narrowband noises centered at 500 Hz.1 The suboptimal threshold improvements with duration observed in both studies are consistent with nonuniform temporal weighting of ITD; that is, not all parts of a sound's duration contributed equally to ITD judgments. Although the data do not indicate which parts of a sound received greatest weight, the authors of both reports hypothesized that cues available in the initial part of a sound (i.e., at sound onset) received greater weight than later cues. This “onset effect,” as termed by Houtgast and Plomp (1968), shares features with subsequent reports of “stimulus-onset dominance” (Houtgast and Aoki, 1994) or simply “onset dominance” (Freyman et al., 1997; Stecker and Hafter, 2002; Freyman et al., 2010) in binaural hearing. In most cases, the authors of those studies have ascribed the results to initial cues rather than to onset cues carried by the envelope itself, but the use of whole-waveform delays leaves unclear the role of the envelope per se as compared to the initial portion of the sound (see Abel and Kunov, 1983, p. 959).

Subsequent studies have confirmed the particular importance of initial cues in ITD-based lateralization of modulated high-frequency sounds. Stecker and Brown (2010), for example, measured ITD thresholds for filtered click trains with static ITD (condition “RR”) or with ITD that changed monotonically over time in conditions “R0” (peak ITD at onset, decreasing to 0 at sound offset) and “0 R” (0 ITD at onset, increasing to peak value at offset). For slow click rates (100 Hz), R0 and 0 R thresholds were quite similar. At higher rates (500 Hz), ITD thresholds were markedly elevated when onset clicks carried zero ITD (0 R). Stecker and Brown argued that this onset dominance likely reflected the progressive loss of ongoing envelope ITD beyond ∼ 150 Hz modulation rate (Bernstein and Trahiotis, 2002). Importantly, no such limit is expected to exist for low-frequency fine-structure ITD. In fact, ITD thresholds for low-frequency pure tones improve with increasing frequency from 250 Hz to well beyond 500 Hz (Bernstein and Trahiotis, 2002; Brughera et al., 2013), suggesting that sensitivity to ongoing fine-structure ITD is not limited to slow patterns of input from the auditory periphery, as is apparently the case for envelope ITD at high frequencies.

Based on the arguments above, it seems reasonable to expect temporally uniform sensitivity to fine-structure ITD carried in the ongoing portion of a pure tone. A number of observations challenge that view, however. These suggest, instead, that the initial fine-structure ITD may be more salient than the ongoing cycle-by-cycle ITD. First, as described above, the results of Houtgast and Plomp (1968) demonstrated nonuniform temporal weighting of ITD in low-frequency narrowband noises. Second, Abel and Kunov (1983) demonstrated the importance of early fine-structure cues in the lateralization of pure tones varying in envelope shape, amplitude, frequency, and duration. Sounds were presented with whole-waveform ITD values large enough to produce opposition between fine-structure and envelope cues. Experiment 1 of that study demonstrated that psychometric functions relating performance to fine-structure ITD varied with both rise/fall time and peak amplitude, but were basically identical for cases matching in initial envelope slope [25 ms rise/fall at 60 dB sound pressure level (SPL) compared to 200 ms rise/fall at 80 dB SPL]. Experiment 3 demonstrated further that, for any given rise/fall time, performance was unaffected by the duration of peak amplitude (25 or 200 ms). Both results suggest that for sounds without strong envelope cues (rise/fall times greater than ∼25 ms), judgments were based on the fine-structure ITD present during the initial rising segment of the envelope (i.e., at sound onset), rather than the later ongoing fine-structure delay or the opposing envelope delay.2 Third and finally, Dietz et al. (2013) recently demonstrated, using a periodically amplitude modulated binaural-beat stimulus centered at 500 Hz, that lateralization follows the fine-structure ITD carried during the rising segment of each modulation cycle, even when the envelope is itself diotic.3 A similar phenomenon occurring at the overall onset of a brief gated sound could offer an explanation for the results of Houtgast and Plomp (1968) and Abel and Kunov (1983). It would also present an important similarity between the processing of ITD in rapidly modulated high-frequency sounds (Stecker and Brown, 2010) and low-frequency sounds, as suggested by the similarity of results obtained by Hafter and Dye (1983) and Houtgast and Plomp (1968). Here, we adapt the approach of Stecker and Brown (2010) to revisit the study of Houtgast and Plomp (1968) and determine if cues present at sound onsets dominate the processing of fine-structure ITD at 500 Hz as they do for envelope ITD at high frequencies.

METHODS

All procedures, including recruitment, consenting, and testing of human subjects followed the guidelines of the University of Washington Human Subjects Division and were reviewed and approved by the cognizant Institutional Review Board.

Subjects

Six subjects participated in the experiment. One was the second author (subject 0510); the remainder were paid subjects naive to the purpose of the experiment. All subjects reported normal hearing and demonstrated pure-tone detection thresholds < 10 dB hearing level (HL) at octave frequencies spanning 250–8000 Hz.

Stimuli

Stimuli were 500-Hz sinusoids presented at 65 dB SPL over closed circumaural earphones (Stax 4070). Tone duration was 40, 80, 160, 320, or 640 ms including 20 ms raised-cosine ramps applied diotically at onset and offset. Reference stimuli were presented diotically (0 ITD), whereas target stimuli carried a fine-structure ITD = Δt that favored the right ear. ITD values of target stimuli were either constant over the stimulus duration (in condition RR), or varied dynamically due to a slight interaural frequency difference (i.e., the stimuli presented short, non-repeating, segments of “binaural beats”). The frequency difference was adjusted so that the change in ITD over the stimulus duration equaled Δt.4 In condition 0 R, sinusoidal phases were aligned at sound onset but increasingly favored the right ear over time so that ITD = Δt at sound offset. In condition R0, ITD = Δt at sound onset but decreased over time to reach 0 at sound offset. Thus, Δt represented the peak value of ITD over the stimulus duration. In all cases, Δt was limited to within ± 600 μs to avoid ambiguous localization caused by mismatching periods across the ears or multiple rotations of the binaural-beat stimulus. Note that while conditions R0 and 0 R presented Δt at sound onset and offset, respectively, the envelope onsets and offsets were themselves diotic.

Procedure

Testing took place in a double-walled sound-attenuating chamber (IAC, Bronx, NY). ITD discrimination was measured using a four-interval two-alternative forced-choice (4I2AFC) procedure, with ITD targets appearing randomly in either the second or third of four intervals. Other intervals presented diotic reference stimuli. Intervals were separated by an interstimulus interval of 600 ms. On each trial, subjects indicated by button press which interval (2 or 3) contained the target stimulus. Feedback regarding the correct response was indicated by light-emitting diode immediately after each response.

ITD thresholds were obtained in each condition using a two-down one-up adaptive procedure with two interleaved but independent tracks (Levitt, 1971). Target ITD Δt was set to 600 μs at the start of each run, and adjusted by a scaling factor of 0.2 for the first 4 of 12 reversals and 0.05 thereafter. ITD threshold was estimated as the geometric mean of the final eight reversals recorded in each track. Subjects completed between three and seven practice runs (condition RR, 200 ms duration) to gain familiarity with the procedure and achieve stable thresholds prior to completing four runs per experimental condition, presented in random order. Thresholds were measured at durations of 40, 80, 160, 320, and 640 ms in condition RR; 80 and 320 ms in conditions 0R and R0. Eight threshold estimates were obtained per condition (one from each track on four separate runs) for each subject.

Analysis

Geometric mean thresholds for individual subjects were computed across runs in each experimental condition. Group-average thresholds were computed by taking the mean across subjects for each experimental condition after normalizing5 by each subject's mean threshold in condition RR at 80 ms duration. Threshold improvement with signal duration in condition RR was quantified by linear regression of log normalized threshold onto log duration (Hafter and Dye, 1983); slopes were computed for each subject and for the group-mean threshold data. Finally, for each subject and tested duration, the log normalized threshold obtained in condition R0 was subtracted from that obtained in condition 0R to obtain difference scores (i.e., threshold ratios) quantifying the advantage of access to ITD early versus late in the stimulus. Group-average difference scores were computed as the mean difference score across subjects.

Statistical testing followed a two-level nonparametric bootstrap approach (Efron and Tibshirani, 1986; Howell, 2010).6 At the individual-subject level, threshold estimates were resampled with replacement 1000 times. The average across runs was recomputed for each bootstrapped sample. Bootstrapped percentile confidence intervals at α = 0.05 were computed using the 2.5 and 97.5 percentile points of the resulting sampling distribution. The 1000 bootstrapped samples for each subject were then used as input to second-level resampling at the group-average level. Bootstrapped subject thresholds were resampled with replacement across subjects, and the group mean recomputed for each resulting bootstrapped sample. The resulting sampling distribution was used to compute group-level confidence intervals following the same procedure as for the individual subject data.

To assess improvement with duration in condition RR, regression slopes were calculated for each bootstrapped sample in the same manner as for the raw data. Confidence intervals were calculated from the appropriate sampling distributions (i.e., using first-level bootstrapping for individual subjects, and second-level bootstrapping for the group average). Similarly, 0R-R0 difference scores were computed for each first-level bootstrapped sample to compute confidence intervals on individual-subject data, and resampled across subjects to estimate the sampling distribution of the group-average difference score. The proportion of bootstrapped difference scores falling at or below 0 (i.e., the p-value of a one-tailed confidence interval) was used to quantify the statistical significance of this difference (0R > R0) at the group level.

RESULTS AND DISCUSSION

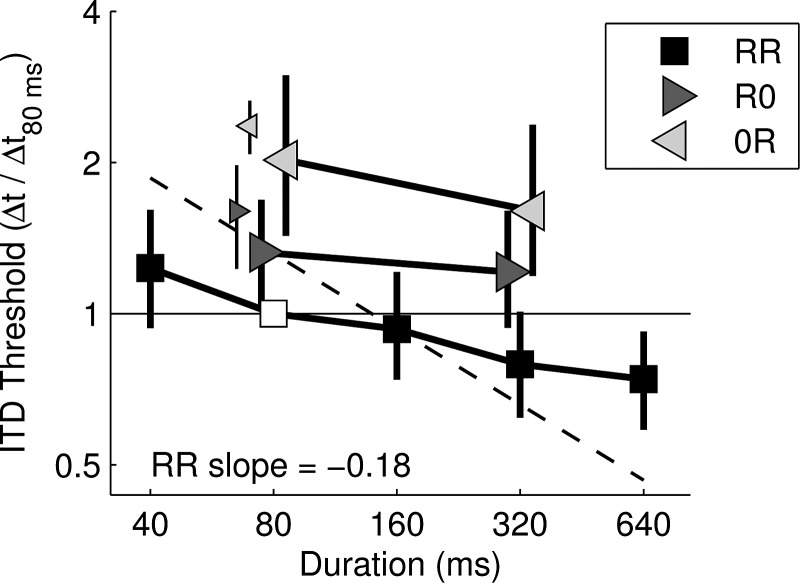
Figure 1 plots across-subject mean normalized threshold ITD against tone duration for the three ITD conditions tested in this study (squares: RR, leftward-pointing triangles: 0R, rightward-pointing triangles: R0). Thresholds were normalized to each subject's threshold at 80 ms tone duration (open square). Small symbols plot, for comparison, data collected in an independent set of nine subjects by Diedesch et al. (2012). Error bars indicate bootstrapped 95% confidence intervals, and the dashed line indicates the theoretical improvement slope of −0.5, arbitrarily passing through the threshold value at 160 ms tone duration. The corresponding data for individual subjects appear in Fig. 2, which plots individual-subject ITD thresholds (i.e., prior to normalization). The shaded gray region in each panel of Fig. 2 indicates a range of values equal to 1.73–2.0 times the thresholds obtained in condition RR. As discussed in more detail later, these represent threshold predictions for conditions R0 and 0R, in the case of temporal averaging of ITD in all conditions (the range reflects various assumptions regarding duration and internal noise). Although subjects differed in their overall sensitivity to ITD (as indicated by the range of thresholds obtained), key features of the results were similar across subjects. First, thresholds improved gradually with increasing duration, most clearly in condition RR. Second, the rate of threshold improvement was significantly less than expected for optimal integration of ITD-related information over the stimulus duration (dashed line). Third, ITD thresholds were lowest in condition RR and tended to be highest in condition 0R.

Figure 1.

Normalized ITD thresholds (vertical axis), averaged across subjects, as a function of tone duration (horizontal axis). Thresholds were measured for sounds carrying static ITD (condition RR, black squares) and for sounds carrying dynamic ITD that was greatest early (condition R0, rightward-pointing triangles) or late in the duration (condition 0R, leftward-pointing triangles). Thresholds were normalized relative to each subject's threshold obtained in condition RR for 80-ms tone duration (open symbol). Error bars indicate bootstrapped 95% confidence intervals for all other conditions. The dashed line indicates the slope of optimal improvement with sound duration (−0.5 in log-log coordinates). Inset text indicates the log-log slope of best fit to RR threshold data. Smaller symbols plot comparison data from a separate replication at 80 ms duration with nine new subjects (Diedesch et al., 2012). Error bars on those data present conventional (i.e., single level and not bootstrapped) 95% confidence intervals computed across subjects.

Figure 2.

Symbols plot ITD thresholds in microseconds (vertical axis) against tone duration (horizontal axis) for individual subjects (in separate panels) for conditions RR (squares), R0 (rightward-pointing triangles), and 0R (leftward-pointing triangles). For purposes of comparison, the shaded gray region in each panel reproduces the RR threshold data, elevated by a factor of 1.73–2.0 (see text). Other formatting as in Fig. 1.

Improvement in ITD threshold with tone duration

Houtgast and Plomp (1968) found ITD thresholds to improve with increasing signal duration but at a rate less than expected for uniform temporal weighting of ITD (i.e., if listeners' sensitivity to ITD had been constant throughout the duration). Results of the current study are consistent with that observation. In condition RR, ITD thresholds improved with increasing duration, consistently across subjects. The log-ITD versus log-duration slopes are indicated in Figs. 12, and plotted in the upper panel of Fig. 3. These ranged from −0.09 to −0.27 (−0.18 for mean data), consistently and significantly shallower (p < 0.001)7 than the optimal improvement slope of −0.5 (dashed line). Slope values were similar to those reported by Houtgast and Plomp (1968) for 500 Hz narrowband noises (−0.23 and −0.25 for two subjects), and by Hafter and Dye (1983) for high-frequency impulse trains presented at 2 ms ICI (ranging −0.08 to −0.33 across four subjects, with a mean of −0.22). The close correspondence of improvement slopes for rapidly presented high-frequency click trains, low-frequency narrowband noises, and low-frequency pure tones suggests that nonuniform temporal weighting of ITD does not depend strongly on the regularity of the stimulus or the place of cochlear excitation.

Figure 3.

Upper panel: Bars plot the slope obtained by linear regression of log threshold onto log duration (condition RR) for each subject; error bars present boot strapped 95% confidence intervals on each estimate. Group average data appear at far right of plot. In every case, slopes were significantly shallower than the optimal improvement slope of −0.5 (dashed line). Lower panel: Bars plot the ratio of ITD thresholds obtained in conditions 0R and R0 (i.e., the log 0R-R0 difference scores, converted to a simple ratio) at 80 ms (gray) and 320 ms (white) duration, along with bootstrapped 95% confidence intervals. Three subjects show significant threshold elevations in condition 0R. Other subjects appear equally sensitive to ITD appearing early or late in the sound, despite their inability to optimally benefit from increasing duration (upper panel). Small symbols at far right of lower panel plot 0R/R0 threshold ratios calculated from thresholds reported by two other studies. DBS: Diedesch et al. (2012) employed stimuli identical to the current study (500 Hz pure tones), 80 ms duration (nine subjects); SB: Stecker and Brown (2010) employed 4000 Hz filtered click trains, 16 clicks at 2 ms interclick interval (nine subjects).

Asymmetrical sensitivity to ITD carried by sound onsets and offsets

For high-frequency narrowband impulse trains presented at 2-ms ICI, Stecker and Brown (2010) found significantly lower thresholds for ITD delivered early (condition R0) versus late (0R) in the stimulus. They interpreted that result as consistent with the dominance of ITD cues present at sound onset over weaker ITD cues available in the ongoing envelope (cf. Bernstein and Trahiotis, 2002). In the current study, the same pattern of lower thresholds for condition R0 than 0R was observed in the group average data,8 and in a subsequent replication by Diedesch et al. (2012, small symbols in Fig. 1). The difference was greatest at 80 ms duration, for which 0R thresholds were on average 1.53 times larger than R0 thresholds. At 320 ms duration, average 0R thresholds were 1.32 times larger than in condition R0. The result (better ITD sensitivity in condition R0 than 0R) is also consistent with the original hypothesis of Houtgast and Plomp (1968) that a greater contribution of the sound onset underlies the small effect of duration on ITD threshold at 500 Hz. That is, sound onsets may play a dominant role in ITD processing at both low and high frequencies, even when the onset of the envelope is itself diotic. A similar phenomenon has been reported in the lateralization of 500 Hz binaural beat stimuli subjected to periodic diotic amplitude modulation at a rate of 32 Hz (Dietz et al., 2013). In that study, listeners' perception of lateral position was strongly dominated by the fine-structure ITD associated with the rising slope of the periodic modulation envelope. The utility of ongoing ITD cues (i.e., those not accompanied by positive envelope slopes) is thus apparently less, as compared to ITD cues at sound onset, regardless of whether the ITD is carried in the fine structure of a low-frequency sound or the envelope of a rapidly modulated high-frequency sound. This result stands in contrast to the expectation that 500 Hz tones should afford stronger relative ongoing ITD cues than should rapidly modulated high-frequency sounds. Along with the similarity of improvement slopes across frequency, this result lends support to the hypothesis of Colburn and Equissaud (1976) that identical central mechanisms are involved in binaural processing regardless of stimulus frequency.

Although the asymmetry between R0 and 0R thresholds was clearly evident in the average data, individual subjects varied substantially in this regard (see Fig. 3, lower panel), indicating the likelihood that listeners differed in respect to listening strategies or decision rules. In particular, three of the subjects presented only small and non-significant differences between these conditions. Included among this group were listeners with the lowest overall thresholds (subjects 0601 and 1012). Importantly, all produced rather shallow ITD-versus-duration functions that would have led Houtgast and Plomp (1968) and Hafter and Dye (1983) to conclude that onsets dominated in every case. Is it possible that some listeners were able to make use of ITD regardless of its position within the stimulus, despite their apparent inability to optimally benefit from increasing sound duration?

Individual differences are further summarized in Fig. 3. The upper panel plots threshold-duration slopes obtained in condition RR for each subject tested. In every case, thresholds improved with duration (indicated by negative slopes), but more shallowly than expected for temporally uniform ITD weighting (slopes were all significantly above −0.5). In two cases (subjects 0601 and 1004), slopes did not significantly differ from zero, a rather extreme departure from optimal processing consistent with duration-independent processing (e.g., sampling only the endpoints). The slope data very consistently indicate temporally nonuniform processing of ITD in these stimuli.

The lower panel of Fig. 3 quantifies the relation between ITD thresholds obtained in conditions 0R and R0. In contrast to the strong consistency of the RR slope data, appreciable individual differences are apparent in listeners' ability to discriminate fine-structure ITD on the basis of cues available at onset (in condition R0) and offset (condition 0R). As mentioned above, half of the tested subjects demonstrated no significant difference between these conditions (i.e., threshold ratio of 1), consistent with temporally symmetric weighting of ITD cues, whereas the other half demonstrated significant threshold elevations in condition 0R consistent with dominance of onset cues. It is not clear whether the observed differences indicate discrete subgroups within the population or a continuum of performance. Although it is well beyond the scope of the current manuscript to quantitatively describe the listening population in these terms, additional relevant data have been reported in abstract form by Diedesch et al. (2012), who replicated the 80-ms conditions of the current study in an independent group of nine listeners. Corresponding 0R/R0 threshold ratios for each of those subjects are plotted as small symbols at the right of Fig. 3; the data cover a similar range to those of the current study and suggest a similar range of intersubject variability. Also plotted for comparison are 0R/R0 threshold ratios computed from ITD thresholds for 4000 Hz filtered impulse trains reported by Stecker and Brown (2010). Note that across all three studies, ratios were either greater than or close to 1, indicating that ITD sensitivity near sound onset was equal to or (in most cases) better than ITD sensitivity near sound offset. In no case was significantly better discrimination observed for cues near offset.

Theoretical implications

Effective ITD of stimuli with dynamic ITD

If listeners utilize ITD equally well early and late in the duration of a dynamic stimulus (i.e., if they exhibit uniform or otherwise symmetric temporal weighting), R0 and 0R thresholds should be equal to one another, and elevated relative to condition RR by an amount that depends on the nature of the internal noise and other factors. Bear in mind that the total ITD in each case is roughly half the total ITD in the RR condition, although the value is reduced by onset and offset gating. The optimal temporal integration of ITD cues in conditions 0R and R0 thus varies somewhat with tone duration, ranging from $\Delta \mathrm{t/}\sqrt{3}$ (for temporally uncorrelated internal noise and negligible gating effects, as at long tone duration) to approximately Δt/2 (at shorter durations or for a single internal noise source). That range (1.73–2.0 times the RR threshold) is indicated by the shaded gray region in each panel of Fig. 2. Data for subject 0601 fall within this range for both 0R and R0, suggesting an ability to utilize ITD early and late in the stimulus equally well despite an apparent inability to benefit from ITD distributed throughout all temporal portions of the sound (as evidenced by his threshold-duration slope of only −0.09). That pattern is consistent with “U-shaped” temporal weighting (as observed for interaural level differences at high frequency; Stecker and Brown, 2012) that emphasizes cues near onset and offset over cues appearing intermediately within the stimulus, or with a decision rule based on the maximum, rather than integrated, ITD (see below). In other cases (e.g., subjects 0510, 1005, 1012), R0 thresholds closely matched RR thresholds, consistent with a strong dominance of early over late ITD cues.

The role of instantaneous ITD magnitude

Another factor that could influence dynamic-ITD thresholds is the relative detectability of instantaneous ITD cues of different magnitudes. If the relationship between detectability and cue value is nonlinear—for example, if larger ITD values contribute more to the overall detection than do smaller values—or the decision variable reflects the maximum ITD integrated over a finite temporal window, the result will be temporally nonuniform ITD weighting that emphasizes instants of extreme ITD, regardless of when they occur. In the limit, such a mechanism represents detection based on the maximum rather than the average ITD over the tone duration, and would correctly predict shallow threshold-duration slopes, along with optimal or better 0R and R0 thresholds as given by some subjects (values below the gray line in Fig. 2), but not the temporal asymmetries observed between 0R and R0 thresholds in this study. It is possible, in fact, that some listeners adopted a similar strategy here, although others clearly did not, as evidenced by their failure to benefit from ITD late in the sound. Although a thorough consideration would lie outside the scope of this paper, the potential impact of such effects should be considered in weighing the evidence for purely temporal weighting of binaural cues.

The salience of ongoing ITD cues in 500 Hz pure tones

A puzzling aspect of the result, at least initially, is the apparent contradiction between ITD processing at low frequencies (where salient ongoing, cycle-by-cycle, cues are expected) and in modulated high frequency sounds, where the salience of ongoing cues depends strongly on the modulation rate (see Stecker and Brown, 2010). That is, the current results suggest that in regard to the temporal weighting of ITD, unmodulated low frequency stimuli are more similar to rapidly modulated high-frequency sounds than to slowly modulated high-frequency sounds, since the former appear strongly dominated by ITD cues occurring at sound onset while the latter offer salient ITD cues throughout their durations. On closer examination, however, the puzzle might be partly resolved: As the modulation rate of a high-frequency sound (such as a filtered impulse train) increases, the effective modulation depth of its neural representation is increasingly diminished by peripheral as well as central transformations (Bernstein and Trahiotis, 2002; Ballestero et al., 2014). At some point, the representation of a high-frequency modulated sound approximates that of a steady tone at the modulation frequency, and may be treated similarly by the auditory system. Like the steady 500-Hz tone employed here, the overall “envelope” of the transformed representation would lack the characteristic of slowly repeated amplitude increases, and instead feature a single overall onset (cf. “synchronized” and “nonsynchronized” responses to amplitude modulation described in central auditory neurons by Bartlett and Wang, 2007). The current results suggest similar temporal weighting of ITD for both such cases (unmodulated low-frequency tones and rapidly modulated high-frequency sounds). The “special” case, then, is that of slow modulations at high frequency, which appear capable of signaling ITD effectively with each modulation cycle, similarly to the case for slow modulations at low frequency (Dietz et al., 2013).

Thus, although the results of this study are not consistent with our initial expectation of salient ongoing fine-structure ITD cues at 500 Hz, they are consistent with the conclusion of Houtgast and Plomp (1968) that “…the onset of the [500 Hz] signal contributes much more to the lateral position perceived than the ongoing part does,” and of Abel and Kunov (1983) that “…phase as well as envelope and intensity information is part of the precedence effect.” The emerging picture is one in which the initial segment of the gated tone (possibly the segment containing the amplitude increase) plays a dominant role in shaping listeners' perception of the tone's lateral position. That view is in fact quite consistent with several recent studies demonstrating the importance of binaural cues occurring at moments of positive slope in the stimulus envelope (Nelson and Takahashi, 2010; Baxter et al., 2013; Dietz et al., 2013). The current results lend additional support to that view, and suggest strong similarities between binaural cue processing at low and high frequencies.

SUMMARY AND CONCLUSIONS

Nonuniform temporal weighting of ITD at 500 Hz

ITD thresholds improved with increasing duration of a 500 Hz pure tone from 40 to 640 ms. The rate of this improvement was less than would be expected, based on a statistical averaging of ITD over the entire duration. Both results replicate those reported by Houtgast and Plomp (1968) for narrowband noises also centered at 500 Hz and suggest that listeners do not weight ITD cues uniformly over the sound duration. One possibility suggested by Houtgast and Plomp (1968) is that sound onsets contribute more strongly to ITD discrimination, as has been previously shown for modulated high-frequency sounds (Stecker and Brown, 2010).

Temporally asymmetric weighting of ITD at 500 Hz

Averaged across subjects, ITD thresholds were significantly better for sounds carrying ITD early (condition R0) rather than late (condition 0R) in their duration. That result is consistent with a dominance of onset or early arriving ITD over cues appearing later in the ongoing sound. That pattern was not consistently observed across individual subjects, some of whom appeared equally sensitive to ITD occurring early or late in the sound. Importantly, despite this difference, none of the subjects showed evidence of uniform temporal weighting in their threshold-versus-duration slopes. Rather, the results suggest that binaural discrimination of unmodulated low-frequency tones relies primarily on cues available near sound onset, and for some individuals, sound offset.