Imaging and modeling of flow in porous media using clinical nuclear emission tomography systems and computational fluid dynamics

Abstract

This paper presents experimental and modeling aspects of applying nuclear emission tomography to study fluid flow in laboratory packed porous media columns of the type frequently used in geophysics, geochemistry and hydrology research. Positron emission tomography (PET) and single photon emission computed tomography (SPECT) are used as non-invasive tools to obtain dynamic 3D images of radioactive tracer concentrations. Dynamic sequences obtained using ¹⁸F-FDG PET are used to trace flow through a 5 cm diameter × 20 cm tall sand packed column with and without an impermeable obstacle. In addition, a custom-made rotating column setup placed in a clinical two-headed SPECT camera is used to image ^99mTc-DTPA tracer propagation in a through-flowing column (10 cm diameter × 30 cm tall) packed with recovered aquifer sediments. A computational fluid dynamics software package FLUENT is used to model the observed flow dynamics. Tracer distributions obtained in the simulations in the smaller column uniformly packed with sand and in the column with an obstacle are remarkably similar to the reconstructed images in the PET experiments. SPECT results demonstrate strongly non-uniform flow patterns for the larger column slurry-packed with sub-surface sediment and slow upward flow. In the numerical simulation of the SPECT study, two symmetric channels with increased permeability are prescribed along the column walls, which result in the emergence of two well-defined preferential flow paths. Methods and results of this work provide new opportunities in hydrologic and biogeochemical research. The primary target application for developed technologies is non-destructive, non-perturbing, quantitative imaging of flow dynamics within laboratory scale porous media systems.

1. Introduction

Sediment columns are commonly used as experimental tools in geochemistry, geophysics, hydrology and similar fields. The sediment is placed in a column and observed for an extended period of time under controlled physical and chemical environment; column sizes range from sub-centimeter diameter and a few centimeters length to tens of centimeters in diameter and a meter or more in length. In a typical experiment, the column is held vertically with water pumped upward through the column at rates that simulate groundwater seepage flow. Adequate design, process control and interpretation of the results of such an experiment greatly benefit from having knowledge of the internal configuration of the column material and compounds pumped through it. Porosity distribution, chemical properties, content of contaminant-reducing materials, geometry of flow paths or 3D flow vector fields are all important and complex parameters to constrain. In order to preserve the integrity of the on-going experiment, non-invasive methods of evaluating these parameters are preferred, for which tomographic imaging (x-ray, optical, magnetic resonance, nuclear emission) is well suited. A recent review of most non-invasive column imaging methods as well as systematically presented motivation for the development of such methods is provided in (Werth et al., 2010). In this paper, we will focus on the nuclear emission tomography, which is not directly discussed in (Werth et al., 2010). Our hypothesis is that this method can provide unique knowledge of the column medium parameters and the tracer propagation geometry, which is not always accessible using other column imaging technologies.

Tomographic nuclear emission imaging methods include positron emission tomography (PET) and single photon emission computed tomography (SPECT). Both methods have been actively used in medicine and non-medical applications for several decades. As a result, the equipment and expertise are both commercially available and already exist at many research universities and institutions, opening a way to wide spread application of these techniques in the earth sciences. In both modalities, the three-dimensional distribution of a radioactive tracer concentration within an object of interest is measured. Spatial resolution of these techniques varies from 3–10 mm scale when scanning patients to less than a millimeter in small animal imaging. In dynamic PET or SPECT, a series of 3D distributions are obtained, forming a 4D dataset of activity concentration as a function of position and time. PET and SPECT differ by the types of radioisotopes used and by the approach to data acquisition. The common features of the two techniques are their non-invasive nature, robustness and extremely high sensitivity: pico- and femtomolar concentrations of radioactive materials can provide sufficient amounts of tracer activity to obtain useful imaging information without altering the dominate geochemical conditions within the experiment (Wernick and Aarsvold, 2004; Cherry et al., 2003).

PET has been used to study sediment columns and similar objects since the 1990s. Degueldre et al (Degueldre et al., 1996) and Maguire et al. (Maguire et al., 1997) described PET application for the study of rock samples. Hoff et al. (Hoff et al., 1996) applied PET to the study of the internal properties of construction materials. Khalili et al. (Khalili et al., 1998) used PET to visualize flow in porous sediments. More recently, a large body of PET research of transport of water and salt solutions in geomaterials was presented by a group in Leipzig, Germany (Richter et al., 2005; Gründig et al., 2007; Kulenkampff et al., 2008). Since flow velocities studied in hydrogeological experiments are low, 10⁻⁴ cm/sec or less, the flow residence time in a typical column is of the order of hours or days. At these time scales, some of the popular PET radioisotopes are not usable because of their short half-lives (¹⁵O: t_1/2 ≈ 2 min, ¹³N: t_1/2 ≈ 10 min, ¹¹C: t_1/2 ≈ 20 min). Most of the studies cited above use ¹⁸F (t_1/2 ≈ 110 min), and some also use ⁶⁴Cu (t_1/2 ≈ 12.7 hrs) or ¹²⁴I (t_1/2 ≈ 4.2 days).

In comparison to positron emission tomography, SPECT imaging of sediment columns is scarcely reported. One possible explanation for this fact is that neither PET nor SPECT geometries are convenient for the task of imaging columns. A standard arrangement for a column is vertical, while the gantry bores of clinical SPECT and PET scanners are typically horizontal. Also, uninterrupted upward flow of water or tracer solution is expected, while SPECT acquisition implies that the contrast distribution within the field of view does not change while the gantry rotates around the imaged object to acquire the projection data. Perret et al. (Perret et al., 2000) reconstructed tomographic images of soil columns, but horizontal column positioning was used and the flow was interrupted during image acquisition. Lear et al. (Lear et al., 2010) studied vertical columns using a SPECT camera as a simple gamma camera acquiring only planar projection images rather than 3D distributions. In addition, Lear used redox-sensitive, non-conservative tracer designed to image redox conditions as opposed to flow dynamics. Overall, application of true tomographic capabilities of SPECT to study 3D flow fields and 4D contaminant distributions in soils and sediments largely remains an unexplored field.

Given a 4D dataset, another major challenge in the practical implementation of the nuclear imaging methods to study flow in sediment columns is relating the 4D radiotracer distribution in the column to the fluid flow field and sediment attributes such as porosity and permeability. In order to establish a connection between the radiotracer distribution data and the water flow, we construct a computational fluid dynamics (CFD) model of the system based on the basic laws of fluid dynamics and a model of a sediment-filled column as a column of porous medium. Parameters describing the medium (sediment) such as porosity, permeability and diffusivity can be adjusted to achieve the same tracer distribution for different time frames as observed experimentally. Radiotracer propagation can be simulated using “virtual ink”, a method of modeling non-reactive contrast agents previously applied to visualize blood flow in cerebral aneurysms (Rayz et al., 2010).

The goal of this paper is to describe a successful implementation of nuclear emission imaging methods to the study of fluid flow in sediments, to compare the imaging experiments and CFD models of flow in porous medium, and to outline how these methods can be applied in sediment column research. Section 2 describes the column set-up and the imaging experiments, section 3 describes the computational modeling details, section 4 presents the imaging and modeling results for flow in similar systems, and section 5 discusses the advantages and limitations of the presented methods for geosciences applications.

2. Materials and methods

2.1. Nuclear Emission Tomography

Below, we list some of the basic facts about nuclear emission tomography necessary for understanding our work. A proper introduction to the field is available in (Wernick and Aarsvold, 2004) and (Cherry et al., 2003). (Perret et al., 2000) also gives a simple description of SPECT technology.

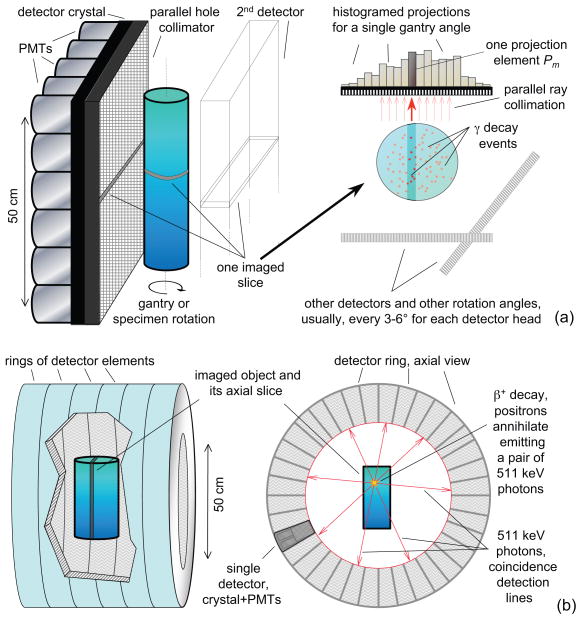
• In both PET and SPECT, a radioactive tracer is injected into the studied specimen. Gamma-ray detectors of the scanner measure the intensity of radiation emitted by radioactive decay or the tracer. The two modalities differ by the type of radioactivity and by the detection geometry. Basic principles of the scanning set-up and geometry are shown in Figure 1.

• The objective of nuclear emission tomography is to compute the image, an intensity distribution of radioactive decay; it is proportional to the radiotracer concentration distribution v(x, y, z).

• Mathematically, nuclear emission tomography solves the inverse problem of finding an unknown discrete v_n from a set of measured projections. Each projection P_m is a Poisson random variable, its mean P̃_m given by

  $${\stackrel{\sim }{P}}_m=\sum _n{S}_{mn}{v}_n,$$ (1)

  where the system matrix S_mn is calculated based on the imaging modality and configuration of the system. For a fixed m, the sum (1) can usually be approximated by a weighted line integral of v.

• There are several well-studied algorithms of image reconstruction, including analytical and iterative methods. In this work, we use statistical reconstruction methods that are proven to provide a good model of the physics of image generation and acquisition.

Figure 1.

General scheme of using (a) single photon emission computed tomography (SPECT) and (b) positron emission tomography (PET) to image a column-shaped object. Radiation detectors consisting of scintillation crystals and photomultiplier tubes (PMTs) measure γ-rays emitted either directly in SPECT or indirectly through positron recombination in PET.

2.2. Experiments A and B: small column studies using PET

In Experiments A and B, a 5 × 20 cm (diameter × length) glass column was studied using ¹⁸F-fluorodeoxyglucose (¹⁸F-FDG) PET.

Experimental set-up

The diagram of the setup is provided in Figure 2. In Experiment A, approximately 75% of the length of the column was slurry-packed with lab-grade quartzite sand, the remaining portion occupied by the column plumbing components. This arrangement assured minimal interaction between radiotracer and the column material, giving the best experimental approximation to the uniform porous medium. In Experiment B, the column was re-packed with a 12.5 × 25 mm (diameter × height) solid nylon cylinder inserted in the center of the column, in-line with the longitudinal axis, 10 cm from the entrance frit. The goal of this modification was to study the uniform flow around an impermeable object. The column was rigidly mounted in a vertical position in the center of the PET gantry. Tap water was pumped through the column with constant flow rate of 0.5 ml/min using a peristaltic pump through 1-mm inner diameter tubing.

Figure 2.

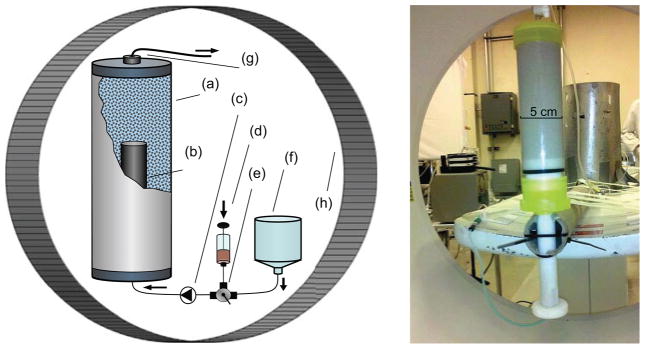
Small column PET experiment setup (Experiments A and B). Components: (a) column filled with hydrated sand, (b) insert used in Experiment B, (c) peristaltic pump, (d) activity source, 1-ml syringe in Experiment A, 0.5 L in Experiment B, (e) three-way valve, (f) deionized tap-water tank, (g) column outlet, (h) PET gantry.

Imaging

The columns were imaged on Siemens ECAT HR PET scanner. In Experiment A, concentrated activity, 2.6 mCi (96.2 MBq, 10⁻⁹ mol), 1mL, was injected as a bolus at the column inlet, corresponding to a delta-like input function (time-dependence of the activity concentration at the inlet). In Experiment B, a step-function input function was used: the input was switched from water to FDG solution, 23.9 mCi (0.884 GBq, 10⁻⁸ mol) in 270 mL, at constant flow rate of 0.5 mL/min. Dynamic image acquisition continued for 6 hours. The acquisition frame durations were the following: fifteen 20 sec frames, five 60 sec frames, and seventy 300 sec frames. Experiment A data were reconstructed using 2D filtered backprojection (FBP) with corrections made for attenuation, randoms, and scatter. For each dynamic frame, 47 slices with thickness 3.13 mm were reconstructed with in-plane pixel size of 2.2 mm. Experiment B data were reconstructed using the ML-EM algorithm with the appropriate corrections.

Velocity analysis

In order to estimate cross-sectional velocity distribution in the column, the following analysis tool was applied to the dynamic image frames. Image intensity representing the tracer concentration was denoted as f(x, y, z, t). Pixels of the column cross-section were indexed, and then for each pixel n with coordinates (x_n, y_n) and for each time frame t, the instantaneous position of the tracer bolus was defined as

$$z_n(t)=\underset{z}{\text{argmax}}f(x_n,y_n,z,t)$$ (2)

The slope of z_n(t) is proportional to the longitudinal component of the flow velocity at cross-sectional pixel n.

2.3. Experiment C: larger column studied using SPECT

In Experiment C, a 10 × 30 cm quartz glass column packed with recovered field materials was imaged using ^99mTc-DTPA dynamic SPECT.

Experimental set-up

The diagram of the setup is provided in Figure 3. The column was slurry-packed with sediment from the DOE Integrated Field Research Site (IFRC) in Rifle, Colorado (Anderson et al., 2003; Williams et al., 2009) and mounted on a custom designed rotating stage in a vertical position. Vertical positioning, as opposed to horizontal, is expected to reduce preferential flow channels and flow fingering and to allow escape of any gasses formed during reactive flow. The column was placed between the detector heads of GEs VG3 Millennium SPECT-CT camera. A computer-controlled stepper motor rotated the column about its vertical axis. At the inlet (1 mm-diameter tubing), the flow was somewhat dispersed through a star-shaped pattern cut into the bottom inlet plate, which proved to provide better dispersion than a dispersion frit. Anoxic artificial ground water mixed to reflect field conditions (Li et al., 2009) was pumped up the column at 1.25 ml/min using a Waters 590 HPLC pump. ^99mTc-DTPA, 30 mCi (1.1 GBq, 60 picomol) diluted in 3 mL of groundwater, was delivered to the inlet line using a syringe drive at 0.1 mL/min. During the 30-minute interval of activity delivery, the HPLC pump rate was reduced to 1.15 mL/min, thus achieving a constant flow rate at the inlet of 1.25 mL/min and a 30 minute-wide rectangle-shaped radiotracer input function. The testing and characterization of the ^99mTc-DTPA as a conservative tracer is described elsewhere (Vandehey et al., 2011).

Figure 3.

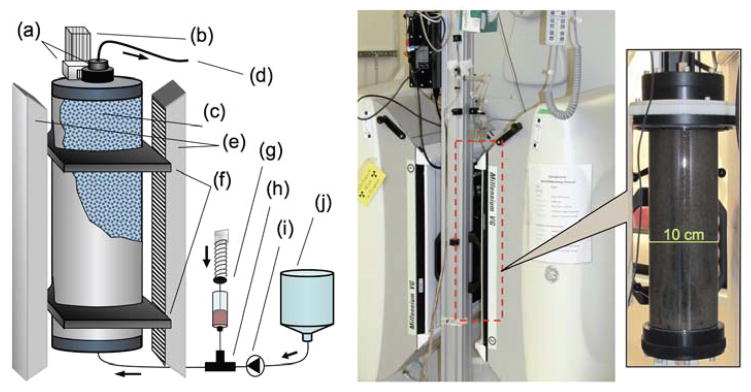
A diagram and a photograph of Experiment C. (a) Stepper-motor rotating the column, (b) stand, (c) glass column filled with Rie site sediment, (d) outlet, (e) SPECT detector heads, (f) sliding mounts, (g) activity delivery system with a syringe drive, (h) T-shaped connector, (i) HPLC-pump, (j) deoxyginated groundwater tank.

Imaging

In order to obtain tomographic datasets, the column was rotated about its vertical axis while a dynamic planar image sequence was acquired by the scanner. Image acquisition was synchronized with the stepper motor rotating the column so that an equivalent of a continuous-rotation sinogram was acquired. During each dynamic study, 120 projections (128 × 128 pixels, 4.42 mm pixel size) were acquired in 6 minutes as the column rotated 360°. For each 6-minute acquisition, the projection data acquired by both detector heads were combined, cropped and reshaped to form a single 28 × 88 × 120 sinogram. A total of 180 sinograms were acquired every 8 minutes over a 24-hour period.

Each sinogram was reconstructed using 25-iterations of a standard ML-EM algorithm. The ray-driven system matrix was calculated including continuous rotation correction, divergent-ray geometric response correction, and attenuation correction. Since the water/tracer flow was not stopped for the time of acquisition, a certain amount of motion blurring was introduced to the data. However, with mean flow velocities (based on the flow rate) below 0.5 mm/min, the motion blurring was expected to be within the image spatial resolution of 4.42 mm.

Attenuation correction was realized in two-stages. First, the projection data were adjusted to take into account attenuation by the stationary elements of the column mounting setup, indexed as (f) in Figure 2. Then, later time frames of the activity distribution inside the column were reconstructed without attenuation correction and used to build a virtual 3D column. Uniform attenuation coefficient of μ = 0.255 cm⁻¹ was assigned to every point inside the virtual column and used to repeat the reconstruction with the attenuation correction. The value of attenuation coefficient μ was measured independently by two methods: a pre-study transmission CT scan and a measurement of the attenuation of a uniform intensity ^99mTc rod source.

3. Computational modeling

This section explains computational fluid dynamics modeling of the water and tracer solution flow in a column.

Theory

The physical variables and system parameters used to model fluid flow in the medium are:

• U – velocity vector of the fluid;

• ρ – density of the fluid;

• μ – viscosity of the fluid;

• γ – porosity of the medium¹;

• K – permeability of the medium;

• p – pressure (includes both applied pressure and gravity).

These variables and parameters are sufficient to formulate the basic equations of fluid flow in the first level of approximation. Second-level parameters to be considered in the future include tensor elements of the porosity (at this stage, we assume isotropic pores, so γ is a scalar between 0 and 1), permeability, and chemical exchange parameters. In order to describe the velocity field of the fluid, we use the flow continuity equation

$$\nabla \cdot (\gamma \mathbf{U})=0,$$ (3)

and Navier-Stokes equation for porous medium

$$\frac{\partial }{\partial t}(\rho \gamma \mathbf{U})+\mathbf{U}\cdot \nabla \cdot \left(\rho \gamma \mathbf{U}\right)-\mu \gamma {\nabla }^2\mathbf{U}+\gamma \nabla p=-\frac{\gamma \mu }{K}\mathbf{U}.$$ (4)

Setting γ = 1 turns the left hand side of equation (4) into the standard Navier-Stokes equation – the equivalent of equations of motion for fluid flow. The right hand side is the momentum sink term that is responsible for the non-inertial nature of flow in porous medium. The density ρ is constant, assuming incompressible liquid. Generally, both K and γ variables are location-dependent and coupled with each other. However, since a few percent change in the porosity can correspond to orders of magnitude change in the permeability, we use K as the only variable parameter of the system at this stage.

Flow modeling

Numerical solution of equations (3)–(4) is implemented using standard CFD software packages FLUENT and CFX (ANSYS, Inc., Canonsburg, PA, USA). The spatial mesh for the solution is generated using Hypermesh software (Altair Engineering, Troy, MI). Computational domains include pure fluid (inlet and outlet tubes) and porous medium (column). In experiment B only, a solid domain representing an impermeable object that partially obstructs the flow of liquid was added.

The boundary conditions for the Navier-Stokes equations were no-slip (zero tangential and normal velocity) at the wall and uniform velocity profile at the inlet. Initial conditions were zero velocity and pressure throughout the computational domain. A Cartesian coordinate system was used in the CFD model (in the general case of non-uniform permeability we could not use a symmetrical domain to reduce the computational cost).

Tracer model

A non-reacting tracer injection was simulated by using virtual ink: a passive scalar function C assigned to each computational cell (Rayz et al., 2010). The distribution of the tracer at each time step was calculated by solving an advection-diffusion equation

$$\frac{\partial C}{\partial t}+U\cdot \nabla C=D{\nabla }^{2}C,$$ (5)

where D is the diffusion coefficient, C represents the local concentration of the tracer, and the steady flow velocities U are obtained from equations (3–4). Diffusion effects were neglected as being much slower than the advection by setting D = 0 throughout the domain. This pure advection equation is identical to the level-set equation, which is widely used in numerical simulations to track the interface between different materials (liquid-solid, liquid-gas, and liquid-liquid). Initially, the concentration of the tracer was uniformly zero throughout the domain. The value of the scalar at the inlet was set to 1 during the injection of the tracer and zero otherwise. The time intervals of the tracer injection (input function) matched the time intervals used in the experiments. As the tracer was advected through the media, the regions where the scalar value was 1 were filled with tracer, while the regions where its value was zero were tracer-free. Due to the Eulerian nature (which represents the concentration C as the volume average over the control volume) of this method and certain amount of numerical diffusion, the value of the scalar obtained in the numerical solution is not always 0 or 1 but can assume values in between. The flow regions with the scalar value above a certain threshold can be readily visualized with a color coding scheme. There is a one-way coupling between the Navier-Stokes and advection-diffusion equations, so the distribution of the tracer at each time step will be computed after velocity field solution is obtained, thus tracer concentration has no effect on the velocity field. The described approach is somewhat different from a more common approach to modeling flow in geophysics using Darcy’s law. Navier-Stokes and continuity equations describe the exact physical model of the system, hence all of the approximations are made only at the parameter selection level.

Numerical simulations

Three studies have been performed to match the system and flow parameters used in experiments A, B, and C. In each of the simulations, the width and length of the column matched that used in the experiments described in the previous section. Inside the column, a porosity value of γ = 0.5 and permeability value K = 10⁻⁸ m⁻² were used.

Experiment A

Uniform medium. The simplest experiment was with uniform γ and K in a column with no additional obstacles. This was aimed at computing the fluid velocity, and the pressure distributions and characteristic tracer profile for fluid flow in uniform porous medium. The single bolus input function was modeled as a 4-second-wide rectangle function.

Experiment B

Uniform medium with an obstacle. The goal of this experiment was to obtain the tracer propagation profile for fluid flow around an impermeable object. The 12.5 × 25 mm obstacle was modeled by modifying the computational mesh of the numerical study A to include a solid domain in the center of the column. Step-function input-function was used.

Experiment C

Non-uniform medium. The goal of this experiment was to model flow propagation in the medium with non-uniform permeability and porosity. Two preferential flow paths were modeled by setting the permeability to K = 10⁻⁴ m⁻² inside a 1 cm-wide region along two opposing walls of the column and along the bottom 1 cm-wide slice of the column. The regions of increased permeability extended along the column length with an angular span of 0.1 rad (5.7°). A 30-minute rectangle input function was used. Nine hours of the tracer propagation were simulated. A vertical cross-section image was saved to the system every 10 minutes of model time.

4. Results

Below, three imaging experiments described in Section 2 are compared to the results of the corresponding numerical studies described in Section 3.

Experiment A

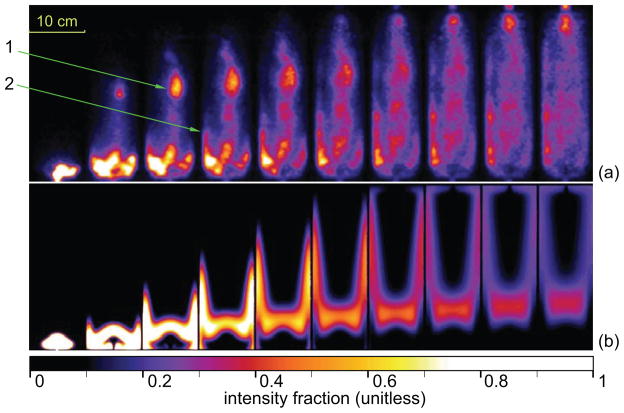
Figure 4 shows a series of intensity profiles of tracer distribution both in the PET-imaged (a) and numerically simulated (b) columns with uniform porosity. The two image series exhibit significant similarity between the experimental and the simulated tracer flow in uniformly porous medium, notably the inverted “V”-like shape of the tracer distribution formed by the diverging flow geometry near the inlet, then propagated across the column with minor deformations.

Figure 4.

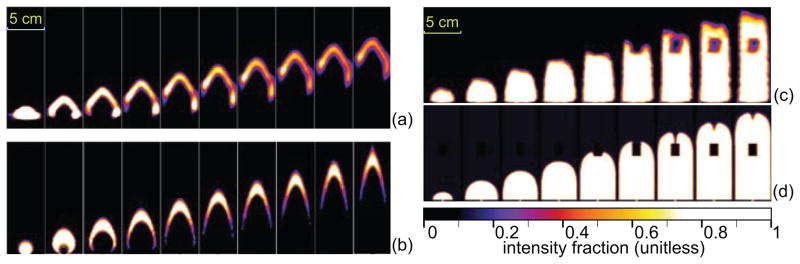
Time-ordered (left to right) longitudinal sections through the sand-filled 16 × 5 cm portion of the column in (a) imaging experiment A, (b) numerical study A, (c) imaging experiment B, (d) numerical study B. Approximately the lower 80% of the column shown in both (c) and (d). PET images are decay-corrected so the image intensity is proportional to the tracer concentration. The time variables for the frames individual frames were selected to visually match the propagation of the tracer edge in PET and simulation image sequences. Since quantitative information on tracer concentration is not available at this time, proportional color scheme was selected with brightness and contrast adjusted for best visibility of the tracer bolus.

Experiment B

Figure 4 shows the tracer propagation profiles for PET-imaged (c) and CFD-simulated (d) fluid flow around an impermeable object with a step-function tracer input function. Visual comparison of the simulated and the measured profiles shows significant similarity, especially at the early time frames, before the tracer front reaches the obstacle. As the front flows around the obstacle, it develops a somewhat asymmetric shape and decreased contrast, most likely caused by the asymmetric placement of the impermeable insert in the experimental column.

Experiment C

Figure 5 shows vertical longitudinal sections through dynamic SPECT images and numerical simulation of flow in a medium with non-uniform porosity. Since the preferential flow-channel positions were selected arbitrarily prior to the study, the two image series show significant differences. Most notably, while both preferential flow paths in the CFD simulation images are within the imaging plane, the main flow path in the real system moves out of the imaging plane near the bottom of the column and reenters the imaging plane first at about 2/3 of the column length and them immediately before the outlet. In addition, rather than the two flow paths being identical, the flow path on the left side of the cross section in the real system is less pronounced. Despite the fact that the system that was modeled was a highly simplified version of what is likely to exist, it still shows many qualitative similarities to the real system. We list several essential features of tracer behavior in non-uniform medium that are common for both image sets below:

Figure 5.

Tracer propagation in inhomogeneous medium: (a) Experiment C, longitudinal cross-sectional slices of the 10 × 30 cm column, reconstructed every 36 minutes. (b) numerical study C results, sampling times adjusted to synchronize the simulated and experimental images. Proportional color scale adjusted for best visual comparison between the datasets. SPECT images were decay corrected so that the image intensity is proportional to the tracer concentration. Arrow 1 shows the point where the main flow path enters the cross-section plane. Arrow 2 indicates a minor preferential flowpath.

• The flow behavior near the bottom of the column is likely driven by the higher-velocity inlet jet, first creating a semi-spherical shape of the tracer distribution, and then the same-shape dark spot, as the tracer input (rectangle function) is followed by tracerless water.

• A significant difference between the image series in Figure 5 is the visibility of the trailing edge of the contrast bolus: it is clearly visible in the simulation but hardly visible in the SPECT results. The exact nature of this effect is unclear, although it is unlikely that it is caused by chemical absorption of ^99mTc-DTPA, which is shown to be a conservative tracer for Rifle sediments in (Vandehey et al., 2011).

• Most of the tracer transport occurs through the preferential flow paths.

• A body of the activity outside of these flow paths propagates up the column at a relatively slow rate.

• A significant amount of flow dispersion at porous scale results in a visible blurring of the image intensity (proportional to the tracer concentration), especially outside of the main flow paths.

Visualization

In addition to the cross-sectional slices, several other display methods can be used to visualize flowpaths in the column. Figure 6 shows four dynamic time frames of the tracer propagation using cross-sectional planes and isosurfaces. The main flowpath and minor flowpaths are clearly visible, as are the effects of tracer mixing with the activity-free water.

Figure 6.

Visualization of the tracer propagation in Experiment C, at four time points, 10 min, 1 hr, 2hrs and 5hrs after injection. Each time frame shown both on four cross-sectional planes and as an isosurface computed at 1/3 of the color axis maximum.

Velocity analysis

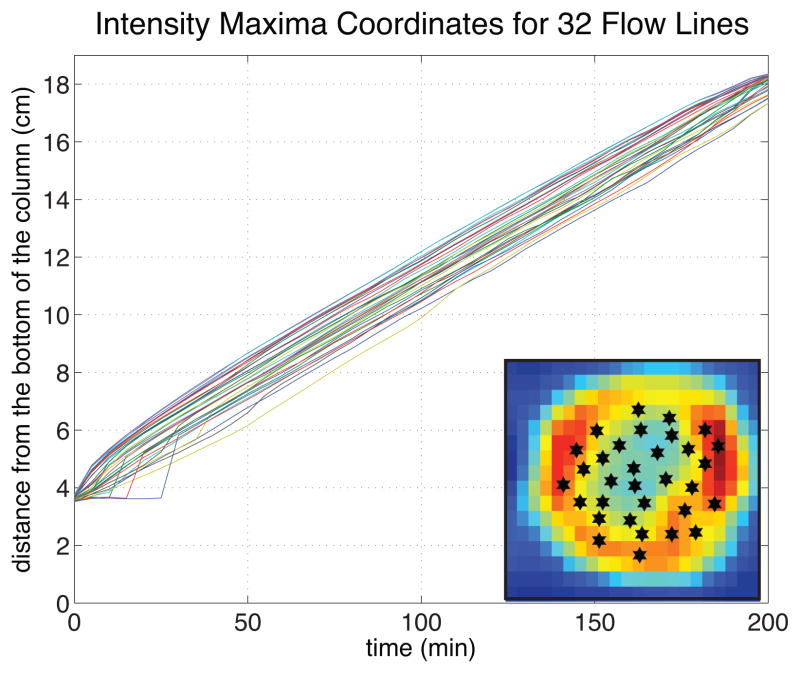
In the process of calculating the flow fields during the CFD simulation, FLUENT software computes the velocities inside the porous domain. In the uniform medium case (experiment A), the velocity field is uniform everywhere except for relatively small regions near the inlet and the outlet. This is a distinct feature of flow in the medium, since velocities in the free flowing fluid in a pipe generally vary depending on the distance to the pipe walls. In Figure 7 we show a plot of the maximum intensity lines for several points within the column cross-section for Experiment A calculated using equation (2). The slope of each of these curves corresponds to the axial (z) velocity component at fixed (x, y). The fact that the curves are parallel straight lines through most of their lengths confirms that velocity is cross-sectionally and longitudinally uniform in most of the column. The value of velocity evaluated from the plot is approximately 6.7 × 10⁻² cm/min. Multiplying this value by the column cross-sectional area 2.5²π cm², we obtain that the flow rate has to be 1.3 γ ml/min, where γ is the porosity of the medium. The measured flow rate in the column is 0.5 ml/min, which gives us γ ~ 0.4, a realistic estimate of porosity for sand.

Figure 7.

Tracer bolus propagation lines in Experiment A calculated using equation (2). Parallel lines indicate cross-sectionally uniform velocity distribution. Converging lines at times less than 20 min and more than 180 min correspond to divergent flow near the inlet and converging flow near the outlet. Insert in the lower right corner of the plot shows arbitrarily chosen cross-sectional positions of the 32 flow lines matched against the longitudinal projection of the column intensity distribution 2.5 hrs after the bolus injection.

5. Discussion

Experiments A and B demonstrate successful application of PET to imaging vertical columns with column sizes comparable to those already reported in the literature. In nuclear emission tomography, it is generally considered that in order to obtain good images, the width of the imaged object should correspond to five attenuation lengths or less. An attenuation length is the thickness of material that reduces the intensity of the penetrating radiation by the factor of 1/e. For the 511 keV γ-ray, this distance of five attenuation lengths corresponds to about 50 cm for water and biological tissues and 25 cm for soils and sediments, implying that column diameters as large as 25 cm can be imaged by PET. Thus, PET with ¹⁸F presents a convenient method of measuring 3D distributions of tracer as it propagates through the column at water seepage flow rates of 10⁻² cm/sec. Similar or slower flow rates can be studied using other long half-life PET isotopes, such as ⁷⁶Br, ⁶⁴Cu or ¹²⁴I.

Good qualitative agreement between the numerical studies and experiments A and B and lack of such agreement in experiment C demonstrate the limits of computational approach based on an exact model within fluid dynamics. While modeling flow in a homogeneous medium can be used to develop and validate methods of extracting material parameters of the medium from dynamic image sequences, modeling flow in a heterogeneous system with unknown medium parameters distributions (which is commonly found in real sediment columns) is a much more complex task. Exact CFD simulations are computationally intensive and time consuming even for the uniform medium; introduction of non-uniform porosity and permeability further increases the complexity of the problem and often leads to instabilities in the numerical solution of the Navier-Stokes equation. We will continue to build numerical models of flow through inhomogeneous medium both using the method presented in section 3 and simpler models of solute transport in medium, such as Darcy’s flow. A working flow model will allow us to calculate local porosity and permeability distributions in columns from the dynamic sets of PET or SPECT images.

The most novel aspect of the presented research is the application of SPECT to obtain 3D tracer distributions in a large vertical column with continuous fluid flow. This method allows continuous monitoring of technetium distribution within a column in a non-invasive manner, without the need to take physical samples of the fluid or sediment material. As mentioned in the introduction, the method is highly sensitive and allows imaging with trace amounts of the radioisotope. The total injected technetium in Experiment C is about 60 picomol, at a concentration of 1.5 picomol/mL. The contrast resolution in Figure 5 is at least 2–3 nCi/pixel, which translates to the ability to resolve differences in concentration of 10⁻¹⁵ mol/L at sub-centimeter length scales.

Our future research in the area of sediment column imaging will focus both on improving the methodology of image acquisition and analysis, and on applying this technique to specific problems in geochemistry, geophysics, hydrology and similar fields. The most immediate practical application of technetium imaging is to study problems related to subsurface transport properties and immobilization strategies of technetium (VII), a prevalent radioactive contaminant (Lear et al., 2010; Burke et al., 2005; Plymale et al., 2011). In particular, the column described in Experiment C is currently used in an extended imaging study with both an active technetium(VII) tracer and a chemically conservative tracer applied to see the effects of anoxic environments and bacterial activity on technetium immobilization, distribution of biogenic divalent iron and flowpath variability.

6. Conclusions

A highly-sensitive non-invasive method of imaging sediment columns using clinical PET and SPECT cameras had been developed and compared to computer simulations of fluid flow in a porous medium obtained using FLUENT software. ¹⁸F-FDG PET was used to image small columns filled with homogeneous material. Dynamic 3D image sequences acquired using PET exhibit significant qualitative similarities to simulated tracer distribution images computed for the flow in a medium with uniform porosity and permeability. A custom-designed experimental arrangement allowed acquisition of tomographic SPECT images in a vertical column with continuously upward flow of the tracer solution. Dynamic 3D sequences of ^99mTc-DTPA distributions in the column were acquired and reconstructed, revealing the inhomogeneous nature of the sediment. Numerical simulations of tracer flow in medium with non-uniform porosity and permeability exhibit the same essential features of the flow as observed in the tomographic images. However, the significant and important differences between the imaged flow patterns within even this relatively simple system using actual field materials and the modeled flow dynamic emphasize the need for non-invasive flow quantification in the interpretation of packed sediment column experiments. The fact that these measurements are rarely done significantly limits the utility of these types of experiments and has probably lead to much incorrect data interpretation. Routine use of nuclear emission tomographic techniques could address this problem and serve an important role within the earth sciences community. The current work presented new tracer options and new column imaging apparatus in order to help bring about that routine application.

Research Highlights.

• Non-destructive and non-perturbing imaging method applied to study sediment columns.

• Nuclear emission tomography (PET and SPECT) clinical scanners used in earth science research.

• PET and SPECT are used to image contaminant transport and flow dynamics in sediment columns

• Computational fluid dynamic (CFD) simulations are able to model flow in porous medium.

• 4D PET and SPECT flow dynamics imaging results compare well with CFD simulations.