Estimating Causal Effects in Observational Studies using Electronic Health Data: Challenges and (Some) Solutions

Abstract

Electronic health data sets, including electronic health records (EHR) and other administrative databases, are rich data sources that have the potential to help answer important questions about the effects of clinical interventions as well as policy changes. However, analyses using such data are almost always non-experimental, leading to concerns that those who receive a particular intervention are likely different from those who do not in ways that may confound the effects of interest. This paper outlines the challenges in estimating causal effects using electronic health data and offers some solutions, with particular attention paid to propensity score methods that help ensure comparisons between similar groups. The methods are illustrated with a case study describing the design of a study using Medicare and Medicaid administrative data to estimate the effect of the Medicare Part D prescription drug program on individuals with serious mental illness.

Introduction

Healthcare has entered the age of “Big Data.” Electronic health data, including electronic health records (EHR) used for clinical care as well as medical billing and other administrative records, are rich data sources for answering important questions about the effects of medical and health systems interventions. They often offer large samples, extensive clinical information, longitudinal data, and details that include the timing, intensity, and quality of the interventions received by individuals. These data sources are currently being used to answer questions ranging from whether a drug is effective to the impact of large-scale health system changes like “pay-for-performance” incentive programs.1–4

Big data allows us to obtain answers to questions that are difficult to answer using randomized trial designs. For example, large administrative datasets are frequently used by pharmaceutical researchers to discern rare but dangerous side-effects of medications that were approved for sale based on trials of a few thousand persons but may eventually be used by millions of people per year.5,6 Moreover, such large scale datasets can better reflect “real-world” use (ie, effectiveness) of medical interventions rather than carefully contrived experimental use (ie, efficacy).7 However, big data will not inherently necessarily solve all of our problems, and in fact, these data sources create some new problems for researchers. As stated in a brief written by AcademyHealth (p. 2), “Access to large amounts of data does not in itself guarantee correct or useful answers to CER [comparative effectiveness research] questions.”8

Randomized trials are generally seen as the best way to estimate causal effects; however, they are often infeasible, especially in comparative effectiveness and patient centered outcomes research. This may be because of ethical concerns (eg, using a placebo comparison to study a treatment already thought to be generally effective, such as flu shots for the elderly), logistical concerns (eg, when interested in long-term outcomes, such as physical functioning 10 years after cardiac surgery), need for a large representative sample (not just those who would choose to enroll in a randomized trial), or lack of resources to carry out a large-scale randomized trial. In these cases we can use data available on a set of individuals who received the intervention of interest, and a set of individuals who did not. Electronic health data can be a crucial element of these types of studies, but analyses using these data are nearly always non-experimental: we simply observe which treatments or interventions individuals receive, with no ability to randomize individuals. Although this often has benefits in terms of the representativeness of the sample and external validity,9 it can be challenging to obtain accurate estimates of causal effects due to selection bias. That is, individuals who receive an intervention may be meaningfully different from those who did not on factors such as income or health status such that it is difficult to simply say if any resulting benefits or harms are due solely to the intervention. In formal terms, selection bias can result in confounding, which is discussed in more detail below.

Because many of the fundamental concerns are the same, in this paper we define our data of interest broadly to include both electronic health records themselves (eg, e-charts compiled at doctor’s offices, geared to track individual clinical experience and status) as well as administrative data (eg, Medicare claims, geared towards program financial monitoring). Because these two broad types of data sources are becoming more intertwined as quality, access, and cost issues are jointly considered in this age of healthcare reform, we feel it is useful to consider them together.10,11 For example, in Maryland since 2006, many outpatient clinic administrative billing claims to that state’s public mental health system must be accompanied by “outcomes measurement system” records that track a person’s level of function from intake to discharge and at six month intervals. Such tracking, though not essential to process accounts receivable and payable, has obvious use in tracking clinical outcomes the state covers.12 This sort of data represents an enormous resource for studies aiming to estimate causal effects. In particular, they often offer large sample sizes of diverse patient populations, longitudinal records over many years, and (at least in some cases) useful details about personal status (eg, living situation, work history), symptom levels, and overall level of functioning indicators (eg, daily living skill and/or well-being ratings). However, access to big data does not automatically ensure accurate inferences. As with any study aiming to estimate causal effects, careful design and thoughtful strategies are needed to draw valid conclusions.

As a primary motivating example for expanded and appropriate use of big data, here we describe an approach for addressing confounding in an ongoing study of the Medicare prescription drug benefit (Medicare Part D) on the cost and health outcomes of individuals with serious (ie, persistent and disabling) mental illness (SMI) who were dually eligible for Medicare and Medicaid. The Medicare prescription drug program first began to offer commercial prescription drug coverage to its beneficiaries in 2006.13,14 For people enrolled in both Medicare and Medicaid, commonly called dual eligibles or “duals,” the advent of the Medicare prescription drug program meant an abrupt transition from Medicaid drug coverage to a private prescription drug plan on January 1, 2006. Among policymakers and advocates there was concern that the transition to Medicare coverage could result in greater formulary restrictions and higher out-of-pocket costs, leading to lower medication access and continuity.13 Moreover, this concern is intensified for vulnerable subpopulations, including persons with SMI. In this study, we compare the dual eligibles to individuals eligible only for Medicaid, who thus retained their Medicaid prescription drug coverage. The data to be used are complex Medicare and Medicaid billing claims data, which includes event-based and time-stamped diagnoses, procedures, treatment venue, medication, and demographic information. The challenge, of course, is that the dual eligibles generally are different from those individuals eligible only for Medicaid, as they must typically be older or sicker to obtain access to both programs jointly.15

There are few resources to guide researchers interested in addressing selection bias using large datasets. Danaei and colleagues illustrate different approaches for simulating a randomized clinical trial using EHR data.16 Sengwee and colleagues address the advantages and disadvantages of individual variable adjustment and confounder summary scores when using data from multiple databases.17 Without clear guidance on how to address confounding, in our review of the literature we found that researchers apply a variety of approaches in CER studies, ranging from multivariable adjustment to matching on a single variable to propensity score approaches. For example, Pantalone et al. used multivariable adjustment;3 Lee, Y.Y. et al. matched based on BMI level18; and Tannen et al. used propensity score weighting.4

This paper presents a tutorial on methods to reduce confounding in non-experimental studies using electronic health datasets; it focuses particularly on methods known as propensity score methods, which help facilitate the comparison of “like with like.” There are other strong non-experimental designs, including instrumental variables, regression discontinuity, and interrupted time series, which are beyond the scope of this paper. See AcademyHealth and West et al. for more discussion of those approaches.8,19 It is important to note that here we focus on just one of several methods to deal with confounds evident in electronic health datasets and that more generally it is important to tailor the design for each research question. We also do not address other data complications such as censoring, missing data, or attrition.

Causal Inference Framework

This paper relates to studies that aim to estimate the causal effect of some intervention, treatment, or exposure relative to some comparison condition. For a given individual, this effect is the comparison of the outcome that would be observed at a given point in time (eg, medication continuity in 2006) if the person receives the treatment of interest (the “potential outcome under treatment,” denoted Y_i(1)) to the outcome that would be observed if that person receives the comparison condition instead (the “potential outcome under control,” denoted Y₀(1)). In our motivating example in Table 1, the potential outcome under treatment is medication continuity in 2006 if an individual was a dual eligible in January of 2006. The potential outcome under control is that person’s medication continuity outcome in 2006 if he or she was not a dual eligible. Interestingly, these ideas of potential outcomes can be seen even in popular media, such as in the iconic and classic movie “It’s a Wonderful Life,” where an angel lets George Bailey see the “potential outcomes” in a world where he never existed, and compare those to the “potential outcomes” in the world in which he was born and lived.

Table 1.

Example of Potential Outcomes

Subject	Dual Eligible Status	Medication Continuity (days of prescriptions in the year) if in only Medicaid (ie, if drugs covered by Medicaid) Y(0)	Medication Continuity (days of prescriptions in the year) if in Medicare and Medicaid (ie, if drugs covered by Medicare Part D) Y(1)
Person A	0	330	?
Person B	1	?	140
Person C	0	172	?
Person D	0	10	?
Person E	1	?	296

Unfortunately, in what is known as the “fundamental problem of causal inference,”20 in the real world we can never observe both of these potential outcomes for the same person: at a given point in time, each person either receives the treatment or receives the control condition. We do not have an angel coming down and showing us what would have happened under the other treatment condition. In other words, we have a missing data problem where (at least) half of the potential outcomes are missing. Individual causal effects are thus very hard to estimate, but we can use statistical techniques to estimate average causal effects. We can think of these techniques as ways to estimate the missing potential outcomes; ie, ways to fill in the question marks in Table 1.

Randomization is perhaps the best-known way of estimating average causal effects. Randomization works by assigning individuals to treatment or control groups by chance (eg, “coin flips”), thereby avoiding self-selection into treatment groups. In terms of Table 1, this means that the people with observed values of Y(1) are only randomly different from those with missing values for Y(1) or, more formally, that the average value of Y(1) that we observe (the average among the people actually in the treatment group) is an unbiased estimate of the average value of Y(1) across the full sample. This means that the difference in observed outcomes in the treatment and control groups provides an unbiased estimate of the actual treatment effect. (Of course this works best in large samples, where the equivalence between the randomized groups is more likely. Moreover, while randomization does not guarantee that an experiment will yield unbiased estimates, since other complexities may arise (such as attrition or non-compliance), it certainly reduces the risk of bias due to confounding factors).

The challenge is that in the absence of randomization we can no longer be sure that the people in the treatment group are representative of what would happen to the control group members if they had instead been treated. In our case example, we simply observe which individuals receive the treatment (eg, Medicare Part D drug coverage). In this study, and in any non-experimental study, there is the danger of confounding. Confounding occurs when we misattribute a difference between the treatment and control groups to the intervention, but the difference is actually due to a third factor that is associated with both the intervention and outcome.21 For example, coffee drinking is correlated with both smoking and pancreatic cancer, but it is not the case that coffee drinking causes pancreatic cancer, whereas smoking does.22 Analyses that do not account for confounding (eg, smoking levels) can lead to incorrect treatment effect estimates. Intuitively, confounding implies that groups receiving different treatments differ on some variables related to outcomes, and thus it is difficult to disentangle differences in outcomes that are due to the treatments from differences in outcomes due to these other pre-existing differences between groups. In our case study examining the Medicare Part D program, the treatment group members (dual eligibles) are likely sicker, older, and may additionally have a support network helping them negotiate the Medicare and Medicaid bureaucracy so they can successfully engage with both systems. It is important to note that standard regression models that simply try to adjust for these differences through regression make the unconfounded treatment assignment assumption described further below and also assume correct functional form of the outcome regression model (see Stuart for more details23). This assumption of the correct functional form is part of the motivation of the propensity score methods discussed further below, as it can be particularly problematic if the treatment and comparison groups look quite dissimilar on the observed characteristics.

In non-experimental settings it is helpful to think about trying to replicate what would happen (and what the data would look like) if we actually did have randomization.24–27 In particular, we can aim to replicate the following key features of an experiment:

• Clear definition of treatment and comparison conditions

• Clear inclusion and exclusion criteria for the study

• Methods to adjust for differences in observed characteristics between groups as a way to mitigate the inherent differences. These methods are the focus of this paper

Cochran (1965) nicely summarizes this approach by encouraging researchers to carefully design their non-experimental studies by considering hypothetical ones based on more rigorous designs: “The planner of an observational study should always try to ask himself the question, ‘How would the study be conducted if it were possible to do it by controlled experimentation?’” (p. 236).28

The primary formal assumption underlying many non-experimental methods is that of “unconfounded” (or “ignorable”) treatment assignment, also known as “ignorability,” “no hidden bias,” or “no unobserved confounders.”29 The assumption is that, once we adjust for the observed characteristics, there is no hidden bias due to unobserved characteristics—that is, there are no additional, unobserved, variables that would bias the treatment effect estimate. In our motivating case study this would be violated if, for example, less severely ill individuals received Medicare coverage because they were able to negotiate and survive the 24-month waiting period for Medicare enrollment (which in turn also affected the study outcomes), and severity of illness was unobserved.15

The “Achilles heel” of non-randomized studies is this worry about unobserved confounders. Those concerns are generally dealt with using two strategies. The first is careful selection of comparison subjects, minimizing the danger of “hidden bias” through careful design. To this end, it is important to understand the process by which individuals choose or are assigned the interventions they receive. The second is sensitivity analysis, to assess sensitivity to such “hidden bias.” We discuss both of these strategies in more detail below.

One of the components of careful selection of comparison subjects involves clever design and thoughtfulness. This might include, for example, ensuring that all individuals in the study sample would have been eligible to receive the new treatment of interest but there was some random process resulting in some receiving it and others not, or identifying groups that are likely to be similar even on variables that we do not observe. For example, in a study of asthma treatment, air pollution levels are an important potential confounder. One way to remove the confounding effects of varying pollution levels is to compare individuals who live in the same geographic area. Rosenbaum discusses the idea of “design sensitivity,” and provides the aspects of a study design that are likely to make it more robust to unobserved confounders, including factors such as a dose-response relationship and using a test statistic tailored to the hypothesized pattern of effects.26

Zubizarreta et al. (2012) provide an example of these ideas of careful design and design sensitivity in practice, estimating the effect of earthquake exposure on Post Traumatic Stress Disorder symptoms.30 The design elements used by Zubizarreta include comparing extreme exposures (high to low) to test for the presence of a dose-response relationship; obtaining close matches on a large set of covariates (methods discussed further below); and tying the analysis procedure to the research question, which hypothesized that there would be no effects for most individuals but large effects for a small subset of individuals. By using a hypothesis test (Stephenson’s test) that specifically allowed for that pattern of effects (large effects on a small subset of individuals), they were able to have much more robustness to unobserved confounding than if a simple t-test or more standard approach were used, which generally assume a constant treatment effect for everyone.

Another way to address worries about unobserved confounders is through clever designs that take advantage of some “natural experiment” that exists in the world; this is known as “instrumental variables” analyses. An appropriate instrumental variable is one that strongly predicts whether or not someone receives the treatment of interest, but that does not directly affect outcomes.31 A common example in pharmacoepidemiology is to use prescribers’ prescribing preferences as an instrument for drugs received.32 The idea is that which prescriber a given patient happens to see is somewhat random and likely affects which drug an individual is first prescribed (eg, a particular provider may happen to prescribe Cox-2 inhibitors rather than nonselective nonsteroidal anti-inflammatory drugs (NSAID’s) for pain control), but (the argument is) that provider’s prescribing preference likely does not affect patients’ outcomes directly.33,34 Another common instrumental variable is distance, for example, estimating the effect of cardiac catheterization using distance to a cardiac catheterization-providing hospital as an instrument for that procedure (under the argument that the distance does not affect outcomes directly, except through whether or not someone gets cardiac catheterization).35 We will not discuss instrumental variables in more detail here; see Newhouse and McClellan and both papers by Rassen et al. for overviews of the approach.31,33,34

Propensity Score Methods

Propensity score methods are a common approach for estimating causal effects in non-experimental studies. They are useful when it is not possible to identify a plausible instrumental variable, but when a large set of confounders are observed. Propensity score methods aim to equate the treatment and comparison groups on a set of observed characteristics. The idea is to replicate a randomized experiment by finding treatment and comparison individuals who look only randomly different from one another, at least with respect to the observed confounders. Intuitively, to do this equating we could, for each treated subject, try to find someone with the same values of all of the observed confounders: same age, same medical history, same location, etc. Of course this is often infeasible given limited sample sizes and large numbers of confounders (for an example and more detailed discussion see Stuart).36 Even in large electronic health datasets with very large sample sizes, there may not be sufficient sample size to find an exact match on all covariates. As a simple example, even 10 binary confounders creates 1,024 different combinations of those confounders; even with very large sample sizes it is not realistic to be able to find exact matches across treatment and comparison groups on all 10 covariates.

Propensity scores enable the formation of groups that look only randomly different from one another on the observed covariates without requiring exact matches on all of those covariates. The propensity score itself is defined as the probability of receiving the treatment, given the observed covariates. Properties of the propensity score detailed by Rosenbaum and Rubin prove its usefulness as a summary measure of the full set of covariates for this purpose of forming comparable groups.29

It is common practice to use the following four steps when using propensity scores in a study, and we strongly recommend the fifth step also listed below:

1. Estimate the propensity score. It is often estimated using logistic regression, although newer machine learning methods have also been found to work well, especially when there are many covariates to include, as is likely the case when using electronic health datasets.37

2. Use the propensity scores to equate the groups through matching, weighting, or subclassification. The simplest form of matching involves selecting, for each treated subject, the comparison subject with the closest propensity score. Weighting weights the treatment and comparison groups by a function of the propensity score to look like one another, similar to the idea of survey sampling weights. Finally, subclassification forms subgroups of individuals with similar propensity scores (eg, 10 subclasses, defined by propensity score deciles). See Stuart for more details on these approaches.23 Weighting is illustrated in further detail below.

3. Check how well the equating worked. Since the goal is to form groups that look similar on the observed covariates (thus reducing bias in the treatment effect estimate), we can see how well it worked by comparing the distributions of the covariates in the treatment and comparison groups. We hope that after the procedure used in Step 2 the groups will be “balanced” in that they will have similar covariate distributions: similar means, variances, and ranges for each variable. We will see an example of this below. A lack of good balance after Step 2 may indicate that either an alternate approach needs to be used in Step 2, or the data is not sufficient to answer the question of interest—perhaps that there are just too many differences between the individuals receiving the treatment and control conditions.

4. Estimate the treatment effect. Using the propensity score equating method from Step 2 and verified in Step 3, effects are then estimated by comparing outcomes in the equated groups. With matching, this involves comparing outcomes in the matched groups. With weighting, we will use weighted regressions to compare outcomes. With subclassification, effects are estimated separately within each subclass and then aggregated. Again, see Stuart for details.23

5. Sensitivity analysis to unobserved confounding. Back to the “Achilles heel” of non-experimental studies, the concern is that there may still be unobserved differences between the groups even if the balance checking step (Step 3 above) indicates that the groups look similar on observed covariates. Accordingly, we recommend a fifth step (which is currently less commonly done than Steps 1–4): to assess how sensitive results are to an unobserved confounder. In particular these methods ask questions such as: “How strongly related to treatment and to outcome would some unobserved confounder have to be to change my study results?” Other approaches posit an unobserved confounder and obtain adjusted impact estimates if that confounder existed, given its assumed characteristics (eg, its prevalence, its associations with treatment, etc.). See Liu, Kuramoto, and Stuart for an overview of these approaches.38

Example

In this section we detail the design of a study to estimate the effects of the Medicare prescription drug program (Medicare Part D) on individuals with SMI. To focus on the design, we discuss only Steps 1–3 above and will not discuss either the resulting estimated effects or the sensitivity analysis following effect estimation. The Medicare Part D program was implemented in 2006; it represented the largest change to the Medicare program since its inception in 1965.14 The program provided stand-alone prescription drug coverage with the goals of increasing access to medicines and reducing out-of-pocket pharmaceutical costs. However, for individuals dually eligible for Medicare and Medicaid (“duals”), it meant transitioning from state governed Medicaid drug coverage to potentially more restrictive coverage commercial health insurance coverage administrated by Medicare; this could mean greater barriers to access medicines, such as need for more prior authorizations, step therapy requirements, or formulary exclusions.13,14 There was concern that these changes would particularly affect individuals with SMI. This study aims to estimate the effect of the Medicare Part D program on dual eligible individuals with SMI in terms of their medication continuity and outcomes such as inpatient admissions, mortality, and costs of care.

The data used are Medicare (federally archived) and Medicaid (state archived) claims from 2004–2009. Both data sources are collected principally for financial (eg, billing and federal Medicaid match calculation) purposes, though they are also utilized by state and federal authorities for quality and access monitoring. The Medicare data was obtained via a formal data use agreement (DUA) with the Centers for Medicare and Medicaid Services (CMS), facilitated by a contractor they have long-retained (www.resdac.org/cms-data). Individual-level medical and pharmacy claims data were obtained from CMS by providing them a “finder file” of duals evident in state Medicaid files obtained directly from Maryland’s Medicaid Management Information System (MMIS) files. These files are maintained and regularly analyzed at the The Hilltop Institute under a long-standing DUA with Maryland’s Medicaid authority. Both the state and federal files contain individual, event-level (ie, date stamped) transactional data that records diagnostic and procedure code information for all medical claims, and national drug code information for pharmacy claims. Additionally, the state Medicaid files yield enrollment periods, eligibility categories, and various demographic indicators (age, race, region) for all persons included in our SMI study cohort. Cross-linking between Medicare and Medicaid files was done by using a Social Security number or unique state Medicaid identifiers.

The first step in answering this question about the Medicare Part D program is to define it cleanly, and to identify appropriate treatment and comparison groups. The intervention group was defined as those individuals eligible for both Medicare and Medicaid as of January 1, 2006—the first day when the Part D program was in effect. The comparison group was defined as those eligible for only Medicaid because they retained Medicaid drug coverage throughout the study period.

We further restricted the sample to meet certain criteria, similar to inclusion and exclusion criteria in a randomized trial, to ensure better comparability and common measures across sample members. In particular we restricted the sample to individuals in Maryland. This ensures that all individuals in the sample were affected by the same state-level factors and policies. This is an important constraint because Medicaid eligibility and benefits vary by state.15 Accordingly, bias could creep in had we compared dual eligibles in one state with Medicaid only individuals in another, given differences in health policies and systems between states. To narrow our focus on persons with unique yet prevalent medical vulnerability, we further limited the sample to individuals with a diagnosis for schizophrenia, bipolar, or depressive disorders in 2004 or 2005. This represented our primary sample of interest. We excluded individuals who enrolled in a Medicare Advantage plan in 2005 or 2006 (the outcome year of primary interest), because neither Medicare nor Medicaid data includes individual-level claims for the minority of individuals who opted to engage in such prospective payment managed care arrangements. We also required continuous enrollment in 2005 in order to have complete and consistent data for all individuals during that year-long baseline time period.

These constraints resulted in an initial sample of 4,149 dual eligibles and 8,905 Medicaid-only individuals. Variables in the propensity score model included mental health diagnoses, baseline year (2005) cost and utilization experience, demographic characteristics, and somatic (ie, non-psychiatric) diagnoses (as detailed below).

Using this sample we combined propensity score methods with a difference-in-differences design, comparing changes in utilization before and after the Part D program in a set of individuals affected by the Part D program (“duals”) and a comparable set of individuals not affected by the Part D program (Medicaid only). This was done by utilizing longitudinal data on all individuals in the cohort of interest, covering the time period before the Medicare Part D program was implemented (January 1, 2006) as well as after. In particular, the study aimed to reduce bias by (1) equating dual eligible individuals and Medicaid-only individuals on baseline values of the primary outcomes of interest, and (2) defining the outcome as the change in the outcome measure (eg, medication continuity) from baseline (pre-2006) to follow-up.

The covariates used in the procedure were variables available from the Medicare and Medicaid administrative data files, which revealed their psychiatric (ie, schizophrenia, bipolar/mania, or depression) and somatic (ie, diabetes, hypertension, high cholesterol, cardiovascular, cancer, or renal) illnesses; demographics; and baseline (2004–2005) measures of the key outcomes of interest. These were selected because we believed these characteristics would help distinguish duals from non-duals and also predict the outcomes of interest. Controlling for a large set of observed confounders is particularly important for obtaining accurate effect estimates. This helps satisfy the assumption of no unmeasured confounding. Steiner et al. in particular show that non-experimental studies yield the most reliable answers when the groups are similar on baseline values of the outcomes.39 Studies that do not have access to such variables (or, eg, when the outcome of interest is something like mortality, for which a baseline value is somewhat meaningless) should think carefully about other baseline variables that are likely to be highly predictive of the key outcomes. In our example, this helped motivate our inclusion of both baseline measures of the outcomes of interest (eg, medication continuity) as well as common somatic illnesses that would help predict future health care utilization.

Step 1 of the propensity score process involves fitting a model predicting dual eligible status (dual eligible vs. not) as a function of the confounders listed above (demographics, mental illnesses, somatic illnesses, etc.). Each individual’s propensity score is then the predicted value from that model: their predicted probability of being a dual eligible, given their observed characteristics. In the matching procedure used in Step 2 (see below) we used logistic regression for this model. In the weighting procedure used in Step 2 we used a generalized boosted model, which is a machine learning regression tree-based method that allows prediction of a binary variable (dual eligible status) as a function of a set of covariates.40,41

As Step 2 in the propensity score process, we considered two propensity score approaches for equating the groups: 1:1 matching, which selects one Medicaid-only individual for each dual eligible, and “weighting by the odds,” which weights the Medicaid-only group to look like the duals. In particular, the treated individuals (duals) receive a weight of 1 and the comparison individuals (Medicaid-only) receive a weight of the propensity score over one minus the propensity score (p/(1-p), where p is the propensity score). Non-duals who look dissimilar to the duals (as evidenced by having small propensity scores; a low probability of being a dual) will receive relatively small weights; non-duals who actually look quite similar to the duals (as evidenced by having large propensity scores; a high probability of being a dual) will receive higher weights. Both of these procedures (1:1 matching and weighting by the odds) estimate what is known as the “average treatment effect on the treated” (ATT), which in this case is the effect of the Medicare Part D program on the dual eligibles (those affected by the policy change). One-to-one matching was implemented using the MatchIt package for R; the weighting was implemented using the twang package for R.4,41 (MatchIt can also be run via SPSS.42 Stata has a user-defined program pscore and psmatch2. Propensity score and matching can also be implemented using SAS, but requires substantial programming. See this webpage for more details on software packages available for implementing propensity score methods: http://www.biostat.jhsph.edu/~estuart/propensityscoresoftware.html.)

We ran both weighting and 1:1 matching on the data, but selected weighting as our preferred approach for two primary reasons. First, and most importantly, weighting led to better covariate balance (detailed below) so, as recommended by Harder, Stuart, and Anthony, we proceeded with that approach.43 Second, weighting allowed us to retain the full sample in the analysis. All duals are included as the “treatment” group, and all non-duals are included but weighted relative to their similarity to the duals.

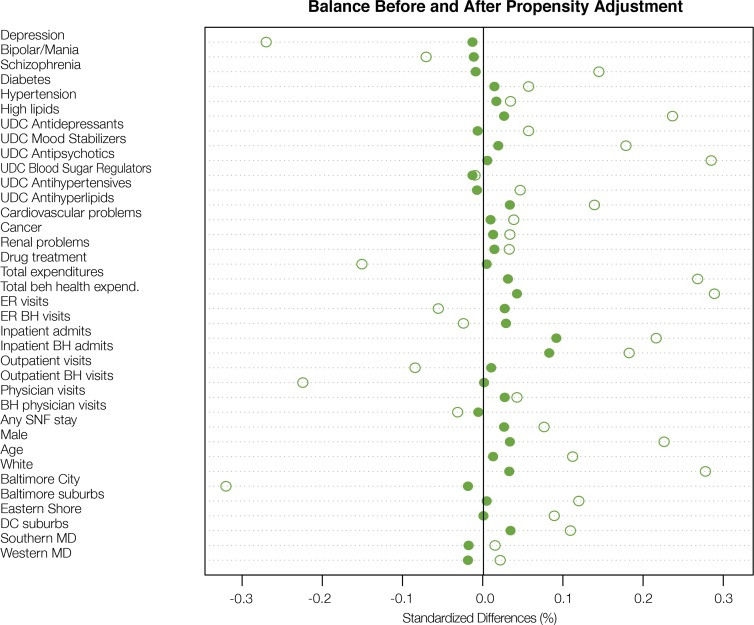
In Step 3 of the propensity score approach we found that the weighting was very successful at reducing differences in the covariates between the dual eligible and Medicaid-only groups. This is illustrated in Figure 1, which shows the standardized difference for each covariate before (hollow circles) and after (solid circles) weighting. The standardized mean difference is a commonly used balance measure, and is the difference in means divided by the standard deviation for that covariate (using weighted means as appropriate). We see that the weighting reduced nearly all of the standardized differences, and after weighting all standardized biases were less than 0.2, a threshold used to indicate adequate balance.23 It is particularly reassuring that the baseline measures of some of the key outcomes (eg, unique day counts [UDC] of six types of prescription drugs) are very well balanced after weighting. There still remains some difference on inpatient admissions and inpatient behavioral health admissions (a subset of inpatient admissions), with the dual eligibles having higher admission rates, but even on these variables the standardized difference is less than 0.15. Overall, Figure 1 shows that the propensity score weighting has served to make the weighted set of Medicaid-only individuals quite comparable to the dual eligibles, at least on this set of observed characteristics. (As reference, a less successful result would be one where many standardized biases remained larger than 0.1 or 0.2 in absolute value even after the propensity score equating, or one where the standardized biases after the equating were larger than before). Now that this design is set, with the propensity weights defined, outcome analysis can proceed by examining differences in outcomes between the weighted groups, for example, by running a regression model using weighted least squares.

Figure 1.

Standardized differences across experimental groups (duals vs. non-duals) on covariates before and after propensity score weighting. Blue hollow circles indicate standardized difference before weighting; solid red circles, after weighting.

Complications when using Electronic Health Datasets

Above we have outlined a study that used an electronic health dataset and propensity score methods to estimate the causal effect of the Medicare Part D program on medication continuity, and demonstrated that our propensity score weighting approach created intervention and control groups that are highly balanced across a large number of observed characteristics. These methods have the potential to help make more reliable statements about causal effects using these complex datasets. However, a number of challenges also arise when trying to use such data to answer causal questions.

An obvious question is how to wade through the large number of observations in electronic health datasets. In particular, how to select the covariates to include in the propensity score procedure. The best strategy is to first use substantive knowledge to select the variables believed to be related to both the treatment received and the outcome (ie, confounders), with particular attention paid to variables believed to be strongly predictive of outcomes. As mentioned above, if baseline (pre-treatment) measures of the outcome are available they should certainly be included. In cases where such substantive knowledge is not available, Schneeweiss et al. have proposed a “high-dimensional propensity score” (HDPS) approach that uses a data driven approach (informed by substantive knowledge) to find the variables that are most strongly correlated with both treatment and outcome.44

Of course even when there are a large number of variables in the dataset, it is possible that important confounders are not observed. This is likely a particular challenge when using billing records not supplemented by medical record data. For example, Polsky et al. found that medical claims were not sufficient for estimating the effect of treatments for chemotherapy-induced anemia; clinical measures such as baseline hemoglobin greatly enhanced the ability to obtain accurate effect estimates.45 Another challenge with administrative data in particular is that it will typically include only final paid claims, which may not fully reflect the care actually provided; or in the case of our pharmacy claims, a filled and paid for prescription does not verify that the patient actually used the medication as instructed. See Hersh et al. for a discussion of these challenges in electronic health datasets.46

Even assuming that an administrative record is thorough enough in terms of the measurement of confounders, measurement error is of course a challenge with all of these datasets. This might include comparability of the data entered by different doctors, and, more generally, data not being collected for research purposes, with possible little attention to validity or reliability. Other concerns include respondent bias in billing data in particular, such as up-coding (to maximize reimbursement and access to services), and how to account for changes in coding over shifts that are secondary to clinical practice or even due to non-medical policy changes (eg, database recording procedures).

This paper has focused on a simple situation with a single point in time treatment initiation date, covariates (ideally) measured before that point in time, and outcomes (ideally) measured after. However, many large electronic health datasets actually consist of repeated measures of the same individuals; for example, billing claims or updated health information every time an individual goes in for an appointment. This leads to two complications. The first is that large electronic health datasets will contain only partially standardized information because these datasets are principally tools used by various parties to track and record individual patient issues or to facilitate reimbursement. The second is that the treatments themselves may be long-acting and time-varying (eg, an individual going on and off an antipsychotic medication), requiring complex methods that can handle time-varying confounders, treatments, and outcomes. See Faries, Ascher-Svanum, and Belger for an overview of approaches and considerations47; one particularly common method for estimating causal effects in complex longitudinal settings is marginal structural models.48,49

Conclusions

In summary, electronic health databases offer enormous potential, with extensive data on large numbers of patients, often measured for many years. However, extensive data on its own cannot answer causal questions; even the most extensive dataset available will never have both potential outcomes observed for each individual. Thus, care is still required to think carefully about how to obtain the best answers to research questions involving causal effects. This involves clear statement of the research problem, careful consideration of confounders and other threats to validity, and then clever design to minimize or eliminate those threats, as illustrated in the Medicare Part D program example. We have shown that propensity score methods can be used successfully with an electronic health dataset to create groups of exposed (Part D participants, “duals”) and unexposed (non-Part D participants; “Medicaid-only”) who look similar to one another on a broad range of baseline characteristics, including demographics, lagged year pharmaceutical utilization, morbidity, and diagnoses. We hope that this paper will prompt further use of these data, and further attention to their strengths and their limitations.