An elastic rod model to evaluate effects of ionic concentration on equilibrium configuration of DNA in salt solution

Abstract

As a coarse-gained model, a super-thin elastic rod subjected to interfacial interactions is used to investigate the condensation of DNA in a multivalent salt solution. The interfacial traction between the rod and the solution environment is determined in terms of the Young–Laplace equation. Kirchhoff’s theory of elastic rod is used to analyze the equilibrium configuration of a DNA chain under the action of the interfacial traction. Two models are established to characterize the change of the interfacial traction and elastic modulus of DNA with the ionic concentration of the salt solution, respectively. The influences of the ionic concentration on the equilibrium configuration of DNA are discussed. The results show that the condensation of DNA is mainly determined by competition between the interfacial energy and elastic strain energy of the DNA itself, and the interfacial traction is one of forces that drive DNA condensation. With the change of concentration, the DNA segments will undergo a series of alteration from the original configuration to the condensed configuration, and the spiral-shape appearing in the condensed configuration of DNA is independent of the original configuration.

Introduction

In a salt solution, geometrical configuration of a DNA chain is determined by interaction between the DNA chain and the solution molecules. This interaction should be, in essence, characterized by von de Waals force or electrostatic force. However, if a DNA chain is regarded as a thin elastic rod, the interaction of the DNA chain with the solution molecules can be modeled by the interfacial traction between the rod and solution [1].

Studies of modeling of DNA as an elastic rod can be traced back to the 1970s. Benham [2, 3] and Le Bret [4, 5] firstly used the elastic model to analyze the equilibrium configuration of DNA. In the framework of this model, varied subjects related with the DNA configuration were investigated extensively [6–10]. Some geometrical configurations appearing in the DNA condensation have been explained perfectly. Recently, Cherstvy used the elastic model to further investigate the effect of counterions and attractive inter-segmental DNA–DNA interactions on molecular spatial conformations and the low-dielectric DNA core on the elastic DNA properties [9–11] in a micro field. Up to the present, it has been confirmed that the elastic rod model is adequate for characterizing the geometrical configuration and deformation of DNA. Some recent reviews can be found in references [12–16].

A series of experiments have shown that, as a polyelectrolyte, geometrical configuration of DNA in a multivalent salt solution is directly influenced by the ionic concentration of the salt solution [6, 17–28]. At low salt, the DNA chain manifests itself in a sparse interwound configuration; while at high salt, the DNA condenses into a toroidal structure. Recently, Huang used the elastic rod model to calculate the equilibrium configuration of DNA subjected to the rod-solution interfacial traction, and discussed the change of DNA configuration with the ionic concentration of solution [1]. However, in that work, the influences of the ionic concentration on the interfacial traction and elastic modulus of DNA are given in a vague way, being lack of a mathematical description. Therefore, the aim of this paper is to establish some models characterizing the influences of the ionic concentration on the interfacial traction and elastic modulus of DNA, and investigate the equilibrium configuration in the salt solution with different concentration.

The paper is divided into five parts. In the second section, basic equations given in [1] are summarized. In the third section, we propose two models that they characterize the rod-solution interfacial traction and the elastic modulus of DNA changing with the ionic concentration of the salt solution. In the fourth section, the influence of the ionic concentration on the equilibrium configuration of DNA is calculated and discussed in detail. Finally, some conclusions are given and the paper is closed.

Basic equations

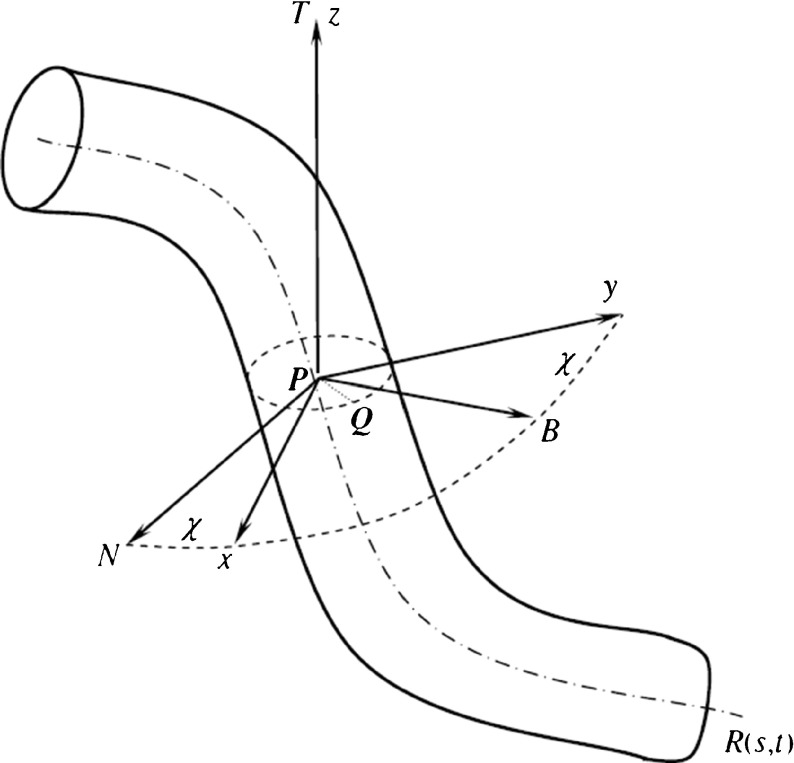
Consider a polymer filament immersed in a solution. The filament can be modeled by a thin flexible circular rod [2–8, 13, 19–26]. The central axis of the rod is a spatial curve R(s, t): R²→R³ parameterized by arc length s and time t. As shown in Fig. 1, the Frenet frame P-NBT and a local orthonormal basis P-xyz are simultaneously set on each cross section of the rod. P is a point on the curve R(s, t). In P-xyz, x-axis and y-axis are the two principal inertia axes of the cross section through the point P. The angle between the principal normal PN and x-axis (or the binormal PB and y-axis) is called the twisting angle, denoted by χ.

Fig. 1.

The thin rod model of DNA

In the initial state of rod, the curvature and torsion of the axis are κ₀ and τ₀, respectively. The initial twisting angle is χ₀. Relative to the coordinates P-xyz, the Kirchhoff equations are written with the index symbols as follows [25]:

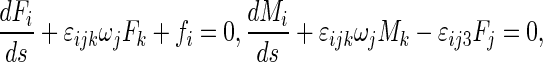1

where F_i and M_i are the stress resultant and principal moment acting at the center of cross section, ω_i the curvature-twisting vector, and ε_ijk the permutation sign. f_i refers to the interfacial traction distributed along the central axis R(s, t). In a solution, f_i is a coarse-grained model to characterize molecular and electrostatic interactions between the DNA chain and solution. As a coarse-grained model, we suppose that f_i is described by interfacial pressure between solution and the rod modeling the DNA chain. So it can be derived from the Young–Laplace equation

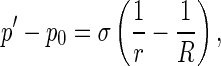2

where R and r are two principal curvature radii in which r is the radius of the rod cross section, p₀ is a constant pressure applied on the interfacial surface by solution, and p′ is the pressure on the interfacial surface by the rod. In (2), we have reckoned a principal curvature radius as positive if it is drawn into the interior of rod.

In terms of the action and reaction law, the pressure p applied on the rod by the interfacial surface is equal to p′ in magnitude, but they are opposite in direction. So, in coordinates P-xyz, p can be decomposed into

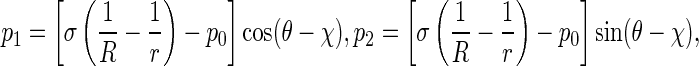3

where 𝜃 is the angle between PQ and PN. It has been proven that R can be written as [1]

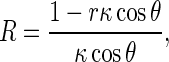4

where κ is the curvature of the rod axis. Substituting (4) into (3) and integrating along the perimeter of the rod cross section leads to

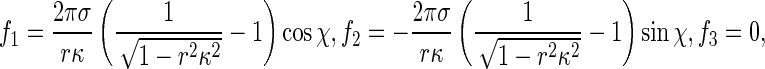5

which characterize interfacial effects between the rod and solution. Clearly, −1 < rκ < 1.

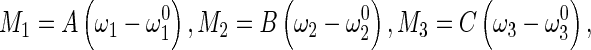6

where 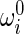denotes the initial curvature-twisting vector. A and B are the bending stiffness with respect to x-axis and y-axis, respectively. C is the twisting stiffness. Assume the rod is isotropic. Then, A, B and C are written as

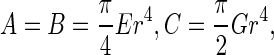7

where r is the radius of the rod cross section. E is the elastic modulus, and G the shear modulus that is equal to E/2(1+ν). Here, ν is the Poisson ratio and it is a constant with ν=0.23 [25]. By the curvature κ, torsion τ and twisting angle χ, the curvature-twisting vector ω_i can be represented as [25]

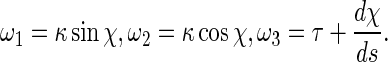8

Inserting (5), (6), and (8) into (1) leads to:

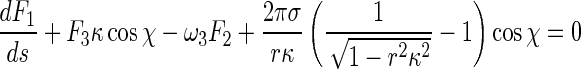9

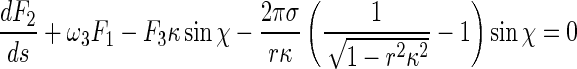10

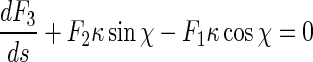11

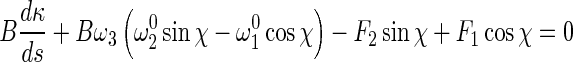12

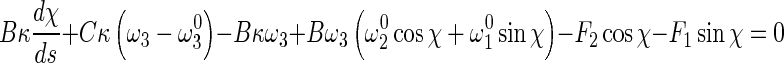13

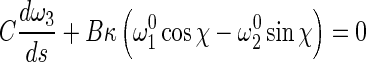14

Let τ=ω₃−dχ/ds, then (13) leads to

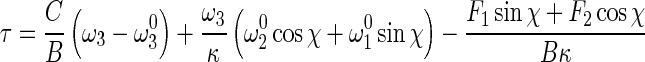15

From (9–15), we can get the value of the curvature κ, torsion τ and twisting angle χ, and with the Frenet–Serret formula of curve as follows:

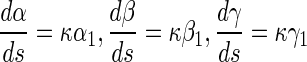16

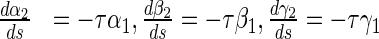17

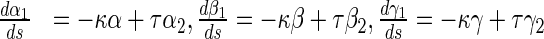18

Relative to the coordinates P-xyz, we can solve the direction cosine ( α , β, γ) of the tangential vector with a point of the curve. So the configuration of the rod is determined by the equation below:

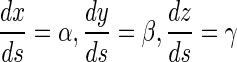19

From (9–15), it is clear that the curvature κ, torsion τ, and twisting angle χ depend only on the interfacial energy and elastic properties of the rod. Therefore, the configuration of a rod is determined by competition between the interfacial energy and elastic strain energy of the rod.

Effects of solution concentration on interfacial traction and elastic modulus

As indicated in (5), the interfacial tractions are influenced by the interfacial tension σ between the rod and the solution, whereas σ depends directly on the concentration of the solution. Therefore, the interfacial tractions change with the concentration of solution. The relationship between them can be characterized by the Gibbs adsorption equation, which reads [37]

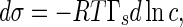20

where c denotes the concentration, Γs is adsorbed amount, T and R are absolute temperature and the gas constant, respectively. On the other hand, Γs is also concentration-dependent. This dependence can be given by the Langmuir adsorption equation below [36, 37]:

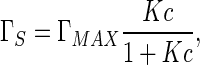21

where Γ_MAX is the maximum concentration when the solution arrives at saturation state, and K is the absorption constant. Substituting (21) into (20) and then calculating integration, we have

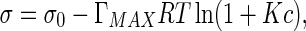22

where σ₀ is the interfacial tension of pure solvent. Equation (22) shows the interfacial tension decreases with the concentration increasing.

Besides effects on the interfacial tractions, the concentration has the influences on the elastic modulus of polymer filament. This is because the change of concentration will cause the Kuhn length of polymer chain altered, whereas the Kuhn length is a main factor to determine the elastic modulus of polymer material. In general, the correlation between the Kuhn length and concentration is described by the Poisson–Boltzmann theory [38, 39], which reads

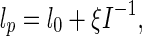23

where l_p denotes the persistence length, l₀ and ξ are two constants, and I is the ionic strength that is defined as [38]

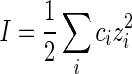24

where c_i is the concentration of ionic species i, and z_i is its charge. For the convenience of analysis, in the following examples we choose the NaCl solution with monovalent Na ⁺. So z_i= 1. With help of the freely jointed chain model, the elastic modulus of polymer filament can be represented as [42]

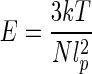25

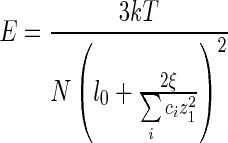
by the Kuhn length, where k is Boltzmann constant, T is the absolute temperature and N is the number of Kuhn length, which is the ratio of the contour length L of DNA and Kuhn segments length b[43]. Substituting (23) and (24) into (25) leads to

26

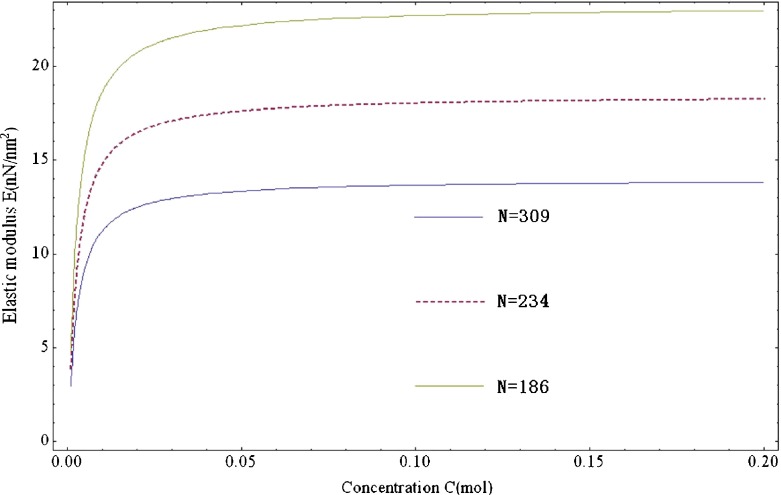
To summarize (22) and (26), we can find that the change of concentration will make elastic modulus and the interfacial tractions simultaneously varied. Figure 2 illustrates the change of elastic modulus with the ions concentration of solution. Therefore, we can implement the self-assembly of polymer filament by adjusting the concentration of solution. Some examples for DNA will be given in next section.

Fig. 2.

The change of elastic modulus with concentration from 1–2 mM for the freely jointed chain model with the parameter of k=1.38×10⁻²³ J/K, T=293 K, ξ=0.324

Analysis and conclusions

In this section, we use (9–19) to solve numerically the equilibrium configuration of DNA under the action of interfacial traction.

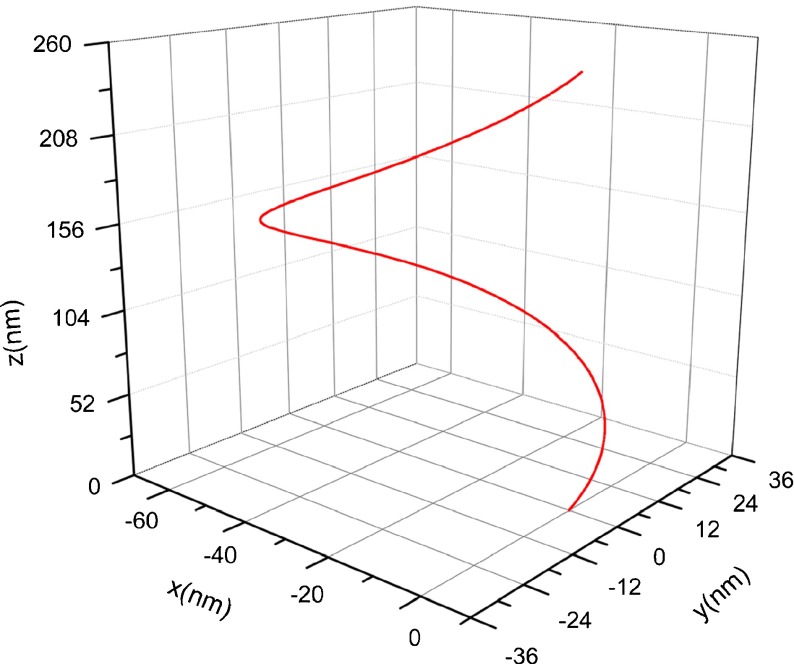
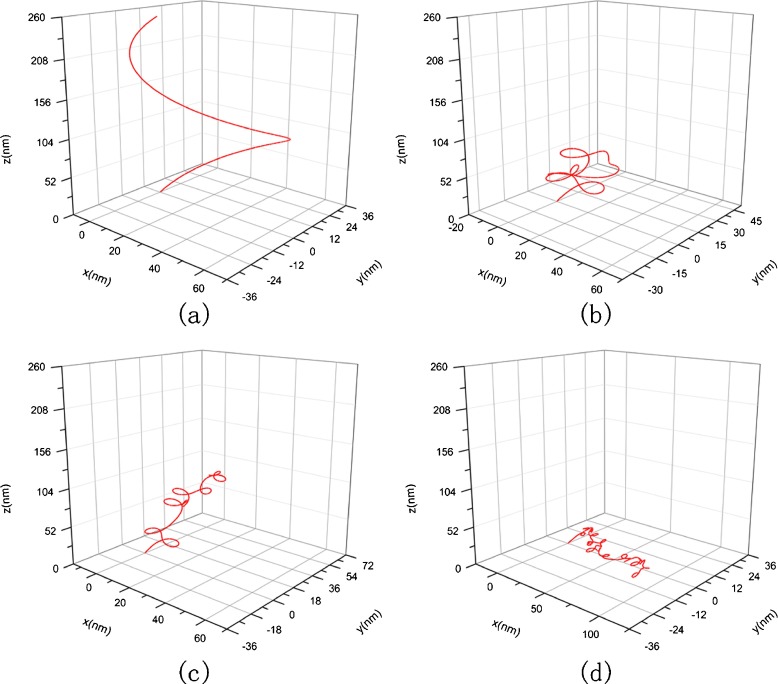
Consider a segment of DNA strand whose original configuration is a helix, as shown in Fig. 3. The length of the DNA segment is of nanometer order of magnitude. Relative to an orthogonal coordinates system, the helix curve is characterized by the equation below:

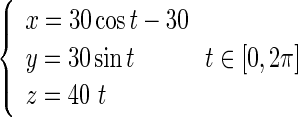27

It is easy to give that the curvature and torsion of the helix curve are 0.012 nm⁻¹ and 0.016 nm⁻¹, respectively. When the DNA segment is immersed into a new solution environment, it will deform from the original configuration into the condensed configuration due to the change of interfacial traction.

Fig. 3.

Original configuration of DNA

As discussed in Section 3, the interfacial tension and elastic modulus of DNA are influenced by the concentration of solution. Therefore, the change of DNA configuration with the concentration of intracellular solution will be investigated in the following section. When calculation, we take r= 1.0 nm[33], Γ_MAX=5.35×10⁻⁶mol/m²[41], K=100 [41], l₀=53 nm, b=0.106 μm, ξ=0.324 [38], T=293 K, L=32.8 μm [43], and N=309(N=L/b) [43].

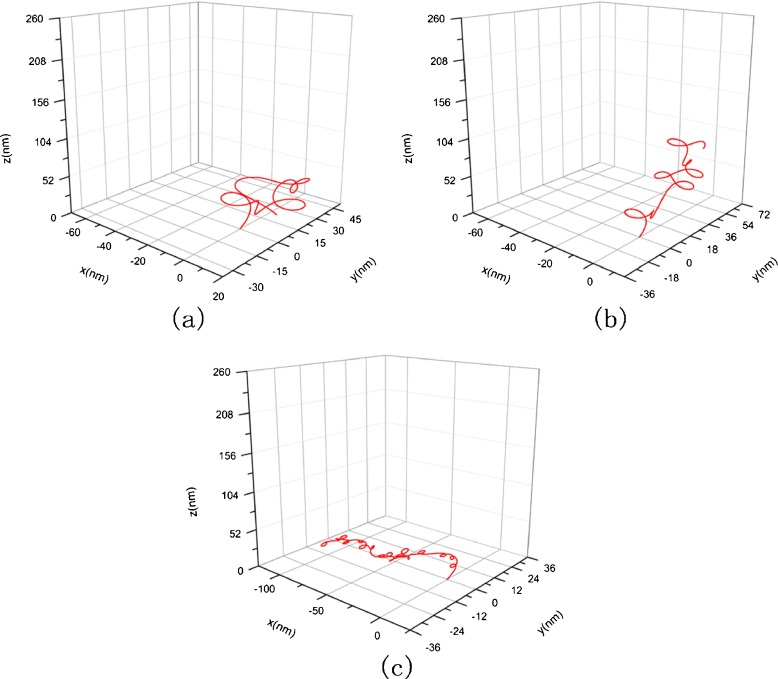
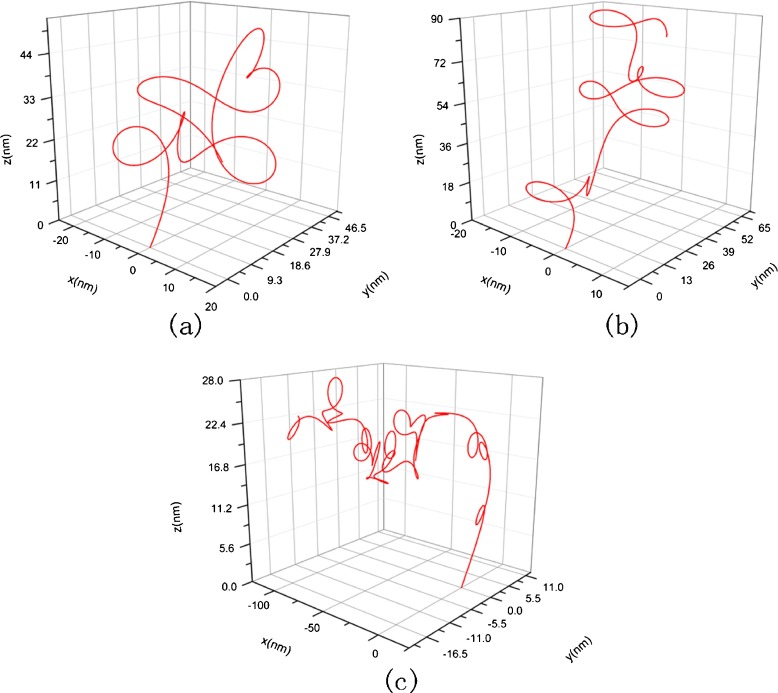
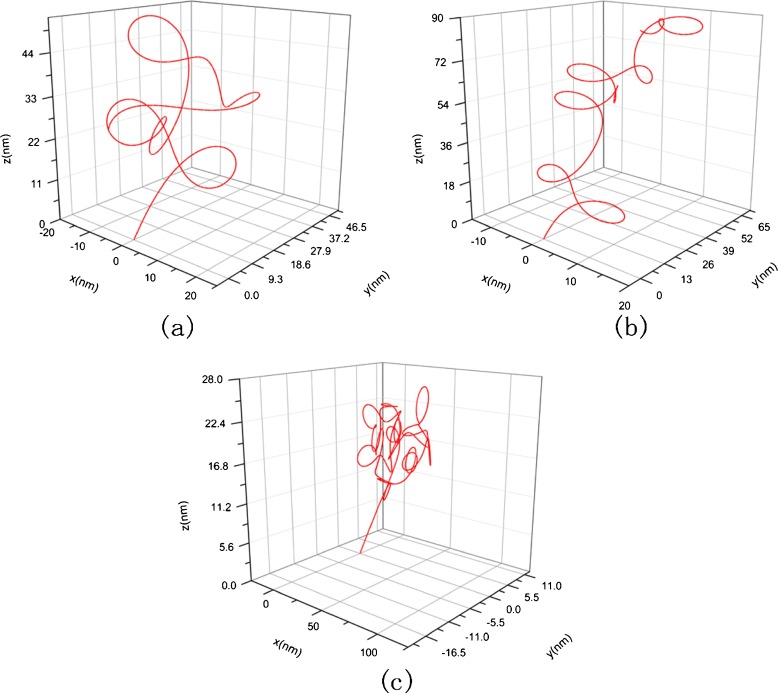
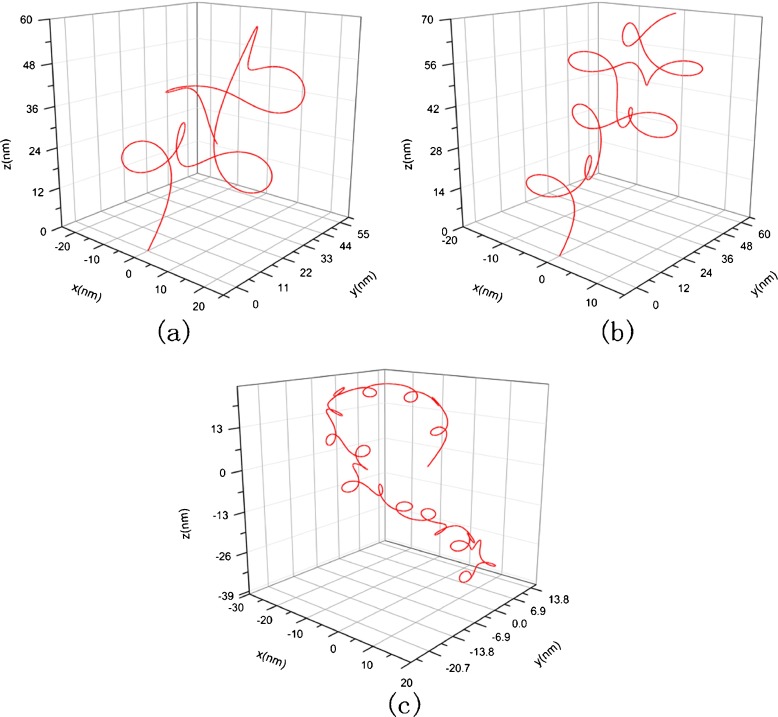
Using the classical Runge–Kutta algorithm, we calculate three condensed configurations corresponding to the original configuration in Fig. 3 in three solutions whose concentration are 1 mM, 10 mM, and 150 mM, respectively. The initial condition takes F₁=F₂=F₃= 0, κ₀= 0.012, τ₀= 0.016, χ₀=0 and x = y = z = 0. The results are shown in Figs. 4 and 5, where Fig. 5 is amplification to Fig. 4 in resolution. From them, one can see that the DNA segment coils into a compact “helix” spontaneously under the interfacial traction. The mechanism to produce this change can be attributed to the correlation between the interfacial traction and the curvature of the rod. When the interfacial traction is applied on the rod, the curvature of rod will alter; conversely, the change of the curvature will cause the interfacial traction to be altered. As thus, the coupling effects between the interfacial traction and the curvature of the rod make the rod (DNA) coil.

Fig. 4.

Condensed helical configuration corresponding to Fig. 3. a c = 1 nM, σ = 7.14×10⁻² nN/nm, E =2.982 nN/nm², G = 1.21 nN/nm², b c = 10 nM, σ=6.38×10⁻² nN/nm, E = 12.6 nN/nm², G = 5.1 nN/nm², c c = 150 nM, σ=3.61×10⁻² nN/nm, E =15.42 nN/nm², G = 6.27 nN/nm²

Fig. 5.

The amplification to Fig. 4 in resolution

The diameter of the helix in Fig. 4a is about 5 nm. This magnitude is nearly 120 times smaller than the diameter of the DNA segment in Fig. 3. Meanwhile, the total size of Fig. 4a reduces to about six times than that of Fig. 3. So, relative to the original configuration, the condensed configuration of the DNA segment seems like a cluster. The change of configuration with concentration is shown in Fig. 4a, b, and c. It can be seen that with the concentration rising, the shape of the DNA segment will change, and the spatial domain occupied by the DNA segment will increase in size. This result can be attributed to the fact that the increase of concentration makes elastic modulus and the interfacial traction simultaneously decrease. Just as implied by (5), the interfacial traction tends to reduce the curvature of a cured DNA segment. Therefore, a curved DNA segment will stretch due to the interfacial traction dropping. Meanwhile, the decrease of elastic modulus causes stretching more easily. Thus, when the concentration rises, the DNA segment will undergo a change from a compact state into a sparse state

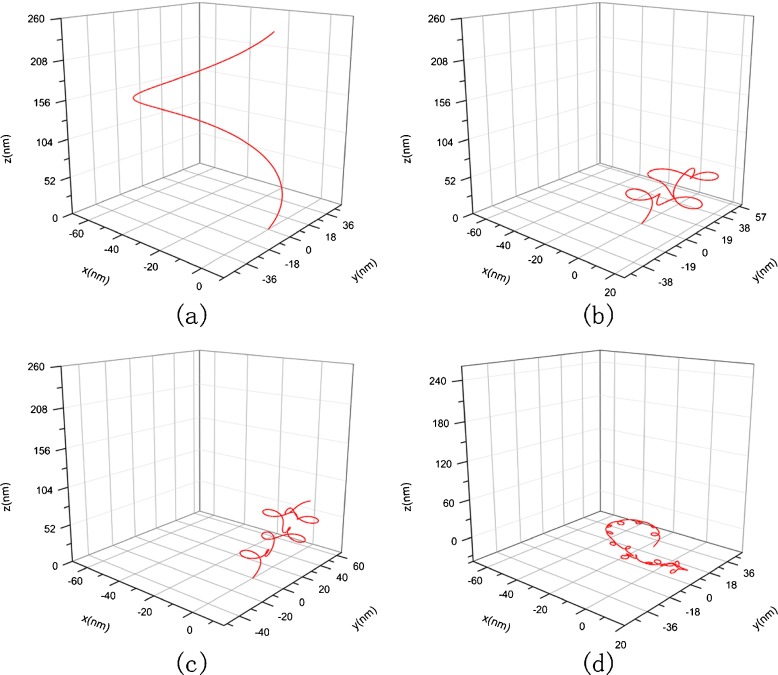
The DNA segments in Figs. 6 and 7 have the same physical properties and arc length as that in Fig. 3. Their differences consist only in their configurations. Figure 6a represents a helical line with spiral direction as opposed to Figs. 3 and 7a is an elliptical helix with κ₀=0.0125, τ₀=0.0125. The value of initial curvature and torsion are depicted in terms of the following equation [40]:

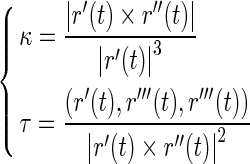28

where r(t) is the parametric equation of a spiral line and r(t),r(t),r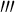(t)are the first-, second-, third-order derivative of r(t), and t represents the arc length.

Fig. 6.

Original configuration as opposed to spiral direction of Fig. 3 and its condensed helical configuration. a Original conformation with κ ₀=−0.012, τ ₀=−0.016, b κ ₀=−0.012, τ ₀=−0.016, c = 1 nM, σ=7.14×10⁻² nN/nm, E =2.982 nN/nm², G =1.21 nN/nm², c κ ₀=−0.012, τ ₀=−0.016, c = 10 nM, σ=6.38×10⁻² nN/nm, E =12.6 nN/nm², G =5.1 nN/nm², d κ ₀=−0.012, τ ₀=−0.016, c = 150 nM, σ=3.61×10⁻² nN/nm, E =15.42 nN/nm², G =6.27 nN/nm²

Fig. 7.

Original and condensed helical configuration of DNA with κ ₀=0.0125, τ ₀=0.0125. a Original conformation, b c = 1 nM, σ=7.14×10⁻² nN/nm, E = 2.982 nN/nm², G = 1.21 N/nm², c c = 10 nM, σ = 6.38 × 10⁻² nN/nm, E = 12.6 nN/nm², G =5.1 nN/nm², d c = 150 nM, σ = 3.61 × 10⁻² nN/nm, E =15.42 nN/nm², G = 6.27 nN/nm²

The changes of two DNA segments with different original configuration with the concentration of solution are shown in Figs. 6 and 7, respectively. Comparing them with Fig. 3, we can see that three DNA segments with different original configuration all twist to a spiral curve in solution with the same concentration. This interesting result show that the condensed configuration of DNA is of spiral shape, being independent of the original configuration. However, the size and spinning direction of the spiral curve are correlated with the original configuration.

Figures 8 and 9 are amplifications to Figs. 6 and 7 in resolution, respectively.

Fig. 8.

The amplification to Fig. 6 in resolution, a κ ₀ =-0.012, τ ₀= 0.016, c = 1 nM, σ= 7.14 × 10 ⁻² nN/nm, E = 2.982 nN/nm ², G = 1.21 nN/nm ², b κ ₀ =-0.012, τ ₀= 0.016, c = 10 nM, σ= 6.38 × 10 ⁻² nN/nm, E = 12.6 nN/nm ², G = 5.1 nN/nm ², c κ ₀ = -0.012,τ ₀= 0.016, c = 150 nM, σ= 3.61 × 10 ⁻² nN/nm, E = 15.42 nN/nm ², G = 6.27 nN/nm ²

Fig. 9.

The amplification to Fig. 7 in resolution, a c = 1 nM, σ = 7.14 × 10 ⁻² nN/nm, E = 2.982 nN/nm ², G = 1.21 nN/nm ², b c = 10 nM, σ = 6.38 × 10 ⁻² nN/nm, E = 12.6 nN/nm ², G = 5.1 nN/nm ², c c = 150 nM, σ = 3.61 × 10 ⁻² nN/nm, E = 15.42 nN/nm ², G = 6.27 nN/nm ²

Figures 4, 6, and 7 reveal that the equilibrium configuration of DNA has non-uniform curvature. This is caused by competition between the interfacial traction and elastic strain energy. In general, the elastic strain energy tends to make the curvature of DNA axis become uniform, but the interfacial traction causes the DNA chain bending more easily due to that it is curvature-dependent. Since one end of DNA axis is fixed and another end is free, this constraint gives rise to that deformability is different along the axis of DNA. In the free end, the DNA is easy to be bent under the interfacial traction. So it is just the difference of deformability to cause curvature being non-uniform along the axis of DNA. The non-uniform curved DNA shapes can be observed in some electron micrographs from the DNA condensation experiments (e.g., [19, 32]), but no measured data on the DNA curvature have been given up to the present. In addition, Schlick gave some examples of DNA seguments with non-uniform curved deformation [44].

Figures 4, 6, and 7 also show that no preferred direction occurs in the configuration of the rod. This is because the free end of the rod is controlled by the interfacial traction dependent on the curvature. Under the action of different interfacial traction, the position and orientation of the free end are different, so the configuration of the rod manifests no preferred direction.

Conclusions

A three-dimensional elastic rod model is established to investigate the equilibrium configuration of DNA under the action of interfacial interactions induced by the changes of ion concentration. Using this model, we account for the effect of concentration on the equilibrium configuration of DNA. Some conclusions are summarized as follows:

1. Equations (22) and (26) characterize how the ion concentrations effect the interfacial tension and elastic modulus of DNA. With the concentration rising, the interfacial traction and elastic modulus of DNA tend to decrease.

2. The interfacial tractions act as a source to spin DNA. The equilibrium configuration of DNA is completely determined by competition between the interfacial energy and elastic strain energy of DNA.

3. Due to the change of concentration, the DNA segments will undergo a series of alteration from the original configuration to the condensed configuration.

4. When the concentration changes, the spiral shape appearing in the condensed configuration of DNA is independent of the original configuration. However, the size and spinning direction of the spiral curve are correlated with the original configuration.

Finally, it should be pointed out that although what we solve is an initial value problem of (9–15), this initial value problem is equivalent to a boundary value problem with one endpoint fixed and another endpoint free, because the stress resultant F_i acting on the beginning endpoint is zero.