THz time scale structural rearrangements and binding modes in lysozyme-ligand interactions

Abstract

Predicting the conformational changes in proteins that are relevant for substrate binding is an ongoing challenge in the aim of elucidating the functional states of proteins. The motions that are induced by protein-ligand interactions are governed by the protein global modes. Our measurements indicate that the detected changes in the global backbone motion of the enzyme upon binding reflect a shift from the large-scale collective dominant mode in the unbound state towards a functional twisting deformation that assists in closing the binding cleft. Correlated motion in lysozyme has been implicated in enzyme function in previous studies, but detailed characterization of the internal fluctuations that enable the protein to explore the ensemble of conformations that ultimately foster large-scale conformational change is yet unknown. For this reason, we use THz spectroscopy to investigate the picosecond time scale binding modes and collective structural rearrangements that take place in hen egg white lysozyme (HEWL) when bound by the inhibitor (NAG) ₃. These protein thermal motions correspond to fluctuations that have a role in both selecting and sampling from the available protein intrinsic conformations that communicate function. Hence, investigation of these fast, collective modes may provide knowledge about the mechanism leading to the preferred binding process in HEWL-(NAG) ₃. Specifically, in this work we find that the picosecond time scale hydrogen-bonding rearrangements taking place in the protein hydration shell with binding modify the packing density within the hydrophobic core on a local level. These localized, intramolecular contact variations within the protein core appear to facilitate the large cooperative movements within the interfacial region separating the α- and β- domain that mediate binding. The THz time-scale fluctuations identified in the protein-ligand system may also reveal a molecular mechanism for substrate recognition.

Electronic Supplementary Material

The online version of this article (doi:10.1007/s10867-014-9341-4) contains supplementary material, which is available to authorized users.

Introduction

The conformational changes in a protein that take place upon the formation of a ligand-protein complex are one of the greatest challenges for researchers studying protein interactions. Although an immense amount of progress has been made in predicting the induced modes of proteins that undergo structural, ;collective rearrangements upon binding, it is clear that this is not a trivial task. Two distinct models have been proposed for comprehending the conformational fluctuations associated with the bound and unbound forms of proteins. One of the earliest views embraced an induced-fit model [1, 2], where the ligand itself prompts conformational changes in the protein upon binding. More recently a contrasting view has suggested that the inherent protein fluctuations may predetermine the possible set of conformations [3, 4] that can be accessed by the ligand upon binding (conformational selection). In fact, growing evidence suggests that the structural changes induced in a protein after ligand binding are constrained by the protein low frequency modes that are available even before binding has taken place [5]. In this paradigm, the intrinsic modes that are perturbed during complex formation are viewed as thermally accessible fluctuations along the protein’s inherent low frequency motions [6]. These modes are characterized by a high degree of collectivity and require the least amount of energy to reach a given conformation. It has been demonstrated computationally that the most accessible of these low frequency collective modes provides an uphill route away from the natural, lowest energy configuration into an alternate conformation that is predisposed for binding and recognizing the ligand [7].

Analytical approaches used for studying protein dynamics have successfully been employed to predict protein global modes of motion. Through this approach, it has been recognized that the detected low frequency protein modes may both facilitate functional motions and also provide a mechanism for stabilizing the protein states that arise in response to binding [8, 9]. In this work we use TeraHertz (THz) time-scale spectroscopy to experimentally analyze the structural fluctuations that take place in an enzyme after binding an inhibitor. Our aim is to address a few fundamental questions: (1) how does a small molecule modify the global dynamics of a protein on a picosecond time scale and (2) how do the detected picosecond time scale fluctuations influence both binding and molecular recognition. We present results that demonstrate that both the protein and the solvent low frequency modes play an important role in ligand binding on a fast time scale. The solvent, which has long been known to play an important role in protein–ligand binding interactions [10, 11], seems to be particularly crucial in destabilizing the barriers that separate the unliganded dominant protein mode from succeeding low energy functional motions that arise with binding.

Methods

Sample preparation

Hen egg white lysozyme (HEWL) was purchased from Sigma-Aldrich (St. Louis, MO). To remove excess salt and other particles from the sample prior to the experiment, the lysozyme sample was dissolved in water and run through a desalting spin column with a buffer consisting of 10 mM NaH ₂PO₄ and 0.01 mM EDTA at pH 7.0. The concentration of the sample was determined by UV absorbance using a standard curve derived from a series of dilutions at 280 nm. The lysozyme sample used in the experiments was initially prepared by diluting the stock protein sample to a concentration of 1 mg/ml. 20 μL ( ∼20 μg) of the diluted sample was subsequently placed on a high resistivity silicon window and excess water was removed by applying a low, steady flow of N ₂ gas over the sample droplet for approximately 10 minutes. The resulting protein film was subsequently rehydrated by equilibrating the partially dried sample in a vacuum sealed container with the vapor pressure of a saturated salt solution at 20 °C for a minimum of 5 days [12]. For the experiments discussed in this manuscript, a relative humidity (RH) of 97% was obtained from the vapor pressure of a saturated K ₂SO4 solution [13]. Previous experimental measurements on hydrated, unoriented HEWL film samples prepared from saturated salt solutions in this manner have revealed (via thermal gravimetric analysis) that samples equilibrated at 97% RH result in a hydration level of approximately 0.8 g/g. At this hydration level, the water molecules available in the hydration layer are sufficient for completing both the first and second hydration shell of the protein [14] and has been shown to relate to a biologically relevant hydration level [15] in HEWL.

The prepared film sample was placed in a sealed transmission cell consisting of two high resistivity silicon substrates and a saturated salt solution was placed at the bottom of the cell to ensure that hydration was maintained throughout the experiment. Experiments with D ₂O as the solvent were prepared in a similar manner except that the lysozyme sample was dissolved in D ₂O rather than water (see Supplementary Information Fig. S8). The tri-N-acetyl-D-glucosamine, (NAG) ₃ was also purchased from Sigma and the HEWL-(NAG) ₃ samples were prepared by adding a slight excess of the substrate relative to the diluted protein in solution. Reaction volumes of 1 mL of the HEWL-(NAG) ₃ solution were created and placed in a 4 °C refrigerator overnight. The samples were prepared for experiment the following day (as hydrated film samples) in a manner analogous to that employed for the unliganded protein. Visible inspection of the film samples after preparation found them to be transparent and without precipitate.

THz absorption spectroscopy experiments

The THz spectroscopy experiments were carried out on a Jasco FT/IR-6000 series spectrometer. The diluted, solid film samples were collected with a liquid helium cooled bolometer in the 15–250 cm ⁻¹ spectral range. The sample cell used in the experiments contained a 0.006 mm thickness polytetrafluoroethylene spacer (Specac Ltd., U.K.) and for each transmission measurement a 25 mm diameter region of the protein sample was illuminated with the THz beam to determine the absorbance. To calculate the absorption spectrum, a background spectrum was initially collected ( I₀). A subsequent measurement of the prepared sample in single beam configuration was also collected. To normalize the infrared measurement, the single beam of the sample ( I) is divided by the background signal ( I₀). The result is a percent transmittance spectrum 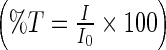. The absorbance spectrum was calculated from the transmittance spectrum by using the relationship

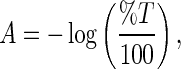1

where A denotes absorbance. Each absorbance spectrum presented in this work is an average of 5 separate spectra. Further, each individual scan consists of 16 averaged scans and the infrared data was collected with a spectral resolution of 4 cm ⁻¹. The 15–100 cm ⁻¹ THz spectra were collected with a 25 micron beam splitter while the data in the 100–250 cm ⁻¹ spectral region was collected with a 12 micron beam splitter. The temperature of the samples was varied using a SPECAC variable temperature cell. Using a combination of refrigerant and the control from the built-in temperature cell-block heaters, the temperature of the sample could be adjusted from −190 °C to 30 °C. Reversibility of the temperature response of the protein and protein-ligand samples, in terms of absorption features and intensity, were used to verify that the seal was maintained throughout the experiment.

It is important to note that the aim of these studies is to analyze the protein dynamics of HEWL in the THz region in the presence of a ligand. Experiments were performed on the ligand alone as well as in the presence of the protein (HEWL-NAG ₃ system). We found no prominent peaks in the experimental spectrum when analyzing the small molecule ligand in the absence of the protein in the ≤ 300 cm ⁻¹ region suggesting that the prominent peaks in the protein-ligand experimental absorption spectra presented in this work arise primarily from motions involving the protein or protein intermolecular motions.

We have elected to work with hydrated, unoriented protein film samples in this investigation rather than hydrated protein powders mainly due to the concern that protein powders are not straightforwardly prepared for transmission experiments in the long wavelength infrared region of the spectrum. This is particularly the case when investigating protein-ligand interactions. When comparing our data to previous THz experiments [16–18] on hydrated samples of lysozyme, it becomes apparent that there are a number of resolved absorption modes in the protein spectra presented in this investigation that are not readily apparent in other studies. It is not entirely clear why this is the case, but one explanation might arise from the types of interactions that we observe in our measurements. Recent far-infrared spectroscopy measurements on hydrated, free standing films [19] of lysozyme and other globular proteins have deduced that the absorption coefficient of biological water differs significantly from that of liquid water. In the free standing film studies distinct features in the globular protein samples could be detected in the absorption spectra. They proposed that the underlying reason is that biological water, which they construed is the only type of water incorporated into the sample preparation, has low absorption in the film samples. Hence, the protein dynamical motions (rather than water) resonate most prominently in the long wavelength infrared region. Based on the analyses that we have conducted in this investigation on HEWL film samples, as well as experiments performed on other protein film samples that we have not presented in this work, we put forward that the resolved protein absorption bands stem from the fact that the unoriented film samples consist mainly of biological water rather than free standing liquid water.

Principal component analysis and elastic network models

All calculations were performed with the ProDy software [20] and visualized with the NMWiz plug-in in VMD ( http://www.ks.uiuc.edu/Research/vmd/). The input for the Elastic Network Models, Gaussian Network Model (GNM) and Anisotropic Network Model (ANM) were the atomic coordinates in PDB format for HEWL (1HEW). In the analyses the C α atoms in the protein structure were used for evaluation. The cut-off distance for the interactions was set at 10.0 Å and 15.0 Å for GNM and ANM, respectively. The spring constant was set to 1.0. The C α atoms from the last 10 ns of the MD simulation of HEWL were used as the structural dataset for the Principal Component Analysis (PCA) calculations. The correlation between the top three PCA modes with the analogous ANM modes was found to be 0.72.

HingeProt prediction software ( http://bioinfo3d.cs.tau.ac.il/HingeProt/hingeprot.html) was also utilized to identify specific hinge-bending residues in HEWL.

Molecular dynamics (MD) simulations

The molecular dynamics (MD) simulations were carried with the Gromacs package ( www.gromacs.org) version 4.5.5 using the Gromacs-43a2 force field. The starting structure of the hen egg white lysozyme configuration was initially downloaded from the protein databank (1HEW). The HEWL simulation was initially set-up by removing the inhibitor from the coordinates. The HEWL sample consisted of 9643 water molecules and 8 Cl⁻ ions. Similarly, the HEWL-(NAG) ₃ simulation consisted of the protein with the inhibitor in place. In this case, the simulation contained 8892 water molecules and 8 Cl⁻ ions. In the simulations, the SPC model of water was used. Energy minimization of the hydrated protein system was carried out by using a steepest descent method to a convergence tolerance of 0.001 kJ mol ⁻¹. The energy minimization was followed by a MD run with constraints for 200 ps in which an isotropic force constant of 100 kJ mol ⁻¹ nm ⁻¹ was used on the protein atoms. During the restrained dynamics simulation, the temperature and pressure of the system were kept constant by weak coupling to a modified velocity rescaled Berendsen temperature [21] and pressure baths and in all cases the protein, water, small molecules, and ions have been coupled to the temperature and pressure baths separately. The final output configurations from the MD simulations with constraints were used as starting configurations for a series of full 20 ns MD simulations. The final simulations were carried out with a 1 fs time step where the bonds between the hydrogen and the other heavier atoms were restrained to their equilibrium values with the linear constraints (LINCS) algorithm [22]. Particle mesh Ewald (PME) method [23] was used to calculate the electrostatic interactions in the simulation and was used with a real-space cutoff of 1.0 nm, a fourth order B-spline interpolation and a Fourier spacing of 0.12 nm. MD simulations for the un-liganded protein in D ₂O were carried out in a similar fashion except that the water molecules in the hydration shell were replaced with heavy water.

Computational data analysis

Velocity Autocorrelation Function

The velocity autocorrelation function (VACF) of atoms from the MD simulations were computed with the extended analysis tools that are included as part of the Gromacs software package. The VACF is defined by

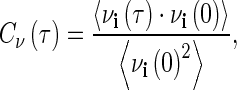2

where v refers to velocity andidenotes an atom or molecule in the simulation system. Fourier transform of the VACF (VACFFT) is used to project out the underlying frequencies of the molecular processes associated with the correlated motions detected in the simulation.

Solvent Hydrogen Bonding

In this analysis, a hydrogen bond is defined by using a geometrical criterion, where the center of mass distance is less than 3.5 Å, the r(O ∙∙∙ cH) distance is smaller than 2.6 Å, and the ∠HO ∙∙∙ O angle is smaller than 30 °.

Radius of Gyration (R _g)

The Radius of gyration (R _g) is used to describe the dimensions or compactness of a polymer structure

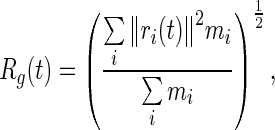3

where m_i is the mass of atomi and r_i is the position of atom ias a function of time with respect to the center of mass of the molecule.

Results

Ligand binding and protein collective modes in the THz region

20–100 cm–1 – Protein Global Modes

One direct way of tackling the problem of ligand-protein molecular recognition is to study the differences between the unbound and the bound structures of the same protein. Both experimental and computational measurements have deduced that the dynamic nature of proteins plays an important role in molecular recognition [8, 9, 24–27]. For our investigation, we use hen egg white lysozyme (HEWL), which is a model globular protein that has been used extensively to study both structural and dynamical properties in proteins. THz spectroscopy is sensitive to the lowest frequency global protein motions and has also recently been presented as a powerful method for probing collective protein motions in lysozyme [16–18, 28, 29] and other proteins as well as solvent motions in the protein hydration shell [18, 21–23]. Additionally, THz spectroscopy also affords direct information about specific protein intra- and intermolecular interactions that are characteristically tied with the chemistry of energy barrier transitions in enzymatic reactions.

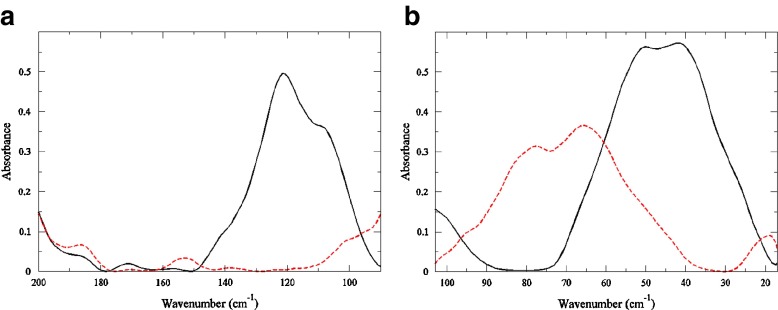
A comparison of the experimental THz spectrum of HEWL with and without the inhibitor (NAG) ₃in the ≤ 100 cm ⁻¹ (Fig. 1a), clearly demonstrates that the global protein modes are affected by the introduction of the inhibitor. It has previously been shown [30] that the protein motions detected in the ≤ 100 cm ⁻¹ region are collective in nature and are typically comprised of backbone fluctuations at a frequency above 25 cm ⁻¹. The unliganded protein sample has prominent peaks at approximately 25 cm ⁻¹ (a shoulder), 40 cm ⁻¹, and 50 cm ⁻¹. Earlier work [16, 17, 29, 31] has suggested that the principal protein modes in HEWL in the ≤ 100 cm ⁻¹ region may be connected with the function of the enzyme. In Fig. 1a, we find that the most significant change in the low frequency spectrum of the bound and unbound protein involves an overall decrease in absorption intensity and a blue-shift of the peaks above 25 cm ⁻¹ in the protein-ligand sample. There is also a small shoulder in the HEWL-(NAG) ₃ sample at 20 cm ⁻¹ that is not present in the unbound sample. Specifically, in the protein-ligand system there are at least 3 possible functional modes in the spectrum. The modes include one at 20 cm ⁻¹ and two others peaks at about 62 cm ⁻¹ and 80 cm ⁻¹. These modes are tentatively assigned to correlated non-polar side-chain fluctuations, intramolecular hydrogen-bond induced fluctuations, and an in-plane collective backbone torsion, respectively. However, it is important to state that the 20 cm ⁻¹ experimental mode lies at the edge of our spectral detection limits.

Fig. 1.

Room temperature experimental THz spectrum of HEWL at 97% RH (black solid line) and HEWL-(NAG)₃ at 97% RH (red dashed line) (a) in the 100–200 cm⁻¹ spectral region and (b) in the 20–100 cm⁻¹ spectral region

100–200 cm ⁻¹ – Protein Segmental Motions

In the frequency region extending up to ∼ 200 cm ⁻¹ (Fig. 1b) we find that the two samples differ dramatically. The HEWL sample contains a large band at 120 cm ⁻¹ that dominates the spectrum in the 100 – 200 cm ⁻¹ region, while the HEWL-(NAG) ₃ sample has no readily distinguishable bands in the same region. The 120 cm ⁻¹ peak in the HEWL spectrum is attributed to a solvent supported (out-of-plane) protein mainchain deformation involving α-helical residues. The differences in the bound and unbound protein spectrum in the THz region suggest two prominent things: (1) the addition of the ligand radically changes the collective dynamics in the protein on a picosecond time scale and (2) the solvent role in this change in dynamics may be significant.

Identifying Protein Functional Motions

Coarse-grained normal mode (NM) analyses [32] and Principal Component Analysis (PCA) [33] are two prevalent methods that have been successfully employed to identify large-scale collective motions in proteins. With the aim of further elucidating the experimental THz spectra obtained from this study, we have utilized both Elastic Network Models (ENMs) and PCAs to try to uncover the nature of the protein global modes detected experimentally. One ENM that provides insight about isotropic fluctuations in biological macromolecules is called Gaussian Network Model (GNM) [32]. In the GNM only the magnitudes of the collective protein fluctuations are revealed, while in the Anisotropic Network Model (ANM) [24] the directions of collective motions are also observed. PCA has long been known as a reliable method for the detection of functional protein modes. But more recently, ANM and GNM have also been noted for being effective in reproducing internal protein motions that compare well with anisotropic temperature factors and crystallographic B-factors obtained experimentally [34].

Intriguingly, both the PCA and ENM components of our investigation offer similar results, although it is probably worth noting that within the ENM analyses, GNM fluctuation predictions agree better with our experimental results than those computed with ANM. We begin by analyzing the two slowest modes from the comparable models. We have focused mainly on the three slowest modes in our analyses because previous investigations [7, 9, 38] have determined that such modes, particularly in the case of ligand-protein complexes, relate in some way to motions that facilitate substrate binding and release. Additionally, we believe that experimentally we are probing the dominant protein (equilibrium) motions in our measurements. The low frequency modes that we detect experimentally are likely those that are larger in amplitude than other modes and are also more likely to be easily accessed in enzyme function in the path away from one global energy minimum to another by means of structural rearrangement. In this view, the differences in the THz spectra that we observe in the bound and unbound form of lysozyme could represent a binding shift in dynamics from one dominant functional mode to another within the range of protein intrinsically favored modes.

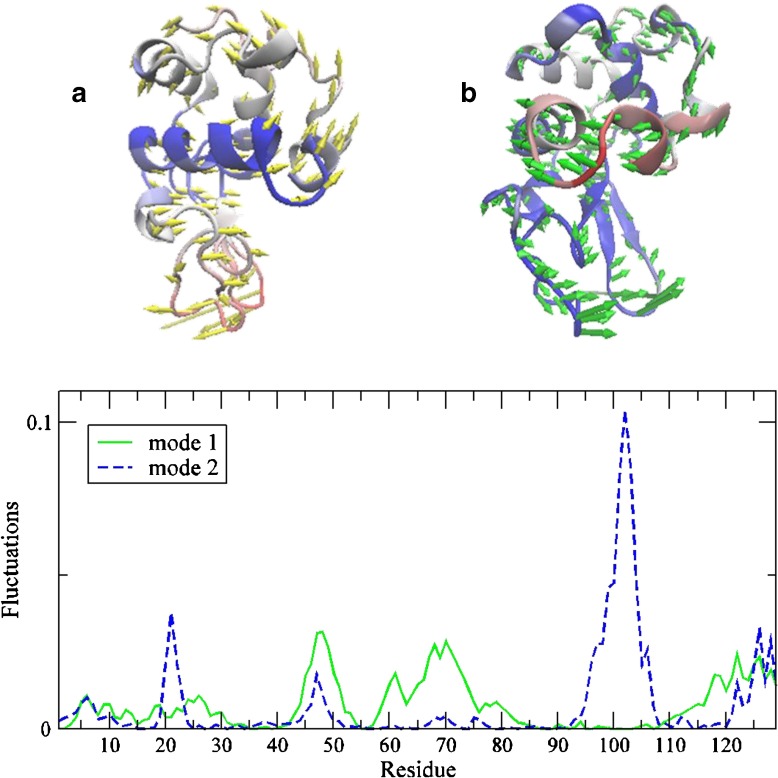
The lowest energy mode (mode 1) reflects a cooperative out-of-plane protein fluctuation that resembles the opening and closing of the protein-binding site (Fig. 2a). Our results are in line with previous computational investigations that have demonstrated that the slowest mode uncovered in both PCA and ENM is associated with the well-studied hinge-bending mode in lysozyme [9, 34]. The second slowest mode (mode 2) is linked with an in-plane cooperative twisting motion of the N-terminal domain with respect to the C-terminal domain (Fig. 2b). Referring back to the experimental THz spectra in the ≤ 100 cm ⁻¹ region (Fig. 1a), we conjecture that the detected bands are comprised primarily of collective backbone fluctuations in this region. One interpretation of the shift in the (experimental) peak frequency of the largest mode upon binding is that there is a change in the global backbone motion of the protein. From previous studies, we have uncovered that the 50 cm ⁻¹ backbone mode reflects an out-of-plane helical fluctuation related to enzyme function [30]. The prominent 80 cm ⁻¹ torsional mode that appears in the protein-inhibitor spectrum implies that a major adjustment in the dominant motion has occurred with binding. Adding further credibility to this hypothesis is the fact that the experimental data in the low frequency region roughly mirrors the slowest modes detected in the ENM results. Although a bold assumption, both MD simulation results and hydrogen-deuterium exchange experiments (see Supplementary Information Fig. S8) appear to support this supposition.

Fig. 2.

Illustration of the two dominant modes from the ANM analysis. Displacement vectors are overlaid with temperature factors depicting mobility where red reflects more mobile regions and blue more rigid regions (a) in the lowest ANM mode, ANM1 and (b) the second lowest mode ANM2. (c) Comparison of the weighted square displacements of the residues along ANM1 (solid green line) and ANM2 (blue dashed line)

It has been proposed that since ENM is capable of identifying collective protein conformational fluctuations without relying on detailed residue specific interactions that it likely reflects low frequency modes involving typically backbone motions [24]. Although still speculative at this stage, it is possible that the experimental data reflects a reconfiguration within the lowest frequency modes on a sub-nanosecond time scale that is also illustrated in ENM/PCA slowest modes. This would permit the ligand to choose the conformation that best fits its own dynamical properties among the range of conformations that are available in the unbound form [2]. In other words, the ligand changes the energy landscape of the protein upon binding.

Hinge-Bending Mode and Protein Intramolecular Interactions

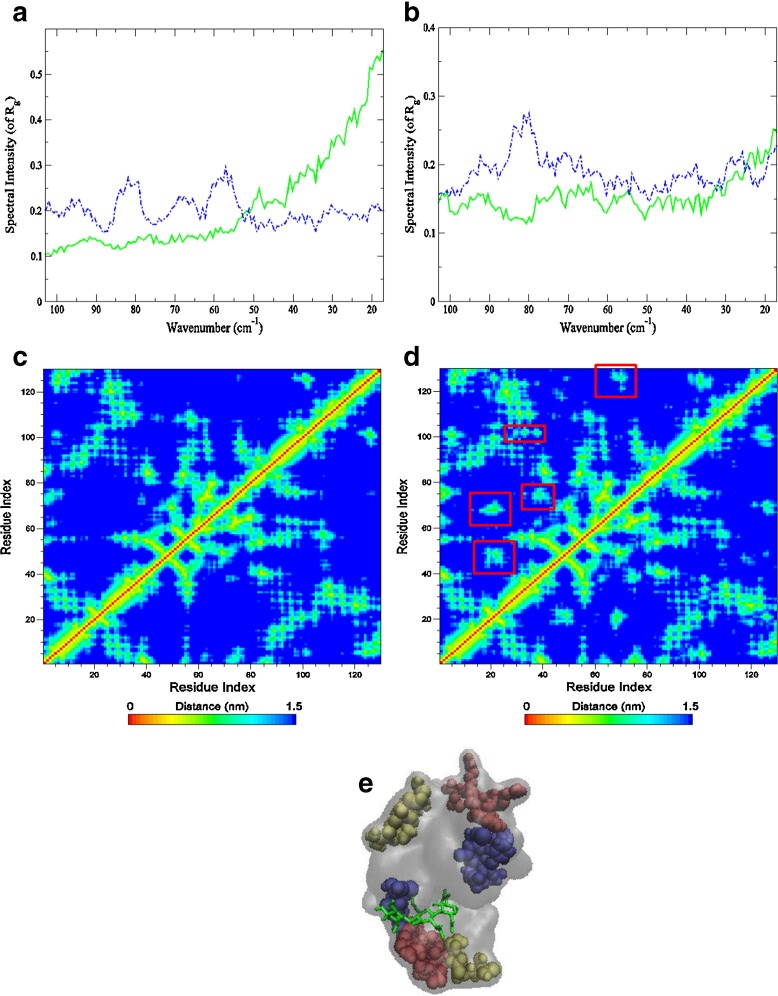
The hinge-bending mode in lysozyme has been a feature of numerous investigations focusing on enzymatic function [27, 35]. Hinge motions, in general, are rotations of a domain about a joint (hinge axis). They follow as a result of binding to another molecule, or as a result of activation of the protein itself. Further, they are typically characterized by large changes in mainchain torsional angles that occur at a localized region (the hinge). When a protein exhibits hinge motion at the region connecting two structural domains, it is usually accompanied by tertiary contact or packing modifications within the protein core. HEWL is a relatively small protein that has two structural domains. The α-domain, comprised of residues 1–35 and 85–129, consist of four α-helices and a short 3 ₁₀-helix. The β-domain includes residues 36–84 that form a triple-stranded antiparallel β-sheet, a long loop, and another 3 ₁₀-helix. In the previous section, using both ENM and PCA methods, a hinge-bending motion in HEWL was revealed. Hinge residues, or residues that are believed to play an important role in mediating the cooperative movement between the two domains, were also identified through this approach [36] (Fig. 2). Gly 102 and Phe 38 are two hinge residues that were recognized as being particularly important in modulating the hinge axis. Both residues form a line that passes through the hinge region of HEWL. Gly 102 is near the bisector of the hinge axis and Phe 38 resides in the loop connecting the α- and β-domain. To further investigate their role in HEWL dynamics on a picosecond time scale, we have turned to molecular dynamics (MD) simulations for specific details about protein interactions that may communicate changes taking place in the protein upon binding. One such parameter is the radius of gyration (R _g), which provides an indication of changes happening within the global structure of the protein. R _g of the individual residues Phe 38 and Gly 102 differ in the unbound and bound form of the confomer, which suggests that the global structure of the protein is altered (at least on a fast time scale) with binding. From the R _g alone, there is no strong indication that the size of the protein has been altered with binding. Although changes in both intramolecular distances related to packing density and the frequency of R _g suggest that a transformation has taken place. From the Fourier Transform of the autocorrelation function of R _g (Fig. 3a-b), it is apparent that the global dynamics of the protein is altered when the inhibitor is present. There is a distinct low frequency mode centered at about 80 cm ⁻¹ in the bound form of the protein that is not apparent in the unbound form. This is a consequence of the twisting of the two domains about the molecular hinge in the protein-ligand complex that would result in closure of the cleft. Accordingly, there is a localized “compactness” of the enzyme that is observed as a decrease in intramolecular distances between specific residues involved in the binding motion (Fig. 3c-e). This is likely the underlying reason the prominent mode at 62 cm ⁻¹ in the experimental HEWL-(NAG) ₃ sample in Fig. 1a that is seemingly absent in the ligand-free protein spectrum. The 62 cm ⁻¹ mode develops from (non-polar) intramolecular side-chain fluctuations that have been found previously [30] to become more prominent when protein intramolecular interactions are increased. Correspondingly, it is possible that the increase in intensity at ∼20 cm ⁻¹ in the protein-ligand sample also reflects localized protein, intramolecular interactions that accompany ligand binding. The 20 cm ⁻¹experimental mode may be associated with delocalized side-chain fluctuations and has been uncovered in numerous protein investigations [37–39].

Fig. 3.

Autocorrelation function spectrum of R _g from the MD simulation of HEWL (solid green line) and HEWL-(NAG) ₃ (dashed blue line) of residue (a) Phe 38 and (b) Gly 102. And the residue contact map displaying the mean distance of residues from the (c) HEWL and (d) HEWL-ligand MD simulation. Areas highlighted in red in the ligand-protein contact map exhibit regions in the protein structure that decrease in residue distance with binding and that differ from the unliganded protein. Contact correlations are further displayed in (e) a color-coded surface rendering of the protein complexed with the ligand depicting the distance changes that arise from binding

Protein Interactions and Potential Energy Barrier Transitions

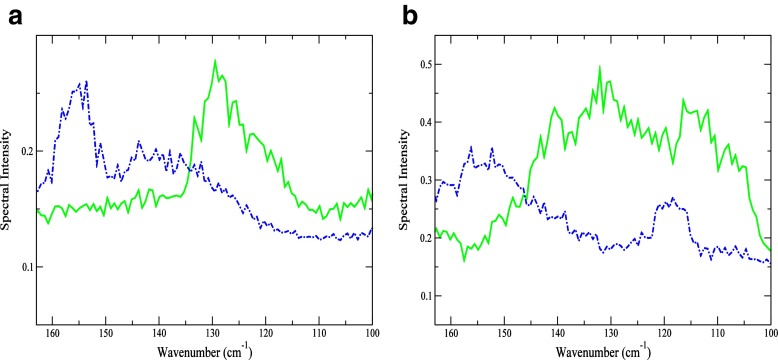
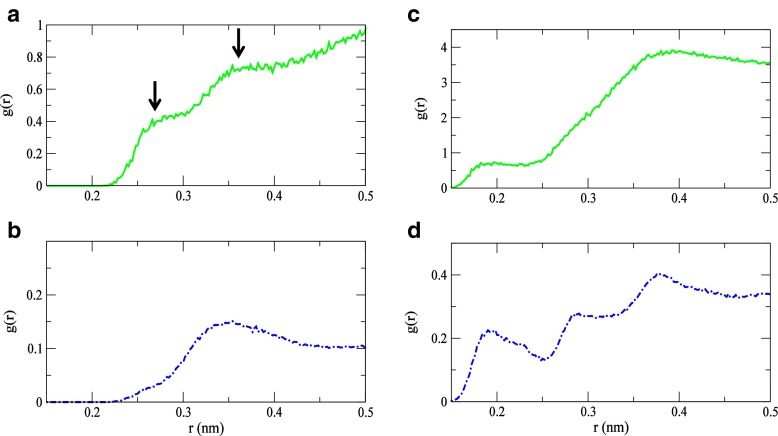
Solvent structural changes surrounding key residues appear to be important in facilitating the transition from the dominant mode of motion in the unbound state to a subsequent functional mode in the bound state. This is particularly apparent if we again consider the two residues that have already been implicated as central players in the cooperative twisting motion in the protein-inhibitor complex. In Fig. 4a comparison of the Fourier Transform of the velocity autocorrelation function (VACFFT) from the MD simulation shows that-in the 100–200 cm ⁻¹ spectral region, both Phe 38 and Gly 102 have a prominent peak at 153 cm ⁻¹ in the bound form that is not present in the unbound protein. The band emanates from a solvent-mediated stretching mode of water molecules with a less structured H-bond arrangement. In the less structured H-bond configuration, the water molecules are arranged in ring-like or open structures rather than a tetrahedral molecular geometry. The variances in water structure in HEWL with and without the ligand become more discernible through a comparison of the radial distribution function (RDF) of the two residues with that of the solvent (Fig. 5) obtained from the MD simulation. The disappearance of the RDF maxima at 2.7 Å in Phe 38 in the protein-inhibitor complex, but the continued presence of a peak at 3.6 Å suggests that apolar hydration in the sample is important, at least on a local level (Fig. 5a). The 2.7 Å peak in the HEWL Phe 38 - solvent RDF reflects carbonyl O∙∙∙ solvent O associations with water molecules in the first hydration shell of the protein. Its absence in the HEWL-(NAG) ₃RDF suggests that the solvent interaction with the residue has been altered with binding. Adding further credence to this assertation is the visible change in the Phe 38 VACFFT peak frequency in the two samples (Fig. 4a). In the unbound protein the VACFFT spectrum contains a prominent peak at 130 cm ⁻¹, while in the bound protein that peak shifts to 153 cm ⁻¹. The shift in peak frequency reveals both a modification in the residue’s tertiary contacts as well as an overall change in the dominant motion of the residue. The peak at 130 cm ⁻¹ is associated with protein intramolecular interactions, mostly involving backbone hydrogen atoms; whereas the 153 cm ⁻¹ mode indicates a solvent-induced water O∙∙∙ hydrogen phenyl ring oscillation. Fast phenyl-ring oscillations at this frequency have been described as localized relaxation processes [40], similar to β-type relaxations, in a diverse number of polymers including proteins.

Fig. 4.

VACFFT spectrum of HEWL (solid green line) and HEWL-(NAG) ₃ (dashed blue line) of hinge residues (a) Phe 38 and (b) Gly 102

Fig. 5.

The calculated solvent-Phe 38 RDF (a) in HEWL and (b) HEWL-(NAG) ₃ and the solvent-Gly 102 RDF in (c) HEWL and (d) HEWL-(NAG) ₃ from the MD simulations

Analogously, a plot of the Gly 102 - solvent RDF in Fig. 5b reveals a similar change in hydration and residue translation frequency in the 100–200 cm ⁻¹ spectral region. In this instance, rather than the disappearance of an RDF peak, we see evidence of more than one type of hydrogen bonding pattern within the solvent H-bonding network in the analysis of the solvent-residue RDF. The Gly 102 - solvent RDF in the protein-ligand complex features clearly discernible peaks at 1.9 Å and 2.8 Å in the solvent region extending to Å from the protein surface. In the unbound protein, there is only one peak in the same region at 1.9 Å that is associated with protein backbone H – water O H-bonding. The 2.8 Å peak in the ligand-protein RDF reflects solvent H-bonding with other atoms in the Gly 102 backbone, principally the carbonyl oxygen and amine nitrogen. Interestingly, the H-bonding pattern of water molecules that are also H-bonded to oxygen and nitrogen backbone atoms in Gly 102, deviate from the more structured arrangement (tetrahedral pattern) of those found in the unbound HEWL sample. This departure also appears to have a profound effect on the general motion of the molecule. In the VACFFT spectrum of Gly 102 (Fig. 4b) there are two clear peaks at 120 cm ⁻¹ and at 153 cm ⁻¹ in the 100–200 cm ⁻¹ region. Both peaks reflect the solvent interaction with the residue backbone. The 120 cm ⁻¹ mode is associated with an out-of-plane solvent induced mainchain torsional fluctuation, while the 153 cm ⁻¹mode describes an in-plane solvent Gly 102 backbone H-stretching motion that takes place with water molecules in a less structured H-bonding configuration. Gly 102 and Phe 38 are not the only residues that have a modification in dynamics due to altered interactions with solvent molecules in the hydration shell. Namely, we see a prominent peak at 153 cm ⁻¹ reflecting the changes in the type of solvent-residue backbone H-bonding in the VACFFT of residues Val 2 and Phe 3 near the N-terminal loop; Leu 25 in Helix B; and Ala 110 found in Helix D. With the exception of Gly 102, the residues connected with the 153 cm ⁻¹ mode are primarily hydrophobic and their interaction with the solvent is apolar in nature. Further, the 153 cm ⁻¹ appears to be predominantly associated with residues residing in the α-domain, hence it is a relatively localized dynamical motion that could, for instance, encourage the formation of a binding surface or perhaps aid in molecular recognition (see Supplementary Information Figs. S1–S7).

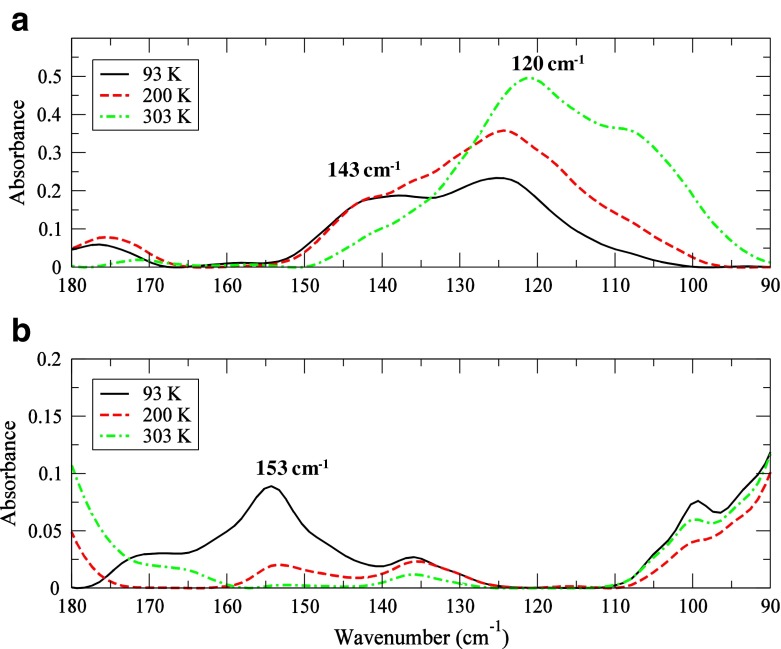
A look at the experimental THz data in the 100–200 cm ⁻¹ spectral region as a function of temperature in Fig. 6 confirms these fluctuations in the protein structure. The 153 cm ⁻¹ mode in Fig. 6b is clearly visible only at the coldest temperature probed (93 K) in the HEWL-(NAG) ₃ sample. The progression of the band intensity as a function of temperature suggests that it stems from a stretching motion. The 120 cm ⁻¹HEWL peak in Fig. 6a, which is rotational in nature, is completely absent in the HEWL-(NAG) ₃ experimental spectrum. Its absence likely means that variation in solvent interaction with the protein backbone is important for facilitating binding on a picosecond time scale. Further, the experimental HEWL spectrum possesses a stretching mode at 143 cm ⁻¹ (Fig. 6a) below the protein glass transition (T _g) that is associated with solvent molecules interacting with residues in an α-helical configuration. The solvent molecules contributing to the 143 cm ⁻¹mode comprise a more structured pattern on a picosecond time scale and their interaction with α-helical residues have been implicated as a marker in the collective helical fluctuation that leads to an opening and closing deformation with respect to the molecular hinge and consequent protein functionality [30]. The distorted H-bonded solvent conformations that we detect in the proximity of Phe 38 and Gly 102 (amongst others) have a rotational freedom that is not observed in water molecules in a more structured H-bonded arrangement. As a result, the detected 80 cm ⁻¹ mode found in these residues arises from a weakening of intramolecular interactions within the protein core as well as coupling to a localized solvent relaxation that promotes a cooperative torsion involving a small number of residues (mode 2). In summary, the solvent appears to enable intramolecular couplings of solute internal degrees of freedom, creating new relaxation pathways and perhaps generating the right conditions needed for destabilizing the potential energy barrier separating the dominant unbound protein mode from the subsequent favorable bound mode.

Fig. 6.

Experimental THz spectrum of (a) HEWL at 97% RH and (b) HEWL-(NAG) ₃ at 97% RH in the 90–180 cm ⁻¹ spectral region at 93 K (black solid line), 200 K (red dashed line), and 303 K (green dashed dotted line)

Previous computational studies focusing on liquid water dynamics in the THz regime [30] have identified an 80 cm ⁻¹ intermolecular mode in the solvent H-bond network that is mainly due to second solvation shell dynamics. Although uncovered computationally, this mode was not expected to contribute significantly to the experimental IR absorption spectrum of liquid water under normal conditions, but was conjectured to be enhanced through solute-induced modifications within the liquid water solvation shell. Additionally an 80 cm ⁻¹ mode has been reported in Raman-induced Kerr-effect spectroscopy measurements on globular proteins [39]. In this case, the 80 cm ⁻¹ mode has been attributed to fluctuations taking place within the protein secondary structure. The assessment of the 80 cm ⁻¹ mode from both studies might agree with our identification of a solvent-induced relaxation mode in HEWL at the same frequency.

Discussion

In this work we have used THz spectroscopy combined with computational methods to capture the picosecond time scale structural rearrangements in HEWL that are brought about through binding to the inhibitor (NAG) ₃. Internal protein motions take place on a wide range of time scales and it has been suggested that they are arranged in a hierarchical tier of interrelated conformations that reside within closely spaced energy levels [41, 42]. In this representation, protein motions are heterogeneous and those sharing similar energies within a particular conformation are said to exist as subsets or substates within the realm of possible protein configurations. Each of these substates reflects a local minimum on the protein free energy landscape and corresponds to a specific protein structure that is accessed via thermal fluctuation [43]. Large-scale conformational changes in proteins entail moving from one protein conformational state to another and typically occur on relatively long time scales ranging from milliseconds to seconds, whereas the fast fluctuations within or between a specific substate happen on a much shorter time scale (femtoseconds to picoseconds) and function as preliminary steps that guide the longer time scale conformational changes. For example, the fast structural fluctuations associated with the rapid interconversion within the accessible substates in an enzyme might act to direct the protein towards a transition state needed to alter the active-site environment required for subsequent longer-term function.

From our results we find that ligand binding modifies the global dynamics of lysozyme and in this case, the solvent role in defining the pathway of molecular binding is significant. The equilibrium fluctuations that are observed experimentally are intimately connected with protein function [44]. Specifically, the THz time scale protein fluctuations detected are directly related to functional relaxational mechanisms that are driven by perturbations originating from introduction of the ligand. The collective backbone mode identified at 80 cm ⁻¹ arises from protein-ligand thermal fluctuations that couple to a picosecond time scale, localized solvent relaxation mode. The modification in collective backbone dynamics reflects a shift in overall protein motion, and consequently a variation in the sampling of the conformational energy landscape [43, 45]. The deviation in dynamics that occurs with ligand binding promotes a cooperative torsion that dynamically reorganizes the interactions of residues both adjacent and distant to the active-site that bias the dynamics of the protein towards one of the alternate protein intrinsic conformations that favor ligand binding. In short, the interaction with the ligand alters the energy landscape of the protein and we speculate that through a fluctuation-driven reconfiguration within its lowest frequency modes, the protein is able to adapt to a new functional conformation. Additionally, we have observed that the fluctuations in the THz regime may play a direct role in modulating substrate-binding affinity in the enzyme binding-pocket. With the use of MD simulation, we have identified an overlap in fluctuations between (NAG) ₃ and the protein that are directly tied to ligand binding. The structural fluctuations shared between the substrate and protein operate to dynamically position the ligand into the HEWL active-site, and as a consequence also shape the environment for binding on a subnanosecond time scale. It is clear that there are still many unanswered questions regarding the role of fast conformational fluctuations in protein function, but thermal equilibrium experiments focusing on the picosecond time scale structural fluctuations in ligand-protein systems may help to illuminate the mechanism(s) in which enzymes are able to readily adapt to a new functional configuration by efficiently sampling from the range of transient structures that form the conformational energy landscape. To this end, we have utilized THz spectroscopy to characterize the subnanosecond collective, internal fluctuations in HEWL as well as to provide detailed insight about the fast, intra- and intermolecular interactions that delineate the principal changes in the protein structure that are observed upon ligand binding.