High Spatial and Temporal Resolution Dynamic Contrast-Enhanced Magnetic Resonance Angiography (CE-MRA) using Compressed Sensing with Magnitude Image Subtraction

Abstract

Purpose

We propose a compressed-sensing (CS) technique based on magnitude image subtraction for high spatial and temporal resolution dynamic contrast-enhanced MR angiography (CE-MRA).

Methods

Our technique integrates the magnitude difference image into the CS reconstruction to promote subtraction sparsity. Fully sampled Cartesian 3D CE-MRA datasets from 6 volunteers were retrospectively under-sampled and three reconstruction strategies were evaluated: k-space subtraction CS, independent CS, and magnitude subtraction CS. The techniques were compared in image quality (vessel delineation, image artifacts, and noise) and image reconstruction error. Our CS technique was further tested on 7 volunteers using a prospectively under-sampled CE-MRA sequence.

Results

Compared with k-space subtraction and independent CS, our magnitude subtraction CS provides significantly better vessel delineation and less noise at 4X acceleration, and significantly less reconstruction error at 4X and 8X (p<0.05 for all). On a 1–4 point image quality scale in vessel delineation, our technique scored 3.8±0.4 at 4X, 2.8±0.4 at 8X and 2.3±0.6 at 12X acceleration. Using our CS sequence at 12X acceleration, we were able to acquire dynamic CE-MRA with higher spatial and temporal resolution than current clinical TWIST protocol while maintaining comparable image quality (2.8±0.5 vs. 3.0±0.4, p=NS).

Conclusion

Our technique is promising for dynamic CE-MRA.

Introduction

High-resolution 3D contrast-enhanced magnetic resonance angiography (CE-MRA) has emerged as a widely accepted and powerful technique for diagnostic assessment of almost all vascular territories. Its non-invasive nature, lack of ionizing radiation and the safety of gadolinium-based contrast agents make CE-MRA an appealing alternative to digital subtraction angiography (DSA) and computed tomography angiography (CTA) (1–5). Furthermore, dynamic (time-resolved) CE-MRA provides simplified scanning logistics and improved evaluation of the hemodynamic consequences of complex vascular anatomy and pathologies while avoiding some of the limitations of traditional single-phase CE-MRA, such as incorrect contrast bolus timing and venous contamination. Dynamic CE-MRI is also used for qualitative and quantitative assessment of tissue perfusion in various oncological applications. However, due to limitations in image acquisition speed, it is difficult to achieve high temporal and spatial resolution at the same time. As a result, typical dynamic CE-MRA acquisitions have lower spatial resolution than conventional CE-MRA. The current clinical set-up in our institution allows acquisition of a chest CE-MRA with 1.1 × 0.9 × 1.2 mm³ spatial resolution within a 24s breath-hold (2,5,6). However, the 24s temporal resolution does not provide adequate speed for capturing the hemodynamics of a rapidly changing vascular contrast kinetics. Therefore, high resolution CEMRA at our institution is typically preceded by a separate dynamic CE-MRA sequence (TWIST) (6,7) using a very small contrast bolus. To obtain an apparent temporal window less than 5s, the TWIST sequence sacrifices through-plane spatial resolution (1 × 1 × 6 mm³) and uses a view-sharing technique (7,8) whereby the k-space center is updated more frequently than the periphery and in turn the under-sampled periphery is shared among neighboring frames. As a result, the temporal footprint of each image frame, which is approximately 10 s, results in temporal blurring of rapidly changing events. Therefore, it is desirable to develop a dynamic CE-MRA acquisition and image reconstruction strategy that can provide a true temporal resolution higher than TWIST, or which can acquire high spatial resolution CE-MRA in a shorter time window than is currently the case.

Recent developments in applying Compressed Sensing (CS) theory (9,10) to shorten MR image acquisitions have opened the door to new approaches for accelerating MRI (11–13). According to CS theory, an image that is sparse in a given transformation domain (i.e. number of significant coefficients in the transformation domain is much smaller than total number of coefficients) can be recovered, sometimes perfectly, using a L1 norm minimization technique based on much fewer samples than specified by the Nyquist sampling limit or even parallel imaging, as long as the samples are obtained incoherently. In MRI, the incoherent sampling can be achieved by randomly skipping k-space lines. CS theory states that the sparser the representation of the signal, the fewer samples are needed to accurately reconstruct the signal. To promote the sparsity of an MR image, different strategies have been previously reported, including wavelet transformation (11), total variation (TV) transformation (13,14), principal component analysis (PCA) (15) and other transformations (16,17). For CE-MRA applications, the images may be very sparse in the image domain even without any transformation (18).

Another strategy to promote sparsity uses subtraction techniques. In dynamic CE-MRA images acquired during a single breath-hold, the blood vessels remain in the same position but the signal intensity of the blood in the vessels changes drastically over time. Therefore, a subtraction of two or more successive temporal frames highlights the region of interest with changing signal intensity due to contrast arrival while suppressing regions without signal intensity change. As a result, subtraction enhances the inherent sparsity of CE-MRA images. This “subtraction sparsity” has previously been shown (19–21) to benefit traditional parallel imaging reconstruction by subtracting the pre-contrast mask k-space data from the contrast-enhanced k-space before any further reconstruction and processing. Trzasko et al. (22) have proposed k-space complex subtraction to improve their Cartesian Acquisition with Projection-Reconstruction like sampling (CAPR), namely Sparse-CAPR, and achieved MRA with a net acceleration of 8X. However, direct k-space complex subtraction suffers from several problems: 1. Direct complex subtraction in k-space imposes an SNR (signal to noise ratio) penalty. 2. MRA is based on blood magnitude enhancement but complex subtraction depends on phase variation and is, therefore, sensitive to phase noise. 3. K-space subtraction requires identical under-sampling patterns between two temporal frames that are being subtracted. 4. Source images are not available, only subtracted images can be produced. However it has been shown that using different sampling patterns for different temporal frames in time-resolved MRI improves CS reconstruction (23). Direct k-space complex subtraction is also feasible if a fully-sampled reference mask image is available (22,24). However, a fully sampled reference image with matching spatial resolution and coverage is generally not reliable for body CE-MRA applications due to limits in breath-holding time and mismatch between multiple breath holds.

To avoid the aforementioned issues of complex k-space subtraction while leveraging subtraction sparsity, we propose here a novel CS algorithm for dynamic CE-MRA that integrates magnitude subtraction into the reconstruction. In our algorithm, the sparsity is enforced in the magnitude-subtracted images of successive temporal frames. In a retrospective under-sampling study, we show that our CS algorithm provides improved reconstruction quality compared to complex k-space subtraction-based methods and conventional CS without reference image subtraction. We further implement our CS algorithm and optimized k-space sampling strategy in a prospectively under-sampled dynamic CE-MRA sequence and describe our initial experience of high temporal resolution (~6s) full-thoracic coverage dynamic CE-MRA with spatial resolution comparable to traditional CE-MRA that is typically acquired in approximately 20–25 s.

Theory

In a dynamic CE-MRA experiment, suppose K₁ is the under-sampled k-space data for temporal frame #n, and K₂ is the under-sampled k-space data for temporal frame #(n+1), then CS images reconstruction corresponds to the minimization of one L2-norm of the difference between estimated and measured samples (the fidelity term) and one or several L1-norm(s) of sparsity penalization(s) (the sparsity terms):

$$I_1=\mathit{argmin}{\Vert U_1\mathcal{F}(I_1)-K_1\Vert }_2^2+\lambda TV(I_1)$$ (1)

$$I_2=\mathit{argmin}{\Vert U_2\mathcal{F}(I_2)-K_2\Vert }_2^2+\lambda TV(I_2)$$ (2)

The fidelity term compares the Fourier transform ( ) of the estimated images (I₁ and I₂) to the measured samples (K₁ and K₂) using the sampling masks (U₁ and U₂). The MRA images are assumed to be piece-wise smooth, thus we use a finite-differences transform (Total Variation, TV(I₁) is the L1-norm of the discrete gradients of I₁) as the sparsifying transform. To take advantage of the k-space subtraction sparsity, one can extend the equation by adding a L1-norm minimization of the reconstructed images after complex k-space subtraction K₂ − K₁ (19,20,22). For dynamic CE-MRA applications, the complex k-space subtraction CS can be formulated as:

$$I_{kd}=\mathit{argmin}{\Vert U_{kd}\mathcal{F}(I_{kd})-(K_2-K_1)\Vert }_2^2+\lambda TV(I_{kd})+\mu {\mid I_{kd}\mid }_1$$ (3)

where I_kd is the unknown subtracted image. The L1-norm |I_kd|₁ promotes blood vessel enhancement and penalizes noise in the background while TV(I_kd) promotes images sparsity.

In current clinical practice of traditional CE-MRA, the pre-contrast mask image is often subtracted from the post-contrast image in magnitude only and the phase of the images are typically not used. To benefit from the “subtraction sparsity” without the aforementioned drawbacks of k-space subtraction, a magnitude subtraction is included in our proposed reconstruction algorithm. The L1 norm of the pixel-wise magnitude difference between the two successive temporal frames, i.e. ||I₂| − |I₁||₁, is used in the sparsity terms instead of the k-space subtracted image. In an iterative algorithm solving for both I₁ and I₂, this magnitude difference is expressed according to each argument variable to find: assuming I₂ fixed, the L1-norm of the magnitude difference is a function of the complex vector I₁: ||I₂| − |I₁||₁ = ||I₂|e^iϕ₁ − I11 with ϕ1 = angle (I1). Similarly: I2 − I11 = |I2 −|I1eiϕ21. Instead of solving each minimization separately, minima I₁ and I₂ are approached iteratively in a single algorithm as shown below:

$$(I_1,I_2)=\mathit{argmin}\left\{\begin{array}{l}{\Vert U_1\mathcal{F}(I_1)-K_1\Vert }_2^2+\lambda TV(I_1)+\mu {\mid \mid I_2\mid e^{i{\varphi }_1}-I_1\mid }_1\\ {\Vert U_2\mathcal{F}(I_2)-K_2\Vert }_2^2+\lambda TV(I_2)+\mu {\mid I_2-\mid I_1\mid e^{i{\varphi }_2}\mid }_1\end{array}\right\}$$ (4)

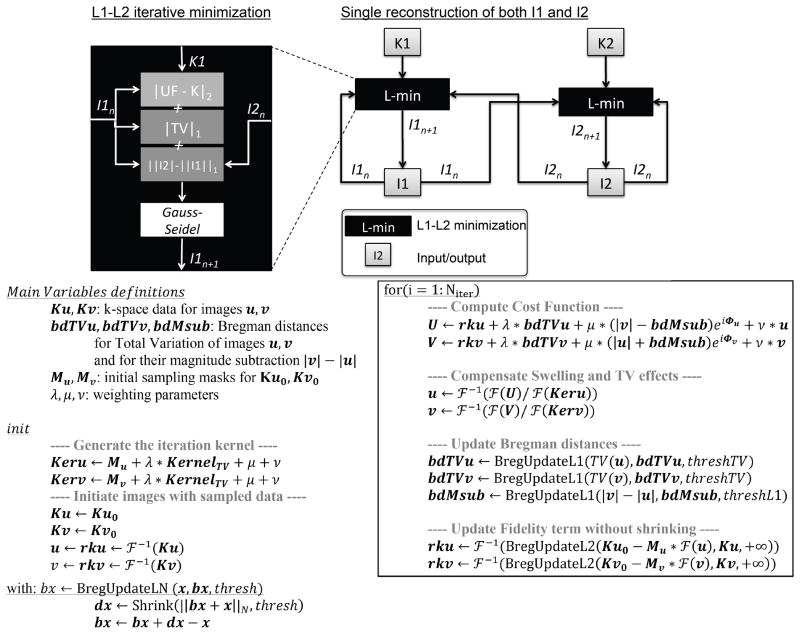
The reconstructions of the 2 volumes become now inter-dependent and both K₁ and K₂ participate in the reconstruction of each volume. The joint function minimization is performed using a single split-Bregman algorithm (25), which is fast, stable and highly parallelizable. The overall solution algorithm is shown in Figure 1. Fidelity and sparsity terms are split into Bregman distances (25). Shrinkage is applied to each distance depending on their norm and residual error is added back to the distance for error minimization (26). A Gauss-Seidel method enables the algorithm to converge towards the function minimum in a small number of iterations.

Figure 1.

Proposed Compressed Sensing algorithm minimizes cost function for both volumes from before and after contrast injection in a single, fast iterative reconstruction. A Gauss-Seidel method is employed to approach the cost function minimum. Cost function is divided into multiple Bregman distances, which are updated accordingly to their norm and a threshold (except for the fidelity term that has no shrinkage, thus the infinite threshold). Thresholds are defined as the median intensity of first Bregman distances after initialization (without thresholding).

Methods

Retrospective study

The study was approved by our institutional review board as Health Insurance Portability and Accountability Act (HIPAA) compliant and written informed consent was obtained before each MRI scan. All imaging was performed on a 1.5 T Avanto MRI system (Siemens Healthcare, Erlangen, Germany) using a combination of 4 to 6 channels with a phased array surface coil (CP mode) and a spine coil. All in vivo data were imported into Matlab (MathWorks, Natick, MA) for offline reconstruction on a dual-core 3.07 GHz station with 24GB RAM.

Imaging protocol

In vivo high-resolution thoracic CE-MRA data were acquired on 6 healthy volunteers. A Cartesian 3D spoiled gradient echo sequence was used for the MRA acquisitions. The imaging parameters include: TE/TR: 0.97/2.3ms, Cartesian matrix size: 512 × 270–294 × 64–96, resolution: 0.98 × 0.98 × 1.3–2.2 mm³, pixel bandwidth=800Hz, flip angle=25°. The sequence was performed both pre- and post-contrast injection. The pre-contrast image was used as a mask reference image. To determine the delay time between initiation of the contrast injection and the arrival of the contrast agent in the ascending aorta, a small bolus of the contrast agent (0.02mmol/kg of body weight, Multihance®) was injected before the pre-contrast mask reference image and a high temporal resolution TWIST (6,7) sequence with view sharing was used to determine the timing of the post-contrast CE-MRA acquisition. Two contrast-enhanced data sets were acquired to capture both arterial and late venous phases. The three MRA data sets (one pre- and two post-contrast) were acquired in three separate breath-holds each less than 25s. To facilitate retrospective comparisons, the acquired k-space was fully sampled with no parallel imaging but with partial Fourier factors of 8/10 along both ky and kz directions to finish the acquisition within a single breath-hold. Thus reference data are accelerated 1.56 times (~1.6X). The through slice spatial resolution (1.3–2.2 mm) was adjusted lower than our standard clinical CE-MRA sequence to allow completion of the partially full-sampled k-space acquisition within a single breath-hold while maintaining adequate spatial and anatomical coverage.

Optimization of k-space under-sampling pattern

The k-space under-sampling pattern is critical to high quality CS reconstruction. 3D Cartesian acquisitions offer various under-sampling options in the ky - kz plane: a radial-like uniform under-sampling in the ky - kz plane (22), a Poisson-Disk random sampling (11,18) or a variable density random sampling (16,27). Different under-sampling schemes were evaluated retrospectively on the fully sampled Cartesian data. Three random sampling schemes were evaluated with varying distributions in the ky - kz plane: a uniform distribution, a variable density distribution and a Poisson-disk distribution with variable density. For all sampling patterns, 10% of the samples were distributed in the center of k-space to fully acquire low frequency points. In the variable density random sampling, each ky – kz sample was defined by its polar coordinates as follow: a zero-centered Gaussian-probability density function was used to generate a random radius value, with a sigma equal to:

$$\mathit{sigma}=0.5\ast max({ky}_{\mathit{max}},{kz}_{\mathit{max}})$$ (5)

And the angle was defined from a uniform random distribution. In the Poisson-disk distribution, each sampled point generates a disk around itself where the probability of a new sample is decreased to ensure maximum spread of the sampling over the ky - kz plane. To simulate a variable density sampling, the disk radius was defined as a function of the distance to the center of k-space (kyc, kzc):

$${\mathit{Radius}}_{\mathit{PDisk}}(ky,kz)=0.25\ast \sqrt{{(ky-\mathit{kyc})}^2+{(kz-\mathit{kzc})}^2}$$ (6)

All proposed under-sampling patterns were applied retrospectively and image quality was compared on reconstructed images using our magnitude subtraction-based CS algorithm.

Algorithm optimization

In a separate pilot study, the weighting parameters in Eqs. (1) to (4) were optimized by retrospectively under-sampling the k-space and minimizing the root mean square error between CS reconstructed images and the images from original k-space. Normalization of the data prior to CS reconstruction by their maximum image intensity allows using the same weighting parameters for a large range of MRA datasets. The optimized weighting parameters were fixed for the rest of our study.

The number of iterations for the reconstruction algorithm is a balance between image quality and reconstruction time. On 3 of the 6 recruited subjects of the retrospective study, we performed the k-space subtraction CS, independent CS and the proposed magnitude subtraction CS using 1–15 iterations for acceleration rates of 4X, 8X and 12X. The optimal number of iterations was defined as when the reconstruction could not improve the results further based on root mean squared error measures and visual assessment.

Retrospective image reconstruction study

Using previously defined under-sampling pattern and number of iterations, different strategies of reconstruction were evaluated: a) reference images from original k-space data after Fourier reconstruction followed by magnitude subtraction of the images; b) separate independent CS reconstructions without subtraction sparsity (Eqs. [1&2]) using retrospectively under-sampled data followed by magnitude subtraction of the CS reconstructed images; c) k-space complex subtraction followed by CS reconstruction of a single subtracted volume (eq. [3]); d) the proposed magnitude subtraction CS reconstruction using both pre- and post-contrast data sets (eq. [4]) followed by magnitude subtraction of the CS reconstructed images. Only subtracted images were compared, as source images are not accessible with the k-space subtraction CS technique. Both 3D volumes and thin-slab maximum-intensity projection (MIP) were provided for quantitative and qualitative evaluation.

Data analysis

Root mean square errors (RMSE) were quantified between the subtraction of the reconstructed volumes and the subtraction of the reference volumes from the original k-space dataset. RMSE were quantified only on the voxels with intensity in the upper 90% of the intensity scale to exclude background noise in the RMSE calculation. Values from the different volunteers were then averaged and reported for different under-sampling rates.

The quality of the images reconstructed at rates 4X, 8X and 12X using the three different methods was graded by 2 experienced radiologists, who were blinded to the information related to subject, reconstruction method and acceleration rate. Three 4-point scales were used for the grading of three aspects of image quality (blood vessel delineation, artifacts and image noise level). The noise level and artifacts were each graded globally (1=severe, 2=moderate, 3=mild, and 4=insignificant noise/artifacts). The quality scoring of blood vessels delineation was focused on selected arteries: aorta, pulmonary arteries tree and subclavian arteries (1=non-diagnostic delineation, 2=main arteries delineated, 3= confident delineation of most arteries but smaller ones, 4=confident delineation of vessels of all sizes). Images were saved as uncompressed DICOM series and presented to the evaluators on a computer workstation side by side, with the order in which they are presented randomized. Subsequent to the scoring by both evaluators, the image volumes for which the difference between the image quality scores given by the two evaluators were greater than 1 were presented to both evaluators in an additional blinded consensus reading session and the consensus scores were included in the final scores. The purpose of the additional consensus reading session was to help avoid any unintended errors during the blinded scoring process. Image volumes for which the score difference was either 1 or no difference were considered normal and were not included in the additional consensus reading.

A one-way ANOVA analysis was performed on scoring data and log-RMSE in order to satisfy the assumptions of ANOVA. The statistical analyses were performed using IBM SPSS Statistics 20.0 software (28). A 5% level of significance was used.

Prospective study

Prospectively accelerated time-resolved high-resolution CE-MRA

A custom sequence was designed and implemented to prospectively under-sample the Cartesian matrix and consequently accelerates the acquisition to obtain a time-series of high-resolution 3D volumes throughout the course of a single contrast bolus within a single breath-hold. Our Poisson-disk random under-sampling was implemented with variable density as described in our retrospective study. In order to reduce image artifacts and signal interferences caused by abrupt changes in the sampled k-space locations, we designed a k-space trajectory as shown in Figure 2. Our k-space trajectory in the ky – kz plane starts from the center of k-space. Samples were sorted according to their radius and angles to generate a spiral-like pattern in this plane. This trajectory samples the low frequency k-space at the beginning of each temporal frame, hence reducing motion sensitivity (29), and it also limits eddy-currents induced by large phase-encoding gradients that potentially affect imaging.

Figure 2.

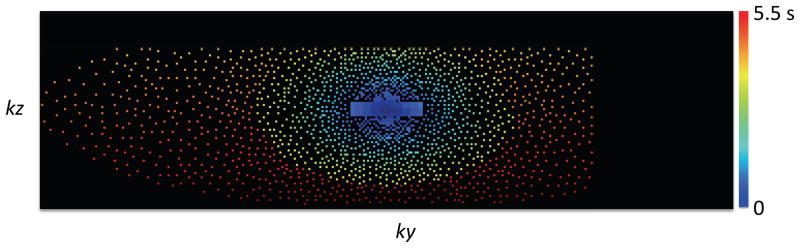
Acquisition trajectory in k-space. A Poisson-Disk random under-sampling is used with variable density and is combined with 8/10 partial Fourier in both ky and kz dimensions. The number of samples is 8% of the total number of samples of the full k-space, resulting in a net acceleration factor of 12.5X. The trajectory is depicted with samples colored according to their time of sampling from the start time of the acquisition.

Imaging protocol for prospectively under-sampled acquisition

Following our retrospective study, 7 additional volunteers were scanned using the prospectively under-sampled sequence at 1.5 T. A small timing bolus was first injected (0.005 mmol/kg of body weight) and a low resolution TWIST was used to determine the timing of the contrast agent’s arrival in ascending aorta. Subsequently, two additional contrast boluses (gadofosveset trisodium), were injected (0.01 mmol/kg for each bolus), each of which was immediately followed by either the clinical TWIST protocol (6,7) or the proposed magnitude-subtraction CS CE-MRA. The order in which TWIST or CS CE-MRA was acquired was randomized. For the CS CE-MRA acquisition, a time-series of high-resolution dynamic CE-MRA using our proposed sequence was acquired over a 35s period timed. The time gap between the two injections (TWIST and the proposed CS CE-MRA) was greater than 10min for all subjects and the total dose for each volunteer was 0.025 mmol/kg. The net acceleration rate for our prospective study was 12.5X. The first frame was defined as a mask to be subtracted from other frames for background suppression as shown in Eq. 4. The subject was asked to hold his/her breath for as long as possible and then to take shallow breath until the end of the acquisition. Imaging parameters for our sequence were as follows: TE/TR: 0.97/2.3ms, matrix size: 448 × 270–322 × 72–80, resolution: 1.12 × 1.12 × 2.0 mm³, pixel bandwidth=860Hz, flip angle=25°. The number of slices and slice thickness were adapted to match the volunteer’s thorax size while maintaining the same temporal resolution among subjects. Partial Fourier factors of 8/10 along both ky and kz were applied and net acceleration factor including the partial Fourier factors was 12.5X using described variable density Poisson-disk scheme. This enables a temporal resolution of 5.9s per frame for a total of 6 volume-frames to be acquired within a single breath-hold. The same sampling pattern was applied to all frames. CS CE-MRA data were subsequently imported in Matlab for offline CS reconstruction.

Images reconstruction and evaluation for time-series CE-MRA

Volume-frames were reconstructed pair-wise (volumes 1&2, 2&3, 3&4, etc.) using proposed magnitude-subtraction CS. The first reconstructed volume, without contrast present in the vessels, was subtracted to other volumes as a mask to suppress background tissues. Reconstructed images were visually compared to the TWIST (6,7) images at similar time points. The overall image quality (blood vessel delineation) of the 7 dynamic CE-MRA volumes and the TWIST volumes were scored and compared in the same blinded fashion as the retrospective study.

Results

Algorithm optimization

For the proposed magnitude subtraction CS reconstruction algorithm shown in Eq. 4, the minimal RMSE between CS reconstructed images and reference images corresponded to optimal weighting parameters: λ = 10⁻³ and μ = 10⁻⁵, which was subsequently used in later part of our study.

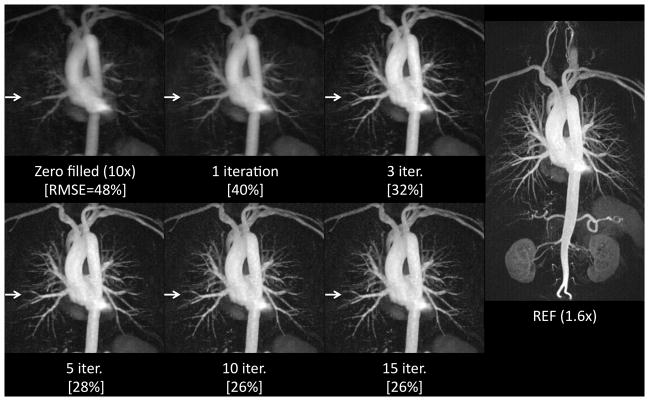
Figure 3 shows the impact of the number of iterations on image quality and main vessels contrast. The split-Bregman algorithm allows fast convergence. During our preliminary study on 3 of the 6 subjects recruited in the retrospective study, the RMSE or visually assessed image quality did not improve after 10 iterations, regardless of reconstruction technique or acceleration rate. Therefore, the number of iteration is set to 10 in this work regardless of the type of reconstruction. This fast convergence of split Bregman algorithm enables a fast reconstruction of the 2 volumes within 4–6 minutes per coil on our dual-core 3.07 GHz station.

Figure 3.

The proposed Compressed Sensing reconstruction using a Split-Bregman minimization converges within approximately 10 iterations. While the reconstructed Maximum Intensity Projection (MIP) from initial zero-filled under-sampled data is blurred (arrows), the CS reconstructed MIP recovers most of the details after only 10 iterations of our proposed algorithm. Root mean-square errors [RMSE] (shown as the percentile numbers at the bottom of each image) between reconstructed images and references images confirm the error does not improve after 10 iterations.

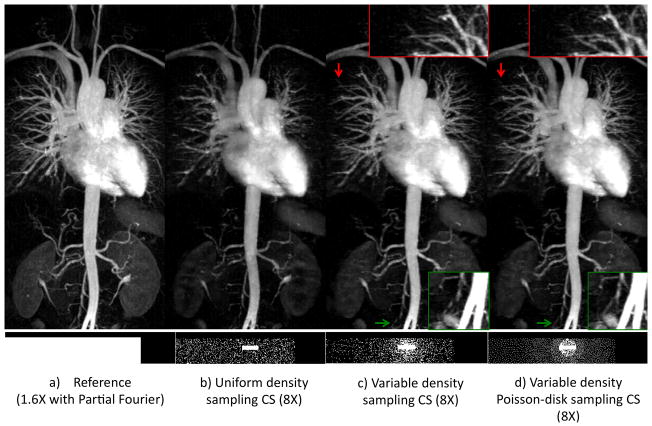
Optimized under-sampling pattern

Figure 4 shows sampling strategy is critical in the image reconstruction quality. Comparing images reconstructed with the proposed magnitude-subtraction CS algorithm from data with the same under-sampling rate, uniform random sampling provides poor image quality and limited details of small blood vessels. The variable density Poisson-disk random sampling offers reduced reconstruction error (23% RMSE compared to 34% RMSE for uniform random sampling) even at an under-sampling rate of 8X. Small blood vessels are better delineated and contrast is improved using the variable density Poisson-disk random sampling. The variable density sampling also provides improved image quality compared to uniform density sampling. In our study, the variable density Poisson-disk random sampling was used for all subsequent experiments with 10% of the acquired samples distributed in the k-space center and partial Fourier factors of 8/10 in both ky and kz.

Figure 4.

Image quality varies from different under-sampling patterns using the proposed magnitude subtraction CS technique. Maximum intensity projections (MIP) (TOP) from different ky - kz under-sampling schemes (BOTTOM) of the same acceleration rate (8X) show different levels of blood vessels details while the same CS reconstruction algorithm was used. A variable density sampling pattern in c) and d) result in considerably better image quality and contrast compared to a uniform density random under-sampling in b). Image quality is similar between the variable density sampling (slightly better at red arrows) and the Poisson-disk variable density sampling (slightly better at green arrows) but the latter is preferred for its even distribution over k-space.

Impact of under-sampling rates on image quality

The impact and limits of the acceleration using our proposed CS are shown in Figure 5. Our technique provides excellent image quality that is highly comparable with the reference at 6X. At a net acceleration rate of 8X, the image quality is comparable to the reference in regard to vessel delineation, with slight signal loss in smaller vessels. Our algorithm was able to provide generally good quality reconstruction at 10X and 12X with excellent delineation of major vessels but noticeable resolution and SNR loss, which is expected due to the high acceleration rates.

Figure 5.

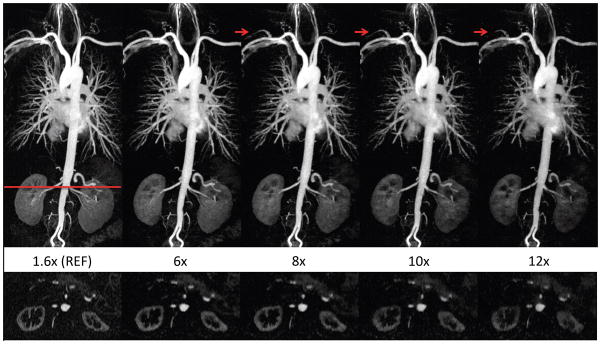
The proposed image reconstruction at acceleration rates up to 12X. Thin MIP images (TOP) reconstructed using our magnitude-subtraction CS algorithm with increasingly under-sampling rates demonstrate image quality that is comparable to the reference at rates up to 8X. At rates 10X–12X, blurring and signal loss is noted in the coronal MIP (top) and axial reformatted image (BOTTOM), which results in incomplete visualization of a few arteries (arrows).

Comparison between CS image reconstruction strategies

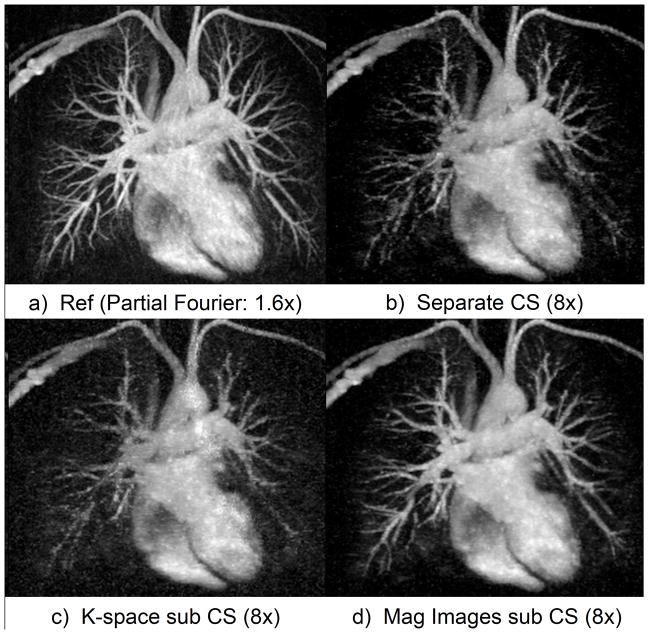
Figure 6 compares the different CS reconstruction strategies for a contrast-enhanced MRI dataset retrospectively under-sampled by 8X. The independent CS reconstruction (Fig. 6b) does not show all details in the reference image, especially small blood vessels, as it does not benefit from the “subtraction sparsity” between the successive temporal frames. This strategy results in the worst RMSE (Table 1) for all under-sampling rates. The strategy of complex k-space subtraction before CS reconstruction uses the redundancy to enforce sparsity. This indeed reduces the error compared to independent CS reconstruction, although not significantly (p=0.44). However the k-space subtraction strategy suffers loss of SNR and anatomical details (Fig. 6c). The proposed magnitude-subtraction CS reconstructs images with accurate details and sharp contrast (Fig. 6d) at under-sampling rate of 8X. The cost of under-sampling can be observed in Fig. 6.d when compared to reference image (Fig. 6a) as the smaller blood vessels are not reconstructed in their full length. But the contrast and delineation of the main circulation tree are accurately with no obvious reconstruction artifact. This accuracy is confirmed by RMSE quantification in Table 1. Magnitude-subtraction CS reconstructed images have lower RMSE than independent reconstruction CS at 4X, 8X and 12X (p<0.01 for all acceleration rates) and lower than k-space subtraction CS at 4X and 8X (p<0.05 for both acceleration rates). Quantified RMSE increases almost linearly with the under-sampling rate.

Figure 6.

Thin MIP chest CE-MRA (zoomed, same windowing level). Our proposed magnitude subtraction CS (d) reconstructs excellent image quality, close to reference (a) from highly under-sampled data while subtracted images from independent CS reconstruction (b) of each volume suffers from image degradation. Image quality is inferior using k-space subtraction CS reconstruction (c) due to high noise and loss of details.

Table 1.

Root-mean square errors (RMSE) average values and standard deviations between reconstructed images and reference images (in percent).

Rate	K-space sub. CS	Independent CS	Mag. sub. CS
4X	24.54% ± 6.72 % (*)	29.37% ± 12.95 % (*)	17.47% ± 9.12 %
8X	30.78% ± 8.64 % (*)	35.17% ± 13.17 % (*)	27.08% ± 10.46 %
12X	38.50% ± 7.84 %	43.39% ± 10.88 % (*)	37.90% ± 8.36 %

^*denotes statistical significance (p<0.05) when compared with the proposed magnitude subtraction CS technique at the same acceleration rate.

Image quality score

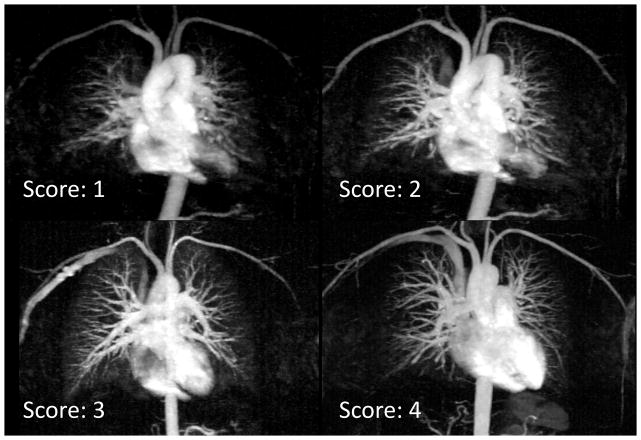
Image scores (Table 2) varied greatly between reconstruction methods and acceleration rates. Reference image (REF) scored very high in vessel delineation (3.8 ± 0.4), image artifacts (3.5 ± 0.8) and noise (3.7 ± 0.5). Under-sampling k-space significantly compromised vessel delineation and noise levels regardless of the reconstruction technique for rates of 8X and above (p<0.05). The proposed technique resulted in better vessel delineation than k-space subtraction or independent CS (p<0.05 for either comparison) at 4X acceleration. In terms of noise, the proposed technique received significantly higher image quality scores than k-space subtraction CS (p<0.05) at all rates (4X, 8X and 12X), and received higher scores than independent CS at 4X (p<0.05). The average scores of the proposed technique over 6 healthy volunteers were the highest (best) among the three techniques for all three acceleration rates, although only the score comparisons marked as (*) in Table 2 were statistically significant. To demonstrate the typical image quality in our scoring, Figure 7 shows example images that were scored 1 – 4, respectively, in vessel delineation.

Table 2.

Image quality scores (average value ± standard deviation, on 1–4 scales) in terms of vessel delineation, artifacts and noise of 3 different reconstruction methods at acceleration rates 4X, 8X and 12X using retrospectively under-sampled data from 6 healthy volunteers.

	Vessel Delineation
	K-space Sub. CS	Independent CS	Mag. Sub. CS
4X	3.1 ± 0.5 (*)	3.2 ± 0.5 (*)	3.8 ± 0.4
8X	2.5 ± 0.6	2.7 ± 0.4	2.8 ± 0.4
12X	2.0 ± 0.4	2.1 ± 0.5	2.3 ± 0.6

	Artifacts
	K-space Sub. CS	Independent CS	Mag. Sub. CS
4X	3.0 ± 0.4	3.1 ± 0.5	3.5 ± 0.6
8X	2.7 ± 0.5	2.8 ± 0.6	3.0 ± 0.6
12X	2.3 ± 0.7	2.5 ± 0.7	2.6 ± 0.7

	Noise
	K-space Sub. CS	Independent CS	Mag. Sub. CS
4X	2.5 ± 0.7 (*)	2.8 ± 0.5 (*)	3.6 ± 0.6
8X	2.0 ± 0.7 (*)	2.3 ± 0.6	2.6 ± 0.7
12X	1.7 ± 0.6 (*)	2.0 ± 0.6	2.2 ± 0.8

^*denotes statistical significance (p<0.05) when compared with the proposed magnitude subtraction CS technique at the same acceleration rate.

Figure 7.

Examples of typical images scored from 1 to 4 in blood vessel delineation. The image scored 4 has excellent delineation of major and smaller vessels. The images that were scored 3 and 2 have progressively more inferior delineation of smaller vessels. Images scored 1 are considered non-diagnostic.

Prospective time-resolved high-resolution CE-MRA

Prospective CS CE-MRA was successfully performed on 7 subjects. The under-sampling of k-space at a rate of 12.5X allowed the acquisition of one complete volume every 5.9 seconds with no view sharing. This temporal resolution was sufficient to resolve the pulmonary and systemic vascular phases of contrast enhancement during a single breath hold. The reconstruction of different temporal frames reconstructed using our proposed technique shows the contrast agent bolus dynamics, and clearly distinguishes contrast first-passage in the pulmonary and systemic circulation (Figure 8), which is typically not possible using conventional high-resolution CE-MRA sequence. Compared with the TWIST sequence that is currently used for dynamic CE-MRA, we were able to achieve 3-fold higher through-plane resolution (2mm vs. 6mm) and a significantly shorter temporal footprint (5.9s vs. ~10s), while maintaining similar spatial coverage and spatial resolution. The image quality scores of our prospective CS CE-MRA (2.8±0.5) were similar to TWIST (3.0±0.4, p=NS), albeit with thinner slices and shorter temporal footprint. Based on the data from the 7 subjects in the prospective study, the average scores of the prospective CS CE-MRA images at 12.5X were higher than the retrospective study (2.8±0.5 vs. 2.3±0.6).

Figure 8.

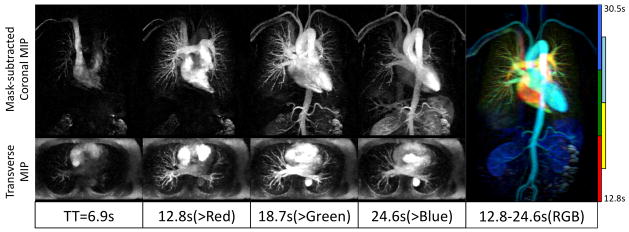
Prospectively under-sampled (12.5X) dynamic high-resolution CE-MRA using our proposed algorithm enables delineation of blood vessels and visualization of dynamic arrival of contrast bolus. A high-resolution 3D volume is acquired every 5.9s with no view sharing. Thin MIPs are reconstructed in coronal planes (after mask subtraction, 10cm thick) and transverse planes (without background suppression, 6cm thick). The color-coded MIP (Right) illustrates both high-resolution vascular structure and dynamic information. Color indicates post-injection time.

Discussion

In this study, we describe a novel image acquisition and reconstruction method for dynamic CE-MRA using a CS algorithm with integrated magnitude subtraction to promote sparsity. In our algorithm, the reconstruction of successive temporal frames is considered as a single reconstruction problem and the magnitude difference of the two successive temporal frames is used as the sparsifying transform. This approach is superior to independent CS reconstruction or direct k-space subtraction based sparsifying methods. Based on our retrospective study, the CS algorithm and k-space under-sampling pattern was optimized. We further demonstrated high quality dynamic CE-MRA images using our custom made prospectively under-sampled CE-MRA sequence with optimized k-space view order. The optimization of not only the CS image reconstruction algorithm but also the k-space under-sampling pattern and acquisition view order in our study enables us to evaluate CS image quality in a prospective fashion.

This study relies on a set of fixed weighting parameters that were optimized for a sample of similar CE-MRA datasets. The normalization of the data prior to image reconstruction enables us to use the same weighting parameters for a large number of MRA datasets, particularly for dynamic high-resolution CE-MRA as seen in our results. Our optimization study showed little RMSE variation while changing weighting parameters by up to 2 orders of magnitude (from: λ = 10⁻² and μ = 10⁻⁶ to: λ = 10⁻⁴ and μ = 10⁻⁴). Therefore, we do not anticipate adjusting these weighting parameters or using reweighting CS approaches (30) is needed for the reconstruction of any new CE-MRA datasets either using significantly smaller boluses or using different contrast-enhanced techniques such DCE-MRI perfusion.

The proposed CS reconstruction algorithm uses Total Variation (TV) as representation of images sparsity. The assumption here is that MRA images are piecewise smooth, with sharp interfaces between body tissues. Mutli-resolution analysis, such as wavelets analysis (11,31), may provide an improved representation of images sparsity but require additional computation. We preliminarily tested wavelets in our retrospective study by replacing Total Variation with 2 levels-Daubechies wavelets and observed no significant improvement of images quality (results not presented) while the computation time and memory allocation (due to data being extended to dyadic sizes) were significantly increased. Therefore we choose to maintain our use of TV as an efficient and fast sparsifying transform. However, numerous previous studies demonstrated high quality CS reconstructions using wavelet as the sparsifying transform (11,31,32) and more thorough evaluations of using wavelets in our algorithm are needed. The other aspect of the algorithm promotes sparsity using magnitude subtraction of 2 consecutively acquired volumes. The equation (4) could be re-written using complex subtraction but the consequence is an increase in noise that eventually affects image reconstruction quality.

One limitation to CS implementation in clinical practice is its computation load. CS requires usually both large amounts of computer memory to handle data and long computation time. While we designed our images reconstruction using Matlab for offline reconstruction, our algorithm is highly parallelizable for distribution over multiple CPU, GPU or FPGA. This is one of the main features of the split-Bregman approach as it avoids array reduction steps (33). Also this approach is fast, with only 10 iterations to converge in about 5 minutes per coil element without the use of parallelization. This reconstruction time opens the possibility of implementation on GPU-enabled MRI scanners to provide images within scalable time for the clinical practice. However the split-Bregman requires a significant amount of computer memory, at least (2N_b +1) times the reconstructed images matrix size, where N_b is the number of Bregman distances defined for the cost function. In our case, the reconstruction needs 2*(3) + 1=7 times the memory necessary for the output. Considering a 512×320×80 complex matrix of floats with a readout oversampling factor of 2, 12 coil elements and 6 temporal frames, we would need at least 7*15=105 GB of memory available for images reconstruction. To overcome this problem, in our algorithm, we applied a Fourier transform in the fully sampled readout dimension first and the remaining reconstruction was performed separately for each ky – kz slice. This strategy allowed us to perform the image reconstruction using less than 1GB memory per thread. This solution is only available for Cartesian sampling and may enable the proposed algorithm to be implemented easily on commercial MRI scanners. Alternative strategies to reduce memory use include techniques such as coils compression (34,35).

The retrospective part of our study focuses on the reconstruction of a set of 2 volumes: the mask pre-contrast and the contrast-enhanced volume. For a clinical dynamic CE-MRA acquisition, more than two temporal frames are typically acquired. To benefit from the temporal dimension, several k-t CS approaches (36,37) can be proposed here. We use the subtraction sparsity here as it benefits from the inherent specific sparsity of CE-MRI and has a low computation cost. A simple extension of the proposed algorithm is to consider only 2 consecutive volumes at a time, as is in our prospective study in this paper. This approach reduces the reconstruction sensitivity to motion but presents a limited use of the time-dimension within the CS reconstruction. CS would benefit from the sparsity over the whole time-dimension, in which intensity varies mostly due to contrast travel through the circulation system. However, breathing motion could hamper the subtraction sparsity at the core of the algorithm over the 35s duration of the acquisition. The background signal would need to be redefined over the time-series to reflect the mechanisms behind intensity variation. It is important to note the subtraction sparsity CS assumes only blood vessels intensity varies from one frame to the other. Thus the subtraction technique is sensitive to motion, especially complex subtraction. Magnitude subtraction becomes sensitive to motion if motion-induced intensity variations are on the same scale as the variations induced by the contrast agent travel. We did not notice motion-artifact amplification with our magnitude subtraction technique but the issue requires further investigation to be well understood. One solution to the application of the subtraction sparsity on the whole time dimension is the inclusion of 3D non-rigid registration in the reconstruction as it has been proposed recently (38).

One of the drawbacks of complex k-space subtraction strategies is that the sampled k-space locations must be sampled in the reference image as well to enable direct k-space subtraction. Although shown to be effective in aliasing artifact reduction (36,39), varying under-sampling pattern from one temporal frame to the next is however not an option for k-space subtraction based approaches. Our proposed magnitude-subtraction CS technique is fully compatible with such a varying sampling pattern. Another benefit of our technique is the ability to vary the under-sampling rate over time to match the dynamic of the observed phenomenon. This feature is highly employed in audio and video encoding to adapt the update rate to the content of the stream. Its application to MRA could allow for a higher frame rate during the first pass of the contrast agent and a slower update rate before and after. These features have not been explored in this study but they are a possible extension of proposed technique to further improve clinical practice of CS CE-MRA.

In our CS algorithm, taking advantages of the sparsity and redundant information in dimensions other than the three spatial dimensions is very important. The proposed magnitude subtraction CS algorithm focuses on the time dimension. The multiple coil elements dimension has not been considered here so as to focus our study on CS only. The extension of proposed reconstruction technique by combining it with parallel imaging can potentially improve reconstructed images quality and allow even higher acceleration rates. Both an image-based parallel imaging, like SENSE (40) or a k-space based method, like SPIRiT (41), could be considered as an enhancement of the algorithm. The Poisson-disk random distribution featured in this study has the advantage of being highly compatible with k-space based parallel imaging reconstruction (41) as the samples are spread out over the entire k-space.

The concept of time-resolved high-resolution CE-MRA has been previously proposed (4,7,22,42) with the use of view sharing. View-sharing increases the apparent temporal resolution by dividing the k-space into multiple portions: the k-space center portion that holds most of image contrast is updated more frequently and is combined with peripheral k-space that is acquired less frequently and shared between frames. As a result, the temporal footprint of each image frame is longer than the apparent temporal resolution. The longer temporal footprint results in various imaging artifacts (43) and temporal blurring and is inadequate in many applications. Therefore our strategy aims at avoiding view sharing and its associated potential problems while still allowing high temporal resolution.

Using the proposed technique, the image quality score decreased significantly from 4X to 12X. However, according to our scoring criteria in the Methods section, scores 2–4 are considered diagnostic. The difference between scores 2–4 are mainly in the delineation of smaller blood vessels. Therefore, although the average image quality scores of the proposed technique decreased from 3.8 at 4X to 2.3 at 12X, all images provided good delineation of major blood vessels. The typical 12X image provided some delineation of smaller vessels, and our typical 8X images provided excellent delineation of major vessels and most of the smaller vessels. Our examples in Fig. 7 demonstrate typical images quality scored from 1–4, respectively. We note that the average image scores of the 12.5X prospective CS CE-MRA images were higher than 12.5X images in the retrospective study. This may be because each prospective image volume had only 5.9s temporal footprint, while the retrospective image had >20s. Therefore, the magnitude subtracted image between two successive temporal frames in the prospective CS data has more spatially limited incremental changes in blood vessel intensity, which would translate to increased sparsity (and hence higher image quality) in the subtraction image when compared with the retrospective data.

Although our proposed technique is evaluated in the context of CE-MRA, it may be applicable to additional applications that benefit from acquisition of 5–6 complete 3D volumes within a single breath-hold. Our algorithm can be applied to dynamic contrast-enhanced MRI (DCE-MRI) for perfusion imaging with minimal modification of the sequence. The high spatial and temporal resolution allowed by our technique may facilitate various model-based perfusion quantification using DCE-MRI by sampling the 3D volume more frequently on the signal-time curve. Our technique could benefit perfusion imaging and perfusion quantification for cardiac applications where motion is a source of artifacts and spatial resolution and coverage are limited by the duration of the acquisition of each frame. Similarly perfusion quantification for oncology MRI could benefit from higher temporal and spatial resolution to detect small metastases (44). In addition to various contrast-enhanced imaging applications, our technique can potentially be applied to non-contrast MRA/MRI applications, such as dynamic arterial-spin labeling MRA (45), to shorten the acquisition time of these applications.

Our study has limitations. Firstly, in the prospective part of our study, we used the k-space under-sampling pattern from the retrospective study. However, the temporal changes of k-space data during the full-sampled acquisition that was used in the retrospective study will be different from a prospectively under-sampled dynamic acquisition, hence the optimal under-sampling pattern may be different. Nevertheless, we expect our retrospective study results to provide at least partially optimized under-sampling pattern for a prospective acquisition. Secondly, our technique was only evaluated on healthy volunteers. The performance of our technique on patients will be affected by the potentially radical differences in anatomic sparsity, contrast-arrival kinetics, and ability to hold breath. Therefore, further evaluation of our technique on a cohort of patients is warranted.