Assessing Thalamocortical Functional Connectivity with Granger Causality

Abstract

Assessment of network connectivity across multiple brain regions is critical to understanding the mechanisms underlying various neurological disorders. Conventional methods for assessing dynamic interactions include cross-correlation and coherence analysis. However, these methods do not reveal the direction of information flow, which is important for studying the highly directional neurological system. Granger causality (GC) analysis can characterize the directional influences between two systems. We tested GC analysis for its capability to capture directional interactions within both simulated and in-vivo neural networks. The simulated networks consisted of Hindmarsh-Rose neurons; GC analysis was used to estimate the causal influences between two model networks. Our analysis successfully detected asymmetrical interactions between these networks (p<10⁻¹⁰, t-test). Next, we characterized the relationship between the “electrical synaptic strength” in the model networks and interactions estimated by GC analysis. We demonstrated the novel application of GC to monitor interactions between thalamic and cortical neurons following ischemia induced brain injury in a rat model of cardiac arrest (CA). We observed that during the post-CA acute period the GC interactions from the thalamus to the cortex were consistently higher than those from the cortex to the thalamus (1.983±0.278 times higher, p=0.021). In addition, the dynamics of GC interactions between the thalamus and the cortex were frequency dependent. Our study demonstrated the feasibility of GC to monitor the dynamics of thalamocortical interactions after a global nervous system injury such as CA-induced ischemia, and offers preferred alternative applications in characterizing other inter-regional interactions in an injured brain.

I. Introduction

Structural and functional plasticity is an important property of the brain that confers the unique capability of adaptation to environment and injury [1]. This may be associated with a dynamic nature of synaptic strengths or the `channel capacity' for communication between neurons. From an information theoretic view, this means that the interaction dynamics within or across specific regions can be assessed through mutual functional influences. In fact, the assessment of dynamic neuronal interactions is an important tool in uncovering neural mechanisms that underlie many neuro-pathologies such as epilepsy [2], Parkinson's disease [3] and depression [4].

To understand the dynamics of functional connectivity between brain regions, simultaneous access to the activity of hundreds of neurons along with suitable analysis methods are vitally important. The former has been achieved to a large extent by recent advances in microelectrode technologies [5]. However, analytical methods to reveal complex, directed interactions among neurons or brain regions are still needed. Cross-correlation or coherence methods have been conventionally chosen for such analysis of experimental data recorded under several cognitive or clinical conditions [6–8]. Yet these methods cannot reveal the directionality of mutual influences. Furthermore, these methods restrict the analysis to either the time or the frequency domain. Granger causality (GC) analysis could be a powerful alternative to characterize the directed, asymmetric coupling in the time-frequency domain [9]. Previously, GC analysis has been used to reveal strong cortico-cortical interactions during specific motor behaviors [10] and identify the primary local generator of alpha oscillations [11]. In a study with WAG/Rij rats, GC analysis was used to successfully identify the interdependence between the frontal cortex and the thalamus during spontaneous absence seizures [12]. In addition, in our previous study, we characterized thalamocortical interactions in response to temperature changes with GC analysis [13].

Studies of the dynamic influences between two regions of the brain elucidate each region's role in specific pathologies. For example, the complex circuitry involved in the thalamocortical interactions is critical in neurological disorders such as coma [14], [15]. It is suggested that arousal from coma and subsequent recovery could be dependent on how well these network components communicate [16], [17]. Muthuswamy et al. analyzed individual signals recorded from the thalamus and the cortex, during arousal from coma [14], but did not reveal the mutual thalamocortical influences. It is documented that the thalamocortical network is inherently asymmetric, both structurally [18] and functionally [19]. Moreover, the interactions may vary with frequency bands [20], [21]. Therefore, an analysis in the combined time-frequency domain is important.

Here, we demonstrate that GC analysis can successfully characterize the asymmetric coupling between the thalamus and the cortex under the conditions of brain injury resulting from global ischemia. The estimated interactions with GC analysis were referred to as GC interactions. Of special interest here are the interactions between the ventral posterolateral (VPL) nucleus in the thalamus and the somatosensory cortex because we're interested in arousal from coma along the somatosensory pathway. VPL nucleus is part of the somatosensory pathway and previous studies have found that the VPL nucleus is abundant in neurons which are involved in the thalamocortical interactions [22]. Our objective is to 1) Demonstrate the use of GC analysis to extract directional coupling among neuronal networks, 2) Use a mathematical model, to characterize the relationship between GC interactions and synaptic coupling strengths as the two are not identical [23], and 3) Demonstrate that GC analysis can be used to monitor changes in thalamocortical function during recovery from cardiac arrest (CA) induced global ischemic injury in a rat model.

II. Methods

A. Time and Frequency Domain Formulation of Granger Causality

For two simultaneously recorded signals x and y, if the variance of the prediction error in y can be reduced by incorporating the past information from x, then it can be said that x is “Granger causal” to y [24]. Using an autoregressive model, two discrete random processes, x(t) and y(t) can be modeled either by two autoregressive processes as [9], [23],

$$\begin{array}{cc}\hfill & x\left(t\right)=\sum _{i=1}^k{a}_{x,i}x(t-i)+{\epsilon }_x\left(t\right),\mathrm{Var}\left({\epsilon }_x\right(t\left)\right)={\sigma }_x\hfill \\ \hfill & y\left(t\right)=\sum _{i=1}^k{a}_{y,i}y(t-i)+{\epsilon }_y\left(t\right),\mathrm{Var}\left({\epsilon }_y\right(t\left)\right)={\sigma }_y\hfill \end{array}$$ (1)

or by two joint processes as,

$$\begin{array}{cc}\hfill & x\left(t\right)=\sum _{i=1}^k{a}_{xx,i}x(t-i)+\sum _{i=1}^k{a}_{xy,i}y(t-i)+{\epsilon }_x^{\prime }\left(t\right),\mathrm{var}\left({\epsilon }_x^{\prime }\right(t\left)\right)={\sigma }_x^{\prime }\hfill \\ \hfill & y\left(t\right)=\sum _{i=1}^k{a}_{yx,i}x(t-i)+\sum _{i=1}^k{a}_{yy,i}y(t-i)+{\epsilon }_y^{\prime }\left(t\right),\mathrm{var}\left({\epsilon }_y^{\prime }\right(t\left)\right)={\sigma }_y^{\prime }\hfill \end{array}$$ (2)

Here, ε_x, ε_y, ${\epsilon }_x^{\prime }$, ${\epsilon }_y^{\prime }$ denote the prediction errors and σ_x, σ_y, ${\sigma }_x^{\prime }$, ${\sigma }_y^{\prime }$ denote the variance of the prediction errors. If ${\sigma }_x^{\prime }\langle {\sigma }_x$ then y is Granger causal to x; similarly, if ${\sigma }_y^{\prime }\langle {\sigma }_y$ then x is Granger causal to y. The causal influences from x to y and y to x are then defined as,

$$\begin{array}{cc}\hfill & g_{xy}=\ln \frac{{\sigma }_y}{{\sigma }_y^{\prime }}\hfill \\ \hfill & g_{yx}=\ln \frac{{\sigma }_x}{{\sigma }_x^{\prime }}\hfill \end{array}$$ (3)

where the scalar g is the measure of GC interactions in time domain.

Equations (2) can be transformed to frequency domain as, [9], [23]

$$\left(\begin{array}{c}\hfill X\left(f\right)\hfill \\ \hfill Y\left(f\right)\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill H_{xx}\left(f\right)\hfill & \hfill H_{xy}\left(f\right)\hfill \\ \hfill H_{yx}\left(f\right)\hfill & \hfill H_{yy}\left(f\right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill E_x\left(f\right)\hfill \\ \hfill E_y\left(f\right)\hfill \end{array}\right)$$ (4)

The spectral matrix S(f) can then be calculated using following equation:

$$S\left(f\right)=H\left(f\right)\Sigma H^{\ast }\left(f\right)$$ (5)

where Σ is the covariance matrix of residual error.

The driving strength from x to y and y to x in frequency domain can be defined as,

$$\begin{array}{cc}\hfill & G_{xy}\left(f\right)=-\ln (1-\frac{({\sigma }_x^{\prime }-\frac{{\sigma }_{yx}^{\prime 2}}{{\sigma }_y^{\prime }}){\mid H_{yx}\left(f\right)\mid }^2}{S_{yy}\left(f\right)})\hfill \\ \hfill & G_{yx}\left(f\right)=-\ln (1-\frac{({\sigma }_y^{\prime }-\frac{{\sigma }_{xy}^{\prime 2}}{{\sigma }_x^{\prime }}){\mid H_{xy}\left(f\right)\mid }^2}{S_{xx}\left(f\right)})\hfill \end{array}$$ (6)

where G is the measure of GC interactions in frequency domain.

B. Application of GC Analysis to Simulated Networks

In order to validate that GC analysis is capable of detecting the asymmetry of coupling, we simulated two asymmetrically coupled neural networks, each made up of N=5 Hindmarsh-Rose neurons [25]. Both networks were globally coupled within themselves (every neuron coupled with every other). The effective “local field potentials” (LFPs) were computationally generated from the action potential output of each neural network using a realistic model of the attenuation properties of the extracellular matrix [26]. The simulated uncoupled LFPs dynamics were validated by spectrally matching with LFPs recorded in-vivo. The two networks were then coupled asymmetrically in order to mimic asymmetric thalamocortical interactions. Finally, the simulated LFPs from the two networks were subjected to GC analysis to estimate the synaptic strengths. The two networks of globally coupled HR neurons can be represented by,

$$\begin{array}{cc}\hfill & {\stackrel{.}{x}}_i={\stackrel{.}{y}}_i-a{x}_i^3+b{x}_i^2-z_i+I_i+\sum _{j=1}^N{c}_{ij}{x}_j+\frac{{\alpha }^{\prime }}{N}\sum _{k=1}^N(x_k-x_k^{\prime })\hfill \\ \hfill & {\stackrel{.}{y}}_i=c-d{x}_i^2-y_i\hfill \\ \hfill & {\stackrel{.}{z}}_i=r\left(s\right(x_i-\chi )-z_i)\hfill \end{array}$$ (7)

where (x, y, z) are the variables for the first network and x' is the variable from the second network. The coefficients c_ij represent coupling within each network and α' denotes the coupling strength from the second network to the first network. When describing the second network, the coupling strength is denoted by α.

To simulate LFPs from the average membrane potentials of the HR networks, we used the method developed in [26]. This method uses the experimental observation that LFPs exhibit frequency dependent attenuation over distances. This results in the following equation for LFPs in frequency domain,

$$V_w\left(r_1\right)=\frac{I_w}{4\pi \sigma \left(R\right)}{\int }_{r_1}^{\infty }\frac{\sigma \left(R\right)+iw\epsilon \left(R\right)}{r^{\prime 2}\left(\sigma \right(r^{\prime })+iw\epsilon (r^{\prime }\left)\right)}d{r}^{\prime }$$ (8)

where the distance r' from current source was 500 μm, σ(R)=1.56, ε(R)=10⁻¹⁰, ε(r')=0.01σ(R), R=105 μm, λ=500 μm and σ(r') is defined as

$$\sigma \left(r^{\prime }\right)=\sigma \left(R\right)({\sigma }_0+(1-{\sigma }_0\left){\epsilon }^{-\frac{r^{\prime }-R}{\lambda }}\right)$$

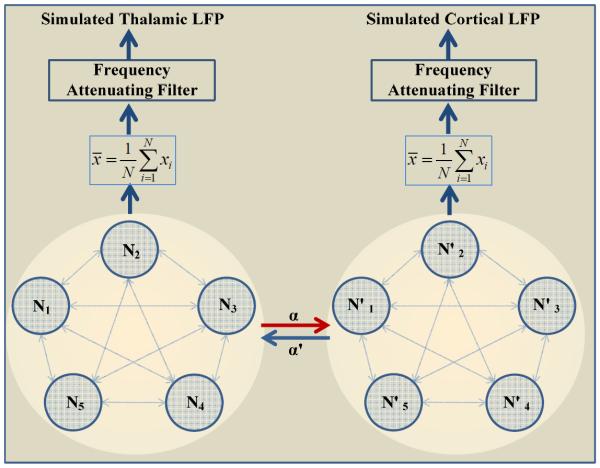
where σ₀ = 2. The inverse Fourier transform gives the LFPs in the time domain, the final output of the model. Fig. 1 shows the entire model schematically.

Fig. 1.

A schematic for simulation of thalamocortical connectivity. Spike trains from two asymmetrically coupled networks (N and N'), each with 5 globally coupled Hindmarsh-Rose neurons were subjected to a realistic model of extracellular, frequency dependent attenuation to simulate the “local field potentials” (LFPs) from each network. α and α' denotes the coupling strength between the two networks. The simulated LFPs were then subjected to GC analysis of connectivity.

The following parameters were adopted so that the simulated LFPs qualitatively matched the in-vivo recordings: a = 1, b = 3, c = 3, d = 4.75, r = 0.015, s = 4, and χ = −1.8. I = [2.5 1.8 2.5 1.8 2.5] and I'= [2.5 2.5 2.5 2.5 2.5]. All coupling strengths within a network, c_ij, were set to random values.

C. Application of GC Analysis to the Animal Model of Cardiac Arrest

GC analysis enables quantitative evaluation of dynamic interactions between two brain signals. In our experiments with arousal from coma after brain injury, we are motivated by the hypothesized interactions between thalamic and cortical structures in the brain [19], [27].

Experimental Protocol

We utilized GC analysis as a measure of thalamocortical interactions in five subjects (Male, Wistar; Charles River, Wilmington, MA). Animals were subjected to asphyxia-induced CA to induce moderate brain injury, and then resuscitated. The rat model has been well established [28], [29]. Briefly, CA was initiated with cessation of mechanical ventilation. Cardiopulmonary resuscitation (CPR) was performed by chest compression until return of spontaneous circulation (ROSC). The protocol was approved by the Institutional Animal Care and Use Committee of the Johns Hopkins University.

LFPs were recorded at 12.2 kHz using the TDT System 3 (Tucker-Davis Technologies, Alachua, FL) for the periods of CA (withdrawal of mechanical ventilation), CPR and a 60 minutes acute recovery. Two pairs of two channel tungsten microelectrodes (FHC, Bowdoin, ME) were used to simultaneously record LFPs from the right forelimb primary somatosensory cortex (S1FL) and the ventral posterolateral (VPL) nucleus in the thalamus. The recorded extracellular data were band-pass filtered (0.5–150 Hz) and the 60 Hz noise was removed using a notch filter. Signals were then down sampled to 300 Hz. Further, we examined every channel for contamination; segments with distinguishable artifacts, such as CPR artifacts, were removed.

Data Analysis

To stably estimate GC interactions and maintain necessary time resolution, we used a moving time-window to segment the LFPs. We chose 1 min as the size of time window and 20 s as the interval of moving steps, since our preliminary analysis showed that the overall results were consistent with various lengths of window and moving steps. We adopted a previously published toolbox for analysis of Granger causality [23]. The order of the autoregression model was determined using the Akaike Information Criterion (AIC) [30]. Here, the AIC dropped monotonically with increasing model order up to a value of 12. However, when the model order was higher than 10, there was just a slight decrease in AIC with the increase in the model order and no obvious change in overall results. Therefore, a model of order 10 was selected.

We previously characterized a sub-band specific change in the information entropy of EEG for five clinical bands and reported a sub-band specific dynamics of EEG entropy during recovery from CA [29], [31]. To measure the frequency-domain dynamics of GC interactions between the thalamus and the cortex for five clinical frequency bands (delta (below 4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (14–30 Hz) and gamma (30–150 Hz)), the sub-band GC interactions, SG, is defined by taking the mean of the GC interactions within a frequency band [32]; that is,

$$SG=\frac{1}{f_H-f_L+1}\sum _{f=f_L}^{f_H}G\left(f\right)$$ (9)

where f_L and f_H are the lowest and highest frequency within a specific band.

III. Results

A. Simulation Studies

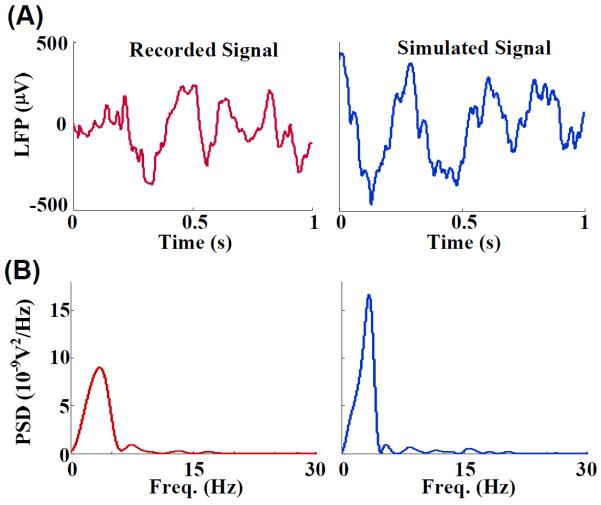
We simulated a pair of asymmetrically coupled networks, each made of five HR neurons that were all connected to each other (see Fig. 1). The coupling strength from one network to another represented the synaptic connections across the two networks. The LFPs from each of the component networks were generated using a theoretical model of extracellular properties of frequency dependent attenuation [26]. Fig. 2(A) shows example trace of LFPs recorded from the somatosensory cortex (forelimb area, S1FL) of an anesthetized rat along with a model LFPs trace simulated using the coupled model networks over a period of one second. The LFPs generated from the model had similar temporal and spectral profile to that of the recorded LFPs from the rat (Fig. 2(B)). The amplitude of the recorded and simulated signals ranged from −350 μV to 244 μV and −460 μV to 440 μV respectively. The power spectra for both signals showed a single dominant peak at 3.6 Hz and 3.4 Hz for recorded and simulated LFPs respectively.

Fig. 2.

(A) Two example traces of LFPs. Left: LFPs recorded from the somatosensory cortex of an anesthetized rat (S1FL), sampled at 300 Hz. Right: LFPs simulated using a model network of five Hindmarsh-Rose neurons (see Fig. 1) subjected to frequency dependent attenuation [26]. (B) Power spectra for the two LFP signals. The similarity between the two signals in the time domain and the frequency domain resulted from a judicious choice of parameters in the model network. The simulated signals were used to characterize the GC interactions as a measure of coupling between two coupled model networks.

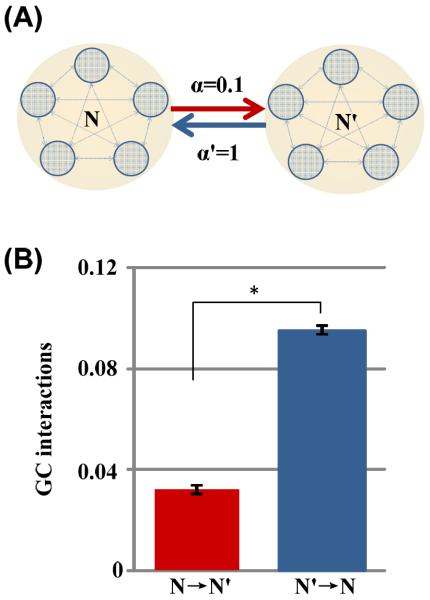
To validate that GC analysis can detect the asymmetry in coupling, we used it to estimate the causal influences between two simulated neural networks. Specifically, we created two coupled neuronal networks (N and N'), each has an output of LFPs. The “electrical synaptic strength” from network N to network N' is 0.1 and 1 for the reverse direction (Fig. 3(A)). GC analysis was applied to 100 realizations with randomized initial conditions. As can be seen in Fig. 3(B), the estimated GC interactions from N to N' is 0.0321±0.0019, which was significantly less than the GC interactions from N' to N (0.0953±0.0016; p<10⁻¹⁰, t-test). Thus, GC analysis successfully reflected the asymmetric influences between the two model networks. Also, the low variability indicated that GC analysis had high reproducibility.

Fig. 3.

(A) The schematic for the two asymmetrically coupled model networks. The “synaptic strength” from network N to N' was α=0.1, and that from N' to N was α'=1. (B) The GC interactions (Mean±SE) from N to N' (red) and that from N' to N (blue) for 100 random samples of simulated LFPs. Note that the estimated GC interactions robustly and reproducibly mimicked the asymmetry in the synaptic strengths, i.e. the GC interactions from network N to N' was significantly less than that from N' to N as set in the model (*, P<10⁻¹⁰, t test).

It should be noted that GC analysis estimates the mutual functional influence between neural networks, and not the underlying strength of synaptic connections that couples them anatomically. This means that we need a characterization of GC interactions with respect to a range of known values of coupling strengths. We implemented this using our simulated network. To establish the relationship between physiological coupling strength and estimated GC interactions, we simulated LFPs for various coupling strengths. Specifically, we set the coupling strengths from network N to N' (α) to be 0.1, and set the coupling from N' to N (α') to increase stepwise from 0 to 2.6. For each combination of coupling strengths, we generated ten seconds of LFPs for five random initial conditions. We calculated the GC interactions between the LFPs of each network for every initial condition and coupling. The changes in GC interactions with α' is shown in Fig. 4. The GC interactions from N' to N showed a linear relationship with α' before it saturated when α' was higher than 2. As expected, the GC interactions from N to N' were less sensitive to the changes in α'. When α' varied from 0.4 to 2, the linear regression fit the GC interactions from N' to N and N to N' with the slopes of 0.1192 (r²=0.9866) and 0.0087 (r²=0.4886) respectively.

Fig. 4.

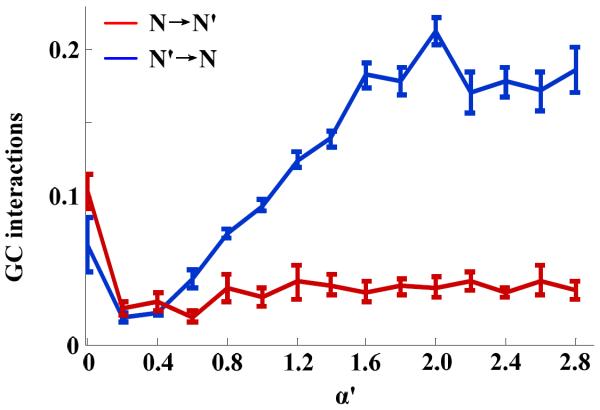
The estimated GC interactions (Mean±SE) as functions of the “synaptic strength” α' in the model coupled networks (see Fig. 1) for a fixed value of α=0.1 (Blue: GC interactions from N' to N; Red: from N to N'). As expected, the estimated GC interactions from network N to N' were less sensitive to changes in α'. While, the estimated GC interactions from N' to N plateaued with increasing α' after an initial proportional increase.

B. Animal Model of Cardiac Arrest

We obtained electrophysiological recording from rats that underwent an asphyxial CA condition. GC analysis was applied to the simultaneously recorded LFPs from the S1FL and the VPL nucleus in the thalamus to detect dynamic changes in thalamocortical interactions following HI brain injury.

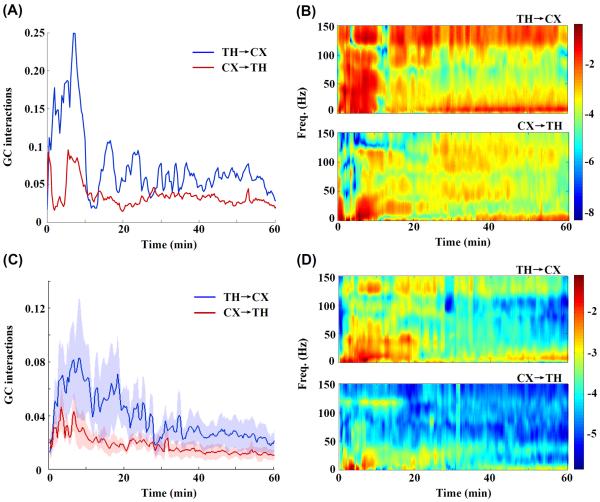
As can be seen in Fig. 5(A), the time-domain interactions in two directions (the thalamus to the cortex and the cortex to the thalamus) were quite asymmetric after the onset of asphyxia. The GC interactions from the thalamus to the cortex had larger values and fluctuations than that from the cortex to the thalamus across the periods of CA and recovery. Table I summarizes the average value of GC interactions from the onset of asphyxia to the end of recording for each rat. The averaged GC interactions from the thalamus to the cortex (0.039±0.027) were significantly higher (1.983±0.278 times higher, p=0.021) than that from the cortex to the thalamus (0.018±0.010)). Furthermore, it is worth noting that the GC interactions from the thalamus to the cortex reached the highest value immediately after resuscitation.

Fig. 5.

(A) The changes in GC interactions over time during to 1hr. after CA in an example rat. The blue curve shows the GC interactions from the thalamus to the cortex (TH→CX) and the red, from the cortex to the thalamus (CX→TH). Time t=0 indicates the onset of asphyxia. (B) Corresponding GC interactions in both directions for the same representative rat are plotted in the time-frequency domain, with the color index indicating the GC interactions. (C) For N=5 rats, the GC interactions (Mean±SE) as a function of time during and 1hr. after CA (Blue: TH→CX; Red: CX→TH) (D) Corresponding mean GC interactions in the time-frequency domain. In the panels B and D, the logarithm of GC interactions was used for plotting purposes to achieve better color contrast. Note that in both the domains, the GC interactions indicated asymmetric interactions between the thalamus and the cortex after CA along with higher GC interactions from the thalamus to the cortex. In addition, the dynamic thalamocortical interactions estimated by GC analysis varied with frequency.

TABLE I.

Mean GC Interactions In Time-domain During Acute Post-CA Period For Each Experimental Rat

	rat #1	rat #2	rat #3	rat #4	rat #5	Mean±SE	P value
TH→CX	0.0239	0.0136	0.0214	0.0598	0.0748	0.0387±0.0121	0.021*
CX→TH	0.0136	0.0087	0.0135	0.0198	0.0355	0.0182±0.0050

TH, thalamus; CX, cortex; GC interactions in TH→CX was significantly higher than CX→TH ((1.983±0.278 times higher, p=0.021,

^*P<0.05)

To explore the features of dynamic interactions in the frequency domain, we employed a frequency decomposition of GC analysis to analyze the causal interactions between the thalamus and the cortex after CA. As can be seen in Fig. 5(B), similar asymmetric interactions between the thalamus and the cortex were observed in the time-frequency domain. Also, the results in the time-frequency domain suggested that the dynamics of thalamocortical GC interactions were frequency dependent. Fig. 6 showed the different dynamics of thalamocortical GC interactions for five clinical bands (delta (below 4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (14–30 Hz) and gamma (30–150 Hz)). Note that, for the delta band, the GC interactions in both directions were approximately equal. For the theta, alpha and beta band, the GC interactions from the thalamus to the cortex showed distinct separation from that from the cortex to the thalamus and starting from 30 min after CA, the GC interactions from the thalamus to the cortex monotonically increased up to the end of recording. In the gamma band, GC interactions diverged at the beginning, and slowly converged during the recovery period.

Fig. 6.

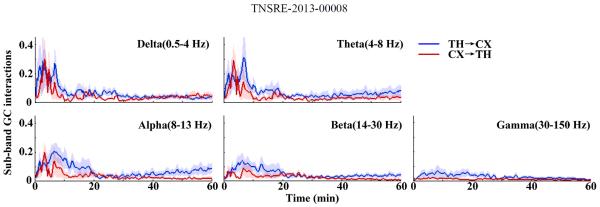
Sub-band GC interactions from the thalamus to the cortex (TH→CX; Blue) and the cortex to the thalamus (CX→TH; Red) of rats (N=5) in one hour after CA for five clinical bands: delta (below 4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (14–30 Hz) and gamma (30–150 Hz). The mean values (lines) and standard errors (shaded areas) were calculated. Note that the dynamic feature of GC interactions between the thalamus and the cortex varied with the frequency bands.

IV. Discussion

Using two simulated, asymmetrically coupled neural networks, we have verified the ability of GC analysis to extract directed coupling strength between neural populations, and characterized the relationship between physiological coupling strength and the GC interactions. Furthermore, we presented the application of GC analysis to the characterization of dynamic neuronal interactions in the context of HI brain injury. For the first time, we demonstrated GC analysis as a viable metric to monitor the dynamics of thalamocortical function after a global ischemic nervous system injury. GC analysis tracked dynamic thalamocortical interactions during CA-induced HI and during the recovery period. GC analysis reflected the asymmetry of thalamocortical interactions in both the time and time-frequency domain. Therefore, GC analysis on thalamocortical interactions provided additional information about not only the strength but also the direction of influences, which could not have been revealed by the conventional methods, such as cross-correlation and coherence methods.

This technique could be widely applicable, for example, in monitoring pain circuits after spinal cord injury [33] or the information flow between the periphery and the central nervous system before and after injury. It should be noted that GC analysis does not in itself characterize causality entirely. It merely tracks the information flow between the subsystems. Implicit assumptions of GC analysis include, most importantly that the underlying dynamics between the two subsystems are taking place on similar time-scales. GC analysis may not be a good choice to characterize information flow between a discrete stochastic subsystems coupled with a continuous oscillatory one. For example, if the underlying system can be modeled as an n-dimensional kicked oscillator, GC analysis may not be able to characterize the information flow. The thalamocortical system of spikes may indeed be such a system and therefore we have focused only on the LFPs from both regions. The two LFP signals are in fact oscillatory and hence well-suited for GC analysis as a measure of interactions.

On the other hand, when applied to a biological network such as neural networks, it should be noted that a functional causal connectivity metric such as GC interactions does not reveal anatomical connections, nor does it directly measure synaptic strength. It provides an overall assessment of dynamic influences of one subsystem over the other, based on an information theoretic framework. In this context, it is important to note that GC analysis cannot distinguish between two coupled subsystems that drive each other from two subsystems coupled to a third common driver system. The characterization of GC interactions, with respect to a range of known values of coupling strength in our study, showed that GC interactions has a linear relationship with coupling strength within certain ranges and saturated for large values of coupling strength. Saturation in GC interactions as a function of synaptic coupling strength was also found in Cadotte et al.'s study with spike train data [34]. As in many nonlinear coupled systems, for a given set of within-network parameters, the two coupled systems reach a point of mutual synchrony (high-correlation) for a high coupling strength. Any further increase in the coupling strength does not contribute further to the mutual exchange of information between the two networks. This might be the reason that GC interactions saturated for higher coupling strengths. In addition, it is worth pointing out that unlike ideal simulated networks, invasive recordings of neural signals inevitably contain different levels of noise, which might affect GC interactions between neural networks. Our future study on GC interactions between simulated networks will include the test of noise-robustness of GC analysis and parametric ranges for different neurons in the participant networks.

Anatomically, the projections from the VPL mainly terminate in layer IV of the cortex, while the feedback to the thalamus is primarily from layer VI [35–37]. Therefore, recordings in different layers of the cortex might lead to variability in estimation of functional interactions between the thalamus and the cortex. In our experiments, the depth of cortical recordings was between layers IV to VI. To better assess the dynamics of interactions in the thalamocortical circuit, cortical signals from the same layer need to be recorded in each experiment. During the experiments, in order to minimize variability between animals, we manually inspected the response latencies upon peripheral tactile stimulation with soft touch.

We have previously developed EEG based biomarkers of coma-arousal after CA, which are capable of quantifying the post-CA evolution of EEG, associated with arousal and neurological outcomes [31], [38–41]. To better understand the relationship between the estimated GC interactions and the arousal level of the brain, future work will focus on comparing and contrasting the recovery of EEG as measured by a qEEG metric such as entropy measures developed by us with the dynamics of GC interactions. Our previous study by analyzing thalamic and cortical activity separately instead of using interactions analysis suggested that the thalamic recovery precedes the cortical recovery during arousal following CA [27]. In this study, we observed that the averaged GC interactions from the thalamus to the cortex were significantly higher than that from the cortex to the thalamus. Those findings might indicate the leading role of the thalamus in arousal from coma. In addition, in our preliminary experiments of this study, we observed that GC interactions from the thalamus to the cortex increased temporarily during immediate recovery phase, which is similar to our previous findings by a modified directed transfer function method [42]. More experiments are needed to gain mechanistic insights into the dynamics of thalamocortical interactions after HI.

Our special interest in understanding thalamocortical dynamical coupling comes from a hypothesis that the thalamus might play a leading role in arousal from coma after CA. According to Poulet et al.'s study, the thalamus plays a key role in controlling cortical states [43]. Previous studies have shown that the vulnerability to HI injury in the cortical and sub-cortical structures is not uniform [14], [44–46]. Furthermore, thalamic nuclei, such as intra-laminar and midline nuclei of the thalamus have long been regarded to affect cortical functioning and participate in the process of arousal [17]. Therefore we expect a measure such as GC analysis to be able to monitor the changes in thalamocortical function in an acute period after a global injury such as CA induced ischemia.

Biographies

Cheng Chen (M'11) was born in Shaoyang, China, on June 19^th, 1989. She received the B.S. degree in biomedical engineering from Zhejiang University, Hangzhou, China, in 2011, the M. S. degree in biomedical engineering from the Johns Hopkins University, Baltimore, MD, in 2013.

From 2011 to 2013, she was a Research Assistant with the Neuroengineering & Biomedical Instrumentation Laboratory, focusing on analyzing electrophysiological responses to hypoxic-ischemic brain injury and therapeutic hypothermia.

Anil Maybhate (M'07) received his Ph.D. in Physics from the University of Pune, India, in 2003. He is currently a lecturer in the Whiting School of Engineering, Johns Hopkins University at Baltimore, MD.

Previously, he has been a postdoctoral fellow at the Weill medical College of Cornell University and later at the Johns Hopkins University's School of Medicine. His research interests include translational biomedical research including modeling of neuronal systems and their applications to neurophysiology. His expertise is in the nonlinear methods of modeling and signal processing for monitoring progress of disease in animal models as well as clinical research.

David Israel was born in Waterbury, Connecticut in 1994. He is in his third year of study at Johns Hopkins University pursuing a B.S. degree in biomedical engineering, applied mathematics and statistics, and economics.

From 2010 to 2011, he worked at the Laboratory for Computational Cognitive Neuroscience at Georgetown University Medical Center in Washington, D.C. There he studied computational models of the visual system, and developed cognitive experiments with wireless EEG integration. From 2011 to 2012 he worked at the Neuroengineering and Biomedical Instrumentation Laboratory at Johns Hopkins University under Dr. Maybhate, researching nonlinear dynamical models of neurons.

Mr. Israel is a student member of the Biomedical Engineering Society. He is the recipient of a travel fellowship for his paper published at the 2012 IEEE Engineering in Medicine and Biology Conference.

Nitish V. Thakor (S'78–M'81–SM'89–F'97) is a Professor of Biomedical Engineering, Electrical and Computer Engineering, and Neurology at Johns Hopkins University, Baltimore, MD, and directs the Laboratory for Neuroengineering. He has been appointed as the Provost Professor, National University of Singapore, and now leads the SiNAPSE Institute, focused on neurotechnology research and development.

His technical expertise is in the areas of neural diagnostic instrumentation, neural microsystem, neural signal processing, optical imaging of the nervous system, rehabilitation, neural control of prosthesis and brain machine interface. He is the Director of a Neuroengineering Training program funded by the National Institute of Health. He has authored 250 refereed journal papers, generated 11 patents, cofounded four companies, and carries out research funded mainly by the NIH, NSF and DARPA. He was the Editor-in-Chief of IEEE Transactions On Neural And Rehabilitation Engineering (2005–2011) and is currently the Editor-in-Chief of Medical and Biological Engineering and Computing journal.

Dr. Thakor is a recipient of a Research Career Development Award from the National Institutes of Health and a Presidential Young Investigator Award from the National Science Foundation. He is a Fellow of IEEE, the American Institute of Medical and Biological Engineering, International Federation of Medical and Biological Engineering, and Founding Fellow of the Biomedical Engineering Society, Technical Achievement Award from IEEE and Distinguished Alumnus award from Indian Institute of Technology, Bombay and University of Wisconsin, Madison.

Xiaofeng JIA received the M. D. degree in clinical medicine from Zhejiang Medical University, Zhejiang, China, in 1994, the M.S. degree in surgery from Shanghai Medical University, China in 1997 and the Ph.D. degree in Surgery (orthopedics) from Fudan University, Shanghai, in 2003.

Dr. Jia has been a Faculty in the Department of Biomedical Engineering, Physical Medicine and Rehabilitation, Johns Hopkins University School of Medicine, Baltimore, MD since 2007. He completed his surgery residency in the Huashan Hospital and Orthopedic Surgery fellowship in the Shanghai 6th People's Hospital, Shanghai. Later, he was an Attending Orthopedic Surgeon in Shanghai 6th People's Hospital and Zhongshan Hospital, Shanghai. His current research interests include novel application of neuro-electrophysiology for detection and restoration of peripheral nerve and spinal cord injury, therapeutic hypothermia of brain and spinal cord after global ischemia injury.

Dr. JIA is a member of the American Academy of Orthopaedic Surgeons, American Association for Hand Surgery, Society of Critical Care Medicine, American Heart Association. He is a recipient of the 2008 Annual Research Awards from American Association for Hand Surgery, the 2009 Top 20 Scientific Exhibits and the 2008 Finalist of Best Overall Poster Award of American Academy of Orthopaedic Surgeons, the Cardiopulmonary, Perioperative and Critical Care Junior Investigator Travel Award from American Heart Association, the Finalist of Research Citation Award from Society of Critical Care Medicine.