Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 10;4:5234. doi: 10.1038/srep05234

Single Shot Coherence Properties of the Free-Electron Laser SACLA in the Hard X-ray Regime

Felix Lehmkühler 1,2,a, Christian Gutt 1,2,6, Birgit Fischer 1,2,7, Martin A Schroer 1,2, Marcin Sikorski 3, Sanghoon Song 3, Wojciech Roseker 1, James Glownia 3, Mathieu Chollet 3, Silke Nelson 3, Kensuke Tono 4, Tetsuo Katayama 4, Makina Yabashi 5, Tetsuya Ishikawa 5, Aymeric Robert 4, Gerhard Grübel 1,2
PMCID: PMC4050387  PMID: 24913261

Abstract

We measured the coherence properties of the free-electron laser SACLA on a single shot basis at an X-ray energy of 8 keV. By analysing small-angle X-ray scattering speckle patterns from colloidal dispersions we found a degree of transverse coherence of βt = 0.79 ± 0.09. Taking detector properties into account, we developed a simulation model in oder to determine the degree of coherence from intensity histograms. Finally we calculated a coherence time of τc = 0.1 fs and a pulse duration of 5.2 fs which corresponds with previous predictions.

The rise of X-ray free electron lasers (XFEL) allows the study of physical and chemical properties that could not be accessed experimentally before. In particular, the ultrashort pulse duration on the order of 10 fs at hard x-ray wavelengths of around 1.5 Å offers the possibility to access physical and chemical processes on molecular time and length scales by single shot x-ray diffraction patterns.

Many of such studies rely on the coherence properties of the X-ray beam. This includes, e.g., the study of dynamic properties via X-ray photon correlation spectroscopy1,2,3, imaging single particles and biological specimens by coherent diffractive imaging4,5, cross correlation techniques to reveal a single particle's shape6 and orientational order in liquids and glasses7, or the imaging of ultrafast magnetization processes8. XFEL sources such as the Linac Coherent Light Source (LCLS) at SLAC9 and SACLA at SPring-810 are based on self-amplified spontaneous emission (SASE)11,12. The SASE process originates from random fluctuation in the electron beam. Therefore, the coherence properties of such an X-ray source differ from optical lasers. In particular, every single X-ray shot is expected to show certain random features because of the stochastic nature of the SASE process. This was observed recently in experiments at the LCLS and in simulations on the longitudinal coherence properties, where a significant shot-to-shot variation has been observed13. In contrast, a SASE beam is expected to show a superior transverse coherence12.

Recently, several studies have been performed on the different FEL sources' coherence properties. In the soft x-ray regime, pinhole and double slit experiments have been performed at FLASH14,15 and LCLS16 in order to study the coherence lengths and times. In further studies, interferometry methods have been used17,18 to determine longitudinal and transverse coherence lengths. In contrast, coherence properties in the range of hard X-ray have been examined by analysing coherent diffraction patterns, so-called speckle patterns, from disordered samples on a shot-to-shot basis13,19. A similar study has been performed at FLASH20. In this study, the degree of coherence is obtained from the speckle contrast. By analysing single shot diffraction patterns from colloidal particles in small angle X-ray scattering (SAXS) geometry, the degree of transverse coherence was found to be almost 113,19. Furthermore, the longitudinal coherence was determined by wide angle scattering (WAXS) experiments on amorphous metals and it also appeared to be very sensitive on the SASE fluctuations3,19.

Here we present a study of the coherence properties of the free-electron laser SACLA in the hard X-ray regime. In contrast to the LCLS, three bunch compressors and short-period in-vacuum undulators are used at SACLA that result in a compact design compared to LCLS10. Furthermore, initial experiments reported pulse durations well below 10 fs21. The question arises if and how this design combined with the short pulse duration have an impact on the coherence properties of the single x-ray pulses. We calculated the degree of coherence for single shots from speckle patterns of colloidal particles at a hard X-ray energy of 8 keV. The number of transverse modes was determined by the need of correcting for the energy bandwidth of the x-ray pulses. The results are supported by simulations of the impact of the charge sharing process of CCD detectors on intensity histograms of speckle patterns. Finally, we estimate the pulse duration from the intensity fluctuations of the beam and compare it to the expected values in the order of 5 fs.

Results

A typical speckle pattern from an amorphous sample together with the azimuthally averaged intensity I(q) is shown in Fig. 1. The experimental details are given in the Methods section. The size of individual speckles depends on set-up parameters only and is given by s = λd/l, with wavelength λ, sample-detector distance d and beam size at the sample l. The experimental speckle size can be determined by calculating the spatial intensity correlation function g(R) = 〈I(r + R)I(r)〉/〈I(r)〉2, that is connected to the coherence properties of the beam via the mutual coherence function γ(R, τ) by g(R) = |γ(R, τ = 0)|2 + 1 at the spatial distance R and time difference τ22. γ(R, τ) is a complex function that contains all information of the coherence properties. The degree of coherence for a single speckle pattern is given by 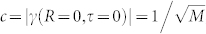Inline graphic, with M denoting the mode number of the beam19,23. By modelling g(R) with a Lorentzian function for both the vertical and horizontal directions, we obtain a beam size of (1.9 ± 0.1) × (1.6 ± 0.1) μm2 (h × v) which corresponds with the directly measured beam size of 1.8 × 1.5 μm2 excellently.

Figure 1.

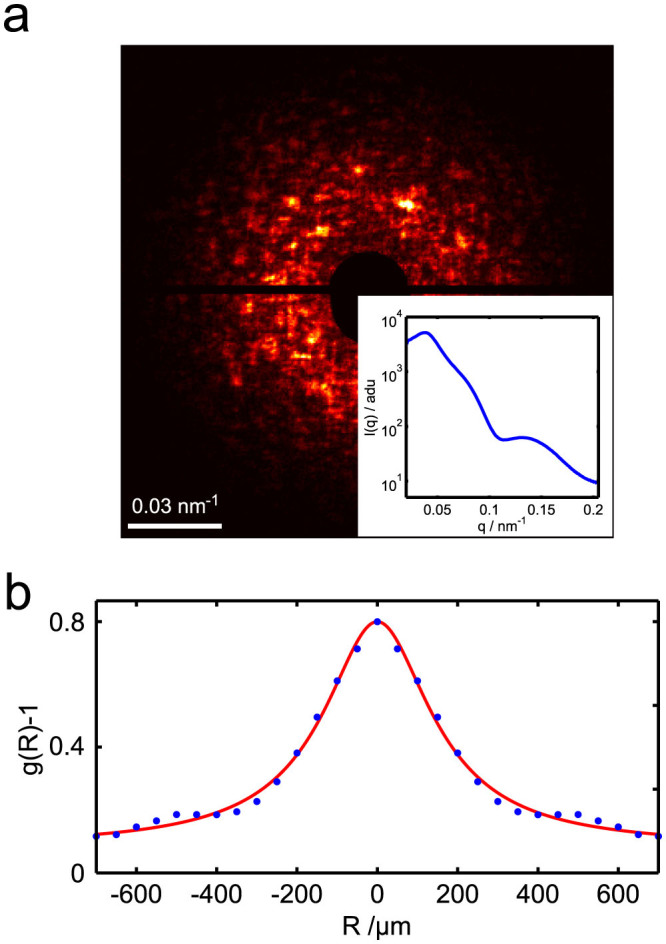
Figure 1

Open in a new tab

(a) Single shot speckle pattern and corresponding I(q) averaged over 500 shots (inset). (b) Typical intensity autocorrelation g(R) and Lorentzian fit to determine the speckle size. Due to the finite size of the extracted region of interest no full decorrelation (g(R) − 1 = 0) can be observed.

By analysing the speckle pattern the most direct quantity that can be accessed is the speckle contrast or visibility βs. It is given by the normalized standard deviation of the intensity yielding22,23,24

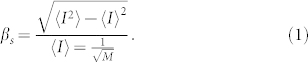graphic file with name srep05234-m1.jpg

Due to the equality 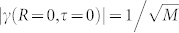Inline graphic, the speckle contrast directly reflects the degree of coherence of the x-ray beam. A fully coherent beam would have a mode number of M = 1 and thus a contrast of βs = 1. The experimentally measured contrast is affected by both the longitudinal and transverse coherence of the x-ray beam yielding βs = βtβl(q), with the transverse coherence βt and a q-dependent correction βl(q) that depends on the energy bandwidth and the scattering geometry19,25,26.

In Fig. 2 (a) the contrast βs is shown for 2000 single shots at q = 0.041 ± 0.001 nm−1. The average scattering intensity in this q-range was 35 photons/pixel. We find an averaged contrast of 〈βs〉 = 0.70 ± 0.08 which can be taken from the histogram of the contrast values as shown in Fig. 2 (b). This corresponds to a mode number of M = 2.0 ± 0.5. The single shot contrast varies from slightly above 0.5 up to some fully coherent shots with contrast values of 1 following an asymmetric distribution. This is demonstrated by the solid line in Fig. 2 (b) reflecting a lognormal distribution. In addition, we did not find any significant variation as a function of q, see Fig. 2 (c). Taking into account the natural bandwidth of the FEL radiation of Δλ/λ = 5 × 10−3, the correction accounting for the effect of the longitudinal coherence can be calculated to19,25

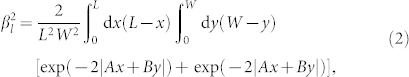graphic file with name srep05234-m2.jpg

with beam size L, sample thickness W, and the coefficients 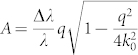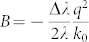Inline graphic, Inline graphic, and k0 = 2π/λ. For the q-range studied here, we find a correction factor of βl = 0.89, i.e. the transverse coherence is found to be βt = βs/βl = 0.79 ± 0.09. This corresponds to a transverse mode number of Mt = 1.6 ± 0.4.

Figure 2.

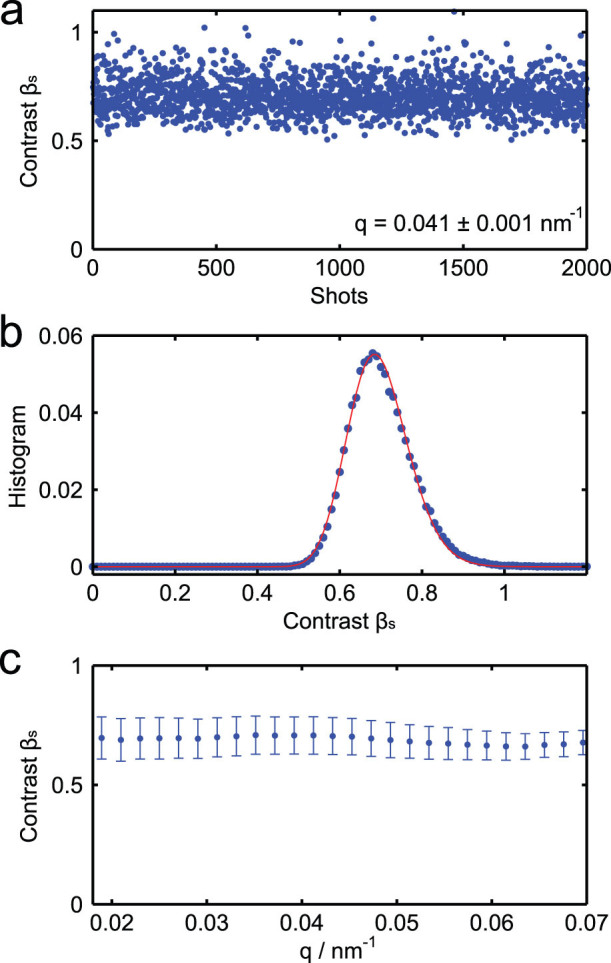
Figure 2

Open in a new tab

(a) Single shot speckle contrast βs from 2000 consecutive shots calculated at q = 0.041 nm−1. (b) Histogram of βs. The solid line represents a lognormal distribution using a mean value of 0.7 and a width of 0.105. (c) Speckle contrast βs as function of q averaged over 2000 consecutive single shots. The error bars represent the standard deviation of the single shot values from the averaged value.

Typically, a certain minimum intensity is necessary for contrast calculation using Eq. 1. At low scattering intensities the contrast is usually obtained by describing the intensity distribution by intensity probability distribution functions2,20,23. This method was shown to sufficiently describe the contrast of low-intensity speckle patterns in particular at large q 3 and by using split-and-delay devices27. Due to charge sharing of neighbouring pixels in the CCD detector and read out noise a continuous histogram is measured with peaks at intensity values corresponding to multiples of single photon events rather than discrete photon events. Typically, experimental intensity values are discretized by rounding up or down to integer values. This may introduce some artifacts. As the ratio of single, double, triple, … photon events is crucial for obtaining the mode number13, the interpretation can have a strong impact on the resulting contrast. At low intensities, such problems can be avoided by using so-called droplet algorithms to identify the location of the photons impacting the pixels of the detector3. However, those algorithms are limited to very low intensities, in particular work best for non-overlapping single photon events28.

Therefore, here we use the experimental, non-discretized intensity histograms and model those by simulations of intensity patterns following a negative binomal distribution and take into account charge sharing effects of the CCD detector29,30 and detector noise, see Methods for details. We used M = 2, which corresponds to the experimental value discussed above, as input parameter for the mode numbers. The results are shown as red line in Fig. 3. For comparison, the black circles represent the discrete values before blurring. In particular, at low intensities the results correspond to the experimental data. At higher intensities (see Fig. 3 (b)), the model describes the general shape of the experimentally obtained histogram very well, however, small differences can be found for 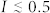Inline graphic and also at higher intensities. We think this is due to the simplicity of our model and due to a better statistic in the simulation model. Because of blurring, real scattering intensities can appear as lower intensities. For example, a single event of intensity I0 hitting the CCD sensor in between two pixels, will appear as two independent events of intensity I0/2. These can not be distinguished from other events of intensity I0/2 in the same pixels. As a result, experimentally obtained mode numbers from intensity histograms may be overestimated.

Figure 3.

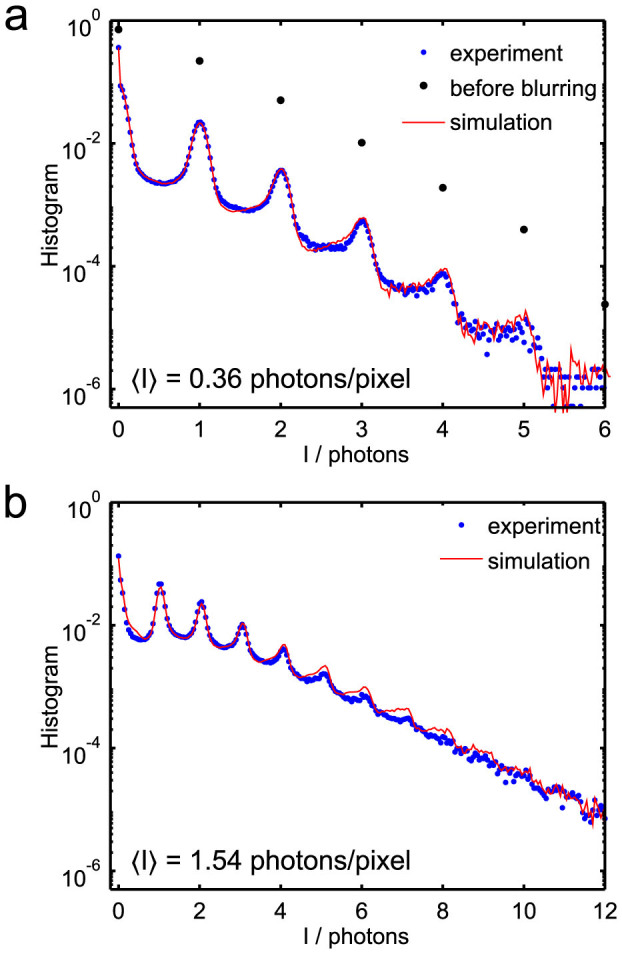
Figure 3

Open in a new tab

Intensity histograms at q = 0.071 ± 0.003 nm−1 (a) and q = 0.053 ± 0.003 nm−1 (b) averaged over 600 consecutive shots and simulation results taking blurring and noise into account.

Finally we want to discuss the impact of the shot-to-shot intensity distribution. Thanks to the energy bandwidth of 40 eV, we estimate the coherence time τc = ξl/c = 0.1 fs, with the speed of light c. The coherence time is proportional to the average x-ray pulse duration 〈tp〉 via 〈tp〉 = Mlτc19, with the average number of temporal modes Ml. We determined Ml from the shot-to-shot intensity distribution via a Gamma-distribution11,23

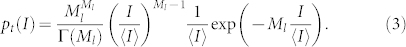graphic file with name srep05234-m3.jpg

This equation is valid at least for the linear FEL regime32. The pulse intensity was measured by a diode located in front of the optical components of the beamline for more than 10000 single shots. The shot-to-shot variation of the beam intensity is displayed in Fig. 4 (a). By fitting its distribution with Eq. 3 we obtain Ml = 52.2 ± 2.0, see Fig. 4 (b). This results in an average x-ray pulse length of tp = 5.2 ± 0.2 fs which perfectly corresponds to other recent results from SACLA21.

Figure 4.

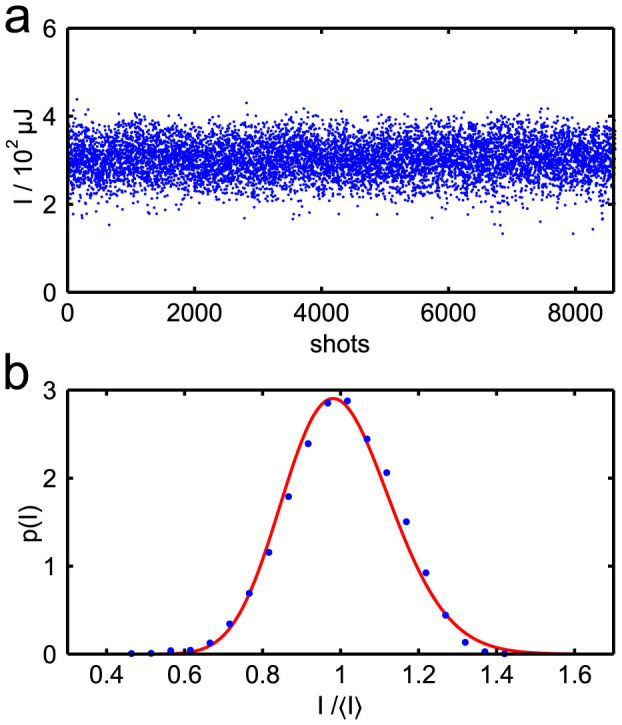
Figure 4

Open in a new tab

(a) Shot to shot variation of the beam intensity. (b) Intensity distribution. The solid line is a fit of Eq. 3 yielding Ml = 52.2 ± 2, the mean intensity was 〈I〉 = 300 μJ.

Discussion

In conclusion, we present a study on the coherence properties of the hard x-ray free-electron laser SACLA based on the analysis of single shot speckle patterns from colloidal particles. The size of the speckles in horizontal and vertical directions are in perfect agreement with expected values. We found a degree of transverse coherence of 0.79 ± 0.09 corresponding to a mode number of M = 1.6. The degree of transverse coherence is affected by set-up and machine parameters such as bunch compression schemes, saturation length, and photon wavelength resulting in observed values below 1. This is in agreement with expectations from FEL theory12,31 and previous experiments16,19,20.

By using a simple simulation model, we were able to model experimental intensity histograms. Because of the model's simplicity, the illustration of the values in the histogram is vague, i.e. they are blurred. This blurring's origin is related to the charge sharing and the noise level which is present in CCD detectors used in modern x-ray scattering experiments. Such simulation methods will help to determine contrasts more efficiently, in particular for weak scattering intensities where time-consuming droplet algorithms are used to overcome the effects of charge sharing3. However, we want to note that the simple simulation model discussed here does not give a full description of such influences. Further knowledge of detector properties is needed for a full understanding of our observations.

Methods

Sample

We synthesized the silica colloidal particles by using a modified Stöber method33,34. The particles were dispersed in water at a volume fraction of about 5%. They had a mean radius of 41 nm with a polydispersity of 10% which was determined by a form factor analysis (see following section). After the preparation the dispersion was filled into a quartz capillary (diameter of about 0.7 mm) which has been sealed by melting the glass.

Experiment

The experiment was performed at SACLA's EH3 of BL3 at a photon energy of 8 keV. With a bandwidth of 5 × 10−3 at a repetition rate of 20 Hz35, the pulse energy was (300 ± 40) μJ. The beam was focalized with KB mirrors to a size of 1.8 × 1.5 μm2 (h × v) at the sample position. The beam size was measured in the vertical and horizontal directions by knife edge scans. The sample capillaries were placed into a holder that was mounted in the MAXIC sample chamber of BL336. To resolve the structure factor of the samples, the detector (dual multiport charge coupled device (MPCCD)38, i.e. two sensors with 1024 × 512 pixels each with individual pixel size of 50 μm × 50 μm) was placed at a distance of 3 m behind the sample. The accessible q-range was limited by the beam stop and the size of the detector to 0.02 nm−1 < q < 0.34 nm−1. For each sample at least 10000 single shot speckle patterns were taken. These were averaged and azimuthally integrated to obtain I(q) as shown in Fig. 1. We measured several 1000 speckle patterns from a diluted dispersion (volume fraction 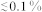Inline graphic) in order to extract the particle form factor. This was fitted by a form factor of a sphere convoluted with a size distribution to account for the polydispersity39. At the volume fraction of 5% used for the coherence analysis a structure factor reflecting particle-particle correlations was visible39, see Fig. 1.

Charge sharing simulations

Depending on the detector used, the photons impinging on the CDD sensor generate a charge cloud of different sizes, typically in the order of 10 μm37. This may result in shortcomings, e.g. an intensity of 1.4 can either be achieved by one photon with negligible charge sharing and less charge sharing contribution from neighbouring pixels, or e.g. by two photons (or more) with non-negligible charge sharing contribution. The impact of charge sharing of the CCD pixels and noise was estimated by computer simulations. Therefore, we used several 500 × 500 pixel grids with values corresponding a negative binomal distribution at an average intensity of 0.36 and 1.54 photons per pixel (identical to the experimental data), respectively. The negative binomal distribution function pb(I) is given by23

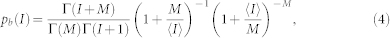graphic file with name srep05234-m4.jpg

where I is the intensity in number of photons, 〈I〉 its average, and Γ the Gamma-function. The initial mode number was set to M = 2, matching the result discussed above. Each pixel pattern was blurred by a random Gaussian distribution to model the charge sharing of pixels given by

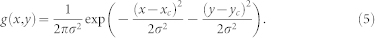graphic file with name srep05234-m5.jpg

Here, x, y denote the pixel coordinate and xc, yc the random center of the Gaussian. After that, Gaussian noise was added to the pattern. The amplitude of the charge sharing parameter σ and the noise were adapted to match the experimentally obtained histograms. Therefore, we calculated an averaged histogram from 600 single shots showing low intensities at q = 0.071 ± 0.003 nm−1, see Fig. 3 (a). The intensities in histograms are scaled for the ADU (Analog-Digital Unit) value for 1 photon of I(1 photon) = 124.7 adu. By comparing the simulated histogram with the averaged experimental one we find σ ≈ 0.15 for the strength of charge sharing and a width of Gaussian noise of σnoise ≈ 0.1 photons. The effect of charge sharing is only slightly above the expected value for the MPCCD detector of 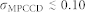Inline graphic pixels38.

Author Contributions

F.L., C.G., W.R., M.Y., T.I. and G.G. designed research. T.K., K.T. and M.Y. prepared the experimental setup. B.F. synthesized and prepared the samples. F.L., C.G., B.F., M.A.S., M.S., S.S., J.G., M.C., S.N., K.T., T.K., A.R. and G.G. performed the experiment. F.L., C.G., W.R. and G.G. analyzed and modeled the data. F.L. and C.G. wrote the manuscript text. All authors reviewed and discussed the manuscript.

Acknowledgments

We thank the Hamburg Centre for Ultrafast Imaging (CUI) for financial support. The Linac Coherent Light Source (LCLS) at SLAC National Accelerator Laboratory, is an Office of Science User Facility operated for the U.S. Department of Energy Office of Science by Stanford University. The XFEL experiments were performed at the BL3 of SACLA with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2013A8010).

References

  1. Grübel G., Stephenson G. B., Gutt C., Sinn H. & Tschentscher T. XPCS at the European X-ray free electron laser facility. Nucl. Instr. Methods 262, 357–367 (2007). [Google Scholar]
  2. Gutt C. et al. Measuring temporal speckle correlations at ultrafast x-ray sources. Opt. Exp. 17, 55–61 (2009). [DOI] [PubMed] [Google Scholar]
  3. Hruszkewycz S. O. et al. High Contrast X-ray Speckle from Atomic-Scale Order in Liquids and Glasses. Phys. Rev. Lett. 109, 185502 (2012). [DOI] [PubMed] [Google Scholar]
  4. Chapman H. N. et al. Femtosecond diffractive imaging with a soft-X-ray free-electron laser. Nature Phys. 2, 839–843 (2006). [Google Scholar]
  5. Seibert M. M. et al. Single mimivirus particles intercepted and imaged with an X-ray laser. Nature 470, 78–86 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Starodub D. et al. Single-particle structure determination by correlations of snapshot X-ray diffraction patterns. Nat. Commun. 3, 1276 (2012). [DOI] [PubMed] [Google Scholar]
  7. Wochner P. et al. X-ray cross correlation analysis uncovers hidden local symmetries in disordered matter. Proc. Natl. Acad. Sci. 106, 11511–11514 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Wang T. et al. Femtosecond Single-Shot Imaging of Nanoscale Ferromagnetic Order in Co/Pd Multilayers Using Resonant X-Ray Holography. Phys. Rev. Lett. 108, 237202 (2012). [DOI] [PubMed] [Google Scholar]
  9. Emma P. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nature Photon. 4, 641–647 (2010). [Google Scholar]
  10. Ishikawa T. et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nature Photon. 6, 540–544 (2012). [Google Scholar]
  11. Saldin E. L., Schneidmiller E. A. & Yurkov M. V. The Physics of Free Electron Lasers (Springer-Verlag, Berlin, 2000). [Google Scholar]
  12. Saldin E. L., Schneidmiller E. A. & Yurkov M. V. Statistical and coherence properties of radiation from x-ray free-electron lasers. New J. Phys. 12, 035010 (2010). [Google Scholar]
  13. Lee S. et al. Single shot speckle and coherence analysis of the hard X-ray free electron lases LCLS. Opt. Exp. 21, 24647–24664 (2013). [DOI] [PubMed] [Google Scholar]
  14. Singer A. et al. Transverse-Coherence Properties of the Free-Electron-Laser FLASH at DESY. Phys. Rev. Lett. 101, 254801 (2008). [DOI] [PubMed] [Google Scholar]
  15. Singer A. et al. Spatial and temporal coherence properties of single free-electron laser pulses. Opt. Express 20, 17480–17495 (2012). [DOI] [PubMed] [Google Scholar]
  16. Vartanyants I. A. et al. Coherence Properties of Individual Femtosecond Pulses of an X-ray Free-Electron Laser. Phys. Rev. Lett. 107, 144801 (2011). [DOI] [PubMed] [Google Scholar]
  17. Schlotter W. F. et al. Longitudinal coherence measurements of an extreme-ultraviolet free-electron laser. Opt. Lett. 35, 372–374 (2010). [DOI] [PubMed] [Google Scholar]
  18. Singer A. et al. Hanbury Brown-Twiss Interferometry at a Free-Electron Laser. Phys. Rev. Lett. 111, 034802 (2013). [DOI] [PubMed] [Google Scholar]
  19. Gutt C. et al. Single Shot Spatial and Temporal Coherence Properties of the SLAC Linac Coherent Light Source in the Hard X-ray Regime. Phys. Rev. Lett. 108, 024801 (2012). [DOI] [PubMed] [Google Scholar]
  20. Mai D. D. et al. Single pulse coherence measurements in the water window at the free-electron laser FLASH. Opt. Exp. 21, 13005–13017 (2013). [DOI] [PubMed] [Google Scholar]
  21. Inubushi Y. et al. Determination of the Pulse Duration of an X-ray Free Electron Laser Using Highly Resolved Single-Shot Spectra. Phys. Rev. Lett. 109, 144801 (2012). [DOI] [PubMed] [Google Scholar]
  22. Nugent K. A. Coherent methods in the X-ray sciences. Advances in Physics 59, 1 (2010). [Google Scholar]
  23. Goodman J. W. Speckle Phenomena in Optics (Roberts and Company, Greenwood Village, 2007). [Google Scholar]
  24. Dixon P. K. & Durian D. J. Speckle Visibility Spectroscopy and Variable Granular Fluidization. Phys. Rev. Lett. 90, 184302 (2003). [DOI] [PubMed] [Google Scholar]
  25. Sutton M. http://www.physics.mcgill.ca/mark/coherence/yorick/highqbeta.pdf (2007), date of access:25/03/2014.
  26. Abernathy D. L. et al. Small-Angle X-ray Scattering Using Coherent Undulator Radiation at the ESRF. J. Synch. Rad. 5, 37–47 (1998). [DOI] [PubMed] [Google Scholar]
  27. Roseker W. et al. Hard x-ray delay line for x-ray photon correlation spectroscopy and jitter-free pump-probe experiments at LCLS. Proc. SPIE 8504, 85040I (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Chushkin Y., Caronna C. & Madsen A. A novel event correlation scheme for X-ray photon correlation spectroscopy. J. Appl. Cryst. 45, 807–813 (2012). [Google Scholar]
  29. Tsunemi H., Yoshita K. & Kitamoto S. New technique of the X-ray efficiency measurement of a charge-coupled device with a subpixel resolution. Jpn. J. Appl. Phys. 36, 2906–2911 (1997). [Google Scholar]
  30. Yoshita K., Tsunemi H., Miyata E., Gendreau K. C. & Bautz M. W. Improvement of the Position Resolution of the CCD for X-Ray Use. IEEE Trans. Nucl. Sci. 46, 100–106 (1999). [Google Scholar]
  31. Saldin E. L., Schneidmiller E. A. & Yurkov M. V. Diffraction effects on the self-amplified spontaneous emission FEL. Opt. Comm. 186, 185–209 (2000). [Google Scholar]
  32. Saldin E. L., Schneidmiller E. A. & Yurkov M. V. Statistical properties of radiation from VUV and X-ray free electron laser. Opt. Comm. 148, 383–403 (1998). [Google Scholar]
  33. Stöber W., Fink A. & Bohn E. Controlled growth of monodisperse silica spheres in the micron size range. J. Coll. Int. Sci. 26, 62 (1968). [Google Scholar]
  34. Fischer B., Autenrith T. & Wagner J. Highly Charged Inorganic-Organic Colloidal Core-Shell Particles. Langmuir 26, 6201–6205 (2010). [DOI] [PubMed] [Google Scholar]
  35. Tono K. et al. Beamline, experimental stations and photon beam diagnostics for the hard x-ray free electron laser of SACLA. New J. Phys. 15, 083035 (2013). [Google Scholar]
  36. Song C. et al. Multiple application X-ray imaging chamber for single-shot diffraction experiments with femtosecond X-ray laser pulses. J. Appl. Cryst. 47, 188–197 (2014). [Google Scholar]
  37. Abboud A. et al. Sub-pixel resolution of a pnCCD for X-ray white beam applications. J. Instrum. 8, P05005 (2013). [Google Scholar]
  38. Kameshima T. et al. Development of an X-ray Pixel Detector with Multi-port Charge-Coupled Device for X-ray Free-Electron Laser Experiments. Rev. Sci. Instrum. 85, 033110 (2014). [DOI] [PubMed] [Google Scholar]
  39. Westermeier F. et al. Structure and short-time dynamics in concentrated suspensions of charged colloids. J. Chem. Phys. 137, 114504 (2012). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES