Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 10;4:5241. doi: 10.1038/srep05241

Robust ferromagnetism in monolayer chromium nitride

Shunhong Zhang 1, Yawei Li 2, Tianshan Zhao 1, Qian Wang 1,2,a
PMCID: PMC4050403  PMID: 24912562

Abstract

Design and synthesis of two-dimensional (2D) materials with robust ferromagnetism and biocompatibility is highly desirable due to their potential applications in spintronics and biodevices. However, the hotly pursued 2D sheets including pristine graphene, monolayer BN, and layered transition metal dichalcogenides are nonmagnetic or weakly magnetic. Using biomimetic particle swarm optimization (PSO) technique combined with ab initio calculations we predict the existence of a 2D structure, a monolayer of rocksalt-structured CrN (100) surface, which is both ferromagnetic and biocompatible. Its dynamic, thermal and magnetic stabilities are confirmed by carrying out a variety of state-of-the-art theoretical calculations. Analyses of its band structure and density of states reveal that this material is half-metallic, and the origin of the ferromagnetism is due to p-d exchange interaction between the Cr and N atoms. We demonstrate that the displayed ferromagnetism is robust against thermal and mechanical perturbations. The corresponding Curie temperature is about 675 K which is higher than that of most previously studied 2D monolayers.

Two dimensional (2D) materials have received intensive attention1,2,3 owing to the birth of graphene4. Materials in low dimensions can have electronic and magnetic properties that are fundamentally different from those of bulk phases. For instance, cubic boron nitride (BN) is an insulator whereas BN nanofilms can be intrinsically metallic5. Bulk MoS2 is an indirect band gap semiconductor while monolayer MoS2 has a direct bandgap of 1.90 eV, making it a promising material for nanoelectronics and valleytronics2,3. In this work, we explore the possibility of achieving highly spin-polarized ferromagnetism in chromium nitride (CrN) by altering its dimensionality.

Transition metal nitrides (TMNs) constitute a large family of materials with rich fundamental properties and vast technological applications. They have traditionally been used at extreme conditions of temperature and pressure due to their superhardness, high melting points, and outstanding corrosion resistance. In this family, CrN, a prototypical TMN, is particularly interesting not only because it combines all the favorable properties of TMNs but also due to its high thermal stability, good electrical conductivity6, and especially its biocompatibility giving rise to its applications on medical implants and devices, such as artificial joints and cutting tools7. CrN has challenged both theoretical and experimental investigations8,9,10,11,12,13,14,15,16,17 for its rare “itinerant antiferromagnetism”11. Currently, two typical phases have been identified: the rocksalt-structured phase with Fm-3m symmetry and paramagnetic (PM) order, and the orthogonal phase with Pnma symmetry and antiferromagnetic (AFM) order8,11. Driven by magnetic stress induced lattice distortion, the former phase can transform into the latter at a very low external pressure10,13. However, neither the rocksalt-structured nor the orthogonal phase exhibits net magnetization despite remarkable local magnetic moments observed.

Previous studies have demonstrated that magnetism of nanomaterials differs from that of bulk materials in a fundamental way because both magnetic coupling and magnetic moments are strongly dependent on coordination number and dimensionality-related quantum confinements. For example, in nanoscale, the AFM coupling between Cr atoms can be switched to ferromagnetic (FM) by means of introducing nitrogen18 or oxygen atoms19. The magnetic coupling between the Mn/Cu dopants in dilute magnetic semiconductors (DMSs) is highly dependent on dimensionality, namely, exhibiting FM coupling configuration in 1D GaN nanowires20,21,22 while having AFM coupling in the 2D thin films23, which implies the possibility of achieving ferromagnetism in CrN system by altering its dimensionality. What's more, even in the AFM phase of bulk CrN there exists ferromagnetic layers8,11. These inspired us to carry out the following study to seek a FM CrN system as it may have applications in spintronics as well as biotechnology.

Results

Structure search

We first revisit CrN in bulk phase to test the methods that we used. Full relaxations of the lattices and atomic positions are performed for the rocksalt phase of CrN with both the FM and AFM coupling configurations of the Cr atoms, respectively. The FM configuration is found to be energetically less favorable than the AFM one by an energy difference of 210 meV, which is in good agreement with previous results6 as well as the fact that bulk CrN is an AFM material at low temperature. We then begin the study of CrN in two-dimensional form. A thorough exploration on the potential energy surface (PES) of 2D CrN is needed to identify the thermodynamically stable structure. We perform unbiased structural searches by means of the CALYPSO (Crystal structure AnaLYsisby Particle Swarm Optimization)24 technique based on the biomimetic Particle Swarm Optimization (PSO) algorithm, which has successfully predicted a series of 2D crystals25,26,27,28,29,30,31 with a considerably high efficiency. Without any priori structural information, our blind structure search converges to a planar one-atomic-thick structure with an optimized lattice constant of 2.82 Å and Cr-N bond length of 1.99 Å, irrespective to the choice of supercell size Z (Z represent the number of formula units in a supercell,) as shown in Figure 1 (See the Supplementary Information for details on the structure search).

Figure 1. CrN in 2D form.

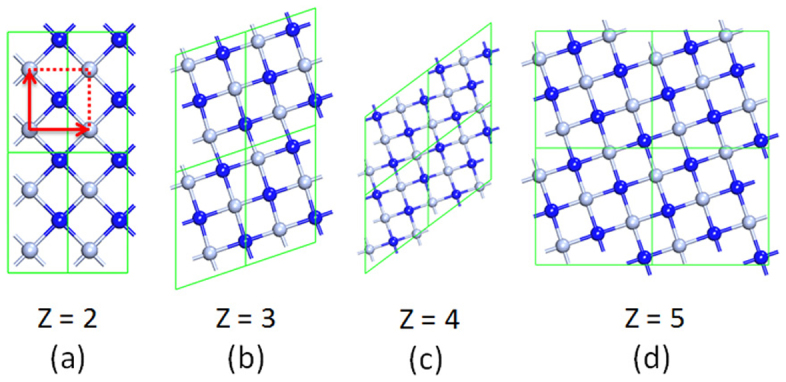
Figure 1

Open in a new tab

The 2D structures of CrN predicted by CALYPSO with respect to the number of formula units Z per supercell. Silver and blue balls represent Cr and N ions, respectively. For clarity all structures are shown in 2 × 2 supercells (green lines). The red lines denote the lattice basis vectors of the unit cell.

Preferred Magnetic Configuration

The predicted 2D CrN structure turns out to be surprisingly simple, which can be viewed as a monolayer of the rocksalt-structured CrN(100) surface. To search for the magnetic ground state of this monoatomic thick structure, we calculate the spin polarization energy32, namely, the energy difference between the nonmagnetic and magnetic configurations. Our calculations yield a large energy gain of 1.6 eV/unit cell upon spin polarization, indicating that the magnetic configuration is highly preferred and the monolayer CrN might be a good magnetic material. In the spin polarized configuration, the bond length of Cr-N is 1.99 Å, which is 4.7% larger than that of the nonmagnetic configuration. Each unit cell carries a net magnetic moment of 3.00 μB, which arises mainly from the Cr 3d orbitals (3.19 μB) and the neighboring N atom is polarized antiferromagnetically with a magnetic moment of −0.37 μB. This is because the Cr ions in this nanosheet have valance state of +III based on the chemical stoichiometry and the electronic configuration of Cr3+ is 3d3. We then consider a low spin configuration by constraining the total magnetic moment of a unit cell to be 1 μB. The calculated total energy of the low spin configuration is 0.95 eV higher than that of the high-spin state. In addition, we find the lattice constants undergo a expansion from 2.70 Å × 2.70 Å (the NM state) to 2.73 Å × 2.75 Å (low-spin state) to 2.82 Å × 2.82 Å (high-spin state), and the Cr-N bond length changes from 1.90 Å to 1.94 Å to 1.99 Å, accordingly. This indicates that spin polarization can effectively release the strain and stabilize the system.

To further determine the most preferable magnetic coupling between the Cr atoms in this predicted CrN nanosheet, we perform spin polarized total energy calculations for the two typical collinear magnetic configurations, namely, the FM and AFM states, within a 2 × 2 supercell. The FM state is found to be 632 meV lower in energy than the AFM one, indicating that the monolayer CrN is FM. Such a magnitude of energy difference is observable in experiments. Figure 2 shows the spin charge density distributions (ρ↑-ρ↓) for both the FM and AFM coupling configurations. We note that large spin charge accumulates around the Cr3+ sites in both the two cases, resulting in large local magnetic moments. However, the spin charge distribution of the N 2p electrons appears differently: In the FM ground state, the N 2p electrons are strongly spin polarized antiferromagnetically with the Cr ions, while in the AFM configuration the net spin polarization in the ligands is negligible, resembling that in its bulk counterpart16.

Figure 2. Magnetic coupling configurations of the monolayer CrN.

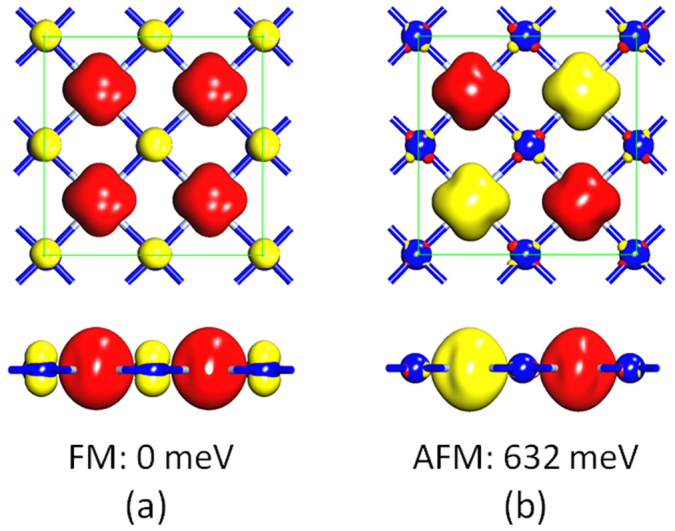
Figure 2

Open in a new tab

Top and side views of the optimized geometry and spin charge density isosurface (isovalue: 0.2 e/Å3) of (a) the FM and (b) AFM configurations of the monolayer CrN. Red and yellow isosurfaces correspond to spin up and spin down charge density, respectively. Green squares denote the 2 × 2 supercell.

Dynamic Stability

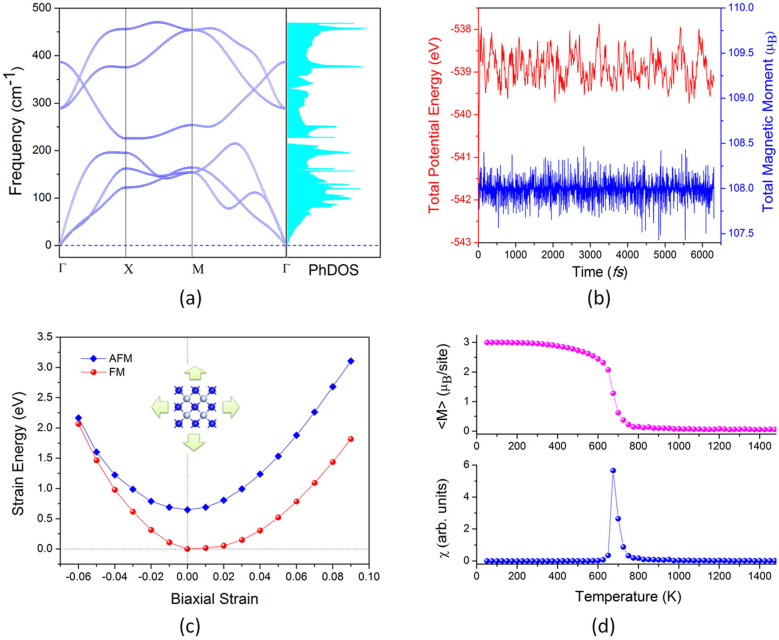
To ensure that the CrN nanosheet can be practically utilized as a FM material, we first examine its dynamical stability by calculating its phonon spectra. The Phonon dispersion and frequency density of states (PhDOS) are displayed in Figure 3(a). All vibrational modes are found to be real in the whole Brillouin Zone, indicating this structure is dynamically stable and can exist as a freestanding 2D crystal.

Figure 3. Structural and magnetic stability of the monolayer CrN.

Figure 3

Open in a new tab

(a) Phonon dispersion and frequency DOS (in arbitrary unit) of the monolayer CrN.The high symmetry q point path in the Brillouin Zone is Γ(0,0) → X (1/2, 0) → M (1/2, 1/2) → Γ (0, 0). (b) Variations of the total potential energy and total magnetic moment with respect to simulation time. (c)Strain energy of the FM and AFM configurations under the biaxial strains. The inset shows the 2 × 2 supercell used to calculate the strain energy. (d) Variations of the average magnetic moment per unit cell and magnetic susceptibility (χ) with respect to temperature.

Thermal Stability

We then examine the thermal stability of the monolayer CrN. We construct a large supercell of 6 × 6 containing 36 formula units to minimize the constraint induced by periodicity. Ab initio molecular dynamics (MD) simulations33,34,35 are performed at 300 K with a time step of 1 fs using Nosé heat bath scheme36 to investigate whether the FM monolayer is thermally stable at room temperature. The atomic configuration of the monolayer remains nearly intact after heated for more than 6 picoseconds. The variations of the total potential energy and total magnetic moment with respect to simulation time are plotted in Figure 3(b), showing that the monolayer is thermally stable as both of them remain almost invariant during the simulation. We further gradually increase heating temperature and find the structure can survive up to 600 K. MD simulations are also carried out for a 4√2 × 4√2 supercell containing 32 formula units. We find, again, neither structural reconstruction nor magnetic phase transition occurs when the structure is heated at room temperature (see Figure S2 in Supplementary Information for details). These results demonstrate that the FM monolayer CrN, once synthesized, is stable and can stay robust at room temperature.

To check if any possible structure reconstruction or buckling pattern37 could happen, we create a single-layer PbO-type structured CrN which is ubiquitous in many layered crystals38. We find, upon full relaxation, the PbO-type structure of CrN spontaneously converges to the planar monolayer sheet, indicating the outstanding stability of this CrN structure.

Magnetic Stability

We further study the stability of the FM order of the monolayer CrN against the in-plane strains. CrN thin films, in reality, usually grow on certain substrates like MgO (100) surface9,39. The synthesized thin films might endure some external strain, either compressive or tensile stain, due to the possible lattice mismatch. We calculate the strain energy for both the FM and AFM configurations under the isotropic biaxial in-plane strain. The results are plotted in Figure 3(c). Although the exchange energy decreases with the compressive biaxial strain and increases with the tensile strain, the FM state is found to always lie lower in energy than the AFM configuration in a wide range of the biaxial strains from −6% to 8%. This indicates that the FM order in the monolayer CrN can remain virtually undisturbed from the in-plane strains. A noteworthy trend in the strain energy curves is that the FM state becomes less competitive upon increasing the compressive biaxial strain, which is reminiscent of previous prediction on the bond length contraction induced AFM ordering in the Mn-doped GaN thin films23.

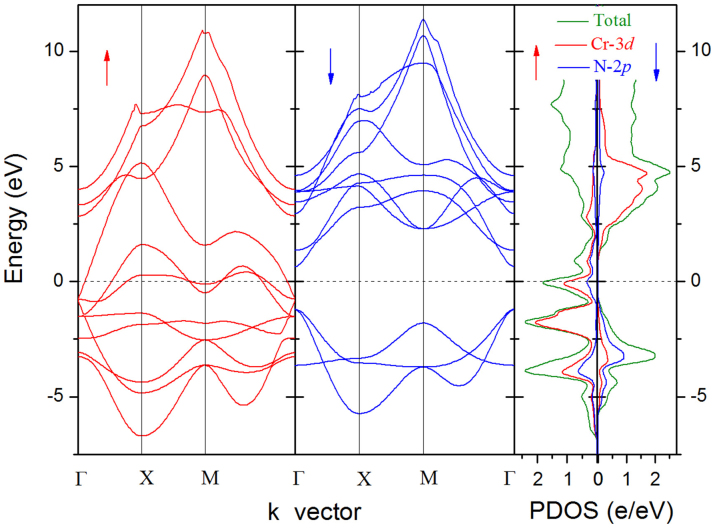
Figure 4. Electronic properties.

Figure 4

Open in a new tab

Spin-polarized electronic band structure (Red: spin up channel; Blue: spin down channel) and PDOS of the monolayer CrN. The Fermi level is shifted to 0 eV.

Estimation of Curie temperature

Having confirmed the structural and magnetic stability, we then quantitatively study the stability of the FM ordering against thermal perturbation by estimating its Curie temperature. To this end we carry out Metropolis Monte Carlo (MC) simulations based on 2D Ising model40. According to the classical Heisenberg model, the Hamiltonian of a 2D lattice can be expressed as 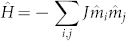Inline graphic, where mi corresponds to the magnetic moments (in μB) at site i (each unit cell is treated as one site, and for each site four spin states are considered, namely, two high spin sates, S = 3/2 and S = −3/2, and two low spin states, S = 1/2 and S = −1/2, and J refers to the Heisenberg direct exchange parameter, which can be obtained by J = (1/8)Eex/2m2, where Eex represents the exchange energy of the AFM and FM states in the 2 × 2 supercell. The factors of 1/8 and 1/2 correspond to the eight exchange pairs in the supercell and the double count of each pair in the summation, respectively. Substituting Eex = 632 meV and m = 3 into the formula, we get J = 4.39 meV. For simplicity, only the nearest neighbor exchange interaction is taken into account in the Hamiltonian. In order to reduce the periodic constraints, a 50 × 50 supercell is used to mimic the monolayer sheet. The variations of average magnetic moment per unit cell and magnetic susceptibility with respect to temperature are plotted in Figure 3(d). We note that the magnetic moment remains in the high spin state in the low-temperature range and then drastically drops to near zero and the magnetic susceptibility appears a sharp peak at a critical temperature, showing a thermal-induced FM-to-PM phase transition. The Curie temperature is estimated to be around 675 K, which is higher than that of most previously studied 2D systems34,35,40,41,42,43,44,45,46,47,48. This implies that ferromagnetism in the monolayer CrN is robust and can be detected at room temperature.

Electronic Properties

Bulk CrN is known as a “borderline Mott insulator”14, to investigate the electronic properties of the monolayer sheet, we calculate the spin-polarized electronic band structure. The results are plotted in Figure 4. We note although the band dispersion relationships in both spin channels are similar, it exhibits metallic feature in the spin-up channel characterized by the Fermi level crossing the partially occupied valance bands in the Brillouin zone and semiconducting feature in spin-down channel, indicating that the monolayer CrN is half-metallic. We further calculate the total density of states (DOS) and orbital resolved partial DOS at the Cr and N sites to explore the origin of the half-metallicity and ferromagnetism. There is a remarkable DOS peak at the Fermi level which is only contributed by the spin up channel. The partial DOS shows an explicit spin splitting in both the Cr 3d and N 2p states. The overlap between the Cr 3d and N 2p orbitals leads to the significant DOS near the Fermi level in spin-up channel, thus results in the half-metallicity as well as the ferromagnetism. Observably, the N 2p orbitals play key role in mediating the magnetic coupling between the Cr atoms.

Bilayer Stacking: structural and magnetic configurations

So far, we have established the viability of realizing robust ferromagnetism in the monolayer CrN. It would be intriguing to see how the structural and magnetic configurations change when the two CrN monolayers are stacked to form bilayer CrN. To address this concern we build two typical bilayer models, namely, AA and AB stacking, as shown in Figure 5. Our calculated results show that the AB stacking is energetically more favorable than the AA stacking. The binding energy between the two monolayers is 1.428 eV and 0.641 eV, and the optimized interlayer distance is 2.09 Å and 3.18 Å for the AB and AA stacking patterns, respectively, showing different bonding characters, namely, weak interaction in the AA stacking and a strong bonding with a hybrid ionic and covalent feature in the AB stacking. This is different from the situations of graphene and BN sheets which have weak interactions between layers, but is similar to the case of Fe-phthalocyanine sheets, where the interaction between the two layers is strong. However, a single Fe-phthalocyanine sheet can be synthesized on an insulating substrate49, where the Fe-phthalocyanine sheet only weakly interacts with the substrate44. Therefore, we can expect that our predicted CrN sheet could be grown on some insulating substrates. Since ferromagnetism of the monolayer CrN is energetically robust against antiferromagnetism, for simplicity we first assume that the intra-layer coupling is FM like a freestanding monolayer, and for each stacking pattern we consider two inter-layer couplings, namely, FM and AFM. We relax the lattice and atomic positions with inclusion of Grimme's potential50 to compensate for missing van der Waals interactions in standard DFT calculations. Total energy calculations show that the AB stacking FM coupling configuration has the lowest energy among all the considered bilayer models. We then enlarge the AB stacking model to a 2 × 2 supercell to examine the intra-layer magnetic coupling. Three possible magnetic coupling configurations: FM (both intra- and inter layer couplings are FM), partial AFM (intra-layer FM and inter-layer AFM), and AFM (both intra- and inter-layer couplings are AFM) are considered. The calculated total energy relative to the FM state for the partial AFM and AFM state are 248 meV and 209 meV, respectively. This confirms that the bilayer CrN is also FM. Therefore, we can conclude that the CrN monolayer, either in freestanding form or stacked in energetically favorable patterns, can exhibit robust ferromagnetism.

Figure 5. Stacking pattern of Bilayer CrN.

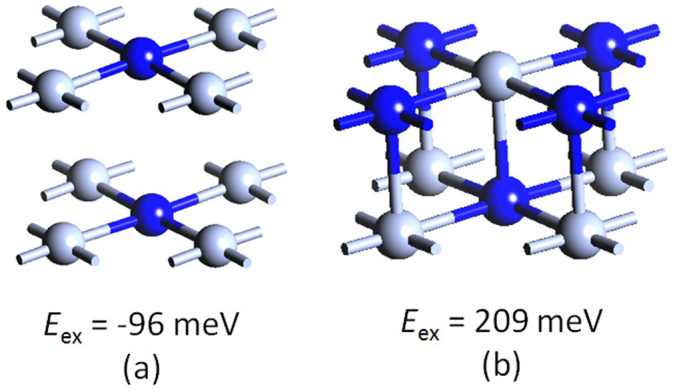
Figure 5

Open in a new tab

(a) AA stacking and (b) AB stacking. The exchange energies (define as energy difference between the AFM and FM configurations) of possible magnetic configurations are presented. Here FM and AFM refer to inter-layer magnetic coupling.

Discussion

To better understand the ferromagnetism of the monolayer CrN, it is worth recalling the following facts. (1) Chromium, due to its unique electronic configuration of [Ar]3d54s1 and the small energy gap between the 3d and 4s orbitals, can exist in different oxidation states, namely, 0, +2, +3, and +6, which can be used to tune the structural and magnetic properties of Cr-containing materials by changing its bonding feature. (2) In a Cr2 dimer, Cr atom binds strongly with the other Cr atom and the resulting sextuple bonding yields a large binding energy (1.44 eV) and a very short bond length (1.68 Å). Small clusters of Cr containing five atoms or fewer are all AFM51. In the bulk phase, Cr is also AFM52. However, the structures and magnetic properties of these small clusters can be drastically modified by doping a nitrogen atom18, where the nearest-neighbor Cr atoms are coupled antiferromagnetically to the N atom and hence ferromagnetically with each other. Similarly, in the ground state of the monolayer CrN, the two nearest Cr atoms are too far apart to allow significant direct overlap of the unpaired electron wave functions, the coupling involves the N 2p orbitals polarized antiferromagnetically to the 3d orbitals of Cr atoms. This lowers the energy of the system and makes the Cr atoms couple ferromagnetically to each other. Thus, the mechanism responsible for the FM coupling in the monolayer CrN can be classified as the p-d exchange mechanism53. (3) To achieve highly spin polarized ferromagnetism, usually it is necessary to introduce transition metal atoms. The observed magnetism originated from 2p electrons in the currently studied systems like porous graphene or hydrogenated35 or fluorinated graphene is weak. Among 3d transition metals, Cr and Mn have been widely used as dopants in semiconductors such as GaN or GaAs or ZnO to introduce magnetism due to their unique electronic configurations. However, it is challenging to regularly dock Cr or Mn atoms into the bulk phases and even on the 2D structures because of the clustering of TM atoms resulting from strong d-d orbital interactions. Recent experimental advances have demonstrated that 2D phthalocyanine-based organometallic (labeled as TM-Pc) sheets40,49 and tetragonal transition-metal-based 7,7,8,8-tetracyanoquinodimethane molecule coordination sheets (labeled as TM@TCNQ)54 have been successfully synthesized with the TM atoms regularly and separately distributed, providing the possibility of synthesizing and the 2D CrN sheet experimentally and detecting the ferromagnetism. (4) Different from Mn-containing 2D sheets where Mn2+ and Mn3+are neurotoxic55, as they can enter the brain by crossing the blood−brain barrier and cause permanent neurological disorder, the explored 2D CrN sheet is biocompatible, where trivalent chromium (Cr3+) in CrN is biologically active56, widely found in food and supplements, meanwhile nitrogen can also improve biocompatibility significantly57.

Summary

Motivated by design of novel 2D magnetic materials and inspired by the chemical control of magnetic coupling in molecules and clusters18,19, a comprehensive theoretical study on geometry, stability, electronic properties and ferromagnetism of the monolayer CrN sheet is performed. We find CrN, a well-known AFM or PM material in bulk phases, can become spontaneously FM when sliced into one-atom-thick nanosheet. The switching between AFM or PM to FM couplings is brought by tailoring the dimensionality and the origin of ferromagnetism is ascribed to p-d exchange mechanism. The well-defined atomic configuration and intrinsic ferromagnetism of the monolayer CrN suggest it is superior to other 2D magnetic materials: (1) Unlike other 2D Cr-containing sheets such as Cr-Pc and TM@TCNQ monolayers, which are AFM, the CrN nanosheet predicted here is both stable and FM, and the ferromagnetism can be sustained against mechanical and thermal perturbations; (2) Unlike other TM-based 2D materials which needs external stimulus like chemical functionalization34,35,58, carrier injection34,44 or external strain42 to switch on or enhance the FM order, the 2D CrN sheet possesses intrinsic ferromagnetism with a very high Curie temperature of 675 K, which is much higher than that of previously reported 150 K and 140 K for Mn-Pc sheet40 and MnO2 monolayer42, respectively; (3) Unlike conventional Cr or Mn doped DMSs where semiconductors are used as matrix to host the magnetic dopants, and magnetism, in most cases, comes from the clustering of TM atoms, in the monolayer CrN, Cr ions are individually held at the specific sites in a 2D crystal structure, and couple instrically ferromagnetically with each other. The Curie temperature is much higher than the highest Tc value achieved experimentally in Mn-doped GaAs. In addition, CrN thin film has been widely used as a coating material owing to its outstanding corrosion-resistance10. Therefore, the displayed high stability, robust ferromagnetism and the intriguing biocompatibility make this monolayer CrN sheet a very promising candidate for applications in spintronics, biodevices and functional coating techniques. We hope that the present study will stimulate further experimental effort in this direction.

Methods

Our first principles calculations are based on spin-polarized Density Functional Theory (DFT). All-electron Projector Augmented Wave (PAW) method implemented in Vienna Ab initio Simulation Package (VASP)59 is used to investigate the ground state structural, electronic and magnetic properties of CrN in the bulk and monolayer phases. For N and Cr, 2s22p5 and 3d54s1 electrons are treated as valence electrons, respectively. Considering the localization character of Cr 3d electrons, GGA+U formalism is adopted to describe the strong on-site Coulomb interaction. We choose the simplified (rotationally invariant) approach due to Dudarev et al.60, which involves only one parameter, namely, the effective U (U–J, where U is the onsite Coulomb repulsion and J is the onsite Hund exchange coupling). We set the effective U value to be 3 eV, which has been widely used in both bulk14,17,61,62 and low-dimensional40,44,63,64 systems that contain Cr or other 3d transition metal atoms and provided reasonable results. 2D structure searches are carried out using the CALYPSO methodology24,25,26 in combination with VASP for local optimizations and total energy calculations. Phonon properties are calculated using Density Functional Perturbation Theory (DFPT)65 implemented in the Quantum ESPRESSO suite66. Ab Initio Molecular Dynamics (AIMD) simulations are performed to examine the thermal stability. Detailed computational procedures are provided in the Supplementary Information.

Author Contributions

Q.W. designed the project; S.Z. performed the calculations; S.Z., Y.L., T.Z. and Q.W. analyzed the results and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep05241-s1.doc (2MB, doc)

Acknowledgments

This work is partially supported by grants from the National Natural Science Foundation of China (NSFC-11174014, NSFC-21273012), the National Grand Fundamental Research 973 Program of China (Grant No. 2012CB921404), and the Doctoral Program of Higher Education of China (20130001110033).

References

  1. Butler S. Z. et al. Progress, Challenges, and Opportunities in Two-Dimensional Materials Beyond Graphene. ACS Nano 7, 2898–2926 (2013). [DOI] [PubMed] [Google Scholar]
  2. Xu M., Liang T., Shi M. & Chen H. Graphene-Like Two-Dimensional Materials. Chem. Rev. 113, 3766–3798 (2013). [DOI] [PubMed] [Google Scholar]
  3. Chhowalla M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013). [DOI] [PubMed] [Google Scholar]
  4. Novoselov K. S. et al. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
  5. Zhang Z. & Guo W. Intrinsic Metallic and Semiconducting Cubic Boron Nitride Nanofilms. Nano Lett. 12, 3650–3655 (2012). [DOI] [PubMed] [Google Scholar]
  6. Weimer A. W. Carbide, nitride and boride materials synthesis and processing. (Springer, 1997). [Google Scholar]
  7. Fuentes G. G. et al. Recent advances in the chromium nitride PVD process for forming and machining surface protection. J. Mater. Process. Technol. 167, 415–421 (2005). [Google Scholar]
  8. Corliss L. M., Elliott N. & Hastings J. M. Antiferromagnetic Structure of CrN. Phys. Rev. 117, 929–935 (1960). [Google Scholar]
  9. Inumaru K., Koyama K., Imo-oka N. & Yamanaka S. Controlling the structural transition at the Néel point of CrN epitaxial thin films using epitaxial growth. Phys. Rev. B 75, 054416 (2007). [Google Scholar]
  10. Rivadulla F. et al. Reduction of the bulk modulus at high pressure in CrN. Nat. Mater. 8, 947–951 (2009). [DOI] [PubMed] [Google Scholar]
  11. Bhobe P. A. et al. Evidence for a Correlated Insulator to Antiferromagnetic Metal Transition in CrN. Phys. Rev. Lett. 104, 236404 (2010). [DOI] [PubMed] [Google Scholar]
  12. Filippetti A., Pickett W. E. & Klein B. M. Competition between magnetic and structural transitions in CrN. Phys. Rev. B 59, 7043–7050 (1999). [Google Scholar]
  13. Filippetti A. & Hill N. A. Magnetic Stress as a Driving Force of Structural Distortions: The Case of CrN. Phys. Rev. Lett. 85, 5166–5169 (2000). [DOI] [PubMed] [Google Scholar]
  14. Herwadkar A. & Lambrecht W. R. L. Electronic structure of CrN: A borderline Mott insulator. Phys. Rev. B 79, 035125 (2009). [Google Scholar]
  15. Alling B., Marten T. & Abrikosov I. A. Questionable collapse of the bulk modulus in CrN. Nat. Mater. 9, 283–284 (2010). [DOI] [PubMed] [Google Scholar]
  16. Botana A. S., Tran F., Pardo V., Baldomir D. & Blaha P. Electronic structure of CrN: A comparison between different exchange correlation potentials. Phys. Rev. B 85, 235118 (2012). [Google Scholar]
  17. Steneteg P., Alling B. & Abrikosov I. A. Equation of state of paramagnetic CrN from ab initio molecular dynamics. Phys. Rev. B 85, 144404 (2012). [Google Scholar]
  18. Wang Q., Sun Q., Rao B. K., Jena P. & Kawazoe Y. Nitrogen-induced magnetic transition in small chromium clusters. J. Chem. Phys. 119, 7124–7130 (2003). [Google Scholar]
  19. Tono K., Terasaki A., Ohta T. & Kondow T. Chemical Control of Magnetism: Oxidation-Induced Ferromagnetic Spin Coupling in the Chromium Dimer Evidenced by Photoelectron Spectroscopy. Phys. Rev. Lett. 90, 133402 (2003). [DOI] [PubMed] [Google Scholar]
  20. Wang Q., Sun Q. & Jena P. Ferromagnetism in Mn-Doped GaN Nanowires. Phys. Rev. Lett. 95, 167202 (2005). [DOI] [PubMed] [Google Scholar]
  21. Xiang H. J. & Wei S.-H. Enhanced Ferromagnetic Stability in Cu Doped Passivated GaN Nanowires. Nano Lett. 8, 1825–1829 (2008). [DOI] [PubMed] [Google Scholar]
  22. Wang Q., Sun Q., Jena P. & Kawazoe Y. Ferromagnetic GaN−Cr Nanowires. Nano Lett. 5, 1587–1590 (2005). [DOI] [PubMed] [Google Scholar]
  23. Wang Q., Sun Q., Jena P. & Kawazoe Y. Antiferromagnetic Coupling Driven by Bond Length Contraction near the Ga1-xMnxN Film Surface. Phys. Rev. Lett. 93, 155501 (2004). [DOI] [PubMed] [Google Scholar]
  24. Wang Y., Lv J., Zhu L. & Ma Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010). [Google Scholar]
  25. Luo X. et al. Predicting Two-Dimensional Boron–Carbon Compounds by the Global Optimization Method. J. Am. Chem. Soc. 133, 16285–16290 (2011). [DOI] [PubMed] [Google Scholar]
  26. Wang Y. et al. An effective structure prediction method for layered materials based on 2D particle swarm optimization algorithm. J. Chem. Phys. 137, 224108 (2012). [DOI] [PubMed] [Google Scholar]
  27. Wu X. et al. Two-Dimensional Boron Monolayer Sheets. ACS nano 6, 7443–7453 (2012). [DOI] [PubMed] [Google Scholar]
  28. Luo X. et al. Two-Dimensional Superlattice: Modulation of Band Gaps in Graphene-Based Monolayer Carbon Superlattices. J. Phys. Chem. Lett. 3, 3373–3378 (2012). [Google Scholar]
  29. Yu X., Li L., Xu X.-W. & Tang C.-C. Prediction of Two-Dimensional Boron Sheets by Particle Swarm Optimization Algorithm. J. Phys. Chem. C. 116, 20075–20079 (2012). [Google Scholar]
  30. Zhou L.-J., Zhang Y.-F. & Wu L.-M. SiC2 Siligraphene and Nanotubes: Novel Donor Materials in Excitonic Solar Cells. Nano Lett. 13, 5431–5436 (2013). [DOI] [PubMed] [Google Scholar]
  31. Dai J., Zhao Y., Wu X., Yang J. & Zeng X. C. Exploration of Structures of Two-Dimensional Boron–Silicon Compounds with sp2 Silicon. J. Phys. Chem. Lett. 4, 561–567 (2013). [DOI] [PubMed] [Google Scholar]
  32. Peng H. et al. Origin and Enhancement of Hole-Induced Ferromagnetism in First-Row d0 Semiconductors. Phys. Rev. Lett. 102, 017201 (2009). [DOI] [PubMed] [Google Scholar]
  33. Du A., Sanvito S. & Smith S. C. First-Principles Prediction of Metal-Free Magnetism and Intrinsic Half-Metallicity in Graphitic Carbon Nitride. Phys. Rev. Lett. 108, 197207 (2012). [DOI] [PubMed] [Google Scholar]
  34. Kan E. et al. Two-Dimensional Hexagonal Transition-Metal Oxide for Spintronics. J. Phys. Chem. Lett. 4, 1120–1125 (2013). [DOI] [PubMed] [Google Scholar]
  35. Zhou J. et al. Ferromagnetism in Semihydrogenated Graphene Sheet. Nano Lett. 9, 3867–3870 (2009). [DOI] [PubMed] [Google Scholar]
  36. Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984). [Google Scholar]
  37. Zhang Z., Liu X., Yakobson B. I. & Guo W. Two-Dimensional Tetragonal TiC Monolayer Sheet and Nanoribbons. J. Am. Chem. Soc. 134, 19326–19329 (2012). [DOI] [PubMed] [Google Scholar]
  38. Hsu F.-C. et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl. Acad. Sci. 105, 14262–14264 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Constantin C., Haider M. B., Ingram D. & Smith A. R. Metal/semiconductor phase transition in chromium nitride(001) grown by rf-plasma-assisted molecular-beam epitaxy. Appl. Phys. Lett. 85, 6371–6373 (2004). [Google Scholar]
  40. Zhou J. & Sun Q. Magnetism of Phthalocyanine-Based Organometallic Single Porous Sheet. J. Am. Chem. Soc. 133, 15113–15119 (2011). [DOI] [PubMed] [Google Scholar]
  41. Zhou J., Wang Q., Sun Q. & Jena P. Intrinsic ferromagnetism in two-dimensional carbon structures: Triangular graphene nanoflakes linked by carbon chains. Phys. Rev. B 84, 081402 (2011). [Google Scholar]
  42. Kan M., Zhou J., Sun Q., Kawazoe Y. & Jena P. The Intrinsic Ferromagnetism in a MnO2 Monolayer. J. Phys. Chem. Lett. 4, 3382–3386 (2013). [DOI] [PubMed] [Google Scholar]
  43. Li X., Zhou J., Wang Q., Kawazoe Y. & Jena P. Patterning Graphitic C–N Sheets into a Kagome Lattice for Magnetic Materials. J. Phys. Chem. Lett. 4, 259–263 (2013). [DOI] [PubMed] [Google Scholar]
  44. Zhou J. & Sun Q. Carrier induced magnetic coupling transitions in phthalocyanine based organometallic sheet. Nanoscale 6, 328–333 (2013). [DOI] [PubMed] [Google Scholar]
  45. Giesbers A. J. M. et al. Interface-Induced Room-Temperature Ferromagnetism in Hydrogenated Epitaxial Graphene. Phys. Rev. Lett. 111, 166101 (2013). [DOI] [PubMed] [Google Scholar]
  46. Zhang C.-W. & Yan S.-S. First-Principles Study of Ferromagnetism in Two-Dimensional Silicene with Hydrogenation. J. Phys. Chem. C. 116, 4163–4166 (2012). [Google Scholar]
  47. Kan M., Adhikari S. & Sun Q. Ferromagnetism in MnX2 (X = S, Se) Monolayers. Phys. Chem. Chem. Phys. 16, 4990–4994 (2014). [DOI] [PubMed] [Google Scholar]
  48. Tan J., Li W., He X. & Zhao M. Stable ferromagnetism and half-metallicity in two-dimensional polyporphyrin frameworks. RSC Adv. 3, 7016–7022 (2013). [Google Scholar]
  49. Abel M., Clair S., Ourdjini O., Mossoyan M. & Porte L. Single Layer of Polymeric Fe-Phthalocyanine: An Organometallic Sheet on Metal and Thin Insulating Film. J. Am. Chem. Soc. 133, 1203–1205 (2010). [DOI] [PubMed] [Google Scholar]
  50. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006). [DOI] [PubMed] [Google Scholar]
  51. Cheng H. & Wang L.-S. Dimer Growth, Structural Transition, and Antiferromagnetic Ordering of Small Chromium Clusters. Phys. Rev. Lett. 77, 51–54 (1996). [DOI] [PubMed] [Google Scholar]
  52. Fawcett E. Spin-density-wave antiferromagnetism in chromium. Rev. Mod. Phys. 60, 209–283 (1988). [Google Scholar]
  53. Mizokawa T. & Fujimori A. p-d exchange interaction for transition-metal impurities in II-VI semiconductors. Phys. Rev. B 56, 6669–6672 (1997). [DOI] [PubMed] [Google Scholar]
  54. Ma Y., Dai Y., Wei W., Yu L. & Huang B. Novel Two-Dimensional Tetragonal Monolayer: Metal–TCNQ Networks. J. Phys. Chem. A 117, 5171–5177 (2013). [DOI] [PubMed] [Google Scholar]
  55. Huang P. et al. Differential toxicity of Mn2+ and Mn3+ to rat liver tissues: Oxidative damage, membrane fluidity and histopathological changes. Exp. Toxicol. Pathol. 64, 197–203 (2012). [DOI] [PubMed] [Google Scholar]
  56. Eastmond D. A., MacGregor J. T. & Slesinski R. S. Trivalent Chromium: Assessing the Genotoxic Risk of an Essential Trace Element and Widely Used Human and Animal Nutritional Supplement. Crit. Rev. Toxicol. 38, 173–190 (2008). [DOI] [PubMed] [Google Scholar]
  57. Carrero-Sánchez J. C. et al. Biocompatibility and Toxicological Studies of Carbon Nanotubes Doped with Nitrogen. Nano Lett. 6, 1609–1616 (2006). [DOI] [PubMed] [Google Scholar]
  58. Wu M., Zeng X. C. & Jena P. Unusual Magnetic Properties of Functionalized Graphene Nanoribbons. J. Phys. Chem. Lett. 4, 2482–2488 (2013). [Google Scholar]
  59. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  60. Dudarev S. L., Botton G. A., Savrasov S. Y., Humphreys C. J. & Sutton A. P. Electron-energy-loss spectra and the structural stability of nickel oxide:An LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998). [Google Scholar]
  61. Alling B., Marten T. & Abrikosov I. A. Effect of magnetic disorder and strong electron correlations on the thermodynamics of CrN. Phys. Rev. B 82, 184430 (2010). [Google Scholar]
  62. Sato K. et al. First-principles theory of dilute magnetic semiconductors. Rev. Mod. Phys. 82, 1633–1690 (2010). [Google Scholar]
  63. Zhou J., Wang Q., Sun Q., Kawazoe Y. & Jena P. Strain-Induced Spin Crossover in Phthalocyanine-Based Organometallic Sheets. J. Phys. Chem. Lett. 3, 3109–3114 (2012). [DOI] [PubMed] [Google Scholar]
  64. Zhou J. & Sun Q. Absorption induced modulation of magnetism in two-dimensional metal-phthalocyanine porous sheets. J. Chem. Phys. 138, 204706–204707 (2013). [DOI] [PubMed] [Google Scholar]
  65. Baroni S., de Gironcoli S., Dal Corso A. & Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001). [Google Scholar]
  66. Paolo G. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep05241-s1.doc (2MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES