Optimal lamellar arrangement in fish gills

Significance

It is generally assumed that shapes encountered in nature have evolved in a way as to maximize the robustness of a species. Nevertheless, given nature’s notoriously complex designs, it is often unclear what is being optimized. The lamellar pattern of fish gills is one of the few cases in which optimization in nature can be well defined. We demonstrate that the lamellar pattern of fish gills has been optimized, such that fish display interlamellar spaces of similar dimension regardless of body mass or species, thereby revealing the primary evolutionary pressure on fish gills. This natural optimization strategy demonstrates how control of the channel arrangement in microfluidic devices enhances heat and mass transfer.

Abstract

Fish respire through gills, which have evolved to extract aqueous oxygen. Fish gills consist of filaments with well-ordered lamellar structures, which play a role in maximizing oxygen diffusion. It is interesting that when we anatomically observe the gills of various fish species, gill interlamellar distances (d) vary little among them, despite large variations in body mass (M_b). Noting that the small channels formed by densely packed lamellae cause significant viscous resistance to water flow, we construct and test a model of oxygen transfer rate as a function of the lamellar dimensions and pumping pressure, which allows us to predict the optimal interlamellar distance that maximizes the oxygen transfer rate in the gill. Comparing our theory with biological data supports the hypothesis that fish gills have evolved to form the optimal interlamellar distances for maximizing oxygen transfer. This explains the weak scaling dependence of d on M_b: d ∼ M_b^1/6.

Fish gills have evolved exclusively in aquatic creatures to extract aqueous oxygen. Because oxygen has considerably low solubility and diffusivity in water, the efficiency of respiration is critical (1). Gills consist of plate-like structures called filaments that are covered by an array of lamellae enclosing a capillary blood network, as shown in Fig. 1 (1, 2). Oxygen-rich water passes through the narrow channels formed by the lamellar layers, where oxygen diffuses into the capillaries. The densely packed lamellar structure is advantageous because it provides a large surface area for oxygen transfer; however, it also generates considerable viscous resistance. This resistance is overcome by pumping. Fish typically adopt one of the following two pumping mechanisms: branchial pumping and ram ventilation. Most teleost fish, members of the diverse group of ray-finned fish, use branchial pumping, and muscular compression in the pharynx enables water flow through the gills. In ram ventilation, which is used by many pelagic fish, the dynamic pressure generated by their swimming drives water flow into the gills (3).

Fig. 1.

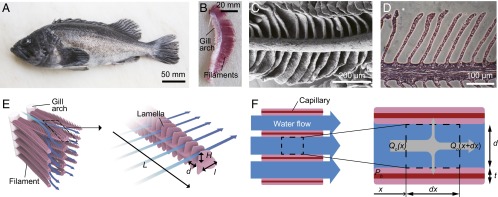
The branchial apparatus of a rockfish Sebastes schlegelii. (A) Sebastes schlegelii having gills on both sides of the pharynx. (B) The gill arch and filaments. (C) SEM image of a gill filament. (D) H&E-stained cross-section of a gill filament. (E) A schematic illustration of gill morphology. Plate-like filaments hanging on branchial arches are covered with lamellae enclosing a blood capillary network. The blue arrows indicate the direction of water flow from the gill arches to the operculum. The well-ordered lamellar structures provide arrays of microchannels where oxygen diffuses to the capillaries. (F) A schematic illustration of the top view of the interlamellar channels. The dashed box corresponds to the control volume for the mass-transfer analysis.

Most previous studies on the structure of fish gills have focused on the dependence of the total surface area of the gill upon the body size and species of fish (1, 4, 5). We consider the convective oxygen transfer that occurs in fish gills. As water passes through the narrow lamellar channels, increased viscous resistance impedes water flow at a given pumping pressure, which is limited by muscle power or swimming speeds; this leads to a lowering of the oxygen transfer rate. Hence, the flow rate within the gaps of the lamellae and the extended surface area play important roles in determining the oxygen transfer rate. The number of lamellae per unit length of gill filament determines both the surface area for diffusion and the size of the water channels. Therefore, we investigate the relationship between lamellar distance and oxygen transfer rate, an aspect that previously has seldom been explored.

Results

Theoretical Analysis.

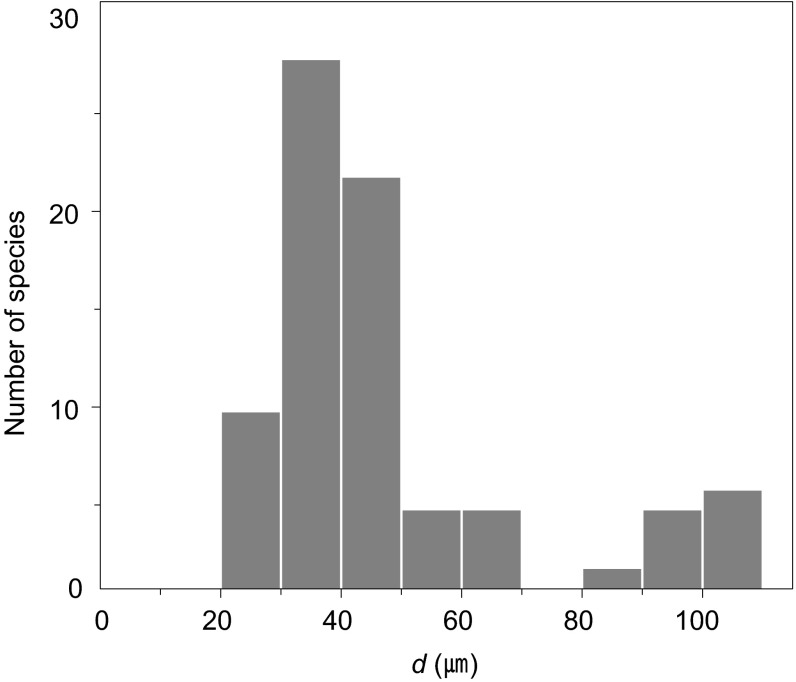
We compiled interlamellar distances in a broad range of fish species, as shown in Fig. 2. It is remarkable that whereas the body mass of these species varies over six orders of magnitude from 0.1 g to 100 kg, the interlamellar distances vary within a very small range, ∼20–100 μm (6, 7). To explain the relatively uniform interlamellar distances, we mathematically modeled the oxygen transfer rate in fish gills, which is driven by the gradient of oxygen partial pressure. For an infinitesimal control volume shown in Fig. 1F, the conservation of oxygen can be written as dQ_o/dx = −hßs(P_w − P_b), where Q_o is the oxygen flow rate, h the convective mass transfer coefficient, β the oxygen solubility coefficient of water, s the wetted perimeter of the control volume, P_w the average oxygen partial pressure in water, and P_b the oxygen partial pressure on the lamellar surface. The oxygen flow rate can be expressed in terms of the water flow rate through the channel Q_w as Q_o = Q_wβP_w. Because the lamellar height H ∼400 μm is typically much greater than the interlamellar distance d ∼40 μm, as shown in Fig. 2 (2, 8–11), s ∼2H, which allows us to write

$$Q_{w}d{P}_w/dx+2hH\left(P_w-P_b\right)=0.$$ [1]

Fig. 2.

Distribution of interlamellar distances for 75 fish species. The gill interlamellar distances of most fish species range from 20 to 110 μm despite immense variation in their body masses, from 10⁻¹ to 10⁵ g. We assumed that the lamellar thickness is negligible compared with the interlamellar distance, and estimated the interlamellar distance d as a reciprocal of the number of lamellae per unit length of the gill filament (2, 6). Detailed data and their sources are provided in Table S1.

For the characteristic flow speed through interlamellar channels u ∼0.01 m/s (2, 11), water density ρ ∼1,000 kg/m³, viscosity μ ∼0.001 Pa·s, interlamellar distance d ∼10 μm, and lamellar length l ∼1 mm, the ratio of inertial to viscous effects, prescribed by the Reynolds number Re = ρud²/(μl) ∼10⁻³, implies that the flow within the interlamellar channel is laminar with negligible entrance effects. Accordingly, h is given by h = ShD_w/2d, where Sh is the Sherwood number, the ratio of convective to diffusive mass transfer (12), which is estimated as 7.5, and D_w, the oxygen diffusion coefficient in water (13), is 2 × 10⁻⁹ m²/s.

To solve Eq. 1 for P_w as a function of x, we first consider the x dependency of P_b. One expects that P_b approximates the partial pressure of oxygen in the capillaries due to negligible diffusive resistance between the lamellar surface and the capillaries (1). Hemoglobin in the capillaries rapidly combines with oxygen molecules, thus stabilizing the partial pressure of oxygen at a relatively low value (14–17). Hence, the relative variation in partial pressure in capillaries to that in water ΔP_b/ΔP_w << 1, allowing us to neglect the variation of P_b with x. Solving Eq. 1 yields P_w(x) = (P_wo − P_b)exp(−2bhx/Q_w) + P_b, where P_wo is the partial pressure of oxygen at the entrance x = 0. Because the rate of oxygen transfer to the blood capillaries in a single interlamellar channel is Q_wβ(P_wo − P_w(l)), the total oxygen transfer rate in a gill filament having N interlamellar channels is given by M_o ∼ Q_wβ(P_wo − P_w(l))N. Although the lamellar thickness t may depend on the fish species or the maturity of the individual, we assume that t/d < 1 and N ∼ L/(d + t) ∼ L/d, as evidenced by many species such as Thunnus albacares, Micropterus dolomieu, and Tetrapturus audax (2, 6).

The stream-wise momentum conservation can be described by the Poiseuille flow solution, Q_w = Hd³ΔP_h/(12 μl), where ΔP_h is the pressure difference applied across the channel (Fig. 1E). Combining this solution with the aforementioned expressions for M_o and P_w, we finally obtained M_o as a function of d and other parameters, including μ, D_w, l, and ΔP_h. Differentiating M_o with respect to d thus yields the optimal interlamellar distances d that maximize M_o:

$$d^4=72\mu D_w{l}^2/\mathrm{\Delta }{P}_h.$$ [2]

Because μ and D_w are material properties, our model suggests that the optimal lamellar arrangement depends exclusively on the lamellar length l and pumping pressure ΔP_h.

Experimental Validation.

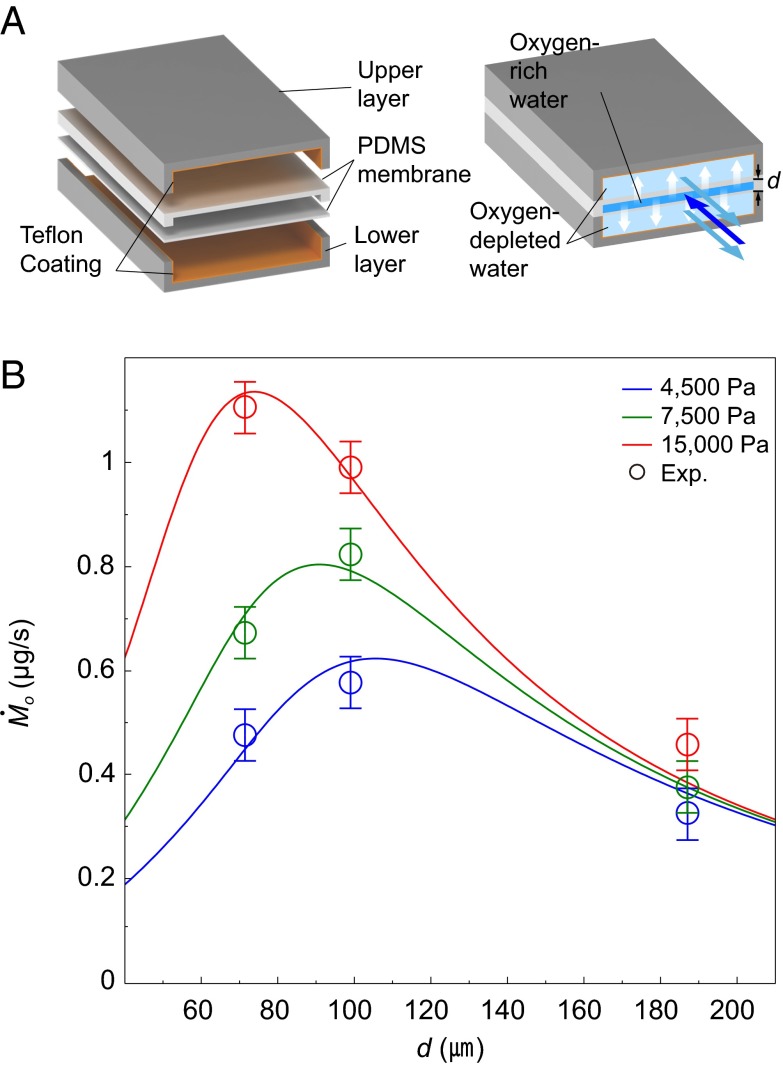
We tested the validity of our theory for M_o as a function of d and ΔP_h, by conducting experiments using a microfluidic chip that mimics a fish gill. As shown in Fig. 3A, an engineered gill was constructed of multiple layers of polydimethylsiloxane (PDMS), so that an oxygen-rich water channel was sandwiched between two neighboring channels of counterflowing oxygen-depleted water. Oxygen diffused across the thin PDMS membranes from oxygen-rich to oxygen-depleted water streams, which were pumped into the channels by syringe pumps. Measuring the oxygen concentration at the outlet of the oxygen-rich channel for various channel dimensions and pumping pressures yielded the oxygen transfer rate M_o as a function of d and ΔP_h for the fixed filament length L = 1 mm. The results, shown in Fig. 3B, indicate that the empirical measurements support our theory.

Fig. 3.

Measurement of oxygen transfer rate using a microfluidic chip that mimics a fish gill. (A) A schematic illustration of the PDMS microchannels. Oxygen-rich water passes through the central channel sandwiched by two oxygen-depleted water channels. Oxygen diffuses across the PDMS membranes. (B) The oxygen transfer rate M_o vs. the interlamellar distance d for different pumping pressures. The lines and circles correspond to the theoretical predictions and the experimental results, respectively. Reynolds numbers range from 0.002 to 0.3. Characteristic error bars are shown.

Discussion

Our modeling result, Eq. 2, allows us to correlate the lamellar distance and length at a given pumping pressure. Pumping pressures in fish gills primarily depend on the pumping mechanisms. For most teleost fish using branchial pumping, the pumping pressure is reported to range from 5 to 50 Pa (18). Pelagic teleost fish that typically use ram ventilation swim at cruising speeds of v = 0.7–2 m/s, resulting in a dynamic pressure (1/2)ρv² ∼0.2–2 kPa, which exceeds branchial pumping pressure (19). Among the species that use ram ventilation, some pelagic elasmobranch fish have developed a unique gill structure called the interbranchial septum; this structure generates primary resistance to water flow, such that only a small fraction of the dynamic pressure on the order of 20 Pa is applied to the interlamellar channels (11).

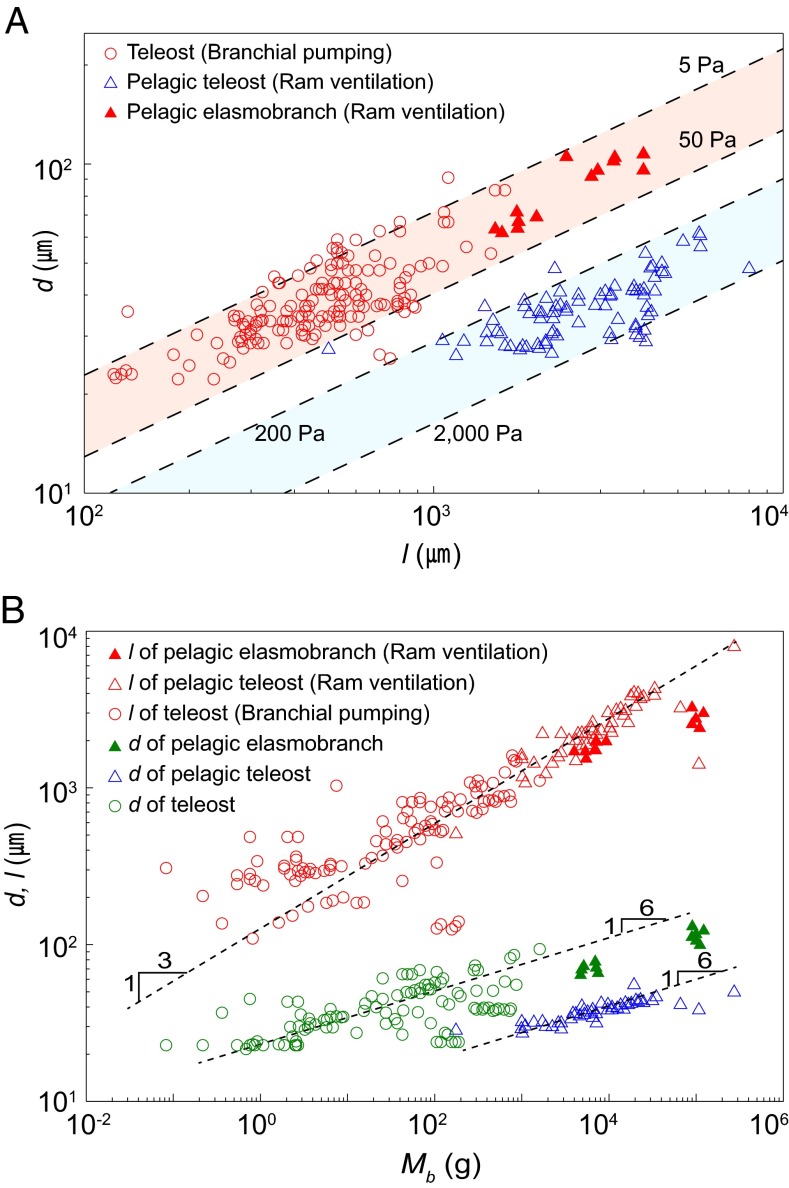
We compared the proposed model, Eq. 2, with biological data (Fig. 4). A comparison of the interlamellar distance vs. lamellar length in the gills of 75 species is indicated in Fig. 4A. Most of the data points are clustered within the anticipated interlamellar distance range for each pumping mechanism, which is consistent with our theory. Fig. 4B shows the correlation between interlamellar distance and body mass. Assuming a geometric similarity across fish species (20), a characteristic body length should be proportional to the cube root of the body mass M_b. We found that the lamellar length l indeed scales as M_b^1/3, despite the variation in gill shapes (1) (Fig. 4B). On the basis of Eq. 2, which predicts that the optimal interlamellar distance d should be scaled as l^1/2 for a given pressure condition, we obtain d ∼M_b^1/6. This scaling, a very weak dependency of d on M_b, explains the biological data provided in Fig. 4B, and thus reveals the origin of the relatively uniform interlamellar distance over six orders of magnitude of body mass.

Fig. 4.

Biological data for the lamellar dimensions of fish gills. (A) The dependence of interlamellar distance on lamellar length. The dotted lines indicate the range of optimal conditions depending on the pumping pressure. The pumping pressures for fish using branchial pumping and for pelagic teleost fish using ram ventilation typically range from 5 to 50 Pa (18) and from 0.2 to 2 kPa (19), respectively. For pelagic elasmobranch fish using ram ventilation but having interbranchial septa, the applied pressure for the interlamellar channel is ∼20 Pa (11). (B) The dependence of lamellar length and interlamellar distance on body mass. Owing to the geometric similarity of fish species, the lamellar length l scales as l ∼M_b^1/3; combining the scaling with our model’s prediction, d ∼l^1/2, yields d ∼M_b^1/6.

Our mass-transfer analysis, experiments with a microfluidic chip, and comparison with biological data allowed us to identify the primary evolutionary pressure in gills: maximization of the oxygen transfer rate for a given pumping pressure. The optimum is reached at an interlamellar distance that increases the surface area for oxygen diffusion but does not markedly impede water flow. The morphology of fish gills exemplifies the natural design strategy, whereby size change is accommodated by proliferation of the exchange surface, and not by alteration of the basic size and geometry of the exchange unit. Similar examples can be found in other biological systems, such as blood capillary size (20), red blood cell size (20), and the choanocytic system of calcareous sponges (21). This natural optimization strategy found in fish demonstrates how the control of channel arrangement in microfluidic devices enhances heat and mass transfer, a critical issue faced in many practical situations, including microheat exchangers (22) and laboratory-on-a-chip systems for drug delivery (23) and biochemical analysis (24).

Materials and Methods

Mass-Transfer Experiments Using an Engineered Gill.

We fabricated an engineered gill system consisting of PDMS microchannels, where gas transfer occurs across the membranes separating the channels. The PDMS structure was constructed using a 10:1 mixture of Sylgard-184 (Dow Corning) cured by baking for 30 min at 80 °C in a vacuum oven. We coated the inner wall of the upper and lower layers with 0.6 wt% Teflon-AF (DuPont 601S2 and 3M Fluorinert Electronic Liquid FC40) to prevent oxygen diffusion out of the channels. All three channels had identical widths of 2 mm and lengths of 70 mm. The membrane thickness was 20 μm. We changed the height of the central channel from 70 to 190 μm, and the heights of the other channels were fixed at 200 μm. Sodium sulfite was used to control the concentration of dissolved oxygen in water. Channel flow was achieved using a syringe pump (Harvard PHD 22/2000). Reynolds numbers range from 0.002 to 0.3, and the flow is laminar. An oxygen microsensor (Unisense OX-100) was used to measure the partial pressure of oxygen at the outlet of the central channel.

Scanning Electron Microscopy.

The gill of a rockfish, Sebastes schlegelii, was fixed in Karnovsky fixative solution and then postfixed with 1% osmium tetroxide in a 0.05 M cacodylate buffer. The specimen was dried in a drying device (Baltzer CPD030) after partial dehydration using a graded ethanol series. The dried specimen was coated with a thin layer of platinum in a sputter coater (Bal-Tec SCD005) and examined using a field-emission scanning electron microscope (Carl Zeiss SUPRA 55VP).