Dynamics of spontaneous flipping of a mismatched base in DNA duplex

Significance

Spontaneous flipping of a single DNA base to an extrahelical position is a fundamental issue in DNA biophysics. The dynamics of such spontaneous flipping of a lesion or mismatched base is an important biophysical feature of DNA to discriminate damaged base from normal Watson–Crick paired ones. It is therefore closely related to repair enzymes' function to recognize base lesions, a mechanism on which almost all organisms rely to maintain their genome integrity. However, it has remained challenging to obtain reliable thermodynamics and kinetics data on this process. By developing experimental and theoretical techniques, we determined the free energy and rates of DNA spontaneous base flipping, providing further insights into its molecular mechanism.

Abstract

DNA base flipping is a fundamental theme in DNA biophysics. The dynamics for a B-DNA base to spontaneously flip out of the double helix has significant implications in various DNA–protein interactions but are still poorly understood. The spontaneous base-flipping rate obtained previously via the imino proton exchange assay is most likely the rate of base wobbling instead of flipping. Using the diffusion-decelerated fluorescence correlation spectroscopy together with molecular dynamics simulations, we show that a base of a single mismatched base pair (T–G, T–T, or T–C) in a double-stranded DNA can spontaneously flip out of the DNA duplex. The extrahelical lifetimes are on the order of 10 ms, whereas the intrahelical lifetimes range from 0.3 to 20 s depending on the stability of the base pairs. These findings provide detailed understanding on the dynamics of DNA base flipping and lay down foundation to fully understand how exactly the repair proteins search and locate the target mismatched base among a vast excess of matched DNA bases.

A base in normal B-DNA spontaneously swinging out of the double helix to an extrahelical position is known as spontaneous base flipping. The dynamics of such base flipping is a fundamental issue in DNA biophysics. It is also related to how DNA repair or modification proteins search and fix the lesion bases to maintain the genome integrity or modify the DNA. Although extensive structural studies have found that many DNA base repair/modification proteins completely flip their target base out extrahelically (so-called enzymatic base flipping) (1–5), it is still under debate (6–11) whether the base flipping occurs spontaneously (9, 10, 12) or not (6–8). Accurate information on the dynamics of spontaneous base flipping is therefore of high interest and importance.

However, the study of spontaneous base flipping is deemed to be difficult. The probability is extremely low for a single base to flip out of the DNA double helix in the absence of proteins. Hence only sensitive relaxation methods are able to detect such kind of fluctuation under equilibrium. As a well-known relaxation method, NMR has been applied to tackle this problem through the imino proton exchange assay (9, 13–17). In this assay, it is assumed that the exchange of the imino proton (in either G or T base) with the catalysts in the solution occurs only when the base flips out (13), and the extrapolated imino proton exchange rate at an infinite catalyst concentration is taken to be the base-flipping rate (14, 15, 17). According to these NMR studies the lifetime of the extrahelical state is on the order of microseconds, and that of the intrahelical state ranges from milliseconds to hundreds of milliseconds, depending on the stability of individual base pairs. MacKerell and coworkers as well as others have done extensive theoretical investigations and found that the target imino proton on the base already becomes accessible to the solvent for proton exchange when the base pair opens to an angle of only 30°, which is still within the potential well of the hydrogen bonding interaction (18–21). Hence, “All of the conformations that undergo exchange cannot be considered as base-flipped states” and “the rate constants measured from imino proton exchange may not necessarily be appropriate for the interpretation of enzymatic flipping studies” (21). In other words, the fluctuation probed by the NMR studies should be reassigned to base wobbling instead of flipping. Another well-known relaxation method, fluorescence correlation spectroscopy (FCS) coupled with fluorescence resonance energy transfer (FRET), has been applied to investigate many DNA conformational dynamics [e.g., DNA bubble breathing (22) and base zipping–unzipping (23)]. However, FRET measurement is sensitive to distance roughly from 2 to 7 nm, whereas the single-base flipping takes place at a distance shorter than 2 nm. The FRET–FCS study on spontaneous base flipping is therefore extremely difficult if not impossible. Indeed, we have not been able to find such kind of reports in the literature.

On the other hand, many efforts have been made, by fast mixing the double-stranded DNA (dsDNA) with repair proteins, to monitor the enzymatic base flipping (24–26). However, this ensemble fast-mixing strategy cannot provide independent and direct kinetic information for the spontaneous base flipping. The observed kinetics of the base flipping is the result of coupling between protein and DNA, and the derivation of the base-flipping rate strongly relies on the assumed damage searching model (9, 25). Nevertheless, an extrahelical base-trapping strategy similar to the enzymatic base flipping was adopted previously to measure the out-flipping rate of matched base pairs (27), where β-cyclodextrin was used as a host molecule to bind and stabilize the extrahelical bases. The formation of the host–guest complex induces melting of DNA duplex below its normal melting temperature, and this melting rate is taken to be the rate of the spontaneous base flipping of matched base pairs (27). However, flipping out a single base in a stable dsDNA is physically different from opening base pairs during the melting of a dsDNA molecule. What this study truly measured may not directly correspond to the rate of single-base outward flipping, but the accumulated rate of unzipping all of the base pairs instead (21, 28). In addition, the introduction of the host–guest complex stabilizes the base open state, so that the energetics and kinetics (especially the extrahelical lifetime of the flipped-out state) must be drastically different from that in a natural condition. Other host molecules, such as bisacrindine (BisA), were found to stabilize the double-helix structure when they bind to a mismatch-containing dsDNA molecule (29), but we have not seen a report on the dynamics of the single-base flipping using the extrahelical trapping strategy by these host molecules. The fundamental dynamic properties of the spontaneous flipping of a single base are still missing.

Previous studies on dynamics of dsDNA bubbling (22), zipping–unzipping (23), and DNA hairpin folding (30) imply that the relaxation time of spontaneous single-base flipping should be on the order of 10 ms. Although the conventional FCS (31) and single-molecule imaging based on total internal reflection fluorescence microscopy (TIRFM) (32) are powerful tools for dynamic studies under equilibrium, their time windows are not suitable for relaxations around 10 ms. The conventional FCS is suitable for a relaxation faster than hundreds of microseconds due to the restriction from molecular diffusion, whereas the time resolution given by single-molecular TIRFM is typically around 50 ms to preserve sufficient signal-to-noise ratio. Other single-molecule techniques, such as scanning confocal single-molecule imaging (32, 33) and single-molecule trapping (34), may have the potential to provide suitable time window, but to the best of our knowledge, they have not been applied to study spontaneous flipping of a single base.

Here, following the “big object attaching” strategy (35), we used our previously demonstrated diffusion-decelerated FCS (ddFCS) technique (30). The ddFCS technique efficiently elongates the presence of the tested molecules in the laser illumination region, allowing an observation in the 0.01 ms∼1-s range. Meanwhile, a fluorescence labeling based on the photoinduced electron transfer (PET) was designed to probe conformational fluctuations with a distance shorter than 1 nm. By improving the FCS technique from FRET–FCS to PET–ddFCS, we were able to observe the dynamics of spontaneous flipping of a single base. We measured the rate and equilibrium constants at different temperatures, from which the thermodynamic and dynamic parameters (i.e., the reaction free energy, enthalpy, entropy, out- and inward flipping activation energy, and preexponential factor of the rate constant) of the investigated mismatched base pairs can be derived. We also applied enhanced sampling molecular simulations (36) to characterize the mechanistic and molecular details of the single-base flipping. Our computational and experimental results are in good agreement. These data have offered fundamental understanding on the dynamics of the spontaneous single-base flipping.

Results and Discussion

Fluorescent Labeling for PET Study of Spontaneous Base Flipping.

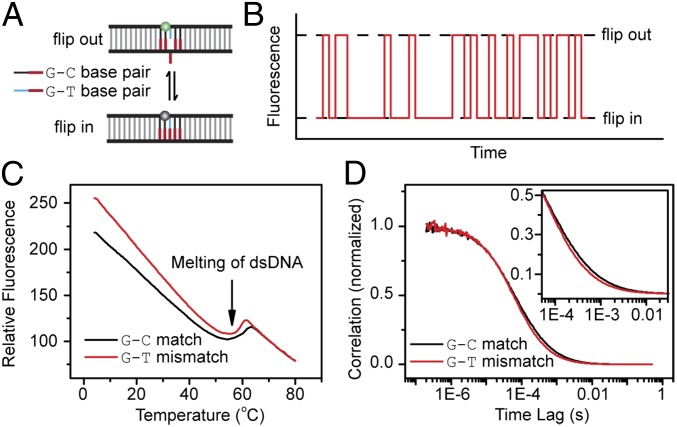
To translate the flipped-in and -out states in base flipping to different fluorescence states, we introduced tetramethylrodamine (TMR) dye into a dsDNA molecule as a fluorescent reporter. Among the four normal nucleotide bases (A, T, C, G) in a DNA molecule, the G base has prominent PET quenching on TMR when they are close to <1 nm, and can serve as a quencher for TMR. To probe the spontaneous base flipping in the dsDNA of G–T mismatched base pair (G–T mismatch), we introduced two G–C matched base pairs on each side of the G–T mismatched base pair as two clamps to avoid the mismatch-induced DNA bubble breath (22). The five G bases line up on the same strand of the DNA duplex opposite the TMR-labeled DNA strand. TMR was labeled to the C base neighboring the G–T mismatch to form a PET pair (Fig. S1 and Table S1). We would expect that when the tested G base of the G–T mismatch stays in the intrahelical conformation, the five stacked G bases show a high quenching efficiency and TMR is in a dark state, whereas when the mismatched G base flips out of the DNA duplex, TMR turns into a bright state because the flipped G base moves away from the chromophore (Fig. 1A). Considering the spatial distribution of the dye-linker group (37, 38), the fluorescence increase does not occur unless the base flips out to a significant extrahelical position (>90°). The dynamics of the spontaneous base flipping in the mismatched G–T pair would then be encoded in the fluorescence fluctuation (Fig. 1B). The static fluorescence experiment confirmed our hypothesis: the fluorescence of the G–T mismatch is higher than that of the G–C match (Fig. 1C) due to the higher probability of the G base to spontaneously flip out in the G–T mismatch than in the G–C match.

Fig. 1.

TMR–PET-based fluorescence assay for probing dynamics of spontaneous base flipping. (A) The scheme of fluorescence labeling. The green and gray balls are the TMR in relatively fluorescent and dark states, respectively. The mismatched base from either strand can flip out. (B) Schematics of fluorescence fluctuation as the mismatched base pair spontaneously flips. (C) Melting curves of the G–T mismatch (red) and the G–C match (black). (D) Conventional FCS curves of the G–T mismatch (red) and the G–C match (black) at 25.0 ± 0.5 °C. A slight difference was observed at the millisecond range (Inset).

Conventional FCS Is Incapable of Accurately Characterizing the Relaxation of Spontaneous Base Flipping.

We recorded the FCS curves of both the G–T mismatched and G–C matched dsDNA in a conventional way. The additional correlation decay at the millisecond time scale in the FCS curve of the G–T mismatch compared with that of the G–C match implies that the mismatch brings a relaxation process (Fig. 1D). However, it is widely accepted that the conventional FCS cannot be used to quantitatively characterize the kinetics with the relaxation time on the order of 1 ms or longer due to the interference and limitation of molecular diffusion (30, 35). The disparity of the FCS curves shown in Fig. 1D may contain dynamic information of spontaneous flipping of the mismatched G–T pair, but the rates cannot be accurately determined (Fig. S2).

Fluorescence Fluctuation Was Insignificant in Matched G–C Base Pair but Clear in Mismatched G–T Pair.

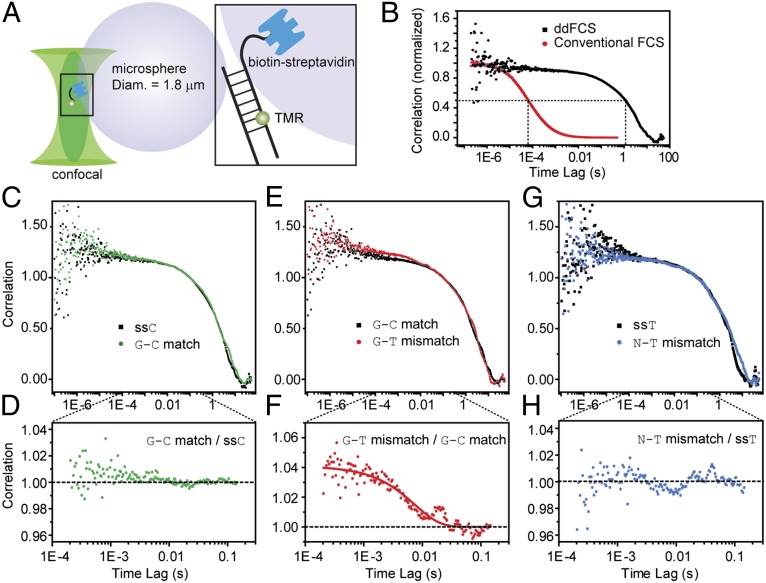
We applied ddFCS by attaching the dsDNA molecule to a 1.8-μm–diameter polystyrene microsphere so that the diffusion coefficient of the particle was dramatically decreased (Fig. 2A) (30). This ddFCS assay prolongs the presence of sample molecules in the confocal volume to ∼1 s and completely decouples the millisecond relaxation from the diffusion correlation, providing a much wider time window (Fig. 2B) for conformational fluctuation analysis. To find out whether we could detect the G base flipping in the G–C match, we took a single-stranded DNA (ssDNA) (ssC, Table S1) as the control molecule. In the conventional FCS experiment, the ssDNA cannot be used as the control for the dsDNA because of their different molecular sizes and configurations, and consequently different diffusion constants. However, in the ddFCS experiment the DNA molecules were immobilized onto a microsphere ∼10³-fold bigger in diameter, so that the diffusion correlation in the ddFCS curve was dominated by the microsphere. Hence, the diffusion correlations of the ssDNA and dsDNA immobilized microspheres will be essentially identical. Because there is no appreciable quenching process in the ssDNA within our time window of interest (0.1–100 ms), any difference between the ddFCS curves of ssDNA and dsDNA indicates that there is detectable conformational fluctuation in the dsDNA. Comparing the G–C match with the control ssDNA, their ddFCS curves were found to be identical (Fig. 2 C and D). This observation indicates that with our labeling strategy, neither fluctuations from dsDNA conformational motion nor TMR–dsDNA interaction in the G–C match can be detected within the respected time range. This result showed that the probability for the G–C Watson–Crick pairs to flip out from its intrahelical position is too small to be detected in the current experimental scheme. On the other hand, a single-exponential decay with the characteristic time of ∼10 ms was clearly seen in the ddFCS curve of the G–T mismatch (Fig. 2 E and F), suggesting that a conformational fluctuation is induced by the G–T mismatch site and is translated into fluorescence correlation decay.

Fig. 2.

Spontaneous flipping of a mismatched G–T base pair. (A) Schematic illustration of the ddFCS assay. (B) Comparison of the conventional FCS (red) and ddFCS (black) curves of the G–C match. (C) The ddFCS curve of the G–C match (green) is identical with that of the control ssC (black). (D) The ratio of correlation by dividing the ddFCS curve of the G–C match over that of ssC. (E) The ddFCS curve of the G–T mismatch (red) exhibits conformational fluctuation compared with that of the G–C match (black). (F) The ratio of correlation by dividing the ddFCS curve of the G–T mismatch over that of the G–C match. (G) The ddFCS curve of the N–T mismatch (blue) is identical with that of the control ssT (black). (H) The ratio of correlation given by dividing the ddFCS curve of the N–T mismatch over that of the ssT. All of the ddFCS data were taken at T = 32.5 ± 0.2 °C.

Fluorescence Fluctuation in G–T Mismatch Is Due to Spontaneous Single-Base Flipping.

The fluorescence correlation decay seen in the G–T mismatch can be associated with either the base flipping itself and/or other conformational fluctuations brought by the mismatch site, such as the increasing DNA backbone flexibility (spontaneous fluctuations of the backbone, different from the simultaneous backbone distortion with the base flipping) (39–42) and/or insertion of the dye molecule into the space left over by the flipped-out base. To estimate the contributions from other possible conformational changes rather than the base flipping, we replaced the G base of the G–T pair with an abasic nucleotide (the N–T mismatch) to mimic all possible mismatch-induced conformational and TMR-associated fluctuations except for the G base flipping (Fig. 2 G and H, Fig. S1, and Table S1). As shown in Fig. 2 G and H, the ddFCS curve of the N–T mismatch is consistent with that of the control ssDNA molecule ssT (Table S1) as well as ssC and the G–C match, indicating that only the G base flipping is registered in the fluorescence fluctuation in the G–T mismatch shown in Fig. 2 E and F, because any detectable fluctuation within the time range of 0.1–100 ms except the G base flipping would also have been seen in the N–T mismatch.

The identity of the ddFCS curves among the ssDNAs, G–C match, and N–T mismatch already ruled out the possibility that the observed exponential decay in the G–T mismatch is due to the motion of the TMR dye. To provide further evidence, we also performed fluorescence anisotropy measurements on various samples (Fig. S3 and Table S1). It is known that when the dye molecule is attached to the end of dsDNA, it caps to the DNA duplex as if an additional base (43). It therefore has a longer rotational relaxation time (represented as higher fluorescence anisotropy) than that of free TMR or TMR attached to an ssDNA (Fig. S3 and Table S1). The anisotropy of TMR labeled in the middle of the dsDNA was significantly lower than that attached to the end of the dsDNA (Fig. S3 and Table S1), suggesting that the TMR labeled in the middle of dsDNA is less trapped than that of the end-capped TMR. According to our previous studies, the end-capped TMR swings on the order of microseconds (see supporting information of ref. 30). It is therefore unlikely that the observed correlation decay at 10 ms represents the motion of the TMR-linker group, because the middle-labeled TMR swings even faster than the end-capped ones.

Observation of Spontaneous Flipping in Mismatched T–T and C–T Pairs.

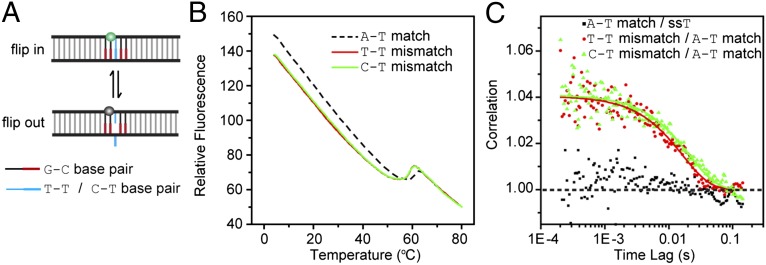
To extend this PET-ddFCS–based base-flipping assay to other mismatches, we replaced the tested G–T and control G–C base pairs with the mismatched T–T/C–T and matched A–T base pairs, respectively (Fig. 3A and Table S1). Compared with the 5-G PET pathway of the G–C match, the A–T match has an A–T pair in the middle of the four guanines. Therefore, TMR stays in a relatively brighter fluorescent state owing to the lower quenching efficiency. When the A–T pair is replaced by a mismatched T–T or C–T pair, the spontaneous outward flipping of the mismatched base facilitates the accessibility of TMR to the G bases, and it results in darker states due to higher quenching efficiency (Fig. 3A). Indeed, the steady-state fluorescence intensities of the C–T and T–T mismatches are lower than that of the A–T match (Fig. 3B), supporting the hypothesis that the outward flipping of the mismatched C–T and T–T base pairs caused additional quenching of TMR. Again, the ddFCS of the A–T match was found to be identical to that of the control ssDNA (Fig. 3C), indicating that, akin to the case of the G–C match, the spontaneous outward flipping of the A–T match also has an undetectable probability, whereas significant single-exponential decays with the relaxation time of ∼20 ms were found in the correlation functions of both the T–T and C–T mismatches (Fig. 3C). With the same argument as for the G–T mismatch, we can prove that this relaxation process is only associated with the T–T/C–T base flipping based on the control experiments of the abasic N–T mismatch (Fig. 2 G and H) and anisotropy measurement (Fig. S3 and Table S1). To provide additional tests, we also probed the spontaneous flipping of the O⁶meG–T and O⁶meG–C pairs, which have varied base-pairing stability (44). Both their behaviors are consistent with our expectation (Fig. S4 and Tables S1 and S2).

Fig. 3.

Spontaneous flipping of the mismatched T–T and C–T base pairs. (A) The scheme of fluorescent labeling. The green and gray balls are the TMR in relatively fluorescent and dark states, respectively. The mismatched base from either strand can flip out. (B) Melting curves of the T–T mismatch (red), C–T mismatch (green), and A–T match (black dash). (C) The ratio of correlation by dividing the ddFCS curve of the A–T match over that of ssT (black square), and that given by dividing the ddFCS curves of the T–T (red circle) and C–T (green triangle) mismatches over that of the A–T match. All of the ddFCS data were taken at T = 32.5 ± 0.2 °C.

Extraction of Dynamic and Thermodynamic Parameters from Obtained ddFCS Data.

As proved above, the correlation function of the G–C and A–T match (G_WC) represents the diffusion correlation (G_diff) of the DNA–microsphere complex only, whereas that of the G–T, T–T, and C–T mismatch (G_MM) represents a combined correlation of diffusion (G_diff) and spontaneous base flipping (G_flip). The G_flip can therefore be obtained through G_flip(τ) = G_MM(τ)/G_WC(τ) = 1+α exp(−τ/τ_flip) (31), in which α and τ_flip can be obtained by fitting the G_flip curves of the G–T (Fig. 2F), T–T, and C–T mismatches (Fig. 3C), respectively. According to the FCS theory, α and τ_flip are related to the equilibrium constant (K = k_flip-out/k_flip-in) and kinetic rate constants (k_flip-out + k_flip-in, where k_flip-out and k_flip-in are the out- and inward base-flipping rate constant, respectively) (45, 46). Therefore, K as well as k_flip-out and k_flip-in of all three mismatches can be derived (see SI Text and Fig. S5 for details of the data analysis).

Table 1 shows the equilibrium constants and kinetic parameters of the G–T, T–T, and C–T mismatches at 32.5 °C. As shown in Table 1, the probability of the spontaneous outward flipping is small for all of the tested mismatches, and bases prefer to stay inside the double helix even for mismatched pairs. The inward base-flipping rate (the lifetime of the extrahelical base) of all three mismatches is about the same, whereas the outward flipping rate (the lifetime of the intrahelical base) of the G–T mismatch is notably slower (longer) than that of the T–T and C–T mismatches. The mismatched G–T pair is known to form two H bonds between the two bases (14) and is therefore more stable and has a longer lifetime in the intrahelical conformation. When the mismatched bases flip out of the DNA duplex they encounter similar solvent environment. The flipped-out bases of the G–T, T–T, and C–T mismatches are expected to spend about the same time in the extrahelical conformation.

Table 1.

Thermodynamics and kinetics of spontaneous base flipping at 32.5 ± 0.2 °C

DNA	K	kflip-in, s−1	kflip-out, s−1	τout, s	τin, s
G–T mismatch	(4.7 ± 0.3) × 10−4	105 ± 42	(4.9 ± 2.0) × 10−2	(9.6 ± 3.9) × 10−3	20.4 ± 8.5
T–T mismatch	(4.4 ± 0.6) × 10−2	58 ± 2	2.5 ± 0.4	(17.4 ± 0.7) × 10−3	0.39 ± 0.05
C–T mismatch	(4.5 ± 0.3) × 10−2	76 ± 53	3.4 ± 2.4	(13.0 ± 9.2) × 10−3	0.30 ± 0.21

K is the equilibrium constant for outward flipping of mismatched base pairs. τ_out = 1/k_flip-in and τ_in = 1/k_flip-out are the lifetimes of the flipping base staying in the extrahelical and intrahelical positions, respectively. Errors are propagated from that of α and τ_flip (mean ± SD, n = 3).

The spontaneous outward-flipping rate obtained herein is about 10⁴-fold slower than that obtained through the imino proton exchanges assay (9, 14, 17). It has been pointed out by previous studies that the imino proton exchange takes place before overcoming the stacking energy barrier (18), and the much faster “base-flipping” rate measured by the imino proton exchange should be a localized fluctuation of base wobbling which allows the base pair to open a small angle (21) and is irrelevant to the significant enzymatic base flipping. In our labeling strategy, because of the broad spatial distribution of the dye due to the flexible linker (37, 38), the fluorescence changes only when the base flips out to an extrahelical angle (>90°) far away from its intrahelical position. The significant base flipping in a mismatched base pair as probed in the present study could be pertinent to the enzymatic base flipping that overcomes the stacking energy barrier and exhibits a much slower relaxation rate.

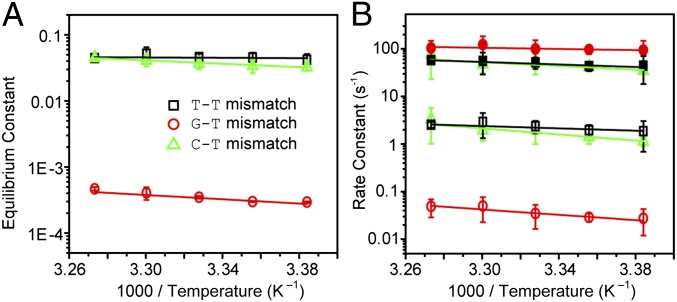
Subsequently, we measured the equilibrium constant and rates of the spontaneous base flipping of all three tested mismatches at different temperatures (Fig. 4 A and B), from which reaction free energy, enthalpy, and entropy and forward and backward activation energies were derived (Table S3). As expected, the equilibrium constant of the mismatched bases to spontaneously flip out of the DNA duplex increases as the temperature increases (Fig. 4A), and both the out- and inward flipping of the G–T, T–T, and C–T mismatches also speed up as the temperature increases (Fig. 4B). The relation between rate and temperature follows the Arrhenius equation. The reaction free energy at 32.5 °C is 4.66 ± 0.04 kcal/mol for the G–T mismatch, significantly greater than both the T–T (1.89 ± 0.08 kcal/mol) and C–T (1.89 ± 0.04 kcal/mol) mismatches. These results are in good agreement with the notion that the mismatched G–T pair possesses two hydrogen bonds. For the same reason, similar trend is seen in the reaction enthalpy (Table S3). On the other hand, the activation energy for the extrahelical base to flip back into the duplex is lower in the G–T mismatch (3.1 ± 1.8 kcal/mol) than both the T–T (5.9 ± 0.8 kcal/mol) and C–T (9.8 ± 2.5 kcal/mol) mismatches. The lower flip-in barrier in G–T is the major reason that the relaxation of the base flipping is faster in the G–T mismatch than both the T–T and C–T mismatches. In other words, because of the lower activation energy the extrahelical state of G–T mismatch has a slightly shorter life time (Table 1). It is widely known that the thermodynamic and kinetic properties of a base pair are sequence sensitive. The equilibrium and rate constants of spontaneous single-base flipping should vary with the surrounding matched base pairs even for the same mismatched base pair.

Fig. 4.

Temperature dependence of the thermodynamics and kinetics of spontaneous flipping of mismatched base pairs. (A) Equilibrium constants of the T–T (black), G–T (red), and C–T (green) mismatches to spontaneously flip out of the double helix (mean ± SD, n = 3) at different temperatures. (B) In- (solid) and out- (open) ward flipping rates of the T–T (black), G–T (red), and C–T (green) mismatches (mean ± SD, n = 3).

Enhanced Sampling Molecular Simulations on Spontaneous Single-Base Flipping.

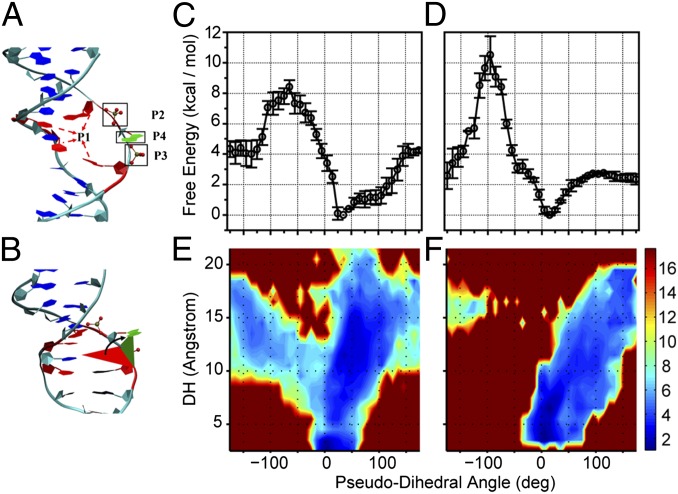
To gain an atomic-detailed insight into the spontaneous flipping of a single mismatched base pair, we performed molecular simulations on a dsDNA containing one single mismatched base pair. Because, as discussed above, the base flipping is a slow process that is beyond the capability of normal molecular dynamics simulations, enhanced sampling techniques are needed. In most previous studies, the umbrella sampling method, for which a predefined reaction coordinate has to be taken, was applied to calculate the free-energy profile for base flipping and has yielded much important information (18, 21, 47, 48). However, Song et al. showed (48) that slightly different preselected reaction coordinates can lead to very different results. In addition, the DNA base flipping is a very complex process likely involving many types of motions of similar time scales. Therefore, it is important to implement a simulation method that allows efficient sampling over many degrees of freedom, namely, not only along the reaction coordinate but also in space orthogonal to it. For this purpose, the recently developed selective integrated tempering sampling (SITS) method (SI Text) (36) was used in this study. SITS enhances the sampling in the energy and configuration space of the system of interest, and allows effective calculations of various thermodynamic properties without preselected reaction coordinates. In such a calculation, a thorough sampling over the conformation space is achieved, and the free-energy profile along any desired collective coordinates can be easily obtained through a simple reweighting process. Two mismatch patterns, G–T and T–T, were studied to investigate the possible variance in the free-energy landscape for base flipping. We adopted the previously used pseudodihedral angle (CPDb) (48) as the coordinate for free-energy mapping to describe the flipped-in and flipped-out states.

Our simulations showed that the flipping of a single base has a much lower free-energy penalty than simultaneous flipping of both bases (Figs. S6 and S7), which is expected based on stacking energy costs. Therefore, the experimentally observed fluctuation must be correlated with a single-base flipping. Through the data analysis the free-energy profiles of the tested bases (G or T) in the dsDNA along the flipping angle CPDb were extracted (Fig. 5 A–D). As expected, the global minima correspond to the G or T base embedded states (∼10°). Compared with the bases in normal Watson–Crick base pairs, the abnormally paired bases (i.e., G and T) have relatively low free energies of reaction (G: ∼4 kcal/mol and T: ∼2 kcal/mol, both in good agreement with the experimental results) for the transition from the intrahelical to the flipped-out states, which is consistent with the higher probability of base flipping for the mismatched bases compared with normal Watson–Crick bases (49). In addition, as seen from Fig. 5 C and D, the spontaneous flipping of either G or T through the major groove has a lower free-energy barrier than that through the minor groove. This observation is consistent with previous umbrella sampling simulations. One also sees from Fig. 5 C and D that the free energy of the flipped-out state in the G–T case is higher than that of the T–T, presumably because two hydrogen bonds can form between the mismatched G–T pair but none between the T–T pair. To understand more details on the free-energy landscape of the base flipping, 2D free-energy profiles using CPDb and DH (the distance between the mass center of the atoms G:N1, O6 and that of T:O2, N3, in which N1–O2 and O6–N3 could form hydrogen bond) as coordinates were also calculated and are shown in Fig. 5 E and F. One interesting feature of these results is that for the G–T mismatch large CPDb values only appear with large DH values. In contrast, for the T–T mismatch, relatively large CPDb values can be observed even when the DH value is small. Such observations indicate that the flipping of G is restricted by its hydrogen bonds with T. The absence of hydrogen bond between two mismatched Ts allows the direct flipping (change of CPDb) of the base. The flipping of the base on the other strand for both the G–T and T–T mismatches was also studied by simulations and it follows a trend similar to that described above.

Fig. 5.

Selective integrated tempering sampling of the mismatched G–T and T–T base pairs. (A) The definition of the pseudodihedral for the base flipping (CPDb). P1 is the center of mass of the two flanking base pairs (red) above and below the flipping base, P2 and P3 are the centers of mass of the flanking phosphate groups, and P4 is the center of mass of the five-member ring of the flipping purine (or the entire six-membered ring for a flipping pyrimidine). The dihedral is made of the two triangular planes which share a common side defined by P2 and P3. The base opening angle is defined by the dihedral angle. (B) The pseudodihedral is shown with the triangular plane defined by the points P1, P2, and P3 (red) and the plane defined by the points P2, P3, and P4 (green). (C and D) Calculated free energy along the pseudodihedral angle CPDb. (C) G flipping in the G–T base pair. (D) T flipping in the T–T base pair. (E and F) Calculated free energy along the pseudodihedral angle CPDb and the distance DH. (E) G flipping in the G–T base pair. (F) T flipping in the T–T base pair. Due to the higher free-energy barrier, the observed events for the base flipping through the minor groove pathway are fewer than through the major groove pathway, so that error bar of free energy along the minor groove is larger.

Conclusion

By implementing the PET-ddFCS assay, we were able to investigate the dynamics of spontaneous single-base flipping in a mismatched base pair in a DNA duplex with, to our knowledge, unprecedented thermodynamic and dynamic details. The experimental and theoretical methods are complementary with consistent results obtained. We showed that the extrahelical lifetimes of the G–T, T–T, and C–T mismatched bases are on the order of 10 ms, whereas their intrahelical lifetimes range from 0.3 to 20 s depending on the stability of the intrahelical states. Because the G–T mismatch is a common lesion encountered in DNA damage that is processed by dedicated repair systems from bacteria to humans (4), our result may also play important roles in understanding the mechanism of enzymatic searching on the damaged site or other relevant events.

Methods and Materials

Detailed information of optical setup can be found in SI Text. SI Text also includes experimental procedures for FCS measurement, steady-state fluorescence experiments, and oligonucleotide synthesis. FCS data processing and molecular simulation are described in SI Text.